Cryptanalysis of an Image Encryption Algorithm Based on Combined Chaos for a BAN System, and Improved Scheme Using SHA-512 and Hyperchaos
Abstract
1. Introduction
- The security of the recent image encryption algorithm in [14] is scrutinized and some defects are unveiled.
- A total break of the algorithm is done under proposed simple cryptanalysis that recovers the plain-image and nullifies the claim of excellent attack resistance ability of the algorithm made in [14].
- An improved scheme is proposed based on SHA-512 and a 4D hyperchaotic system to settle the issues of plain-image insensitivity and weak keys with strong encryption quality.
2. Wang et al. Image Encryption Algorithm
| E = Wang_Encryption(I(i, j)) | |
| W.1. | Read the plain-image I(i, j) and form its data matrix T of dimension M × N. |
| W.2. | Set initial values of map (1) and generates 1D chaotic sequence X = {x1, x2, …, xn1} of length n1 = M × N1, where N1 = N − ceil(N/2) |
| W.3. | Create a 2D sub-chaotic matrix SI from sequence X of Logistic map of size M × N1. |
| W.4. | Set initial values of map (2) and generates another 1D chaotic sequence Y = {y1, y2, …, yn2} of length n2 = M × N2, where N2 = N − N1 |
| W.5. | Construct another 2D sub-chaotic matrix SK from sequence Y of size M × N2. |
| W.6. | Combine the two sub-chaotic matrices SI and SK to get 2D chaotic matrix ECM×N = {SIM×N1; SKM×N2}. |
| W.7. | Perform the XOR operation on data matrix T (of plain-image I) and chaotic matrix EC to get final encrypted image E as: |
| for i = 1 to M do for j = 1 to N do | |
| E(i, j) = bitxor(T(i, j), EC(i, j)) | |
| endfor | |
| endfor | |
| W.8. | Exit |
3. Security Defects
3.1. Weak Keys
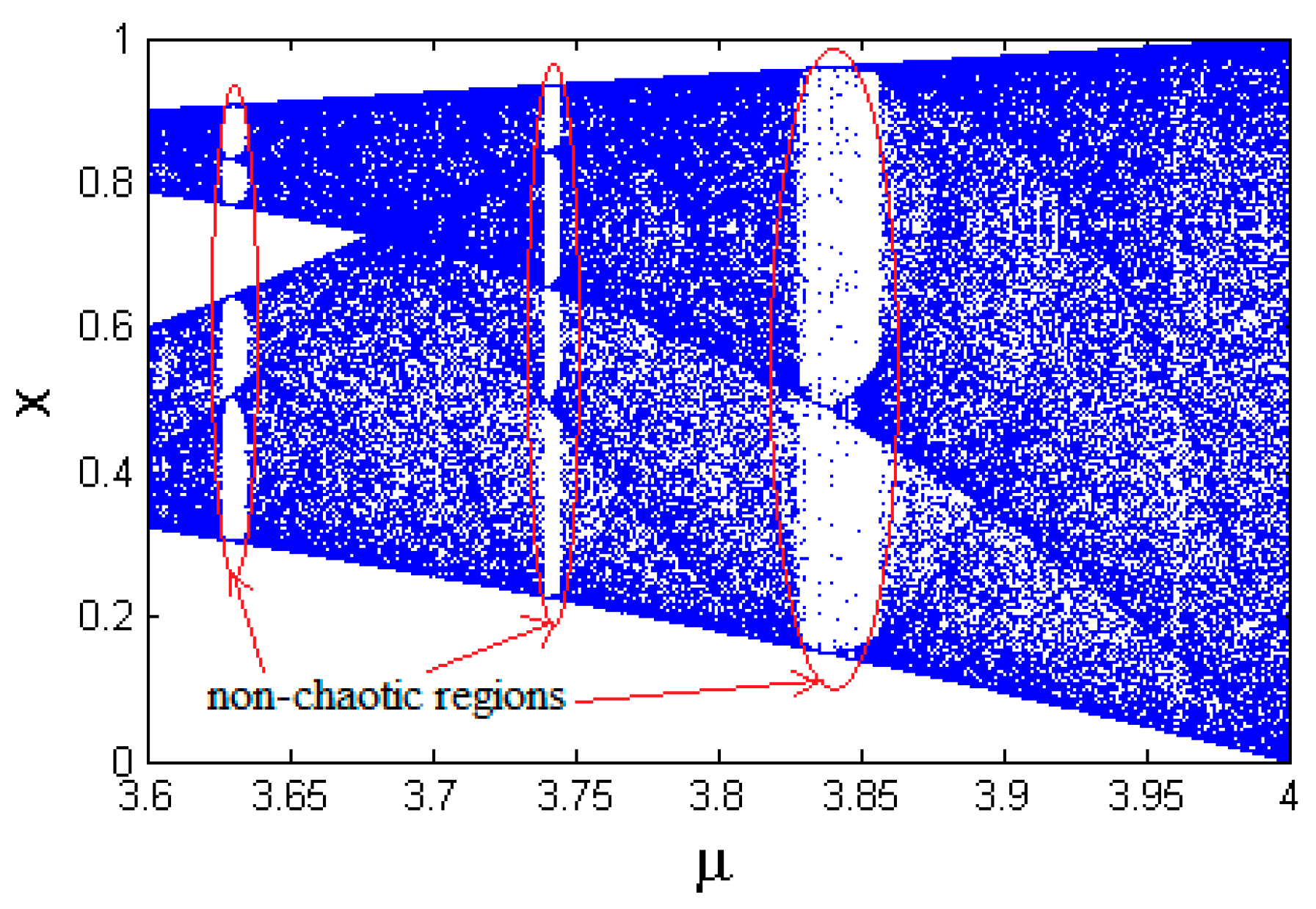
3.2. Sub-Chaotic Matrices SI and SK Are Fixed
3.3. Lack of Sensitivity to Change in Plain-Image
4. Proposed Cryptanalysis
5. Proposed Improved Image Encryption Scheme
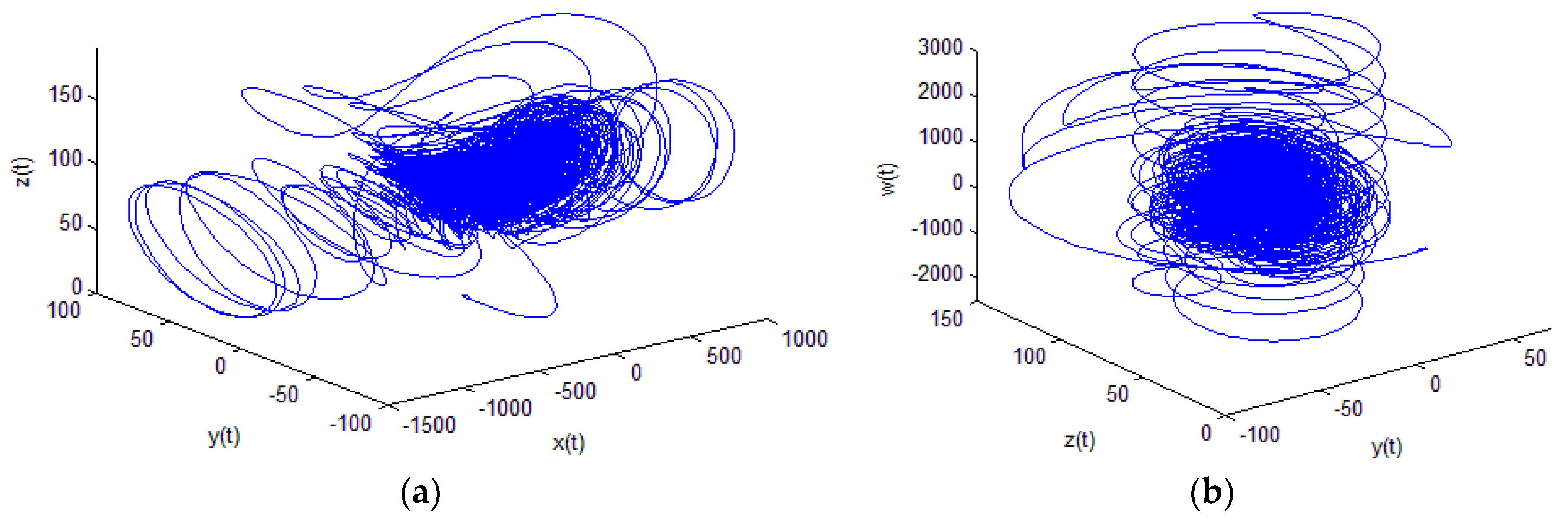
5.1. 4D Hyperchaotic System
- It consists of 7 system parameters, which enlarge heavily the key space of the respective security primitive and make the exhaustive attack impractical.
- It has a maximum lyapunov exponent of 25.6206 which is quite high and it is largest among all available 4D hyperchaotic systems. A larger positive lyapunov exponent shows that system trajectories vary more sharply in phase space and makes system’s dynamics more complicated by establishing stronger sensitivity to initial conditions [32]. However, the lyapunov exponent of most of the 1D chaotic maps are less than 1, including the logistic map and skew tent map in (1) and (2).
- The range of Kaplan–Yorke dimensions for 60 ≤ r ≤ 166 is 3.2801 ≤ DKY ≤ 3.3241, which is also much larger than most of the existing 4D hyperchaotic systems.
- It exhibits largest topological entropy, in hyperchaotic systems, which is not less than log(3).
5.2. SHA-512
5.3. Algorithm
- Step 1.
- Take proper input values for initial conditions x(0), y(0), z(0), w(0), parameters a, b, c, d, e, f, r.
- Step 2.
- Read the plain image I (gray-scale or RGB image).
- Step 3.
- Transform the input image I into 1D sequence of pixels of length say L (=MN for gray image and 3 MN for color image).
- Step 4.
- Compute hash digest of 512-bits using SHA-512 on 1D image sequence I in Step 3, say Hwhere, each Hi = {hi1, hi2, hi3, ..., hi8} is i-th byte in hash H.H = H1, H2, H3, …, H63, H64
- Step 5.
- Update the initial conditions of system (3) and parameter r [60, 166] according to the following Formulas (4)–(8)where, the function bin2dec(Hi) converts input binary data Hi to its equivalent decimal value.
- Step 6.
- Iterate the hyperchaotic system (3) with updated initial conditions and parameter for L times to generate four chaotic sequences X(i), Y(i), Z(i) and W(i), where i = 1 to L.
- Step 7.
- Do the following to perform masking operation on 1D image sequence I = {I1, I2, I3, …, IL} for i = 1 to L as
- Step 8.
- Perform the inverse of Step 3 on 1D sequence E to get the encrypted image.
- Step 9.
- Exit
6. Performance Analysis of Improved Scheme
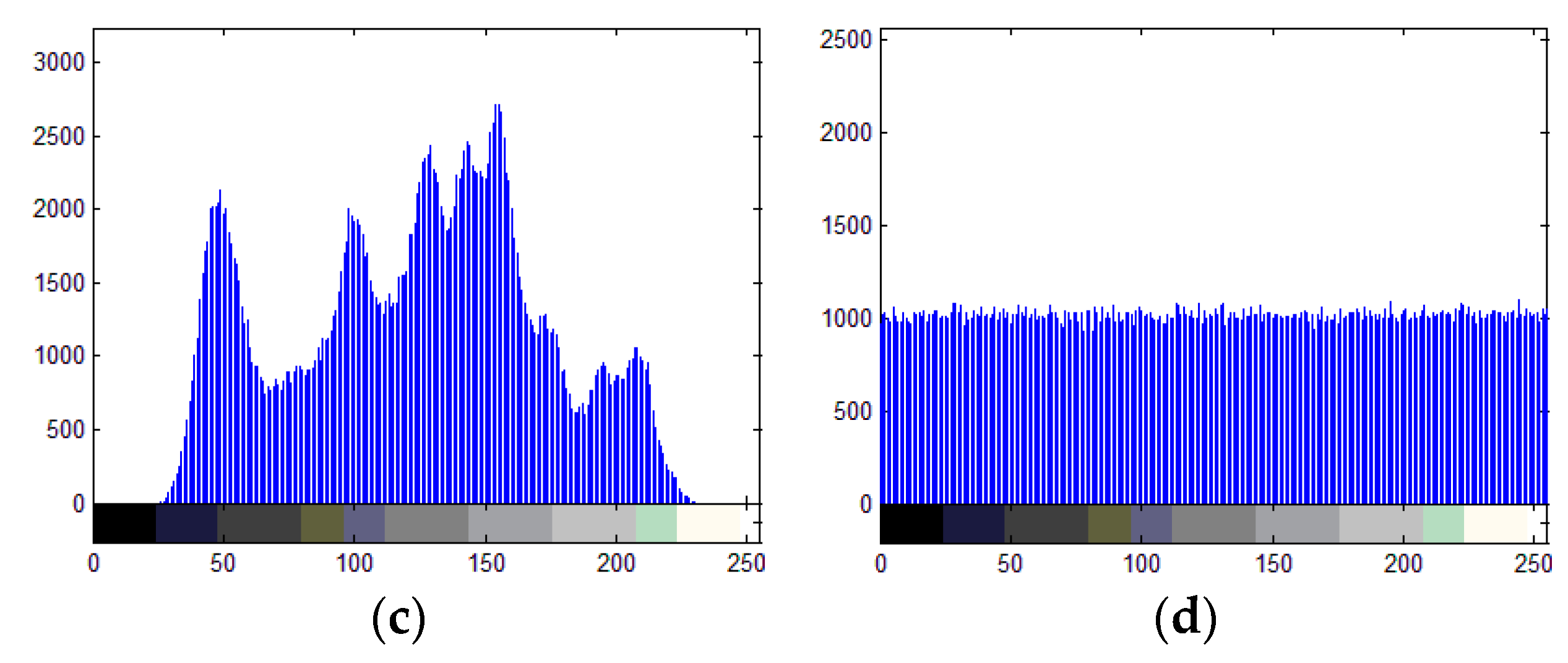
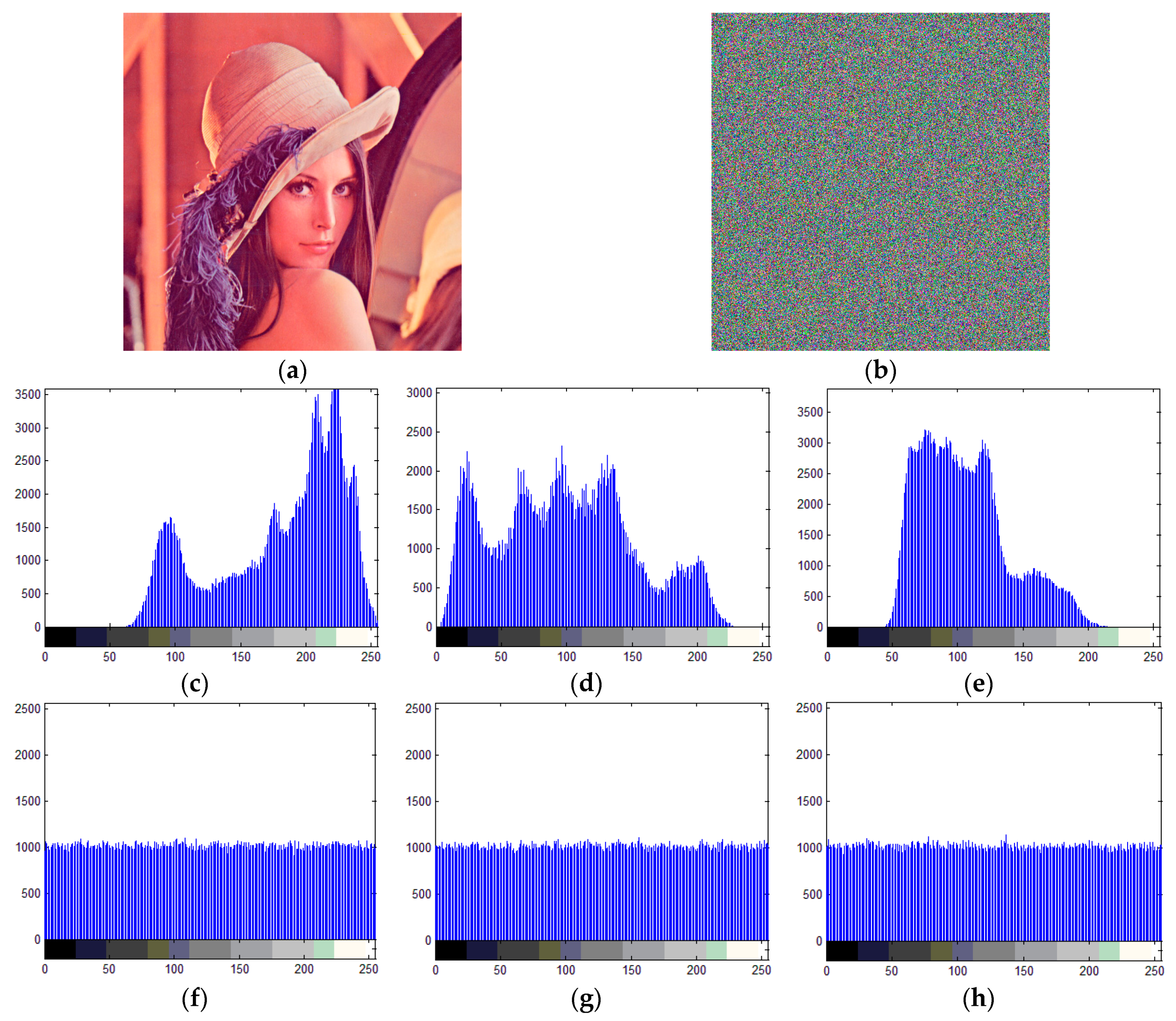
6.1. Histogram Analysis
6.2. Pixels Correlation Analysis
6.3. Image Entropy Analysis
6.4. Number of Pixel Change Rate (NPCR) and Unified Average Changing Intensity (UACI) Analysis for Plain-Image Sensitivity
6.5. Key Space Analysis
6.6. Computation Efficiency
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Patel, M.; Wang, J. Applications, challenges, and prospective in emerging body area networking technologies. IEEE Wirel. Commun. 2010, 17, 80–88. [Google Scholar] [CrossRef]
- Jovanov, E.; Milenkovic, A. Body Area Networks for Ubiquitous Healthcare Applications: Opportunities and Challenges. J. Med. Syst. 2011, 35, 1245–1254. [Google Scholar] [CrossRef] [PubMed]
- Milenkovic, A.; Otto, C.; Jovanov, E. Wireless sensor networks for personal health monitoring: Issues and an implementation. Comput. Commun. 2006, 29, 2521–2533. [Google Scholar] [CrossRef]
- Javadi, S.S.; Razzaque, M.A. Security and Privacy in Wireless Body Area Networks for Health Care Applications. Signals Commun. Technol. Wirel. Netw. Secur. 2013, 165–187. [Google Scholar] [CrossRef]
- Li, M.; Lou, W.; Ren, K. Data security and privacy in wireless body area networks. IEEE Wirel. Commun. 2010, 17, 51–58. [Google Scholar] [CrossRef]
- Poon, C.; Zhang, Y.-T.; Bao, S.-D. A novel biometrics method to secure wireless body area sensor networks for telemedicine and m-health. IEEE Commun. Mag. 2006, 44, 73–81. [Google Scholar] [CrossRef]
- Ahmad, M.; Ahmad, T. A Framework to Protect Patient Digital Medical Imagery for Secure Telediagnosis. Procedia Eng. 2012, 38, 1055–1066. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Vasilakos, A.V.; Fang, H. ECG-Cryptography and Authentication in Body Area Networks. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1070–1078. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Li, M.; Yu, S.; Yuan, J. BANA: Body area network authentication exploiting channel characteristics. IEEE J. Sel. Areas Commun. 2013, 9, 1803–1816. [Google Scholar] [CrossRef]
- Zhao, Z. An Efficient Anonymous Authentication Scheme for Wireless Body Area Networks Using Elliptic Curve Cryptosystem. J. Med. Syst. 2014, 38. [Google Scholar] [CrossRef] [PubMed]
- Carmen, P.-L.; Ricardo, L.-R. Notions of Chaotic Cryptography: Sketch of a Chaos Based Cryptosystem; Applied Cryptography and Network Security: Intechopen, UK, 2012. [Google Scholar]
- Sufi, F.; Han, F.; Khalil, I.; Hu, J. A chaos-based encryption technique to protect ECG packets for time critical telecardiology applications. Secur. Commun. Netw. 2010, 4, 515–524. [Google Scholar] [CrossRef]
- Fu, C.; Meng, W.-H.; Zhan, Y.-F.; Zhu, Z.-L.; Lau, F.C.; Tse, C.K.; Ma, H.-F. An efficient and secure medical image protection scheme based on chaotic maps. Comput. Biol. Med. 2013, 43, 1000–1010. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Si, M.; Pang, Y.; Ran, P.; Wang, H.; Jiang, X.; Liu, Y.; Wu, J.; Wu, W.; Chilamkurti, N.; et al. An encryption algorithm based on combined chaos in body area networks. Comput. Electr. Eng. 2018, 65, 282–291. [Google Scholar] [CrossRef]
- Ahmad, M.; Alam, M.Z.; Ansari, S.; Lambić, D.; Alsharari, H.D. Cryptanalysis of an image encryption algorithm based on PWLCM and inertial delayed neural network. J. Intell. Fuzzy Syst. 2018, 34, 1323–1332. [Google Scholar] [CrossRef]
- Bard, G.V. Algebraic Cryptanalysis; Springer: Berlin, Germany, 2009. [Google Scholar]
- Alvarez, G.; Li, S.; Hernandez, L. Analysis of security problems in a medical image encryption system. Comput. Biol. Med. 2007, 37, 424–427. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Bhat, P.S.; Kumar, S.; Min, L.C. Transmission and storage of medical images with patient information. Comput. Biol. Med. 2003, 33, 303–310. [Google Scholar] [CrossRef]
- Zhu, Z. An Efficient Authentication Scheme for Telecare Medicine Information Systems. J. Med. Syst. 2012, 36, 3833–3838. [Google Scholar] [CrossRef] [PubMed]
- Muhaya, F.T.B. Cryptanalysis and security enhancement of Zhu’s authentication scheme for Telecare medicine information system. Secur. Commun. Netw. 2014, 8, 149–158. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, P.; Wen, Q.; Jin, Z.; Zhang, H.; He, L. A Secure and Efficient Authentication and Key Agreement Scheme Based on ECC for Telecare Medicine Information Systems. J. Med. Syst. 2013, 38, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Islam, S.H.; Khan, M.K. Cryptanalysis and Improvement of Authentication and Key Agreement Protocols for Telecare Medicine Information Systems. J. Med. Syst. 2014, 38, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.-B.; Zhu, Z.-L.; Yang, B.-Q.; Liu, W.-Y.; Zhu, H.-F.; Zou, M.-Y. Cryptanalysis and Improvement of an Efficient and Secure Medical Image Protection Scheme. Math. Probl. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Chen, L.; Wang, S. Differential cryptanalysis of a medical image cryptosystem with multiple rounds. Comput. Biol. Med. 2015, 65, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C; John Wiley & Sons: Indianapolis, IN, USA, 2015. [Google Scholar]
- Kerckhoffs’s Principle. Available online: http://crypto-it.net/eng/theory/kerckhoffs.html (accessed on 13 February 2018).
- Hua, Z.; Zhou, B.; Zhou, Y. Sine-Transform-Based Chaotic System with FPGA Implementation. IEEE Trans. Ind. Electr. 2018, 65, 2557–2566. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Zhang, H.-L. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
- Li, P.; Wang, X.-Y.; Fu, H.-J.; Xu, D.-H.; Wang, X.-K. A New Color Image Encryption Based On High-Dimensional Chaotic Systems. Int. J. Mod. Phys. B 2014, 28, 1450024. [Google Scholar] [CrossRef]
- Ahmad, M.; Ahmad, T. Securing multimedia colour imagery using multiple high dimensional chaos-based hybrid keys. Int. J. Commun. Netw. Distributed Syst. 2014, 12, 113. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.-Y.; Kadir, A. Color image encryption using Choquet fuzzy integral and hyper chaotic system. Optik 2013, 124, 3527–3533. [Google Scholar] [CrossRef]
- Chen, L.; Tang, S.; Li, Q.; Zhong, S. A new 4D hyperchaotic system with high complexity. Math. Comput. Simul. 2018, 146, 44–56. [Google Scholar] [CrossRef]
- Maashri, A.A.; Pathuri, L.; Awadalla, M.; Ahmad, A.; Ould-Khaoua, M. Optimized Hardware Crypto Engines for XTEA and SHA-512 for Wireless Sensor Nodes. Indian J. Sci. Technol. 2016, 9, 1–7. [Google Scholar] [CrossRef]
- Ahmad, I.; Das, A.S. Hardware implementation analysis of SHA-256 and SHA-512 algorithms on FPGAs. Comput. Electr. Eng. 2005, 31, 345–360. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Zhang, Y.-Q.; Bao, X.-M. A colour image encryption scheme using permutation-substitution based on chaos. Entropy 2015, 17, 3877–3897. [Google Scholar] [CrossRef]
- Ahmad, M.; Alam, M. Z.; Umayya, Z.; Khan, S.; Ahmad, F. An image encryption approach using particle swarm optimization and chaotic map. Int. J. Inf. Technol. 2018, 10, 247–255. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Fu, C.; Yu, H.; Zhang, L. A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 846–860. [Google Scholar] [CrossRef]
- Bashir, Z.; Wątróbski, J.; Rashid, T.; Zafar, S.; Sałabun, W. Chaotic Dynamical State Variables Selection Procedure Based Image Encryption Scheme. Symmetry 2017, 9, 312. [Google Scholar] [CrossRef]
- Dong, C. Color image encryption using one-time keys and coupled chaotic systems. Signal Process. Image Commun. 2014, 29, 628–640. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Gong, P. A fast color image encryption scheme using one-time S-Boxes based on complex chaotic system and random noise. Opt. Commun. 2015, 338, 340–347. [Google Scholar] [CrossRef]
- Chai, X.-L.; Gan, Z.-H.; Lu, Y.; Zhang, M.-H.; Chen, Y.-R. A novel color image encryption algorithm based on genetic recombination and the four-dimensional memristive hyperchaotic system. Chin. Phys. B 2016, 25, 100503. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K.; Chen, Y.; Liu, X. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. Image Commun. 2017, 52, 6–19. [Google Scholar] [CrossRef]
- Zhu, C.; Sun, K. Cryptanalyzing and Improving a Novel Color Image Encryption Algorithm Using RT-Enhanced Chaotic Tent Maps. IEEE Access 2018, 6, 18759–18770. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H.; Kurths, J. Color image DNA encryption using NCA map-based CML and one-time keys. Signal Process. 2018, 148, 272–287. [Google Scholar] [CrossRef]
- Wong, K.-W.; Kwok, B.S.-H.; Yuen, C.-H. An efficient diffusion approach for chaos-based image encryption. Chaos Solitons Fractals 2009, 41, 2652–2663. [Google Scholar] [CrossRef]
- Mao, Y.; Chen, G.; Lian, S. A Novel Fast Image Encryption Scheme Based On 3D Chaotic Baker Maps. Int. J. Bifurc. Chaos 2004, 14, 3613–3624. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, K.-W.; Yu, H.; Zhu, Z.-L. An image encryption scheme using reverse 2-dimensional chaotic map and dependent diffusion. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2066–2080. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.-W.; Liao, X.; Xiang, T.; Chen, G. A chaos-based image encryption algorithm with variable control parameters. Chaos Solitons Fractals 2009, 41, 1773–1783. [Google Scholar] [CrossRef]




| Proposed | Ref. [14] | Ref. [37] | Ref. [38] |
|---|---|---|---|
| 0.000329 | −0.00114 | 0.0045 | 0.005497 |
| Component | Proposed | Ref. [14] | Ref. [39] | Ref. [40] | Ref. [41] |
|---|---|---|---|---|---|
| Red | 0.000626 | 0.0027 | 0.0017 | 0.0026 | −0.0031 |
| Green | 0.0000219 | −0.0019 | 0.0027 | 0.0051 | 0.0160 |
| Blue | −0.000475 | 0.0003 | 0.0043 | 0.0009 | −0.0190 |
| Proposed | Ref. [14] | Ref. [37] | Ref. [38] |
|---|---|---|---|
| 7.999419 | 7.9964 | 7.999319 | 7.9994 |
| Component | Proposed | Ref. [14] | Ref. [39] | Ref. [40] | Ref. [41] |
|---|---|---|---|---|---|
| Red | 7.999328 | 7.9974 | 7.9898 | 7.99734 | 7.9993 |
| Green | 7.999322 | 7.9969 | 7.9901 | 7.99716 | 7.9993 |
| Blue | 7.999277 | 7.9884 | 7.9902 | 7.99688 | 7.9993 |
| Proposed | Ref. [14] | Ref. [37] | Ref. [38] | |
|---|---|---|---|---|
| NPCR | 99.627 | nearly 0 | 99.62 | 99.6002 |
| UACI | 33.452 | nearly 0 | 33.48 | 33.463 |
| Component | Proposed | Ref. [14] | Ref. [39] | Ref. [40] | Ref. [41] | |
|---|---|---|---|---|---|---|
| Red | NPCR | 99.627 | ≈0 | 99.613 | 99.647 | 99.60 |
| UACI | 33.473 | ≈0 | 33.439 | 33.425 | 33.25 | |
| Green | NPCR | 99.631 | ≈0 | 99.611 | 99.623 | 99.60 |
| UACI | 33.496 | ≈0 | 33.465 | 33.275 | 33.28 | |
| Blue | NPCR | 99.624 | ≈0 | 99.615 | 99.594 | 99.60 |
| UACI | 33.478 | ≈0 | 33.469 | 33.439 | 33.31 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.; Al Solami, E.; Wang, X.-Y.; Doja, M.N.; Beg, M.M.S.; Alzaidi, A.A. Cryptanalysis of an Image Encryption Algorithm Based on Combined Chaos for a BAN System, and Improved Scheme Using SHA-512 and Hyperchaos. Symmetry 2018, 10, 266. https://doi.org/10.3390/sym10070266
Ahmad M, Al Solami E, Wang X-Y, Doja MN, Beg MMS, Alzaidi AA. Cryptanalysis of an Image Encryption Algorithm Based on Combined Chaos for a BAN System, and Improved Scheme Using SHA-512 and Hyperchaos. Symmetry. 2018; 10(7):266. https://doi.org/10.3390/sym10070266
Chicago/Turabian StyleAhmad, Musheer, Eesa Al Solami, Xing-Yuan Wang, M. N. Doja, M. M. Sufyan Beg, and Amer Awad Alzaidi. 2018. "Cryptanalysis of an Image Encryption Algorithm Based on Combined Chaos for a BAN System, and Improved Scheme Using SHA-512 and Hyperchaos" Symmetry 10, no. 7: 266. https://doi.org/10.3390/sym10070266
APA StyleAhmad, M., Al Solami, E., Wang, X.-Y., Doja, M. N., Beg, M. M. S., & Alzaidi, A. A. (2018). Cryptanalysis of an Image Encryption Algorithm Based on Combined Chaos for a BAN System, and Improved Scheme Using SHA-512 and Hyperchaos. Symmetry, 10(7), 266. https://doi.org/10.3390/sym10070266





