Abstract
We consider an alternative formula for time delay in gravitational lensing. Imposing a smoothness condition on the gravitationally deformed paths followed by the photons from the source to the observer, we show that our formula displays the same degrees of freedom as the standard one. In addition to this, it is shown that the standard expression for time delay is recovered when small angles are involved. These two features strongly support the claim that the formula for time delay studied in this paper is the generalization to the arbitrary angles of the standard one, which is valid at small angles. This could therefore result in a useful tool in Astrophysics and Cosmology which may be applied to investigate the discrepancy between the various estimates of the Hubble constant. As an aside, two interesting consequences of our proposal for time delay are discussed: the existence of a constraint on the gravitational potential generated by the lens and a formula for the mass of the lens in the case of central potential.
1. Introduction
One of the first modern cosmological models [1] was proposed by Albert Einstein in 1917: a static, spatially closed and temporally infinite universe with positive spatial curvature. This model, known as Einstein static universe, although unstable, had the nice feature to be completely determined: the request of staticity fixes the content of the universe, which is composed by matter, curvature and a cosmological constant . However, in 1929, Hubble showed that the universe is expanding, ruling out the Einstein model [2]. The value of the expansion speed of the universe, later characterized by the Hubble constant , was measured to be 500 . Then, the value of was revised along the 20th century, with a controversy about the measurements made by Sandage [3] (50 ) and de Vaucouleurs [4] (100 ). Only in the early 2000s the HST project found a value of km/s/Mpc [5].
After these works, the measurements of refined more and more, to reach the most recent direct estimate of the expansion rate of the Universe: [6]. The most important modern techniques arise from the study of the perturbations of the Cosmic Microwave Background (CMB) [7], the Supernovae 1A (SN 1A) [6] and the effect of Gravitational Lensing (GL) [8,9,10,11,12,13]. Nevertheless, the different measurements are not compatible one with each other, and still a slight tension about the correct value of does remain [14].
The discrepancy could be caused by a statistical fluctuations or could be evidence of new physics. To solve this puzzle, different theoretical scenarios have been proposed. For instance, it has been showed on general basis that dynamical dark energy [15,16] or a specific quintessence model [17] can solve the tension. Other possibilities have also been considered, such as dark matter-neutrinos interactions [18,19].
Our contribution towards an attempt to solve the disagreement [20] concerns the theoretical analysis of the time delay and its connection to . In the standard analysis [21], the time delay is calculated adding two contributions: the Shapiro delay from the gravitational potential of the lens and the geometric delay due to the deformations of the ray paths, approximated by straight lines [21]. The formula we are considering in this work derives from a different approach which allows to compute the time delay directly in a single shot, rather than two [20].
The two formulas for time delay, the standard one [21] and the one we are proposing [20], at first sight look quite different. In particular, our proposal seems to depend on more degrees of freedom. In this paper we show that, imposing a reasonable condition of smoothness on the paths of the photons, the parameters of our formula coincide with those characterizing the standard one, and, most remarkably, we prove that the standard formula is the the small angles limit of the one we are proposing, so turns out to be more general.
Furthermore, a weak point of the measurement of through GL is the determination of the gravitational potential generated by the lens, which is a crucial quantity in GL, and which, in general is not a known quantity. This is, therefore, an important issue [11], which motivated us to study a possible check of consistency for the supposed gravitational potential .
The paper is organized as follows. In Section 2 we briefly summarize the model underlying our formula for time delay. In Section 3 we impose a smoothness condition to the paths followed by the photons and we derive the analytical expression of the new parameters in terms of the ones already present in the standard formula. The main result achieved in this paper is contained in Section 4, where we show that our formula is the generalization of the standard formula to the arbitrary angles. In Section 5 a consistency check is proposed in order to select a gravitational potential among different possibilities. In Section 6 we make the exercise of applying our formula to the simple case of central potential generated by the lens, obtaining a formula for the mass of the lens. However, the mass of the lens is generally unknown, being also possibly generated by dark matter. Phenomenological consequences concerning this point, as well as comparison with known results, are also discussed in this Section. Our results are summarized in the concluding Section 7.
2. The Model
In Ref [20] we have obtained a new formula to determine the Hubble constant using time delay between multiple images of lensed objects (Throughout this paper we adopt the notations of [22]).
where , , , , are parameters defined in Figure 1, is the redshift of the generic point X and
where are the four parameters corresponding to radiation, matter, curvature and vacuum and respectively. The GL potentials () are defined as follows
where is the angular diameter distance of the point Y from the observer X. is the gravitational potential generated by the lens and the integral is performed over past directed geodesic paths emanating from the observer. Finally, are the coefficients of the Taylor series, which can be easily computed and can be found in Ref [20].
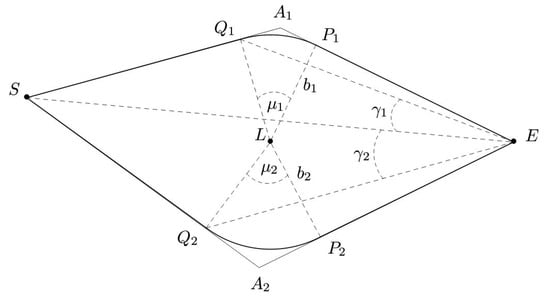
Figure 1.
S = source. L = lens. E = observer. = impact parameters. = approximated paths of the photons from S to E, indexed by .
Equation (1) was built in the framework of a new theoretical model for GL whose geometry is described in Figure 1. Our approach led to the well known time delay formula [21]
The assumptions on which our model is built are:
- The space is divided into two regions: the first, far from L, where , and the second, close to L, where .
- We approximate the curve by an arc of a circle centered in L. We want to point out that this is not a necessary condition: the arc of a circle is a good choice to represent , but it is not the only one possible.
- The universe is spatially flat, compatibly with observations [23].
According to assumption 1, we chose and as the points which divide the photons trajectory : from S to and from to E photons are in the region where , and so they run along straight lines (thanks to assumption 3); from to , instead, photons are in the region where , and so they moves on a curved trajectory, which we choose to describe with the arc of a circle in Figure 1.
There are at least two different geodesics along which photons can move from S to E and this causes the time delay [21].
These assumptions led us to the time delay Equation (4), which relates to .
3. Smoothness Condition
In Ref [20] we emphasized that Equation (1), as it stands, is not well suited for actual calculations of time delay, in the hope of softening the discrepancy among the existing estimates of . The reason is that the geometry is not uniquely defined because we have placed no constraints on , , , and which, consequently, are free parameters. It is easy to show that imposing on a smoothness condition of the paths uniquely fixes the parameters appearing in the new Equation (1) which, therefore, are not free. The next task is to show that (1) can be written in terms of the parameters appearing in the usual Equation (4). In other terms, no new degrees of freedom have been introduced in our reformulation of the time delay formula. Moreover, expressing the new formula by means of the parameters appearing in (4), makes easier the comparison of the two results, rendering, at the same time, more clear the domain of application of our new approach. Let us consider for the moment only one path, as in Figure 2. The equation of the straight line passing through is
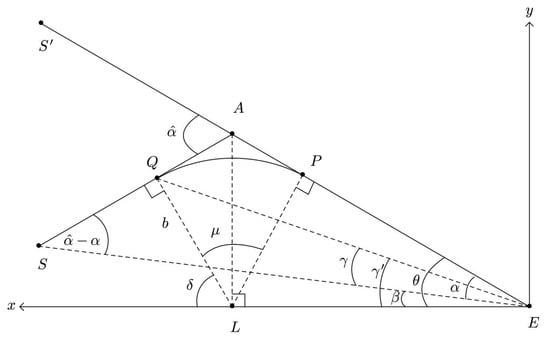
Figure 2.
The geometry within which we will develop our calculation. Only one path is displayed.
The equation of the circle centered in L of radius b to which belongs the arc is
Analogously, the equation of the straight line is
where is defined as in Figure 2, which makes clear that
Now we are able to obtain the value of as defined in Figure 2
Now we observe that
hence
and the angles and are related by Ref [22]
We have now all the tools to write Equation (1) in terms of the parameters appearing in the usual one (4). Let us rewrite (1) as
where
Using (7) we can write the first contribution to as
We are then able to write in (18) as follows
The exact expression for the time delay (1), using (18), is then given by the sum of the three terms (22), (26) and (27). We stress that the two expressions for time delay (1) and (4) are expressed by means of the same parameters: no new degrees of freedom have been introduced.
We conclude this Section with a few words concerning the possibility of a comparison with other proposals of alternative formulae for the time delay. The most important quests where gravitational time delay occurs are the determination of the Hubble constant [12] and the tests of General Relativity [24]. In all these cases the formula which is used is the one appearing in Ref [21], namely Equation (4). At most, the Equation (4) is heuristically modified, as done in Ref [12] in order to take into account the multiple galaxies at different redshifts close in projection to the strong lens system. Actually, formulae for time delay have also been given for very particular cases, like, for instance, in Ref [25] for lensing by Schwarzschild black hole and naked singularities, and in Ref [26] where is considered the time delay generated by black holes and massless wormholes in massive gravity, but the interest of these latter expressions for time delay is mainly formal, rather than phenomenological. In this paper, instead, we propose the first attempt to go beyond the standard formula for time delay, resting on basic grounds of General Relativity. As a matter of fact, we rely only on the definitions of angular distance and of redshift in Cosmology. Therefore, for what concerns the formula presented in this paper, the most pertinent comparison is only with the standard Equation (4).
4. Small Angles Limit
In this section we show that the standard formula for time delay (4) is recovered in the small angles limit of our Equation (1). This is a remarkable result, because it proves that Equation (1) is the generalization of the standard one to the arbitrary angles. To get this result, the crucial step is that the formula , written in the form (18), is expressed in terms of the same degrees of freedom appearing in the standard Equation (4).
Let us consider Equation (16) and let us suppose that all the angles involved are very small. Up to the second non vanishing order, we get
Now we are able to expand in the small angles limit the time delay Equation (1) term by term, according to (18). For what concerns (22), we have
Using (31), (32) and (34) in Equation (18) we obtain the following formula
which is precisely the formula already present in literature (4) and currently used in the determination of through GL. We can therefore conclude that
This remarkable fact justifies our claim: our time delay Equation (18), which is equivalent to (1) once the smoothness condition is imposed, is the generalization at the arbitrary angles of the standard expression (4), and, differently from (4), it has been obtained in one shot only without having to consider two distinct steps (geometrical and Shapiro).
Some comments are in order concerning the relation between the result presented in [20] and the one obtained in this paper. In Ref [20], the Equation (1) for time delay has been proposed which, a priori, was supposed to be an alternative to the standard one (4). It was indeed derived in a different way, in particular without adding together two independent contributions, namely the Shapiro and the geometrical ones, but, rather, by means of a single reasoning, namely a refinement of the approximation concerning the path of the photon in its way from the source through the observer. The resulting Equation (1) appears to depend on more degrees of freedom than the standard one, and only for a particular, arbitrary albeit reasonable, choice of the parameters, the two formulae were shown to coincide. This, evidently, is not sufficient to claim that the new formula generalizes the standard one. At most, it is possible to conclude that the two formulae coincide in a subset of the space of parameters. In this paper we do not make any assumption on the parameters. Instead, we impose a condition of smoothness on the path followed by the photons. Doing this, quite unexpectedly, we find the remarkable result that the degrees of freedom collapse into the standard ones. This is the first clue that the new formula is a generalization of the old one, rather than something different and alternative. The definitive proof of this statement is contained in Section 4, where it is shown that, going to small angles, the standard formula is recovered. This demonstration is the main achievement of this paper. Of course, the breakthrough would be the use of this more general formula in physical situations where the angles involved are not small, and therefore the standard formula cannot be used. At the moment, however, the actual technology does not allow the quantitative observation of the phenomenon of gravitational lensing at large, or at least not too small, angles.
5. A Constraint on the Lens Gravitational Potential
The time delay Equation (4) or, equivalently (1), allows to determine . The crucial physical quantity for the time delay is the gravitational potential originated by the lens L. In most cases, is not known but rather is assumed to belong to a certain class, or inferred by some theoretical considerations [11]. We will denote with the assumed potential, which, hopefully, should not be very far from the real one, which we shall call . Our aim is to provide a consistency relation for , by means of which it will be possible to check if represents a realistic assumption for the real gravitational potential of the lens or not. From now on we will use the subscript “hp” for the quantities deduced from and the subscript “phys” for their actual values. Once the potential has been assumed, from Ref [22]
where is the transverse gradient of the potential with respect to the path, we can compute the angle which, consequently, not necessarily coincides with . From the experimental knowledge of and of , and once that are determined, we can predict the position of the source . An obvious check for would be
where identifies the actual position of the source S. Unfortunately, the exact position of the source is rarely known. What is generally known, instead, is its redshift , from which, using (2), the distance can be computed. Therefore, the check of consistency reduces to
which is a necessary condition for . We can compute explicitly as follows.
From (13) and (11) we have
and the equations of the straight lines passing through and S are
where, again, . From (41) we get the coordinates of the source S
The small angles limit and gives
and hence the distance of the source is
6. Determination of the Lens Mass for Central Potential
To give a simple example of how our time delay formula can be used for phenomenological calculations, let us consider the textbook case of spherically symmetric potential , being aware that this is not a realistic assumption for actual gravitational potentials generated by the lens. It is a known result [22] that in this case the angles are given by
where M is the mass of the lens L and is the angular diameter distance between L and E. Inserting (47) in (46) we obtain
and hence
Using the relation between the angular diameter distance d and the proper distance r [23]
we can conclude that
This is a general result, valid for all spherically symmetric lenses. The lesson from this simple example, is that in principle it is possible to estimate the mass of a lens with central gravitational potential, like a star or a black hole, once the angular diameter distances , , the observed angle and the redshifts are known. It is interesting to compare the results coming from the mass Equation (51) with those obtained using the corresponding formula existing in literature.
If a circularly symmetric lens is considered and if lens, source and observer are collinear, as a consequence of the rotational symmetry of the lens system, the source is imaged as a ring. The radius of the ring, called Einstein radius, is given by
where , and are the angular diameter distances. From (52), it is possible to estimate the mass inside the Einstein ring, which is given by
This is the standard formula provided in the literature (see for example [27]). If the source and the lens are misaligned, multiple images can be observed. In this case, it is possible to measure the relative distances between each image and the lens, called and for a two-images lens system, but it is also possible to extract an “effective” Einstein radius by performing a fit assuming a particular mass distribution of the lens. It has been shown that the assumed mass distribution model only partly affects the Einstein ring extraction [28,29], and since the Einstein angle is an average between the lens center and multiple images, in the case of a two images system the angle is usually replaced with .
This is usually a good approximation for systems with nearly symmetric image configuration () where the mass enclosed within is accurate to within ∼5% as reported in Ref [29]. The Equation (51) is indeed a generalisation of the standard formula and reduces to the standard formula if .
To test the validity of the lens mass estimation, a comparison between the standard Equation (52) and the formula for the mass of the lens obtained in this paper (51), which uses explicitly and , is provided. To have a fair comparison and to verify the applicability of (51), the formula is applied to a subset of quasar lenses listed in the CASTLES webpage [30] satisfying the following requirements: first of all, the source and the lens redshifts have to be known. Complex lens systems such as multiple galaxies or cluster of galaxies are excluded and only quasar lenses with a planar geometry with two lens images are chosen. Finally, the observed angles and must be known data. Five quasar lenses have been identified to fulfill the previous criteria. Our study shows that in the case of , the standard formula is a good approximation of Equation (51) and as it can be seen in Table 2: for QJ0158-4325 the correction is negligible, while for SDSS1226-0006 the correction is of the order of .
For , the standard formula starts to show a significant discrepancy with respect to the formula obtained in this paper. The limit of the standard formula is overcome by Equation (51) that can indeed be applied for any angle configuration.
An ideal outcome of our study would be the determination of the dark matter fraction in the lens galaxy in a more precise way. To do that, a more appropriate potential has of course to be used to take into account the density distribution of dark matter in a galaxy. This additional study represents a future development of our work.
The parameters for the five considered lenses are reported in Table 1.

Table 1.
Lenses parameters 1.
We considered a flat CDM universe, with , and km/s/Mpc. The calculated masses using the parameters reported in Table 1 are reported in Table 2, where and are calculated using (51) and (53), respectively.

Table 2.
Lenses parameters 2.
We stress that the results contained in Section 5 and Section 6, are secondary with respect to the main one obtained in the previous Sections, namely the generalized formula for time delay. These are mathematical achievements with predictive consequences, and, in our opinion, represent interesting applications of the new formula for time delay, with possible phenomenological implications. The first is a no-go theorem for the possible gravitational potentials generated by the lens, whose determination is currently object of intensive research. The second consequence is the determination of Equation (51) for the total mass which deviates the path of the photon. By total we mean the sum of bot visible and dark matter. This formula, which holds for the particular case of spherical symmetric mass distributions, has been compared with Equation (53), which is the one currently used in the same situations, of which the new mass formula appears to be a refinement. In the few cases we considered as a test, we found interesting deviations from the existing estimates, which deserve further investigations.
7. Conclusions
In this paper, we improved the analysis of the time delay contained in a previous work [20], where we obtained a new expression for , characterized, however, by the presence of several apparently free parameters, whose presence renders that expression unsuitable for phenomenological considerations. Although, as we showed, its validity is enforced by the fact that, for certain values of its parameters, it reduces to the standard one [21]. Both in the standard approach and in ours, the paths followed by the photons from the source to the observer, modified by the presence of the lens, were approximated either by straight lines (as in Ref [21]) or by straight lines and an arc of a circle (as in Ref [20]), not joining in a smooth way.
There are two main results presented in this paper. The first is that, imposing a smoothness condition on the photon rays, the number of free parameters drastically reduces, with the outcome that no new degrees of freedom are introduced with respect to the standard formula for time delay. The second outcome is represented by the fact that we were able to show that our formula exactly reduces to the standard one in the small angles limit, which means that our expression for time delay generalizes the standard one to generic angles. In addition, we gave a consistency check for the gravitational potential generated by the lens. Although this physical quantity is crucial for the GL effect, and in particular for the determination of the Hubble constant by means of the time delay formula, its exact expression is rarely known, and all the considerations are made on the basis of conjectured potentials. For instance, the GL effect could be generated also by dark matter distributions, of which, at most, only hypothetical maps exist. A criterion for selecting among different guesses on the gravitational potential generating the GL effect is therefore useful.
Finally, to give a taste of the possible applications of our formula, we applied our results to the case of a central gravitational potential, obtaining an expression for the mass of the lens, which, again, is generally unknown. Although different situations exist, for which the spherical symmetry is a good approximation, realistic gravitational potentials generated by the lenses are in general far more complicated. Our aim here is only to show which might be the phenomenological applications of our formula. The signal of the particular case of a spherically symmetric gravitational potential is the presence of only two images, which are aligned with the lens. We analyzed five situations where our Equation (51) for the mass can be successfully applied, and we compared our results to those obtained with the mass formula traditionally used in case of central potentials (53). The promising outcome is that our formula reproduces the results obtained in the usual way, but, quite remarkably, also extends the range of application of the standard one to any angle configuration. This approach could give hints on the dark matter present in high z galaxies: from their luminosity it is possible to estimate the value of their mass, which could be compared to our theoretical prediction. This would be interesting in situations where it is not possible to use standard methods, such as the study of the galaxy rotations curve, due to the high distances involved.
Author Contributions
Conceptualization, N.A., M.B. and N.M.; Methodology, N.A., M.B. and N.M.; Formal Analysis, N.A., M.B. and N.M.; Investigation, R.C., A.D., C.R. and S.T.; Data Curation, R.C., A.D., C.R. and S.T.; Writing & Original Draft Preparation, N.A., M.B., R.C., A.D., N.M., C.R. and S.T.; Writing, Review & Editing, N.A., M.B. and N.M.; Supervision, N.M.
Funding
This research received no external funding.
Acknowledgments
N.M. thanks the support of INFN Scientific Initiative SFT: “Statistical Field Theory, Low-Dimensional Systems, Integrable Models and Applications”. Luca Panizzi and Davide Ricci are gratefully acknowledged. We thank Laura Massa Trucat for a careful reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Einstein, A. Cosmological Considerations in the General Theory of Relativity. Math. Phys. 1917, 1917, 142–152. [Google Scholar]
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Sandage, A.; Tammann, G.A. Steps toward the Hubble constant. VII—Distances to NGC 2403, M101, and the Virgo cluster using 21 centimeter line widths compared with optical methods: The global value of H sub 0. Astrophys. J. 1976, 210, 7–24. [Google Scholar] [CrossRef]
- De Vaucouleurs, G.; Peters, W.L. Hubble ratio and solar motion from 200 spiral galaxies having distances derived from the luminosity index. Astrophys. J. 1981, 248, 395–407. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Gibson, B.K.; Ferrarese, L.; Kelson, D.D.; Sakai, S.; Mould, J.R.; Kennicutt, R.C., Jr.; Ford, H.C.; Graham, J.A.; et al. Final results from the Hubble Space Telescope key project to measure the Hubble constant. Astrophys. J. 2001, 553, 47–72. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Suyu, S.H.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Rusu, C.E.; Sluse, D.; Treu, T.; Wong, K.C.; Auger, M.W.; Ding, X.; et al. H0LiCOW—I. H0 Lenses in COSMOGRAIL’s Wellspring: Program overview. Mon. Not. R. Astron. Soc. 2017, 468, 2590–2640. [Google Scholar] [CrossRef]
- Sluse, D.; Sonnenfeld, A.; Rumbaugh, N.; Rusu, C.E.; Fassnacht, C.D.; Treu, T.; Suyu, S.H.; Wong, K.C.; Auger, M.W.; Bonvin, V.; et al. H0LiCOW II. Spectroscopic survey and galaxy-group identification of the strong gravitational lens system HE0435–1223. Mon. Not. R. Astron. Soc. 2017, 470, 4838–4857. [Google Scholar] [CrossRef]
- Rusu, C.E.; Fassnacht, C.D.; Sluse, D.; Hilbert, S.; Wong, K.C.; Huang, K.-H.; Suyu, S.H.; Collett, T.E.; Marshall, P.J.; Koopmans, T.T.L.V.E. H0LiCOW—III. Quantifying the effect of mass along the line of sight to the gravitational lens HE 0435–1223 through weighted galaxy counts. Mon. Not. R. Astron. Soc. 2017, 467, 4220–4242. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Auger, M.W.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Halkola, A.; Rusu, C.E.; Sluse, D.; Treu, A.S.T.; et al. H0LiCOW—IV. Lens mass model of HE 0435–1223 and blind measurement of its time-delay distance for cosmology. Mon. Not. R. Astron. Soc. 2017, 465, 4895–4913. [Google Scholar] [CrossRef]
- Bonvin, V.; Courbin, F.; Suyu, S.H.; Marshall, P.J.; Rusu, C.E.; Sluse, D.; Tewes, M.; Wong, K.C.; Collett, T.; Fassnacht, C.D.; et al. H0LiCOW—V. New COSMOGRAIL time delays of HE 0435–1223: H0 to 3.8 percent precision from strong lensing in a flat ΛCDM model. Mon. Not. R. Astron. Soc. 2017, 465, 4914–4930. [Google Scholar] [CrossRef]
- Refsdal, S. On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect. Mon. Not. R. Astron. Soc. 1964, 128, 307. [Google Scholar] [CrossRef]
- Luković, V.V.; D’Agostino, R.; Vittorio, N. Is there a concordance value for H0? Astron. Astrophys. 2016, 595, A109. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Linder, E.V.; Silk, J. Constraining Dark Energy Dynamics in Extended Parameter Space. Phys. Rev. D 2017, 96, 023523. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; Pérez, J.D.C. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. B 2017, 774, 317. [Google Scholar] [CrossRef]
- Valentino, E.D.; Linder, E.V.; Melchiorri, A. Vacuum phase transition solves the H0 tension. Phys. Rev. D 2018, 97, 043528. [Google Scholar] [CrossRef]
- Wilkinson, R.J.; Boehm, C.; Lesgourgues, J. Constraining Dark Matter-Neutrino Interactions using the CMB and Large-Scale Structure. JCAP 2014, 1405, 011. [Google Scholar] [CrossRef]
- Valentino, E.D.; Bøehm, C.; Hivon, E.; Bouchet, F.R. Reducing the H0 and σ8 tensions with Dark Matter-neutrino interactions. Phys. Rev. D 2018, 97, 043513. [Google Scholar] [CrossRef]
- Alchera, N.; Bonici, M.; Maggiore, N. Towards a new proposal for the time delay in gravitational lensing. Symmetry 2017, 9, 202. [Google Scholar] [CrossRef]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Addison-Wesley: San Francisco, CA, USA, 2004; 513p. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008; 593p. [Google Scholar]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Keeton, C.R. Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities. Phys. Rev. D 2008, 77, 124014. [Google Scholar] [CrossRef]
- Jusufi, K.; Sarkar, N.; Rahaman, F.; Banerjee, A.; Hansraj, S. Deflection of light by black holes and massless wormholes in massive gravity. Eur. Phys. J. C 2018, 78, 349. [Google Scholar] [CrossRef]
- Schmidt, R.; Webster, R.L.; Lewis, G.F. Weighing a galaxy bar in the lens Q2237 + 0305. Mon. Not. R. Astron. Soc. 1998, 295, 488–496. [Google Scholar] [CrossRef]
- Oguri, M.; Rusu, C.E.; Falco, E.E. The stellar and dark matter distributions in elliptical galaxies from the ensemble of strong gravitational lenses. Mon. Not. R. Astron. Soc. 2014, 439, 2494–2504. [Google Scholar] [CrossRef]
- Suyu, S.H. Cosmography from two-image lens systems: Overcoming the lens profile slope degeneracy. Mon. Not. R. Astron. Soc. 2012, 426, 868–879. [Google Scholar] [CrossRef]
- CASTLES Catalogue. Available online: https://www.cfa.harvard.edu/castles (accessed on 27 June 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).