Research on Electronic Voltage Transformer for Big Data Background
Abstract
1. Introduction
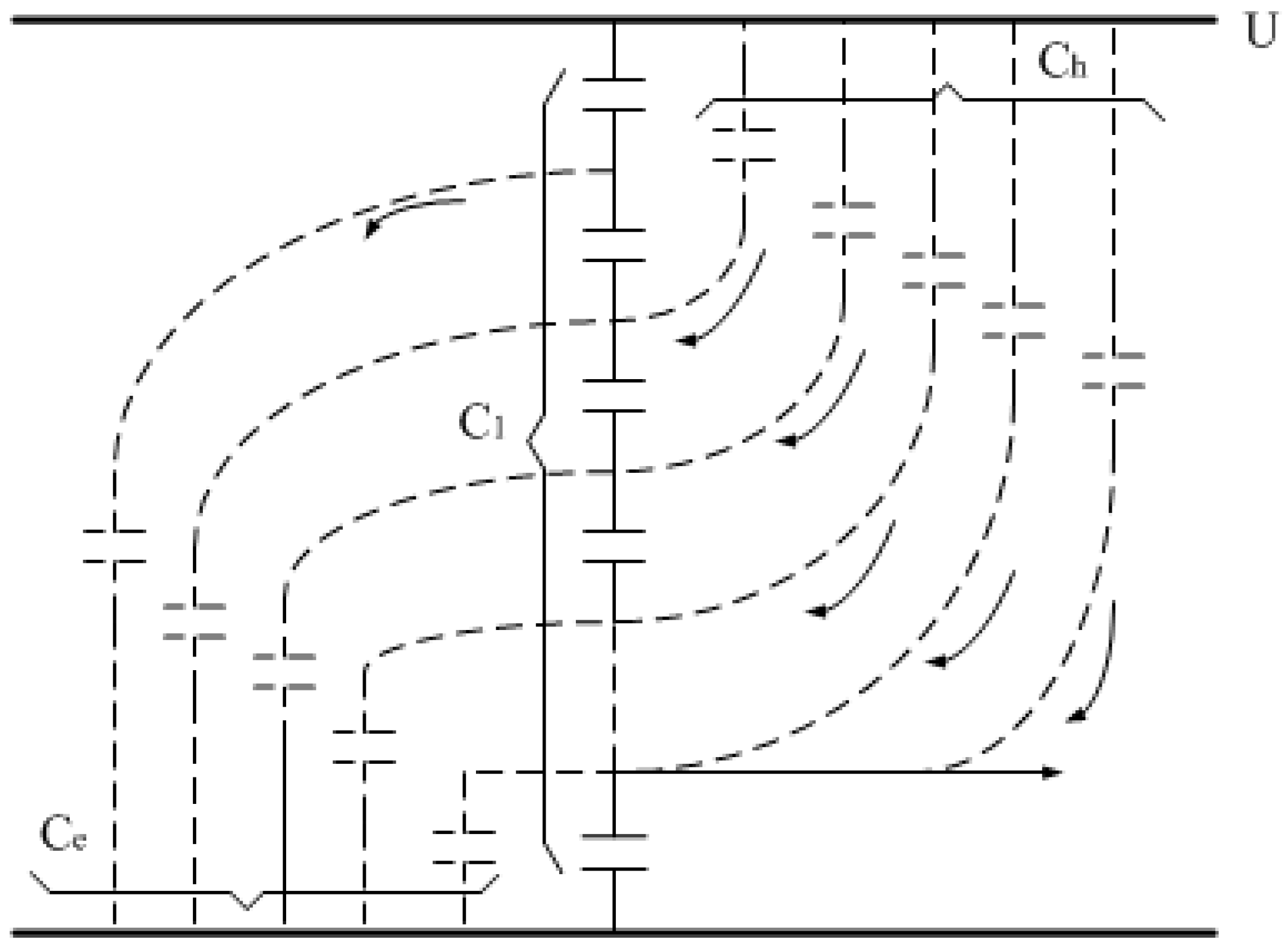
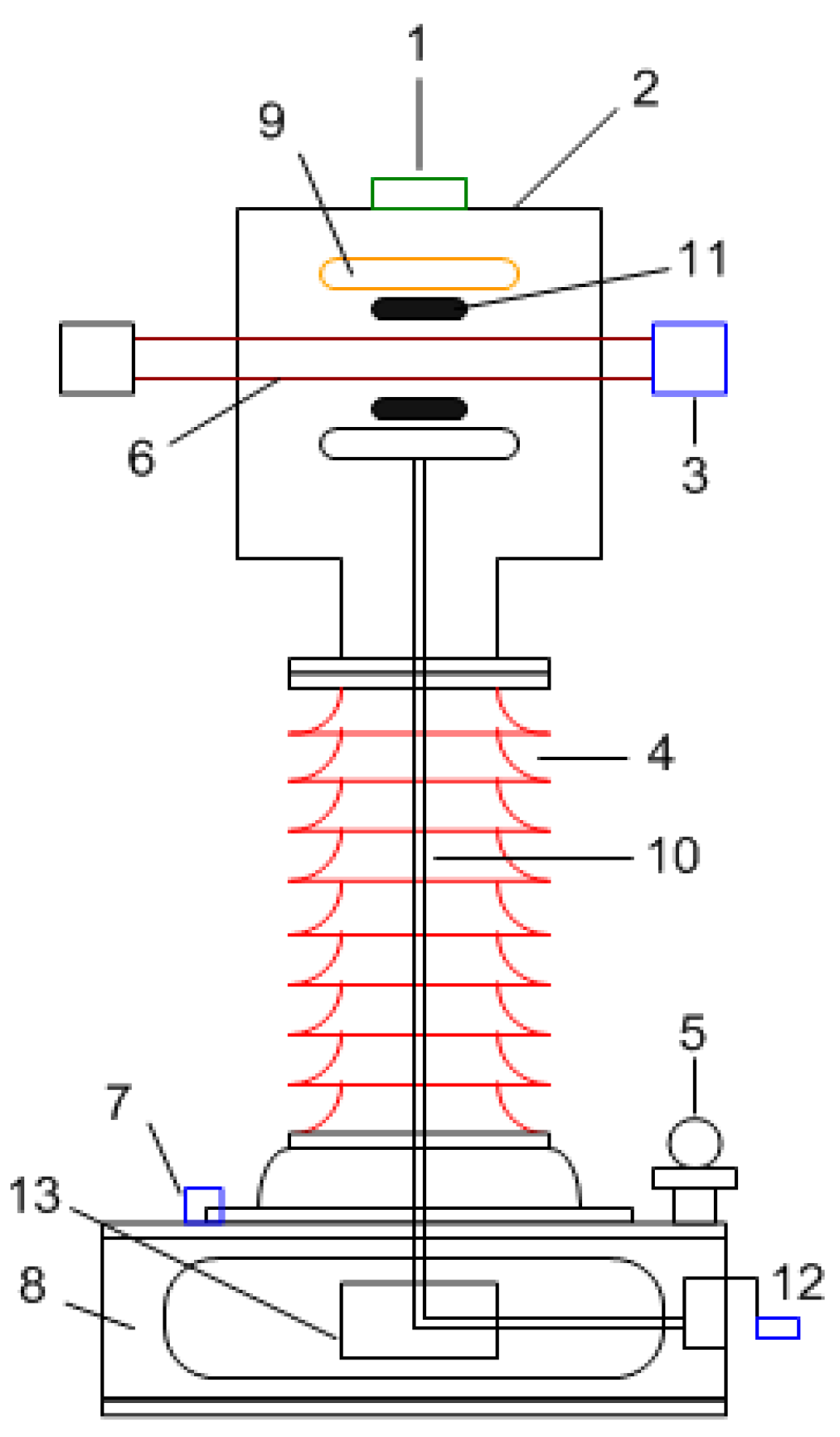
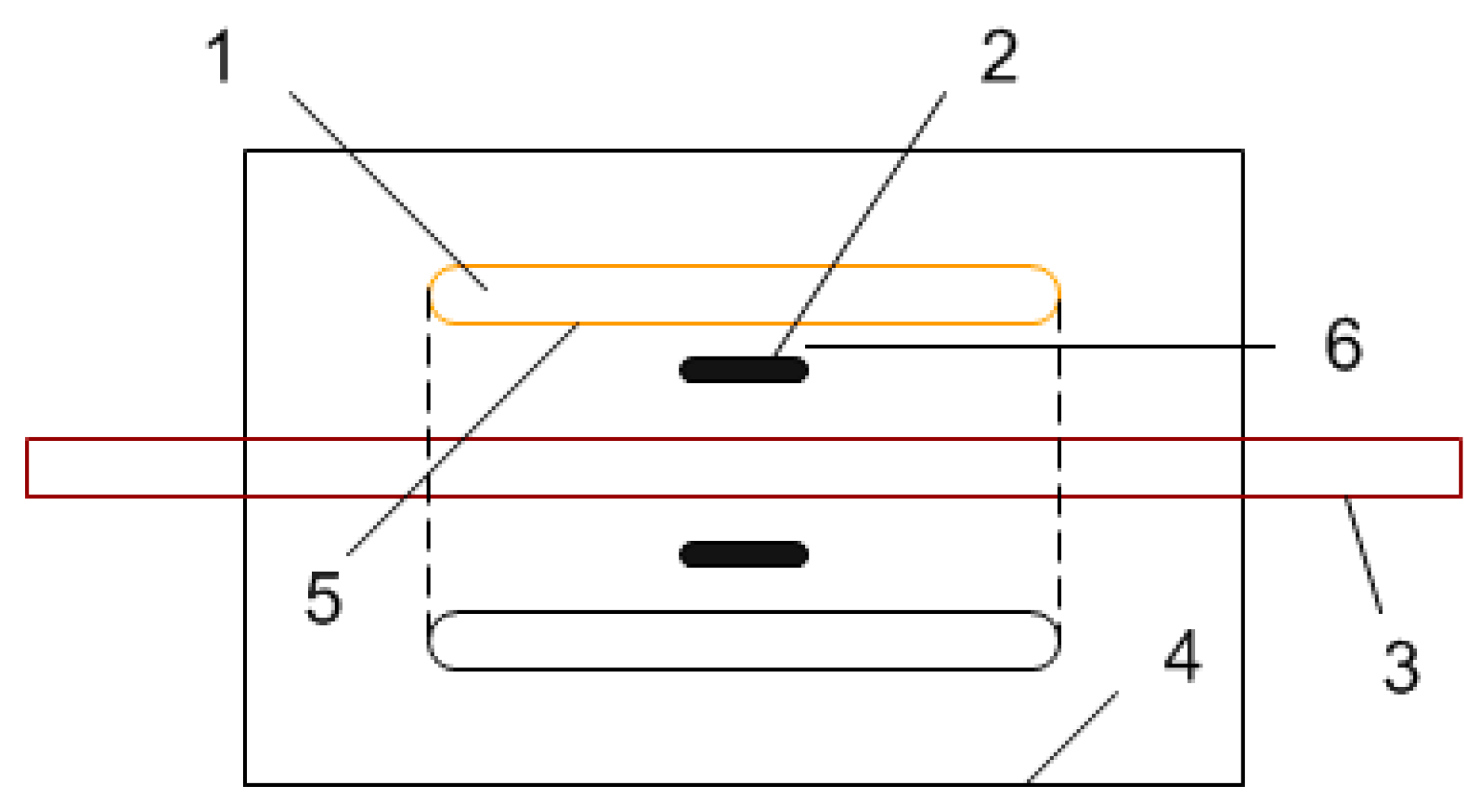
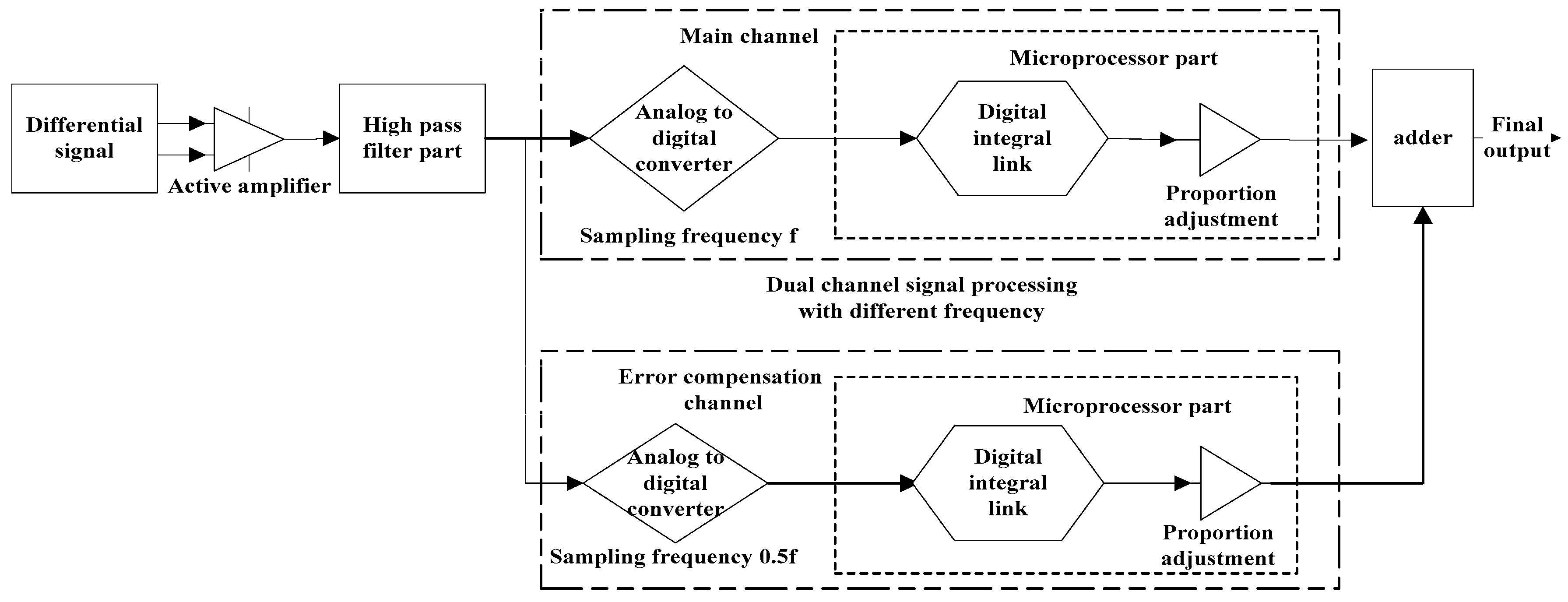
2. Principle and Structure
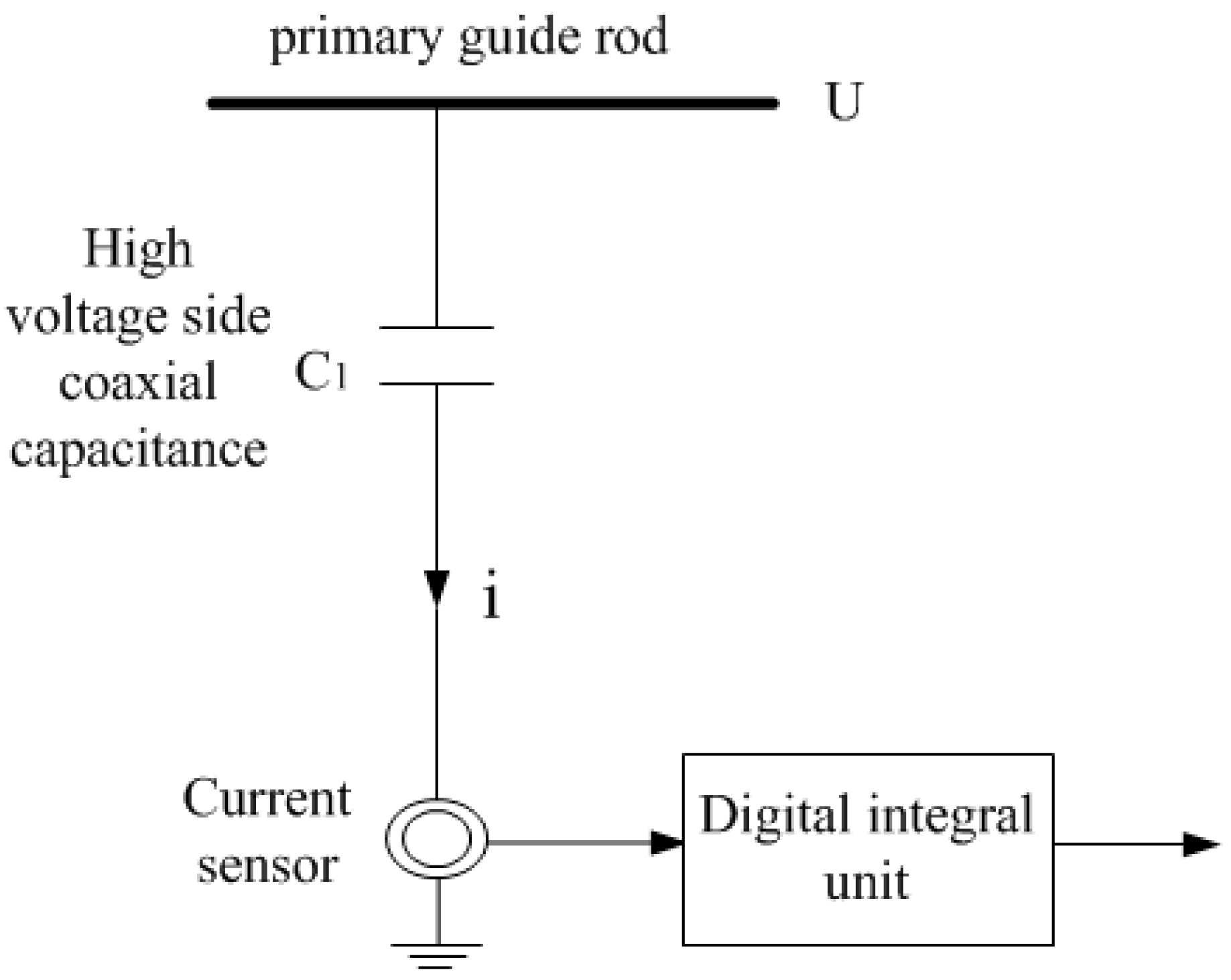
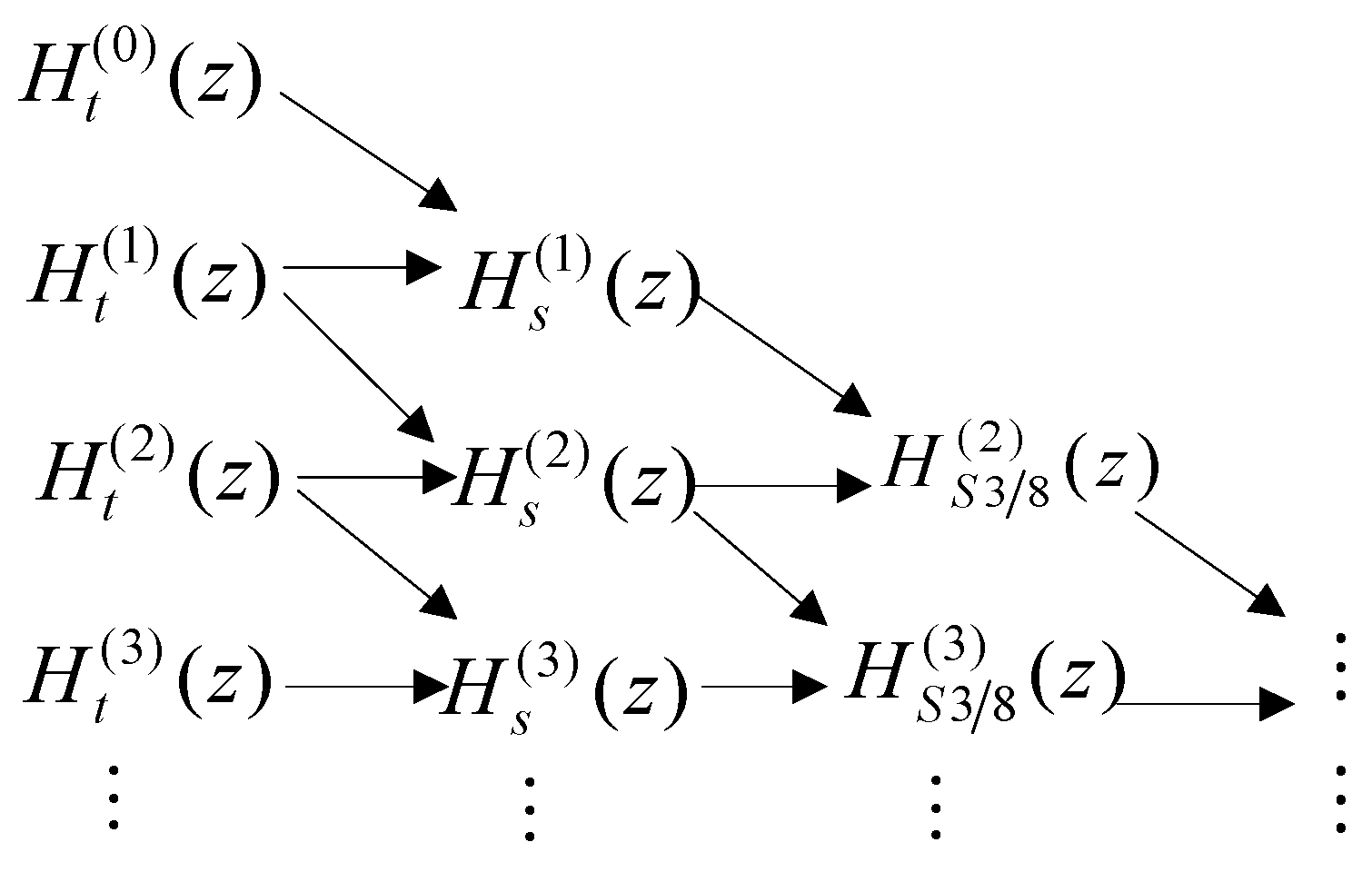
3. High-Precision Digital Integrator
- (1)
- Improving the sampling frequency has obvious effects on improving the amplitude characteristic of the digital integrator.
- (2)
- The complex Simpson formula is more accurate than the complex trapezoidal formula, and the error is reduced faster [15].
4. Performance Analysis
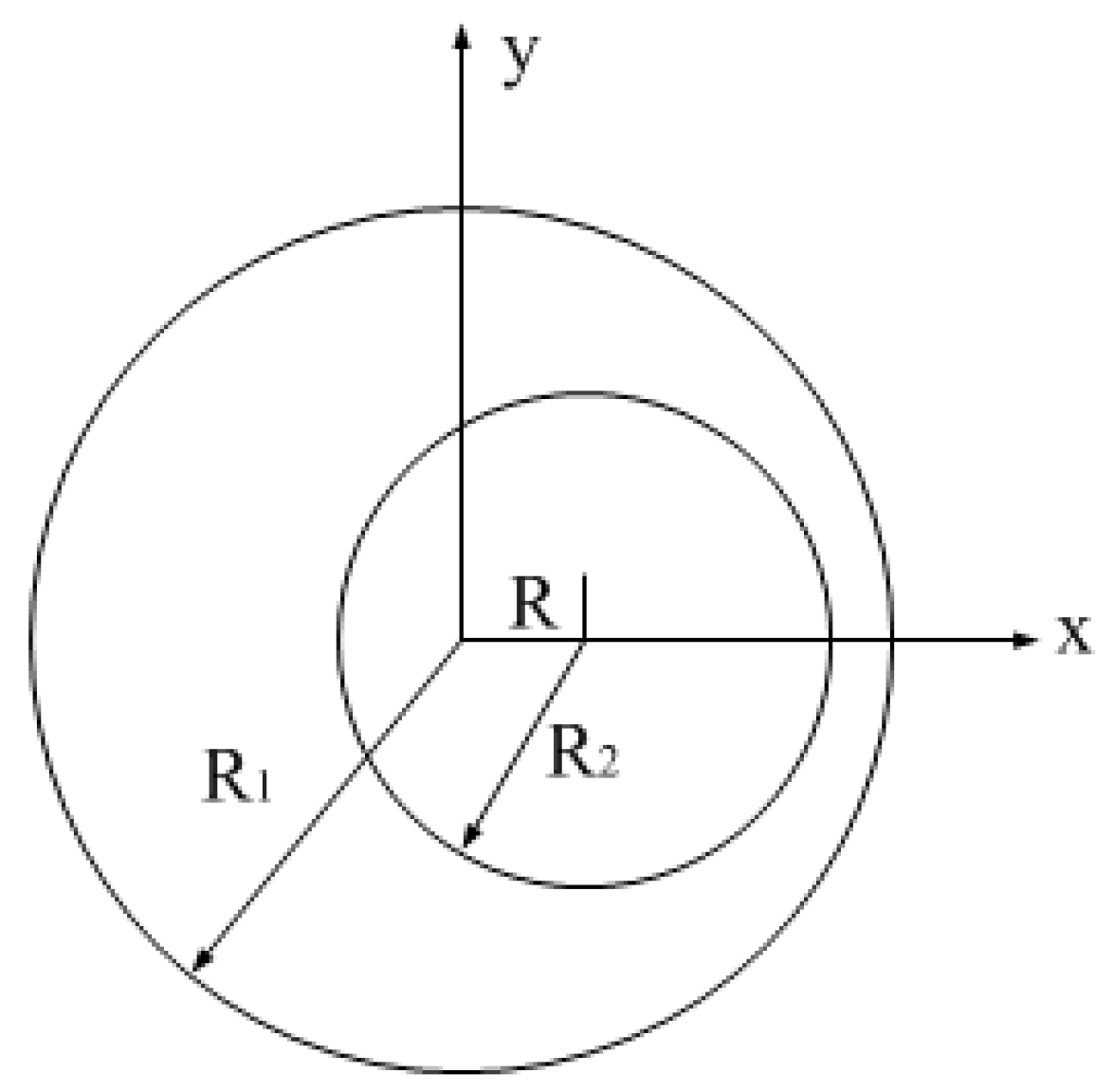
4.1. Analysis of Position Influence of the SF_6 Coaxial Capacitor
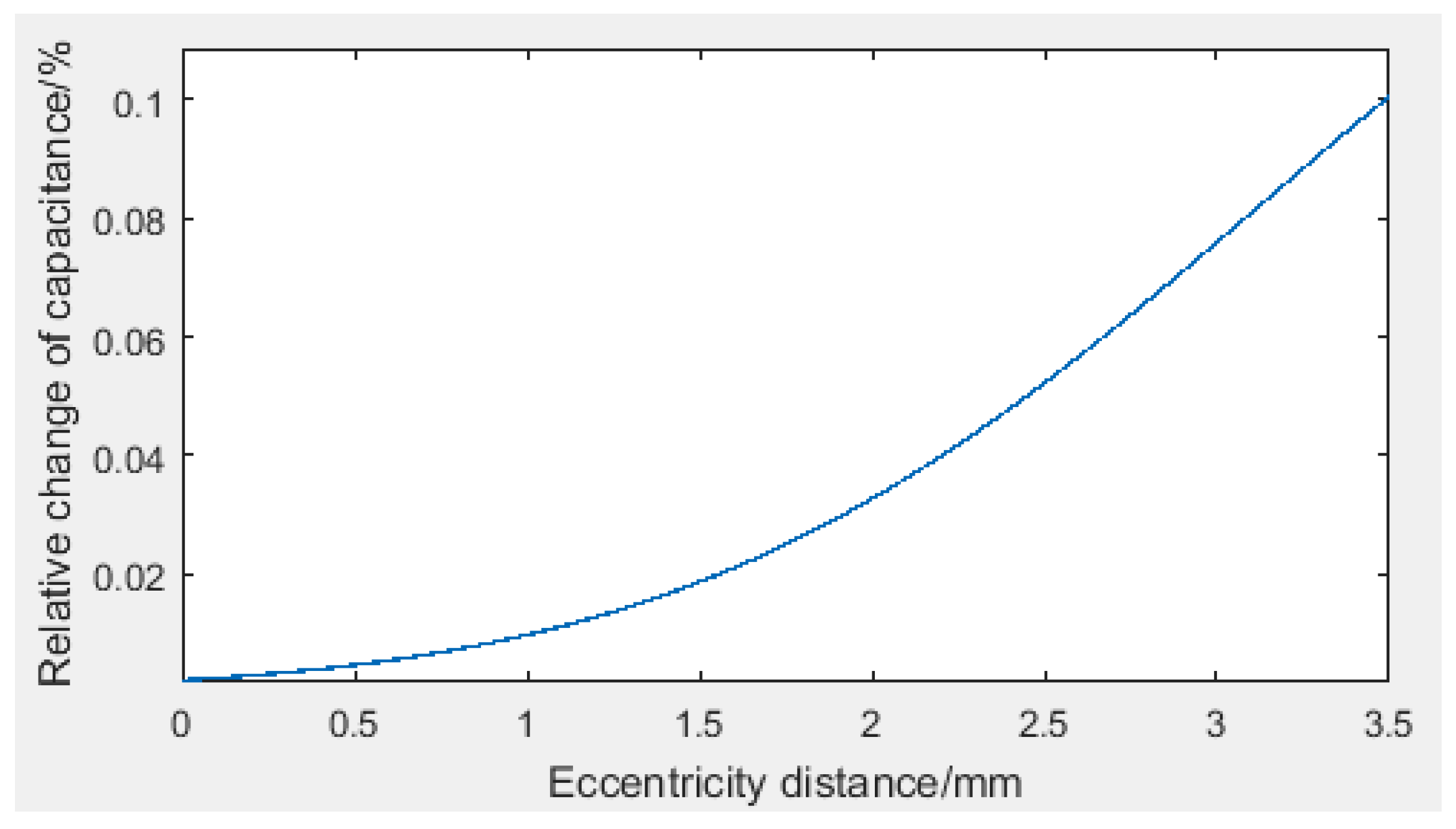
4.1.1. Calculation of Off-Axis Capacitance
4.1.2. Calculation of the Deflection Angle Capacitance
4.1.3. Off-Axis Distance Allowed in Practice
4.2. Analysis of Temperature Performance and Pressure Performance of the Coaxial Capacitor
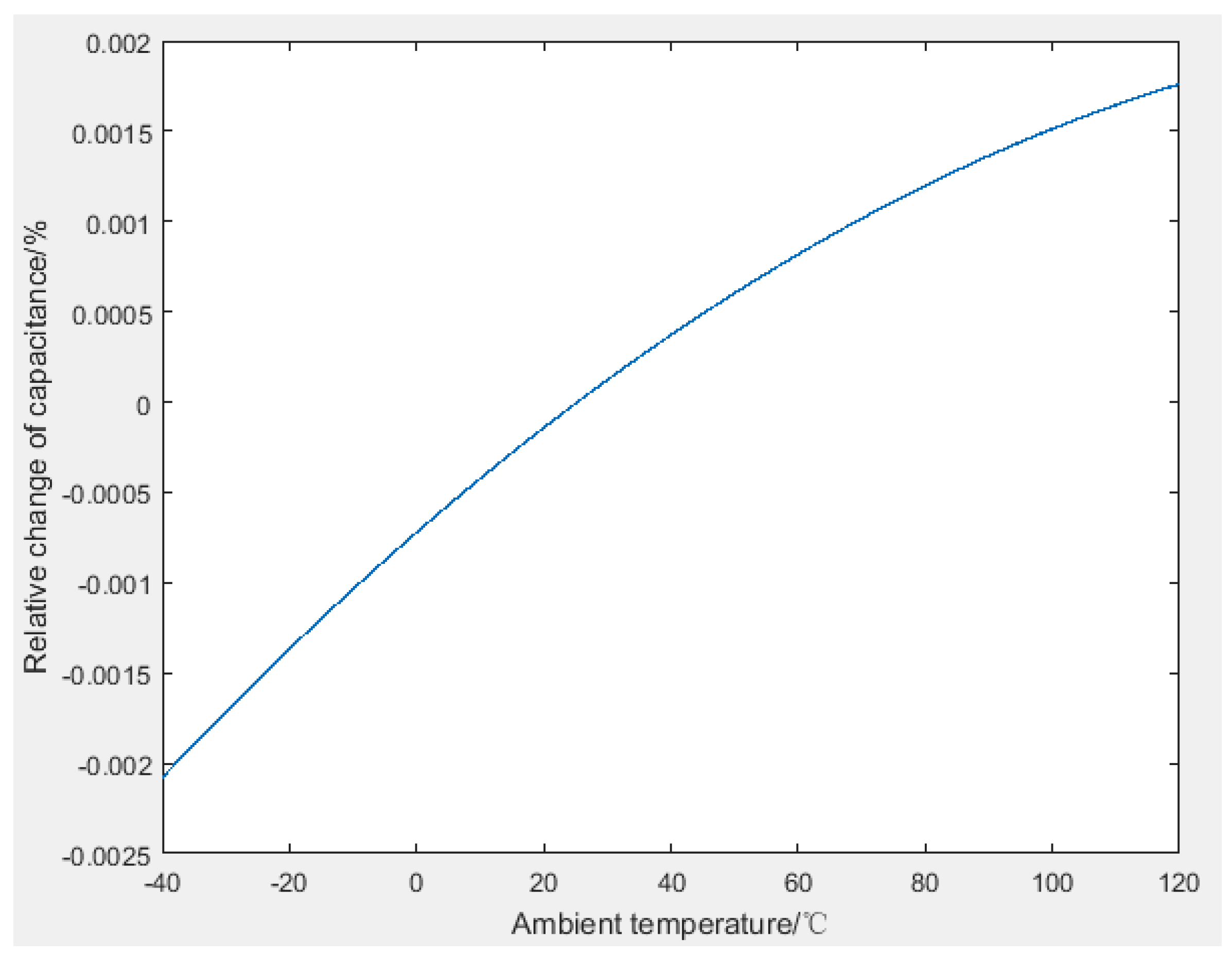
4.2.1. The Relationship between the Capacitance and the Temperature When the Density Does Not Change
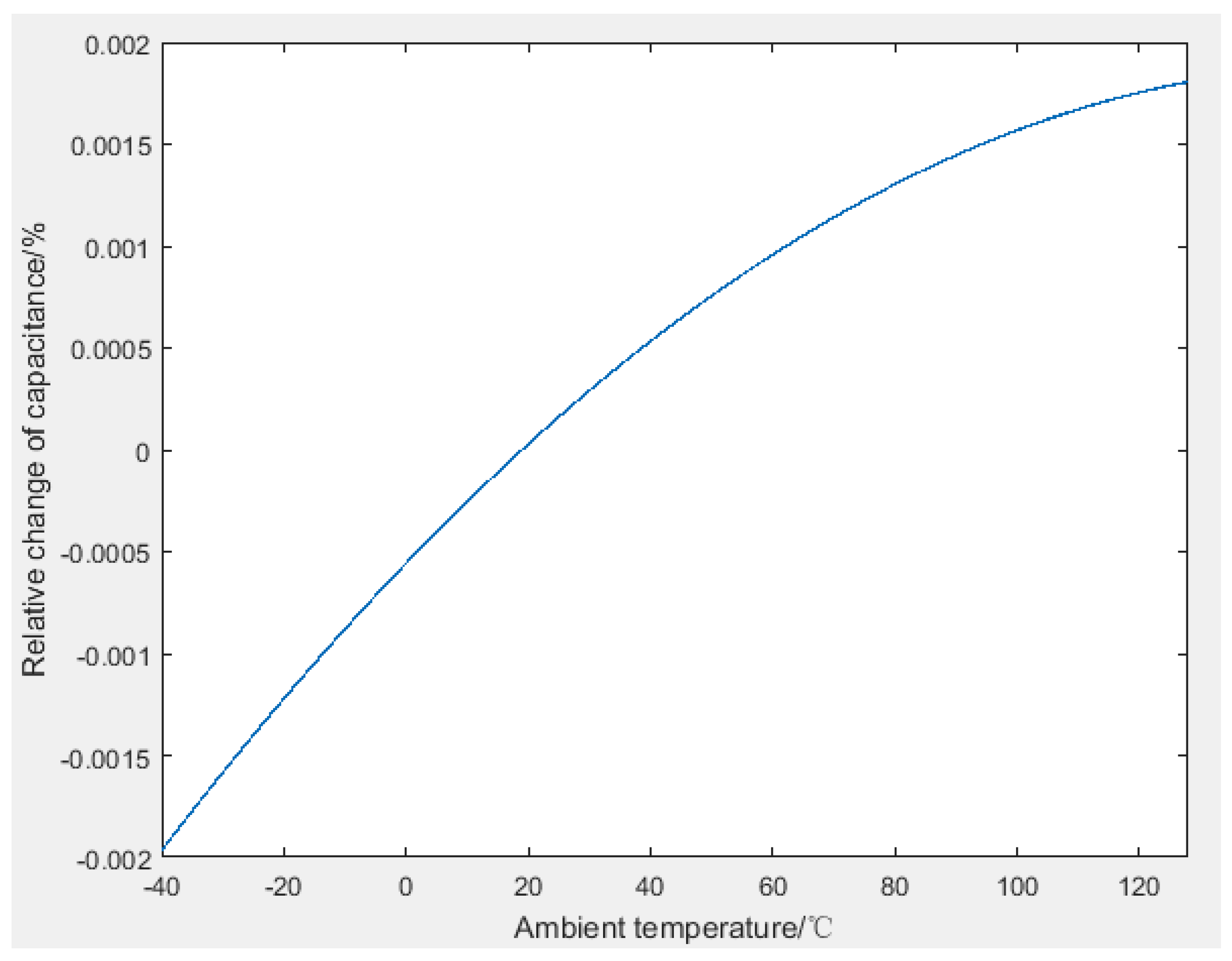
4.2.2. The Relationship between the Capacitance and the Temperature When the Density Changes
5. Experimental Results and Analysis
5.1. Basic Accuracy Test
5.2. Partial Discharge Test
5.3. EMC (Electromagnetic Compatibility) Test
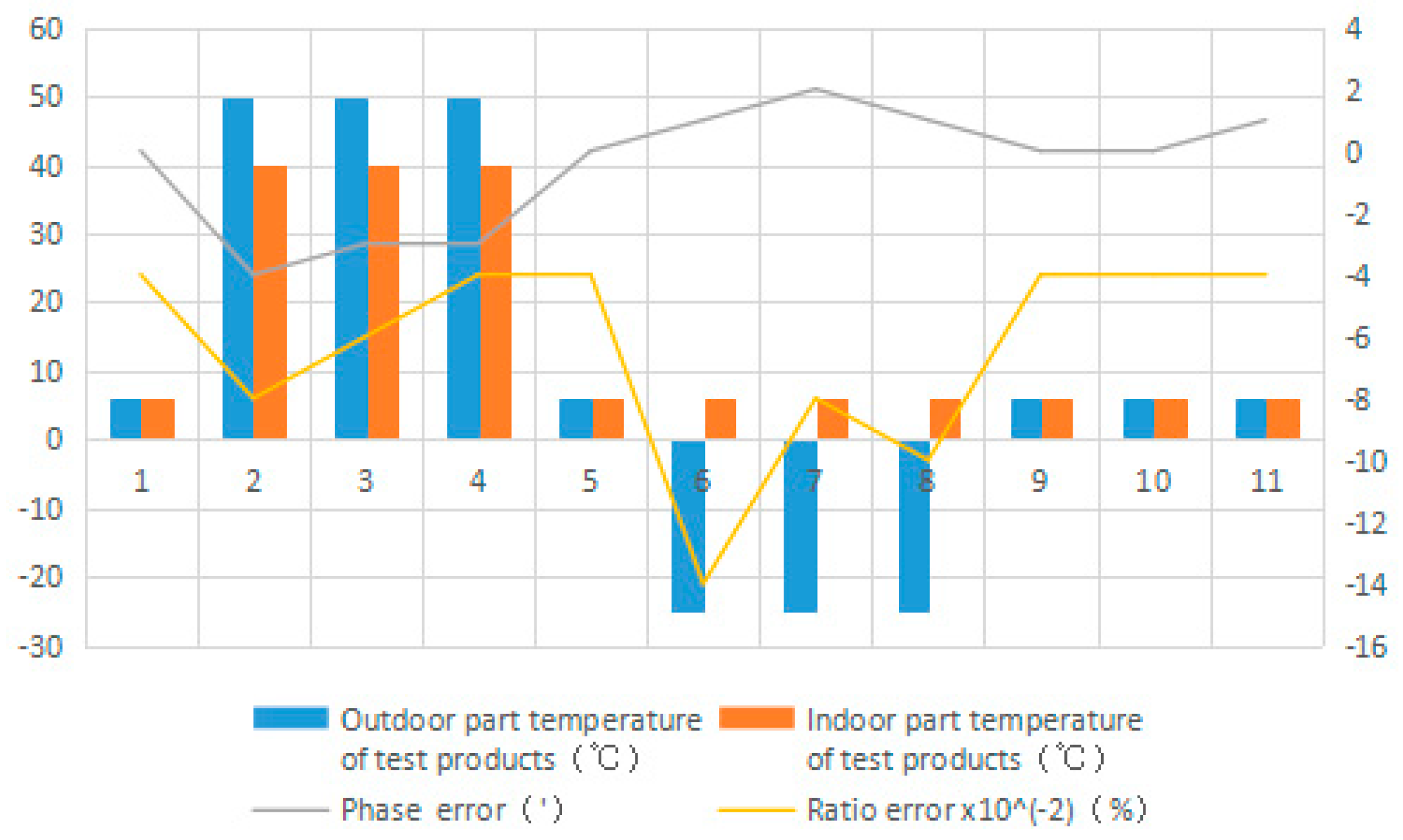
5.4. Temperature Cycle Test
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ch | parasitic capacitance for the high-voltage side (F); |
| Ce | parasitic capacitance to the ground (F); |
| Ced | equivalent parasitic capacitance to the ground (F); |
| C1 | capacitance C1 of the high-voltage side (F); |
| ε0 | permittivity of vacuum (8.85 × 10−12 F/m); |
| l | width of the capacitor ring (m); |
| D1 | diameter of the the capacitor ring (m); |
| D2 | diameter of the primary conductor (m); |
| i | capacitance current (A); |
| u | primary voltage (V); |
| R1 | inner radius of the coaxial cylindrical conductor shells (m); |
| R2 | outer radius of the coaxial cylindrical conductor shells(m); |
| P | pressure (MPa); |
| T | temperature (K); |
| ρ | density (Kg/m3); |
| k | Boltzmann constant (1.38 × 10−23 J/K); |
| molecular radius of the SF_6 gas (2.27 × 10−10 m). |
References
- Refaat, S.S.; Abu-Rub, H. Smart grid condition assessment: concepts, benefits, and developments. Power Electron. Drives 2016, 1, 147–163. [Google Scholar]
- Turner, M.; Liao, Y.; Du, Y. Comprehensive Smart Grid Planning in a Regulated Utility Environment. Int. J. Emerg. Electr. Power Syst. 2015, 16, 265–279. [Google Scholar] [CrossRef]
- Tu, C.; He, X.; Shuai, Z.; Jiang, F. Big data issues in smart grid—A review. Renew. Sustain. Energy Rev. 2017, 79, 1099–1107. [Google Scholar] [CrossRef]
- Munshi, A.A.; Yasser, A.-R.M. Big data framework for analytics in smart grids. Electr. Power Syst. Res. 2017, 151, 369–380. [Google Scholar] [CrossRef]
- Kovacevic, U.; Bajramovic, Z.; Jovanovic, B.; Lazarević, D.; Djekić, S. The construction of capacitive voltage divide for measuring ultrafast pulse voltage. In Proceedings of the IEEE Pulsed Power Conference (PPC), Austin, TX, USA, 31 May–4 June 2015; pp. 1–5. [Google Scholar]
- Li, N.; Zhang, J.; Chai, Z.; Wang, J.; Yang, B. The Application of Voltage Transformer Simulator in Electrical Test Training. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Harbin, China, 8–10 December 2017; Volume 113. [Google Scholar]
- Xiang, L.; Bei, H.; Yue, T.; Tian, Y.; Fan, Y. Characteristic study of electronic voltage transformers’ accuracy on harmonics. In Proceedings of the China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–6. [Google Scholar]
- Morawiec, M.; Lewicki, A. Power electronic transformer based on cascaded H-bridge converter. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 675–683. [Google Scholar] [CrossRef]
- Santos, J.C.; de Sillos, A.C.; Nascimento, C.G.S. On-field instrument transformers calibration using optical current and voltage transformes. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems Proceedings (AMPS), Aachen, Germany, 24–26 September 2014; pp. 1–5. [Google Scholar]
- Chen, X.S.; Li, Y.S.; Jiao, Y.; Lei, G.C. Distributed Capacitance Calculation Model in GIS Voltage Transformer’s Error Test. Appl. Mech. Mater. 2015, 378, 820–825. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, Q.; Lei, M. Compact system for onsite calibration of 1000 kV voltage transformers. IET Sci. Meas. Technol. 2018, 12, 368–374. [Google Scholar] [CrossRef]
- Lebedev, V.D.; Yablokov, A.A. Studies in electromagnetic compatibility of optical and digital current and voltage transformers. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Tomsk, Russia, 27–29 October 2016; Volume 177. [Google Scholar]
- Yin, X.D.; Jiang, C.Y.; Lei, M.; Xia, S.G.; Zhou, F. Research of Influence of Negative Voltage at Capacitance of Pulse Transformer of Pulse Power Generator. Appl. Mech. Mater. 2013, 2560, 1510–1514. [Google Scholar] [CrossRef]
- Frikha, N.; Huang, L. A multi-step Richardson-Romberg extrapolation method for stochastic approximation. Stoch. Process. Their Appl. 2015, 125, 4066–4101. [Google Scholar] [CrossRef]
- Polla, G. Comparison of Approximation Accuracy and time Integral Process between Simpson Adaptive Method and Romberg Method. J. Interdiscip. Math. 2015, 18, 459–470. [Google Scholar] [CrossRef]
- Li, Z.H.; Hu, W.Z. A high-precision digital integrator based on the Romberg algorithm. Rev. Sci. Instrum. 2017, 88, 045111. [Google Scholar] [CrossRef] [PubMed]
- Glushkov, D.A.; Khalyasmaa, A.I.; Dmitriev, S.A.; Kokin, S.E. Electrical Strength Analysis of SF6 Gas Circuit Breaker Element. AASRI Procedia 2014, 7, 57–61. [Google Scholar] [CrossRef]
- Lee, J.-C. Numerical Study of SF6 Thermal Plasmas Inside a Puffer-assisted Self-blast Chamber. Phys. Procedia 2012, 32, 822–830. [Google Scholar] [CrossRef]
- Ren, M.; Zhou, J.R.; Yang, S.J.; Zhuang, T.X.; Dong, M.; Albarracín, R. Optical Partial Discharge Diagnosis in SF6 gas-Insulated System with SiPM-based Sensor Array. IEEE Sens. J. 2018, 18, 5532–5540. [Google Scholar] [CrossRef]
- IEC 60044-7. Instrument Transformers Part 7: Electronic Voltage Transformers. Available online: https://webstore.iec.ch/publication/156 (accessed on 17 December 1999).
- IEC 61869-6. Instrument Transformers Part 6: Additional General Requirements for Low-Power Instrument Transformers. Available online: https://webstore.iec.ch/publication/24662 (accessed on 27 April 2016).
- GBT 20840.7-2007. Instrument Transformers Part 7: Electronic Voltage Transformers. Available online: http://www.anystandards.com/gbt/elec/20130221/22955.html (accessed on 16 January 2007).
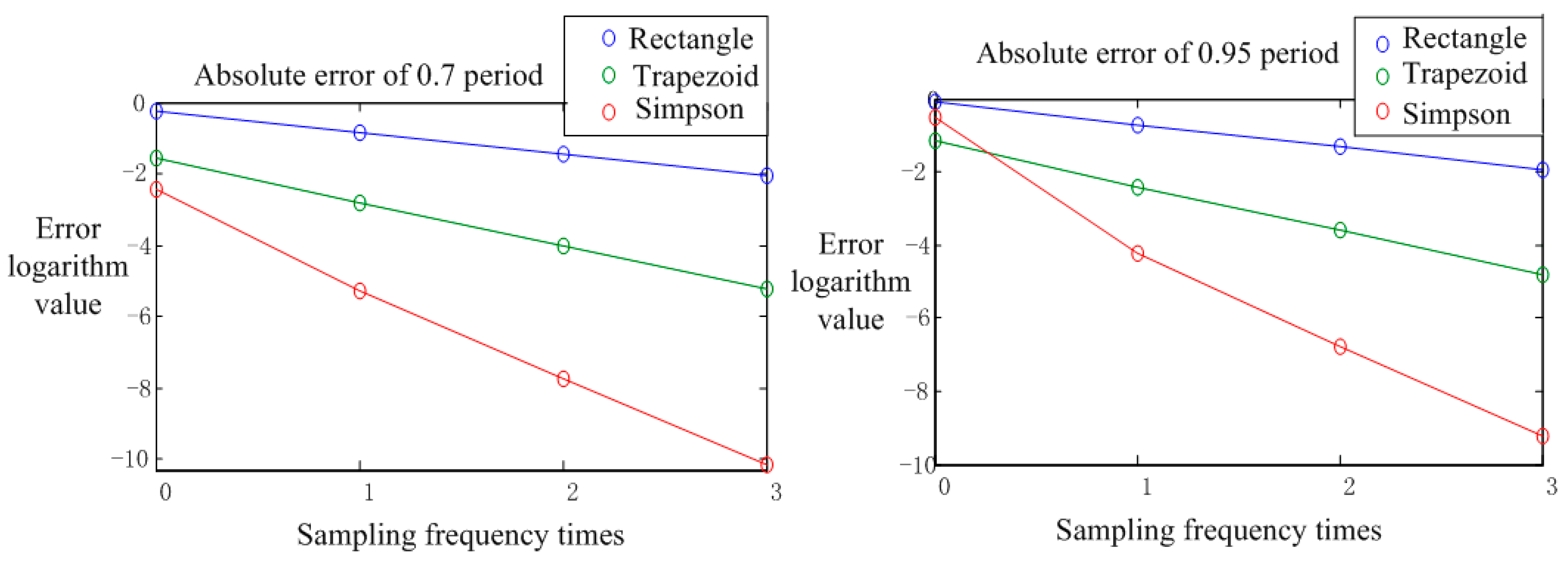

| n | Complex Rectangular Formula R(n)(0) | Complex Trapezoid Formula R(n)(1) | Complex Simpson Formula R(n)(2) | |||
|---|---|---|---|---|---|---|
| = 0.7 | = 0.95 | = 0.7 | = 0.95 | = 0.7 | = 0.95 | |
| 0 | 0.5771 | 0.8215 | 0.0273 | 0.0754 | 0.0035 | 0.32223 |
| 1 | 0.13902 | 0.19056 | 1.5769 × 10−3 | 4.0266 × 10−3 | 5.4254 × 10−6 | 5.7389 × 10−5 |
| Standard Requirements | Test Results of the Tested Electronic Voltage Transformer |
|---|---|
| Preload voltage: 230 kV | Preload voltage: 230 kV |
| Test frequency: 50 Hz | Test frequency: 50 Hz |
| Measurement voltage: 126 kV | Measurement voltage: 126 kV |
| Allowable partial discharge: ≤10 pC | apparent charge: 3 pC |
| Measurement voltage: 87 kV | Measurement voltage: 87 kV |
| Allowable partial discharge: ≤5 pC | apparent charge: 2 pC |
| Detection Project | Performance Evaluation |
|---|---|
| Voltage variations immunity tests | A |
| Voltage dips and short interruptions immunity tests | A |
| Surge immunity test | A |
| Electrical fast transient/burst immunity test | A |
| Damped oscillatory wave immunity test | A |
| Electrostatic discharge immunity test | A |
| Power frequency magnetic field immunity test | A |
| Pulse magnetic field immunity test | A |
| Damped oscillatory magnetic field immunity test | A |
| Radiated, radio-frequency, electromagnetic field immunity test | A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-H.; Wang, Y.; Wu, Z.-T.; Li, Z.-X. Research on Electronic Voltage Transformer for Big Data Background. Symmetry 2018, 10, 234. https://doi.org/10.3390/sym10070234
Li Z-H, Wang Y, Wu Z-T, Li Z-X. Research on Electronic Voltage Transformer for Big Data Background. Symmetry. 2018; 10(7):234. https://doi.org/10.3390/sym10070234
Chicago/Turabian StyleLi, Zhen-Hua, Yao Wang, Zheng-Tian Wu, and Zhen-Xing Li. 2018. "Research on Electronic Voltage Transformer for Big Data Background" Symmetry 10, no. 7: 234. https://doi.org/10.3390/sym10070234
APA StyleLi, Z.-H., Wang, Y., Wu, Z.-T., & Li, Z.-X. (2018). Research on Electronic Voltage Transformer for Big Data Background. Symmetry, 10(7), 234. https://doi.org/10.3390/sym10070234





