1. Symmetry in Crystal Structures—The Past and the Present
Perceived balance when looking at crystals suggests that the category of symmetry is comparable or related to that of harmony. Harmony, derived from the greek word “harmonia” meaning “concordance” or “unison”, is generally understood as the existence of regularity and simplicity. Recapturing this relation using today’s knowledge and possibilities shows an untapped potential. Accordingly, a search for common basic principles of harmony and symmetry actually leads to substantial intersections, which allow for qualitative as well as quantitative conclusions. The foundations of corresponding considerations have their roots already in the time before Christ [
1] and were intensively employed in the beginning of the establishment of crystallography [
2]. The present work reflects historical contributions revealing relations from harmonic principles to the evolution of symmetry in crystals from today’s point of view, leading to a quantitative discussion for isotropic atomic interactions, i.e., with metallic and ionic character of bonding. The balance of interactions is considered between a few atoms and based on that for a growing cluster of atoms in a logical conception, maximizing the number of equilibrium distances. The second part introduces an energy quantification for the cluster motifs on grounds of a single-well pair potential with flexible long- and short-range interaction, and consecutively transfers the obtained high-symmetric motifs to 3D periodic lattices. In dependence on variations of the pair interaction and related potentials, the most common lattice symmetries for elemental crystals of metals and noble gases are derived and summarized within a respective phase diagram.
For thousands of years, the first known historical records going back to the philosopher Thales of Miletus during the ancient times of the Greeks, men have raised the question “What is the universe made of?” In the same era, Democritus, student of Leucippus, stated the existence of underived, indivisible, and indestructible smallest particles of matter, the atoms [
3]. In general, cooling matter to its solid state will restrict the movement of these atoms to restricted positions within the ensemble. Depending on the chemical constituents, most ensembles will form regular patterns with a periodic long-range order, the crystals. The variety of crystal structures is vast and even within an ensemble of fixed chemical composition several modifications or phases can persist simultaneously. However, what causes the atoms to arrange in a certain structure or symmetry and why are certain structures more stable than others? To understand the interaction of atoms, it is essential to focus on the dimensions of the particles within the atoms, the positively charged nuclei made up of protons and neutrons and the negatively charged electrons in its periphery. Since the nucleus is four to five orders of magnitude smaller than the electron cloud, its structure has in most cases minor influence on the formation of crystals. The electronic structure on the other hand governs the distances and coordination of the atoms within the crystal structure and can therefore be considered fundamental in this respect [
4].
As early as in ancient Greece at the time of the philosophers Pythagoras and Plato the
five corpora regularia—tetrahedron, octahedron, cube, dodecahedron, and icosahedron (see
Figure 1)—stood for the harmony of the universe. In the 4th century BC Plato, according to whom these geometric bodies are named, described them in his work “Timaios”. A short time later, in the 3rd century BC, the Greek mathematician Euclid pursued the hypotheses of Proclus with his essay “The Elements”, especially in the 13th book, developing a comprehensive geometric theory of Platonic bodies based on the golden ratio [
5]. About 1000 years later the natural philosopher Kepler revisits the theory of the Platonic solids in his books “Mysterium Cosmographicum” and “Harmonice mundi” [
6] for his first, later rejected model of the solar system and the description of the world’s harmony in the sense of musical proportions. Weiss, known as the founder of the geometric crystallography, as well as J. G. Graßmann, father of the famous mathematician Graßmann, referred according to literature [
7] to the musical analogy in crystallography. Graßmann states, in respect to ratios of musical tones and segments formed by faces of the same zone of crystals: “crystal polyhedron is a fallen asleep chord—a chord of the molecular fluctuations made in time of its formation”. In the late 1890s, the famous crystallographer Goldschmidt further extended the laws of harmonic ratios from crystals to other fields in his “Theory of Harmony”, among others, the theory of sounds [
2,
8,
9]. In 1884, the German mathematician Klein wrote his book “Vorlesungen über das Ikosaeder” (“Lectures on the Icosahedron” [
10]), in which he elucidates this highest symmetric representative of the Platonic solids as the foundation of geometry and related mathematical fields, such as group theory and the theory of differential equations. Recently, the scientists Curl, Kroto and Smalley and the physicist Shechtman received the Nobel Prize for Chemistry for the discovery of the Fullerene C
in 1996 and for the discovery of quasi-crystals in 2011, respectively, both structures with icosahedral symmetry.
Symmetry in physics today is generally defined as the property of a system to be invariant with respect to particular transformations. Each symmetry reduces the necessary amount of information for the complete description of the system. With regard to an infinitely extended crystal, the structure is coming into congruence with itself after application of the transformation. In 3D space, this applies first and foremost to the translations, which—except for aperiodic crystals such as quasi-crystals and modulated phases [
11]—regularly reproduce the structural units in the three dimensions. The complete set of translations determines the translational lattice of a crystal structure. Starting from an arbitrary point of this lattice, there is an infinitely large quantity of pairwise nonparallel translational triplets or lattice vectors. Due to the redundancy within the volumes, it makes sense to restrict the description to as small a volume unit as possible. In addition to the translations, the angles between two lattice vectors reflect further symmetries of the grid. For lattice vectors of equal length, rotations of angles
and
as well as their multiples can map the lattice on itself. These symmetries additionally reduce the volume required for the complete structural information and lead to seven possible lattice types or systems for the description of all crystals. They also provide the basis for the combination with further compatible symmetry operations such as mirror planes. In order of precedence, the principle of visible symmetries of these angles to avoid redundancy is stronger than the principle of volume reduction of the translational cell, which manifests itself in additional lattice points within the cell, i.e., centering, and leads to the 14 Bravais Lattices. Summarizing all possible symmetry combinations within 3D space in groups, the so-called 230 space groups represent the complete set (for a detailed elaboration see e.g., [
12]).
This common starting point to describe the symmetry of crystal structures uniquely classifies existing crystals. Nevertheless, it tells little about balance, stability, and formation of symmetry during the initial steps of crystal growth. In this respect, it is more beneficial to refer in a bottom-up approach to the smallest building blocks and atomic configurations, which gradually build up the translations and ultimately form the space-filling crystal. This connection of clusters as
a bridge across the disciplines of physics and chemistry has been outlined for instance by Jena et al. [
13] on the basis of examples in the different fields. The Platonic Solids as representatives of the highest symmetry, i.e., with the greatest possible number of transformation invariances as discussed in the last section, play a central role in this picture. The five polyhedra can be divided into three symmetry groups, the tetrahedral group with the self-dual tetrahedron, the hexahedral group with cube and dual octahedron, and the icosahedral group with dodecahedron and dual icosahedron. (Dual polyhedra have interchanged vertices and faces. Duality preserves the symmetry and is closely related to reciprocity, chirality, and polarity.) Only polyhedra from the first two groups can be arranged in a space-filling manner and commonly occur in three-dimensionally periodic crystals of common unary equilibrium phases (see
Figure 2), although this does not hold for the tetrahedron as exclusive motif. For the last group, at least one coexisting non-platonic atomic configuration is necessary, which by thermodynamically means would require energetic degeneracy of the additional non-platonic atomic configuration or a second atomic species as further degree of freedom to be adequate for the ground state structure, as is the case e.g., in quasi-crystals, metal-organic frameworks, or the more complex binary intermetallic phases of the Frank-Kasper group (topologically regarded as close-packed spheres [
14] combining periodic and aperiodic symmetry). In general, a high symmetry entails a high degree of degeneracy for the atoms in the structure. Thus, high symmetric structural coordination permits a maximum of inter-atomic equilibrium distances and thus energetically favors the ground state, as discussed in the following section.
2. Atomistic Crystal Growth Process
The following consideration for the growth of a crystalline solid is based on the assumption that all constituting particles are atoms of equivalent type, which form a cluster step by step, i.e., atom by atom, similarly to an evolutionary structure prediction algorithm and in this respect much simpler than recent general approaches for complex crystal structures [
15]. In the present picture, the only reason for the cohesion of the cluster is the distance-dependent two-particle interaction or respective pair potential
with a stable minimum, e.g., a Morse type potential. An overall minimization of the binding energy of the entire cluster as the sum of all two-particle interactions defines the ground state of the cluster, with total energy
for atoms
i,
j at positions
,
. For the infinite crystal, this approach is similar to the Madelung sum [
16] without the alternating sign of consecutive shells. In addition to the pair energy at equilibrium distance
, the total energy depends in particular on the geometric spacing ratios of the smallest structural units and the according development of the pair potential for deviations from the equilibrium distance.
The presence of one initial atom, which can be regarded as an isolated 0-dimensional point, is not yet subject to any interaction. The second atom entering the cluster, is arranged at the equilibrium distance around the first atom. Seen within the three-dimensional space, each point of a spherical surface with radius fulfills the condition of the lowest total energy. By defining a position, the first dimension is spanned and a bond is formed, which mediates the distance of both atoms.
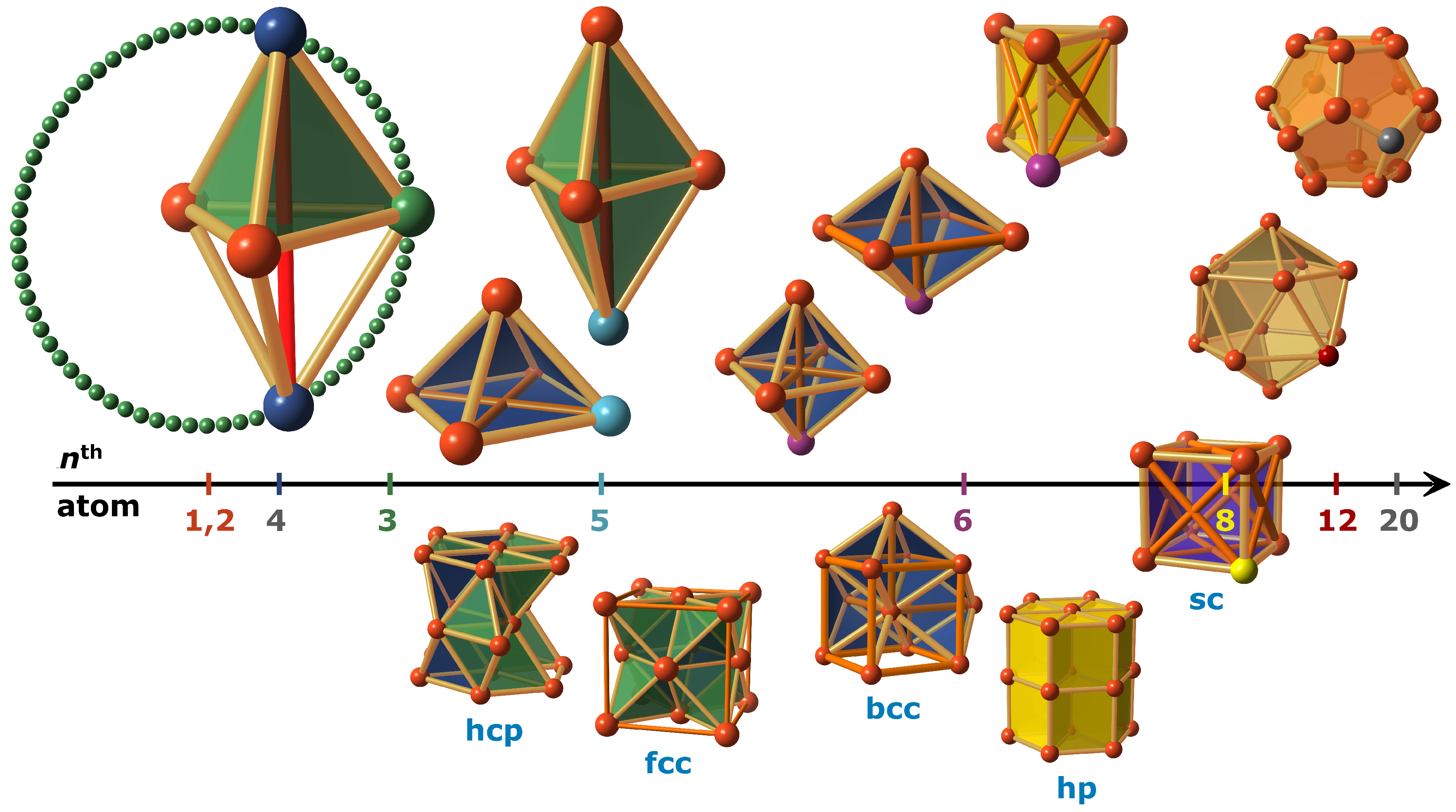
A third added atom has the freedom of a circular orbit around the bond between the first two atoms for energy-favored positioning (see
Figure 3). A total energy of three degenerate bonds is realized according to the equilibrium distance of the two-particle potential. An equilateral triangular surface is formed after positioning, which spans the second spatial dimension.
The following fourth atom can similarly fulfill the condition of minimum energy by placing it at one of the two tetrahedron positions along the orthogonal axis of gravity of the equilateral triangle, thereby implementing three further, i.e., a total of six, two-particle interactions at equilibrium distances. The formed tetrahedron is the first volumetric unit in three dimensions and has no inversion symmetry. It has an initial volume of
and an according density result, although there is no 3D crystal structure consisting of tetrahedra only. The densest known packing of regular solid tetrahedra amounts to 85.6% in the form of double-tetrahedra arrangement [
17], neglecting energy considerations in between the tetrahedra.
For the fifth atom in this series, the limitations of 3D space do not allow this atom to form all new bonds at equilibrium distance. The degeneration for all bonds in the most stable ground state is lifted. For the first time, a compromise must be found for the positioning, which now depends on the distance-dependent course of the pair potential. Two cases are possible: On the one hand, the fifth atom can attach itself to the second tetrahedral position of the original equilateral triangle, which results in three further equilibrium bonds. In this configuration, there is a single long bond (
) between the tips of the resulting di- or double-tetrahedron that affects the balance of the atomic bonds. A shortening of this bond necessarily results in a shortening of the six equilibrium bonds to the tips or an elongation of the three central equilibrium bonds (see
Figure 3). Energetically, the high potential gradient for the long distance bond (energy gain) counteracts the potential increase for changing the other equilibrium bonds (energy loss). On the other hand, the fifth atom can also be added to one of the faces of the tetrahedron forming a square pyramid. This configuration entails two further equilibrium distances and two additional moderately longer distances (
, diagonals of the square). Depending on the course of the pair potential, either the pyramid configuration or the configuration of the double-tetrahedron is energetically favored.
When a sixth atom is added to the cluster, it can continue the tetrahedron principle and attach itself to one face of the double-tetrahedron. Three new equilibrium bonds and two further longer bonds now also play a role in the total energy balance. If the pyramid configuration is retained, an octahedron, another highly symmetric platonic body again with 12 equilibrium distances and three moderately longer bonds (
) or its bcc variant with eight equilibrium distances, five moderately longer bonds and two longer bonds is formed (
Figure 3). The prism is a further non-platonic possibility to place the sixth atom. With only nine equilibrium distances and six moderately longer bonds on the squares, it always has a slightly higher total energy than the regular octahedron, as holds for the bcc-octahedron. Due to the small number of longer bonds, a phase transformation from an original tetrahedron configuration is immediately possible, again depending on the specific pair potential. Further symmetry transformations can occur for all other platonic bodies, i.e., the dice at eight atoms, the dodecahedron at 12 atoms, and the icosahedron at 20 atoms. The dodecahedron or icosahedron is even more stable if filled with an additional atom at the center (see
Section 3).
In summary, this consideration is governed by the principle of a maximum number of equilibrium distances. This intrinsically delivers a high degree of packing density. Due to the restricted nature of three-dimensional space, the geometrical atomic arrangements in the crystal growth process are limited. The principle leads to the smallest configurations or structural units for a few atoms that continue in the crystal up to the macroscopic scale and describes very well the crystal structures formed by elements. From the combination of tetrahedral and octahedral configuration, a dense crystal lattice of hexagonal close-packed symmetry (hcp) with stacking sequence ABAB or of face-centered cubic symmetry (fcc) with stacking sequence ABCABC is formed. The ground state symmetry and according natural stacking sequence may already result from the structural decision of the fifth atom towards the hexagonal anisotropy given by the defined direction of the double-tetrahedron axis or the octahedral domination and respective cubic symmetry. Tetrahedral units can be dismissed at the cost of octahedral distortions to form the macroscopic crystal solely of octahedra as is evident in the body-centered cubic lattice (bcc). Although surface energy has been neglected in the picture so far, qualitatively the structural freedom of smooth nucleus surfaces is expected to favor certain crystal symmetries but will play a decreasing and rapidly vanishing role for growing crystallites. An early phase transformation to the configuration of the cube or the prism leads to the simple cubic lattice (sc) and the simple hexagonal lattice (hp). Filling 3D space with dodecahedra or icosahedra is not possible without further degrees of freedom. With the help of further structural units, this is in principle feasible (e.g., quasi-crystals, metal-organic frameworks), but leads to a considerably smaller number of equilibrium bonds per volume.
3. Pair Potentials and Structural Stability
The discussed atomistic crystal growth process is based on the assumption of a universal pair potential
to account for all interactions between the atoms [
18]. Sophisticated three- or many-body interactions or their projection into the pair potential in terms of a double-well with metastable second minimum to introduce angle specific atomic alignments, have not been necessary to derive the rigid and high-symmetric lattices in the previous section. Although this simplification entails restrictions in describing certain non-pair interaction based effects, such as planar atomic arrangements for clusters of a few atoms known for instance for Au
up to
[
19] or B
up to
[
20]. The Morse Potential [
21] is a commonly used pair potential with one stable minimum that includes a harmonicity of vibrational modes, the temperature dependence of the equilibrium distance as well as the description of unbound states and bond breaking. The form with zero bond-dissociation energy
is usually written as
with well-depth
, equilibrium bond distance
, and the reciprocal well-width
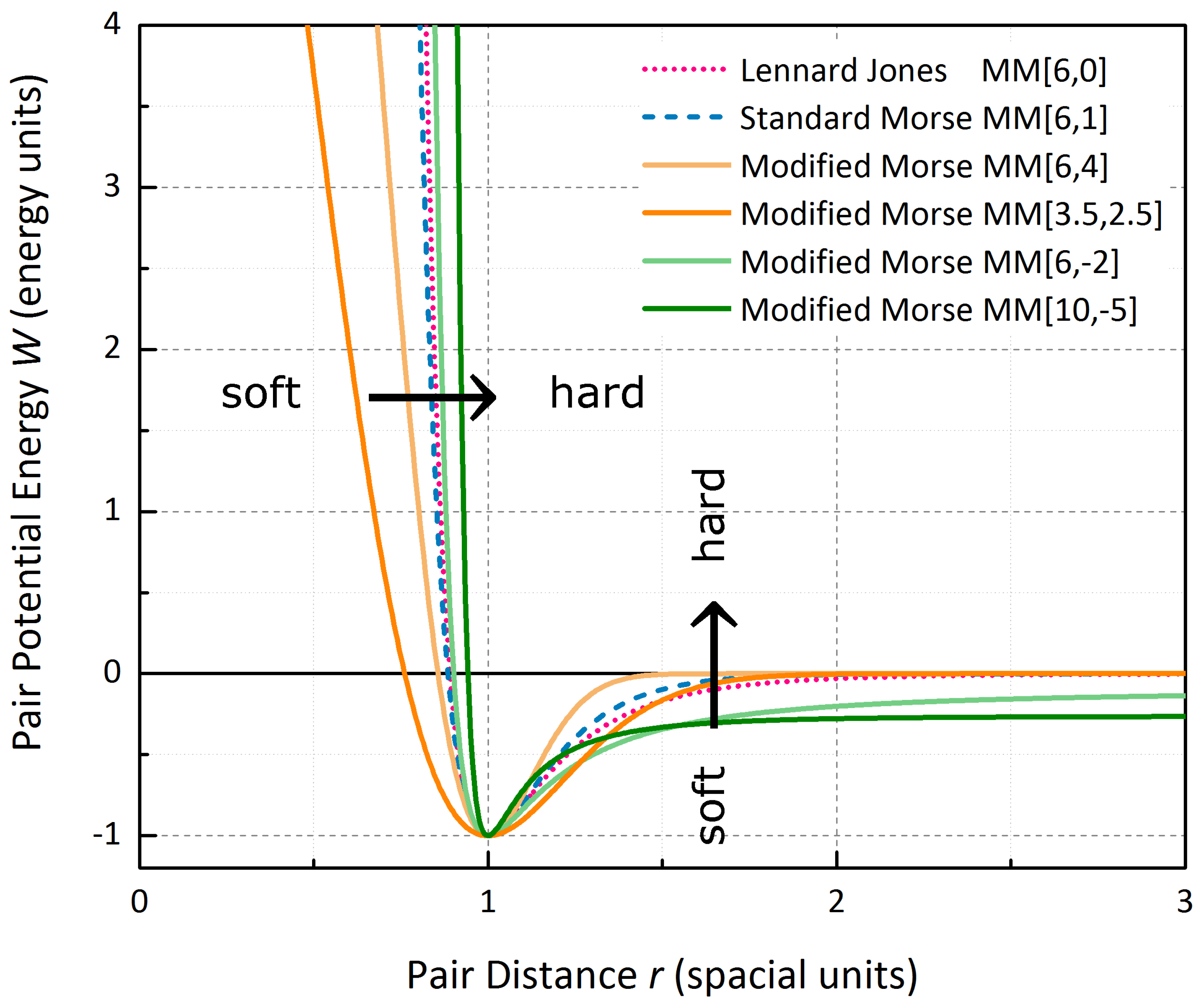
a. The potential is very rigid. In case of unary phases
and
act as two universal scaling factors, for the total energy as well as a homogeneous lattice expansion. The only parameter that qualitatively varies the bond network is the reciprocal well-width
a, so that for comparison
will be fixed for the following considerations and
will be used to classify a specific Morse Potential. To provide more flexibility, and in particular to control long- and short-range interaction independently by a second qualitative parameter
, a Modified Morse Potential
has been introduced [
22], with
for
and
for
. For
the original Morse Potential is retained, whereas
yields the well-known Lennard-Jones Potential [
23].
Extensive modeling has been performed for Morse as well as Lennard-Jones type potentials and clusters of various sizes [
24]. As discussed in [
22], both types are mid-ranged pair potentials that predominantly favor icosahedral structures with few exceptions of decahedral or face-centered cubic symmetry for certain “magic” numbers. Generalizing this conclusion for increasing cluster size towards the limit of a 3D periodic crystal, the icosahedral symmetry cannot prevail and in the case of large clusters, the face-centered cubic symmetry would present the only stable structure solution for these potentials (—although for the infinite crystal we find in addition a significant parameter range for hcp symmetry, see Figure 5). In contrast, with the separation of short- and long-range interaction, the Modified Morse Potential offers the freedom to find new stable structures. For clusters up to a size of 210 atoms, this increase of stable structures has been demonstrated for two examples [
22]: a potential with softer long-range and harder short-range interaction
, and a potential with harder long-range and softer short-range interaction
.
The following results present the extension and related energy optimization for 3D periodic crystals. They provide a bridge from the pair potential cluster modeling towards the crystallographic systematization of Ruhnow [
25], who derives five basic atomic arrangements for unary phases: sc, bcc, fcc, hcp, and the diamond arrangement. According to Ruhnow, about 100 atoms are necessary for the nucleus to establish the energetically favored stable structural state, following the principles of simplicity, high symmetry, and dense packing. He further connects the high symmetric structural motifs in crystals to specific atomic shapes [
26]. In contrast, the Platonic solids or high symmetric structural units in the present study occur without any inner-atomic structure and solely based on the assumption of two-particle interactions and a minimum of total energy.
3.1. Stability of Structural Motifs
We used the Modified Morse Potential in comparison to the Standard Lennard-Jones (
) and Morse (
) Potentials to perform structural relaxations of the Platonic Solids as well as high symmetric non-Platonic structural motifs.
Table 1 summarizes the results of the relaxation, including the deviation of the relaxed nearest neighbor bond length
from the equilibrium distance
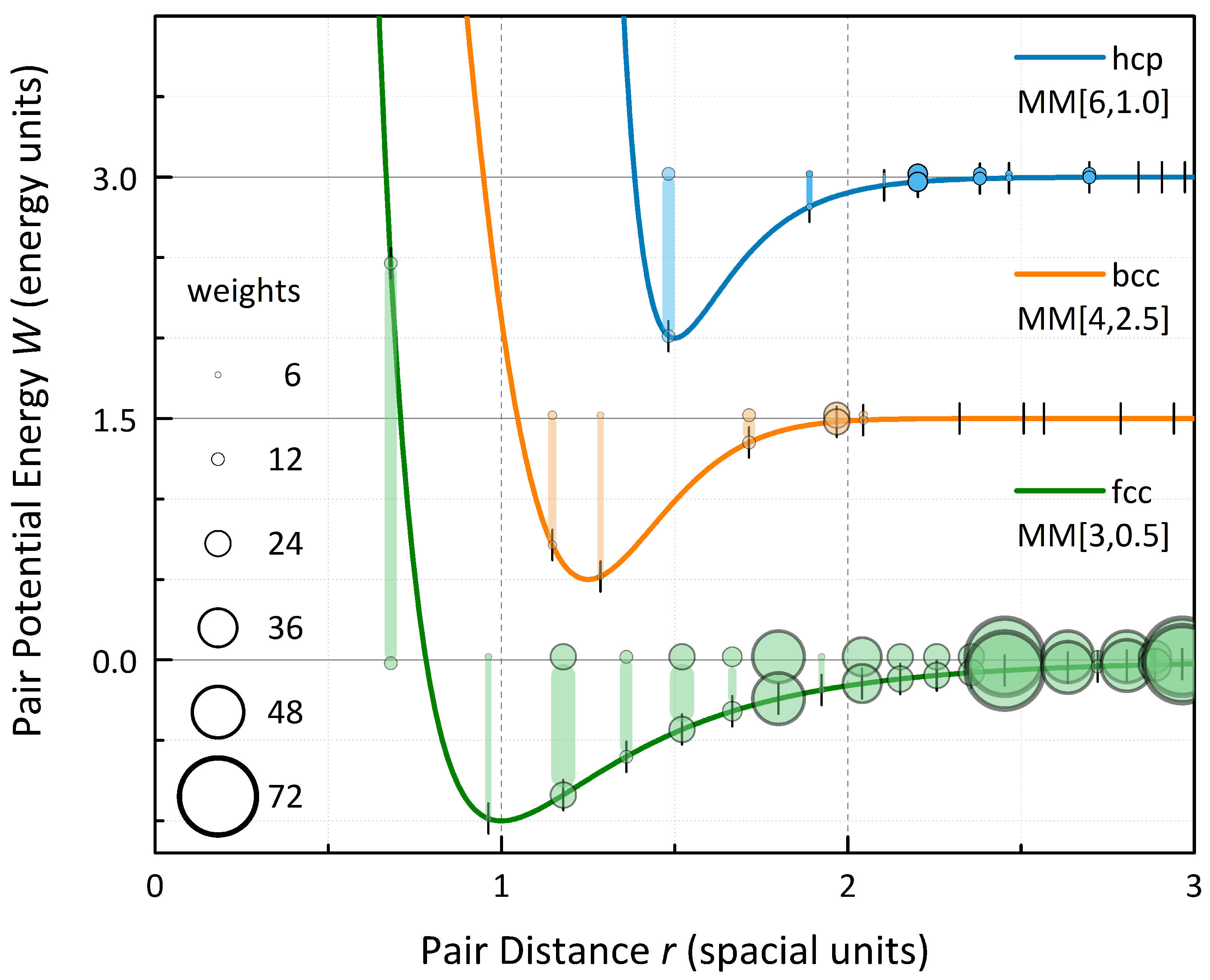
spacial units. Two specific examples,
with a comparably soft short-range and
with a hard short-range and wide long-range interaction (see
Figure 4), demonstrate how the stability of the motifs is severely dependent on the course of the pair potential.
Since all contributions above the equilibrium distance
stabilize the cluster, in general an increase of binding energy with increasing number of atoms can be expected. The rigid geometry of the high symmetric motifs, most dominantly the next-nearest neighbor contributions and the specific potential value at their pair distance, however, have a strong impact on the stability of certain motifs. As shown in
Table 1, smaller clusters up to the octahedron exhibit similar total energies with respect to changes in the pair potential, whereas the dodecahedron can more than double its total energy in case of a wide long-range interaction (
). It can even replace the icosahedron, with or without center atom, which constitutes the most stable motif for most potential variations. For the potential
, the cube can also supersede the octahedron, which is more stable in all other cases.
Regarding the leading contribution of the nearest neighbors, it is not surprising that the most remarkable relaxations take place for the soft short-range. Next to the dodecahedron, the cube is most affected and thus less rigid, whereas the icosahedron shows unexpectedly small relaxation.
3.2. Stability of Unary Structures
In the following stability discussion the potential-dependent total energy is compared for the extension of the motifs to high-symmetric unary-type 3D lattices, namely the five basic arrangements sc, bcc, fcc, hcp, and diamond as well as the hp symmetry as a sixth representative. With the exception of double hexagonal close-packed (dhcp) symmetry for some elements of the lanthanides and actinides, this set makes up the vast majority of elemental crystal structures of metals and noble gases (about 83%) that comply with isotropic interactions [
27]. For reasons of completeness the diamond-type of structure is included in this comparison, although it is a consequence of non-isotropic covalent bonding. The inherent high symmetry for the chosen set provides rigid structures with only one free parameter, specifying the homogeneous structural expansion for a given pair potential.
The principle of close-packing corresponding to a maximum number of equilibrium distances is evident for 3D periodic crystals as well as clusters. The relaxation is much more prominent than for the isolated motifs, since long-range interactions favor a shrinking and balance the energy gain of the first coordination shell.
It is evident from the calculated data that in terms of energetic stability, the structures constitute three groups (see
Table 2): the close-packed fcc and hcp together with bcc as most stable group, the primitive sc and hp of intermediate stability and the diamond structure with least binding energy. Within the first group, the Standard Morse Potential and the Lennard-Jones Potential slightly favor hcp over fcc, whereas bcc is dominant for a soft short- and hard long-range interaction (
) and fcc wins for a generally broad potential (
). Within the second group, the hp symmetry outperforms the sc symmetry for all potentials taken into account. In terms of relaxation, the diamond double-fcc symmetry is most rigid for the considered potentials with the exception of the very broad
potential, in which case the structure relaxes even more strongly than close-packed fcc and hcp lattices, which overall show good rigidity. Most flexibility on the other hand is obtained for sc symmetry. Whereas bcc relaxes stronger than hcp in the case of Standard Morse and Lennard-Jones Potentials, this reverses for the chosen Modified Morse Potentials, evidently due to the soft short-range interaction.
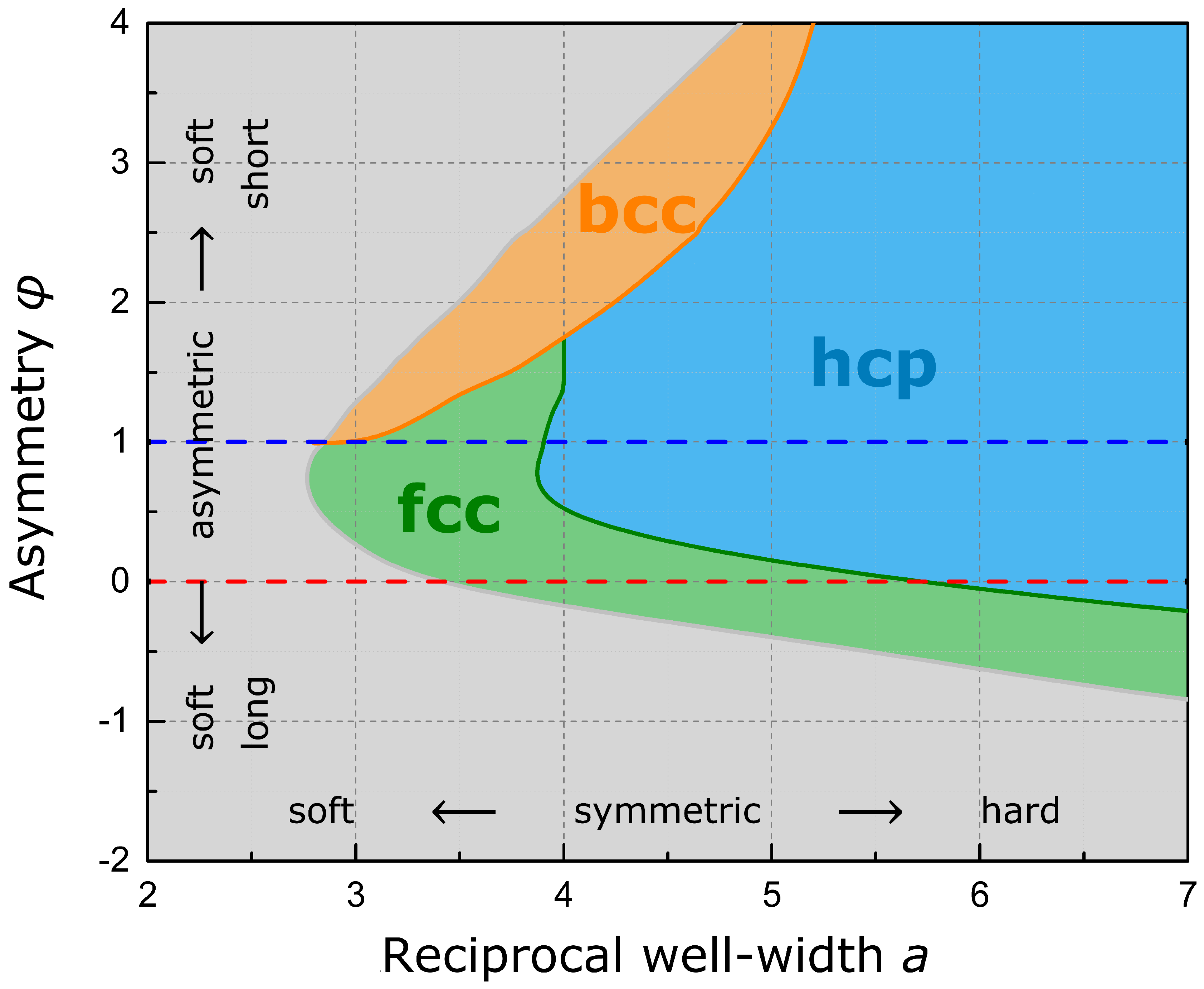
In order to determine the equilibrium phases for a larger span of pair potentials, total energies have been optimized in dependence on the relaxational degree of freedom for the six high-symmetry lattices in focus. The phase diagram given in
Figure 5 summarizes the results for a large grid of parameter pairs
. As is evident from the diagram, both the Standard Morse Potential and the Lennard-Jones Potential cannot stabilize the bcc symmetry—e.g., for alkali metals or transition metals of the vanadium and chromium group. Only a soft short-range, reflecting open electronic shells and a decreased Pauli repulsion, and hard long-range interaction, reflecting increased shielding, will provide this lattice symmetry. This dependence on the potential originates from the fact that for the bcc structure the first two shells are comparably close in distance and comprise two atoms more (in total 14) than the first shell of fcc and hcp (see
Figure 6). A soft short-range interaction is thus beneficial for these two bcc shells. In addition, a hard long-range interaction neglects higher shells, which would favor the consecutive fcc and hcp second and third shells, whereas the third bcc shell is distant and in many way less stabilizing in comparison. A soft long- and short-range interaction and a generally broad well favor fcc, which occurs in particular within the copper and zinc group as well as the noble metals, whereas a symmetric potential with hard interactions favors hcp. Thus, the form of the pair potential, in particular the asymmetric shape of the minimum, favors one or the other structure motif or lattice symmetry, whereas energy partitioning enforced by the strict geometric structural framework governs the equilibrium cell parameters. Considering the close-packed phases, more sophisticated stacking configurations might present additional equilibrium regions which are not captured by the presented phase diagram, in particular in between hcp and fcc. This may comprise stacking sequences like dhcp as well as ordered stacking-faults.
The model may also be used to study the behavior of metals under compression. In the presence of pressure, the atomic relaxation towards equilibrium distances is restricted by boundary condition of stress and strain. Again, the balance between long- and short-range interaction will play a crucial role in determining which lattice symmetry prevails. Examples in the literature are scarce, e.g., the behavior of magnesium [
28] which under compression transforms from hcp to bcc, of thallium [
29] which transforms from hcp to fcc, and of calcium [
30] which transforms from fcc to bcc and then to sc.
The here considered motifs and lattices are of high symmetry and thus low complexity in terms of internal structural degrees of freedom. If symmetry descends, more and more free lattice and structure parameters dominate the arrangement of distances for the equilibrium structure. The assessment of these relaxational degrees of freedom has been in the focus of crystallography for many decades, since the first structures have been determined up to recent attempts from the atomic level [
31], and even with mathematical schemes to generate complexity like cellular automatons [
32]. The presented considerations may give rise to optimization of pair potentials beyond the scope of the Standard Morse Potential, which is widely used, e.g., in Molecular Dynamic Simulations [
33] and Bond Valence Methods [
34]. Enhanced potentials with a broad flexibility, which can be determined from structural data of large structure databases like the ICSD [
35], may then present a convenient way to tackle free internal parameters in structure determination, without computationally expensive quantum-electronic calculations like density functional theory (DFT, see e.g., [
36]) or modern synchrotron methods like Resonant X-ray Diffraction [
37,
38].
5. Conclusions
We presented an atomistic crystal growth model for growing atomic ensembles of the same species starting from the first few atoms and derived a generalization of these units for 3D lattice symmetries of common elemental crystal structures, namely hcp, fcc, bcc, sc, hp and the diamond structure. The model is based on a single well pair potential with isotropic interaction, which is well suited for metallic bonds and noble gases. The stability of the preferred motifs depends on the specific profile of the pair potential, whereas certain profiles may promote early-state phase transformations towards other basic motifs—connected to a specific number of atoms—within the growing cluster.
This picture of cluster formation and crystal growth may be augmented by assigning each cluster a surface. Minimizing the surface energy would be equivalent to a minimum of surface triangles for a cluster. Another enhancement would be the treatment of binary and ternary structures by considering pairwise distinct two-particle interactions. These considerations are beyond the scope of the present work and might be the subject of another article.
We summarized our deductions with a discussion of short- and long-range interaction using the flexibility of a Modified Morse Potential and revealed dependencies to entail specific lattice symmetries. Next to exemplary equilibrium relaxations of hcp, fcc and bcc typical signatures, a phase diagram of stable lattice regions was presented. It is concluded that only a soft short-range and hard long-range interaction can provide the bcc lattice symmetry, whereas a soft long- and short-range and a generally broad will favor fcc and a symmetric potential with hard interactions favors hcp.
Although the Standard Morse Potential is the predominantly used potential in up-to-date atomistic dynamic and bond valence simulations, the authors believe that the range-flexibility of the Modified Morse Potential would highly improve related data analysis and structure predictions. In addition, apart from computationally expensive DFT calculations, the use of enhanced pair-interaction potentials as constraints in conventional structure refinement may increase the accuracy of free internal atomic structure parameters significantly.
In this work we investigated the formation of structural units from simple pair-interaction principles. High symmetry motifs, among them the Platonic Solids, are energetically favored due to a maximum number of equilibrium distances being equivalent to the principle of close-packing. These motifs reflect a balance of atomic distances within the equilibrium atomic arrangement and thus exhibit, according to Platon, a geometric harmony within elemental crystal structures, or in the words of the famous scientist Poincaré:
“It is the harmony of the diverse parts, their symmetry, their happy balance [...] that permits us to see clearly and to comprehend at once both the ensemble and the details”