1. Introduction
Fractals are popular research subjects not only in mathematics but also in physics, chemistry, biology, social science, computer science, engineering and economics. There have been many studies on fractals in the last decade (for details see [
1,
2,
3,
4]). Most classic fractals have two basic features: the first one is self-similarity, and the second one is that their Hausdorff dimensions are larger than their topological dimensions. The Sierpinski Gasket, which is named after Waclaw Sierpinski, is one of the leading examples of fractals. The basic characteristics of the Sierpinski Gasket,
S, are given as follows:
This fractal is the attractor of an iterated function system (IFS). An IFS on a metric space
X is a finite family
of contracting maps
whose contracting factors are
for
. It is well-known that if
is an IFS on a complete metric space
X, then there is unique non-empty compact subset
K of
X such that
The set
K is called the attractor associated with the IFS (for the construction of
S as the attractor of an IFS see Equation (
1)).
The area of the Sierpinski Gasket is zero and its fractal dimension is non-integer. The topological dimension of this fractal is one. It satisfies the open set condition and thus its fractal dimension, the unique real solution of the Moran equation
is
.
That is, Hausdorff dimension of the Sierpinski Gasket is larger than its topological dimension. Therefore, this set exhibits all of the classical properties of fractals.
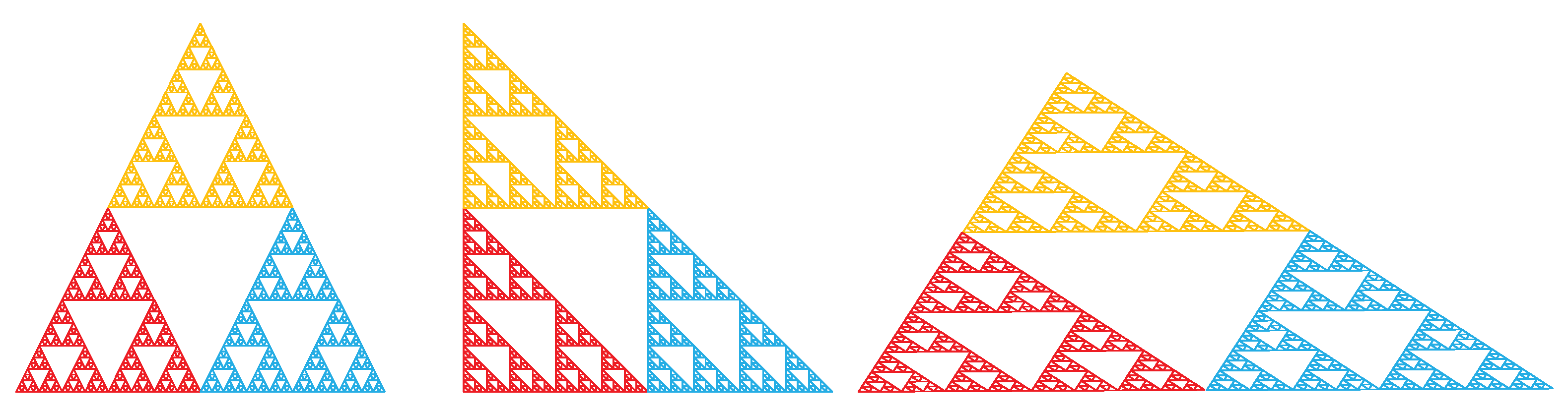
However, none of the above listed features depend on whether the Sierpinski Gasket is constructed on the equilateral, isosceles, scalene triangles or not. The only difference that will occur is the coefficients of the functions with respect to IFS. In other words,
S, which is constructed with the vertices
and
, is the attractor of the iterated function system
such that
It is obvious that if we choose
and
, then we get the classical Sierpinski Gasket as the attractor of the IFS. If these coefficients are taken as
and
, then the right angled Sierpinski Gasket becomes the attractor of the IFS (see
Figure 1).
Besides these characteristics, different geometric properties can be examined by defining the intrinsic metrics on the equilateral, isosceles and scalene Sierpinski triangles. It is well-known that there are different ways to define the Sierpinski Gasket apart from the notion of IFS. By using these alternative definitions, various different properties of this fractal can be obtained. As one of them, the construction of the intrinsic metric on
S can be given in several ways (for details see [
5,
6,
7,
8,
9,
10]).
The general definition of the intrinsic metric on
S is expressed as follows:
for
(for details see [
11]). Throughout this paper, we will only deal with the intrinsic metric obtained from the code representations of points on
S. In [
12], the intrinsic metric on the equilateral Sierpinski Gasket is explicitly formulated as follows:
Definition 1. Let and be two representations respectively of the points A and B on the equilateral Sierpinski Gasket such that for and The distance between A and B is determined by the following formula:where Note that, since there exists at least one shortest path between any two points, the metric
d defined in Equation (3) is a strictly intrinsic metric on the code set of
S ([
12]). Moreover, in [
13], we classify geodesics of the Sierpinski Gasket by using this metric.
In this paper, we give a general formula for the case of different edge lengths of the triangle. That is, we obtain a formula for the intrinsic metric on the code set of the scalene Sierpinski Gasket in Theorem 1. Afterwards, we show the relationship between the coefficients of formulas computed for the equilateral, isosceles and scalene Sierpinski Gasket. Finally, in Propositions 3 and 4, we get some important geometrical properties by using these formulas.
In the following section, we express some basic concepts that are needed to describe the metric given in Equation (
4).
2. Preliminaries
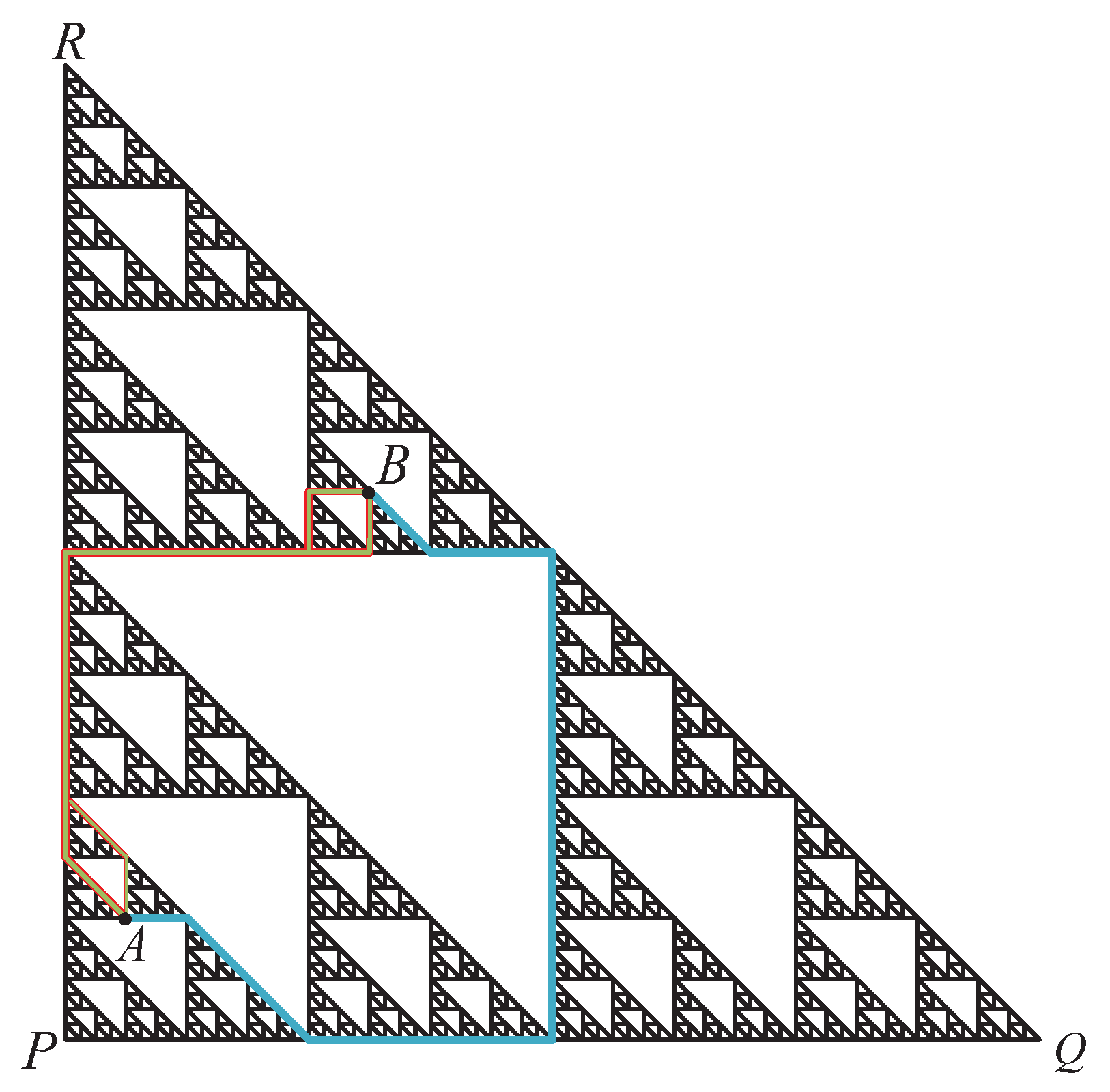
Let us fix
where
for
. The bottom-left part, the bottom-right part and the upper part of
are denoted by
,
and
respectively. Thus, we have the sub-triangle
Hence, the code set of
S is the union of the code sets
and
(see
Figure 2).
From now on, we will define the code representation of a point on
S by using these code sets. The construction above shows that
is a nested sequence of sets such that
The Cantor intersection theorem states that the infinite intersection
is a point on
S, which we denote by
A. A code representation of
A is the infinite word
where
. Note that, if
is the intersection point of any two sub-triangles of
, then
A is called a junction point of
S. In such a case,
A has two different code representations of forms
and
where
and
. (If a point is not in this form, then it has a unique code representation. For example, the vertices
and
R have the code representations
and
respectively). Let
,
and
.
and
are different code representations of
K,
and
are different code representations of
L,
and
are different code representations of
M. Moreover, the code set of all points on the line segment connecting the vertices
P and
Q is
the code set of all points on the line segment connecting the vertices
P and
R is
and the code set of all points on the line segment connecting the vertices
Q and
R is
For the general case, let us fix
where
for
. We now consider the sub-triangles
and
. Let
,
and
. Similarly,
and
are different code representations of
,
and
are different code representations of
,
and
are different code representations of
. Furthermore, the code set of all points on the line segment connecting the vertices
and
is
the code set of all points on the line segment connecting the vertices
and
is
and the code set of all points on the line segment connecting the vertices
and
is
Moreover, it can be easily seen that
owing to the fact that
,
,
and
.
3. The Intrinsic Metric on the Scalene Sierpinski Gasket
Consider a scalene Sierpinski Gasket with vertices and . In the following proposition, we formulate the distance between two different points on a scalene Sierpinski Gasket by using the code representations of these points. Then a special case of this formula will be given on the isosceles Sierpinski Gasket and it will be associated with the formula given in Definition 1 on the equilateral Sierpinski Gasket.
Theorem 1. Suppose that the points A and B on the scalene Sierpinski Gasket have two representations and respectively such that for and Then the distance between A and B is determined by the following formula;such thatwhereand and . Note that we only give a sketch proof since it is long and tedious to show all the cases. However, different cases can be shown in a similar way.
Proof. Suppose that A and B, which are two different points of the scalene Sierpinski, have the code representations and respectively. It is obvious that there exists at least one natural number s such that . Thus, we have and where Let and (or and ). In this case, the shortest paths between A and B must pass through either the point or the line . If and (or and ), then the shortest paths between a and b must pass through either the point or the line . If and (or and ), then the shortest paths between a and b must pass through either the point or the line .
Case 1. Firstly, we will deal with the shortest paths that pass through the point . We thus have and or and . Let us only investigate and because the proof is the same for and . The union of a path between A and and a path between and B gives a path between A and B. If we compute the length of the shortest paths between A and , then the paths between and B can be obtained using a similar argument.
Given and let where . Then we must compute the length of the line segment . Thus, the length of the shortest paths between A and is for some . (For the case and , we actually get ).
If , then we must compute the length of the line where to obtain the length of the shortest path between A and . Hence, this length equals to for some (that is, if and , then ).
If
where
is the intersection point of the sub-triangles
and
, then there are two shortest paths between
A and
. These paths are the union of the line segments
and
or the union of the line segments
and
. So, the length of these paths are exactly obtained as
(In this case,
a has the code representations
or
. For
, if
and
, then we obtain
and
or similarly if
and
, then we get
and
).
Let us now consider
. Notice that, the multiplier
is not included in the computation of the length of the shortest paths between
A and
since
. If
or
, then we must compute the length of the line segment
or the length of the line segment
to get the shortest distance such that
,
where
. In this case, we get
or
respectively for some
.
For the case
, where
is the intersection point of the sub-triangles
and
, there are two paths to obtain the shortest distance between
A and
as before. These paths are the union of the line segments
and
or the union of the line segments
and
. The length of these two paths is
This procedure also continues for smaller triangles. By splicing these shortest paths between “A and ” and “ and B”, we can determine the length of the shortest paths between A and B passing through the point .
Case 2. Now, we will investigate the length of the shortest paths passing through the line segment . In this case, we must figure out the shortest paths between “A and ” and between “B and ”. Note that we can compute the lengths of these shortest paths in the same way as the Case 1. As we add (the length of the path ) to these lengths, we obtain the length of the shortest path passing through .
We now consider the shortest paths passing through the line segment . The shortest paths (thus the corresponding length) between “A and ” and between “B and ” can be obtained similarly. We get the length of the shortest path passing through by adding the length of the path , which equals to , to these lengths.
Also, we can compute the length of the shortest paths passing through the line segment . In this sense, this length is obtained by adding to the length of the shortest paths between “A and ” and between “B and ”.
As a result, the minimum of the lengths obtained from Case 1 and 2 gives us the length of the shortest paths between A and B. □
Remark 1. The length of the shortest paths passing through one of the points , and is the first sum in Equation (4), . And the second value in Equation (4), , gives us the length of the shortest paths passing through one of the line segment , and where is the length of the line segment , and respectively. The metric given in Theorem 1 is equivalent to the metric given in Equation (
2) due to the fact that the metric
d is defined as the minimum of the lengths of the admissible paths connecting the points
A and
B of the scalene Sierpinski Gasket.
The proof of the following proposition is similar to the proof in [
12]. Thus the proof here will be omitted.
Proposition 1. The metric d defined in Theorem 1 does not depend on the choice of the code representations of the points.
Suppose that the points A and B on the isosceles Sierpinski Gasket have the code representations and respectively where for and In Theorem 1, if we choose and , then the distance formula on isosceles Sierpinski Gasket will be as follows:
Corollary 1. The distance between A and B is defined by the following formula:such thatwhereand and . Note that if we take and , then the distance formula on equilateral Sierpinski Gasket is obtained as Definition 1. Hence, Theorem 1 is very useful since it gives us the general case.
We now give an illustrative example which shows the computation of the distance between any two points on an isosceles Sierpinski triangle.
Example 1. Consider an isosceles triangle with vertices and . Let A and B be the points of S whose code representations are and respectively.
We get since the first terms of the code representations of A and B are different. By using Corollary 1, we computeandIt follows thatandwhich shows (see Figure 3). 4. Some Interesting Properties of the Equilateral, Isosceles and Scalene Sierpinski Gaskets
In this section, we give some important geometrical properties with the intrinsic metric on the equilateral, scalene and isosceles Sierpinski Gaskets via the code representations of their points. We first begin with a proposition related to the equilateral Sierpinski Gasket whose proof is given in [
12] as follows:
Proposition 2 ([12]). Let be a sub-triangle of the equilateral Sierpinski Gasket with edge length 1 and let , and be vertices of . If is an arbitrary point of thenwhere . Proposition 2 does not hold for scalene and isosceles Sierpinski Gaskets. That is, there are points
A and
B such that
as shown the following example:
Example 2. Let us consider the scalene Sierpinski Gasket with vertices and . Let A and B be the points of S such that their code representations are and respectively. It is clear that and R have the code representations , , respectively. For the computation of the shortest distance between A and P, we obtain , , , and for and thus . Since , , , and for , we compute . Due to the fact that , , , and for , we get and thus . By using the formula given in Theorem 1, we have Moreover, since we have , , , and for . Owing to the fact that , , , and for , we compute . Given , , , and for , we get . This shows that By the code representations of points, we will demonstrate another property that is obtained on the equilateral Sierpinski Gasket but not on the isosceles and scalene Sierpinski Gaskets. We first recall the definition of the distance of a point to a set:
Definition 2. Let is a metric space and let B be a point of and . Then the distance of B to is determined by Obviously, if , then we get .
Remark 2. It is well-known that the sum of the shortest distances of an arbitrary point on one edge of an equilateral triangle to the other two edges is fixed, and this number is equal to the height of the triangle. In the following proposition, we apply this property to the equilateral Sierpinski Gasket with the intrinsic metric and obtain a remarkable result.
Proposition 3. Let be a sub-triangle of the equilateral Sierpinski Gasket with edge length 1 and let , and be vertices of . If with code representation is an arbitrary point on the edge of , then Proof. Firstly, assume that
. In such a case, the code representation of
is
. Thus,
since
. We will compute
. Let
X be any point on
which is the closest points to
. It is clear that
X has the code representation
where
. Because
,
and
for
, we have
We now show
Let us consider cases
and
separately. If
, then we obtain
. Due to the fact that
, we have
for
. In order to get the closest distance,
must be 2 and thus
for
. Therefore, we get
Similarly, equals to for the case . Following the similar way, the same result is acquired if . Hence, the proof is completed for the special cases and .
We now consider
and
. There exist
and
such that
and
. We choose
m and
n as the first index such that
and
. Let
(the other case is done analogously). As
is on the edge
of
, we get
. Hence, we have
for
and
. Consider any point
X with code representation
on
and any point
Y with code representation
on
which are the closest points to
. In that case,
must be 0 for
. There are only two options for
which are 0 or 2. In the case of
, it is obtained
for
. So,
must be equal to 0 for the computation of the closest distance. In addition, we attain
since
for
. Moreover, we get
for
because
Y is on the edge
(that is,
for
). We thus have
for
. Furthermore, for
, we obtain
and
since
and
. (Note that,
must be equal to 1). For any
, if
, then
and
and if
, then
,
. It follows that
A similar computation shows
This concludes the proof. □
Remark 3. If and are on the sides and of the equilateral Sierpinski Gasket with edge length 1 respectively, then we haveandHowever, Proposition 3 does not hold for every edges of scalene and isosceles Sierpinski Gaskets. Example 3. Consider the scalene Sierpinski Gasket with vertices and . Let A with code representation be a point on the edge of the scalene Sierpinski Gasket. By using the formula given in Theorem 1, we first compute the distance . The code representation of any point on must be in the form where In order to obtain as 0, must be 0 since the term of A equals to zero for . Moreover, we have to take as 0 for owing to the fact that , and . We thus obtain We now compute the distance . The code representation of any point on must be in the form where To get the shortest distance, we must choose as (if we take =2, then we obtain for computation of shortest distance). Furthermore, must be 2 for because , and . Thus we have . So, we havewhich shows By similar calculations, the following result can be given.
Corollary 2. Let S be a scalene or an isosceles Sierpinski Gasket. If A is a point on the shortest edge of S, then the sum of the distances of point A to the other two edges is fixed and this distance equals to the length of the shortest edge.
Proposition 4. Let S be an equilateral Sierpinski Gasket with vertices P, Q and R. Suppose that A is a point on the edge with the code representation where . Then there are many points on that determine the shortest distance of the point A to the line . Additionally, if n is the first index such that , then the set of points on which determines this shortest distance is Proof. Let A be a point on the edge with the code representation where and let n be the first index such that . Consider any point X on with the code representation where
Firstly, suppose that
for
. In this case,
must be 0 for
to obtain the shortest distance between
X and
A. We can choose
as 0 or 2 since
for
, and thus
for
. Additionally,
can be taken 0 or 2 for
because
, and so
for
. This shows that the set of points
X is
We now assume that there exists at least one
for
. Obviously,
must be 0 for
. Note that there are two options for
such as 0 and 2. However, in order to obtain the shortest distance between
X and
A,
has to be 0 since at least one
is 0 for
. Hence, at least one
must be 0. Moreover,
can be taken 0 or 2 for
as
, and thus
for
. Consequently, the set of points
X are
□