1. Introduction
Graph theory is a multidimensional subject in light of its huge applications in both unadulterated and connected science. It is viable in terms of displaying and planning crystal structures, complex systems, and synthetic graphs. There are number of chemical compounds that are organic and inorganic and that have applications in commercial, industrial, and laboratory contexts and in daily life. A relationship exists between synthetic mixes and their atomic structures. Graph theory is an effective territory of arithmetic that has a tremendous scope of utilizations in numerous areas of science, such as chemistry, software engineering, electrical, and electronics. Chemical graph theory is a branch of science in which proficient apparatuses of graph theory are utilized to graphically demonstrate concoctions.
The physical structure of strong materials depends generally on the courses of action of atoms, particles, or atoms that make up the strong holding powers between them. The crystal structure, also referred to as crystalline material or crystalline strong is made out of unit cells, and molecules are organized in 3D on a grid. The schemes of atoms or crystalline material are vital in determining the conduct and properties of a material, such as metals, composites, and artistic materials. The unit cell is the smallest auxiliary unit that can clarify the precious stone structure. The redundancy of the unit cell creates the entire precious stone.
Let be a subatomic diagram, where V is the arrangement of the vertex, called atoms, and E is the edge set, called the chemical bond. The degree of v is the quantity of edges of G occurrence with v. An atomic diagram can be informed by a polynomial, a numerical esteem, an eigenvalue, a topological index, and so forth. There are certain types of topological indices mostly distance-based, degree-based, and distance-based indices. This article is completely dedicated to managing degree-based additive topological indices. A topological index is a number that depicts vital and valuable information about molecular structure. It is a numerical invariant of a subatomic graph and is very valuable we’re comparing their bioactivity and physio-synthetic properties.
In 1975, the very first degree-based index was introduced by Randić [
1]:
In 1988, Bollobás et al. [
2] and Amic et al. [
3] independently proposed the general Randic index. For more details about the important results and chemical properties of the Randić index, we recommend [
4]. The general Randic index is defined as
Estrada et al. [
5] introduced the atom-bond connectivity index:
In 1972, both the first and second Zagreb indices were formulated by Gutman [
6] as follows:
For more details about Zagreb indices, their properties, and important results, see [
7,
8,
9]. Shirdel et al. introduced the hyper Zagreb index in 2013 [
10]. The mathematical representation of this index is as follows:
The fourth version of the atom-bond connectivity index
of a graph
G was introduced by Ghorbhani et al. [
11] and is defined as follows:
where
and
.
Vukicevic et al. [
12] defined the geometric arithmetic index
of a graph
G as follows:
Another well known molecular descriptor is the fifth version of the geometric arithmetic index
of a graph
G. It was introduced by Graovac et al. [
13] and is defined as follows:
2. Applications of Topological Indices
The Randic index is a topological descriptor related to a great deal of synthetic qualities of atoms and was discovered parallel to processing the boiling point and Kovats constants of the particles. The particle bond network (
) index connects to the security of direct alkanes and stretched alkanes and is used to process the strain vitality of cyclo alkanes [
14,
15]. In terms of physico-concoction properties, the
index has prescient control superior to the prescient energy of the Randic connectivity index [
16]. The first and second Zagreb indices were found to be helpful for calculation of the aggregate
-electron energy of the particles inside particular rough articulations [
17]. These are among the graph invariants proposed for the estimation of skeletons of stretching of carbon atoms [
18].
During the last two decades, analysts created substance diagrams, and they arranged and processed particular indices. W. Gao and M. R. Farahani calculated degree-based indices of synthetic structures by utilizing an edge-separated technique [
19]. Gao et al. [
20,
21] created concoction structures in medications and processed overlooked topological indices. As of late, Baig et al. [
22] computed and graphically portrayed topological descriptors of concoction graphs of carbon graphite and precious stone cubic carbon structures. Different utilizations of atomic descriptors of subatomic diagrams and systems are given in the reference list and the references in [
23,
24]. These applications and literature reviews inspired us to investigate new substance diagrams and gem structures and process their topological records.
3. Methods
For the computation of our results, we utilized a strategy for combinatorial registering, a vertex partition strategy, an edge partition technique, graph hypothetical instruments, scientific systems, a degree-counting strategy, and a degrees of neighbors strategy. In addition, we used Matlab for scientific estimations and confirmations. We likewise utilized Maple for plotting numerical results.
4. Bismuth Tri-Iodide
The bismuth tri-iodide
is an outstanding inorganic compound. This dark gray solid is the product of a reaction of bismuth and iodine, which was once of interest in qualitative inorganic analysis [
25]. It has been demonstrated over the years that Bi-doped glass optical strands are among the most promising dynamic laser media. Different kinds of Bi-doped optical strands have been created as a result and have been used to build Bi-doped fiber lasers and optical speakers [
26]. Layered
precious stone is thought to be a three-layered stacking structure, where bismuth atom planes are sandwiched between iodide particle planes, which shape the succession
planes [
27]. The periodic stacking of three layers forms rhombohedral
crystal with
symmetry [
28,
29]. The progressive stacking of one
layer shapes the hexagonal structure with symmetry [
30]. A solitary precious stone of
has been integrated by Nason and Keller [
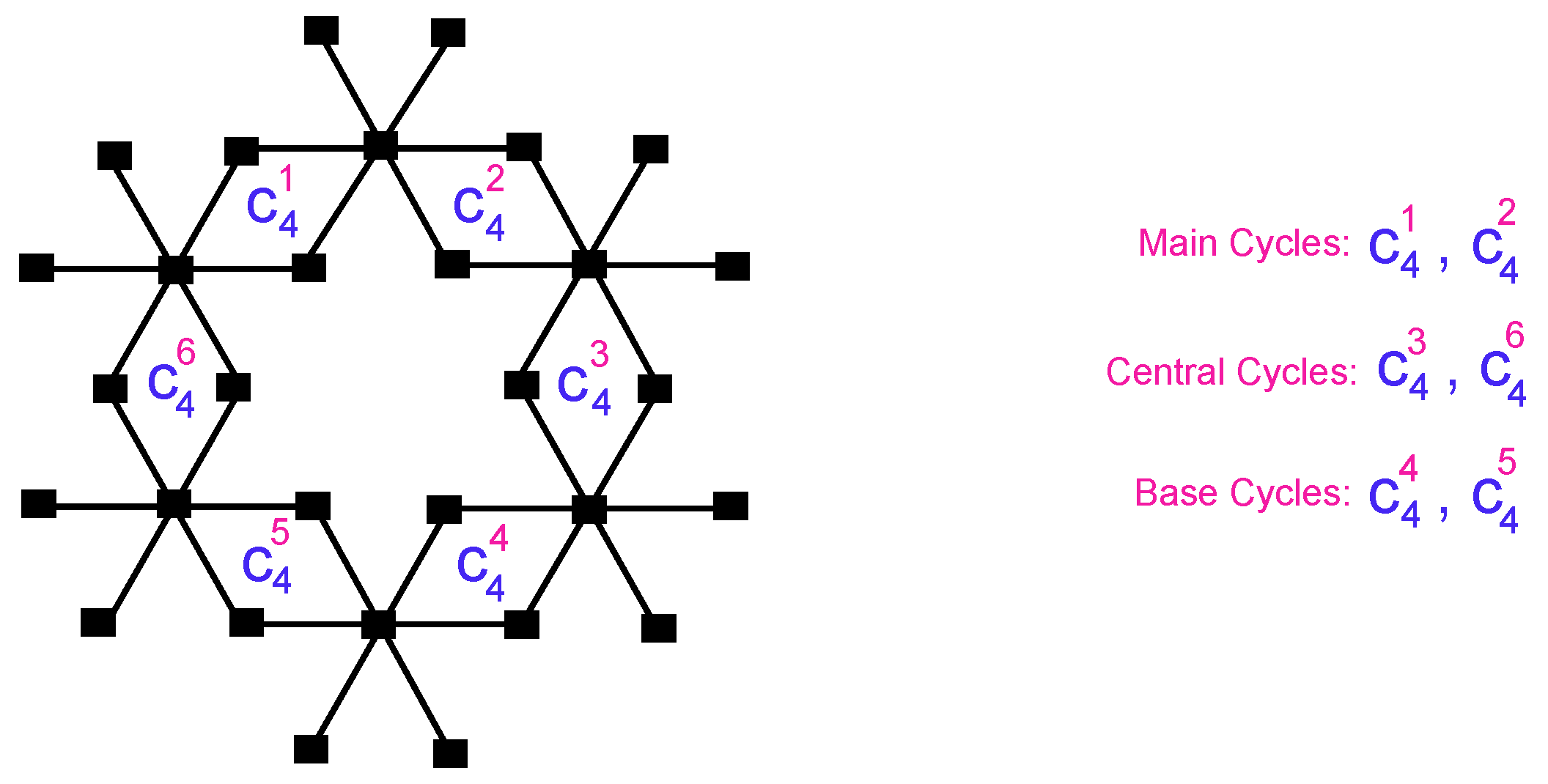
31]. The graph of a solitary unit of bismuth tri-iodide contains six 4-cycles, of which two are on the main, two are in the center, and two are at the base. The bismuth tri-iodide can be organized either straightly (chain) or in a sheet frame [
32].
4.1. Results for Bismuth Tri-Iodide Chain ()
The linear arrangement of bismuth tri-iodide with
m unit cells is called
m-bismuth tri-iodide chain. The unit cell of bismuth tri-iodide
is illustrated in
Figure 1. The cardinality of vertices and edges of bismuth tri-iodide chain
are
and
, respectively. In
chain, the 1 degree vertices are
, the 2 degree vertices are
, and the 6 degree vertices are
. The edge set of
chain is divided into two partitions based on the degree of end vertices. The first edge partition contains
edges
, where
and
. The second edge partition contains
edges
, where
and
.
Table 1 shows the edge partition of bismuth tri-iodide
for
.
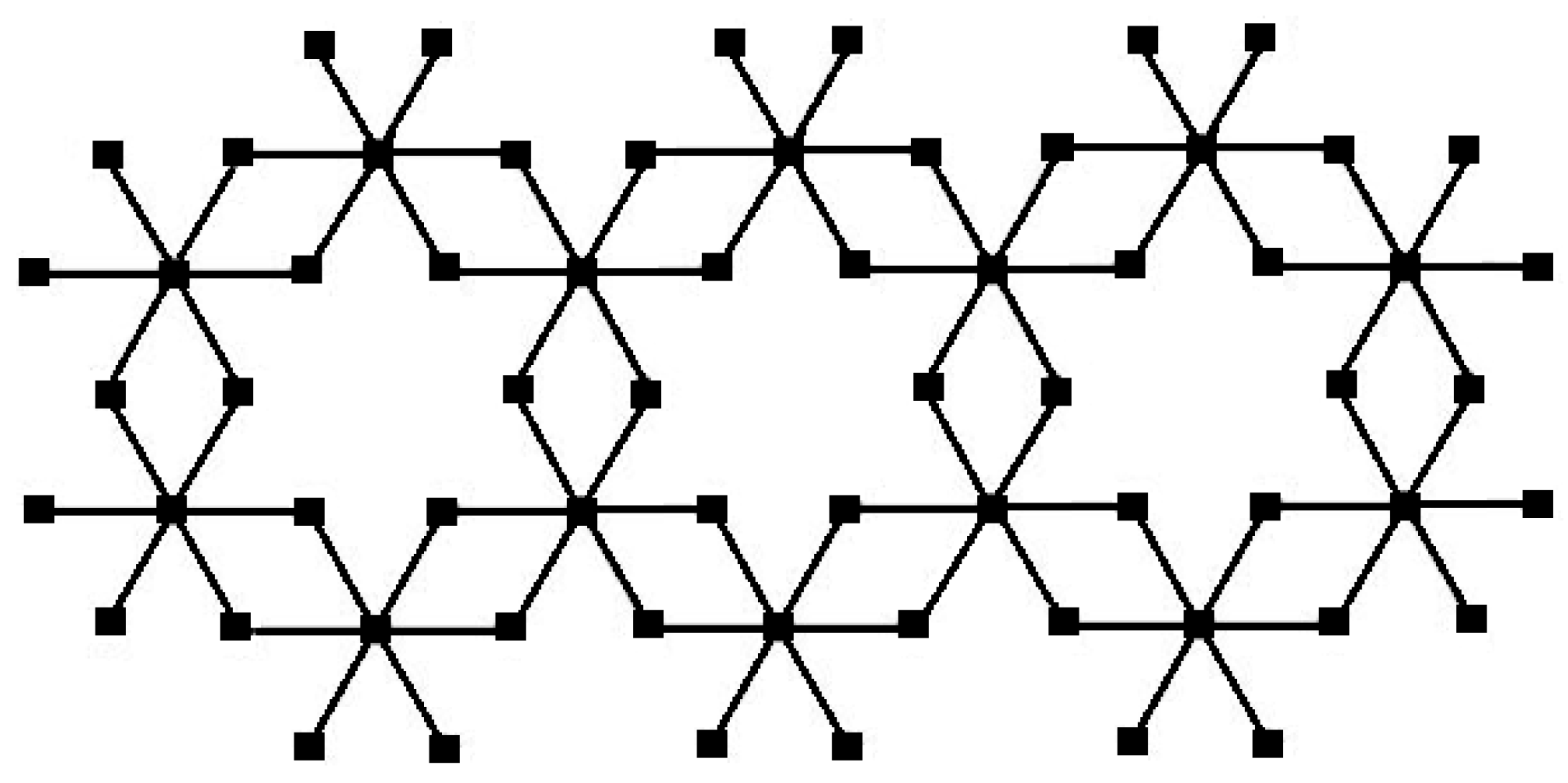
The chain bismuth tri-iodide for
is formed by combining one unit cell of
three times together as shown in
Figure 2.
In the next step, we computed the atom-bond connectivity index, the general Randić index for , the geometric arithmetic index, the fourth atom-bond connectivity index , the fifth geometric arithmetic index , and the first, second, and hyper Zagreb indices. We present these results graphically for the crystal structure of bismuth tri-iodide for both chain and sheet.
Let
G represent the molecular graph of
. Then, from
Table 1, the atom-bond connectivity index is computed as
Let
G be the graph of
. Now, using
Table 1, the geometric arithmetic index is computed as
Let
G be the graph of
. Now, using
Table 1, the general Randić index for
is
Let
G be the graph of
. Now, using
Table 1, the first, second, and hyper Zagreb indices are computed as
The hyper Zagreb index is computed as
Table 2 demonstrates the edge distribution in light of the degree sum of the end vertices of each edge. We find an exact formula for the fourth atom-bond connectivity index and the fifth geometric arithmetic index using
Table 2.
Let
G be the graph of
. Now, using
Table 2, the fourth atom-bond connectivity index is computed as
Let
G be the graph of
. Now, using
Table 2, the fifth geometric arithmetic index is computed as follows:
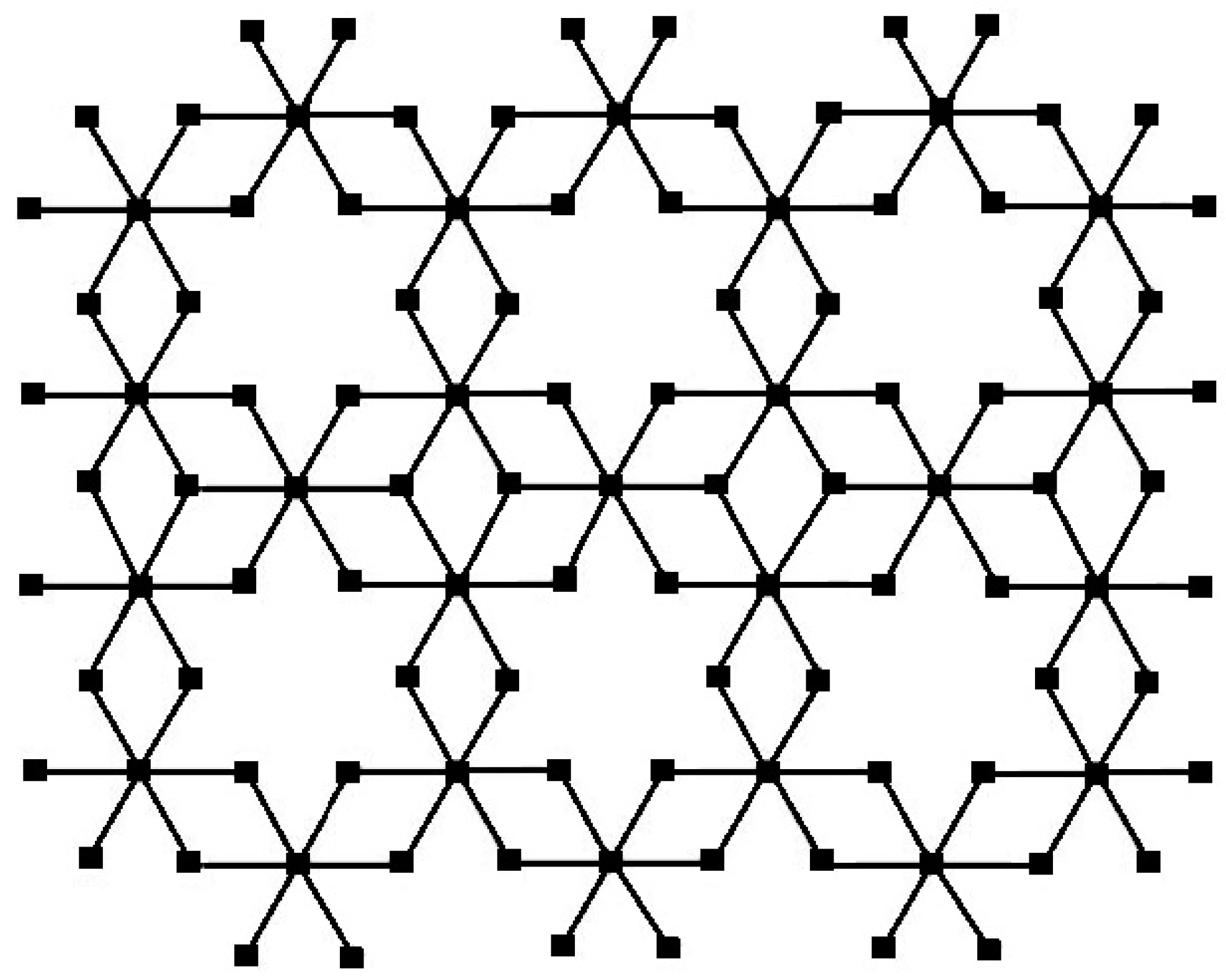
4.2. Results for Bismuth Tri-Iodide Sheet
In this section, the topological additive indices based on the degree and sum of degree of bismuth tri-iodide sheet are computed. The linear arrangement of bismuth tri-iodide with
unit cells is called
bismuth tri-iodide sheet, where
m unit cells are taken as rows and
n unit cells are taken as columns. The graph of bismuth tri-iodide sheet for
and
is represented in
Figure 3.
The cardinality of vertices and edges of bismuth tri-iodide sheet
are
and
, separately. In
sheet, the 1 degree vertices are
, the 2 degree vertices are
, the 3 degree vertices are
, and the 6 degree vertices are
. The edge set of the
sheet is separated into three parcels in light of the level of the end vertices. The main edge parcel contains
edges
, where
and
. The second edge segment contains
edges
, where
and
. The third edge segment contains
edges
, where
and
.
Table 3 demonstrates the edge parcel of the bismuth tri-iodide sheet for
.
Let
G be the graph of
with
. From the edge partition of
, which is given in
Table 3, the atom-bond connectivity index is computed as
Let
G be the graph of
with
. Now, using
Table 3, the geometric arithmetic index is computed as follows:
Let
G be the graph of
with
. Now, using
Table 3, the general Randić index is given:
Let
be a molecular graph of bismuth tri-iodide sheet. Now, using
Table 3, the first, second, and hyper Zagreb indices are computed as
Table 4 demonstrates the edge segment in view of the degree sum of the end vertices of each edge. We derived the exact result for the fourth atom-bond connectivity index and the fifth geometric arithmetic index using
Table 4.
Let
G be the graph of silicon carbide of type
. Now, using
Table 4, the fourth atom-bond connectivity index is computed as
Let
G be a molecular graph of bismuth tri-iodide sheet
. Then, using
Table 4, the fifth geometric arithmetic index is computed as
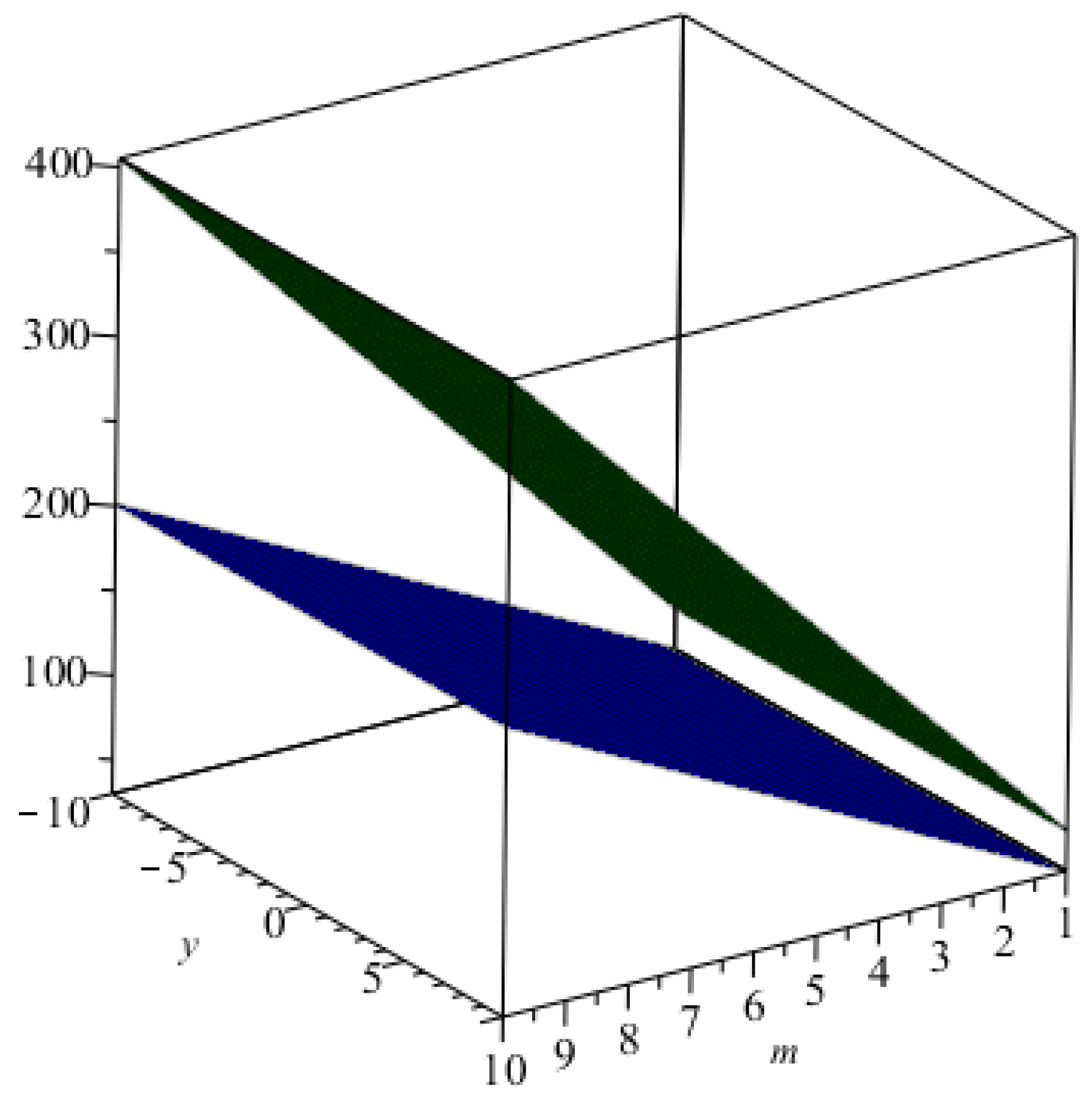
5. Comparisons and Discussion
For the comparison of these indices numerically for
, we computed all indices for different values of
m. Now, from
Table 5, we can easily see that all indices are in increasing order as the values of
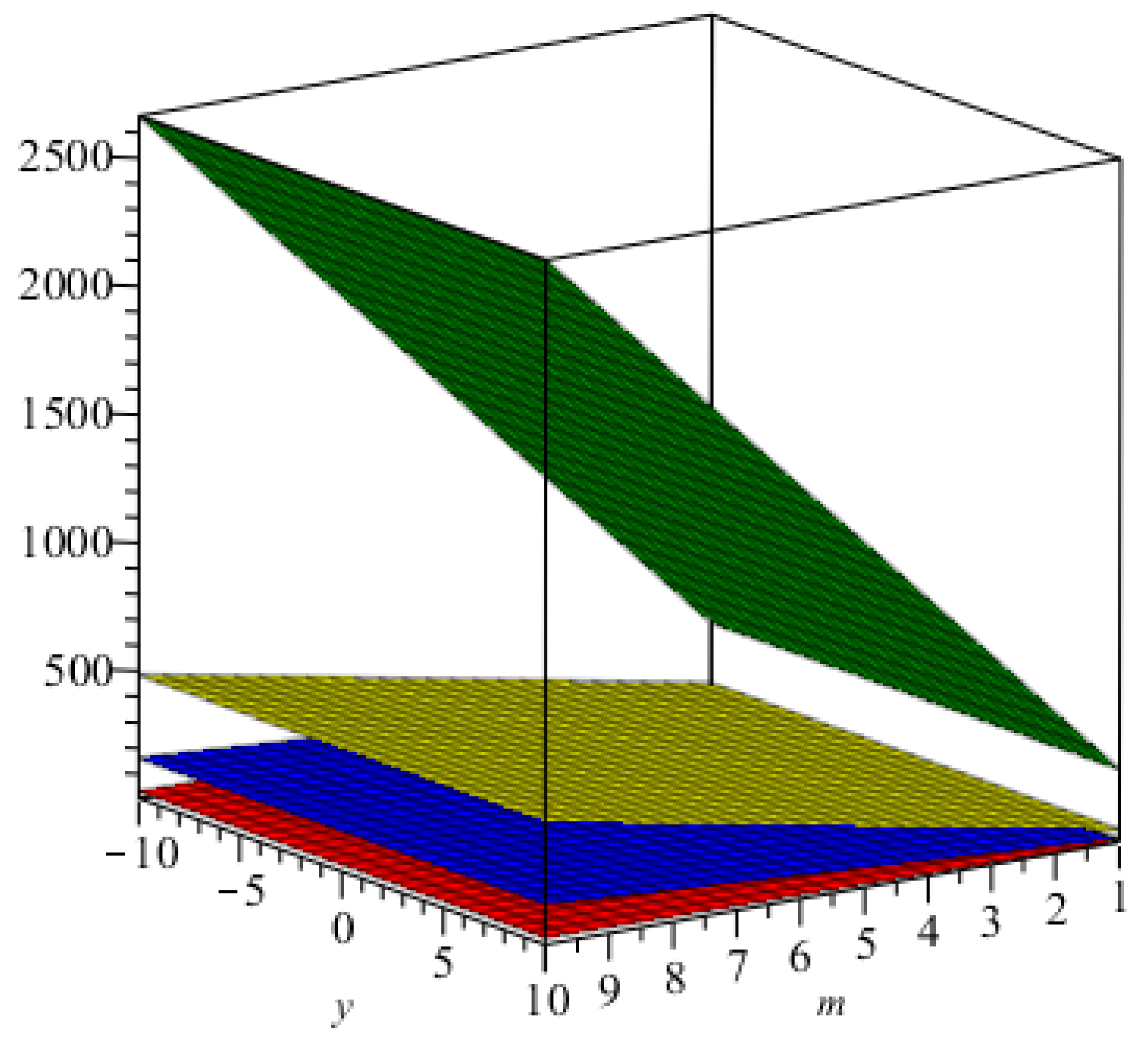
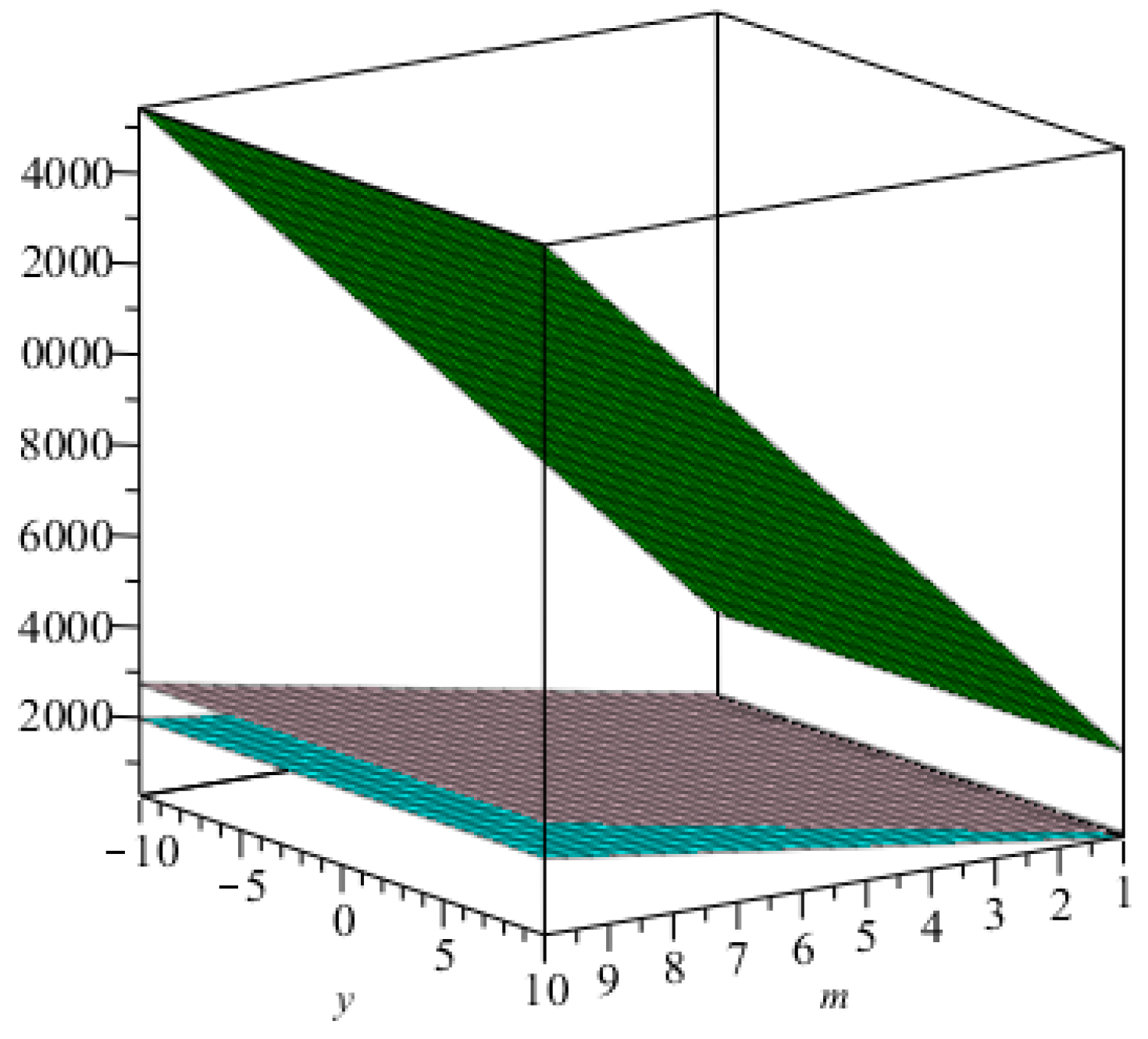
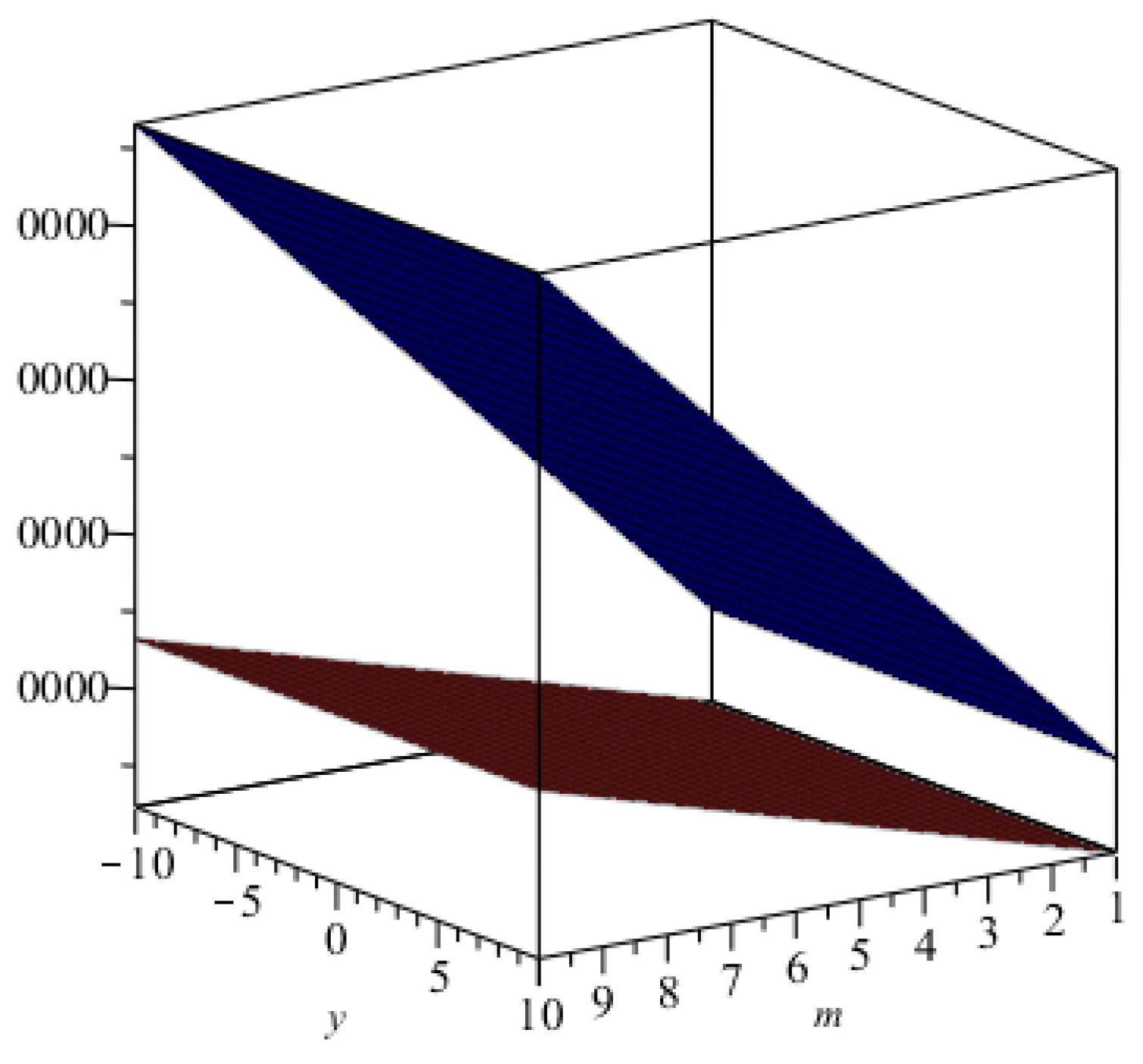
m are increasing. The graphical representations of the topological indices for
are depicted in
Figure 4,
Figure 5,
Figure 6 and
Figure 7 for certain values of
m.
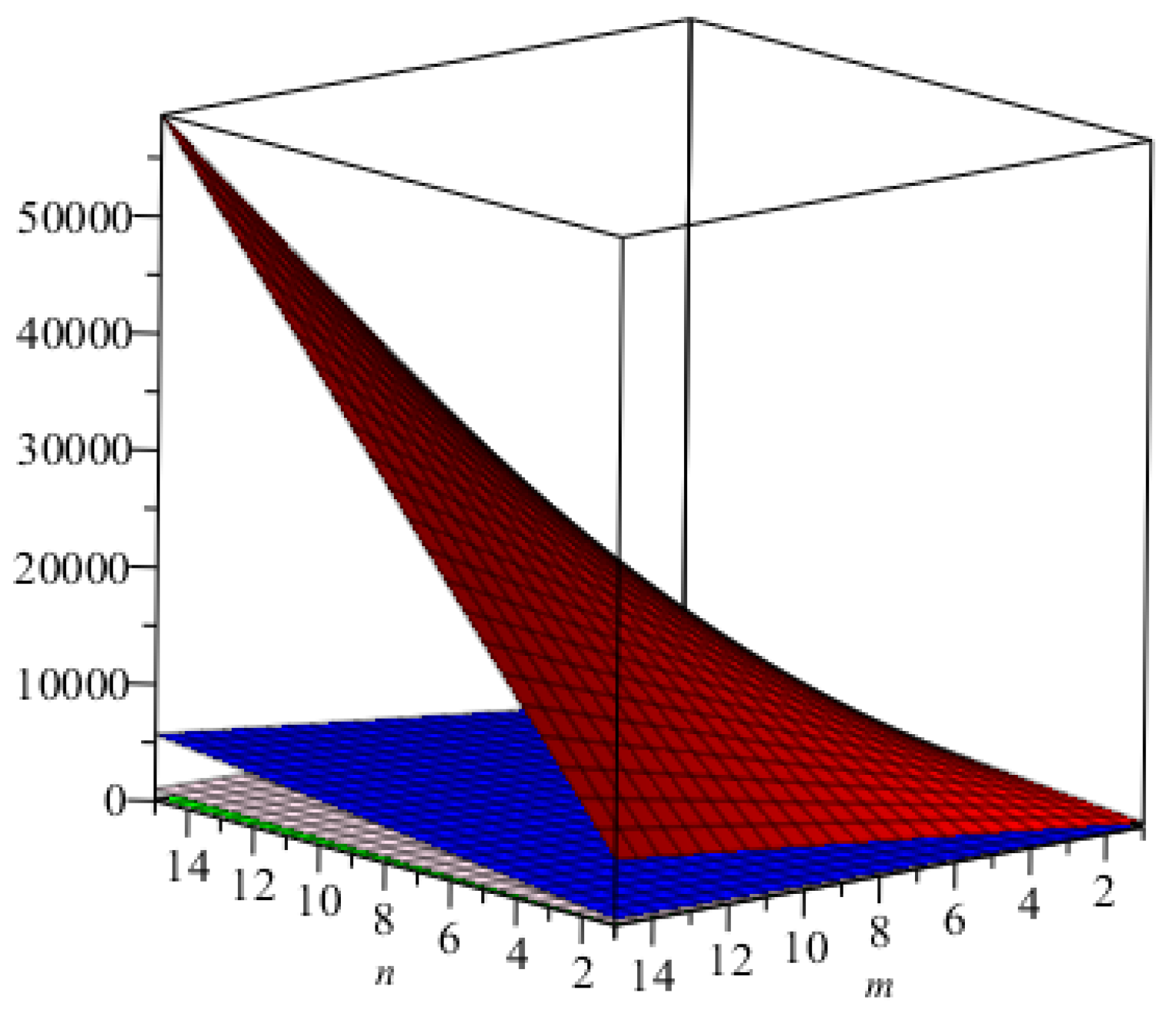
We computed all indices numerically for
for different values of
. We can easily see, from
Table 6, that all indices are in increasing order as the values of
are increasing. The graphical representations of the topological indices for
are depicted in
Figure 8,
Figure 9,
Figure 10 and
Figure 11 for certain values of
.
6. Conclusions
We computed additive degree-based topological indices, the atom-bond network index, the general Randić index, the first, second, and hyper Zagreb indices, the arithmetic index, the fourth atom-bond connectivity index, and the fifth geometric arithmetic index of and .
The Randic index is a topological descriptor that correlates with many chemical characteristics of molecules. It was found that the boiling point of and varies in increasing order for .
The atom-bond connectivity index provides a very good correlation for computing the strain energy of molecules. One can easily see that the strain energy of and is high as the values of increase.
The index has as much predictive power as that of the Randic index, so the index is more useful than the Randic index for , as compared to the Randic index for , in the case of and .
The first and second Zagreb indices were found to occur for the computation of the total -electron energy of molecules; thus, in the case of and , their values provide the total -electron energy in increasing order for higher values of .
However, computation of distance-based and counting-related topological indices for these symmetrical chemical structures are open challenges and have yet to be investigated.
Author Contributions
M.I. contribute for conceptualization, designing the experiments, funding, supervision and analyzed the data. M.K.S. contribute for methodology, software, validation, and formal analysing. M.A.A. and S.A. contribute for performed experiments, resources, some computations and wrote the initial draft of the paper which were investigated and approved by M.I., M.K.S. and A.Q.B. and wrote the final draft. All authors read and approved the final version of the paper.
Funding
This research is supported by the Start-Up Research Grant 2016 of United Arab Emirates University (UAEU), Al Ain, United Arab Emirates via Grant No. G00002233 and UPAR Grant of UAEU via Grant No. G00002590.
Acknowledgments
The authors are grateful to the anonymous referees for their valuable comments and suggestions that improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Randic, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Bollobas, B.; Erdos, P. Graphs of extremal weights. Ars Comb. 1998, 50, 225–233. [Google Scholar] [CrossRef]
- Amic, D.; Beslo, D.; Lucic, B.; Nikolic, S.; Trinajstić, N. The vertex-connectivity index revisited. J. Chem. Inf. Comput. Sci. 1998, 38, 819–822. [Google Scholar] [CrossRef]
- Li, X.; Gutman, I. Mathematical Aspects of Randić Type Molecular Structure Descriptors; Mathematical Chemistry Monographs, No. 1; University of Kragujevac and Faculty of Science: Kragujevac, Serbia, 2006; ISBN 86-81829-67-X. [Google Scholar]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Gutman, I.; Trinajstc, N. Graph theory and molecular orbitals, Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Naeem, M.; Rehman, N.A. Topological Characterization of Carbon Graphite and Crystal Cubic Carbon Structures. Molecules 2017, 22, 1496. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, M.K.; Imran, M.; Ahmad, A. On Zagreb indices, Zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput. 2016, 280, 132–139. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Naeem, M.; Rahman, N.A.; Imran, M. Computing topological indicesof certain networks. J. Optoelectron. Adv. Mater. 2016, 18, 884–892. [Google Scholar]
- Shirdel, G.H.; RezaPour, H.; Sayadi, A.M. The Hyper-Zagreb Index of Graph Operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Ghorbani, M.; Hosseinzadeh, M.A. Computing ABC4 index of nanostar dendrimers. Optoelectron. Adv. Mater.-Rapid Commun. 2010, 4, 1419–1422. [Google Scholar]
- Vukicevic, D.; Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 2009, 46, 1369–1376. [Google Scholar] [CrossRef]
- Graovac, A.; Ghorbani, M.; Hosseinzadeh, M.A. Computing fifth geometric arithmetic index for nanostar dendrimers. J. Math. Nanosci. 2011, 1, 33–42. [Google Scholar]
- Shao, Z.; Wu, P.; Zhang, X.; Dimitrov, D.; Liu, J. On the maximum ABC index of graphs with prescribed size and without pendent vertices. IEEE Access. 2018. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, P.; Gao, Y.; Gutman, I.; Zhang, X. On the maximum ABC index of graphs without pendent vertices. Appl. Math. Comput. 2017, 315, 298–312. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I.; Furtula, B. Survey on geometric-arithmetic indices of graphs. MATCH Commun. Math. Comput. Chem. 2011, 65, 595–644. [Google Scholar]
- Gutman, I.; Ruscic, B.; Trinajstić, N.; Wilcox, C.F. Graph theory and molecular orbitals, XII. Acyclic polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar] [CrossRef]
- Schlter, M.; Cohen, M.L.; Kohn, C.E.; Fong, C.Y. Electronic Structure of BiI3. Phys. Status Solidi (B) 1976, 78. [Google Scholar] [CrossRef]
- Gao, W.; Farahani, M.R. Degree-based indices computation for special chemical molecular structures using edge dividing method. Appl. Math. Nonlinear Sci. 2015, 1, 94–117. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K. Molecular Descriptors of Nanotube, Oxide, Silicate, and Triangulene networks. J. Chem. 2017, 2017, 6540754. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Imran, M.; Jamil, M.K.; Farahani, M.R. Forgotten topological index of chemical structure in drugs. Saudi Pharm. J. 2016, 24, 258–264. [Google Scholar] [CrossRef] [PubMed]
- Baig, A.Q.; Imran, M.; Khalid, W.; Naeem, M. Molecular description of carbon graphite and crystal cubic carbon structures. Can. J. Chem. 2017, 95, 674–686. [Google Scholar] [CrossRef]
- Baig, A.Q.; Imran, M.; Ali, H. On topological indices of poly oxide, poly silicate, DOX, and DSL networks. Can. J. Chem. 2015, 93, 730–739. [Google Scholar] [CrossRef]
- Hayat, S.; Imran, M. Computation of certain topological indices of nanotubes covered by C5 and C7. J. Comput. Theor. Nanosci. 2015, 12, 533–541. [Google Scholar] [CrossRef]
- Iodide, B. McGraw-Hill Dictionary of Scientific and Technical Terms; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Mackay, R.A.; Henderson, W. Introduction to Modern Inorganic Chemistry; CRC Press: Boca Raton, FL, USA, 2002; pp. 122–126. ISBN 0-7487-6420-8. [Google Scholar]
- Smart, L.; Elaine, A.M. Solid State Chemistry: An Introduction; CRC Press: Boca Raton, FL, USA, 2005; p. 40. ISBN 0-7487-7516-1. [Google Scholar]
- Watanabe, K.; Karasawa, T.; Komatsu, T.; Kaifu, Y. Optical Properties of Extrinsic Two-Dimensional Excitons in BiI3 Single Crystals. J. Phys. Soc. Jpn. 1986, 55. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. Crystal Structures, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia, 1964. [Google Scholar]
- Yorikawa, H.; Muramatsu, S. Theoretical Study of Crystal and Electronic Structures of BiI3. J. Phys. Condens. Matter 2008, 20, 325–335. [Google Scholar] [CrossRef]
- Nason, D.; Keller, L. The Growth and Crystallography of Bismuth Tri-Iodide Crystals Grown by Vapor Transport. J. Cryst. Growth 1995, 221. [Google Scholar] [CrossRef]
- Erdmann, H.; Dunlap, F.L. Handbook of Basic Tables for Chemical Analysis; John Wiley & Sons: New York, NY, USA, 1900. [Google Scholar]
Figure 1.
The unit cell of bismuth tri-iodide.
Figure 1.
The unit cell of bismuth tri-iodide.
Figure 2.
The chain bismuth tri-iodide for .
Figure 2.
The chain bismuth tri-iodide for .
Figure 3.
The sheet bismuth tri-iodide for and .
Figure 3.
The sheet bismuth tri-iodide for and .
Figure 4.
The graphical representation of index in blue and that of the index in green.
Figure 4.
The graphical representation of index in blue and that of the index in green.
Figure 5.
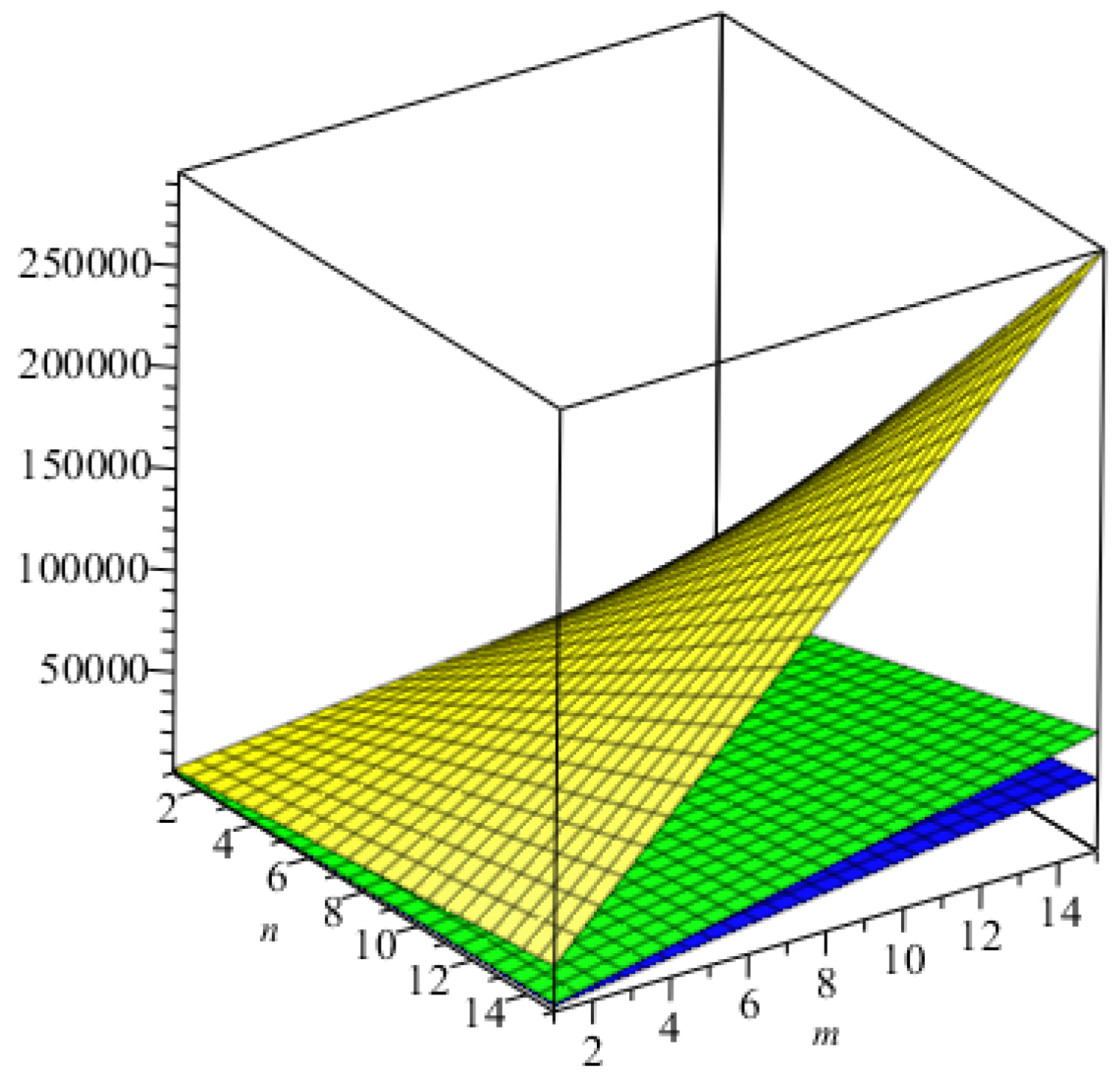
The graphical representation of the Randić index for in green, that for in red, that for in yellow, and that for in blue.
Figure 5.
The graphical representation of the Randić index for in green, that for in red, that for in yellow, and that for in blue.
Figure 6.
The graphical representation of the first, second, and hyper Zagreb indices in cyan, pink, and green, respectively.
Figure 6.
The graphical representation of the first, second, and hyper Zagreb indices in cyan, pink, and green, respectively.
Figure 7.
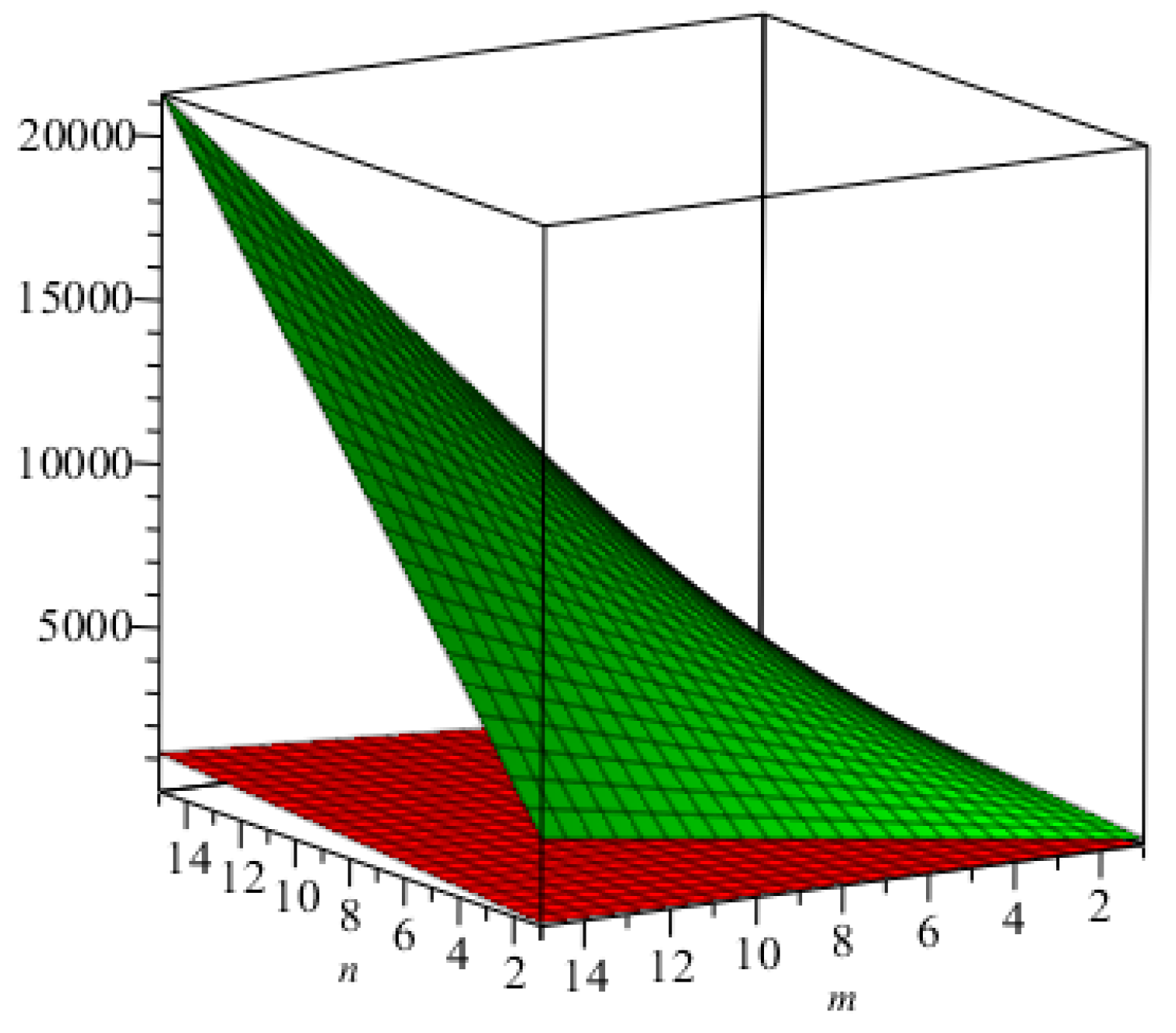
The graphical representation of index in blue and that of the index in brown.
Figure 7.
The graphical representation of index in blue and that of the index in brown.
Figure 8.
The graphical representation of the index in green, and that of the index in blue.
Figure 8.
The graphical representation of the index in green, and that of the index in blue.
Figure 9.
The graphical representation of the Randić index for in red, that for in green, that for in pink, and that for in blue.
Figure 9.
The graphical representation of the Randić index for in red, that for in green, that for in pink, and that for in blue.
Figure 10.
The graphical representation of the first, second, and hyper Zagreb indices in blue, green, and yellow, respectively.
Figure 10.
The graphical representation of the first, second, and hyper Zagreb indices in blue, green, and yellow, respectively.
Figure 11.
The graphical representation of index in blue, and that of the index in brown.
Figure 11.
The graphical representation of index in blue, and that of the index in brown.
Table 1.
Edge partition of .
Table 1.
Edge partition of .
| | |
|---|
| Number of Edges | | |
Table 2.
Edge partition of based on the degree sum of end vertices of each edge.
Table 2.
Edge partition of based on the degree sum of end vertices of each edge.
| | | |
|---|
| Number of Edges | | | |
Table 3.
Edge partition of based on the degree of end vertices of each edge.
Table 3.
Edge partition of based on the degree of end vertices of each edge.
| | | |
|---|
| Number of Edges | | | |
Table 4.
Edge partition of based on the degree sum of the end vertices of each edge.
Table 4.
Edge partition of based on the degree sum of the end vertices of each edge.
| Number of Edges |
|---|
| |
| |
| |
| |
| |
| |
| |
Table 5.
All indices for .
Table 5.
All indices for .
| m | | | | | | | | | | | |
|---|
| 1 | | 288 | 4 | | | | 276 | 360 | 2158 | | |
| 2 | | 552 | | | | | 464 | 624 | 3632 | | |
| 3 | | 816 | | | | | 652 | 888 | 5106 | | |
| 4 | | 1080 | | | | | 840 | 1152 | 6580 | | |
Table 6.
All indices for .
Table 6.
All indices for .
| | | | | | | | | | | |
|---|
| | 360 | | | | | 276 | 360 | 2124 | | |
| | 744 | | | | | 585 | 1248 | 6816 | | |
| | 1128 | | | | | 1736 | 2640 | 14016 | | |
| | 1412 | | | | | 2918 | 4536 | 23724 | | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).