Exponential Aggregation Operator of Interval Neutrosophic Numbers and Its Application in Typhoon Disaster Evaluation

Abstract

In recent years, typhoon disasters have occurred frequently and the economic losses caused by them have received increasing attention. This study focuses on the evaluation of typhoon disasters based on the interval neutrosophic set theory. An interval neutrosophic set (INS) is a subclass of a neutrosophic set (NS). However, the existing exponential operations and their aggregation methods are primarily for the intuitionistic fuzzy set. So, this paper mainly focus on the research of the exponential operational laws of interval neutrosophic numbers (INNs) in which the bases are positive real numbers and the exponents are interval neutrosophic numbers. Several properties based on the exponential operational law are discussed in detail. Then, the interval neutrosophic weighted exponential aggregation (INWEA) operator is used to aggregate assessment information to obtain the comprehensive risk assessment. Finally, a multiple attribute decision making (MADM) approach based on the INWEA operator is introduced and applied to the evaluation of typhoon disasters in Fujian Province, China. Results show that the proposed new approach is feasible and effective in practical applications.

1. Introduction

Natural hazards attract worldwide attention. Typhoons are one of the main natural hazards in the world. When a typhoon makes landfall, the impacted coastal areas experience torrential rain, strong winds, storm surges, and other weather-related disasters [1]. Typhoons can cause extremely serious harm, frequently generating heavy economic losses and personnel casualty [2]. In the last 50 years, economic damage from typhoon disasters around the coastal regions of China has increased dramatically. The Yearbook of Tropical Cyclones in China shows that from 2000 to 2014, on average, typhoon disasters caused economic losses of 45.784 billion yuan (RMB), 244 deaths, and affected 37.77 million people per year [3]. Effective evaluation of typhoon disasters can improve the typhoon disaster management efficacy, preventing or reducing disaster loss. Furthermore, precise evaluation of typhoon disasters is critical to the timely allocation and delivery of aid and materials to the disaster area. Therefore, in-depth studies of typhoon disaster evaluation are of great value.

The evaluation of typhoon disasters is a popular research topic in disaster management. Researchers have made contributions to this topic from several different perspectives [1]. Wang et al. [4] proposed a typhoon disaster evaluation model based on an econometric and input-output joint model to evaluate the direct and indirect economic loss caused by typhoon disasters for related industrial departments. Zhang et al. [5] proposed a typhoon disaster evaluation model for the rubber plantations of Hainan Island which is based on extension theory. Lou et al. [6] adopted a back-propagation neural network method to evaluate typhoon disasters, and a real case in Zhejiang Province of China was studied in detail. Lu et al. [7] used the multi-dimensional linear dependence model to evaluate typhoon disaster losses in China. Yu et al. [1] and Lin [8] asserted that establishing a decision support system is crucial to improving data analysis capabilities for decision makers.

Since the influencing factors of the typhoon disasters are completely hard to describe accurately, the typhoon disasters may include economic loss and environmental damage. Taking economic loss for example, it includes many aspects such as the building’s collapse, the number and extent of damage to housing, and the affected local economic conditions [1]. Therefore, it is impossible to describe the economic loss precisely because the estimation is based on incomplete and indeterminate data. Therefore, fuzzy set (FS) and intuitionistic fuzzy set (IFS) have been used for typhoon disaster assessment in recent years. Li et al. [9] proposed evaluating typhoon disasters with a method that applied an extension of the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method with intuitionistic fuzzy theory. Ma [10] proposed a fuzzy synthetic evaluation model for typhoon disasters. Chen et al. [11] provided an evaluation model based on a discrete Hopfield neural network. Yu et al. [1] studied typhoon disaster evaluation in Zhejiang Province, China, using new generalized intuitionistic fuzzy aggregation operators. He [12] proposed a typhoon disaster assessment method based on Dombi hesitant fuzzy information aggregation operators. However, this review reveals that the application of the neutrosophic sets theory in typhoon disaster assessment has yet to be examined. We believe that neutrosophic sets (NSs) offer a powerful technique to enhance typhoon disaster assessment.

Neutrosophic sets can express and handle incomplete, indeterminant, and inconsistent information. NSs were originally defined by Smarandache [13,14], who added an independent indeterminacy-membership on the basis of IFS. Neutrosophic sets are a generalization of set theories including the classic set, the fuzzy set [15] and the intuitionistic fuzzy set [16]. Neutrosophic sets are characterized by a truth-membership function (T), an indeterminacy-function (I), and a falsity-membership function (F). This theory is very important in many application areas because indeterminacy is quantified explicitly and the three primary functions are all independent. Since Smarandache’s initial proposal of NSs in 1998, the concept has attracted broad attention and achieved several successful implementations. For example, Wang et al. [17] proposed single-valued neutrosophic sets (SVNSs), a type of NS. Ye [18] introduced simplified neutrosophic sets (SNSs) and defined the operational laws of SNSs, as well as some aggregation operators. Wang et al. [19] and Peng et al. [20] defined multi-valued neutrosophic sets and the multi-valued neutrosophic number, as well as proposing the application of the TODIM (a Portuguese acronym of interactive and multi-criteria decision making) method in a multi-valued neutrosophic number environment. Wang et al. [21] proposed interval neutrosophic sets (INSs) along with their set-theoretic operators and Zhang et al. [22] proposed an improved weighted correlation coefficient measure for INSs for use in multi-criteria decision making. Ye [23] offered neutrosophic hesitant fuzzy sets with single-valued neutrosophic sets. Tian et al. [24] defined simplified neutrosophic linguistic sets, which combine the concepts of simplified neutrosophic sets and linguistic term sets, and have enabled great progress in describing linguistic information. Biswas [25] and Ye [26] defined the trapezoidal fuzzy neutrosophic number, and applied it to multi-criteria decision making. Deli [27] defined the interval valued neutrosophic soft set (ivn-soft set), which is a combination of an interval valued neutrosophic set and a soft set, and then applied the concept as a decision making method. Broumi et al. [28,29,30] combined the neutrosophic sets and graph theory to introduce various types of neutrosophic graphs.

When Smarandache proposed the concept of NSs [13], he also introduced some basic NS operations rules. Ye [16] defined some basic operations of simplified neutrosophic sets. Wang et al. [21] defined some basic operations of interval neutrosophic sets, including “containment”, “complement”, “intersection”, “union”, “difference”, “addition”, “Scalar multiplication” and “Scalar division”. Based on these operations, Liu et al. [31] proposed a simplified neutrosophic correlated averaging (SNCA) operator and a simplified neutrosophic correlated geometric (SNCG) operator for multiple attribute group decision making. Ye [32] and Zhang et al. [33] introduced interval neutrosophic number ordered weighted aggregation operators, the interval neutrosophic number weighted averaging (INNWA) operator, and the interval neutrosophic number weighted geometric (INNWG) operator for multi-criteria decision making. Liu et al. [34] proposed a single-valued neutrosophic normalized weighted Bonferroni mean (SVNNWBM) operator and analyzed its properties. Ye [35] proposed interval neutrosophic uncertain linguistic variables, and further proposed the interval neutrosophic uncertain linguistic weighted arithmetic averaging (INULWAA) and the interval neutrosophic uncertain linguistic weighted arithmetic averaging (INULWGA) operator. Peng et al. [36] introduced multi-valued neutrosophic sets (MVNSs) and proposed the multi-valued neutrosophic power weighted average (MVNPWA) operator and the multi-valued neutrosophic power weighted geometric (MVNPWG) operator. A trapezoidal neutrosophic number weighted arithmetic averaging (TNNWAA) operator and a trapezoidal neutrosophic number weighted geometric averaging (TNNWGA) operator have also been proposed and applied to multiple attribute decision making (MADM) with trapezoidal neutrosophic numbers [26]. Tan et al. [37] proposed the trapezoidal fuzzy neutrosophic number ordered weighted arithmetic averaging (TFNNOWAA) operator and the trapezoidal fuzzy neutrosophic number hybrid weighted arithmetic averaging (TFNNHWAA) operator for multiple attribute group decision making. Sahin [38] proposed generalized prioritized weighted aggregation operators, including the normal neutrosophic generalized prioritized weighted averaging (NNGPWA) operator and the normal neutrosophic generalized prioritized weighted geometric (NNGPWG) operator for normal neutrosophic multiple attribute decision making.

As the study of the NS theory has expanded in both depth and scope, effective aggregation and handling of neutrosophic number information have become increasingly imperative. In response, many techniques for aggregating neutrosophic number information have been developed [18,26,31,32,33,34,35,36,37,38]. However, an important operational law is lacking, we are unable to handle information aggregation in which the bases are positive real numbers and the exponents are neutrosophic numbers. For example, when decision makers determine the attribute importance under a complex decision environment, the attribute weights are characterized by incompleteness, uncertainty, and inconsistency, while the attribute values are real numbers. In the existing literature about exponential operational laws and exponential aggregation operator, Gou et al. [39] introduced a new exponential operational law about intuitionistic fuzzy numbers (IFNs), in which the bases are positive real numbers and the exponents are IFNs. Gou et al. [40] defined exponential operational laws of interval intuitionistic fuzzy numbers (IIFNs), in which the bases are positive real numbers and the exponents are IFNs. Lu et al. [41] defined new exponential operations of single-valued neutrosophic numbers (NNs), in which the bases are positive real numbers, and the exponents are single-valued NNs. In addition, they also proposed the single-valued neutrosophic weighted exponential aggregation (SVNWEA) operator and the SVNWEA operator-based decision making method. Sahin [42] proposed two new operational laws in which the bases are positive real numbers and interval numbers, respectively; the exponents in both operational laws are simplified neutrosophic numbers (SNNs), and they introduce the simplified neutrosophic weighted exponential aggregation (SNWEA) operator and the dual simplified neutrosophic weighted exponential aggregation (DSNWEA) operator for multi-criteria decision making. Unfortunately, to date, there are not enough theoretical and applied researches on the exponential operational laws and exponential aggregation operators of interval neutrosophic numbers [43]. This is what we need to do. In order to perfect the existing neutrosophic aggregation methods, we further enriched the theoretical research of the exponential operational laws of interval neutrosophic numbers (INNs) and the applied research of the corresponding interval neutrosophic aggregation method based on [43]. In this paper, we discussed in detail several properties of the exponential operation laws of interval neutrosophic numbers, in which the bases are positive real numbers and the exponents are interval neutrosophic numbers. Then, we investigated in detail several properties of the interval neutrosophic weighted exponential aggregation (INWEA) operator, and applied the operator to aggregate assessment information to obtain comprehensive evaluation value. Additionally, a MADM method based on the INWEA operator is proposed. In the MADM problem, the attribute values in the decision matrix are expressed as positive real numbers and the attribute weights are expressed as INNs. Although traditional aggregation operators of INNs cannot address the above decision problem, the exponential aggregation operators of INNs can effectively resolve this issue.

The remainder of this paper is organized as follows: Section 2 briefly introduces some basic definitions dealing with NSs, INSs and so on. Section 3 discusses the exponential operational properties of INSs and INNs in detail. Moreover, this paper investigates in detail the properties of the interval neutrosophic exponential aggregation (INWEA) operator in Section 4. After that, a MADM method based on the INWEA operator is given in Section 5. Section 6 uses a typhoon disaster evaluation example to illustrate the applicability of the exponential operational laws and the information aggregation method proposed in Section 3. Finally, in Section 7, the conclusions are drawn.

2. Preliminaries

In this section, we review some basic concepts related to neutrosophic sets, single-valued neutrosophic sets, and interval neutrosophic sets. We will also introduce the operational rules.

Definition 1 [13].

Let$X$be a space of points (objects), with a generic element in X denoted by x. A neutrosophic set (NS) A in X is characterized by a truth-membership function T_A(x), an indeterminacy-membership function I_A(x), and a falsity-membership function F_A(x). The function T_A(x), I_A(x) and F_A(x) are real standard or nonstandard subsets of$\left]0^{-},1^{+}\right[$, i.e.,$T_A\left(x\right):X\to \left]0^{-},1^{+}\right[$, $I_A\left(x\right):X\to \left]0^{-},1^{+}\right[$, and$F_A\left(x\right):X\to \left]0^{-},1^{+}\right[$. Therefore, the sum of T_A(x), I_A(x) and F_A(x) satisfies the condition$0^{-}\le \sup T_A\left(x\right)+\sup I_A\left(x\right)+\sup F_A\left(x\right)\le 3^{+}$.

Definition 2 [21].

Let$X$be a space of point (objects) with generic elements in$X$denoted by$x$. An interval neutrosophic set (INS)$\tilde{A}$in$X$is characterized by a truth-membership function${\tilde{T}}_{\tilde{A}}(x)$, an indeterminacy-membership function${\tilde{I}}_{\tilde{A}}(x)$, and a falsity-membership function${\tilde{F}}_{\tilde{A}}(x)$. There are${\tilde{T}}_{\tilde{A}}(x)$, ${\tilde{I}}_{\tilde{A}}(x)$, ${\tilde{F}}_{\tilde{A}}(x)\subseteq [0,1]$for each point$x$in$X$. Thus, an INS$\tilde{A}$can be denoted by

$$\begin{array}{ll}\tilde{A}& =\{<x,{\tilde{T}}_{\tilde{A}}(x),{\tilde{I}}_{\tilde{A}}(x),{\tilde{F}}_{\tilde{A}}(x)>|x\in X\}\\ & =\{<x,[\inf T_{\tilde{A}}(x),\sup T_{\tilde{A}}(x)],[\inf I_{\tilde{A}}(x),\sup I_{\tilde{A}}(x)],[\inf F_{\tilde{A}}(x),\sup F_{\tilde{A}}(x)]>|x\in X\}.\end{array}$$

(1)

Then, the sum of ${\tilde{T}}_{\tilde{A}}(x)$, ${\tilde{I}}_{\tilde{A}}(x)$, and ${\tilde{F}}_{\tilde{A}}(x)$ satisfies the condition of $0\le \sup T_{\tilde{A}}(x)+\sup I_{\tilde{A}}(x)+\sup F_{\tilde{A}}(x)\le 3$.

For convenience, we can use $a=<[T^L,T^U],[I^L,I^U],[F^L,F^U]>$ to represent an interval neutrosophic number (INN) in an INS.

Definition 3 [33].

Let$a_1=<[T_1^L,T_1^U],[I_1^L,I_1^U],[F_1^L,F_1^U]>$and$a_2=<[T_2^L,T_2^U],[I_2^L,I_2^U],[F_2^L,F_2^U]>$be two INNs and$\lambda >0$. Then, the operational rules are defined as follows:

1. 

$a_1\oplus a_2=\langle \left[T_1^L+T_2^L-T_1^L\cdot T_2^L,T_1^U+T_2^U-T_1^U\cdot T_2^U\right],\left[I_1^L\cdot I_2^L,I_1^U\cdot I_2^U\right],\left[F_1^L\cdot F_2^L,F_1^U\cdot F_2^U\right]\rangle ;$

2. 

$a_1\otimes a_2=\langle \left[T_1^L\cdot T_2^L,T_1^U\cdot T_2^U\right],\left[I_1^L+I_2^L-I_1^L\cdot I_2^L,I_1^U+I_2^U-I_1^U\cdot I_2^U\right],\left[F_1^L+F_2^L-F_1^L\cdot F_2^L,F_1^U+F_2^U-F_1^U\cdot F_2^U\right]\rangle ;$

3. 

$\lambda a_1=\langle \left[1-{(1-T_1^L)}^{\lambda },1-{(1-T_1^U)}^{\lambda }\right],\left[{(I_1^L)}^{\lambda },{(I_1^U)}^{\lambda }\right],\left[{(F_1^L)}^{\lambda },{(F_1^U)}^{\lambda }\right]\rangle ;$

4. 

$a_1^{\lambda }=\langle \left[{(T_1^L)}^{\lambda },{(T_1^U)}^{\lambda }\right],\left[1-{(1-I_1^L)}^{\lambda },1-{(1-I_1^U)}^{\lambda }\right],\left[1-{(1-F_1^L)}^{\lambda },1-{(1-F_1^U)}^{\lambda }\right]\rangle .$

Furthermore, for any three INNs $a_1=<[T_1^L,T_1^U],[I_1^L,I_1^U],[F_1^L,F_1^U]>$, $a_2=<[T_2^L,T_2^U],[I_2^L,I_2^U],[F_2^L,F_2^U]>$, $a_3=<[T_3^L,T_3^U],[I_3^L,I_3^U],[F_3^L,F_3^U]>$ and any real numbers $\lambda ,{\lambda }_1>0,{\lambda }_2>0,$ then, there are the following properties:

• $a_1\oplus a_2=a_2\oplus a_1$;
• $a_1\otimes a_2=a_2\otimes a_1$;
• $\lambda (a_1\oplus a_2)=\lambda a_2\oplus \lambda a_1$;
• ${(a_1\otimes a_2)}^{\lambda }=a_1^{\lambda }\oplus a_2^{\lambda }$;
• ${\lambda }_1{a}_1+{\lambda }_2{a}_1=({\lambda }_1+{\lambda }_2)a_1$;
• $a^{{\lambda }_1}\otimes a^{{\lambda }_2}=a^{({\lambda }_1+{\lambda }_2)}$;
• $(a_1\oplus a_2)\oplus a_3=a_1\oplus (a_2\oplus a_3)$;
• $(a_1\otimes a_2)\otimes a_3=a_1\otimes (a_2\otimes a_3)$.

Definition 4 [44].

Let$a=<[T^L,T^U],[I^L,I^U],[F^L,F^U]>$be an INN, a score function$S$of an interval neutrosophic value, based on the truth-membership degree, indeterminacy-membership degree, and falsity-membership degree is defined by

$$S(a)=\frac{2+T^L+T^U-2I^L-2I^U-F^L-F^U}{4}$$

(2)

where$S(a)\in [-1,1]$.

Definition 5.

Let$a=<[T^L,T^U],[I^L,I^U],[F^L,F^U]>$be an INN. Then an accuracy function$A$of an interval neutrosophic value, based on the truth-membership degree, indeterminacy-membership degree, and falsity-membership degree is defined by

$$A(a)=\frac{1}{2}\left(T^L+T^U-I^U\left(1-T^U\right)-I^L\left(1-T^L\right)-F^U\left(1-I^L\right)-F^L\left(1-I^U\right)\right),$$

(3)

where$A(a)\in [-1,1]$.

Definition 6.

Let$a_1=<[T_1^L,T_1^U],[I_1^L,I_1^U],[F_1^L,F_1^U]>$, and$a_2=<[T_2^L,T_2^U],[I_2^L,I_2^U],[F_2^L,F_2^U]>$be two INNs, then the ranking method is defined by

1. 

If$S(a_1)>S(a_2)$, then$a_1>a_2$;

2. 

If$S(a_1)=S(a_2)$, and then$A(a_1)=A(a_2)$, then$a_1>a_2$.

Definition 7 [33].

Let$a_j(j=1,2,\cdots ,n)$be a collection of INNs, and$\omega ={({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)}^T$be the weight vector of$a_j(j=1,2,\cdots ,n)$, with${\omega }_j\in [0,1]$, and${\displaystyle \sum _{j=1}^n{\omega }_j}=1$. Then the interval neutrosophic number weighted averaging (INNWA) operator of dimension$n$is defined by

$$\begin{array}{l}INNWA(a_1,a_2,\cdots ,a_n)={\omega }_1{a}_1+{\omega }_2{a}_2+\cdots {\omega }_n{a}_n={\displaystyle \sum _{j=1}^n{\omega }_j{a}_j}\\ =<[1-{\displaystyle \prod _{j=1}^n{(1-T_j^L)}^{{\omega }_j}},1-{\displaystyle \prod _{j=1}^n{(1-T_j^U)}^{{\omega }_j}}],[{\displaystyle \prod _{j=1}^n{(I_j^L)}^{{\omega }_j}},{\displaystyle \prod _{j=1}^n{(I_j^U)}^{{\omega }_j}}],[{\displaystyle \prod _{j=1}^n{(F_j^L)}^{{\omega }_j}},{\displaystyle \prod _{j=1}^n{(F_j^U)}^{{\omega }_j}}]>.\end{array}$$

(4)

Definition 8 [33].

Let$a_j(j=1,2,\cdots ,n)$be a collection of INNs, and$\omega ={({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)}^T$be the weight vector of$a_j(j=1,2,\cdots ,n)$, with${\omega }_j\in [0,1]$, and${\displaystyle \sum _{j=1}^n{\omega }_j}=1$. Then the interval neutrosophic number weighted geometric (INNWG) operator of dimension$n$is defined by

$$\begin{array}{l}INNWG(a_1,a_2,\cdots ,a_n)={a_1}^{{\omega }_1}\otimes {a_2}^{{\omega }_2}\otimes \cdots {a_n}^{{\omega }_n}={\displaystyle \prod _{j=1}^n{a_j}^{{\omega }_j}}\\ =<[{\displaystyle \prod _{j=1}^n{(T_j^L)}^{{\omega }_j}},{\displaystyle \prod _{j=1}^n{(T_j^U)}^{{\omega }_j}}],[1-{\displaystyle \prod _{j=1}^n{(1-I_j^L)}^{{\omega }_j}},1-{\displaystyle \prod _{j=1}^n{(1-I_j^U)}^{{\omega }_j}}],[1-{\displaystyle \prod _{j=1}^n{(1-F_j^L)}^{{\omega }_j}},1-{\displaystyle \prod _{j=1}^n{(1-F_j^U)}^{{\omega }_j}}]>.\end{array}$$

(5)

3. The Exponential Operational Laws of INSs and INNs

As a supplement, we discussed in detail several properties of the exponential operational laws about INSs and INNs, respectively, in which the bases are positive real numbers and the exponents are INSs or INNs.

Lu and Ye [41] and Ye [43] introduced the exponential operations of SVNSs as follows:

Definition 9 [41].

Let$A=\{\langle x,T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)\rangle |x\in U\}$be a SVNS in a universe of discourse$X$. Then an exponential operational law of the SVNS$A$is defined as

$${\lambda }^A=\{\begin{array}{l}\{\langle x,{\lambda }^{1-T_A\left(x\right)},1-{\lambda }^{I_A\left(x\right)},1-{\lambda }^{F_A\left(x\right)}\rangle |x\in X\},\lambda \in \left(0,1\right),\\ \{\langle x,{(\frac{1}{\lambda })}^{1-T_A\left(x\right)},1-{(\frac{1}{\lambda })}^{I_A\left(x\right)},1-{(\frac{1}{\lambda })}^{F_A\left(x\right)}\rangle |x\in X\},\lambda \ge 1.\end{array}$$

(6)

Definition 10[43].

Let X be a fixed set, $\tilde{A}=\{<x,{\tilde{T}}_{\tilde{A}}(x),{\tilde{I}}_{\tilde{A}}(x),{\tilde{F}}_{\tilde{A}}(x)>|x\in X\}$ be an INS, then we can define the exponential operational law of INSs as:

$${\lambda }^{\tilde{A}}=\{\begin{array}{l}\{\langle x,\left[{\lambda }^{1-\inf T_{\tilde{A}}\left(x\right)},{\lambda }^{1-\sup T_{\tilde{A}}\left(x\right)}\right],\left[1-{\lambda }^{\inf I_{\tilde{A}}\left(x\right)},1-{\lambda }^{\sup I_{\tilde{A}}\left(x\right)}\right],\left[1-{\lambda }^{\inf F_{\tilde{A}}\left(x\right)},1-{\lambda }^{\sup F_{\tilde{A}}\left(x\right)}\right]\rangle |x\in X\},\lambda \in \left(0,1\right),\\ \{\langle x,\left[{\left(\frac{1}{\lambda }\right)}^{1-\inf T_{\tilde{A}}\left(x\right)},{\left(\frac{1}{\lambda }\right)}^{1-\sup T_{\tilde{A}}\left(x\right)}\right],\left[1-{\left(\frac{1}{\lambda }\right)}^{\inf I_{\tilde{A}}\left(x\right)},1-{\left(\frac{1}{\lambda }\right)}^{\sup I_{\tilde{A}}\left(x\right)}\right],\left[1-{\left(\frac{1}{\lambda }\right)}^{\inf F_{\tilde{A}}\left(x\right)},1-{\left(\frac{1}{\lambda }\right)}^{\sup F_{\tilde{A}}\left(x\right)}\right]\rangle |x\in X\},\lambda \ge 1.\end{array}$$

(7)

Theorem 1.

The value of${\lambda }^{\tilde{A}}$is an INS.

Proof. 

(1)

Let $\lambda \in \left(0,1\right)$, and $\tilde{A}=\{<x,{\tilde{T}}_{\tilde{A}}(x),{\tilde{I}}_{\tilde{A}}(x),{\tilde{F}}_{\tilde{A}}(x)>|x\in X\}$ be an INS, where ${\tilde{T}}_{\tilde{A}}(x)\subseteq [0,1]$, ${\tilde{I}}_{\tilde{A}}(x)\subseteq [0,1]$ and ${\tilde{F}}_{\tilde{A}}(x)\subseteq [0,1]$ with the condition: $0\le \sup T_{\tilde{A}}(x)+\sup I_{\tilde{A}}(x)+\sup F_{\tilde{A}}(x)\le 3$. So we can get $\left[{\lambda }^{1-\inf T_{\tilde{A}}\left(x\right)},{\lambda }^{1-\sup T_{\tilde{A}}\left(x\right)}\right]\subseteq [0,1],\left[1-{\lambda }^{\inf I_{\tilde{A}}\left(x\right)},1-{\lambda }^{\sup I_{\tilde{A}}\left(x\right)}\right]\subseteq [0,1]$ and $\left[1-{\lambda }^{\inf F_{\tilde{A}}\left(x\right)},1-{\lambda }^{\sup F_{\tilde{A}}\left(x\right)}\right]\subseteq [0,1]$. Then, we get $0\le {\lambda }^{1-\sup T_{\tilde{A}}\left(x\right)}+1-{\lambda }^{\sup I_{\tilde{A}}\left(x\right)}+1-{\lambda }^{\sup F_{\tilde{A}}\left(x\right)}\le 3$. So ${\lambda }^{\tilde{A}}$ is an INS.

(2)

Let $\lambda \in \left(0,1\right)$, and $0\le \frac{1}{\lambda }\le 1$, it is easy to proof that ${\lambda }^{\tilde{A}}$ is an INS.

Combining (1) and (2), it follows that the value of ${\lambda }^{\tilde{A}}$ is an INS. Similarly, we propose an operational law for an INN. □

Definition 11[43].

Let$a=<[T^L,T^U],[I^L,I^U],[F^L,F^U]>$be an INN, then the exponential operational law of the INN$a$is defined as follows:

$${\lambda }^a=\{\begin{array}{l}\langle \left[{\lambda }^{1-T^L},{\lambda }^{1-T^U}\right],\left[1-{\lambda }^{I^L},1-{\lambda }^{I^U}\right],\left[1-{\lambda }^{F^L},1-{\lambda }^{F^U}\right]\rangle ,\lambda \in \left(0,1\right),\\ \langle \left[{\left(\frac{1}{\lambda }\right)}^{1-T^L},{\left(\frac{1}{\lambda }\right)}^{1-T^U}\right],\left[1-{\left(\frac{1}{\lambda }\right)}^{I^L},1-{\left(\frac{1}{\lambda }\right)}^{I^U}\right],\left[1-{\left(\frac{1}{\lambda }\right)}^{F^L},1-{\left(\frac{1}{\lambda }\right)}^{F^U}\right]\rangle ,\lambda \ge 1.\end{array}$$

(8)

It is obvious that ${\lambda }^a$ is also an INN. Let us consider the following example.

Example 1.

Let$a=<[0.4,0.6],[0.1,0.3],[0.2,0.4]>$be an INN, and${\lambda }_1=0.3$and${\lambda }_2=2$are two real numbers. Then, according to Definition 11, we obtain

$$\begin{array}{ll}{\lambda }_1^a& ={0.3}^{<[0.4,0.6],[0.1,0.3],[0.2,0.4]>}=\langle \left[{0.3}^{1-0.4},{0.3}^{1-0.6}\right],\left[1-{0.3}^{0.1},1-{0.3}^{0.3}\right],\left[1-{0.3}^{0.2},1-{0.3}^{0.4}\right]\rangle \\ & =\langle \left[{0.3}^{0.6},{0.3}^{0.4}\right],\left[1-{0.3}^{0.1},1-{0.3}^{0.3}\right],\left[1-{0.3}^{0.2},1-{0.3}^{0.4}\right]\rangle \\ & =\langle \left[0.4856,0.6178\right],\left[0.1134,0.3032\right],\left[0.2140,0.3822\right]\rangle .\end{array}$$

$$\begin{array}{ll}{\lambda }_2^a& =2^{<[0.4,0.6],[0.1,0.3],[0.2,0.4]>}=\langle \left[{\left(\frac{1}{2}\right)}^{1-0.4},{\left(\frac{1}{2}\right)}^{1-0.6}\right],\left[1-{\left(\frac{1}{2}\right)}^{0.1},1-{\left(\frac{1}{2}\right)}^{0.3}\right],\left[1-{\left(\frac{1}{2}\right)}^{0.2},1-{\left(\frac{1}{2}\right)}^{0.4}\right]\rangle \\ & =\langle \left[{0.5}^{0.6},{0.5}^{0.4}\right],\left[1-{0.5}^{0.1},1-{0.5}^{0.3}\right],\left[1-{0.5}^{0.2},1-{0.5}^{0.4}\right]\rangle \\ & =\langle \left[0.6598,0.7579\right],\left[0.0670,0.1877\right],\left[0.1294,0.2421\right]\rangle .\end{array}$$

Here, when $T^L=T^U$, $I^L=I^U$ and $F^L=F^U$, the exponential operational law for INNs is equal to the exponential operational law of SVNNs [41]. When $0^{-}\le T^U+I^U+F^U\le 1$, the exponential operational law for INNs is equivalent to the exponential operational law of IIFNs [40]. When $T^L=T^U$, $I^L=I^U$, $F^L=F^U$ and $0^{-}\le T^U+I^U+F^U\le 1$, the exponential operational law for INSs is equivalent to the exponential operational law of IFNs [39]. So the exponential operational laws of INNs is a more generalized representation, and the exponential operational laws of SVNNs, IIFNs and IFNs are special cases.

Next, we investigate in detail some basic properties of the exponential operational laws of INNs. We notice that when $\lambda \in \left(0,1\right)$, the operational process and the form of ${\lambda }^a$ are similar to the case when $\lambda \ge 1$. So, below we only discuss the case when $\lambda \in \left(0,1\right)$.

Theorem 2.

Let$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2\right)$be two INNs,$\lambda \in \left(0,1\right)$, then

(1) 

${\lambda }^{a_1}\oplus {\lambda }^{a_2}={\lambda }^{a_2}\oplus {\lambda }^{a_1}$;

(2) 

${\lambda }^{a_1}\otimes {\lambda }^{a_2}={\lambda }^{a_2}\otimes {\lambda }^{a_1}$.

Proof. 

By Definition 3 and Definition 11, we have

(1)

$\begin{array}{l}{\lambda }^{a_1}\oplus {\lambda }^{a_2}\\ =\langle \left[{\lambda }^{1-T_1^L},{\lambda }^{1-T_1^U}\right],\left[1-{\lambda }^{I_1^L},1-{\lambda }^{I_1^U}\right],\left[1-{\lambda }^{F_1^L},1-{\lambda }^{F_1^U}\right]\rangle \oplus \langle \left[{\lambda }^{1-T_2^L},{\lambda }^{1-T_2^U}\right],\left[1-{\lambda }^{I_2^L},1-{\lambda }^{I_2^U}\right],\left[1-{\lambda }^{F_2^L},1-{\lambda }^{F_2^U}\right]\rangle \\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L},{\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right),\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right],\left[\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right),\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right]\end{array}\rangle \\ ={\lambda }^{a_2}\oplus {\lambda }^{a_1}.\end{array}$

(2)

$\begin{array}{l}{\lambda }^{a_1}\otimes {\lambda }^{a_2}\\ =\langle \left[{\lambda }^{1-T_1^L},{\lambda }^{1-T_1^U}\right],\left[1-{\lambda }^{I_1^L},1-{\lambda }^{I_1^U}\right],\left[1-{\lambda }^{F_1^L},1-{\lambda }^{F_1^U}\right]\rangle \oplus \langle \left[{\lambda }^{1-T_2^L},{\lambda }^{1-T_2^U}\right],\left[1-{\lambda }^{I_2^L},1-{\lambda }^{I_2^U}\right],\left[1-{\lambda }^{F_2^L},1-{\lambda }^{F_2^U}\right]\rangle \\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L},{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right),\left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right),\left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right]\end{array}\rangle \\ ={\lambda }^{a_2}\otimes {\lambda }^{a_1}.\square \end{array}$

Theorem 3.

Let$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2,3\right)$be three INNs,$\lambda \in \left(0,1\right)$, then

(1) 

$\left({\lambda }^{a_1}\oplus {\lambda }^{a_2}\right)\oplus {\lambda }^{a_3}={\lambda }^{a_1}\oplus \left({\lambda }^{a_2}\oplus {\lambda }^{a_3}\right)$;

(2) 

$\left({\lambda }^{a_1}\otimes {\lambda }^{a_2}\right)\otimes {\lambda }^{a_3}={\lambda }^{a_1}\otimes \left({\lambda }^{a_2}\otimes {\lambda }^{a_3}\right)$.

Proof. 

By Definition 3 and Definition 11, we have

(1)

$\begin{array}{l}\left({\lambda }^{a_1}\oplus {\lambda }^{a_2}\right)\oplus {\lambda }^{a_3}\\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L},{\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right),\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right),\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right]\end{array}\rangle \\ \oplus \langle \left[{\lambda }^{1-T_3^L},{\lambda }^{1-T_3^U}\right],\left[1-{\lambda }^{I_3^L},1-{\lambda }^{I_3^U}\right],\left[1-{\lambda }^{F_3^L},1-{\lambda }^{F_3^U}\right]\rangle \\ =\langle \begin{array}{l}\left[\begin{array}{l}\left({\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\right)+{\lambda }^{1-T_3^L}-\left({\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\right)\cdot {\lambda }^{1-T_3^L},\\ \left({\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right)+{\lambda }^{1-T_3^U}-\left({\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right)\cdot {\lambda }^{1-T_3^U}\end{array}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right),\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right),\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[\begin{array}{l}{\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}+{\lambda }^{1-T_3^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_3^L}-{\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L}+{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L},\\ {\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}+{\lambda }^{1-T_3^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_3^U}-{\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}+{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\end{array}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right),\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right),\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[\begin{array}{l}{\lambda }^{1-T_1^L}+\left({\lambda }^{1-T_2^L}+{\lambda }^{1-T_3^L}-{\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L}\right)-{\lambda }^{1-T_1^L}\cdot \left({\lambda }^{1-T_2^L}+{\lambda }^{1-T_3^L}-{\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L}\right),\\ {\lambda }^{1-T_1^U}+\left({\lambda }^{1-T_2^U}+{\lambda }^{1-T_3^U}-{\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\right)-{\lambda }^{1-T_1^U}\cdot \left({\lambda }^{1-T_2^U}+{\lambda }^{1-T_3^U}-{\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\right)\end{array}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right),\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right),\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\right]\end{array}\rangle \\ =\langle \left[{\lambda }^{1-T_1^L},{\lambda }^{1-T_1^U}\right],\left[1-{\lambda }^{I_1^L},1-{\lambda }^{I_1^U}\right],\left[1-{\lambda }^{F_1^L},1-{\lambda }^{F_1^U}\right]\rangle \oplus \\ \langle \begin{array}{l}\left[{\lambda }^{1-T_2^L}+{\lambda }^{1-T_3^L}-{\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L},{\lambda }^{1-T_2^U}+{\lambda }^{1-T_3^U}-{\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\right],\\ \left[\left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right),\left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\right],\left[\left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right),\left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\right]\end{array}\rangle \\ ={\lambda }^{a_1}\oplus \left({\lambda }^{a_2}\oplus {\lambda }^{a_3}\right).\end{array}$

(2)

$\begin{array}{l}\left({\lambda }^{a_1}\otimes {\lambda }^{a_2}\right)\otimes {\lambda }^{a_3}\\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L},{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right),\left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right),\left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right]\end{array}\rangle \\ \otimes \langle \left[{\lambda }^{1-T_3^L},{\lambda }^{1-T_3^U}\right],\left[1-{\lambda }^{I_3^L},1-{\lambda }^{I_3^U}\right],\left[1-{\lambda }^{F_3^L},1-{\lambda }^{F_3^U}\right]\rangle \\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L},{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\right],\\ \left[\begin{array}{l}\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)+\left(1-{\lambda }^{I_3^L}\right)-\left(\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)\right)\cdot \left(1-{\lambda }^{I_3^L}\right),\\ \left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)+\left(1-{\lambda }^{I_3^U}\right)-\left(\left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\end{array}\right],\\ \left[\begin{array}{l}\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)+\left(1-{\lambda }^{F_3^L}\right)-\left(\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)\right)\cdot \left(1-{\lambda }^{F_3^L}\right),\\ \left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)+\left(1-{\lambda }^{F_3^U}\right)-\left(\left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\end{array}\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L},{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\right],\\ \left[\begin{array}{l}\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)+\left(1-{\lambda }^{I_3^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right)-\left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right)+\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right),\\ \left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)+\left(1-{\lambda }^{I_3^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)-\left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)+\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\end{array}\right],\\ \left[\begin{array}{l}\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)+\left(1-{\lambda }^{F_3^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right)+\left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right),\\ \left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)+\left(1-{\lambda }^{F_3^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)+\left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\end{array}\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\cdot {\lambda }^{1-T_3^L},{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\cdot {\lambda }^{1-T_3^U}\right],\\ \left[\begin{array}{l}\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)+\left(1-{\lambda }^{I_3^L}\right)-\left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(\left(1-{\lambda }^{I_2^L}\right)+\left(1-{\lambda }^{I_3^L}\right)-\left(1-{\lambda }^{I_2^L}\right)\cdot \left(1-{\lambda }^{I_3^L}\right)\right),\\ \left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)+\left(1-{\lambda }^{I_3^U}\right)-\left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(\left(1-{\lambda }^{I_2^U}\right)+\left(1-{\lambda }^{I_3^U}\right)-\left(1-{\lambda }^{I_2^U}\right)\cdot \left(1-{\lambda }^{I_3^U}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)+\left(1-{\lambda }^{F_3^L}\right)-\left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(\left(1-{\lambda }^{F_2^L}\right)+\left(1-{\lambda }^{F_3^L}\right)-\left(1-{\lambda }^{F_2^L}\right)\cdot \left(1-{\lambda }^{F_3^L}\right)\right),\\ \left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)+\left(1-{\lambda }^{F_3^U}\right)-\left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(\left(1-{\lambda }^{F_2^U}\right)+\left(1-{\lambda }^{F_3^U}\right)-\left(1-{\lambda }^{F_2^U}\right)\cdot \left(1-{\lambda }^{F_3^U}\right)\right)\end{array}\right]\end{array}\rangle \\ ={\lambda }^{a_1}\otimes \left({\lambda }^{a_2}\otimes {\lambda }^{a_3}\right).\square \end{array}$

Theorem 4.

Let$a=<[T^L,T^U],[I^L,I^U],[F^L,F^U]>$and$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2\right)$be three INNs,$\lambda \in \left(0,1\right)$, $k,k_1,k_2>0$, then

(1) 

$k\left({\lambda }^{a_1}\oplus {\lambda }^{a_2}\right)=k{\lambda }^{a_1}\oplus k{\lambda }^{a_2}$;

(2) 

${\left({\lambda }^{a_1}\otimes {\lambda }^{a_2}\right)}^k={\left({\lambda }^{a_2}\right)}^k\otimes {\left({\lambda }^{a_1}\right)}^k$;

(3) 

$k_1{\lambda }^a\oplus k_2{\lambda }^a=(k_1+k_2){\lambda }^a$;

(4) 

${({\lambda }^a)}^{k_1}\otimes {({\lambda }^a)}^{k_2}={\left({\lambda }^a\right)}^{k_1+k_2}$;

(5) 

${({\lambda }_1)}^a\otimes {({\lambda }_2)}^a={\left({\lambda }_1{\lambda }_2\right)}^a$.

Proof. 

By Definition 3 and Definition 11, we have

(1)

$\begin{array}{l}k\left({\lambda }^{a_1}\oplus {\lambda }^{a_2}\right)\\ =k\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L},{\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right),\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right],\left[\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right),\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[1-{\left(1-\left({\lambda }^{1-T_1^L}+{\lambda }^{1-T_2^L}-{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L}\right)\right)}^k,1-{\left(1-\left({\lambda }^{1-T_1^U}+{\lambda }^{1-T_2^U}-{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right)\right)}^k\right],\\ \left[{\left(\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right)\right)}^k,{\left(\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right)}^k\right],\left[{\left(\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right)\right)}^k,{\left(\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right)}^k\right]\end{array}\rangle \\ =\langle \left[1-{(1-{\lambda }^{1-T_1^L})}^k,1-{(1-{\lambda }^{1-T_1^U})}^k\right],\left[{(1-{\lambda }^{I_1^L})}^k,{(1-{\lambda }^{I_1^U})}^k\right],\left[{(1-{\lambda }^{F_1^L})}^k,{(1-{\lambda }^{F_1^U})}^k\right]\rangle \\ \oplus \langle \left[1-{(1-{\lambda }^{1-T_2^L})}^k,1-{(1-{\lambda }^{1-T_2^U})}^k\right],\left[{(1-{\lambda }^{I_2^L})}^k,{(1-{\lambda }^{I_2^U})}^k\right],\left[{(1-{\lambda }^{F_2^L})}^k,{(1-{\lambda }^{F_2^U})}^k\right]\rangle \\ =k{\lambda }^{a_1}\oplus k{\lambda }^{a_2}.\end{array}$

(2)

$\begin{array}{l}{\left({\lambda }^{a_1}\otimes {\lambda }^{a_2}\right)}^k\\ ={\langle \begin{array}{l}\left[{\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L},{\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U}\right],\\ \left[\left(1-{\lambda }^{I_1^L}\right)+\left(1-{\lambda }^{I_2^L}\right)-\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right),\left(1-{\lambda }^{I_1^U}\right)+\left(1-{\lambda }^{I_2^U}\right)-\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right)\right],\\ \left[\left(1-{\lambda }^{F_1^L}\right)+\left(1-{\lambda }^{F_2^L}\right)-\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right),\left(1-{\lambda }^{F_1^U}\right)+\left(1-{\lambda }^{F_2^U}\right)-\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right)\right]\end{array}\rangle }^k\\ =\langle \begin{array}{l}\left[{({\lambda }^{1-T_1^L}\cdot {\lambda }^{1-T_2^L})}^k,{({\lambda }^{1-T_1^U}\cdot {\lambda }^{1-T_2^U})}^k\right],\\ \left[1-{(1-\left(1-{\lambda }^{I_1^L}\right)-\left(1-{\lambda }^{I_2^L}\right)+\left(1-{\lambda }^{I_1^L}\right)\cdot \left(1-{\lambda }^{I_2^L}\right))}^k,1-{(1-\left(1-{\lambda }^{I_1^U}\right)-\left(1-{\lambda }^{I_2^U}\right)+\left(1-{\lambda }^{I_1^U}\right)\cdot \left(1-{\lambda }^{I_2^U}\right))}^k\right],\\ \left[1-{(1-\left(1-{\lambda }^{F_1^L}\right)-\left(1-{\lambda }^{F_2^L}\right)+\left(1-{\lambda }^{F_1^L}\right)\cdot \left(1-{\lambda }^{F_2^L}\right))}^k,1-{(1-\left(1-{\lambda }^{F_1^U}\right)-\left(1-{\lambda }^{F_2^U}\right)+\left(1-{\lambda }^{F_1^U}\right)\cdot \left(1-{\lambda }^{F_2^U}\right))}^k\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[{({\lambda }^{1-T_2^L})}^k\cdot {({\lambda }^{1-T_1^L})}^k,{({\lambda }^{1-T_2^U})}^k\cdot {({\lambda }^{1-T_1^U})}^k\right],\\ \left[\begin{array}{l}\left(1-{(1-\left(1-{\lambda }^{I_2^L}\right))}^k\right)+\left(1-{(1-\left(1-{\lambda }^{I_1^L}\right))}^k\right)-\left(1-{(1-\left(1-{\lambda }^{I_2^L}\right))}^k\right)\cdot \left(1-{(1-\left(1-{\lambda }^{I_1^L}\right))}^k\right),\\ \left(1-{(1-\left(1-{\lambda }^{I_2^U}\right))}^k\right)+\left(1-{(1-\left(1-{\lambda }^{I_1^U}\right))}^k\right)-\left(1-{(1-\left(1-{\lambda }^{I_2^U}\right))}^k\right)\cdot \left(1-{(1-\left(1-{\lambda }^{I_1^U}\right))}^k\right)\end{array}\right],\\ \left[\begin{array}{l}\left(1-{(1-\left(1-{\lambda }^{F_2^L}\right))}^k\right)+\left(1-{(1-\left(1-{\lambda }^{F_1^L}\right))}^k\right)-\left(1-{(1-\left(1-{\lambda }^{F_2^L}\right))}^k\right)\cdot \left(1-{(1-\left(1-{\lambda }^{F_1^L}\right))}^k\right),\\ \left(1-{(1-\left(1-{\lambda }^{F_2^U}\right))}^k\right)+\left(1-{(1-\left(1-{\lambda }^{F_1^U}\right))}^k\right)-\left(1-{(1-\left(1-{\lambda }^{F_2^U}\right))}^k\right)\cdot \left(1-{(1-\left(1-{\lambda }^{F_1^U}\right))}^k\right)\end{array}\right]\end{array}\rangle \\ ={\left({\lambda }^{a_2}\right)}^k\otimes {\left({\lambda }^{a_1}\right)}^k.\end{array}$

(3)

$\begin{array}{l}{k}_1{\lambda }^a\oplus k_2{\lambda }^a\\ =k_1\langle \left[{\lambda }^{1-T^L},{\lambda }^{1-T^U}\right],\left[1-{\lambda }^{I^L},1-{\lambda }^{I^U}\right],\left[1-{\lambda }^{F^L},1-{\lambda }^{F^U}\right]\rangle \\ \oplus k_2\langle \left[{\lambda }^{1-T^L},{\lambda }^{1-T^U}\right],\left[1-{\lambda }^{I^L},1-{\lambda }^{I^U}\right],\left[1-{\lambda }^{F^L},1-{\lambda }^{F^U}\right]\rangle \\ =\langle \left[1-{(1-{\lambda }^{1-T^L})}^{k_1},1-{(1-{\lambda }^{1-T^U})}^{k_1}\right],\left[{(1-{\lambda }^{I^L})}^{k_1},{(1-{\lambda }^{I^U})}^{k_1}\right],\left[{(1-{\lambda }^{F^L})}^{k_1},{(1-{\lambda }^{F^U})}^{k_1}\right]\rangle \\ \oplus \langle \left[1-{(1-{\lambda }^{1-T^L})}^{k_2},1-{(1-{\lambda }^{1-T^U})}^{k_2}\right],\left[{(1-{\lambda }^{I^L})}^{k_2},{(1-{\lambda }^{I^U})}^{k_2}\right],\left[{(1-{\lambda }^{F^L})}^{k_2},{(1-{\lambda }^{F^U})}^{k_2}\right]\rangle \\ =\langle \begin{array}{l}\left[\begin{array}{l}1-{(1-{\lambda }^{1-T^L})}^{k_1}+1-{(1-{\lambda }^{1-T^L})}^{k_2}-\left(1-{(1-{\lambda }^{1-T^L})}^{k_1}\right)\cdot \left(1-{(1-{\lambda }^{1-T^L})}^{k_2}\right),\\ 1-{(1-{\lambda }^{1-T^U})}^{k_1}+1-{(1-{\lambda }^{1-T^U})}^{k_2}-\left(1-{(1-{\lambda }^{1-T^U})}^{k_1}\right)\cdot \left(1-{(1-{\lambda }^{1-T^U})}^{k_2}\right)\end{array}\right],\\ \left[{(1-{\lambda }^{I^L})}^{k_1}\cdot {(1-{\lambda }^{I^L})}^{k_2},{(1-{\lambda }^{I^U})}^{k_1}\cdot {(1-{\lambda }^{I^U})}^{k_2}\right],\left[{(1-{\lambda }^{F^L})}^{k_1}\cdot {(1-{\lambda }^{F^L})}^{k_2},{(1-{\lambda }^{F^U})}^{k_1}\cdot {(1-{\lambda }^{F^U})}^{k_2}\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[\begin{array}{l}1-{(1-{\lambda }^{1-T^L})}^{k_2}{(1-{\lambda }^{1-T^L})}^{k_1},\\ 1-{(1-{\lambda }^{1-T^U})}^{k_2}{(1-{\lambda }^{1-T^U})}^{k_1}\end{array}\right],\\ \left[{(1-{\lambda }^{I^L})}^{k_1}\cdot {(1-{\lambda }^{I^L})}^{k_2},{(1-{\lambda }^{I^U})}^{k_1}\cdot {(1-{\lambda }^{I^U})}^{k_2}\right],\left[{(1-{\lambda }^{F^L})}^{k_1}\cdot {(1-{\lambda }^{F^L})}^{k_2},{(1-{\lambda }^{F^U})}^{k_1}\cdot {(1-{\lambda }^{F^U})}^{k_2}\right]\end{array}\rangle \\ =(k_1+k_2){\lambda }^a.\end{array}$

(4)

$\begin{array}{l}{({\lambda }^a)}^{k_1}\otimes {({\lambda }^a)}^{k_2}\\ ={\langle \left[{\lambda }^{1-T^L},{\lambda }^{1-T^U}\right],\left[1-{\lambda }^{I^L},1-{\lambda }^{I^U}\right],\left[1-{\lambda }^{F^L},1-{\lambda }^{F^U}\right]\rangle }^{k_1}\\ \otimes {\langle \left[{\lambda }^{1-T^L},{\lambda }^{1-T^U}\right],\left[1-{\lambda }^{I^L},1-{\lambda }^{I^U}\right],\left[1-{\lambda }^{F^L},1-{\lambda }^{F^U}\right]\rangle }^{k_2}\\ =\langle \left[{({\lambda }^{1-T^L})}^{k_1},{({\lambda }^{1-T^U})}^{k_1}\right],\left[1-{(1-\left(1-{\lambda }^{I^L}\right))}^{k_1},1-{(1-\left(1-{\lambda }^{I^U}\right))}^{k_1}\right],\left[1-{(1-\left(1-{\lambda }^{F^L}\right))}^{k_1},1-{(1-\left(1-{\lambda }^{F^U}\right))}^{k_1}\right]\rangle \\ \otimes \langle \left[{({\lambda }^{1-T^L})}^{k_2},{({\lambda }^{1-T^U})}^{k_2}\right],\left[1-{(1-\left(1-{\lambda }^{I^L}\right))}^{k_2},1-{(1-\left(1-{\lambda }^{I^U}\right))}^{k_2}\right],\left[1-{(1-\left(1-{\lambda }^{F^L}\right))}^{k_2},1-{(1-\left(1-{\lambda }^{F^U}\right))}^{k_2}\right]\rangle \\ =\langle \begin{array}{l}\left[{({\lambda }^{1-T^L})}^{k_1}\cdot {({\lambda }^{1-T^L})}^{k_2},{({\lambda }^{1-T^U})}^{k_1}\cdot {({\lambda }^{1-T^U})}^{k_2}\right],\\ \left[\begin{array}{l}1-{(1-\left(1-{\lambda }^{I^L}\right))}^{k_1}+1-{(1-\left(1-{\lambda }^{I^L}\right))}^{k_2}-\left(1-{(1-\left(1-{\lambda }^{I^L}\right))}^{k_1}\right)\cdot \left(1-{(1-\left(1-{\lambda }^{I^L}\right))}^{k_2}\right),\\ 1-{(1-\left(1-{\lambda }^{I^U}\right))}^{k_1}+1-{(1-\left(1-{\lambda }^{I^U}\right))}^{k_2}-\left(1-{(1-\left(1-{\lambda }^{I^U}\right))}^{k_1}\right)\cdot \left(1-{(1-\left(1-{\lambda }^{I^U}\right))}^{k_2}\right)\end{array}\right],\\ \left[\begin{array}{l}1-{(1-\left(1-{\lambda }^{F^L}\right))}^{k_1}+1-{(1-\left(1-{\lambda }^{F^L}\right))}^{k_2}-\left(1-{(1-\left(1-{\lambda }^{F^L}\right))}^{k_1}\right)\cdot \left(1-{(1-\left(1-{\lambda }^{F^L}\right))}^{k_2}\right),\\ 1-{(1-\left(1-{\lambda }^{F^U}\right))}^{k_1}+1-{(1-\left(1-{\lambda }^{F^U}\right))}^{k_2}-\left(1-{(1-\left(1-{\lambda }^{F^U}\right))}^{k_1}\right)\cdot \left(1-{(1-\left(1-{\lambda }^{F^U}\right))}^{k_2}\right)\end{array}\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[{({\lambda }^{1-T^L})}^{k_1}\cdot {({\lambda }^{1-T^L})}^{k_2},{({\lambda }^{1-T^U})}^{k_1}\cdot {({\lambda }^{1-T^U})}^{k_2}\right],\\ \left[1-{({\lambda }^{I^L})}^{k_2}{({\lambda }^{I^L})}^{k_1},1-{({\lambda }^{I^U})}^{k_2}{({\lambda }^{I^U})}^{k_1}\right],\\ \left[1-{({\lambda }^{F^L})}^{k_2}{({\lambda }^{F^L})}^{k_1},1-{({\lambda }^{F^U})}^{k_2}{({\lambda }^{F^U})}^{k_1}\right]\end{array}\rangle \\ ={\left({\lambda }^a\right)}^{k_1+k_2}.\end{array}$

(5)

$\begin{array}{l}{({\lambda }_1)}^a\otimes {({\lambda }_2)}^a\\ =\langle \left[{\lambda }_1^{1-T^L},{\lambda }_1^{1-T^U}\right],\left[1-{\lambda }_1^{I^L},1-{\lambda }_1^{I^U}\right],\left[1-{\lambda }_1^{F^L},1-{\lambda }_1^{F^U}\right]\rangle \\ \otimes \langle \left[{\lambda }_2^{1-T^L},{\lambda }_2^{1-T^U}\right],\left[1-{\lambda }_2^{I^L},1-{\lambda }_2^{I^U}\right],\left[1-{\lambda }_2^{F^L},1-{\lambda }_2^{F^U}\right]\rangle \\ =\langle \begin{array}{l}\left[{\lambda }_1^{1-T^L}\cdot {\lambda }_2^{1-T^L},{\lambda }_1^{1-T^U}\cdot {\lambda }_2^{1-T^U}\right],\\ \left[1-{\lambda }_1^{I^L}+1-{\lambda }_2^{I^L}-\left(1-{\lambda }_1^{I^L}\right)\cdot \left(1-{\lambda }_2^{I^L}\right),1-{\lambda }_1^{I^U}+1-{\lambda }_2^{I^U}-\left(1-{\lambda }_1^{I^U}\right)\cdot \left(1-{\lambda }_2^{I^U}\right)\right],\\ \left[1-{\lambda }_1^{F^L}+1-{\lambda }_2^{F^L}-\left(1-{\lambda }_1^{F^L}\right)\cdot \left(1-{\lambda }_2^{F^L}\right),1-{\lambda }_1^{F^U}+1-{\lambda }_2^{F^U}-\left(1-{\lambda }_1^{F^U}\right)\cdot \left(1-{\lambda }_2^{F^U}\right)\right]\end{array}\rangle \\ =\langle \begin{array}{l}\left[{\lambda }_1^{1-T^L}\cdot {\lambda }_2^{1-T^L},{\lambda }_1^{1-T^U}\cdot {\lambda }_2^{1-T^U}\right],\\ \left[1-{\lambda }_1^{I^L}{\lambda }_2^{I^L},1-{\lambda }_1^{I^U}{\lambda }_2^{I^U}\right],\\ \left[1-{\lambda }_1^{F^L}{\lambda }_2^{F^L},1-{\lambda }_1^{F^U}{\lambda }_2^{F^U}\right]\end{array}\rangle \\ =\langle \left[{\left({\lambda }_1{\lambda }_2\right)}^{1-T^L},{\left({\lambda }_1{\lambda }_2\right)}^{1-T^U}\right],\left[1-{\left({\lambda }_1{\lambda }_2\right)}^{I^L},1-{\left({\lambda }_1{\lambda }_2\right)}^{I^U}\right],\left[1-{\left({\lambda }_1{\lambda }_2\right)}^{F^L},1-{\left({\lambda }_1{\lambda }_2\right)}^{F^U}\right]\rangle \\ ={\left({\lambda }_1{\lambda }_2\right)}^a.\square \end{array}$

Theorem 5.

Let$a=<[T^L,T^U],[I^L,I^U],[F^L,F^U]>$be an INN. If${\lambda }_1\ge {\lambda }_2$, then one can obtain${\left({\lambda }_1\right)}^a\ge {\left({\lambda }_2\right)}^a$for${\lambda }_1,{\lambda }_2\in \left(0,1\right)$, and${\left({\lambda }_1\right)}^a\le {\left({\lambda }_2\right)}^a$for${\lambda }_1,{\lambda }_2\ge 1$.

Proof. 

When ${\lambda }_1\ge {\lambda }_2$ and ${\lambda }_1,{\lambda }_2\in \left(0,1\right)$, based on Definition 11, we can obtain

$$\begin{array}{c}{\left({\lambda }_1\right)}^a=\langle \left[{\lambda }_1^{1-T^L},{\lambda }_1^{1-T^U}\right],\left[1-{\lambda }_1^{I^L},1-{\lambda }_1^{I^U}\right],\left[1-{\lambda }_1^{F^L},1-{\lambda }_1^{F^U}\right]\rangle ,\\ {\left({\lambda }_2\right)}^a=\langle \left[{\lambda }_2^{1-T^L},{\lambda }_2^{1-T^U}\right],\left[1-{\lambda }_2^{I^L},1-{\lambda }_2^{I^U}\right],\left[1-{\lambda }_2^{F^L},1-{\lambda }_2^{F^U}\right]\rangle ,\end{array}$$

Since ${\lambda }_1\ge {\lambda }_2$, then ${\lambda }_1^{1-T^L}\ge {\lambda }_2^{1-T^L}$, ${\lambda }_1^{1-T^U}\ge {\lambda }_2^{1-T^U}$, and $1-{\lambda }_1^{I^L}\le 1-{\lambda }_2^{I^L}$, $1-{\lambda }_1^{I^U}\le 1-{\lambda }_2^{I^U}$, and $1-{\lambda }_1^{F^L}\ge 1-{\lambda }_2^{F^L}$, $1-{\lambda }_1^{F^U}\ge 1-{\lambda }_2^{F^U}$.

$$\begin{array}{ll}S({\left({\lambda }_1\right)}^a)& =\frac{2+{\lambda }_1^{1-T^L}+{\lambda }_1^{1-T^U}-2\left(1-{\lambda }_1^{I^L}\right)-2\left(1-{\lambda }_1^{I^U}\right)-\left(1-{\lambda }_1^{F^L}\right)-\left(1-{\lambda }_1^{F^U}\right)}{4}\\ & =\frac{{\lambda }_1^{1-T^L}+{\lambda }_1^{1-T^U}+2{\lambda }_1^{I^L}+2{\lambda }_1^{I^U}+{\lambda }_1^{F^L}+{\lambda }_1^{F^U}-4}{4},\end{array}$$

$$\begin{array}{ll}S({\left({\lambda }_2\right)}^a)& =\frac{2+{\lambda }_2^{1-T^L}+{\lambda }_2^{1-T^U}-2\left(1-{\lambda }_2^{I^L}\right)-2\left(1-{\lambda }_2^{I^U}\right)-\left(1-{\lambda }_2^{F^L}\right)-\left(1-{\lambda }_2^{F^U}\right)}{4}\\ & =\frac{{\lambda }_2^{1-T^L}+{\lambda }_2^{1-T^U}+2{\lambda }_2^{I^L}+2{\lambda }_2^{I^U}+{\lambda }_2^{F^L}+{\lambda }_2^{F^U}-4}{4},\end{array}$$

$$\begin{array}{l}S({\left({\lambda }_1\right)}^a)-S({\left({\lambda }_2\right)}^a)\\ =\frac{{\lambda }_1^{1-T^L}+{\lambda }_1^{1-T^U}+2{\lambda }_1^{I^L}+2{\lambda }_1^{I^U}+{\lambda }_1^{F^L}+{\lambda }_1^{F^U}-4}{4}-\frac{{\lambda }_2^{1-T^L}+{\lambda }_2^{1-T^U}+2{\lambda }_2^{I^L}+2{\lambda }_2^{I^U}+{\lambda }_2^{F^L}+{\lambda }_2^{F^U}-4}{4}\\ =\frac{\left({\lambda }_1^{1-T^L}-{\lambda }_2^{1-T^L}\right)+\left({\lambda }_1^{1-T^U}-{\lambda }_2^{1-T^U}\right)+\left(2{\lambda }_1^{I^L}-2{\lambda }_2^{I^L}\right)+\left(2{\lambda }_1^{I^U}-2{\lambda }_2^{I^U}\right)+\left({\lambda }_1^{F^L}-{\lambda }_2^{F^L}\right)+\left({\lambda }_1^{F^U}-{\lambda }_2^{F^U}\right)}{4}\\ \ge 0.\end{array}$$

Then $S({\left({\lambda }_1\right)}^a)\ge S({\left({\lambda }_2\right)}^a)$, ${\left({\lambda }_1\right)}^a\ge {\left({\lambda }_2\right)}^a$.

Then, when ${\lambda }_1,{\lambda }_2\ge 1$ and ${\lambda }_1\ge {\lambda }_2$, we can know $0\le \frac{1}{{\lambda }_1}\le \frac{1}{{\lambda }_2}\le 1$. As discussed above, we can obtain ${\left({\lambda }_1\right)}^a\le {\left({\lambda }_2\right)}^a$. This completes the proof. □

In what follows, let us take a look at some special values about ${\lambda }^a$:

(1)

If $\lambda =1$, then ${\lambda }^a=\langle \left[1,1\right],\left[0,0\right],\left[0,0\right]\rangle =\langle 1,0,0\rangle$;

(2)

If $a=\langle \left[1,1\right],\left[0,0\right],\left[0,0\right]\rangle =\langle 1,0,0\rangle$, then ${\lambda }^a=\langle \left[1,1\right],\left[0,0\right],\left[0,0\right]\rangle =\langle 1,0,0\rangle$;

(3)

If $a=\langle \left[0,0\right]\left[1,1\right],\left[1,1\right],\rangle =\langle 0,1,1\rangle$, then

$${\lambda }^a=\langle \left[\lambda ,\lambda \right],\left[1-\lambda ,1-\lambda \right],\left[1-\lambda ,1-\lambda \right]\rangle$$

4. Interval Neutrosophic Weighted Exponential Aggregation (INWEA) Operator

Aggregation operators have been commonly used to aggregate the evaluation information in decision making. Here, we utilize the INNs rather than real numbers as weight of criterion, which is more comprehensive and reasonable. In this section, we propose an interval neutrosophic weighted exponential aggregation (INWEA) operator. Furthermore, some characteristics of the proposed aggregation operator, such as boundedness and monotonicity are discussed in detail.

Definition 12.

Let$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2,\cdots ,n\right)$be a collection of INNs, and${\lambda }_i\in \left(0,1\right)\left(i=1,2,\cdots ,n\right)$be the collection of real numbers, and let INWEA:${\mathsf{\Theta }}^n\to \mathsf{\Theta }$. If

$$INWEA\left(a_1,a_2,\cdots ,a_n\right)={{\lambda }_1}^{a_1}\otimes {{\lambda }_2}^{a_2}\otimes \cdots \otimes {{\lambda }_n}^{a_n}.$$

(9)

Then the function INWEA is called an interval neutrosophic weighted exponential aggregation (INWEA) operator, where$a_i\left(i=1,2,\cdots ,n\right)$are the exponential weighting vectors of attribute values${\lambda }_i\left(i=1,2,\cdots ,n\right)$.

Theorem 6[43].

Let$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2,\cdots ,n\right)$be a collection of INNs, the aggregated value by using the INWEA operator is also an INN, where

$$\begin{array}{l}INWEA\left(a_1,a_2,\cdots ,a_n\right)\\ =\{\begin{array}{l}\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right]\rangle ,{\lambda }_i\in \left(0,1\right)\\ \langle \left[{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{1-T_i^L}},{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{I_i^L}},1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{F_i^L}},1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{F_i^U}}\right]\rangle ,{\lambda }_i\ge 1\end{array}\end{array}$$

(10)

and$a_i\left(i=1,2,\cdots ,n\right)$are the exponential weights of${\lambda }_i\left(i=1,2,\cdots ,n\right)$.

Proof. 

By using mathematical induction, we can prove the Equation (10).

(1)

When $n=2$, we have

$$\begin{array}{l}INWEA\left(a_1,a_2\right)={{\lambda }_1}^{a_1}\otimes {{\lambda }_2}^{a_2}\\ =\langle \left[{\lambda }_1^{1-T_1^L},{\lambda }_1^{1-T_1^U}\right],\left[1-{\lambda }_1^{I_1^L},1-{\lambda }_1^{I_1^U}\right],\left[1-{\lambda }_1^{F_1^L},1-{\lambda }_1^{F_1^U}\right]\rangle \\ \otimes \langle \left[{\lambda }_2^{1-T_2^L},{\lambda }_2^{1-T_2^U}\right],\left[1-{\lambda }_2^{I_2^L},1-{\lambda }_2^{I_2^U}\right],\left[1-{\lambda }_2^{F_2^L},1-{\lambda }_2^{F_2^U}\right]\rangle \\ =\langle \begin{array}{l}\left[{\lambda }_1^{1-T_1^L}\cdot {\lambda }_2^{1-T_2^L},{\lambda }_1^{1-T_1^U}\cdot {\lambda }_2^{1-T_2^U}\right],\\ \left[1-{\lambda }_1^{I_1^L}+1-{\lambda }_2^{I_2^L}-\left(1-{\lambda }_1^{I_1^L}\right)\cdot \left(1-{\lambda }_2^{I_2^L}\right),1-{\lambda }_1^{I_1^U}+1-{\lambda }_2^{I_2^U}-\left(1-{\lambda }_1^{I_1^U}\right)\cdot \left(1-{\lambda }_2^{I_2^U}\right)\right],\\ \left[1-{\lambda }_1^{F_1^L}+1-{\lambda }_2^{F_2^L}-\left(1-{\lambda }_1^{F_1^L}\right)\cdot \left(1-{\lambda }_2^{F_2^L}\right),1-{\lambda }_1^{F_1^U}+1-{\lambda }_2^{F_2^U}-\left(1-{\lambda }_1^{F_1^U}\right)\cdot \left(1-{\lambda }_2^{F_2^U}\right)\right]\end{array}\rangle \\ =\langle \left[{\displaystyle \prod _{i=1}^2{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^2{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^2{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^2{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^2{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^2{\lambda }_i^{F_i^U}}\right]\rangle .\end{array}$$

(11)

(2)

When $n=k$, according to Equation (10) there is the following formula:

$$\begin{array}{l}INWEA\left(a_1,a_2,\cdots ,a_k\right)\\ =\langle \left[{\displaystyle \prod _{i=1}^k{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^k{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{F_i^U}}\right]\rangle .\end{array}$$

(12)

When $n=k+1$, we have the following results based on the operational rules of Definition 3 and combining (2) and (3).

$\begin{array}{l}INWEA\left(a_1,a_2,\cdots ,a_k,a_{k+1}\right)\\ =\langle \left[{\displaystyle \prod _{i=1}^k{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^k{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{F_i^U}}\right]\rangle \otimes a_{k+1}\\ =\langle \left[{\displaystyle \prod _{i=1}^k{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^k{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^k{\lambda }_i^{F_i^U}}\right]\rangle \\ \otimes \langle \left[{\lambda }_{k+1}^{1-T_{k+1}^L},{\lambda }_{k+1}^{1-T_{k+1}^U}\right],\left[1-{\lambda }_{k+1}^{I_{k+1}^L},1-{\lambda }_{k+1}^{I_{k+1}^U}\right],\left[1-{\lambda }_{k+1}^{F_{k+1}^L},1-{\lambda }_{k+1}^{F_{k+1}^U}\right]\rangle \\ =\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right]\rangle .\square \end{array}$

Therefore, for the above results we determine that Equation (10) holds for any $n$. Thus, the proof is completed. When ${\lambda }_i\ge 1$, and $0<\frac{1}{{\lambda }_i}\le 1$, we can also obtain

$$\begin{array}{l}INWEA\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)\\ =\langle \left[{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{1-T_i^L}},{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{I_i^L}},1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{F_i^L}},1-{\displaystyle \prod _{i=1}^n{\left(\frac{1}{{\lambda }_i}\right)}^{F_i^U}}\right]\rangle .\end{array}$$

and the aggregated value is an INN.

Here, we discuss the relationship between the $INWEA$ operator and other exponential aggregation operators. When $T^L=T^U$, $I^L=I^U$ and $F^L=F^U$, the $INWEA$ operator of INNs is equivalent to the $SVNWEA$ operator of SVNNs [41].

$$INWEA\left(a_1,a_2,\cdots ,a_n\right)=\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i}}\right]\rangle =SVNWEA\left(a_1,a_2,\cdots ,a_n\right)$$

When $0^{-}\le T^U+I^U+F^U\le 1$, the $INWEA$ operator of INNs is equivalent to the $IIFWEA$ operator of IIFNs [40]. When $T^L=T^U$, $I^L=I^U$, $F^L=F^U$ and $0^{-}\le T^U+I^U+F^U\le 1$, the $INWEA$ operator of INNs is equivalent to the $IFWEA$ operator of IFNs [39]. So the $INWEA$ operator of INNs defined by us is a more generalized representation, and the other exponential aggregation operators of SVNNs, IIFNs and IFNs are special cases.

Theorem 7.

The INWEA operator has the following properties:

(1) 

Boundedness: Let$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2,\cdots ,n\right)$be a collection of INNs, and let$a_{\min }=<[\underset{i}{\min }{T}_i^L,\underset{i}{\min }{T}_i^U],[\underset{i}{\max }{I}_i^L,\underset{i}{\max }{I}_i^U],[\underset{i}{\max }{F}_i^L,\underset{i}{\max }{F}_i^U]>$, $a_{\max }=<[\underset{i}{\max }{T}_i^L,\underset{i}{\max }{T}_i^U],[\underset{i}{\min }{I}_i^L,\underset{i}{\min }{I}_i^U],[\underset{i}{\min }{F}_i^L,\underset{i}{\min }{F}_i^U]>$for$i=1,2,\cdots ,n$,

$$\begin{array}{l}{a}^{-}=\mathrm{INWEA}\left(a_{\min },a_{\min },\cdots ,a_{\min }\right)\\ =\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\min }{T}_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\min }{T}_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{I}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{I}_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{F}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{F}_i^U}}\right]\rangle ,\end{array}$$

$$\begin{array}{l}{a}^{+}=\mathrm{INWEA}\left(a_{max},a_{max},\cdots ,a_{max}\right)\\ =\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\max }{T}_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\max }{T}_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{I}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{I}_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{F}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{F}_i^U}}\right]\rangle ,\end{array}$$

Then$a^{-}\le \mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)\le a^{+}$.

Proof. 

For any $i$, we have $\underset{i}{min}{T}_i^L\le T_i^L\le \underset{i}{max}{T}_i^L$, $\underset{i}{min}{T}_i^U\le T_i^U\le \underset{i}{max}{T}_i^U$, $\underset{i}{min}{I}_i^L\le I_i^L\le \underset{i}{max}{I}_i^L$, $\underset{i}{min}{I}_i^U\le I_i^U\le \underset{i}{max}{I}_i^U$, $\underset{i}{min}{F}_i^L\le F_i^L\le \underset{i}{max}{F}_i^L$, $\underset{i}{min}{F}_i^U\le F_i^U\le \underset{i}{max}{F}_i^U$.

$$\begin{array}{c}{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}\ge {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\min }{T}_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\ge {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\min }{T}_i^U}},\\ 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\le 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{I}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\le 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{I}_i^U}},\\ 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\le 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{F}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\le 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{F}_i^U}},\\ {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}\le {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{mxa}{T}_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\le {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{mxa}{T}_i^U}},\\ 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{I}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{I}_i^U}},\\ 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{F}_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{F}_i^U}},\end{array}$$

Let $\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)=a$, $a^{-}=<[T^{L-},T^{U-}],[I^{L-},I^{U-}],[F^{L-},F^{U-}]>$, and $a^{+}=<[T^{L+},T^{U+}],[I^{L+},I^{U+}],[F^{L+},F^{U+}]>$, then based on the score function, where

$$\begin{array}{l}S(a)\\ =\frac{2+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right)}{4}\\ \ge \frac{2+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\min }{T}_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\min }{T}_i^U}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{I}_i^L}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{I}_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{F}_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\max }{F}_i^U}}\right)}{4}\\ =S\left({\alpha }^{-}\right),\end{array}$$

$$\begin{array}{l}S(a)\\ =\frac{2+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right)}{4}\\ \ge \frac{2+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\max }{T}_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-\underset{i}{\max }{T}_i^U}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{I}_i^L}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{I}_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{F}_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{\underset{i}{\min }{F}_i^U}}\right)}{4}\\ =S\left({\alpha }^{+}\right).\square \end{array}$$

In what follows, we discuss three cases:

(I)

If $S\left(a^{-}\right)<S\left(a\right)<S\left(a^{+}\right)$, then $a^{-}<\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)<a^{+}$ holds obviously.

(II)

If $S\left(a\right)=S\left(a^{-}\right)$, then there is

$T^L+T^U-2I^L-2I^U-F^L-F^U=T^{L-}+T^{U-}-2I^{L-}-2I^{U-}-F^{L-}-F^{U-}$. Thus, we can obtain $T^L=T^{L-}$, $T^U=T^{U-}$, $I^L=I^{L-}$, $I^U=I^{U-}$, $F^L=F^{L-}$, $F^U=F^{U-}$. Hence, there is

$$\begin{array}{l}A(a)=\frac{1}{2}\left(T^L+T^U-I^U\left(1-T^U\right)-I^L\left(1-T^L\right)-F^U\left(1-I^L\right)-F^L\left(1-I^U\right)\right)\\ =\frac{1}{2}\left(T^{L-}+T^{U-}-I^{U-}\left(1-T^{U-}\right)-I^{L-}\left(1-T^{L-}\right)-F^{U-}\left(1-I^{L-}\right)-F^{L-}\left(1-I^{U-}\right)\right)\\ =A(a^{-}).\end{array}$$

So we have $\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)=a^{-}$.

(III)

If $S\left(a\right)=S\left(a^{+}\right)$, then there is

$T^L+T^U-2I^L-2I^U-F^L-F^U=T^{L+}+T^{U+}-2I^{L+}-2I^{U+}-F^{L+}-F^{U+}$. Thus, we can obtain $T^L=T^{L+}$, $T^U=T^{U+}$, $I^L=I^{L+}$, $I^U=I^{U+}$, $F^L=F^{L+}$, $F^U=F^{U+}$. Hence, there is

$$\begin{array}{l}A(a)=\frac{1}{2}\left(T^L+T^U-I^U\left(1-T^U\right)-I^L\left(1-T^L\right)-F^U\left(1-I^L\right)-F^L\left(1-I^U\right)\right)\\ =\frac{1}{2}\left(T^{L+}+T^{U+}-I^{U+}\left(1-T^{U+}\right)-I^{L+}\left(1-T^{L+}\right)-F^{U+}\left(1-I^{L+}\right)-F^{L+}\left(1-I^{U+}\right)\right)\\ =A(a^{+}).\end{array}$$

Hence, we have $\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)=a^{+}$.

Based on the above three cases, there is $a^{-}\le \mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)\le a^{+}$.

(2) 

Monotonity: Let$a_i=<[T_i^L,T_i^U],[I_i^L,I_i^U],[F_i^L,F_i^U]>\left(i=1,2,\cdots ,n\right)$and$a_i^{\ast }=<[T_i^{L\ast },T_i^{U\ast }],[I_i^{L\ast },I_i^{U\ast }],[F_i^{L\ast },F_i^{U\ast }]>$be two collections of INNs. If$a_i\le a_i^{\ast }$, then$\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)\le \mathrm{INWEA}\left(a_1^{\ast },a_2^{\ast },\cdots ,a_n^{\ast }\right)$.

Proof. 

Let $a=\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)=\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right]\rangle ,a^{\ast }=\mathrm{INWEA}\left(a_1^{\ast },a_2^{\ast },\cdots ,a_n^{\ast }\right)=\langle \left[{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}},{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}\right],\left[1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{L\ast }}},1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{U\ast }}}\right]\rangle ,$

If $a_i\le a_i^{\ast }$, then $T_i^L\le T_i^{L\ast }$, $T_i^U\le T_i^{U\ast }$, $I_i^L\ge I_i^{L\ast }$, $I_i^U\ge I_i^{U\ast }$, $F_i^L\ge F_i^{L\ast }$, $F_i^U\ge F_i^{U\ast }$ for any $i$. So we have ${\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}\le {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}}$, ${\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\le {\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{L\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\ge 1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}$.

Thus,

$$\begin{array}{l}S(a)\\ =\frac{2+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right)}{4}\\ \le \frac{2+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{L\ast }}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{U\ast }}}\right)}{4}\\ =S\left({\alpha }^{\ast }\right).\end{array}$$

Hence, there are the following two cases:

(1)

If $S\left(a\right)<S\left(a^{\ast }\right)$, then we can get $\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)<\mathrm{INWEA}\left(a_1^{\ast },a_2^{\ast },\cdots ,a_n^{\ast }\right)$;

(2)

If $S\left(a\right)=S\left(a^{\ast }\right)$, then

$$\begin{array}{l}{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right)\\ ={\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}}\right)-2\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{L\ast }}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{U\ast }}}\right).\end{array}$$

Therefore, by the condition $T_i^L\le T_i^{L\ast }$, $T_i^U\le T_i^{U\ast }$, $I_i^L\ge I_i^{L\ast }$, $I_i^U\ge I_i^{U\ast }$, $F_i^L\ge F_i^{L\ast }$, $F_i^U\ge F_i^{U\ast }$ for any $i$, we can get

${\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}={\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}}$, ${\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}={\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}=1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}=1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}=1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{L\ast }}}$, $1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}=1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}.$

Thus,

$$\begin{array}{l}A(a)\\ =\frac{1}{2}\left({\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right)\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^U}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\right)\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^L}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^U}}\right)\left(1-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^L}}\right)\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^L}}\right)\left(1-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^U}}\right)\right)\right)\\ =\frac{1}{2}\left({\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}}+{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}\right)\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{U\ast }}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}}\right)\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{1-T_i^{L\ast }}}\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{U\ast }}}\right)\left(1-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{L\ast }}}\right)\right)-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{F_i^{L\ast }}}\right)\left(1-\left(1-{\displaystyle \prod _{i=1}^n{\lambda }_i^{I_i^{U\ast }}}\right)\right)\right)\\ =A(a^{\ast }).\end{array}$$

Therefore, $\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)=\mathrm{INWEA}\left(a_1^{\ast },a_2^{\ast },\cdots ,a_n^{\ast }\right)$.

Based on (1) and (2), there is $\mathrm{INWEA}\left(a_1,a_2,\cdots ,a_n\right)\le \mathrm{INWEA}\left(a_1^{\ast },a_2^{\ast },\cdots ,a_n^{\ast }\right)$. □

5. Multiple Attribute Decision Making Method Based on the INWEA Operator

To better understand the new operational law and the new operational aggregation operator, we will address some MADM problems, where the attribute weights will be expressed as INNs, and the attribute values for alternatives are represented as positive real numbers. So, we establish a MADM method.

In MADM problems, let $X=\{x_1,x_2,\cdots x_m\}$ be a discrete set of $m$ alternatives, and $C=\{c_1,c_2,\cdots c_n\}$ be the set of $n$ attributes. The evaluation values of attribute $c_j(j=1,2,\cdots ,n)$ for alternative $x_i(i=1,2,\cdots ,m)$ is expressed by a positive real number ${\lambda }_{ij}\in \left(0,1\right),(i=1,2,\cdots ,m,j=1,2,\cdots ,n)$. So, the decision matrix $R={({\lambda }_{ij})}_{m\times n}$ can be given. The INN $a_j=<[T_j^L,T_j^U],[I_j^L,I_j^U],[F_j^L,F_j^U]>$ is represented as the attribute weight of the $c_j(j=1,2,\cdots ,n)$, here $[T_j^L,T_j^U]\subseteq [0,1]$ indicates the degree of certainty of the attribute $c_j$ supported by the experts, $[I_j^L,I_j^U]\subseteq [0,1]$ indicates the degree of uncertainty of the attribute $c_j$ supported by the experts, and $[F_j^L,F_j^U]\subseteq [0,1]$ indicates the negative degree of the attribute $c_j$ supported by the experts. Then, we can rank the alternatives and obtain the best alternatives based on the given information; the specific steps are as follows:

Step 1

Utilize the INWEA operator $d_i=INWEA\left(a_1,a_2,\cdots ,a_m\right)\left(i=1,2,\cdots ,m;j=1,2,\cdots n\right)$ to aggregate the characteristic ${\lambda }_{ij}$ of the alternative $x_i$.

Step 2

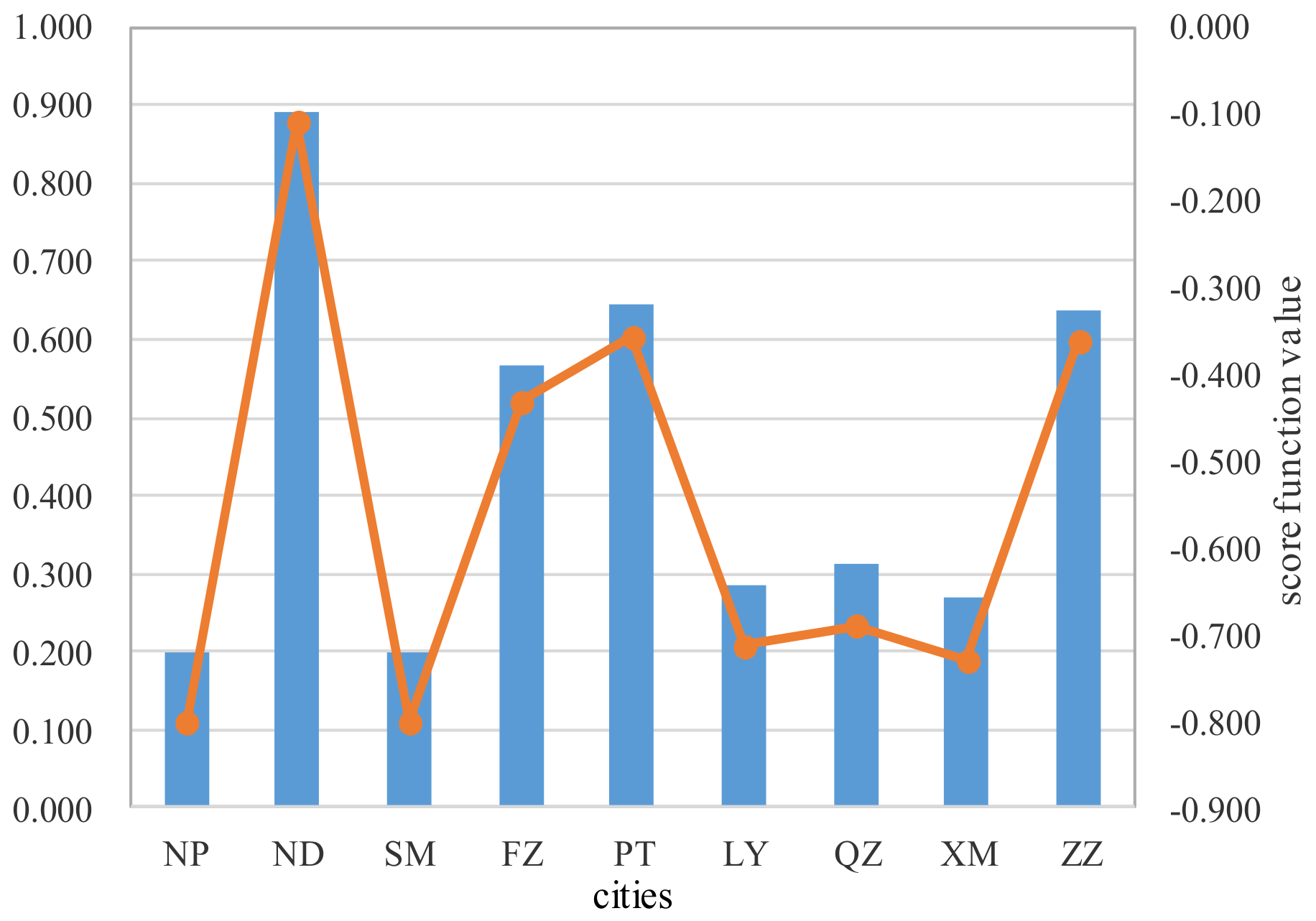
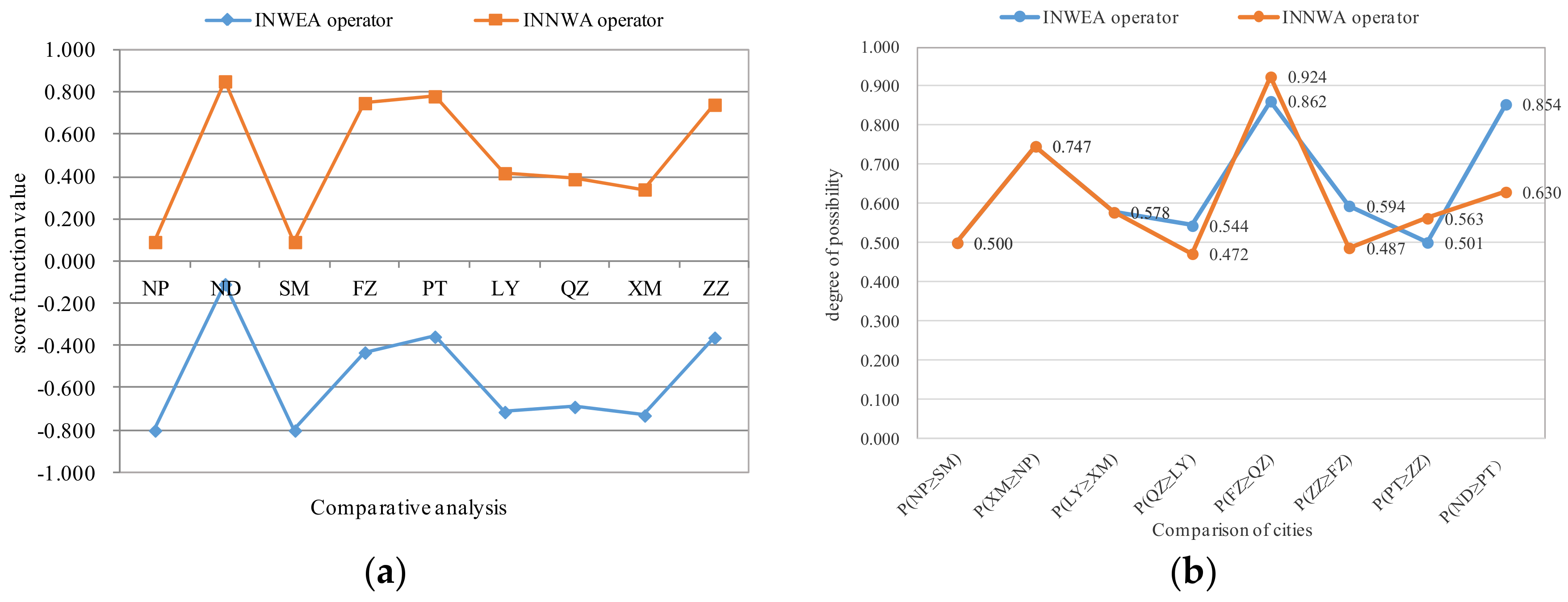
Utilize the score function to calculate the scores $S\left(d_i\right)\left(i=1,2,\cdots ,m\right)$ of the alternatives $x_i\left(i=1,2,\cdots ,m\right)$.

Step 3

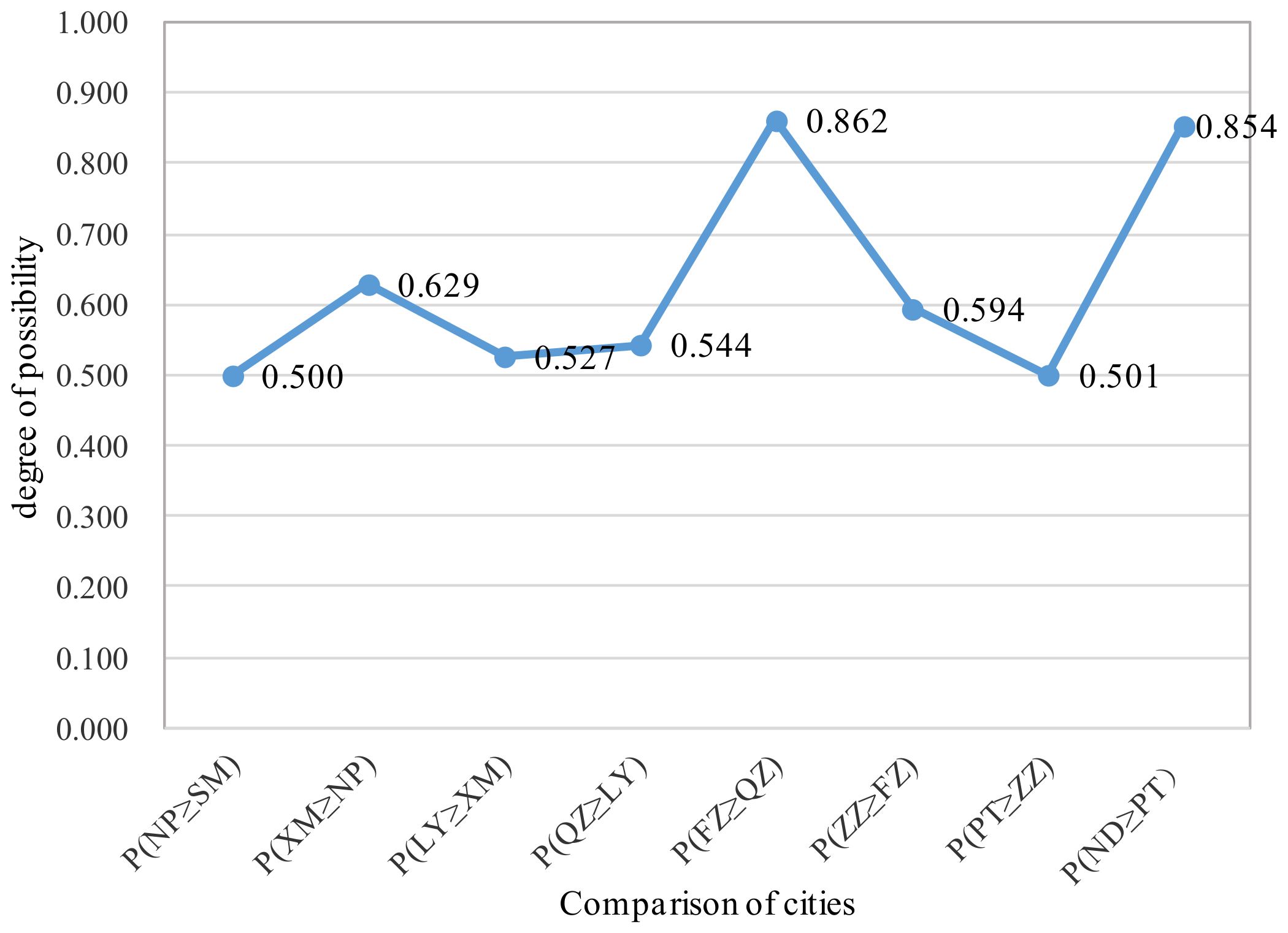
Utilize the scores $S\left(d_i\right)\left(i=1,2,\cdots ,m\right)$ to rank and select the alternatives $x_i\left(i=1,2,\cdots ,n\right)$, if the two scores $S\left(d_i\right)$ and $S\left(d_j\right)$ are equal, then we need to calculate the accuracy degrees $A\left(d_i\right)$ and $A\left(d_j\right)$ of the overall criteria values $d_i$ and $d_j$, then we rank the alternatives $x_i$ and $x_j$ by using $A\left(d_i\right)$ and $A\left(d_j\right)$.

Step 4

End.

6. Typhoon Disaster Evaluation Based on Neutrosophic Information

6.1. Illustrative Example

In China, typhoons are among the most serious types of natural disasters. They primarily impact the eastern coastal regions of China, where the population is extremely dense, the economy is highly developed, and social wealth is notably concentrated. Fujian Province is one of the most severely impacted typhoon disaster areas in both local and global contexts, routinely enduring substantial economic losses caused by typhoon disasters. For example, in 2017, a total of 208,900 people in 59 counties of Fujian Province were affected by the successive landings of twin typhoons No. 9 “Nassa” and No. 10 “Haicang.” There were 434 collapsed houses and 273,300 people were urgently displaced; 26.73 thousand hectares of crops were affected, 101.9 thousand hectares affected, and 2.19 thousand hectares were lost. The typhoon also led to the cancellation of 507 Fujian flights and 139 trains. According to incomplete statistics, the total direct economic loss was 966 million yuan (RNB). We examine the problem of typhoon disaster evaluation in Fujian Province.

We will use several indices to evaluate the typhoon disaster effectively. The assessment indicators $C=\{c_1,c_2,c_3,c_4\}$ include economic loss $c_1$, social impact $c_2$, environmental damage $c_3$, and other impact $c_4$ proposed by Yu [1]. Several experts are responsible for this assessment, and the evaluation information is expressed by positive real numbers and INNs. The assessment decision matrix based on this is constructed $R={({\lambda }_{ij})}_{m\times n}$(see

Table 1. Decision matrix.

	Attributes	c1	c2	c3	c4
Cities
Nanping (NP)		0.2	0.2	0.2	0.2
Ningde (ND)		0.9	0.8	0.7	0.4
Sanming (SM)		0.2	0.2	0.2	0.2
Fuzhou (FZ)		0.8	0.5	0.5	0.3
Putian (PT)		0.7	0.7	0.6	0.3
Longyan (LY)		0.4	0.3	0.3	0.2
Quanzhou (QZ)		0.3	0.4	0.2	0.3
Xiamen (XM)		0.3	0.3	0.3	0.2
Zhangzhou (ZZ)		0.6	0.5	0.8	0.3

), and the ${\lambda }_{ij}$ is positive real numbers. The ${\lambda }_{ij}$ in the matrix indicates the degree of damage to the city in the typhoon. The data between 0 and 1 is used to indicate the degree of disaster received. 0 means that the city is basically unaffected by disasters, 0.2 means that the extent of the disaster is relatively small, 0.4 means that the extent of the disaster is middle, 0.6 means that the degree of disaster is slightly larger, 0.8 means the extent of the disaster is relatively large. 1 means that the extent of the disaster is extremely large. The rest of the data located in the middle of the two data indicates that the extent of the disaster is between the two. The interval neutrosophic weights ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, ${\omega }_4$ for the four attributes voted by experts. Take ${\omega }_1$ as an example to explain its meaning, $[0.6,0.8]$ indicates the degree of certainty of the attribute $c_1$ supported by the experts is between 0.6 and 0.8, $[0.2,0.4]$ indicates the uncertainty of the expert’s support for attribute $c_1$ is between 0.2 and 0.4, and $[0.1,0.2]$ indicates the negative degree of expert’s support for attribute $c_1$ is between 0.1 and 0.2.

$$\begin{array}{c}{\omega }_1=<[0.6,0.8],[0.2,0.4],[0.1,0.2]>,{\omega }_2=<[0.5,0.9],[0.2,0.5],[0.1,0.3]>\\ {\omega }_3=<[0.4,0.7],[0.3,0.6],[0.3,0.5]>,{\omega }_4=<[0.2,0.4],[0.4,0.8],[0.6,0.7]>.\end{array}$$

According to Section 5, Typhoon disaster evaluation using the MADM model contains the following steps:

Step 1

Using the $INWEA$ operator defined by equation (10) to aggregate all evaluation information to obtain a comprehensive assessment value $d_i$ for each city as follows:

When $i=2$, we can get

$$\begin{array}{l}{d}_2^{ND}=INWEA\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)\\ =\langle \left[{\displaystyle \prod _{i=1}^4{\lambda }_i^{1-T_i^L}},{\displaystyle \prod _{i=1}^4{\lambda }_i^{1-T_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^4{\lambda }_i^{I_i^L}},1-{\displaystyle \prod _{i=1}^4{\lambda }_i^{I_i^U}}\right],\left[1-{\displaystyle \prod _{i=1}^4{\lambda }_i^{F_i^L}},1-{\displaystyle \prod _{i=1}^4{\lambda }_i^{F_i^U}}\right]\rangle \\ =<\left[{0.9}^{(1-0.6)}\times {0.8}^{(1-0.5)}\times {0.7}^{(1-0.4)}\times {0.4}^{(1-0.2)},{0.9}^{(1-0.8)}\times {0.8}^{(1-0.9)}\times {0.7}^{(1-0.7)}\times {0.4}^{(1-0.4)}\right],\\ \left[1-{0.9}^{0.2}\times {0.8}^{0.2}\times {0.7}^{0.3}\times {0.4}^{0.4},1-{0.9}^{0.4}\times {0.8}^{0.5}\times {0.7}^{0.6}\times {0.4}^{0.8}\right],\\ \left[1-{0.9}^{0.1}\times {0.8}^{0.1}\times {0.7}^{0.3}\times {0.4}^{0.6},1-{0.9}^{0.2}\times {0.8}^{0.3}\times {0.7}^{0.5}\times {0.4}^{0.7}\right],\\ =<[0.333,0.497],[0.417,0.667],[0.498,0.597]>\end{array}$$

In a similar way, we can get

$d_1^{NP}=<[0.025,0.145],[0.830,0.975],[0.830,0.935]>$,

$d_2^{ND}=<[0.333,0.497],[0.417,0.667],[0.498,0.597]>$,

$d_3^{SM}=<[0.025,0.145],[0.830,0.975],[0.830,0.935]>$,

$d_4^{FZ}=<[0.163,0.352],[0.582,0.837],[0.640,0.764]>$,

$d_5^{PT}=<[0.204,0.374],[0.540,0.796],[0.612,0.721]>$,

$d_6^{LY}=<[0.051,0.196],[0.760,0.949],[0.785,0.897]>$,

$d_7^{QZ}=<[0.057,0.215],[0.751,0.943],[0.758,0.885]>$,

$d_8^{XM}=<[0.045,0.185],[0.774,0.955],[0.791,0.903]>$,

$d_9^{ZZ}=<[0.192,0.383],[0.546,0.808],[0.597,0.718]>$.

Step 2

Using Definition 4 to calculate the score function value of the comprehensive assessment value $d_i$ for each city as follows:

$S\left(d_1^{NP}\right)=-0.801$, $S\left(d_2^{ND}\right)=-0.109$, $S\left(d_3^{SM}\right)=-0.801$, $S\left(d_4^{FZ}\right)=-0.432$,

$S\left(d_5^{PT}\right)=-0.357$, $S\left(d_6^{LY}\right)=-0.714$, $S\left(d_7^{QZ}\right)=-0.690$, $S\left(d_8^{XM}\right)=-0.730$,

$S\left(d_9^{ZZ}\right)=-0.360$.

Step 3

According to Definition 6, the ranking order of the nine cities is $d_2^{ND}\succ d_5^{PT}\succ d_9^{ZZ}\succ d_4^{FZ}\succ d_7^{QZ}\succ d_6^{LY}\succ d_8^{XM}\succ d_3^{SM}$~$d_1^{NP}$. The ranking results of the cities are shown in Figure 1.

Step 4

End.

6.2. Comparative Analysis Based on Different Sorting Methods

To illustrate the stability of the ranking results, the degree of possibility-based ranking method proposed in [33,45] is used in this paper. We obtain the matrix of degrees of possibility of the comprehensive assessment values of nine cities as follows:

$$P=\begin{array}{cc}\begin{array}{l}\begin{array}{l}\\ NP\\ ND\\ SM\\ FZ\\ PT\\ LY\\ QZ\\ XM\\ ZZ\end{array}\end{array}& \begin{array}{l}\begin{array}{lllllllll}NP& ND& SM& FZ& PT& LY& QZ& XM& ZZ\end{array}\\ \left[\begin{array}{lllllllll}0.500& 0.000& 0.500& 0.000& 0.000& 0.344& 0.302& 0.371& 0.000\\ 1.000& 0.500& 1.000& 0.944& 0.854& 1.000& 1.000& 1.000& 0.843\\ 0.500& 0.000& 0.500& 0.000& 0.000& 0.344& 0.302& 0.371& 0.000\\ 1.000& 0.056& 1.000& 0.500& 0.402& 0.913& 0.862& 0.943& 0.406\\ 1.000& 0.146& 1.000& 0.598& 0.500& 1.000& 0.980& 1.000& 0.501\\ 0.656& 0.000& 0.656& 0.087& 0.000& 0.500& 0.456& 0.527& 0.000\\ 0.698& 0.000& 0.698& 0.138& 0.020& 0.544& 0.500& 0.570& 0.038\\ 0.629& 0.000& 0.629& 0.057& 0.000& 0.473& 0.430& 0.500& 0.000\\ 1.000& 0.157& 1.000& 0.594& 0.499& 1.000& 0.962& 0.100& 0.500\end{array}\right]\end{array}\end{array}$$

Here, $ND\succ PT\succ ZZ\succ FZ\succ QZ\succ LY\succ XM\succ SM$~$NP$. The ranking order of the nine cities is also $d_2^{ND}\succ d_5^{PT}\succ d_9^{ZZ}\succ d_4^{FZ}\succ d_7^{QZ}\succ d_6^{LY}\succ d_8^{XM}\succ d_3^{SM}$~$d_1^{NP}$. The ranking results of the cities are shown in Figure 2. As can be seen from the above results, the two sorting results are the same.

6.3. Comparative Analysis of Different Aggregation Operators

In order to illustrate the rationality and predominance of the proposed method, we compare this method with other methods [33]. The comparative analysis is shown in

Table 2. Comparative analysis of different aggregation operators.

Different Aggregation Method	Ranking Result
$INWEA$ operator of our method	$d_2^{ND}\succ d_5^{PT}\succ d_9^{ZZ}\succ d_4^{FZ}\succ d_7^{QZ}\succ d_6^{LY}\succ d_8^{XM}\succ d_3^{SM}$~$d_1^{NP}$
$INNWA$ operator of [33]	$d_2^{ND}\succ d_5^{PT}\succ d_4^{FZ}\succ d_9^{ZZ}\succ d_6^{LY}\succ d_7^{QZ}\succ d_8^{XM}\succ d_3^{SM}$~$d_1^{NP}$

and Figure 3.

First in Step 1, using the $INNWA$ operator proposed by [33] instead of the $INWEA$ operator to aggregate all evaluation information to obtain a comprehensive assessment value $d_i$ for each city, then using Definition 4 to calculate the score function value of $d_i$ as follows:

$$\begin{array}{l}S\left(d_1^{NP}\right)=0.092,S\left(d_2^{ND}\right)=0.853,S\left(d_3^{SM}\right)=0.092,S\left(d_4^{FZ}\right)=0.750,S\left(d_5^{PT}\right)=0.782,S\left(d_6^{LY}\right)=0.418,\\ S\left(d_7^{QZ}\right)=0.389,S\left(d_8^{XM}\right)=0.340,S\left(d_9^{ZZ}\right)=0.742.\end{array}$$

Here, we compare and analyze several aggregation methods to illustrate the advantages of the proposed method.

(1) Can be seen from Table 2 and Figure 3, the two ranking results based on the $INWEA$ operator and the $INNWA$ operator are different. The main reason is that the positions and meanings of the attribute values and the attribute weights are different. For the $INWEA$ operator, its bases are positive real numbers and the exponents are interval neutrosophic numbers. It can deal with the decision making problem, in which attribute values are positive real numbers, and the attribute weights are interval neutrosophic numbers. However, the $INNWA$ operator is just the opposite. It needs to exchange the roles of the attribute values and the attribute weights because its bases are interval neutrosophic numbers and its exponents are positive real numbers. Therefore, it cannot be used to solve the typhoon disaster assessment problem in this paper, and the second ranking results in Table 2 and Figure 3 are unreasonable.

(2) Compared with the existing $SVNWAA$ operator introduced in an SVNN environment [41], our method is a more generalized representation, and the $SVNWAA$ operator is a special case. When the upper limit and lower limit of the INNs are the same, the $INWEA$ operator is equivalent to the $SVNWEA$ operator.

(3) Compared with the existing $IIFWEA$ operator of IIFNs [40] and the $IFWEA$ operator of IFNs [39], our method uses interval neutrosophic weights, which include truth degree, falsity degree, and indeterminacy degree, and can deal with the indeterminate, incomplete, and inconsistent problems. However, the $IIFWEA$ operator and $IFWEA$ operator use intuitionistic fuzzy weights, which only contain truth degree and falsity degree, and cannot handle the assessment problem in this paper. Since IFN and IIFN are only special cases of interval NN, our exponential aggregation operator is the extension of the existing exponential operators [39,40,41].

7. Conclusions

In this paper, a typhoon disaster evaluation approach based on exponential aggregation operators of interval neutrosophic numbers under the neutrosophic fuzzy environment, is proposed. First, this paper introduced the exponential operational laws of INSs and INNs, which are a useful supplement to the existing neutrosophic fuzzy aggregation techniques. Then, we investigated a series of properties of these operational laws. Next, we discussed in detail some favorable properties of the interval neutrosophic weighted exponential aggregation (INWEA) operator.Finally, we applied the proposed decision making method successfully to the evaluation of typhoon disaster assessment. The research in this paper will be helpful to deepen the study of typhoon disaster evaluation and improve decision making for disaster reduction and disaster prevention. In addition, it provides methodological guidance for the handling of typhoon disasters and can improve the government’s ability to effectively improve disaster reduction. In future research, we will expand the proposed method and apply it to other natural disaster assessment problems. We will continue to study related theories of exponential aggregation operators in a neutrosophic fuzzy environment and their application in typhoon disaster assessment. The authors will also study the related theory of single-valued neutrosophic sets, interval-valued neutrosophic sets, bipolar neutrosophic sets, neutrosophic hesitant fuzzy sets, multi-valued neutrosophic sets, simplified neutrosophic linguistic sets, and their applications in typhoon disaster evaluation problems.