Based on the analyses above, we perceived that the energy conservation method was able to estimate surface settlements. It was essential for this method to calculate the energy in shearing the soil. To obtain this energy, the expression for maximum engineering shear strain was required. However, when compared with the expression for surface settlements, the expression for maximum engineering shear strain is rarely researched. In this paper, two different approaches were used to calculate the shear strains and obtain the energy. The first approach obtained the energy indirectly through the differential of the vertical and horizontal displacements, as proposed by other researchers. The second approach obtained the energy directly through fitted expressions from the numerical results.
5.1. Prediction Using the Differential of Empirical Solutions
To obtain maximum shear strains using the differential, vertical and horizontal displacements of surface and subsurface were inevitably required. However, relatively few methods were available to estimate tunneling-induced subsurface settlements. Loganathan and Poulos [
7] presented a closed-form solution for estimating subsurface settlements. Both vertical and horizontal displacements proposed by this method are given by the following equations:
where
z0 is the tunnel depth as measured from the ground surface,
ε0 is the ground loss,
R is the radius of the tunnel, and
vL and
uL are the vertical and horizontal displacements.
Similarly, Mair et al. [
4] also presented an empirical method to estimate subsurface settlements, which is given by the following equations:
where
vmax is the maximum subsurface settlement at depth
z.
Following the work of Grant and Taylor [
16], a distribution of horizontal displacement was proposed by the following equation:
where
H is the distance between the plane of interest and the vector of interest for ground displacements. We assumed that
H was equal to
z0 so as to simplify this equation.
We obtained the differentials of the displacements using Equation (3). Both results of the calculations using the differentials had a similar distribution to that of the numerical maximum engineering shear strain. However, the peak values of the curves had some differences. The analytical curves of the differentials using both methods were illustrated for a depth of 20 m. All of the calculated results with a ground loss of 0.85% are shown in
Figure 3.
Both these shear strain curves were wider than the numerical curves. For the same level of volume loss, Mair et al.’s [
4] results decreased with depth, while Loganathan and Poulos’s [
7] results increased with depth. The middle segments of the curves were concave near the top of the ground, when using Loganathan and Poulos’s results [
7], and near the crown of the tunnel, when using Mair et al.’s results [
4]. Notably, the middle segment of the surface curve using Loganathan and Poulos’s results [
7] was convex, which was the same as that of the numerical surface curve.
In the proposed method,
ε0 is the only unknown in the equations for Δ
W and Δ
E. The equation for Δ
W is a linear term about
ε0, while the equation for Δ
E is a quadratic term about
ε0. The unknown
ε0 is equal to the expression for Δ
E divided by that for Δ
W. Consequently, ground displacements could be predicted once ground loss (
ε0) was obtained. The maximum surface settlements were predicted in four different cases, including at depths of 15 m, 20 m, and 25 m. The results calculated using these two empirical methods were compared with the numerical results, and are shown in
Table 3.
When compared with the numerical results (9.9 mm and 10.7 mm) at depths of 20 m and 25 m, the results using Mair et al.’s method [
4] were 8.0 mm and 11.8 mm, respectively. We perceived that the results obtained using Mair et al.’s method [
4] were suitable at depths ranging from 20 m to 25 m because the peak values of the curves within this range were close to those of the numerical curves. At depths of 15 m and 20 m, the results obtained using Mair et al.’s method [
4] were slightly small. This was the reason for those shear strain curves being wider than the numerical curves. The resultant energy in shearing the soil was slightly large. The peak values near the crown were larger at shallower tunnel depths, and smaller when the tunnel was deeper. The calculated results were smaller at a depth of 15 m, and larger at a depth of 25 m.
The results calculated using Loganathan and Poulos’s method [
7] were slightly small at a depth of 15 m, and considerably smaller when the tunnel was excavated deeper. This was due to the peak values of the shear strain curves increasing radically at depths below the crown of the tunnel. The denominators had a term of (
z0 −
z) in the expressions for vertical and horizontal displacement. When
z was close to
z0, the denominator was extremely small. Thus, the value of shear strain increased radically as the tunnel was excavated deeper. The energy in shearing the soil was extremely large. Accordingly, the obtained ground loss
ε0 was fairly small. On the contrary, the energy in shearing the soil would not increase at shallower tunnel depths. We supposed this method was suitable for shallow tunnels.
The method using the differentials of horizontal and vertical soil displacements was inexact when calculating maximum surface settlements. This was probably due to the profiles of the vertical and horizontal soil displacements not fully conforming to the numerical curves. Additionally, horizontal soil displacement is not studied clearly. The errors using the differentials of horizontal and vertical displacements were beyond estimation. Despite this, the method using the differentials of vertical and horizontal displacements can still be used to calculate surface settlement under specific conditions.
5.2. Prediction Using Fitted Expressions of Numerical Results
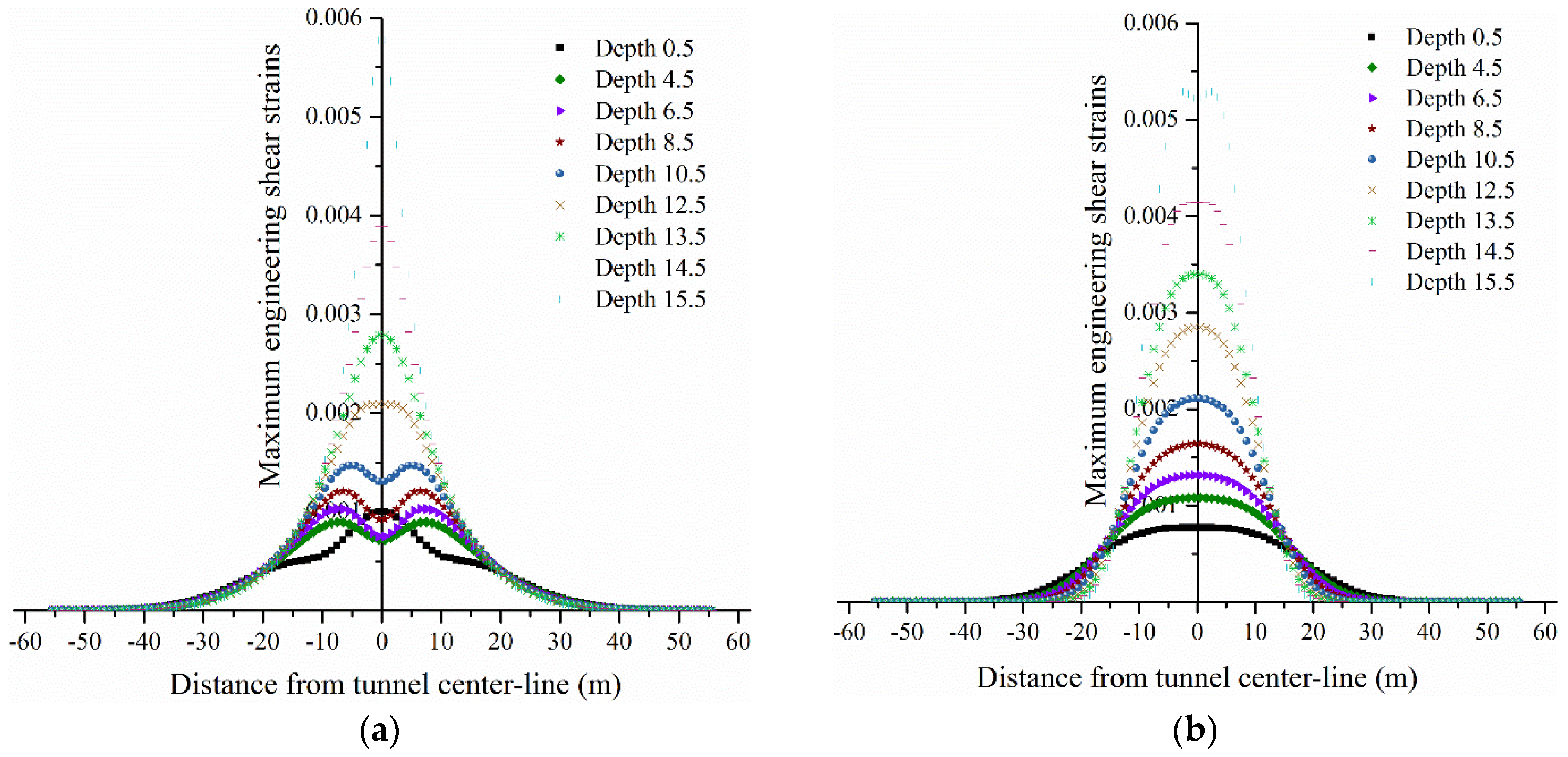
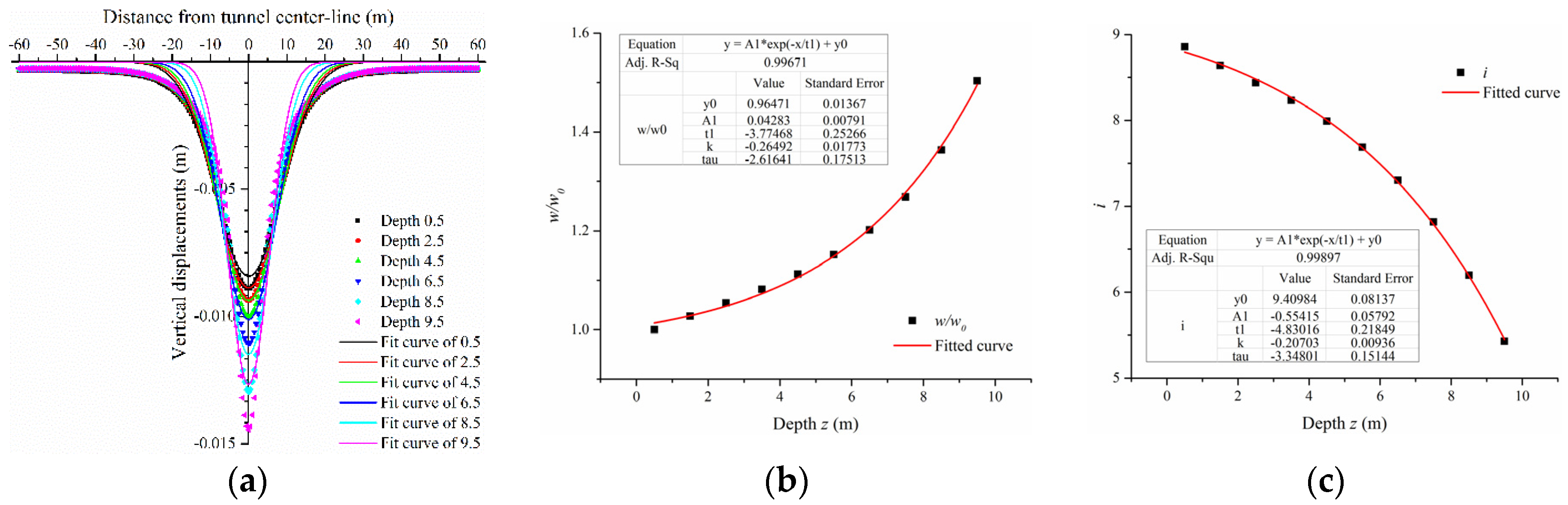
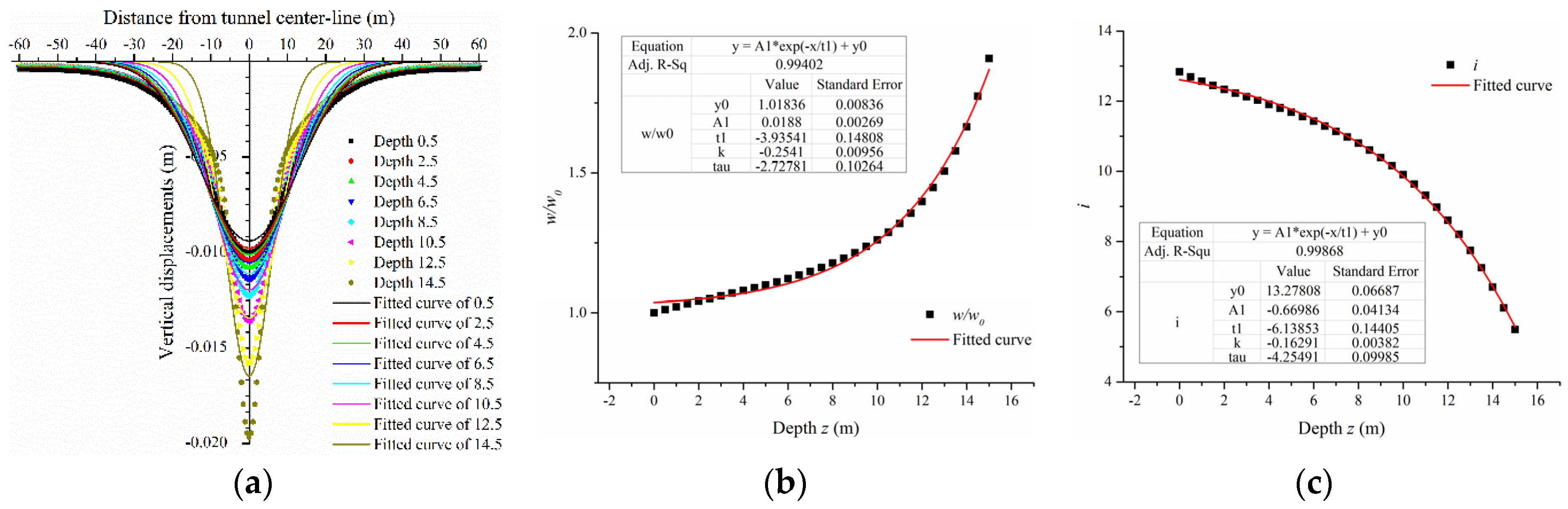
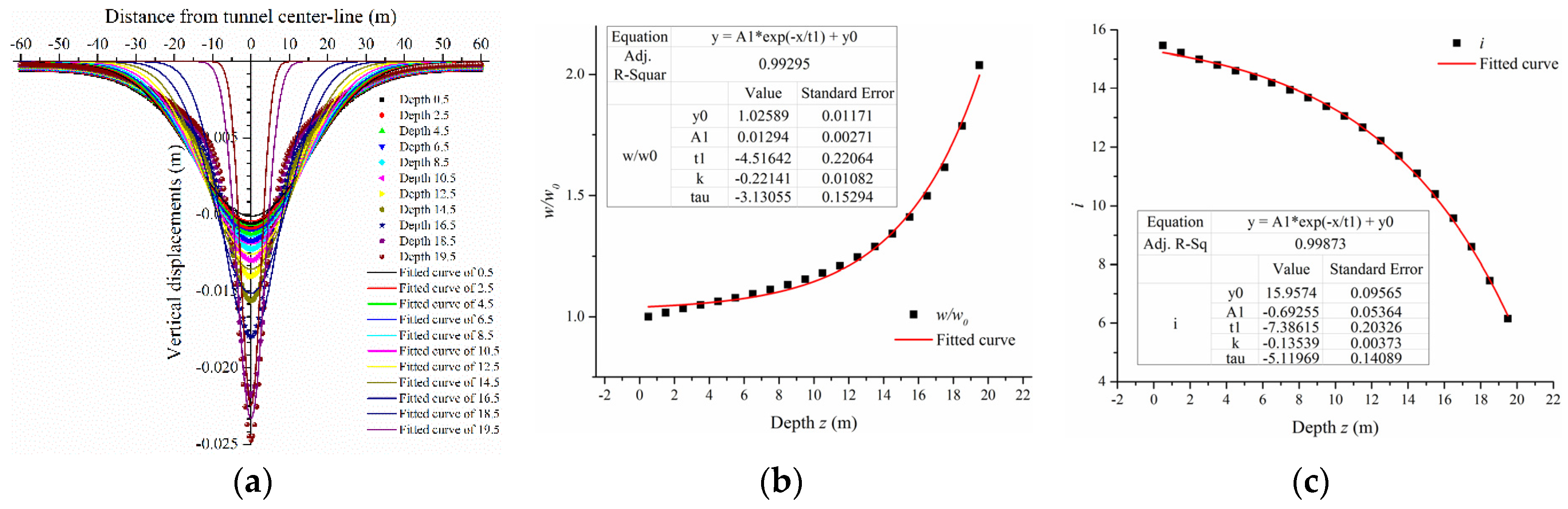
The results of ground settlements and maximum shear strains were obtained and fitted by numerical analyses shown in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9. The vertical displacements satisfied a Gaussian distribution which was similar to Peck’s expression (Mair and Taylor [
17]), and is given by the following equation:
where
w is the maximum displacement occurring at the tunnel centerline at depth
z,
is is the distance to the point of inflexion, and they are both satisfied by exponential functions at depth
z. Note that
w0 is the maximum surface settlement (
x = 0,
z = 0.5) which was later obtained. Accordingly, the fitted expressions were functions related to
w0,
x, and
z.
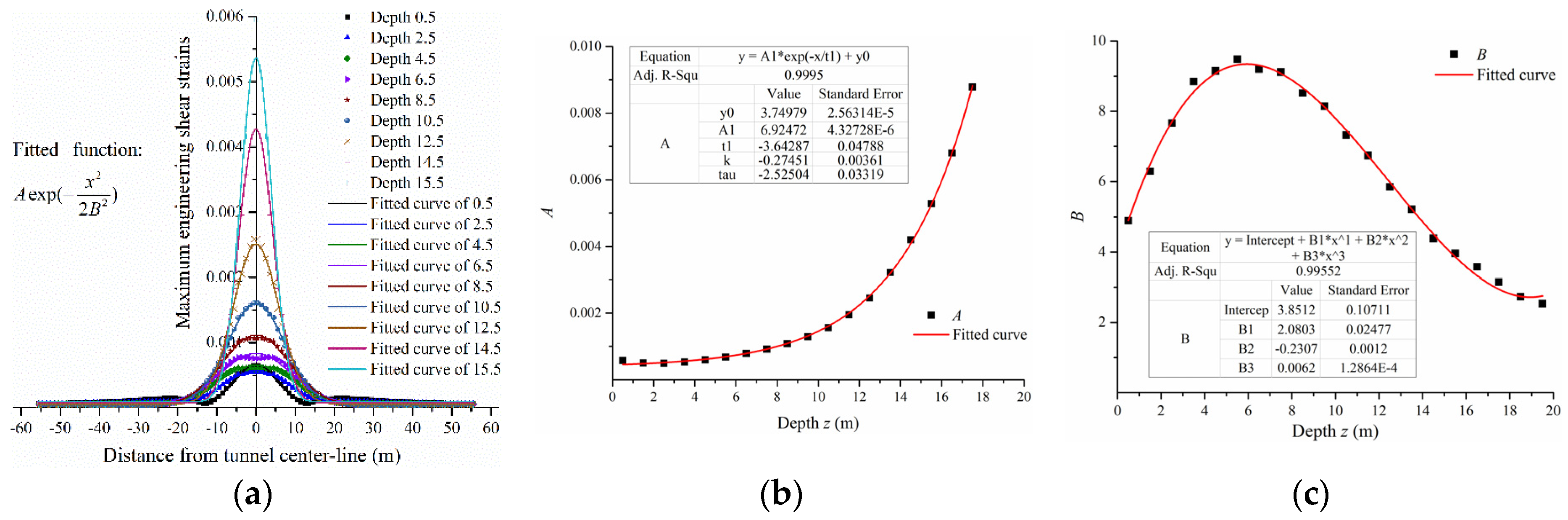
The predictions of maximum shear strains also satisfy a Gaussian distribution, as shown below.
where parameters
A and
B can be fitted by an exponential function and a cubic polynomial function, respectively. Note that the form of fitted functions resembles the Peck function because the maximum shear strain can be the differential of vertical and horizontal displacements. The forms of differential functions do not change due to the properties of differentials of exponential functions. Similarly, parameter
A can also be fitted by an exponential function. The distance to the point of inflexion in the Peck function can be expanded by a polynomial function. Thus, it is suitable to fit parameter
B using a cubic polynomial function. The expressions of all fitted parameters listed above are given in
Appendix A. Note that some data below the crown of the tunnel were not shown, because there was either no data within the tunnel, or the data were extremely large.
As shown in
Figure 4,
Figure 5 and
Figure 6, the vertical displacements were not fitted perfectly. The reason was probably the distinction between the boundary of the numerical simulations and the Gaussian deformation mechanism. The total half-width of the surface settlement trough distributed in Gaussian was assumed to be 2.5
is (Mair et al. [
4]). The soil outside the total width of the surface settlement trough was assumed to be stationary. However, the soil deformed at the same position in the numerical simulations even though the values were fairly small. Additionally, the deeper the buried soil was, the narrower the settlement trough became, and the larger the maximum vertical displacements were. This satisfied the conclusions presented by Fang et al. [
18]. Therefore, the fitted expressions of vertical displacements were not exact at deeper depths. Most maximum values of the fitted expressions were smaller than those of the numerical results. Contrarily, the parameters
w/
w0 and
is were both fitted exactly. The parameter
w/
w0 increased exponentially with an increase in depth
z0, while the parameter
is decreased exponentially.
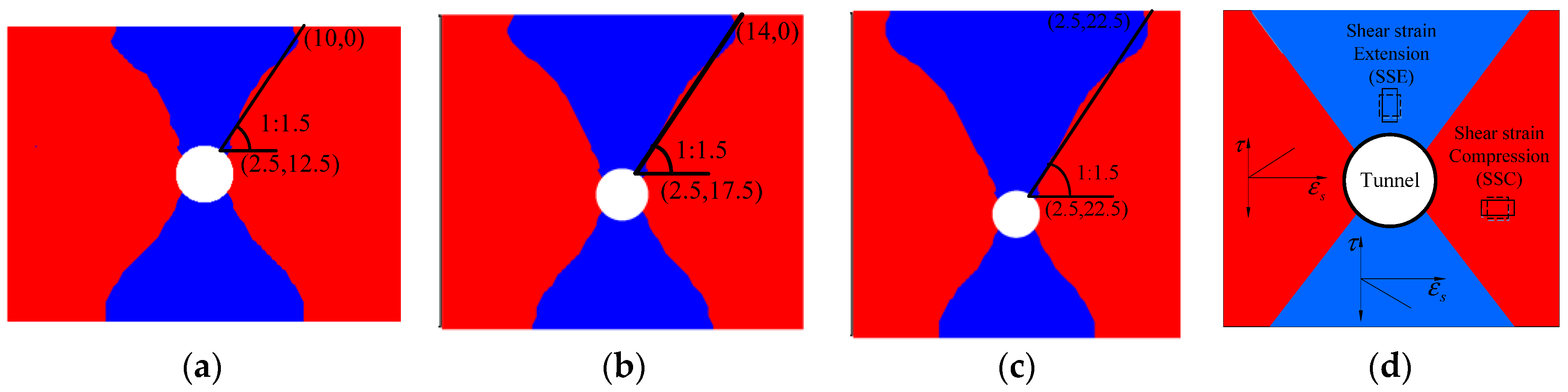
When compared with the vertical displacements, the maximum engineering shear strains were fitted perfectly. The coefficients of determinations of these fitted curves were larger than 0.99. The parameters A and B were also fitted exactly by the extracted results from the fitted expressions at each depth z. The parameter A decreased with an increase in depth z0. We perceived that the coefficients in the expressions changed regularly with overburden depth z0. Maximum engineering shear strain can probably be predicted by an accurate formula which has actual physical meaning. This formula is perhaps relative to the radius of the tunnel r and the overburden depth z0, and it can be studied further.
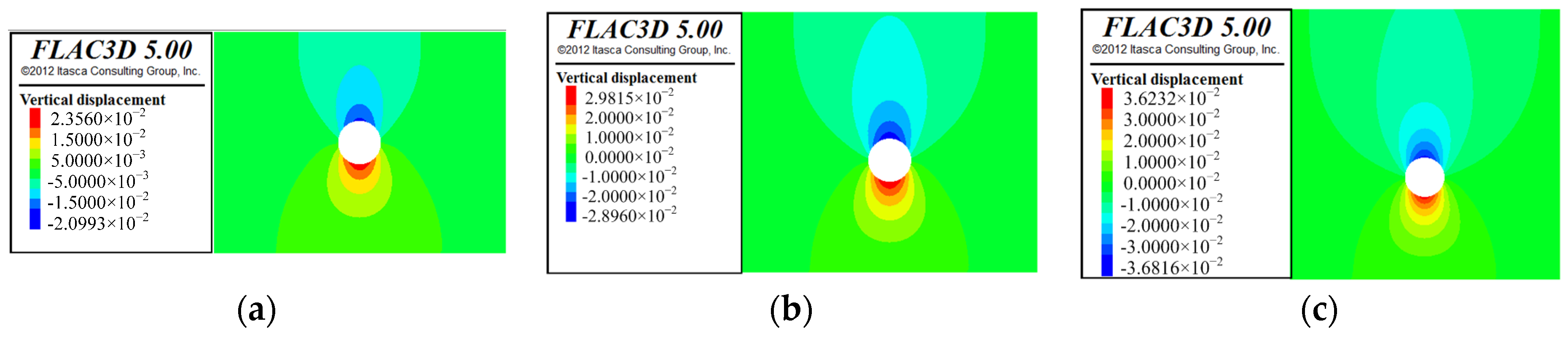
Based on the contours of vertical displacements in
Figure 1, the ground displacements were separated into two different regions. The demarcation line was the location of the arch spring of tunnel. One region of displacement occurred in the upper area of the model, while the other occurred in the lower area of the model. As such, the upper area of the model was selected to calculate the settlement of the soil using Equation (1) and the fitted expressions above.
The mechanism was firstly divided into a series of unit elements (1 m × 1 m). Secondly, the energy of each element was calculated, and then summed to obtain Δ
E and Δ
W. According to the numerical analyses, the negative energy Δ
N was about one-tenth of the total value of Δ
W. Δ
W − Δ
N was modified by a coefficient of 1.2 due to the error between the vertical displacement results from the fitted expression and the numerical simulation. The reason for this treatment was that the vertical displacements from the fitted expressions were smaller than those in the numerical results, which was previously discussed. This was because Δ
W − Δ
N is a function about
w0, and Δ
E is a real number. Thus, all parameters were finally prepared for the calculation of
w0. Using the Matlab software, the maximum surface settlements (
w0) were calculated at depths of 15 m, 20 m and 25 m. All analytical results were compared with the numerical results, and are shown in
Table 4.
The analytical results were 8.9 mm at a depth of 15 m, 10.3 mm at a depth of 20 m, and 11.1 mm at a depth of 25 mm. The maximum error between the calculation and the numerical results was 4.0 percent, and the minimum error was 3.5 percent. The method of calculating ground settlements due to tunneling using fitted expressions was better than that using the differentials of horizontal and vertical displacements. This research has improved the calculation of surface settlements by directly using fitted expressions of maximum engineering shear strains. The maximum engineering shear strains cannot yet be predicted by the arbitrary location of the tunnel z0, and the tunnel diameter r. The fitted expressions are worth studying further so as to calculate the surface and subsurface settlements.