Energy, Christiaan Huygens, and the Wonderful Cycloid—Theory versus Experiment
Abstract
:1. Introduction
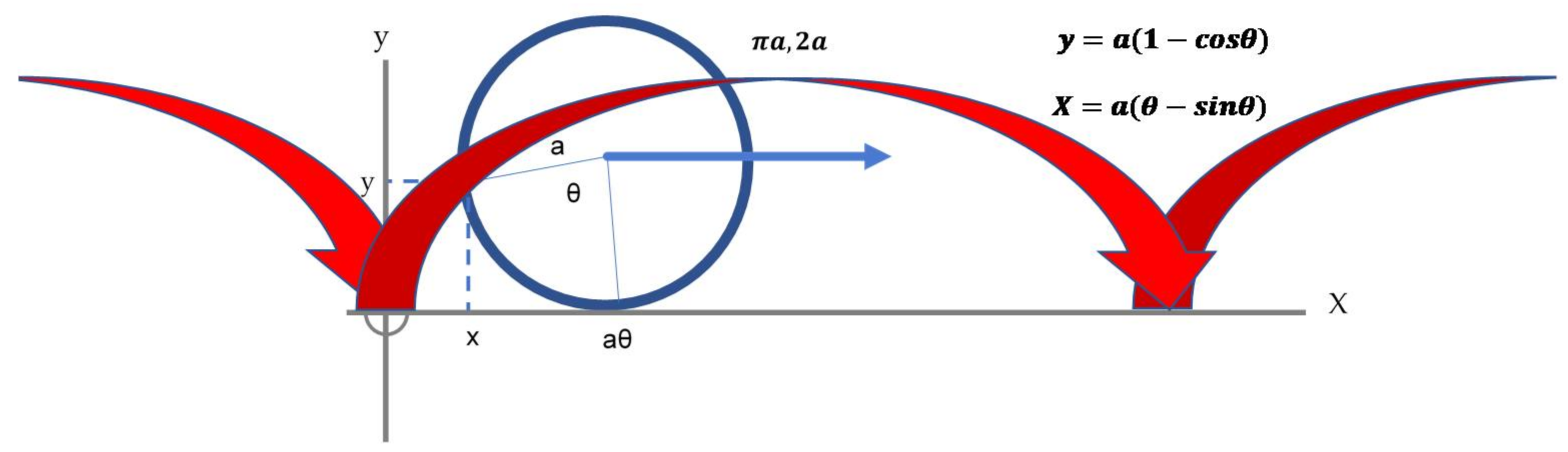
1.1. The Cycloid: Coordinates, Equations of Motion, And Approximations
1.2. Cycloid Coordinates
1.3. Equations of Motion for a Cycloid
1.4. "Get the Ball Rolling"—Correcting for Angular Kinetic Energy
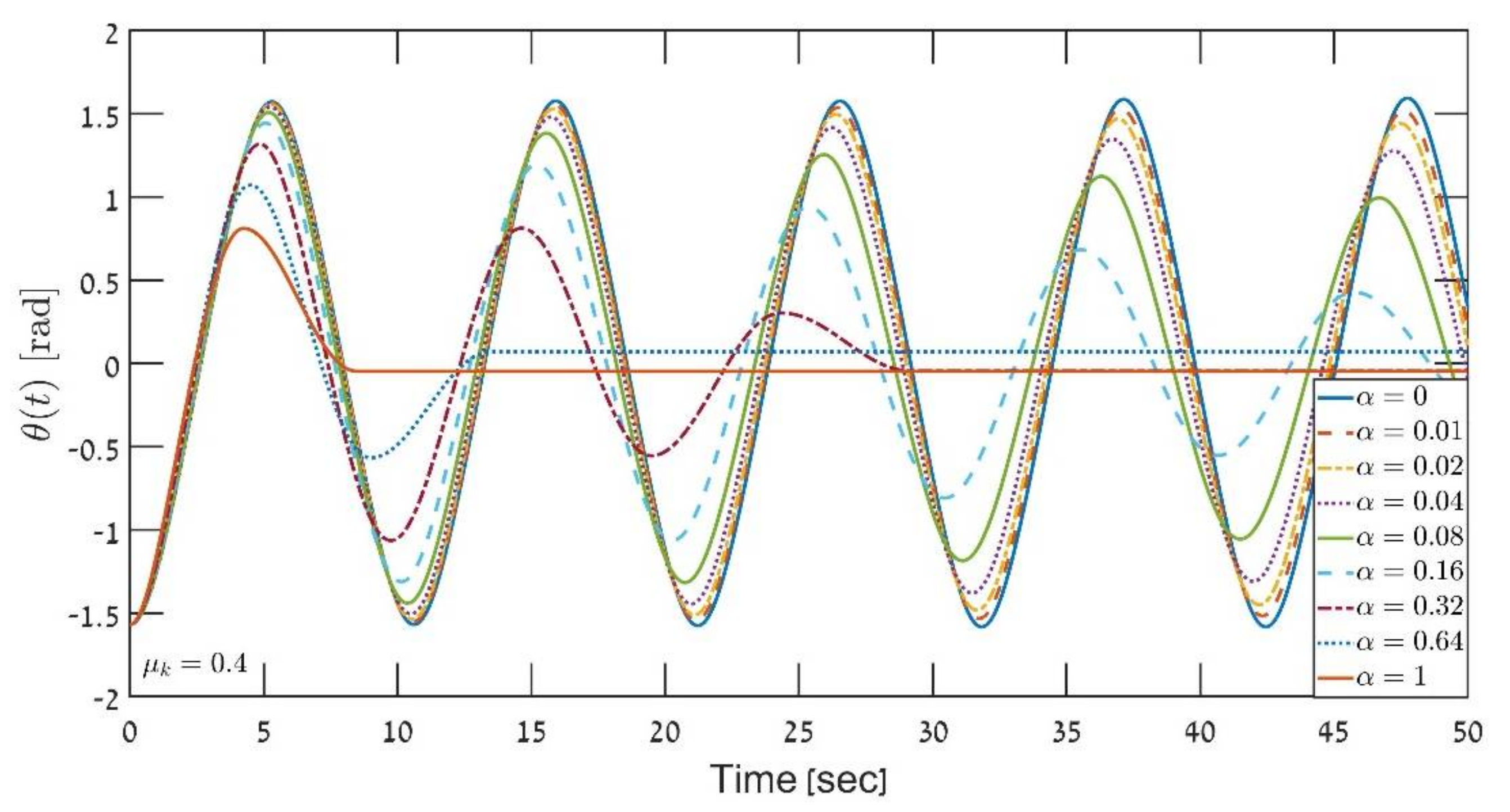
1.5. The Influence of Slipping While Rolling in Motion on Cycloid Pathways
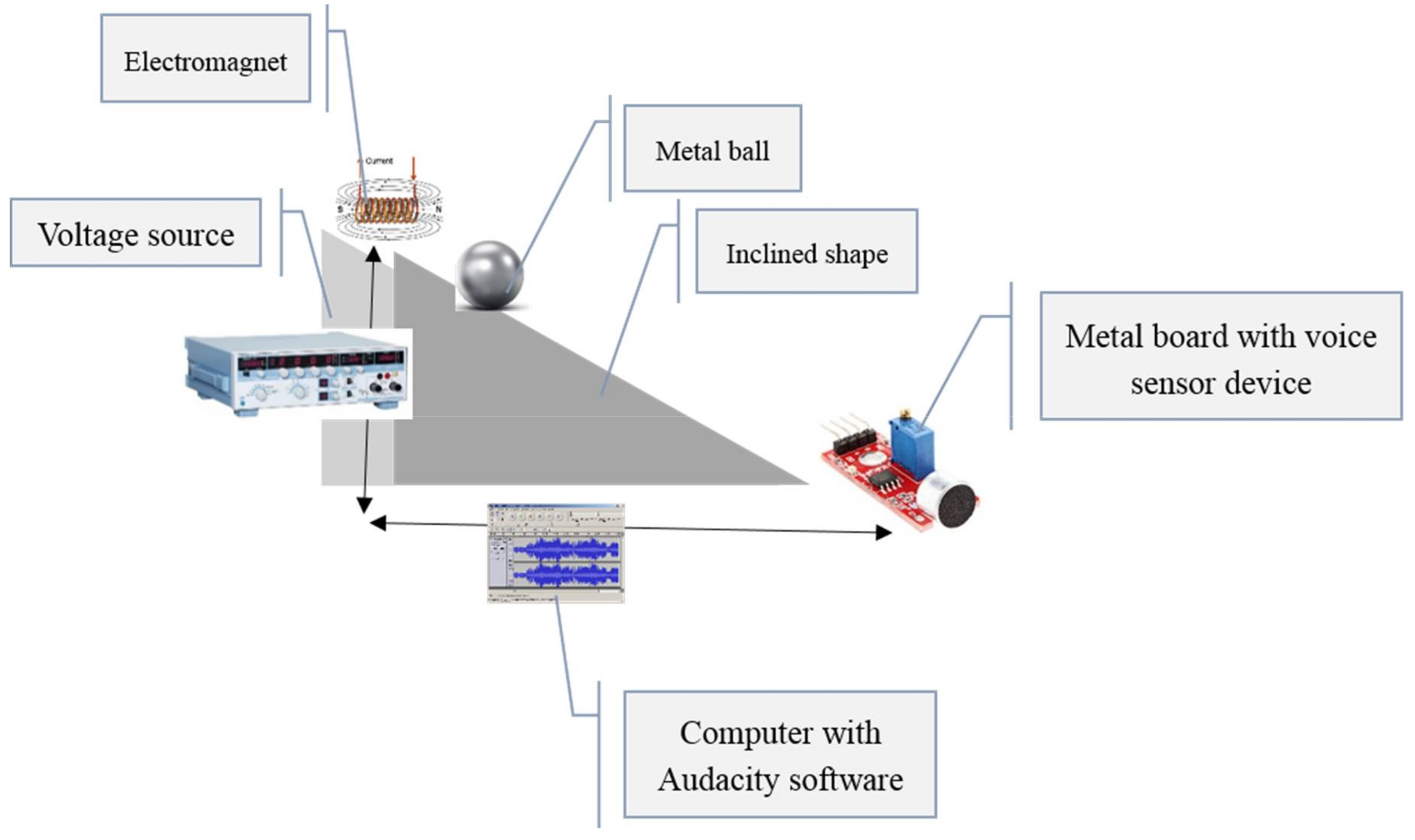
2. Methods
The Experimental System
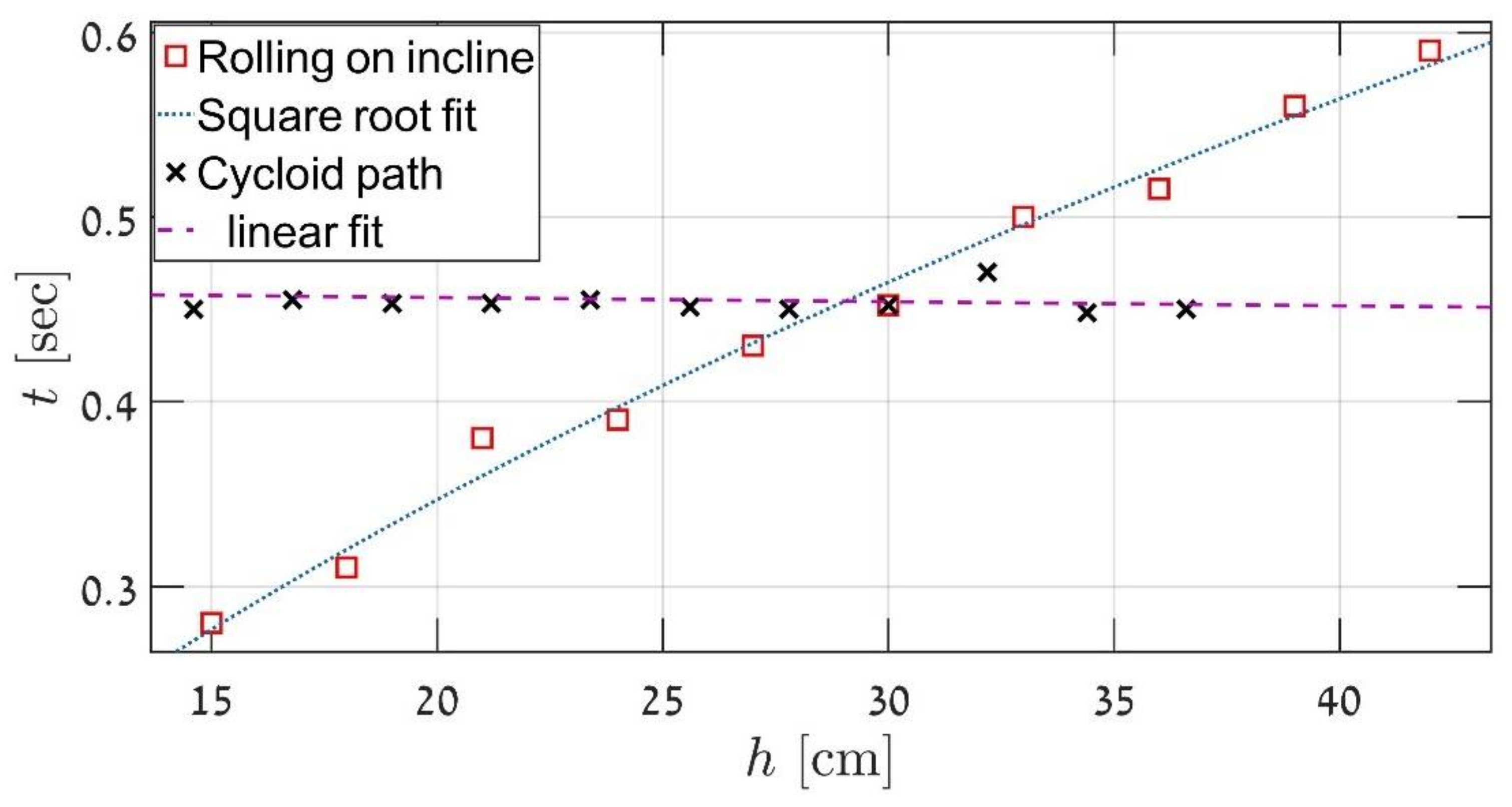
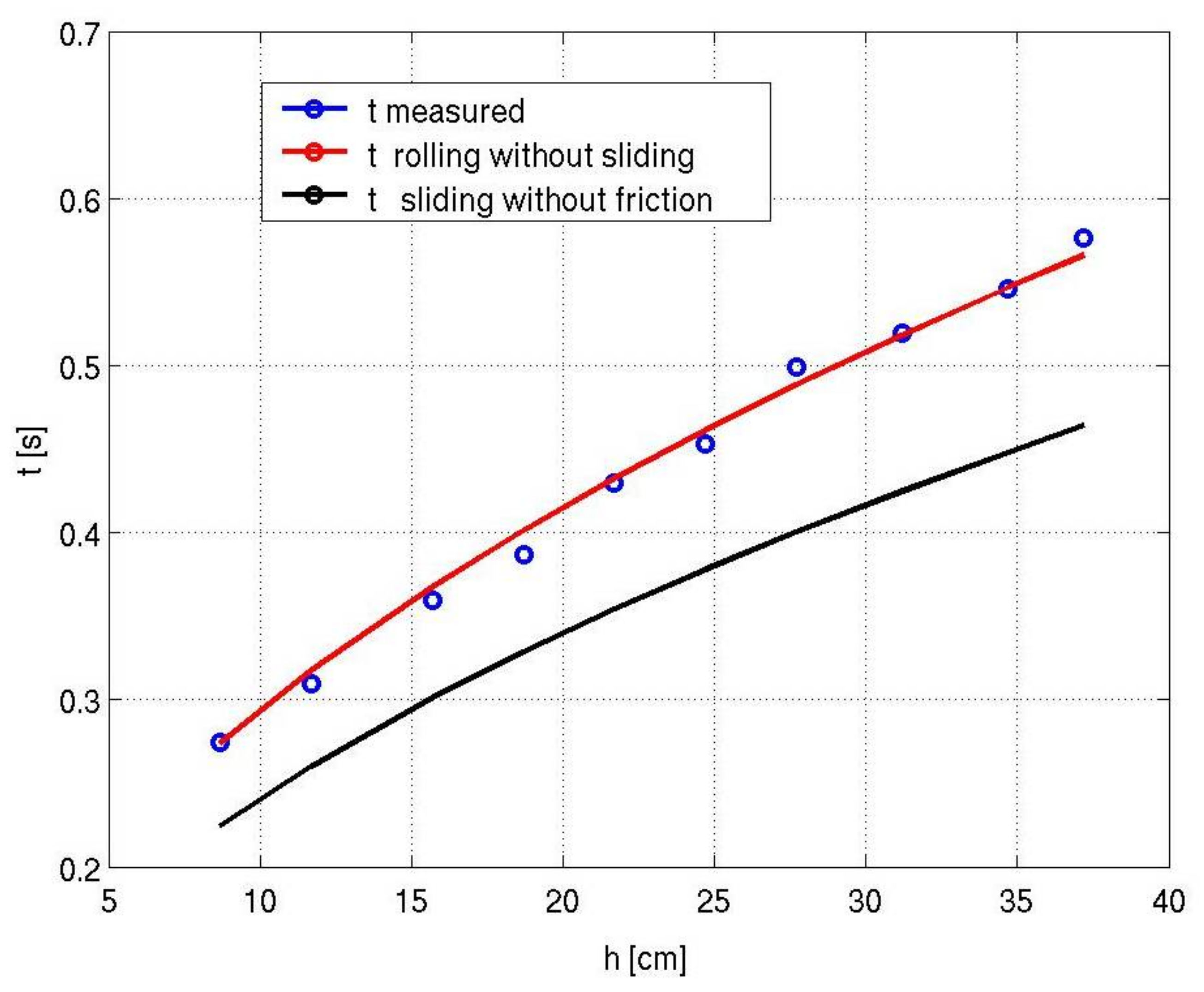
3. Results and Discussion
The Energy Consideration
4. Conclusions
Author Contributions
Conflicts of Interest
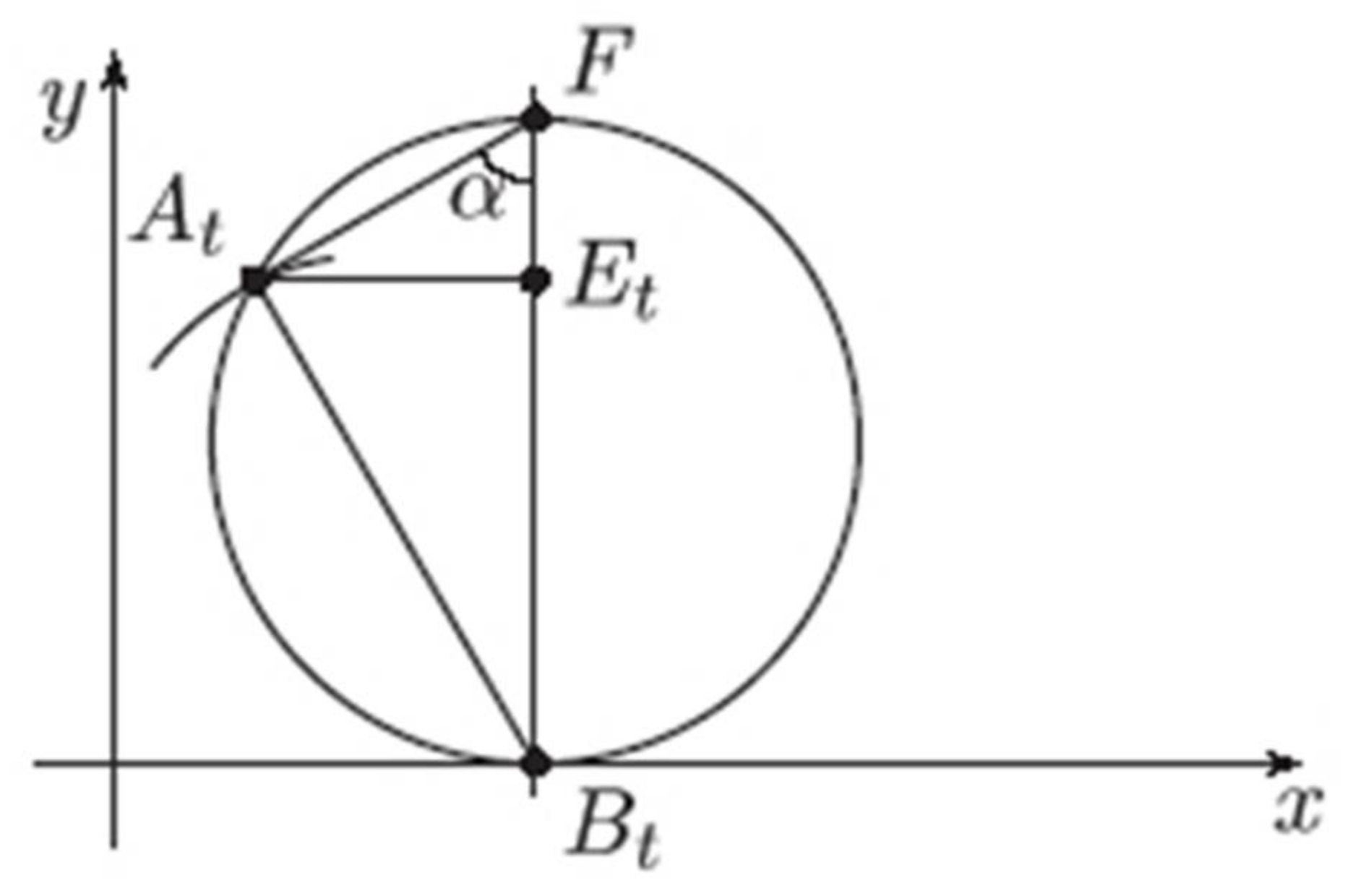
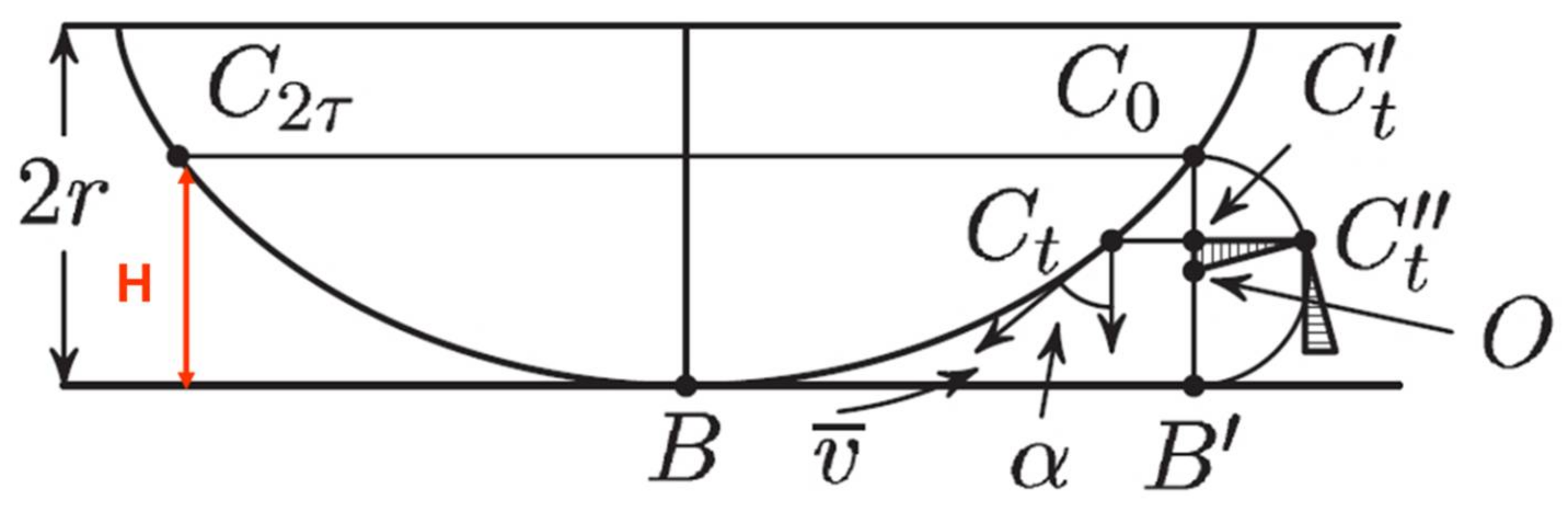
Appendix A. Huygens’ Proof That a Cycloid Is an Isochronic Curve 2
References
- Gindkin, S. Tale of Mathematics and Physicists, 2nd ed.; Springer: Berlin, Germany, 2007; pp. 107–193. [Google Scholar]
- Ben-Abu, Y.; Eshach, H.; Yizhaq, H. Interweaving the Principle of Least Potential Energy in School and Introductory University Physics Courses. Symmetry 2017, 9, 45. [Google Scholar] [CrossRef]
- Yoder, J.G. Unrolling Time; Cambridge University Press: Cambridge, UK, 1988; pp. 115–127. [Google Scholar]
- Mungan, C.E.; Trevor, C.L. Minimum descent time along a set of connected inclined planes. Eur. J. Phys. 2017, 38, 045002. [Google Scholar] [CrossRef]
- Theilmann, F. Approaching the Brachistochrone using inclined planes—Striving for shortest or equal travelling times. Phys. Educ. 2016, 52, 015009. [Google Scholar] [CrossRef]
- Caravlho, S.C.; Sousa, A.S. An inexpensive technique to measure coefficient of friction with rolling solides. Phys. Teach. 2005, 43, 548–550. [Google Scholar]
- Walker, J.; Resnick, R.; Halliday, D. Halliday & Resnick Fundamentals of Physics, 10th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ben-Abu, Y.; Wolfson, I.; Baran, G.; Yizhaq, H. Downhill cycling symmetry breaking: How the rider foils experiment. Phys. Educ. 2017, 52, 065005. [Google Scholar]
- Gluck, P. Balls on an incline roll, slide and skip. Phys. Educ. 2011, 40, 206. [Google Scholar] [CrossRef]
- Benacka, J.; Stubna, I. Ball launched against an inclined plane—An example of using recurrent sequences in school physics. Int. J. Math. Educ. Sci. Technol. 2009, 40, 696–705. [Google Scholar] [CrossRef]
- Ben-Abu, Y. Gate Antiphase of Potassium Channel. Symmetry 2017, 9, 150. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben-Abu, Y.; Wolfson, I.; Eshach, H.; Yizhaq, H. Energy, Christiaan Huygens, and the Wonderful Cycloid—Theory versus Experiment. Symmetry 2018, 10, 111. https://doi.org/10.3390/sym10040111
Ben-Abu Y, Wolfson I, Eshach H, Yizhaq H. Energy, Christiaan Huygens, and the Wonderful Cycloid—Theory versus Experiment. Symmetry. 2018; 10(4):111. https://doi.org/10.3390/sym10040111
Chicago/Turabian StyleBen-Abu, Yuval, Ira Wolfson, Haim Eshach, and Hezi Yizhaq. 2018. "Energy, Christiaan Huygens, and the Wonderful Cycloid—Theory versus Experiment" Symmetry 10, no. 4: 111. https://doi.org/10.3390/sym10040111
APA StyleBen-Abu, Y., Wolfson, I., Eshach, H., & Yizhaq, H. (2018). Energy, Christiaan Huygens, and the Wonderful Cycloid—Theory versus Experiment. Symmetry, 10(4), 111. https://doi.org/10.3390/sym10040111



