Recomputing Causality Assignments on Lumped Process Models When Adding New Simplification Assumptions
Abstract
:1. Introduction
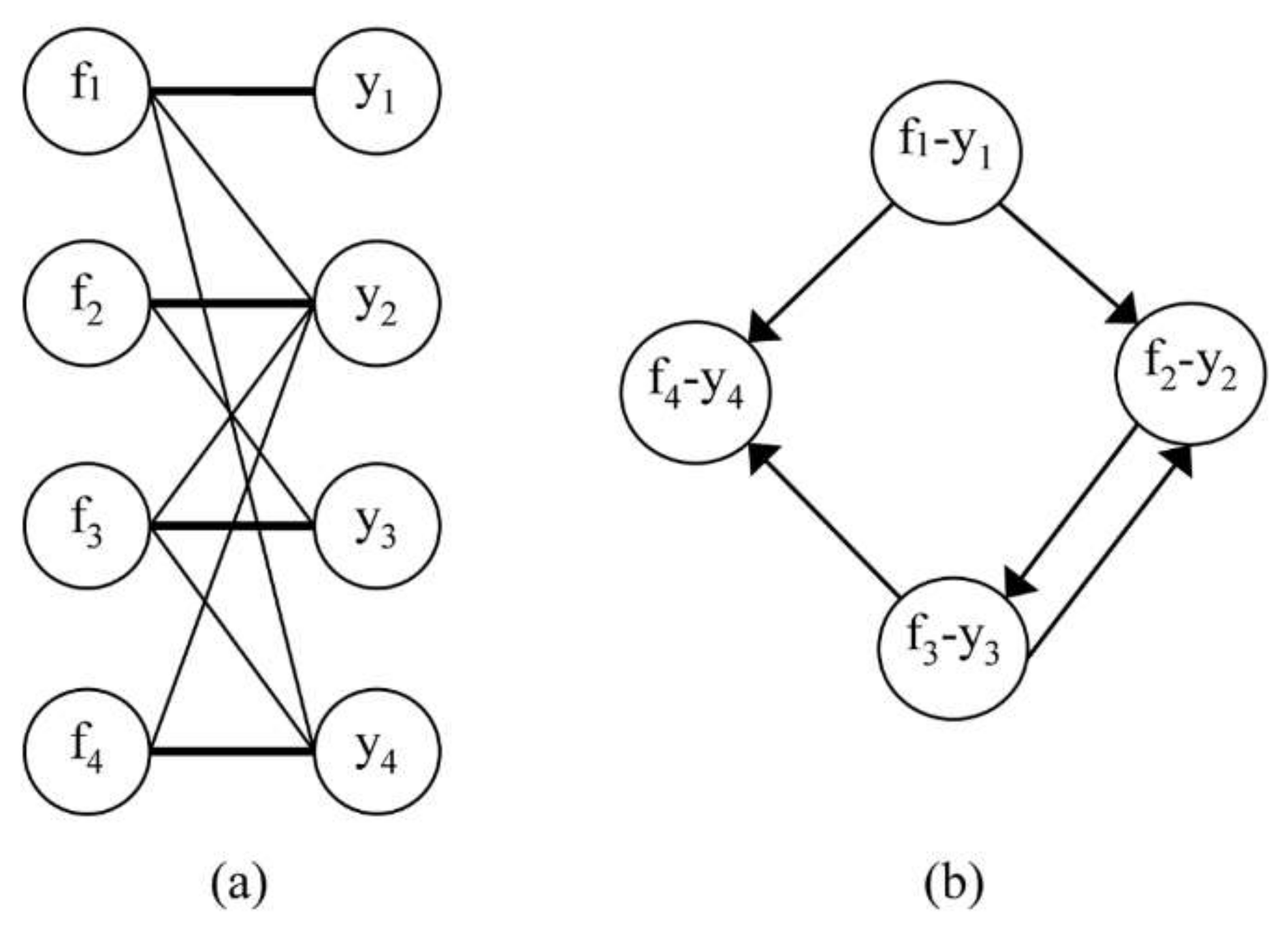
2. Bipartite Graph Preliminzaries
| Algorithm 1. Computing matching of maximum weight on a bipartite graph. |
| Input: A bipartite graph B(L, R, E) and weight function w. Output: Matching of maximum weight. 1: Construction of a direct graph GM(V, EM) with function weight z. 1.1: V = L ∪ R 1.2: EM is defined by: If the undirected edge (l, r) ∈ Mc then the directed edge (l, r) ∈ EM. else if the undirected edge (l, r) ∈ M then the directed edge (r, l) ∈ EM. end if That is, the set of edges EM is: EM = {(l, r)/(l, r) ∈ Mc} ∪ {(r, l)/(l, r) ∈ M} 1.3: The weight function z is defined: If (l, r) ∈ EM then z(l, r) = w (l, r). else if (r, l) ∈ EM then z(r, l) = − w((l, r) end if 1.4: Append a new vertex s linked to all free vertexes of L. 1.5: Append a new vertex t which is the destination of all free vertexes of R. 2: M := ∅ 3: while there exists an augmented path p of minimum cost into GM do 3.1: M := M ∆ p 3.2: Apply steps 1.2 and 1.3 to GM. end while |
3. Hangos’ Method for New Model Assumptions
3.1. Hangos’ Algorithms
- Hangos’ Algorithm 1: it is applied when only one assumption equation e is added. It has the following features:
- -
- The free vertexes on the new graph are ‘e’ and variables from D ∪ S.
- -
- The shortest path from ‘e’ to any variable of D ∪ S is found by a Breadth First Search (BFS).
- -
- The resulting matching is that having the greatest number of edges shared with F.
- -
- The computational cost is O(V + E), where V is the number of vertex in the graph.
- Hangos’ Algorithm 2: it is used when several assumption equations Q are added, and its properties are:
- -
- The vertexes of the new graph become: L′ = L ∪ Q and R′ = R ∪ D ∪ S.
- -
- The weight function w: is defined as follows:The purpose of this function is to provide higher weights to the edges of F to obtain a solution with the maximum number of edges shared with F.
- -
- The maximum matching of maximum weight for w has the greatest number of edges shared with F.
3.2. Problems of Hangos’ Method
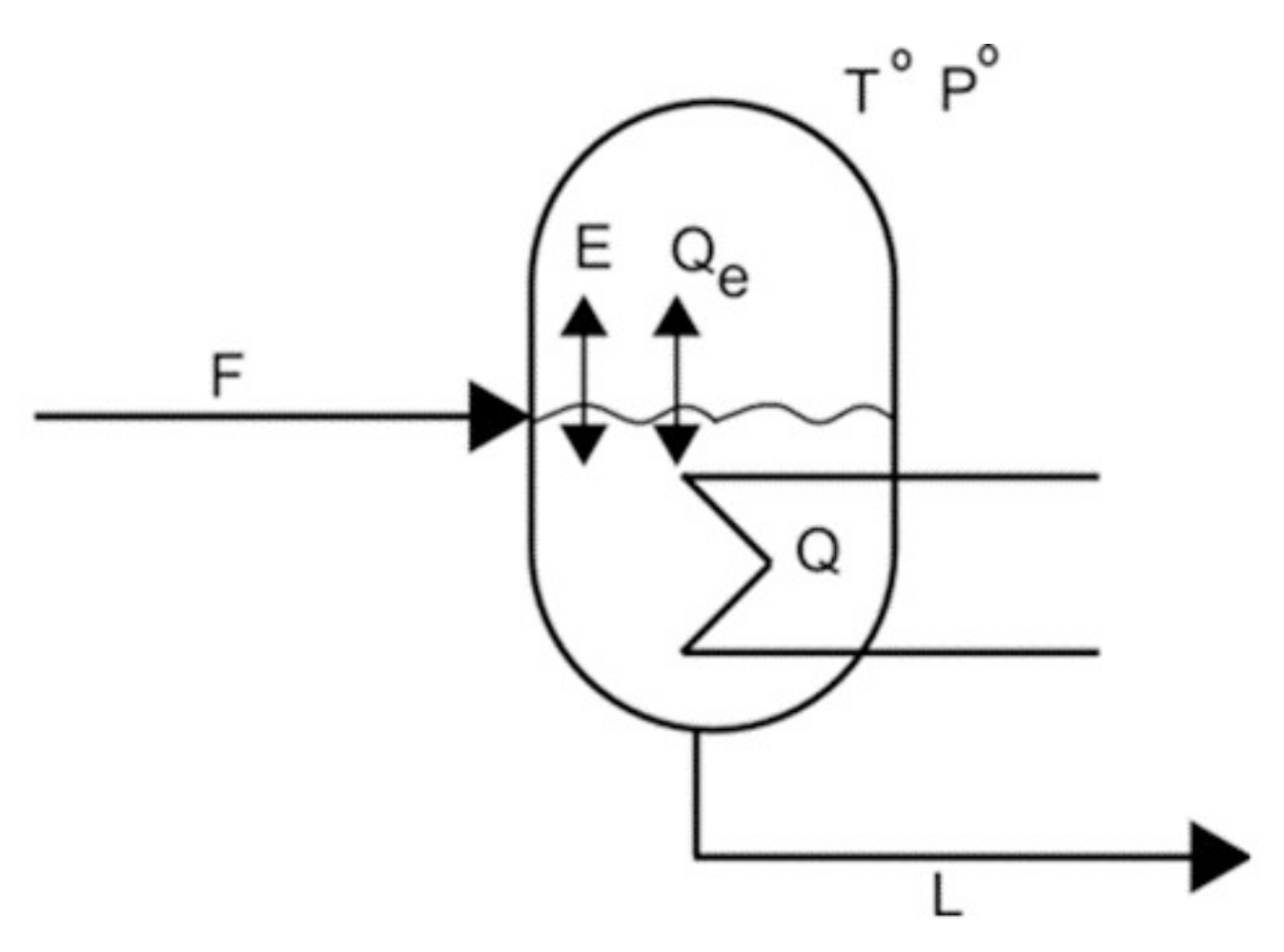
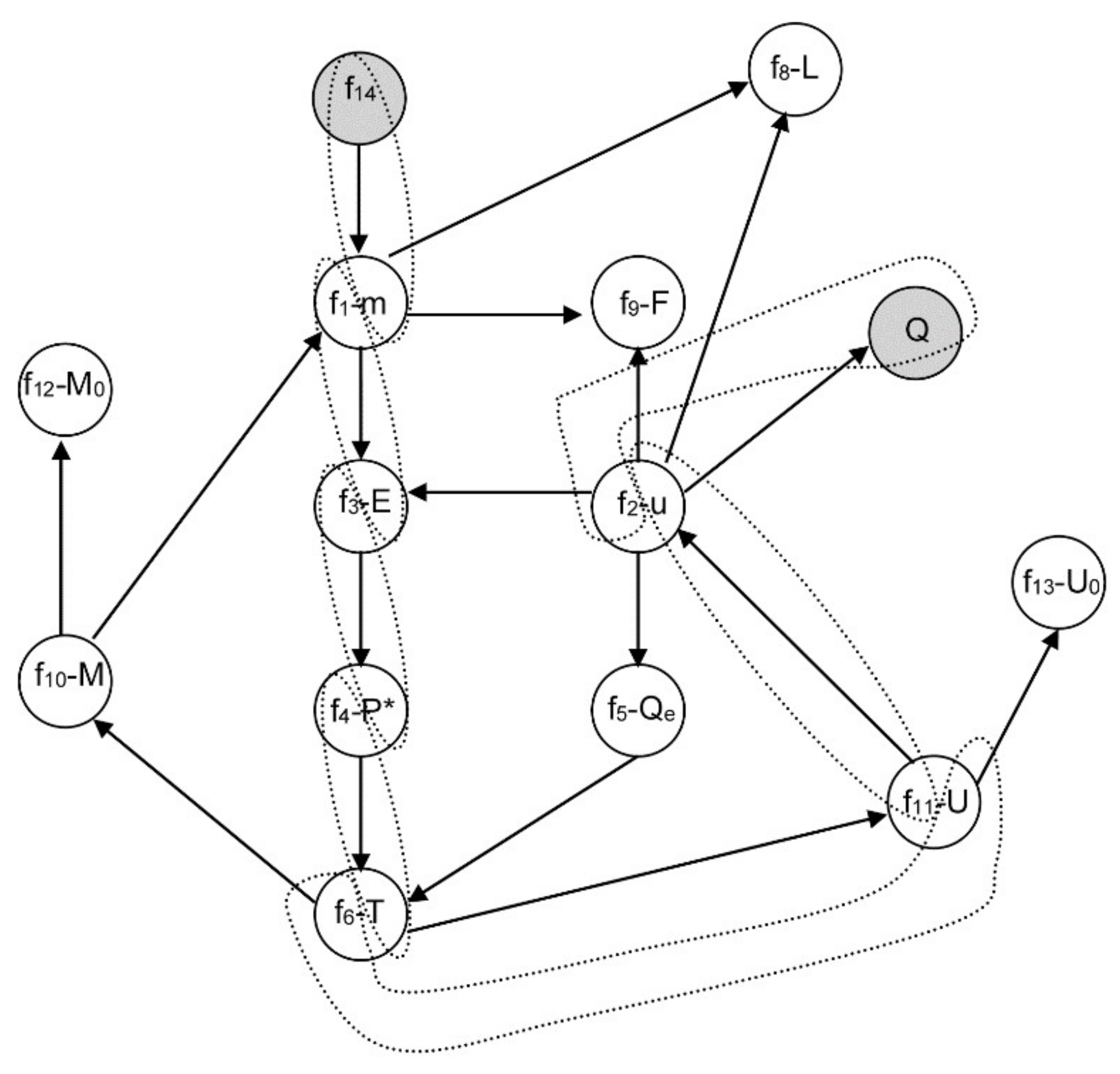
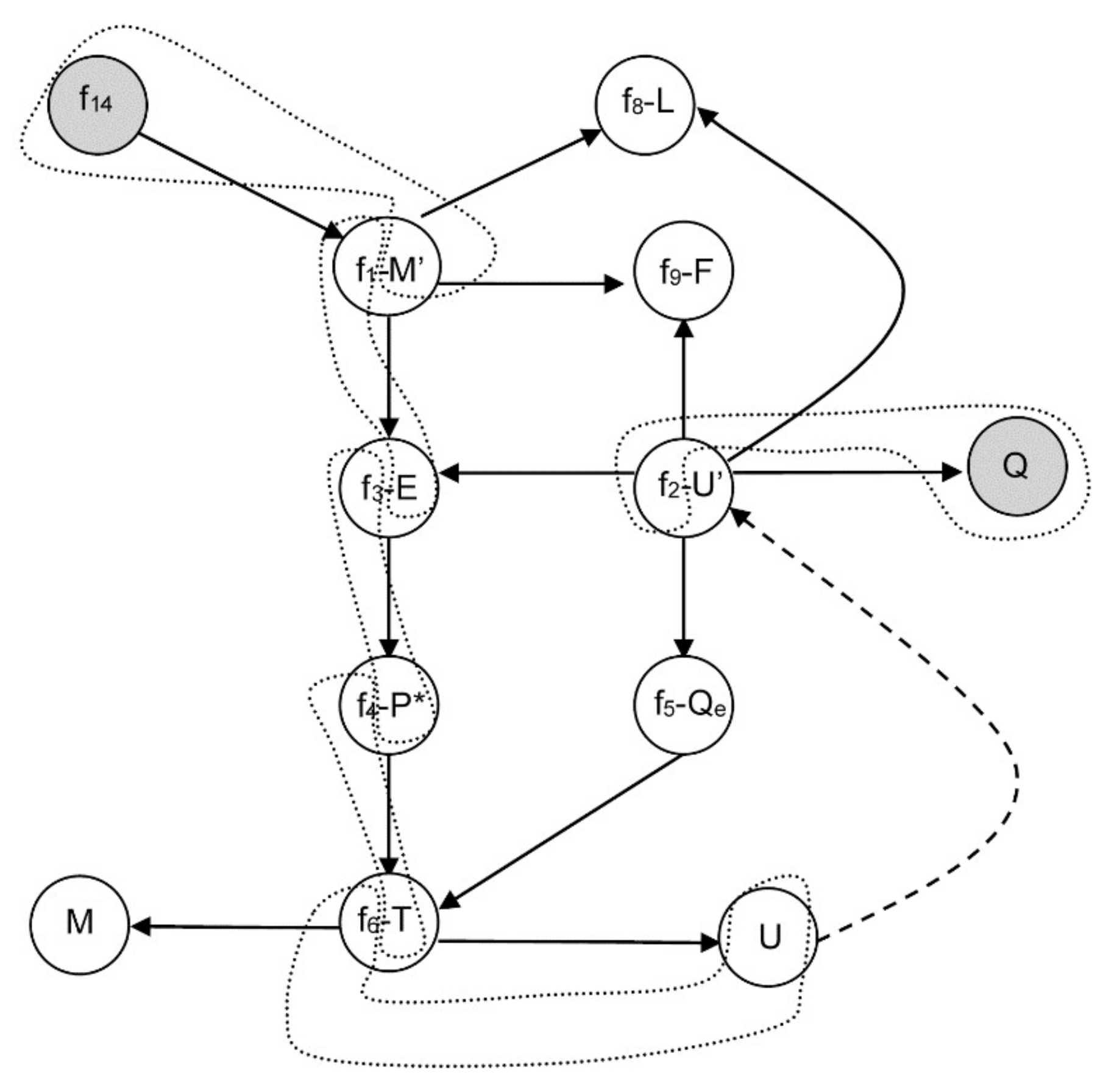
3.2.1. Example 1: Removing Initial Conditions
- From equation f14 (8), m = 0, and consequently, from f1 it is obtained that E is a function of F and L: E = F − L ⇒ E = E(F,L).
- Similarly, from equation f3 with P0 and kLV constant, P* is a function of F and L: .
- From f4, and assuming H invertible: .
- From f5 with T0 and qLV constant: .
- By equation f6 with ce and M constant: .
- Finally, from f2 with hF, hL, hLV constant: ⇒ .
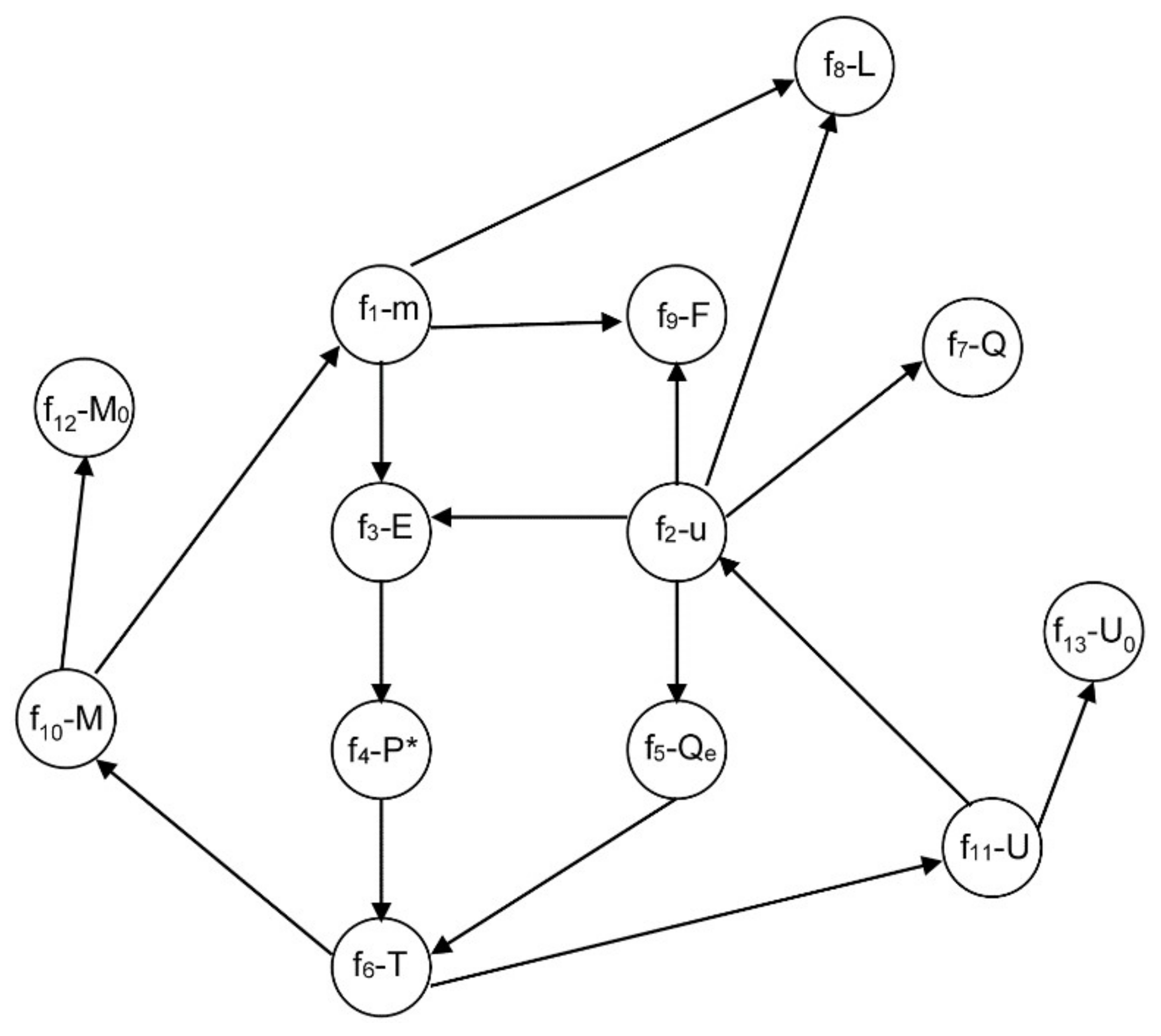
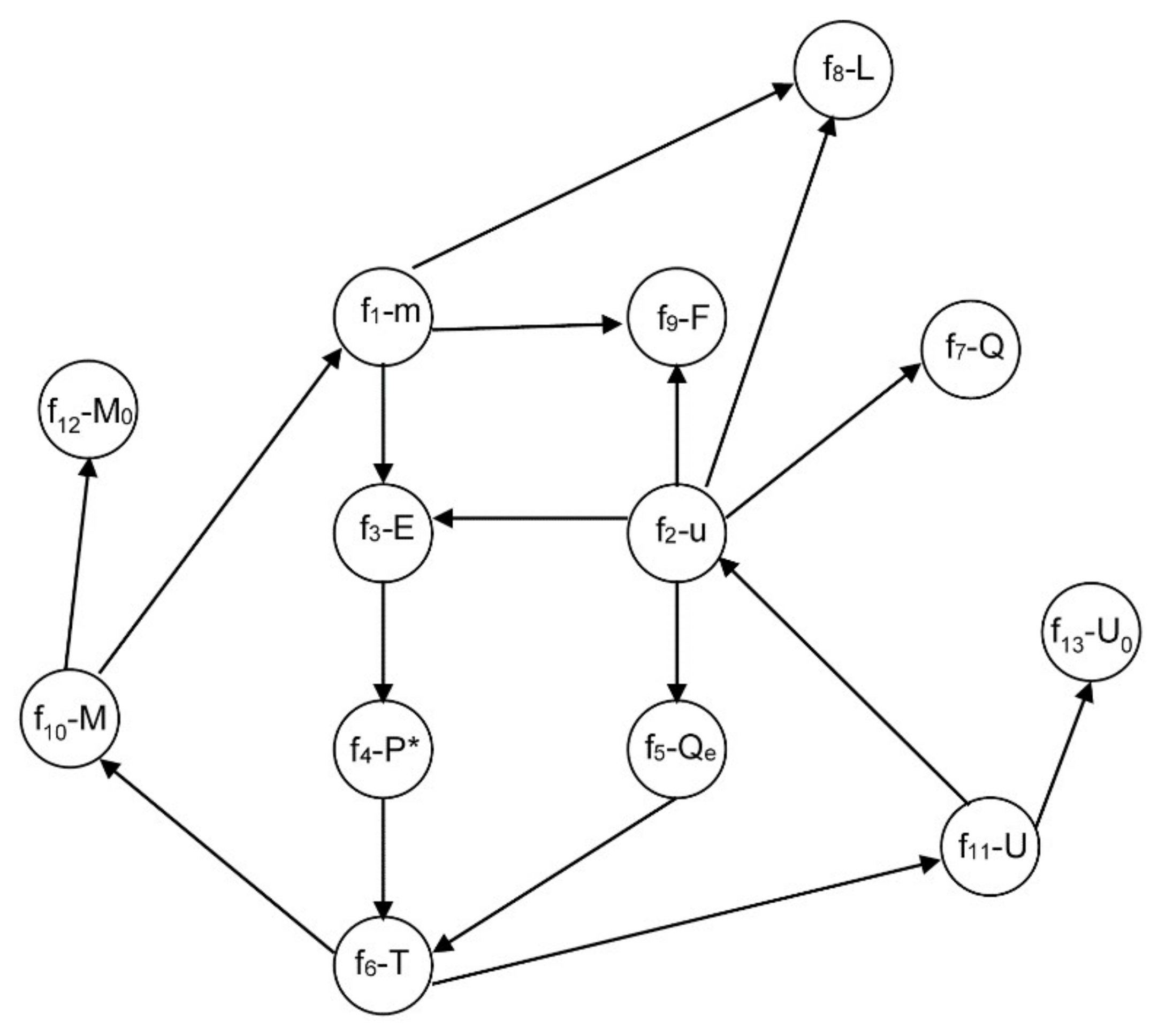
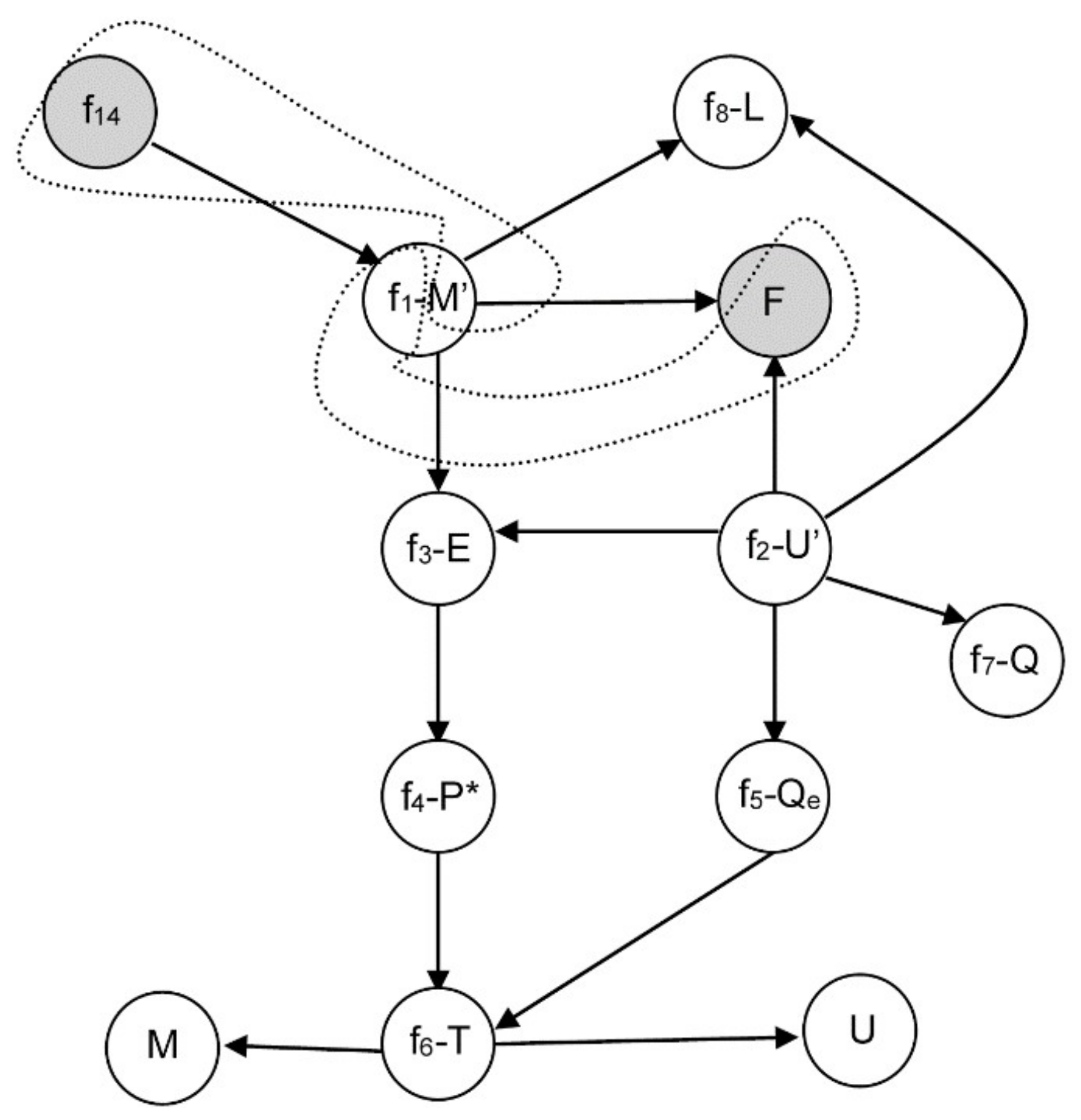
3.2.2. Example 2: Removing an Arbitrary Specification Equation
- Derive equation f11. In this case, equations f13, f6, f10, f12, f4, f3, f1, f8 and f9 must also be derived. After that, a perfect matching is obtained and the index is two, contradicting the previous statement of index one.
- Solve integral f11 by a quadrature method. In this case, it can be thought that no derivative is necessary. However, applying some rules such as the trapezoidal rule, the following results are obtained:To decrease errors, these two formulas are subtracted:Solving the above integral by the trapezoidal rule:and isolating the term u(t + h), the following expression is achieved:The last expression is the numeric derivative of U(t), which shows that the system solution could not converge. Thus, this second alternative is not a good general alternative.
4. Proposed Method by Relaxation of Design Variables
4.1. Basis of the Proposed Method
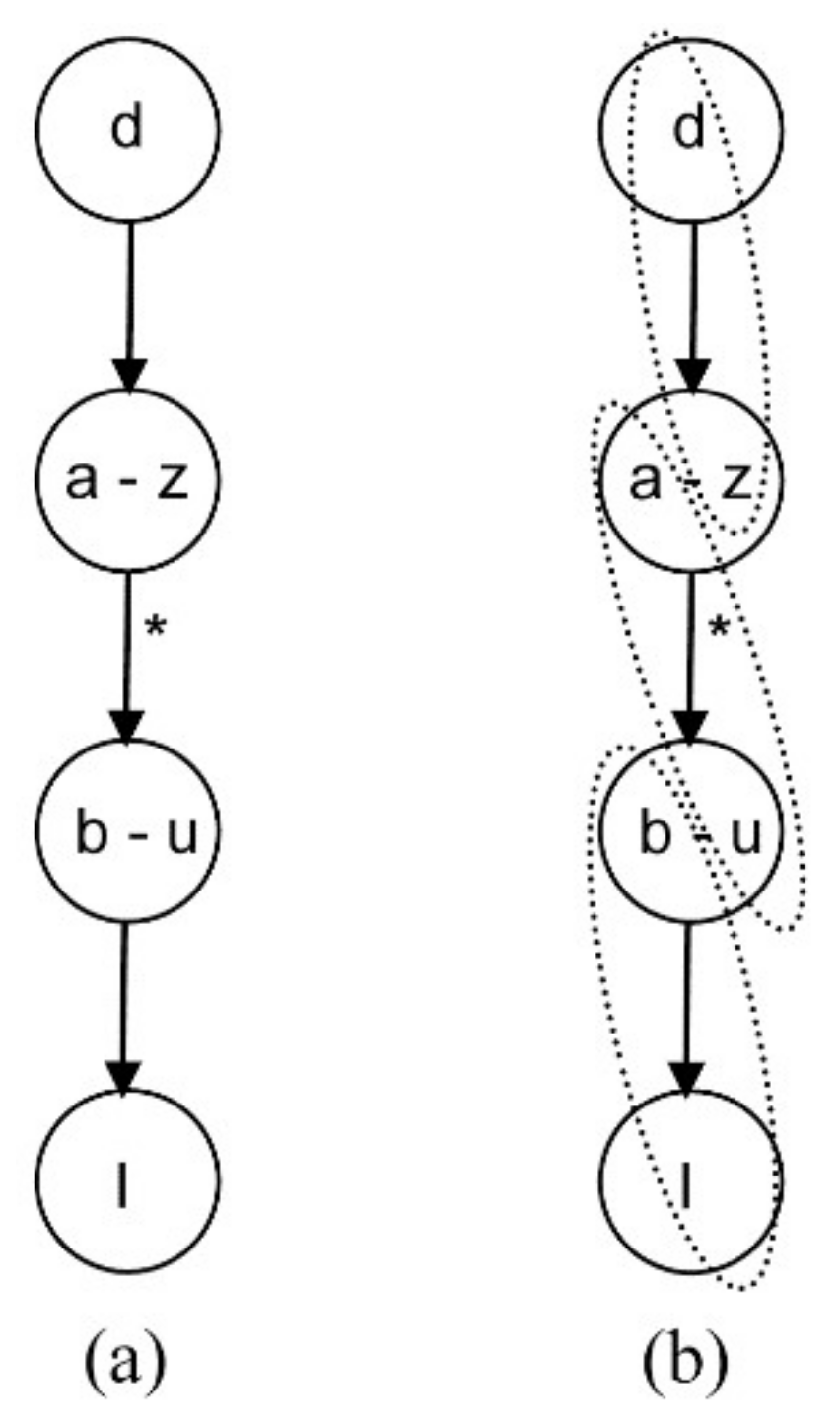
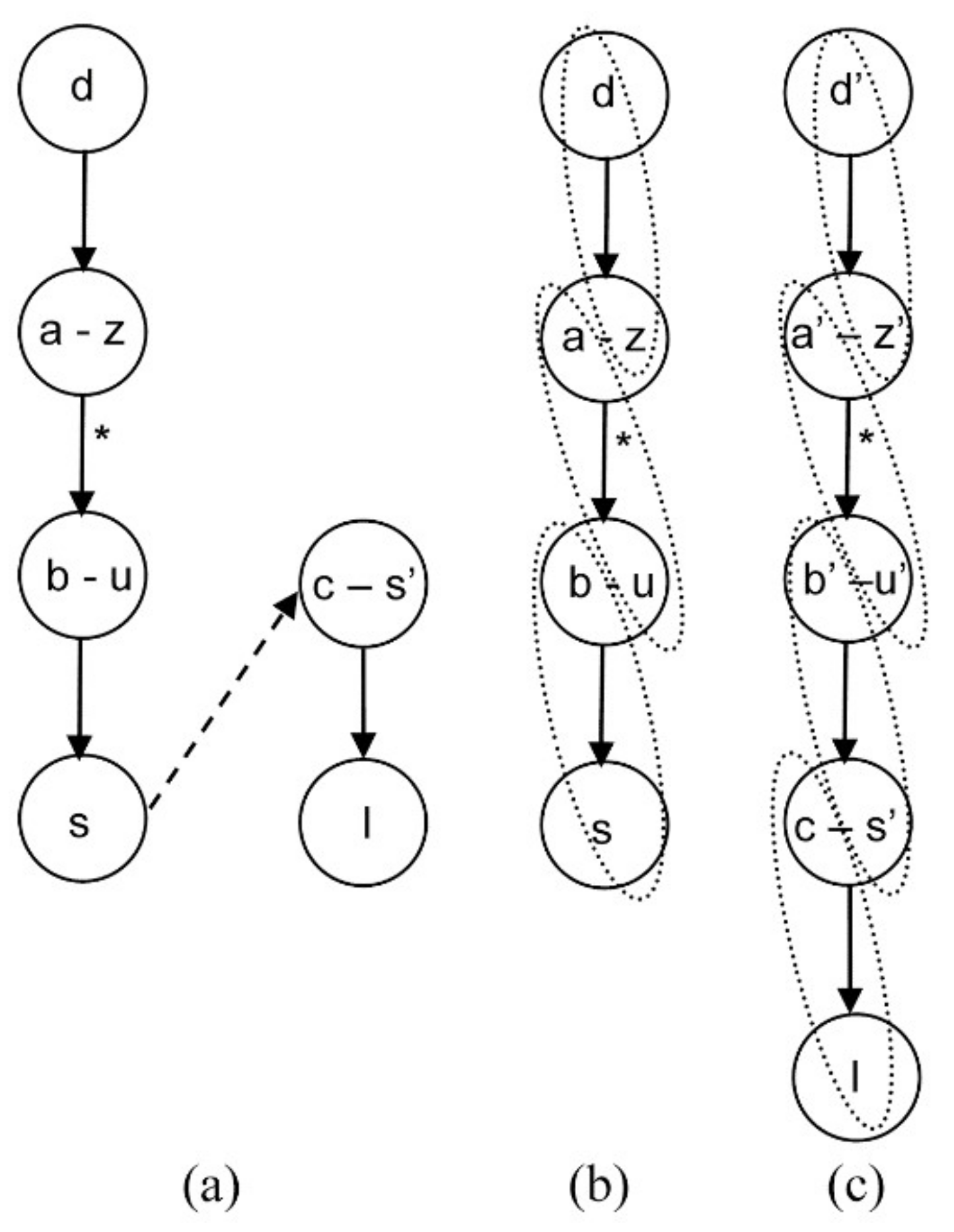
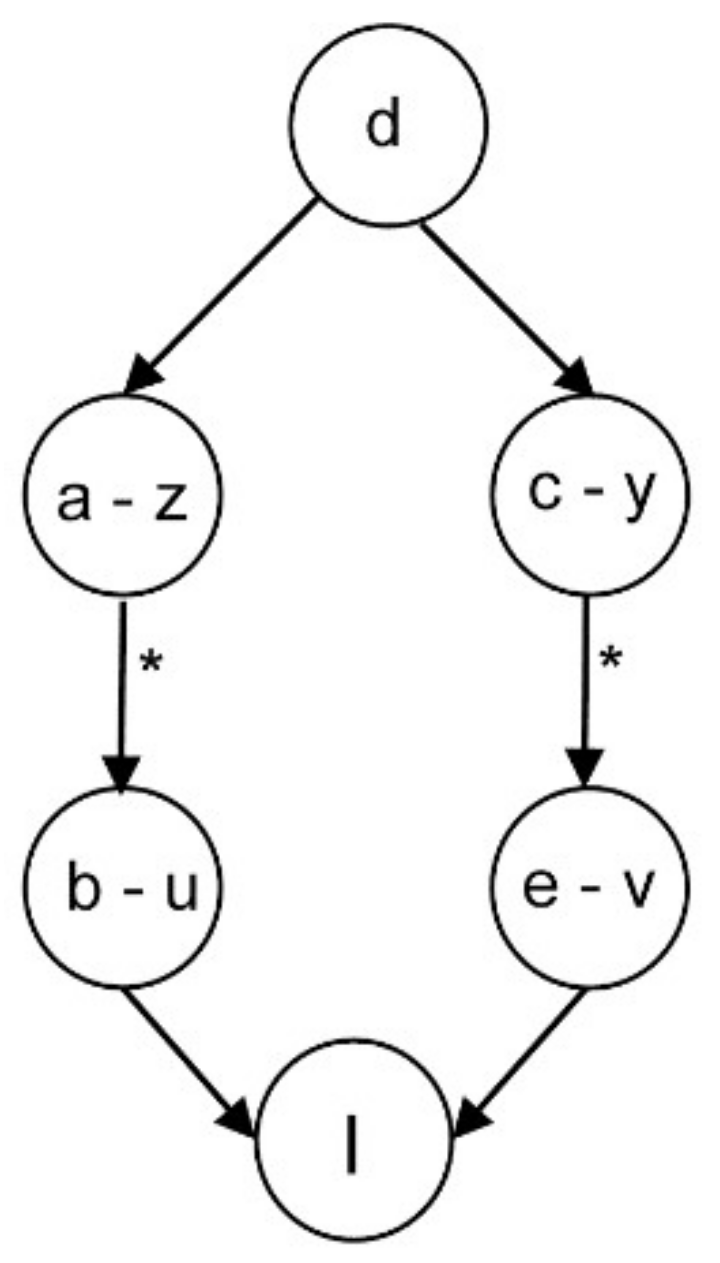
- The capital letters (I, J, K, …) indicate design variables.
- The lowercase letters (a, b, c, …) denote the equation identifier and are placed to the left of the equation-variable node.
- The lowercase letters (u, v, w, …) represent system variables, which are placed to the right of the graph node. In particular, x and s are states and u, v and w denote algebraic variables.
- An arrow marked with an asterisk indicates that there is a path from the first node to the last one.
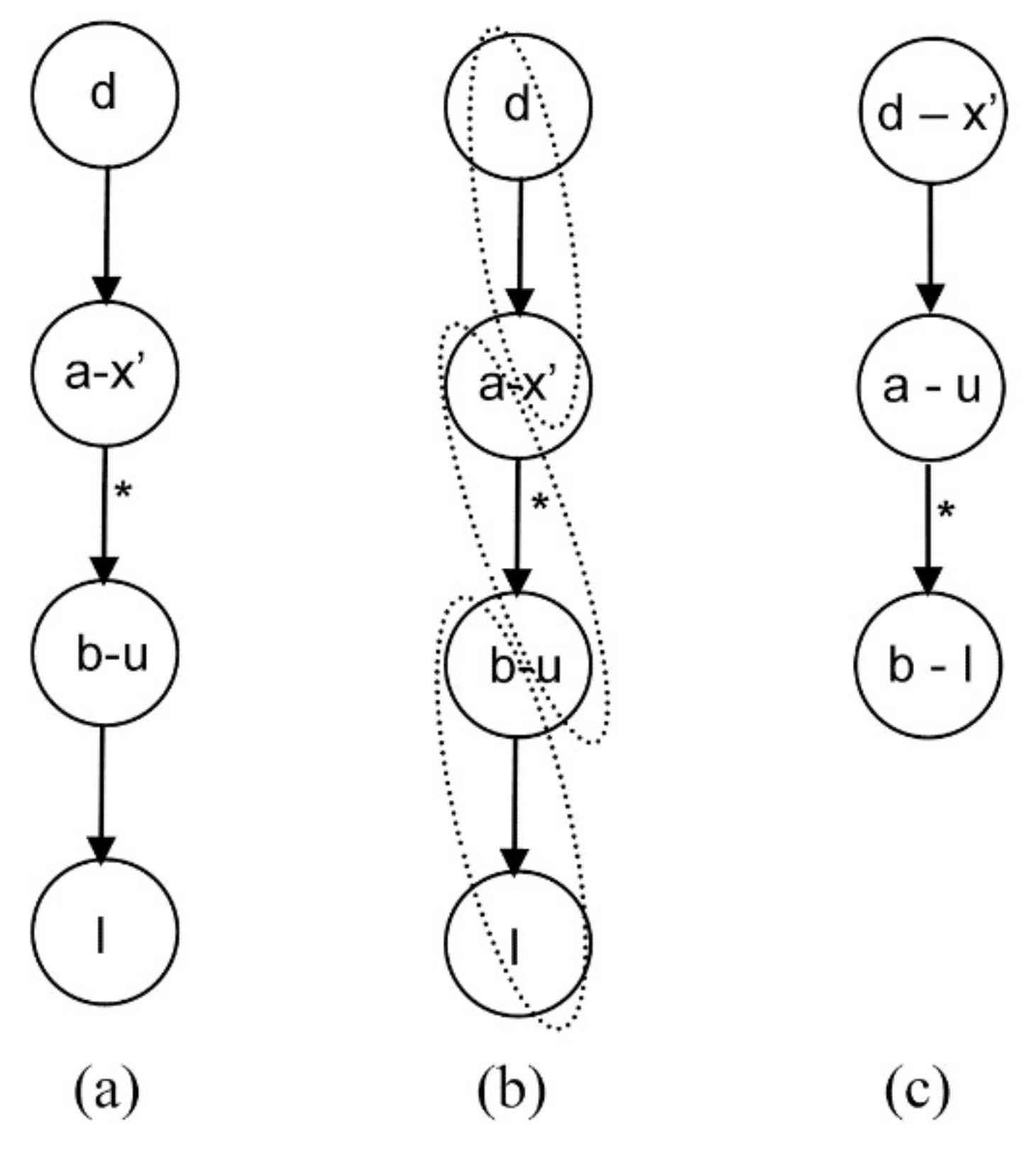
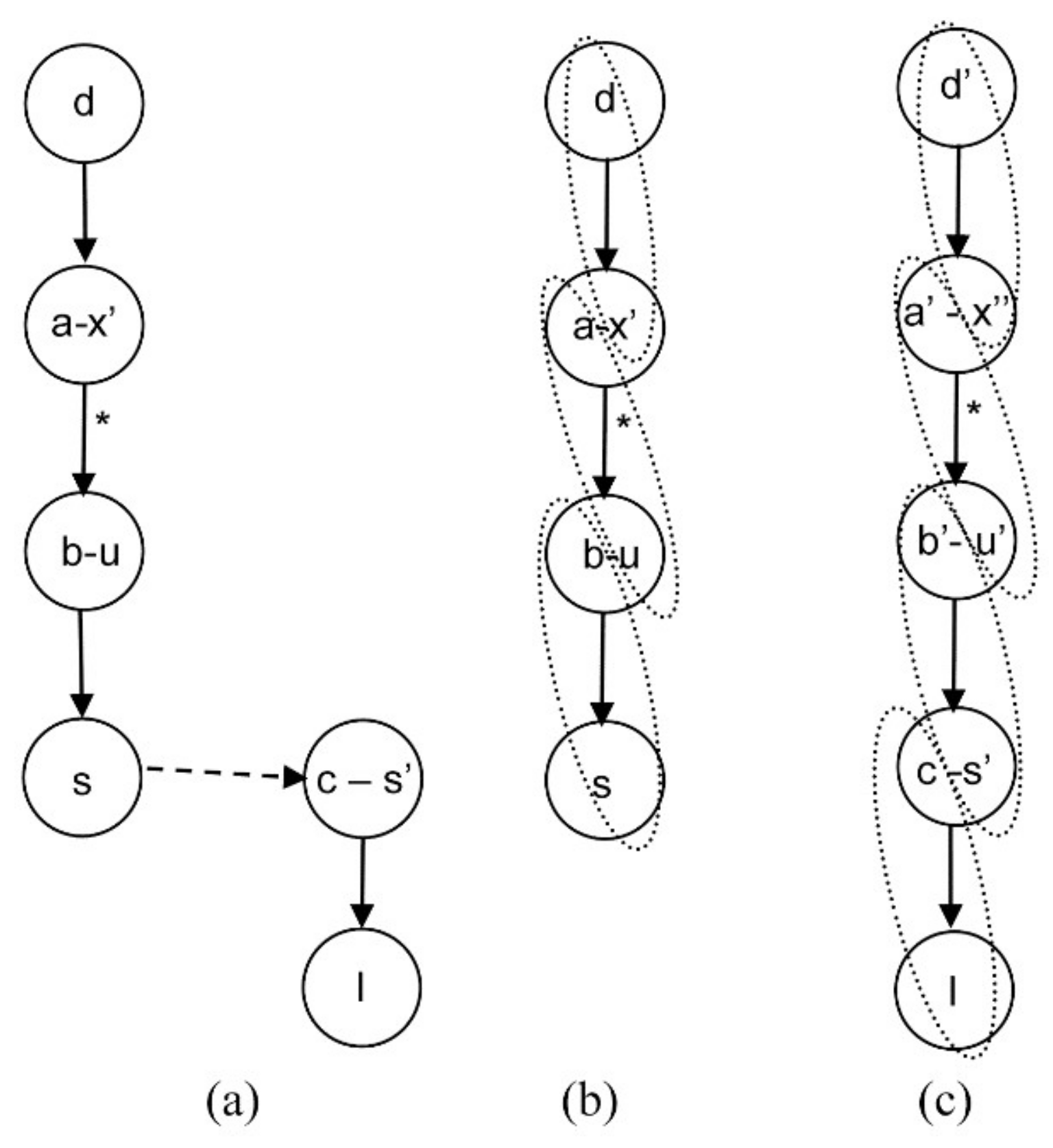
4.1.1. Steady Equation Addition
4.1.2. Algebraic Equation Addition
4.1.3. General Case
4.2. Proposed Algorithm
- (1)
- M ∆ F is decomposed into , where:
- All of the sets pi, di and ci are disjointed.
- pi represents the augmented paths in F. There are k = |M| − |F| > 0 paths of this kind, and all of them have odd length. Moreover, the number of edges of pi in F + 1 is equal to number of edges of pi in M − F, that is:|pi ∩ F| + 1 = |pi ∩ (M − F)| = (|pi| + 1)/2.
- di represents an alternating path of even length. The number of edges of di in F is equal to the number of edges of di in M − F:|di ∩ F| = |di ∩ (M − F)| = |di|/2.
- ci represents cycles, and therefore, their length is even. They fulfill the same equation as di, that is:|ci ∩ F| = |ci ∩ (M − F)| = |ci|/2.
- (2)
- Let M′ = F ∆ (). If M′ is a matching in B and its cardinality is , then:In contrast,
- (3)
- According to our hypothesis, if |M ∩ F| is maximum among all the matchings of cardinality |M|, then: |M ∩ F| |M′ ∩ F|. By (29) and (30):Equation (31) can be simplified to:By replacing the Expressions (27) and (28) into (32):This expression implies that:which is a contradiction. ☐|di| = 0 ∀ i = 1, …, r and |ci| = 0 ∀ i = 1, …., s,
- 1.
- M = F ∆ p1 ∆… ∆ pk.
- 2.
- .
- 3.
- .
- It is known by Lemma 1 that the cardinality of M ∩ F is the maximum among all the maximum matchings. After applying Lemma 2, the desired result is obtained.
- By (26) and (29) of Lemma 2, it follows that:
- By the last expression:As k = |M| − |F|, then:
| Algorithm 2. Find the maximum matching such that |M ∩ F| is highest. |
| Input: A bipartite graph B(L, R, E), weight function w and initial maximum matching F. Output: Matching of maximum weight closest to F. 1: M := F 2: Construction of a direct graph GM (V, EM) with function weight z. 2.1: V = L ∪ R 2.2: EM is defined by: If the undirected edge (l, r) ∈ Mc then the directed edge (l, r) ∈ EM. else if the undirected edge (l, r) ∈ M then the directed edge (r, l) ∈ EM. end if That is, the set of edges EM is: EM = {(l, r)/(l, r) ∈ Mc} ∪ {(r, l)/(l, r) ∈ M} 2.3: The weight function z is defined: If (l, r) ∈ EM then z(l, r) = w (l, r). else if (r, l) ∈ EM then z(r, l) = − w((l, r) end if 2.4: Append a new vertex s linked to all free vertexes of L. 2.5: Append a new vertex t which is the destination of all free vertexes of R. 3: while there exists an augmented path p into GM do 3.1: p = an augmented path of lowest cost in GM 3.2: M := M ∆ p 3.3: Adjust GM by path p. end while |
5. Conclusions
- It relates algebraic and state variables of the assumptions equations to the design variables of the system selected by the user.
- It allows the addition of several assumption equations and obtaining a greater number of common edges with the starting system.
- In the best case, depending on the implementation, the computational cost is O(Q(E + V)), where Q is the number of assumption equations, V the number of vertexes in the bipartite equation-variable graph and E is the number of edges in that graph. Therefore, if the number of assumption equations is small, the cost of the algorithm is linear.
- The algorithm can be combined with an algorithm of index reduction.
Author Contributions
Conflicts of Interest
References
- Garrido, J.; Zafra, A.; Vazquez, F. Object oriented modelling and simulation of hydropower plants with run-of-river scheme: A new simulation tool. Simul. Model. Pract. Theory 2009, 17, 1748–1767. [Google Scholar] [CrossRef]
- Nikolić, D.D. Dae tools: Equation-based object-oriented modelling, simulation and optimisation software. PeerJ Comput. Sci. 2016, 2, e54. [Google Scholar] [CrossRef]
- Fritzson, P.; Engelson, V. Modelica—A Unified object-oriented language for system modeling and simulation. In ECOOP’98—Object-Oriented Programming; Springer: New York, NY, USA, 1998; pp. 67–90. [Google Scholar]
- Piela, P.; Epperly, T.; Westerberg, K.; Westerberg, A. Ascend—An object-oriented computer environment for modeling and analysis—The modeling language. Comput. Chem. Eng. 1991, 15, 53–72. [Google Scholar] [CrossRef]
- Vázquez, F.; Jiménez, J.; Garrido, J.; Belmonte, A. Introduction to Modelling and Simulation with Ecosimpro; Pearson Educacion: Madrid, Spain, 2010; p. 272. [Google Scholar]
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar]
- Navarro, A.; Vassiliadis, V. Computer algebra systems coming of age: Dynamic simulation and optimization of dae systems in mathematica™. Comput. Chem. Eng. 2014, 62, 125–138. [Google Scholar] [CrossRef]
- Cellier, F.E.; Kofman, E. Continuous System Simulation; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Tarjan, R. Depth-first search and linear graph algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Pantelides, C.C. The consistent initialization of differential-algebraic systems. SIAM J. Sci. Comput. 1988, 9, 213–231. [Google Scholar] [CrossRef]
- Cafferkey, N.; Provan, G. An analysis of performance-critical properties of modelica models. IFAC-PapersOnLine 2015, 48, 210–215. [Google Scholar] [CrossRef]
- Unger, J.; Kroner, A.; Marquardt, W. Structural-analysis of differential-algebraic equaion systems—Theory and applications. Comput. Chem. Eng. 1995, 19, 867–882. [Google Scholar] [CrossRef]
- Hangos, K.; Cameron, I. A formal representation of assumptions in process modelling. Comput. Chem. Eng. 2001, 25, 237–255. [Google Scholar] [CrossRef]
- Merchan, V.; Esche, E.; Fillinger, S.; Tolksdorf, G.; Wozny, G. Computer-aided process and plant development. A review of common software tools and methods and comparison against an integrated collaborative approach. Chem. Ing. Tech. 2016, 88, 50–69. [Google Scholar] [CrossRef]
- Jensen, A.K. Generation of Problem Specific Simulation Models within an Integrated Computer Aided System; CAPEC-DTU: Lyngby, Denmark, 1998. [Google Scholar]
- Bogusch, R.; Lohmann, B.; Marquardt, W. Computer-aided process modeling with modkit. Comput. Chem. Eng. 2001, 25, 963–995. [Google Scholar] [CrossRef]
- Moe, H.I. Dynamic Process Simulation: Studies on Modeling and Index Reduction. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1995. [Google Scholar]
- Murota, K. Systems analysis by graphs and matroids. Structural solvability and controllability. SIAM Rev. 1989, 31, 502. [Google Scholar]
- Leitold, A.; Hangos, K. Structural solvability analysis of dynamic process models. Comput. Chem. Eng. 2001, 25, 1633–1646. [Google Scholar] [CrossRef]
- Soares, R.D.P.; Secchi, A.R. Structural analysis for static and dynamic models. Math. Comput. Model. 2012, 55, 1051–1067. [Google Scholar] [CrossRef]
- Hangos, K.; Szederkenyi, G.; Tuza, Z. The effect of model simplification assumptions on the differential index of lumped process models. Comput. Chem. Eng. 2004, 28, 129–137. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Korte, B.; Vygen, J.; Korte, B.; Vygen, J. Combinatorial Optimization; Springer: Berlin, Germany, 2012; Volume 2. [Google Scholar]
- Tassa, T. Finding all maximally-matchable edges in a bipartite graph. Theor. Comput. Sci. 2012, 423, 50–58. [Google Scholar] [CrossRef]
- Micali, S.; Vazirani, V.V. An O(v|v| c |E|) algorithm for finding maximum matching in general graphs. In Proceedings of the 21st Annual Symposium on Foundations of Computer Science, Syracuse, NY, USA, 13–15 October 1980; pp. 17–27. [Google Scholar]
- Gabow, H.N.; Tarjan, R.E. Faster scaling algorithms for general graph matching problems. J. ACM 1991, 38, 815–853. [Google Scholar] [CrossRef]
- Hopcroft, J.E.; Karp, R.M. An n^5/2 algorithm for maximum matchings in bipartite graphs. SIAM J. Comput. 1973, 2, 225–231. [Google Scholar] [CrossRef]
- Mucha, M.; Sankowski, P. Maximum matchings via gaussian elimination. In Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, Rome, Italy, 17–19 October 2004; pp. 248–255. [Google Scholar]
- Goel, A.; Kapralov, M.; Khanna, S. Perfect matchings in O(n\logn) time in regular bipartite graphs. SIAM J. Comput. 2013, 42, 1392–1404. [Google Scholar] [CrossRef]
- Frenkel, J.; Kunze, G.; Fritzson, P. Survey of appropriate matching algorithms for large scale systems of differential algebraic equations. In Proceedings of the 9th International MODELICA Conference, Munich, Germany, 3–5 September 2012; Linköping University Electronic Press: Linköping, Sweden, 2012; pp. 433–442. [Google Scholar]
- Berge, C. Two theorems in graph theory. Proc. Natl. Acad. Sci. USA 1957, 43, 842–844. [Google Scholar] [CrossRef] [PubMed]
- Har-Peled, S. Matchings II. Available online: https://courses.engr.illinois.edu/cs473/fa2015/w/lec/lec/31_matchings_II.pdf (accessed on 8 April 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belmonte, A.; Garrido, J.; Jiménez, J.E.; Vázquez, F. Recomputing Causality Assignments on Lumped Process Models When Adding New Simplification Assumptions. Symmetry 2018, 10, 102. https://doi.org/10.3390/sym10040102
Belmonte A, Garrido J, Jiménez JE, Vázquez F. Recomputing Causality Assignments on Lumped Process Models When Adding New Simplification Assumptions. Symmetry. 2018; 10(4):102. https://doi.org/10.3390/sym10040102
Chicago/Turabian StyleBelmonte, Antonio, Juan Garrido, Jorge E. Jiménez, and Francisco Vázquez. 2018. "Recomputing Causality Assignments on Lumped Process Models When Adding New Simplification Assumptions" Symmetry 10, no. 4: 102. https://doi.org/10.3390/sym10040102
APA StyleBelmonte, A., Garrido, J., Jiménez, J. E., & Vázquez, F. (2018). Recomputing Causality Assignments on Lumped Process Models When Adding New Simplification Assumptions. Symmetry, 10(4), 102. https://doi.org/10.3390/sym10040102






