Abstract
Recently, prediction modelling has become important in data analysis. In this paper, we propose a novel algorithm to analyze the past dataset of crop yields and predict future yields using regression-based approximation of time series fuzzy data. A framework-based algorithm, which we named DAbFP (data algorithm for degree approximation-based fuzzy partitioning), is proposed to forecast wheat yield production with fuzzy time series data. Specifically, time series data were fuzzified by the simple maximum-based generalized mean function. Different cases for prediction values were evaluated based on two-set interval-based partitioning to get accurate results. The novelty of the method lies in its ability to approximate a fuzzy relation for forecasting that provides lesser complexity and higher accuracy in linear, cubic, and quadratic order than the existing methods. A lesser complexity as compared to dynamic data approximation makes it easier to find the suitable de-fuzzification process and obtain accurate predicted values. The proposed algorithm is compared with the latest existing frameworks in terms of mean square error (MSE) and average forecasting error rate (AFER).
1. Introduction
Currently, time series having indecision observations are called fuzzy time series, a term originally defined by Song and Chissom [1,2]. The interpretation obtained from time series is then transformed into fuzzy sets. There is a need for data available in numerous forms multiplied over time. Forecasting is suitable for circumstances where vacillation linked to the outcome is tangible. Time series exploration is an essential mechanism for forecasting the unknown on the basis of its past history. The two significant methods that fit this category are time series and regression. Modern approaches to time series forecasting are influenced by the repetition of history itself. Time series include the recorded values of the variable in the past and also include the present value. This method supports the discovery of arrangements and the inference of future events based on the patterns established as the chief focus material of time series analysis. Solutions to various practical problems related to finance, economics, marketing, and business as well as prediction in economic and sales forecasting, information systems forecasting, stock market prediction, the number of outpatient visits, etc., can be determined using time series.
The idea for the exploratory work on this topic came from an extensive study of work previously done in the niche field of extrapolative demonstration using fuzzy logic. In an agrarian country with a primarily tropical climate, a tropical plant like wheat presents itself as a very lucrative and justifiable topic. To put this into perspective, Asia on its own harvests and ingests more than three quarters of the global wheat production. If economists are to be believed, this dominance by Asia in the global wheat market leads to a reduction in poverty in the region. With an improvement in production and quality of yield, wheat becomes more accessible to people from all walks of life at a lower price, which in turn pushes farmers to invest in sophisticated and valued crops. These crops bring additional income and prosperity to the farmers’ families and improve consumer food products. The sustainable computing and management of natural resources has therefore become an imperative field of study [3]. The assessment and forecasting of wheat manufacture certainly require much effort [4].
Various experimental results have been published where prediction has been shown on different datasets based on time series forecasting. Forecasting and predictions help in combating decision-making problems. Askar [5] proposed an autoregressive moving average model to predict wheat crop yield. Sachin [6,7] worked specifically on predicted rice yield for inventory management using a fuzzy time series model. Narendra [8] proposed a model for a terse-period agricultural protraction estimate. Eǧrioǧlu et al. [9,10] and Wangren et al. [11], on the other hand, implemented a generalized equivalent length breaks implanted for improvement. The former used a genetic approach.
In contrast to the above discussed methods, the proposed method in this study focused on diverse and finer levels of partitions with respect to fuzzy series data. Using this degree approximation method based fuzzy portioning, a higher prediction accuracy was observed. The method of fuzzy partitioning involved the creation of newly generated fuzzy sets based on the underlying data. The time series wheat data undertaken consisted of dynamic data whose feature value changes as a function of time. In partitioning, elements that are more similar than others form members of one set, whereas dissimilar elements form different fuzzy sets. Prediction was done under a fuzzy environment that consisted of ambiguity, improbability, and inaccuracy. The fuzzy intervals were divided based on the frequency of number of times series data. Later, historical time series data analysis was performed by computation of higher order logical fuzzy relations based on the universe of discourse. The novelty of this paper is explained below.
The proposed method used the first 9th and 11th interval time series fuzzy partitioning for wheat production prediction. Based on the interval-based fuzzy partition degree, approximation was applied for real-time wheat produce forecasting. De-fuzzified outputs obtained from approximations were estimated for error and compared with four existing methods. The decision to use fuzzy partitioning in comparison to a regression model was due to the fact that relationships become more complex when dealing with time series data. As proposed in our case, the wheat dataset was dynamic as a function of time, and the use of regression would not produce compact sets. Fuzzy partitioning was a better approach that used degrees of memberships rather than a strict rule as in case of regression. Because the relationship in our time series dataset was not sufficient to apply regression, fuzzy partitioning was a better choice. The method of fuzzy partitioning was closer to human observation behavior as compared to a linear regression model. Furthermore, the new method for forecasting wheat production with a fuzzy time series using degree approximation as a fuzzy relation for forecasting provided lesser complexity in the linear order. Such simplicity was extended to cubic and quadratic polynomial approximation which minimized the time needed to generate relational equations based on complex min-max composition operations, as well as the various hits and trials of the defuzzification process that might be required to achieve better accuracy as used in [6,7,8,9,12] as well as by Singh [13]. Two-set partitioning with lower and higher approximation performed over regression analysis finally helped in selecting a best fit line/values that represents the average across all points in graph [14].
The rest of the paper is organized as follows: Section 2 provides the literature overview about the use and progress of time series-based fuzzy partition for prediction problems. Section 3 gives the complete explanation of the proposed framework for the algorithm formulated. Section 3.1 gives a diagram workflow representation of the framework followed by a numerical example explaining the methodology in brief. In Section 3.2, a detailed explanation of the proposed methodology, which we named data algorithm for degree approximation-based fuzzy partitioning (DAbFP), is given with intermediate results. The fuzzy logic relation (FLR) for different intervals is calculated using the wheat yield dataset for different years. Thereafter, average forecasting error rate (AFER) and mean square error (MSE) formulas are also mentioned. Section 4 lists experiments using different degree polynomials and calculating the AFER and MSE for the corresponding polynomials with their respective plots. The proposed algorithm is compared with the existing methods in terms of AFER and MSE with respect to other algorithms. Finally, Section 5 depicts the final conclusions about the method and its implications over the wheat dataset and also emphasizes its future application and scope.
2. Related Works
2.1. Literature Review
Fuzzy-based time series forecasting is used to examine information which is neither explicit nor precise. Researchers have developed fuzzy time series perceptions and definitions to deal with imprecise and vague information systems where decisions or predictions could be carried out. This was later proposed by Song and Chissom, who also portrayed a special dynamic forecasting process with linguistic values [1,2,15]. Fuzzy forecasting to predict links in social networks has been described by authors in [16]. Later, the authors in [12] formally defined a fuzzy time series model described in Section 2.2.
Qiu, Liu, and Li [17] proposed a particle swarm optimization technique for similar forecasting. Primarily, data dealing with time series from the University of Alabama [18] were used. An average autocorrelation function was framed to give high forecasting accuracy. In order to analyze time series using computed fuzzy logical relations of higher order, Garg et al. [19], Son [20], Hunrag [21,22], Hwang and Chen [23], Lee Wang and Chen [24], Chu and Kim [25], and Sheta [26] developed extensive fuzzy as well as decision based forecasting methods in order to augment forecasting accuracy, each having minor variations. Lee [27] proposed a fuzzy candlestick [28] pattern to store financial expertise. To obtain highly mosaic matrix computations, a multivariate heuristic model was modelled and implemented in [29]. A determination of the interval over varying length was given by Hiemstra [30]. A number of repetitions of fuzzy relationships were used to determine the weights in fuzzy time series data in [31,32,33]. Regular increasing Monotone (RIM) quantifiers were used by Garg et al. [34,35] to design a priority matrix.
Several distinguished and relative works have been done by Klir et al. [36] and Dostal [37] with some native approaches for prediction. The use of optimization techniques in commercial and communal sector was also demonstrated by Dostal [38]. Li et al. [39] introduced fuzzy logic linking to chaos theory. Peters [40,41] extended it to fractal market analysis in capital markets. Trippi [42] represented fuzzy logic to chaos and non-linear dynamics in financial markets. Altroc [43] applied to business and finance using neuro-fuzzy. Hamam et al. [44] evaluated superiority of understanding of haptic centered uses based on fuzzy logic. Alreshoodi [45] researched an experiential learning established on a fuzzy logic method to measure the QOS/QOE correlation for covered video streaming. Doctor et al. [46] entrenched agent-based method for comprehending ambient intellect. Wang et al. [47] generated fuzzy instructions by learning from instances. In [48] a high order approximation for forecasting tourism demands in turkey using fuzzy time series data and artificial neural network is proposed. Another, new approach using fuzzy type-2 logic and fractal theory was given by Castillo and Melin [49]. The experimental study was done to establish the span of breaks with fuzzy time series [50]. A non-linear optimization with polynomial time series is another work presented by authors [51]. The forecasting models based on Event discretization function were placed forward.
In this paper, the dataset used for forecasting wheat production is taken from a source [52]. Son et al. [53] established a fuzzy clustering method for weather forecasting. Also, a neuro-fuzzy system has been designed and evaluated for insurance forecasting [54]. In [54], the authors have used an ensemble learning technique with limited fuzzy weights. Adaptive neuro-fuzzy [55] framework is another work by [56] in field of wheat production forecasts.
In [57], a different dataset for wheat production forecasts using soil properties has been used. Some of the properties of soil like shear strength has been predicted in [58]. Similarly, an adaptive fuzzy rule-based technique with automatic parameter updating has been used to model financial time series in [59]. A systematic approach has been discussed in [60] for detection of structural breaks in time series, namely the fuzzy transform and other method of fuzzy natural logic. It is based on F- transform to calculate slope of time-series. Another problem of the separable verification of fuzzy binary relations has been addressed in [61] providing necessary conditions and a well-organized algorithm for checking the same.
2.2. Mathematical Preliminary
This section presents the preliminaries needed to understand any problem of time series forecasting
Definition 1 [62].
Given F(t) as the group of all possible values of fuzzy time series at time t, F(t − 1) is group of all possible values at t − 1 having Z as a fuzzy relation between F(t) and F(t − 1) where Z is a union of all fuzzy relations defined as:
Then a first order time invariant series model is expressed as
Definition 2 [62].
Let be U the universe of discourse, U = {u1, u2, u3…} and U be a finite set A fuzzy set F of U can be expressed as follows:
where “+” is operator and ”/” is separator.
Definition 3 [63].
Assume that F(t) is a fuzzy time series, and Z (t, t − 1) is a first order model of time series F(t). If
Definition 4 [64].
Given F(t) as the time series data D, with Ft(I) as fuzzy set, then defuzzified value Fd is defined as the z-value with the highest membership degree.
Definition 5 [64].
Given F(t) as the time series data D, with Ft(I) as fuzzy set, a quasi-arithmetic mean for fuzzified output is:
α = 1 for arithmetic means
Forecasting models are categorized as follows:
AR (Autoregressive) Models,
MA (Moving Average) Models,
ARMA (Autoregressive Moving Average) Models,
ARIMA (Autoregressive Integrated Moving Average) Models.
Definition 6 [65].
AR model of a given order r is defined as:
where are independent variables and … are model parameters.
AR(r) model =
(a)
(b)
(c)
Substituting values for parameter aids in prediction.
3. The Proposed Framework
3.1. The Need of This Framework
Recent studies on wheat production forecasts have been conducted in [56,57,58]. Here, the later of an artificial neural network with fuzzy systems have been used for predicting forecast for a 5-degree polynomial in only two periods. In another work, ensemble learning with limited fuzzy weights was used. While the former uses another artificial neural network to forecast production based on energy inputs, another decision making analysis has been done in [66]. Several prediction procedures on case basis has been done by authors in [67,68,69,70]. The above stated method provided prediction using support vector machines based on soil properties. A similar prediction was performed in [7,8,9] where data are not partitioned and fuzzified as per time series.
The proposed method in this paper will take the yield data in reference to time series fuzzified in diverse partitions and give precise prediction. The precision comes from the 9 or 11-level linguistic partition carried out over large time series scale. Our method outperforms the existing 4 methods in terms of RMSE and AFER. Hence, a consolidated framework to perform predictions over multiple and diverse linguistic partitions is needed.
3.2. The Workflow Diagram
In this section, an overview of the proposed framework with simulation steps is given in Figure 1. Table 1 gives the linguistic fuzzy set partitioning while Table 2 gives the frequency distribution over 9 interval partitioning.
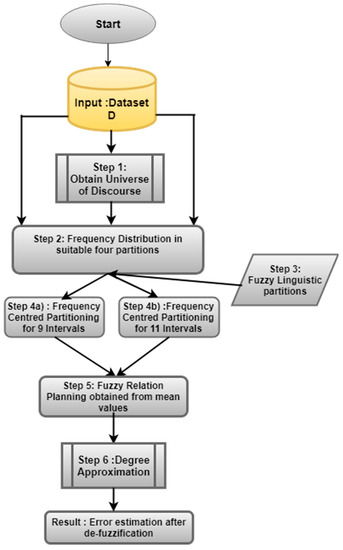
Figure 1.
Degree Approximation-Based Fuzzy Partitioning Algorithm and Applications DAbFP simulation Workflow.

Table 1.
Fuzzy linguistic partitions.

Table 2.
Frequency Distribution (9 Interval).
3.3. DAbFP Algorithm
The proposed algorithm is performed on the source dataset taken under following steps:
Step 1: Let D denotes the source dataset variable.
Using Definition 2, Universe of Discourse (U) is defined as
Step 2: Partition the dataset D into suitable four frequencies to perform subsequent forecasting steps to each group:
Step 3: Using above partitioned data as Dnew, we define fuzzy sets as F1, F2…F7 linguistically mapped over the universe of discourse U defined as follows:
Every partition obtained in the partitioning based on frequency is represented by F(I), where (I) indicates the intervals inside its value exist. The value of the outcome increases on increasing the value of “I”. The same taxonomy helps to provide an evocative vision to the researchers. For instance, every interval can be signified by fuzzy partitions if we are operating on 9 partitions, as presented beneath:
Hence, growth in the suffix (I) is evidently related through greater harvest in the production of wheat and having the same taxonomy. Subsequently, Fuzzy Logic Relationships (FLR) is recognized for the specified group of values. It can be elucidated over the particular instance. Here, q1, q2…q7 fixed length intervals.
Step 4: From above partitioned data as Dnew, we define 11 fuzzy sets as F1, F2…F11 over U. Similar equations (as 5 to 13) are observed for 11 intervals. Here, q1, q2…q11 fixed length intervals.
Step 5: Mean of middle values of fuzzy partitions on the Right-Hand Side of Fuzzy logic relation (FLR) is calculated. This calculation is performed for degree approximation. For instance, in the 2nd order FLR, F4 <- F2, F7. If P and Q are the centers of Interval F2 and F7 respectively then
where for fuzzy partition F4, R is the center. Likewise, for 3rd order FLR:
R = P + Q/2
If F <- F2, F7, F3 where P, Q, R are the centers for Interval F2, F7 and F3 respectively then
S = (P + Q + R)/3
Here, S is the mean fuzzy value for a particular forecast year. It is used in Linear Regression Model as a variable, for thorough de-fuzzification. From this, the results can be used to calculate the forecast value:
Here, n is total number of values while is the fuzzy value at degree.
As per the steps followed in the proposed algorithm, Table 3, Table 4 and Table 5 give the intermediate results. In this section, the concluding part of the devised algorithm is explained with the results presented in Table 6, Table 7, Table 8 and Table 9.

Table 3.
Frequency Centered Partitioning (9 Interval).

Table 4.
Frequency Distribution (11 Interval).

Table 5.
Frequency Centered Partitioning (11 Interval).

Table 6.
(9 INTERVALS, Fuzzy Logic Relation 2nd DEGREE).

Table 7.
(11 INTERVALS, Fuzzy Logic Relation 2nd DEGREE).

Table 8.
9 INTERVALS, Fuzzy Logic Relation 3rd DEGREE.

Table 9.
11 INTERVALS, Fuzzy Logic Relation 3rd DEGREE.
Step 6: After degree approximation based on fuzzy logic relation, defuzzification is performed using regression analysis. On plotting the points, we select a Best Fit line that represents average across all points in graph. Thereafter, the equation of line is estimated which can be linear or polynomial of higher degrees 2, 3, 4, 5 or 6. In the consequent section, we use two important constraints to associate the outcome as stated below:
Average Forecasting Error Rate (AFER) =
Mean Square Error (MSE).
Here, Xi is the actual production cost whereas Yi is the predicted value.
3.4. Numerical Example
In year 1981, Produce = 3552 (fits to F3).
In year 1982, Produce = 4177 (fits to F7).
In year 1983, Produce = 3372 (fits to F2).
In year 1984, Produce = ? (Assume this request to be forecast, let F be the partition where value is contained).
Hence, the above Logical Relationships can assist forecast for a specific year by means of the values obtained for earlier years and then creating a relationship amongst values. Fuzzy Logical Relationship of Order 3 is: F = F2, F7, F3, here F is the forecast partition for produce in year 1984.
Now, an appropriate defuzzification procedure can be functional on these values to forecast value of the harvest in year 1984 (conferred in step 5), agreed that appropriate calculations are done for fuzzy sets which resemble to the fuzzy partitions in the previous years.
4. Results and Discussion
4.1. Linear Polynomial
A linear polynomial relation is defined as:
Here, variable Y provides the value that is predicted. Output for year and the input variable X fed to equation using form (14, 15, 16, which relates to years 1981, 1982, 1983, 1984…). By means of Figure 2a,b, one can calculate the yearly predicted results and then estimating the AFER and MSE as given in Table 10.
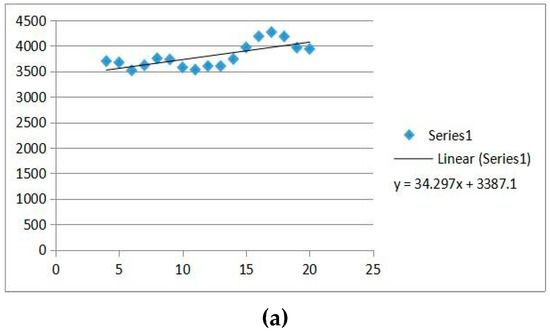
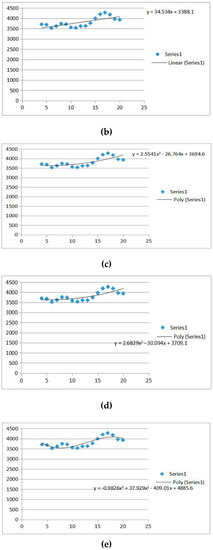
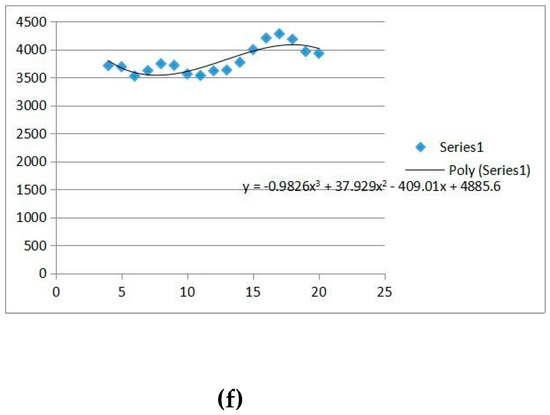
Figure 2.
(a–f): 9th to 11th Interval for fuzzified degree-based approximation AFER and MSE.

Table 10.
MSE and AFER values for all intervals.
4.2. Quadratic Polynomial
A linear polynomial relation is defined as:
Here, variable Y will give the value that is predicted Output for year and the input variable X fed to equation using form (1, 2, 3, 4…., which relates to years 1981, 1982, 1983, 1984…). By means of Figure 2c,d, one can calculate the yearly predicted results and then estimating the AFER and MSE was calculated matching to figure as given in Table 11.

Table 11.
MSE and AFER values for all intervals.
4.3. Cubic Polynomial
The cubic polynomial relation is given as:
Here, variable Y will give the value that is predicted output for each year and input variable X fed to equation using form (1, 2, 3, 4…., which relates to years 1981, 1982, 1983, 1984…). By means of Figure 2e,f, one can calculate the yearly predicted results and then estimating the AFER and MSE matching to figure as given in Table 12.

Table 12.
MSE and AFER values for all intervals.
4.4. Results
From the above analysis, we have computed the mean MSE and AFER values for final predicted values where the degree approximation is computed accordingly. The proposed algorithm is initially compared with baseline method such as Chissom [1,2] on benchmark data for forecasting the enrollments of University of Alabama. The superiority in values in terms of MSE and AFER marks it as a probable candidate for predicting wheat production in future as shown in Table 13. For further performance analysis, the proposed method is hereby compared with existing methods as shown in Table 14 and Table 15 for both 9 and 11 intervals. The proposed algorithm outperforms the existing ones in terms of MSE and AFER; thereby proving to be a best fit for wheat produce prediction. The MSE and AFER of the proposed algorithm comes out to be 362,119.88 and 5,107,713.738 for 3rd degree and 2nd degree polynomial in 9th interval as compared to the MSE of 36,559.88 and AFER AS 11.92547975 for 3rd degree polynomial of Yalaz et al. [64]. Similarly, the values of MSE and AFER are compared in Table 13 and Table 14 for 9th interval 2nd degree polynomial. Also, the evaluation statistics of our proposed algorithm outperforms in 11th interval.

Table 13.
Comparison of MSE and AFER values for one set of intervals with Chissom [1,2] on enrollment data.

Table 14.
Comparison of MSE and AFER values for 9 intervals with existing frameworks.

Table 15.
Comparison of MSE and AFER values for 11 intervals with existing frameworks.
In Figure 3, the FLR 3rd degree MSE is generally higher than FLR 2nd degree MSE except in case of polynomial degree 3. We can infer that Linear FLR 2nd degree polynomial has the lowest MSE among all the cases for 9th interval. It is convenient to estimate a particular case is the best among all others. As it can be inferred from the graph, total 10 cases for 9th interval has been monitored. We have also worked on 8 cases in 11th interval partitioning as shown in Figure 4.
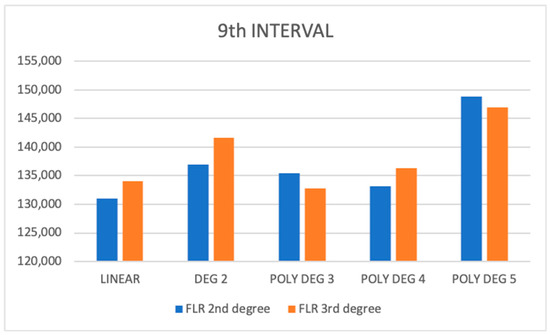
Figure 3.
Comparison of MSE among all degrees in 9th interval.
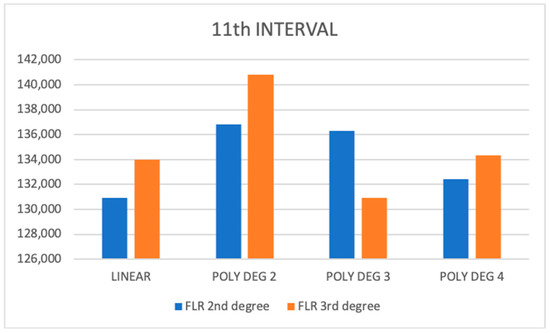
Figure 4.
Comparison of MSE among all degrees in 11th interval.
5. Conclusions
Various researchers in the past have tried to explore this prediction modeling field using fuzzy logic. Further research is needed by researchers around the world. In this paper, we proposed a novel algorithm using fuzzy linear regression to forecast wheat production. The results demonstrated the efficiency of the suggested method. Further studies will focus on accelerating computational time of this method by GPU and examining other wheat problems or exploring advanced methods [70,71,72,73,74,75,76,77,78,79,80,81,82].
Author Contributions
The article conceptualization was done by R.J. and N.J. The methodology was proposed by L.H.S. Software feasibility was validated and tested by S.K. Further the formal analysis with Investigation was performed by R.J. and N.J. The data curation for the experiments was done by S.K. Writing-Original Draft Preparation was done by R.J. and N.J. along with Writing-Review & Editing performed by L.H.S. The project was visualized by N.J. and S.K. under the supervision of R.J. and L.H.S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Compliance with Ethical Standards
The authors declare that they do not have any conflict of interests. This research does not involve any human or animal participation. All authors have checked and agreed the submission.
References
- Song, Q.; Chissom, B. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B. Forecasting enrollments with fuzzy time series-Part, I. Fuzzy Sets Syst. 1993, 45, 1–10. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B. Forecasting enrollments with fuzzy time series-Part II. Fuzzy Sets Syst. 1994, 62, 1–8. [Google Scholar] [CrossRef]
- Song, Q.; Leland, R.; Chissom, B. A new fuzzy time-series model of fuzzy number observations. Fuzzy Sets Syst. 1995, 73, 341–348. [Google Scholar] [CrossRef]
- Choudhury, A.; Jones, J. Crop Yield Prediction Using Time Series Models. J. Econ. Econ. Educ. Res. 2014, 15, 53. [Google Scholar]
- Kumar, S.; Kumar, N. A Novel Method for Rice Production Forecasting Using Fuzzy Time Series. Int. J. Comput. Sci. Issues 2012, 9, 455. [Google Scholar]
- Kumar, S.; Kumar, N. Two Factor Fuzzy Time Series Model for Rice Forecasting. Int. J. Comput. Math. Sci. 2015, 4, 2347–8527. [Google Scholar]
- Kumar, N.; Ahuja, S.; Kumar, V.; Kumar, A. Fuzzy time series forecasting of wheat production. Int. J. Comput. Sci. Eng. 2010, 2, 635–640. [Google Scholar]
- Egrioglu, E.; Aladag, C.; Yolcu, U.; Uslu, V.; Basaran, M. Finding an optimal interval length in high order fuzzy time series. Expert Syst. Appl. 2010, 37, 5052–5055. [Google Scholar] [CrossRef]
- Eğrioğlu, E. A New Time-Invariant Fuzzy Time Series Forecasting Method Based on Genetic Algorithm. Adv. Fuzzy Syst. 2012, 2012, 2. [Google Scholar] [CrossRef]
- Qiu, W.; Liu, X.; Li, H. A generalized method for forecasting based on fuzzy time series. Expert Syst. Appl. 2011, 38, 10446–10453. [Google Scholar] [CrossRef]
- Song, Q. A note on fuzzy time series model selection with sample autocorrelation functions. Cybern. Syst. 2003, 34, 93–107. [Google Scholar] [CrossRef]
- Garg, B.; Beg, M.; Ansari, A. Fuzzy time series model to forecast rice production. In Proceedings of the IEEE International Conference on Fuzzy Systems, Hyderabad, India, 7–10 July 2013. [Google Scholar]
- Huarng, K. Effective lengths of intervals to improve forecasting in fuzzy time series. Fuzzy Sets Syst. 2001, 123, 387–394. [Google Scholar] [CrossRef]
- Huarng, K. Heuristic models of fuzzy time series for forecasting. Fuzzy Sets Syst. 2001, 123, 369–386. [Google Scholar] [CrossRef]
- Hwang, J.; Chen, S.; Lee, C. Handling Forecasting Problems using Fuzzy Time Series. Fuzzy Sets Syst. 1998, 100, 217–228. [Google Scholar] [CrossRef]
- Lee, L.; Wang, L.; Chen, S. Handling Forecasting Problems based on Two-Factors High-Order Time Series. IEEE Trans. Fuzzy Syst. 2006, 14, 468–477. [Google Scholar] [CrossRef]
- Sheta, A. Software Effort Estimation and Stock Market Prediction Using Takagi-Sugeno Fuzzy Models. In Proceedings of the IEEE International Conference on Fuzzy System, Vancouver, BC, Canada, 16–21 July 2006; pp. 171–178. [Google Scholar]
- Chu, S.; Kim, H. Automatic knowledge generation from the stock market data. In Proceedings of the 93 Korea Japan Joint Conference on Expert Systems, Seoul, South Korea, 1993; pp. 193–208. [Google Scholar]
- Wolfers, J.; Zitzewitz, E. Prediction markets in theory and practice. Natl. Bureau Econ. Res. 2006, 1–11. [Google Scholar] [CrossRef]
- Hammouda, K.; Karray, F. A Comparative Study of Data Clustering Techniques. Available online: www.pami.uwaterloo.ca/pub/hammouda/sde625-paper.pdf (accessed on 10 November 2018).
- Babuska, R.; Roubos, J.; Verbruggen, H. Identification of MIMO systems by input-output TS fuzzy models. In Proceedings of the Fuzzy-IEEE’98, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Van Eyden, R.J. Application of Neural Networks in the Forecasting of Share Prices; Finance and Technology Publishing: Haymarket, VA, USA, 1996. [Google Scholar]
- Hiemstra, Y. A stock market forecasting support system based on fuzzy logic. In Proceedings of the Twenty-Seventh Hawaii International Conference on System Sciences HICSS-94, Wailea, HI, USA, 4–7 January 1994. [Google Scholar]
- Chiu, S. Fuzzy model identification based on cluster estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar]
- Gomide, F. A review of: Fuzzy Sets and Fuzzy Logic: Theory and Applications by George Klir and Bo Yuan, Prentice Hall PTR. Int. J. Gen. Syst. 1997, 26, 292–294. [Google Scholar] [CrossRef]
- Ribeiro, R.; Hans-Jürgen, Z.; Yager, R.; Kacprzyk, J. Soft Computing in Financial Engineering; Physica: Heidelberg, Germany, 1999. [Google Scholar]
- Dostál, P. The Use of Optimization Methods in Business and Public Services. In Handbook of Optimization Intelligent Systems Reference Library; Springer: Berlin/Heidelberg, Germany, 2013; pp. 717–777. [Google Scholar]
- Dostál, P. The Use of Soft Computing for Optimization in Business, Economics, and Finance. In Meta-Heuristics Optimization Algorithms in Engineering, Business, Economics, and Finance; IGI Global: Hershey, PA, USA, 2013; pp. 41–86. [Google Scholar]
- Li, Z.; Chen, G.; Halang, W. Anticontrol of Chaos for Takagi-Sugeno Fuzzy Systems, Integration of Fuzzy Logic and Chaos Theory; Springer: Berlin/Heidelberg, Germany, 2006; pp. 185–227. [Google Scholar]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Peters, E.E. Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Trippi, R.R. Chaos & Nonlinear Dynamics in the Financial Markets; Irwin Professional Publishing: Cheney, KS, USA, 1995. [Google Scholar]
- Altrock, C. Fuzzy Logic & Neurofuzzy—Applications in Business & Finance; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Hamam, A.; Eid, M.; El Saddik, A.; Georganas, N.D. Fuzzy logic system for evaluating Quality of Experience of haptic-based applications. In International Conference on Human Haptic Sensing and Touch Enabled Computer Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 129–138. [Google Scholar]
- Alreshoodi, M.; Woods, J. An Empirical Study based on a Fuzzy Logic System to Assess the QoS/QoE Correlation for Layered Video Streaming. In Proceedings of the IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications, Milan, Italy, 15–17 July 2013. [Google Scholar]
- Doctor, F.; Hagras, H.; Callaghan, V. A Fuzzy Embedded Agent based Approach for Realizing Ambient Intelligence in Intelligent Inhabited Environments. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2005. [Google Scholar]
- Wang, L.X.; Mendel, J.M. Generating fuzzy rules by learning from examples. IEEE Trans. Syst. Man Cybern. 1992, 22, 1414–1427. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. A new approach for plant monitoring using type-2 fuzzy logic and fractal theory. Int. J. Gen. Syst. 2004, 33, 305–319. [Google Scholar] [CrossRef]
- Yolcu, U.; Egrioglu, E.; Uslu, R.V.R.; Basaran, M.A.; Aladag, C.H. A new approach for determining the length of intervals for fuzzy time series. Appl. Soft Comput. 2009, 9, 647–651. [Google Scholar] [CrossRef]
- Garg, B.; Beg, M.M.S.; Ansari, A.Q.; Imran, B.M. Fuzzy Time Series Prediction Model, Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 141, pp. 126–137. [Google Scholar]
- Garg, B.; Beg, M.M.S.; Ansari, A.Q.; Imran, B.M. Soft Computing Model to Predict Average Length of Stay of Patient, Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 141, pp. 221–232. [Google Scholar]
- Khuong, M.N.; Tuan, T.M. A New Neuro-Fuzzy Inference System for Insurance Forecasting. In Advances in Information and Communication Technology; Springer: Thai Nguyen, Vietnam, 2016. [Google Scholar]
- Son, L.; Thong, P. Some novel hybrid forecast methods based on picture fuzzy clustering for weather nowcasting from satellite image sequences. Appl. Intell. 2017, 46, 1–15. [Google Scholar] [CrossRef]
- Stathakis, D.; Savin, I.; Nègre, T. Neuro-fuzzy modeling for crop yield prediction. The International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2006, 34, 1–4. [Google Scholar]
- Lee, M.H.; Sadaei, J.H. Introducing polynomial fuzzy time series. J. Intell. Fuzzy Syst. 2013, 25, 117–128. [Google Scholar]
- Jilani, T.A.; Burney, S.M.A.; Ardil, C. Multivariate high order fuzzy time series forecasting for car road accidents. Int. J. Comput. Intell. 2007, 4, 15–20. [Google Scholar]
- Chen, S.M.; Hwang, J.R. Temperature prediction using fuzzy time series. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2000, 30, 263–275. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, J.R. Fuzzy Time Series Forecasting; Aalborg University Esbjerg: Esbjerg, Denmark, 2009. [Google Scholar]
- Detyniecki, M.; Bouchon-meunier, D.B.; Yager, D.R.; Prade, R.H. Mathematical Aggregation Operators and their application to video querying. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.21.17 (accessed on 10 November 2018).
- Yalaz, S.; Arife, A. Fuzzy Linear Regression for the Time Series Data which is Fuzzified with SMRGT Method. Süleyman Demirel Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2016, 20, 405–413. [Google Scholar] [CrossRef]
- Pant Nagar farm, G.B. Pant University of Agriculture and Technology, India. Available online: http://www.gbpuat.ac.in/facility/farm/index.html (accessed on 10 November 2018).
- Khan, M.; Son, L.; Ali, M.; Chau, H.; Na, N.; Smarandache, F. Systematic review of decision making algorithms in extended neutrosophic sets. Symmetry 2018, 10, 314. [Google Scholar] [CrossRef]
- Khoshnevisan, B.; Rafiee, S.; Mahmoud, O.; Mousazadeh, H. Development of an intelligent system based on ANFIS for predicting wheat grain yield on the basis of energy inputs. Inf. Process. Agric. 2014, 1, 14–22. [Google Scholar] [CrossRef]
- Kamali, H.; Shahnazari-Shahrezaei, P.; Kazemipoor, H. Two new time-variant methods for fuzzy time series forecasting. J. Intell. Fuzzy Syst. 2013, 24, 733–741. [Google Scholar]
- Yang, W.; Li, M.; Zheng, L.; Sun, H. Evaluation Model of Winter Wheat Yield Based on Soil Properties. In International Conference on Computer and Computing Technologies in Agriculture; Springer: Cham, Switzerland, 2015; pp. 638–645. [Google Scholar]
- Luna, I.; Ballini, R. Adaptive fuzzy system to forecast financial time series volatility. J. Intell. Fuzzy Syst. 2012, 23, 27–38. [Google Scholar]
- Kasabov, N.K.; Song, Q. DENFIS: Dynamic evolving neural-fuzzy inference system and its application for time-series prediction. IEEE Trans. Fuzzy Syst. 2000, 10, 144–154. [Google Scholar] [CrossRef]
- Aladag, C.; Egrioglu, E.; Yolcu, U.; Uslu, V. A high order seasonal fuzzy time series model and application to international tourism demand of Turkey. J. Intell. Fuzzy Syst. 2014, 26, 295–302. [Google Scholar]
- Pham, B.T.; Son, L.H.; Hoang, T.-A.; Nguyen, D.-M.; Bui, D.T. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Son, L.; Huy, N.Q.; Thong, T.N.; Dung, T.T.K. An effective solution for sustainable use and management of natural resources through webGIS open sources and decision-making support tools. In Proceedings of the 5th International Conference on GeoInformatics for Spatial-Infrastructure Development in Earth and Allied Sciences, Hanoi, Vietnam, 9–11 December 2010. [Google Scholar]
- Tuan, T.; Chuan, P.; Ali, M.; Ngan, T.; Mittal, M.; Son, L. Fuzzy and neutrosophic modeling for link prediction in social networks. Evol. Syst. 2018, 1–6. [Google Scholar] [CrossRef]
- Kadir, M.K.A.; Ayob, M.Z.; Miniappan, N. Wheat yield prediction: Artificial neural network based approach. In Proceedings of the 4th International Conference on Engineering Technology and Technopreneuship (ICE2T), Kuala Lumpur, Malaysia, 27–29 August 2014. [Google Scholar]
- Vovan, T. An improved fuzzy time series forecasting model using variations of data. Fuzzy Optim. Decis. Mak. 2018, 1–23. [Google Scholar] [CrossRef]
- Georgi, C.; Spengler, D.; Itzerott, S.; Kleinschmit, B. Automatic delineation algorithm for site-specific management zones based on satellite remote sensing data. Precis. Agric. 2018, 19, 684–707. [Google Scholar] [CrossRef]
- Paustian, M.; Theuvsen, L. Adoption of precision agriculture technologies by German crop farmers. Precis. Agric. 2017, 18, 701–716. [Google Scholar] [CrossRef]
- Novak, V. Detection of Structural Breaks in Time Series Using Fuzzy Techniques. Int. J. Fuzzy Logic Intell. Syst. 2018, 18, 1–12. [Google Scholar] [CrossRef]
- Grzegorzewski, P. On Separability of Fuzzy Relations. Int. J. Fuzzy Logic Intell. Syst. 2017, 17, 137–144. [Google Scholar] [CrossRef]
- Phuong, P.T.M.; Thong, P.H.; Son, L.H. Theoretical Analysis of Picture Fuzzy Clustering: Convergence and Property. J. Comput. Sci. Cybern. 2018, 1, 17–32. [Google Scholar] [CrossRef]
- Jha, S.; Kumar, R.; Chatterjee, J.M.; Khari, M.; Yadav, N.; Smarandache, F. Neutrosophic soft set decision making for stock trending analysis. Evol. Syst. 2018, 1–7. [Google Scholar] [CrossRef]
- Ngan, R.T.; Son, L.H.; Cuong, B.C.; Ali, M. H-max distance measure of intuitionistic fuzzy sets in decision making. Appl. Soft Comput. 2018, 69, 393–425. [Google Scholar] [CrossRef]
- Giap, C.N.; Son, L.H.; Chiclana, F. Dynamic structural neural network. J. Intell. Fuzzy Syst. 2018, 34, 2479–2490. [Google Scholar] [CrossRef]
- Ali, M.; Son, L.H.; Thanh, N.D.; Van Minh, N. A neutrosophic recommender system for medical diagnosis based on algebraic neutrosophic measures. Appl. Soft Comput. 2018, 71, 1054–1071. [Google Scholar] [CrossRef]
- Ali, M.; Son, L.H.; Khan, M.; Tung, N.T. Segmentation of dental X-ray images in medical imaging using neutrosophic orthogonal matrices. Expert Syst. Appl. 2018, 91, 434–441. [Google Scholar] [CrossRef]
- Ali, M.; Dat, L.Q.; Son, L.H.; Smarandache, F. Interval complex neutrosophic set: Formulation and applications in decision-making. Int. J. Fuzzy Syst. 2018, 20, 986–999. [Google Scholar] [CrossRef]
- Son, L.H.; Tuan, T.M.; Fujita, H.; Dey, N.; Ashour, A.S.; Ngoc, V.T.N.; Chu, D.T. Dental diagnosis from X-Ray images: An expert system based on fuzzy computing. Biomed. Signal Process. Control 2018, 39, 64–73. [Google Scholar] [CrossRef]
- Nguyen, G.N.; Son, L.H.; Ashour, A.S.; Dey, N. A survey of the state-of-the-arts on neutrosophic sets in biomedical diagnoses. Int. J. Mach. Learn. Cybern. 2017, 1–13. [Google Scholar] [CrossRef]
- Ngan, R.T.; Ali, M.; Son, L.H. δ-equality of intuitionistic fuzzy sets: A new proximity measure and applications in medical diagnosis. Appl. Intell. 2018, 48, 499–525. [Google Scholar] [CrossRef]
- Ali, M.; Son, L.H.; Deli, I.; Tien, N.D. Bipolar neutrosophic soft sets and applications in decision making. J. Intell. Fuzzy Syst. 2017, 33, 4077–4087. [Google Scholar] [CrossRef]
- Thanh, N.D.; Ali, M.; Son, L.H. A novel clustering algorithm in a neutrosophic recommender system for medical diagnosis. Cognit. Comput. 2017, 9, 526–544. [Google Scholar] [CrossRef]
- Son, L.H.; Viet, P.V.; Hai, P.V. Picture inference system: A new fuzzy inference system on picture fuzzy set. Appl. Intell. 2017, 46, 652–669. [Google Scholar] [CrossRef]
- Son, L.H.; Tien, N.D. Tune up fuzzy C-means for big data: Some novel hybrid clustering algorithms based on initial selection and incremental clustering. Int. J. Fuzzy Syst. 2017, 19, 1585–1602. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).