Binary Locating-Dominating Sets in Rotationally-Symmetric Convex Polytopes
Abstract
1. Introduction
2. An Integer Linear Programming Model
3. The Exact Values
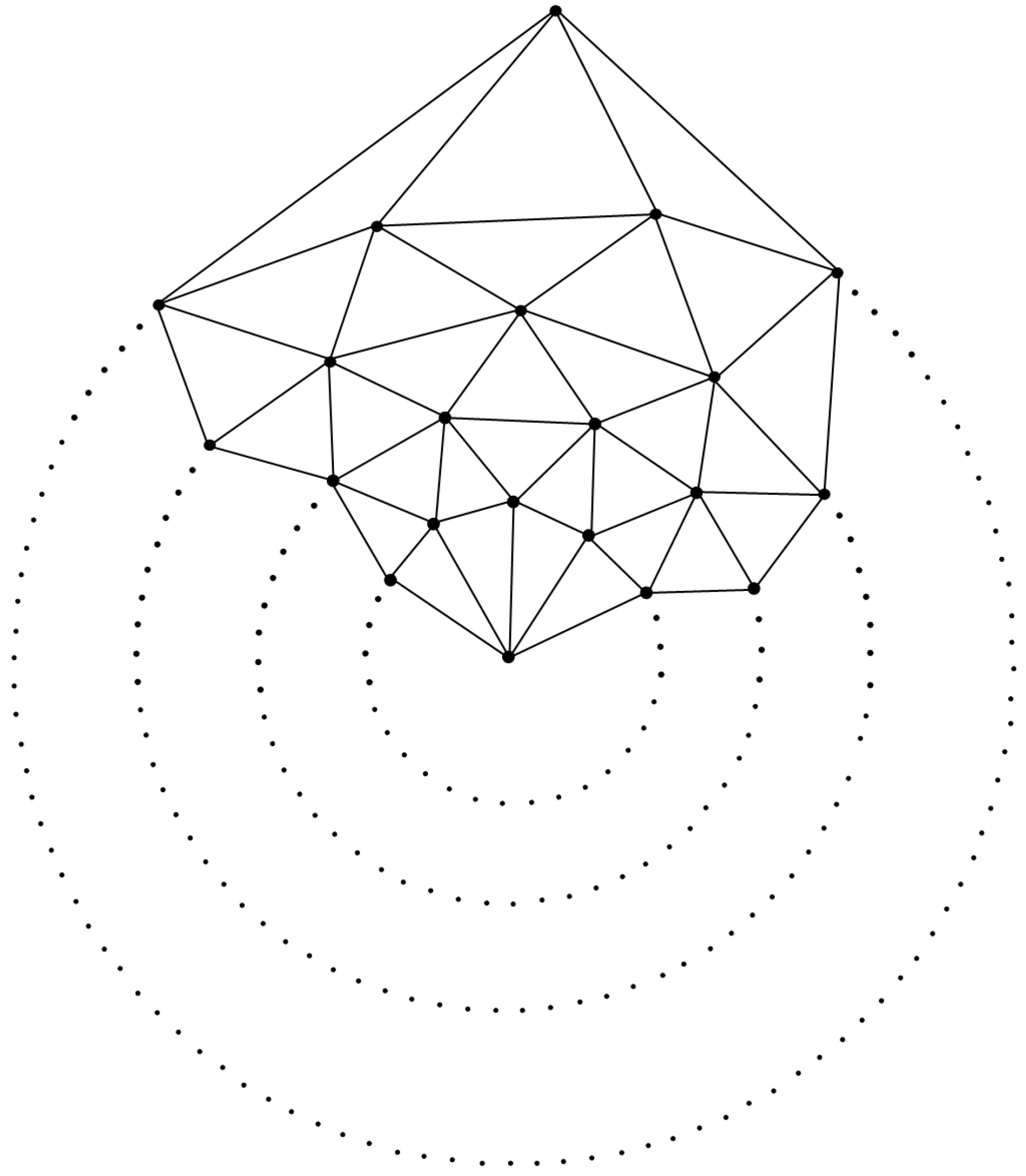
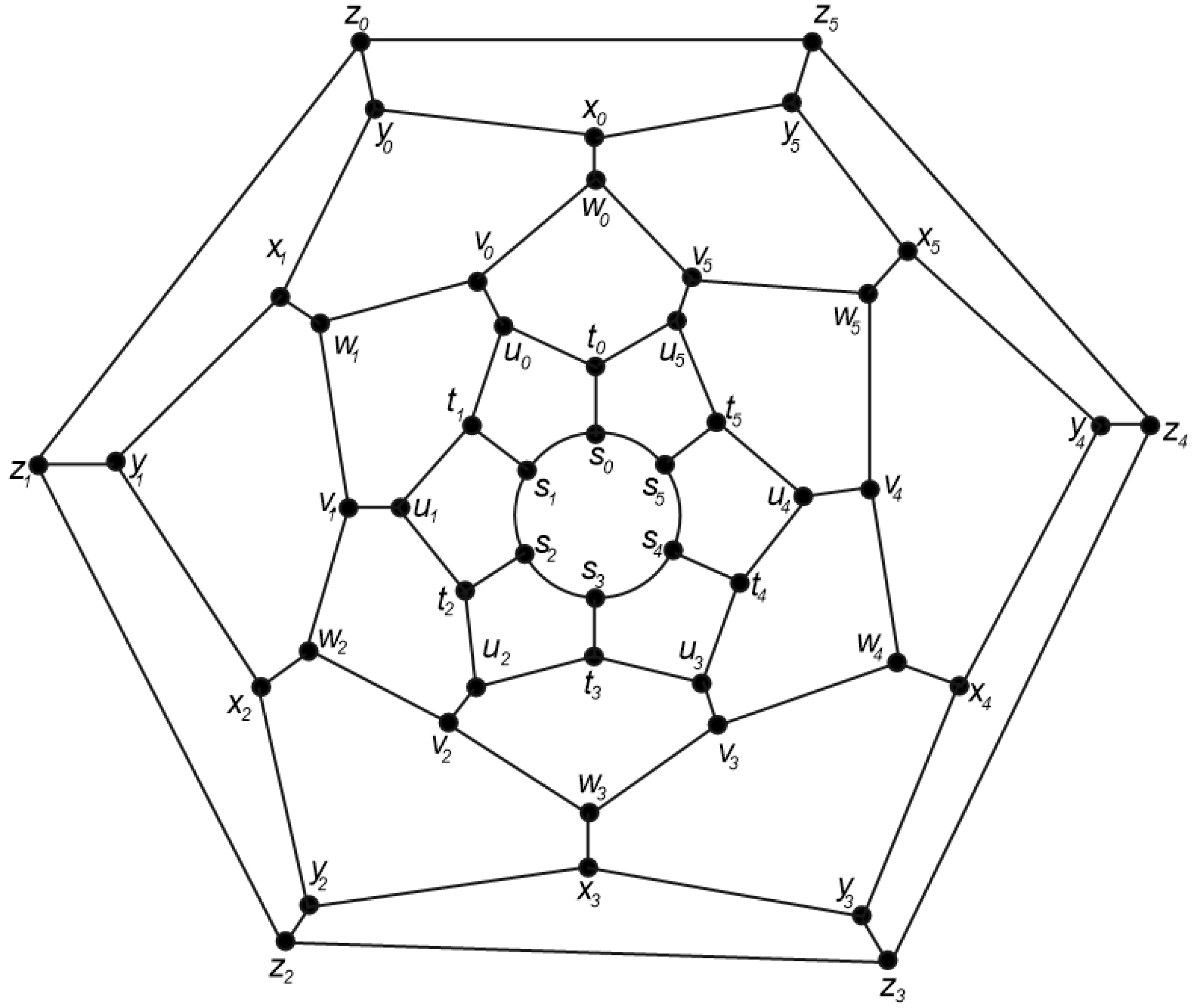
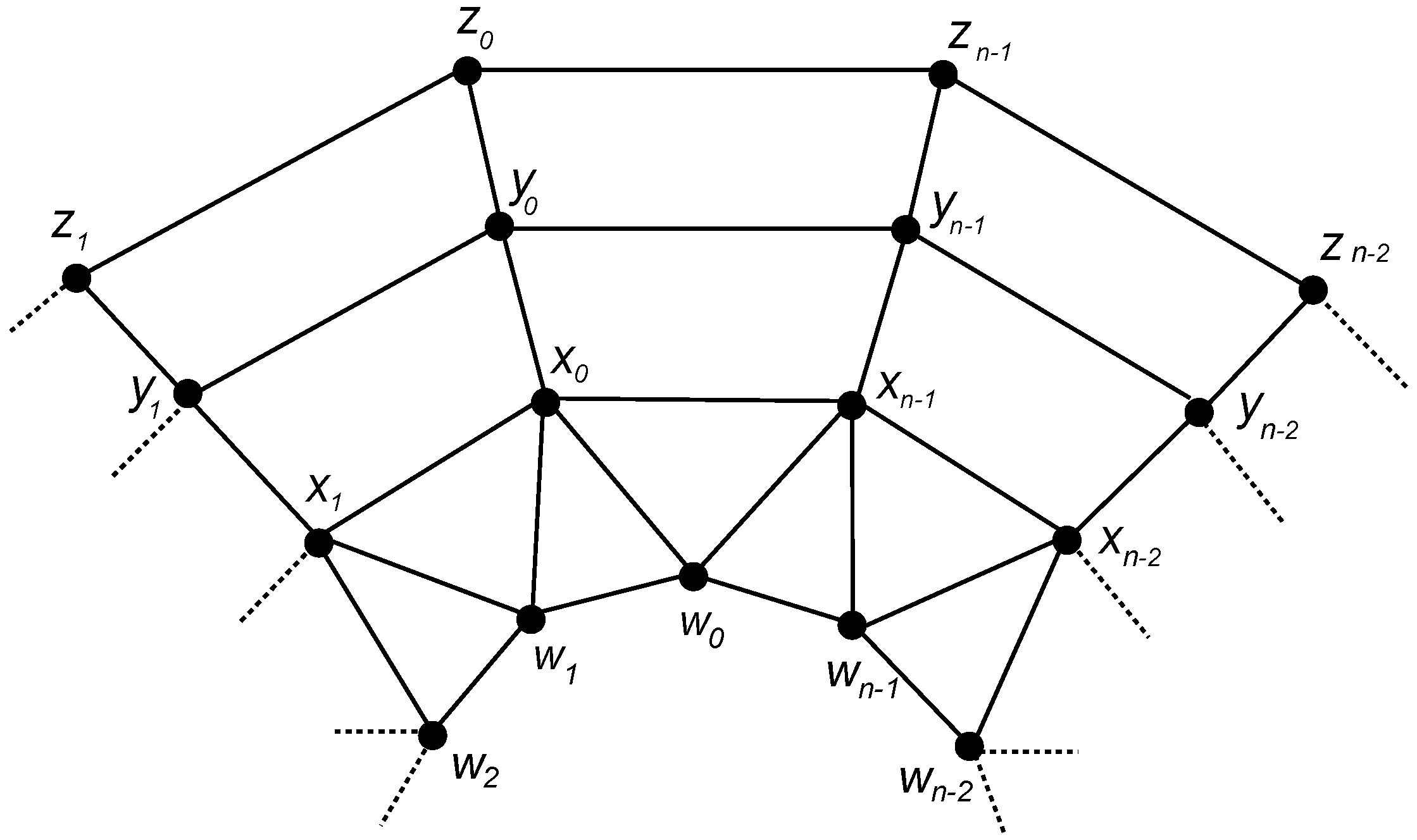
3.1. The Graph of Convex Polytope
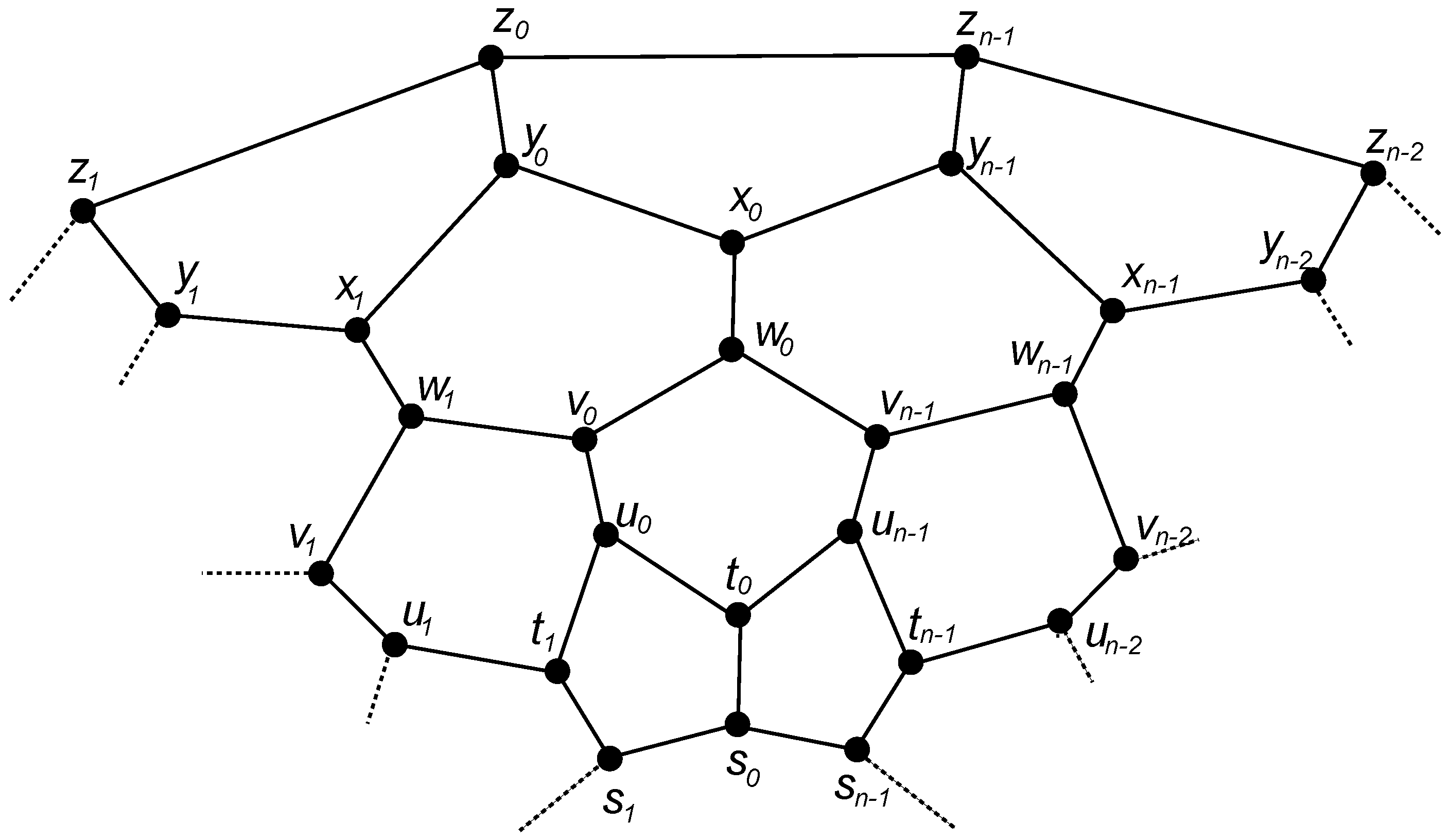
3.1.1. Construction
- (1)
- (2)
- (3)
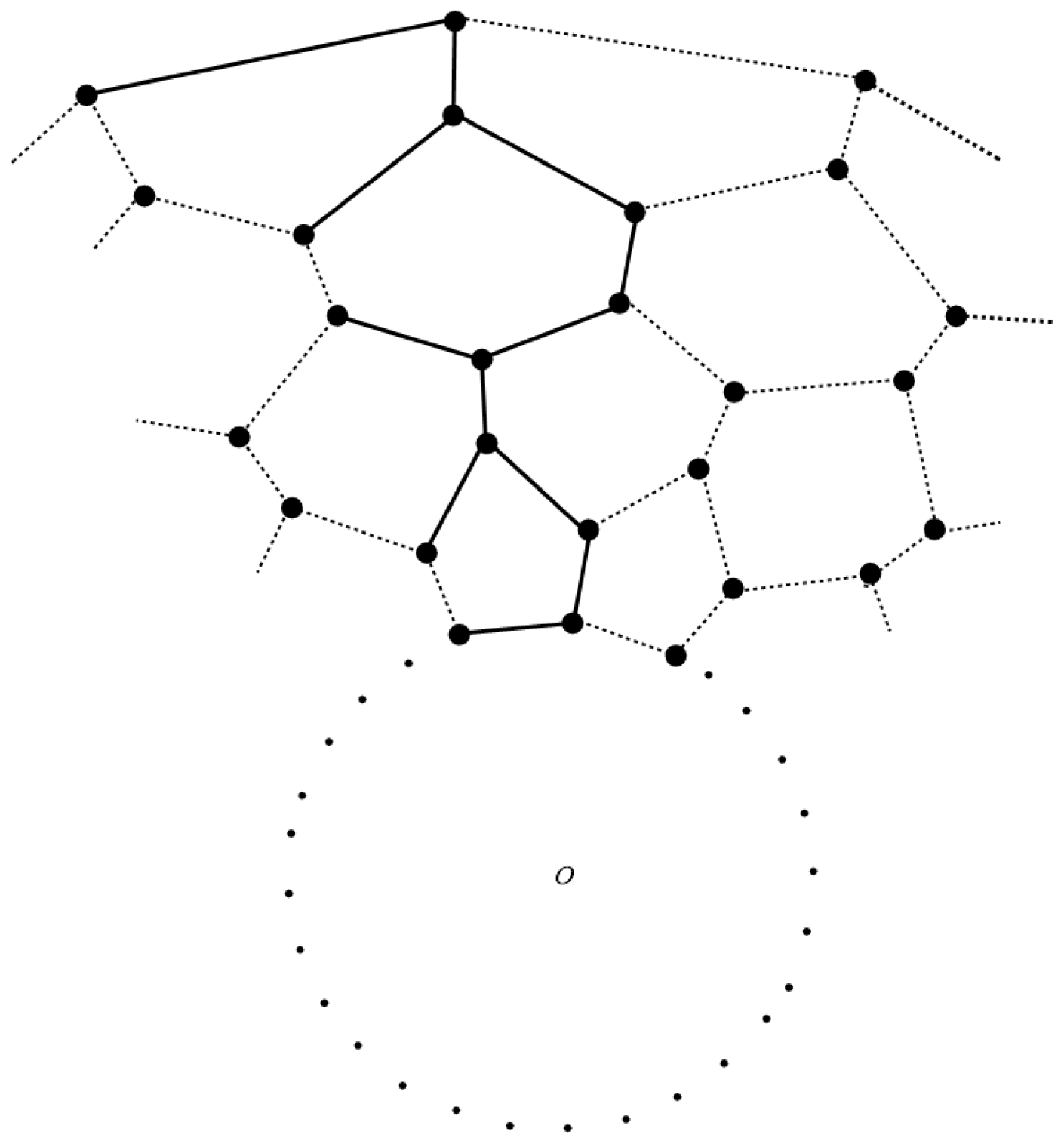
3.1.2. Rotational Symmetry of the Convex Polytopes
3.1.3. Binary Locating-Dominating Number of
- Case 1:
- When .In order to show S to be a binary locating-dominating set, we need to show that the neighborhoods of all vertices in are non-empty and distinct. Table 1 shows these neighborhoods and their intersections. Although some formulas for some intersections can be somewhat similar, but they are distinct.
- Case 2:
- When .As in the previous case, the neighborhoods of all vertices in are non-empty and distinct shown in Table 1.
- Case 3:
- When .Similar to the previous two cases, Table 1 shows that the neighborhoods of all vertices in are non-empty and distinct.
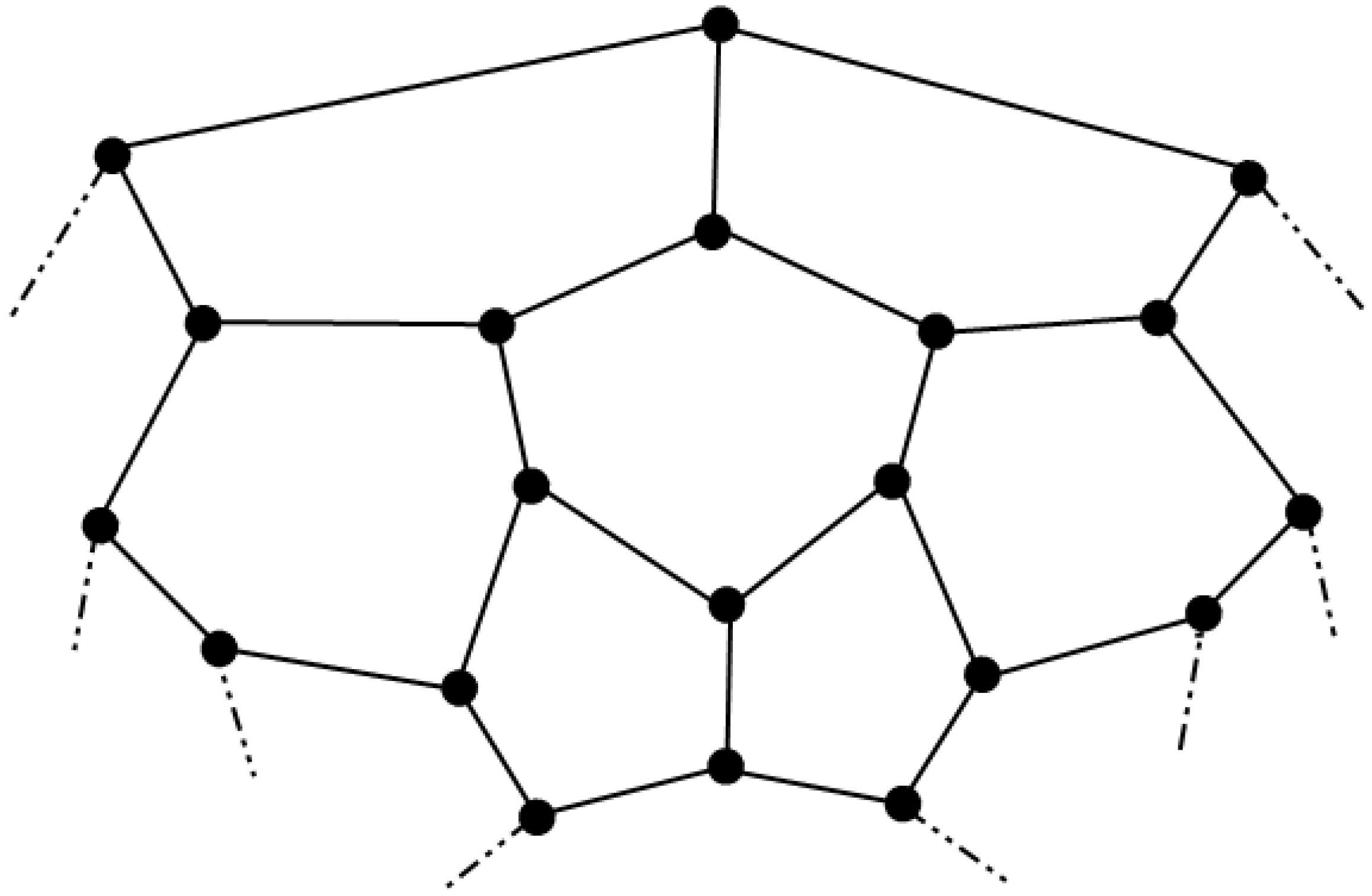
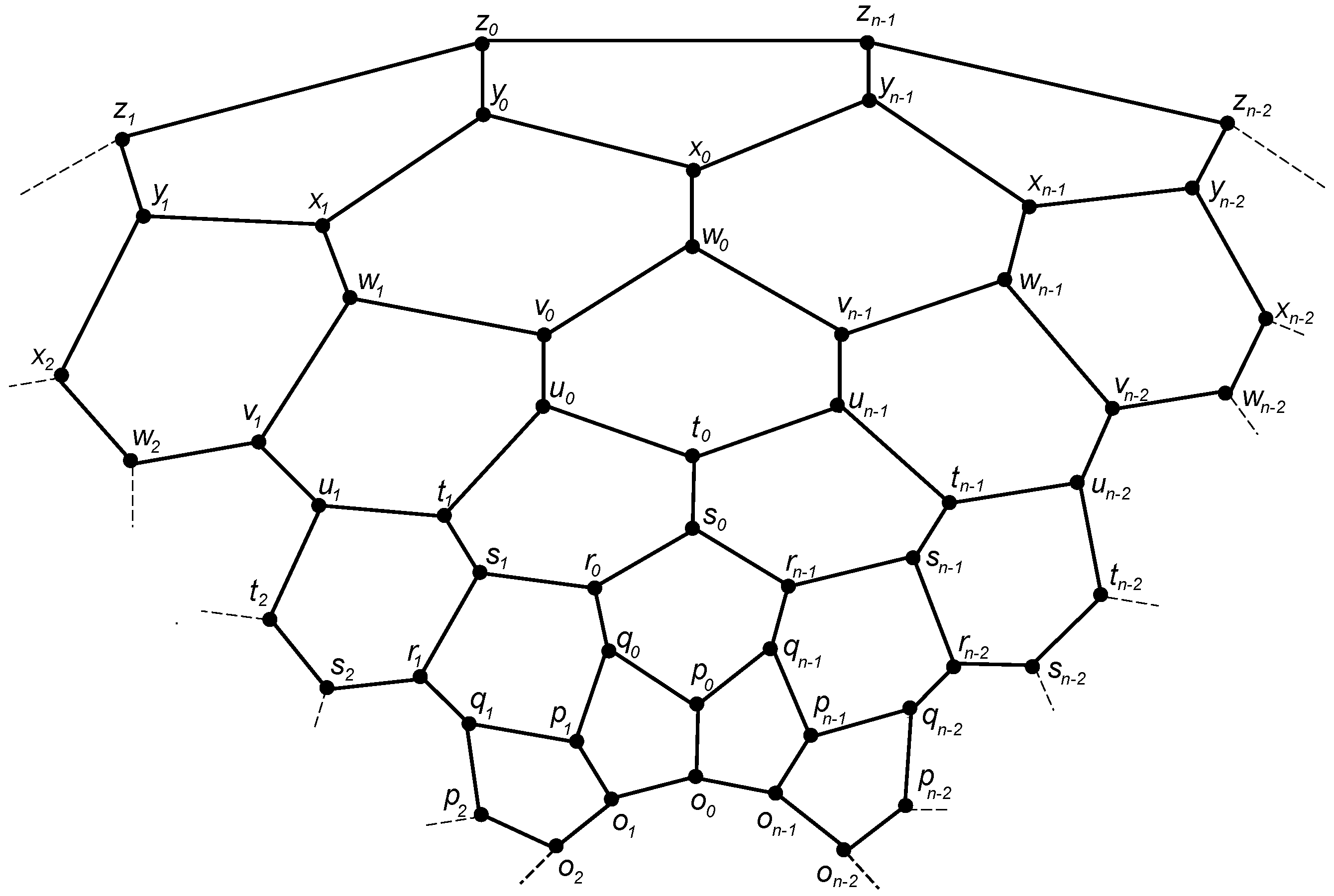
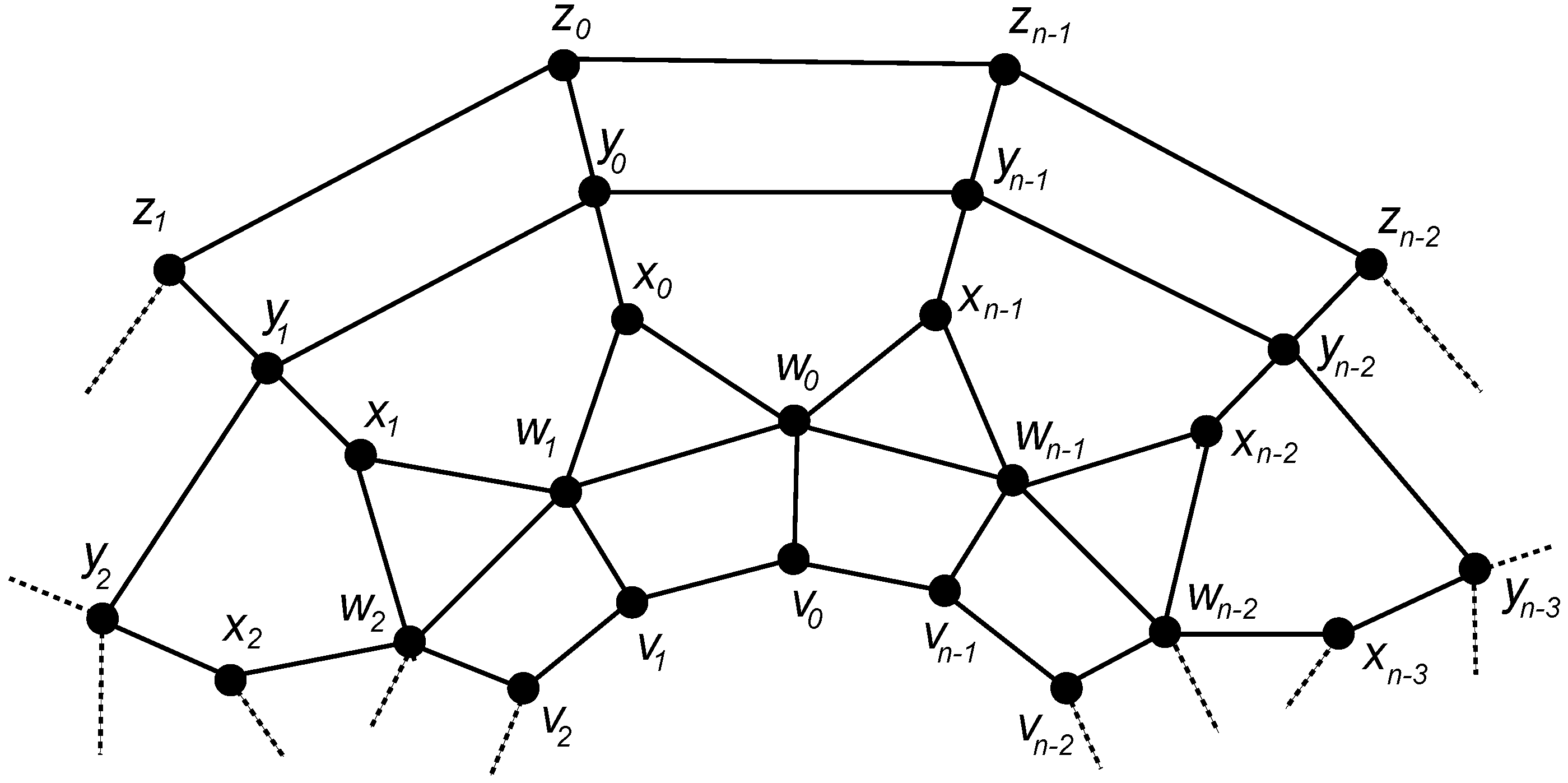
3.2. The Graph of Convex Polytope
3.2.1. Construction
3.2.2. Binary Locating-Dominating Number of
4. Tight Upper Bounds
4.1. The Graph of Convex Polytope
- Case 1:
- When .Table 2 depicts all vertices in S and the intersections of their closed neighborhoods with S. From the second column, we can see that all these intersections are nonempty and distinct. Thus, for any two vertices S, we have . This shows that S is a binary locating-dominating set of .
- Case 2:
- When .Similar to the argument in Case 1, we see from Table 2 that all the intersections are nonempty and distinct. This shows that S is a binary locating-dominating set for , if .
- Case 3:
- When .Similar to the argument in Case 1 and Case 2, we see from Table 2 that all the intersections are nonempty and distinct. This shows that S is a binary locating-dominating set for , if .Thus, from the above discussion, we can say that Case 4 and Case 5 are analogous to above mentioned cases.
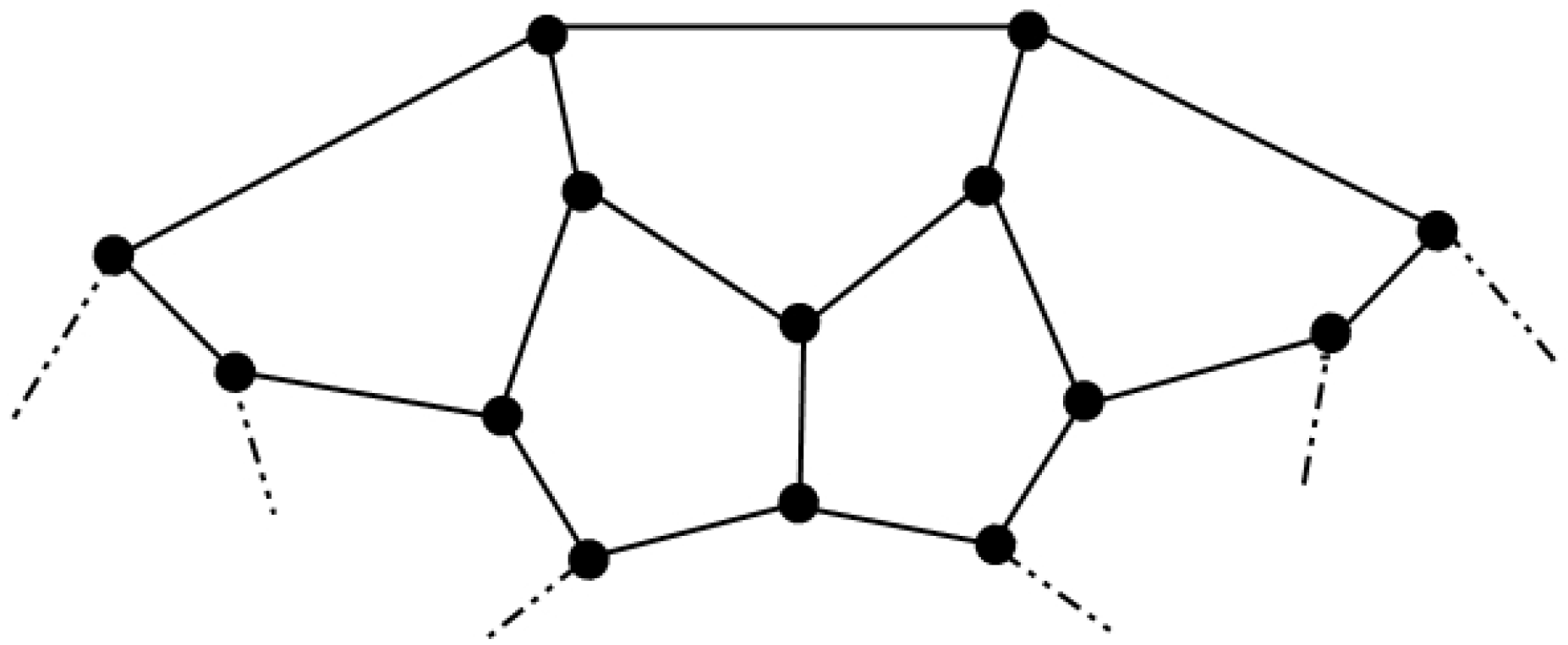
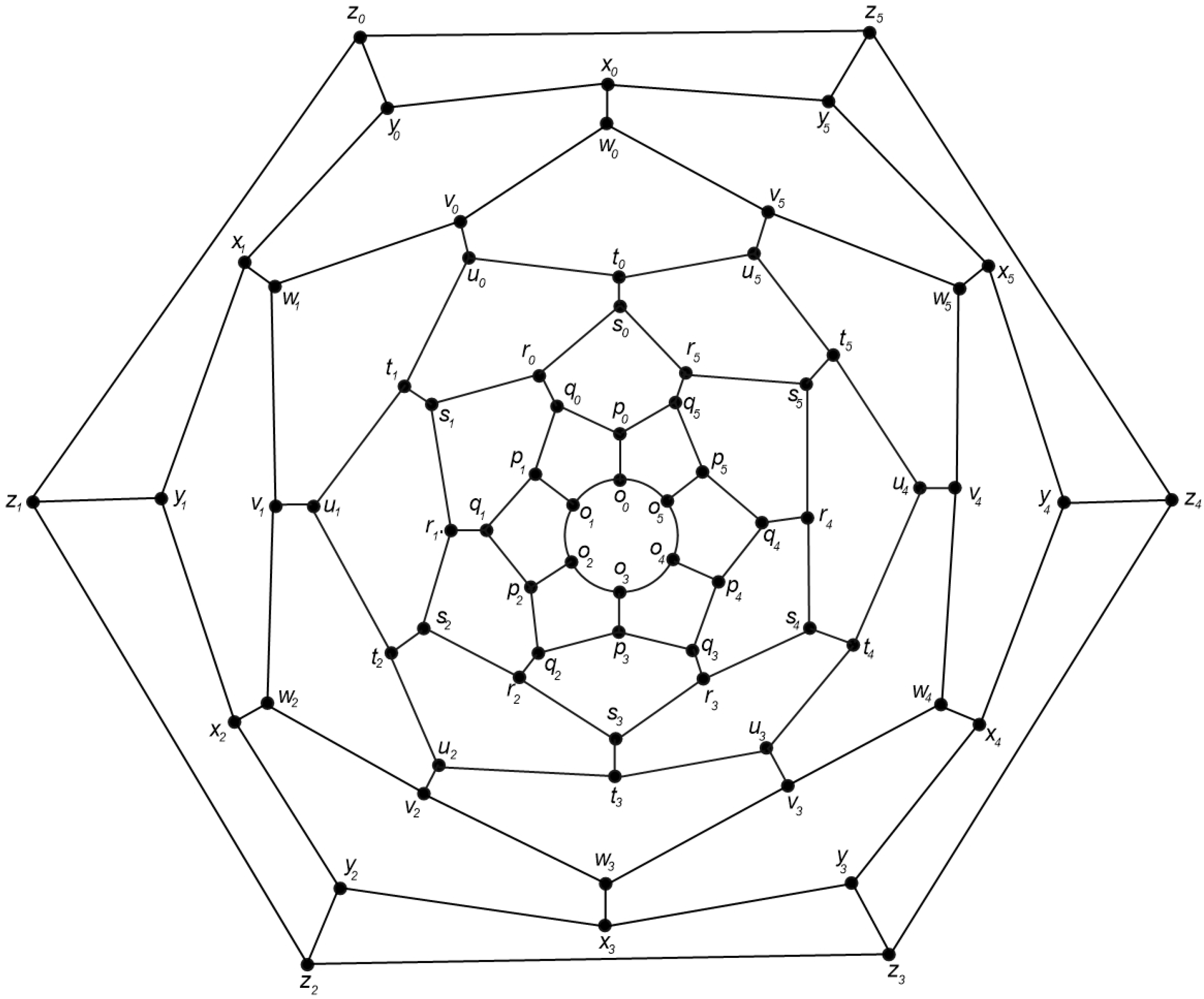
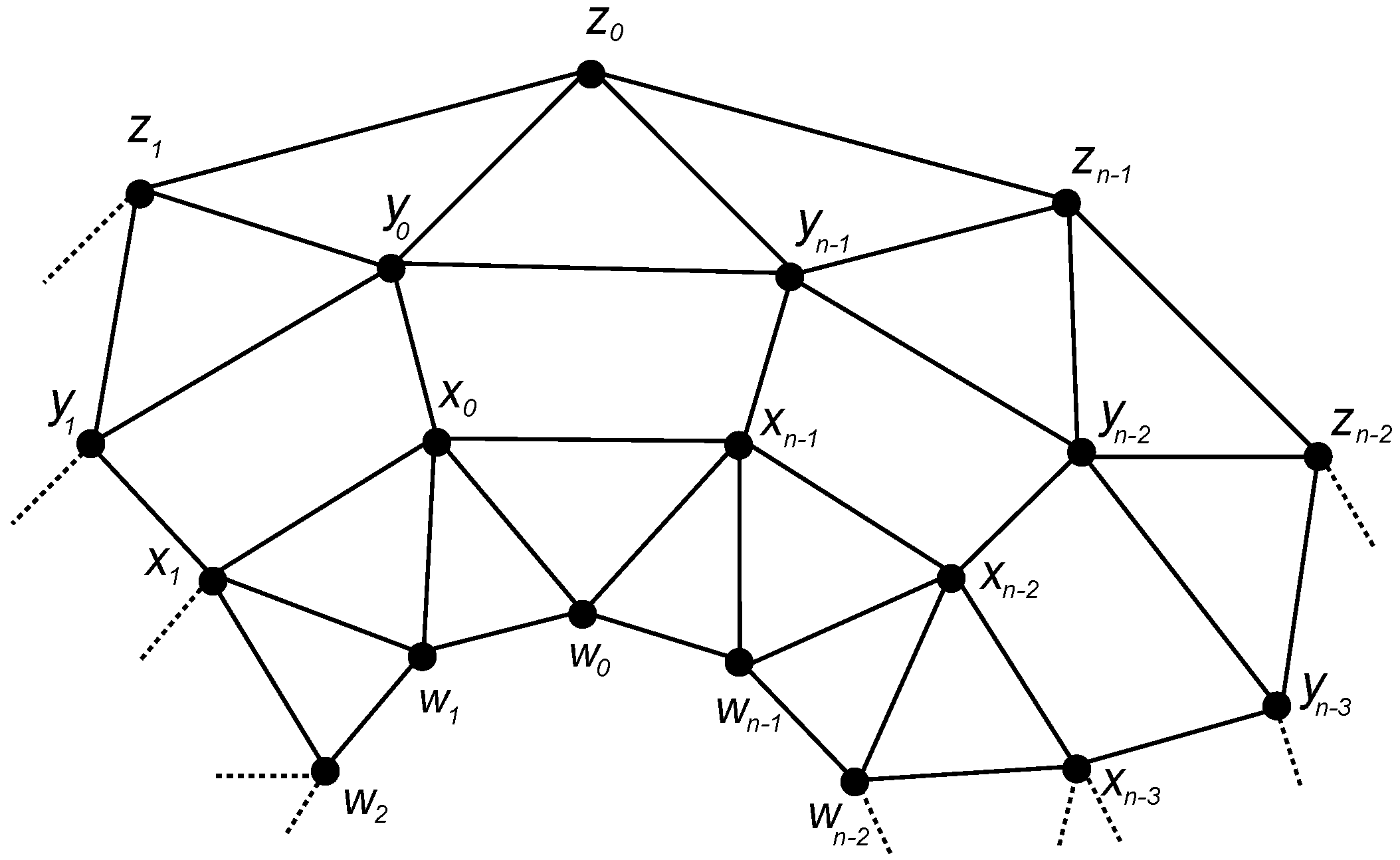
4.2. The Graph of Convex Polytope
4.3. The Graph of Convex Polytope
- Case 1:
- When .In order to show S to be a binary locating-dominating set, we need to show that the neighborhoods of all vertices in S are non-empty and distinct. Table 3 shows these neighborhoods and their intersections. Although some formulas for some intersections can be somewhat similar, but they are distinct.
- Case 2:
- When .As in the previous case, the the neighborhoods of all vertices in S are non-empty and distinct shown in Table 3. Thus, from the above discussion, we can say that Case 3, Case 4 and Case 5 are analogous to the above-mentioned cases.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haynes, T.W.; Hedetniemi, S.; Slater, P. Fundamentals of Domination in Graphs; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Haynes, T.W.; Henning, M.A.; Howard, J. Locating and total dominating sets in trees. Discret. Appl. Math. 2006, 154, 1293–1300. [Google Scholar] [CrossRef]
- Charon, I.; Hudry, O.; Lobstein, A. Extremal cardinalities for identifying and locating-dominating codes in graphs. Discret. Math. 2007, 307, 356–366. [Google Scholar] [CrossRef]
- Honkala, I.; Hudry, O.; Lobstein, A. On the ensemble of optimal dominating and locating-dominating codes in a graph. Inf. Process. Lett. 2015, 115, 699–702. [Google Scholar] [CrossRef]
- Honkala, I.; Laihonen, T. On locating-dominating sets in infinite grids. Eur. J. Comb. 2006, 27, 218–227. [Google Scholar] [CrossRef]
- Seo, S.J.; Slater, P.J. Open neighborhood locating-dominating sets. Australas. J. Comb. 2010, 46, 109–119. [Google Scholar]
- Seo, S.J.; Slater, P.J. Open neighborhood locating-dominating in trees. Discret. Appl. Math. 2011, 159, 484–489. [Google Scholar] [CrossRef]
- Slater, P.J. Fault-tolerant locating-dominating sets. Discret. Math. 2002, 249, 179–189. [Google Scholar] [CrossRef]
- Hernando, C.; Mora, M.; Pelayo, I.M. LD-graphs and global location-domination in bipartite graphs. Electron. Notes Discret. Math. 2014, 46, 225–232. [Google Scholar] [CrossRef]
- Slater, P.J. Domination and location in acyclic graphs. Networks 1987, 17, 5–64. [Google Scholar] [CrossRef]
- Slater, P.J. Locating dominating sets and locating-dominating sets. In Graph Theory, Combinatorics, and Algorithms, Proceedings of the Seventh Quadrennial International Conference on the Theory and Applications of Graphs, Kalamazoo, MI, USA, June 1–5, 1992; Alavi, Y., Schwenk, A., Eds.; John Wiley & Sons: New York, NY, USA, 1995; Volume 2, pp. 1073–1079. [Google Scholar]
- Charon, I.; Hudry, O.; Lobstein, A. Identifying and locating-dominating codes: NP-completeness results for directed graphs. IEEE Trans. Inf. Theory 2002, 48, 2192–2200. [Google Scholar] [CrossRef]
- Charon, I.; Hudry, O.; Lobstein, A. Minimizing the size of an identifying or locating-dominating code in a graph is NP-hard. Theor. Comput. Sci. 2003, 290, 2109–2120. [Google Scholar] [CrossRef]
- Lobstein, A. Watching Systems, Identifying, Locating-Dominating and Discriminating Codes in Graphs. Available online: http://perso.telecom-paristech.fr/~lobstein/debutBIBidetlocdom.pdf (accessed on 16 November 2018).
- Bača, M. Labelings of two classes of convex polytopes. Util. Math. 1988, 34, 24–31. [Google Scholar]
- Bača, M. On magic labellings of convex polytopes. Ann. Discret. Math. 1992, 51, 13–16. [Google Scholar]
- Imran, M.; Baig, A.Q.; Ahmad, A. Families of plane graphs with constant metric dimension. Util. Math. 2012, 88, 43–57. [Google Scholar]
- Imran, M.; Bokhary, S.A.U.H.; Baig, A.Q. On the metric dimension of rotationally-symmetric convex polytopes. J. Algebra Comb. Discret. Appl. 2015, 3, 45–59. [Google Scholar] [CrossRef]
- Imran, M.; Bokhary, S.A.U.H.; Baig, A.Q. On families of convex polytopes with constant metric dimension. Comput. Math. Appl. 2010, 60, 2629–2638. [Google Scholar] [CrossRef]
- Malik, M.A.; Sarwar, M. On the metric dimension of two families of convex polytopes. Afr. Math. 2016, 27, 229–238. [Google Scholar] [CrossRef]
- Kratica, J.; Kovačević-Vujčić, V.; Čangalović, M.; Stojanović, M. Minimal doubly resolving sets and the strong metric dimension of some convex polytopes. Appl. Math. Comput. 2012, 218, 9790–9801. [Google Scholar] [CrossRef]
- Salman, M.; Javaid, I.; Chaudhry, M.A. Minimum fault-tolerant, local and strong metric dimension of graphs. arXiv, 2014; arXiv:1409.2695. [Google Scholar]
- Simić, A.; Bogdanović, M.; Milošević, J. The binary locating-dominating number of some convex polytopes. ARS Math. Cont. 2017, 13, 367–377. [Google Scholar] [CrossRef]
- Hayat, S. Computing distance-based topological descriptors of complex chemical networks: New theoretical techniques. Chem. Phys. Lett. 2017, 688, 51–58. [Google Scholar] [CrossRef]
- Hayat, S.; Imran, M. Computation of topological indices of certain networks. Appl. Math. Comput. 2014, 240, 213–228. [Google Scholar] [CrossRef]
- Hayat, S.; Malik, M.A.; Imran, M. Computing topological indices of honeycomb derived networks. Rom. J. Inf. Sci. Tech. 2015, 18, 144–165. [Google Scholar]
- Hayat, S.; Wang, S.; Liu, J.-B. Valency-based topological descriptors of chemical networks and their applications. Appl. Math. Model. 2018, 60, 164–178. [Google Scholar] [CrossRef]
- Bange, D.W.; Barkauskas, A.E.; Host, L.H.; Slater, P.J. Generalized domination and efficient domination in graphs. Discret. Math. 1996, 159, 1–11. [Google Scholar] [CrossRef]
- Sweigart, D.B.; Presnell, J.; Kincaid, R. An integer program for open locating dominating sets and its results on the hexagon-triangle infinite grid and other graphs. In Proceedings of the 2014 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 25 April 2014; pp. 29–32. [Google Scholar]
- Hanafi, S.; Lazić, J.; Mladenović, N.; Wilbaut, I.; Crévits, C. New variable neighbourhood search based 0-1 MIP heuristics. Yugoslav J. Oper. Res. 2015, 25, 343–360. [Google Scholar] [CrossRef]
- Bača, M. Face anti-magic labelings of convex polytopes. Util. Math. 1999, 55, 221–226. [Google Scholar]
- Imran, M.; Siddiqui, H.M.A. Computing the metric dimension of convex polytopes generated by wheel related graphs. Acta Math. Hung. 2016, 149, 10–30. [Google Scholar] [CrossRef]
- Miller, M.; Bača, M.; MacDougall, J.A. Vertex-magic total labeling of generalized Petersen graphs and convex polytopes. J. Comb. Math. Comb. Comput. 2006, 59, 89–99. [Google Scholar]
- Imran, M.; Bokhary, S.A.U.H.; Ahmad, A.; Semaničová-Feňovčíková, A. On classes of regular graphs with constant metric dimension. Acta Math. Sci. 2013, 33B, 187–206. [Google Scholar] [CrossRef]
- Raza, H.; Hayat, S.; Pan, X.-F. On the fault-tolerant metric dimension of convex polytopes. Appl. Math. Comput. 2018, 339, 172–185. [Google Scholar] [CrossRef]
- Erickson, J.; Scott, K. Arbitrarily large neighborly families of congruent symmetric convex polytopes. arXiv, 2001; arXiv:math/0106095v1. [Google Scholar]
| n | S | S | ||
|---|---|---|---|---|
| n | S | S | ||
|---|---|---|---|---|
| n | S | S | ||
|---|---|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, H.; Hayat, S.; Pan, X.-F. Binary Locating-Dominating Sets in Rotationally-Symmetric Convex Polytopes. Symmetry 2018, 10, 727. https://doi.org/10.3390/sym10120727
Raza H, Hayat S, Pan X-F. Binary Locating-Dominating Sets in Rotationally-Symmetric Convex Polytopes. Symmetry. 2018; 10(12):727. https://doi.org/10.3390/sym10120727
Chicago/Turabian StyleRaza, Hassan, Sakander Hayat, and Xiang-Feng Pan. 2018. "Binary Locating-Dominating Sets in Rotationally-Symmetric Convex Polytopes" Symmetry 10, no. 12: 727. https://doi.org/10.3390/sym10120727
APA StyleRaza, H., Hayat, S., & Pan, X.-F. (2018). Binary Locating-Dominating Sets in Rotationally-Symmetric Convex Polytopes. Symmetry, 10(12), 727. https://doi.org/10.3390/sym10120727





