An Updated Constraint on Variations of the Fine-Structure Constant Using Wavelengths of Fe II Absorption Line Multiplets
Abstract
1. Introduction
2. Atomic Data and Analysis
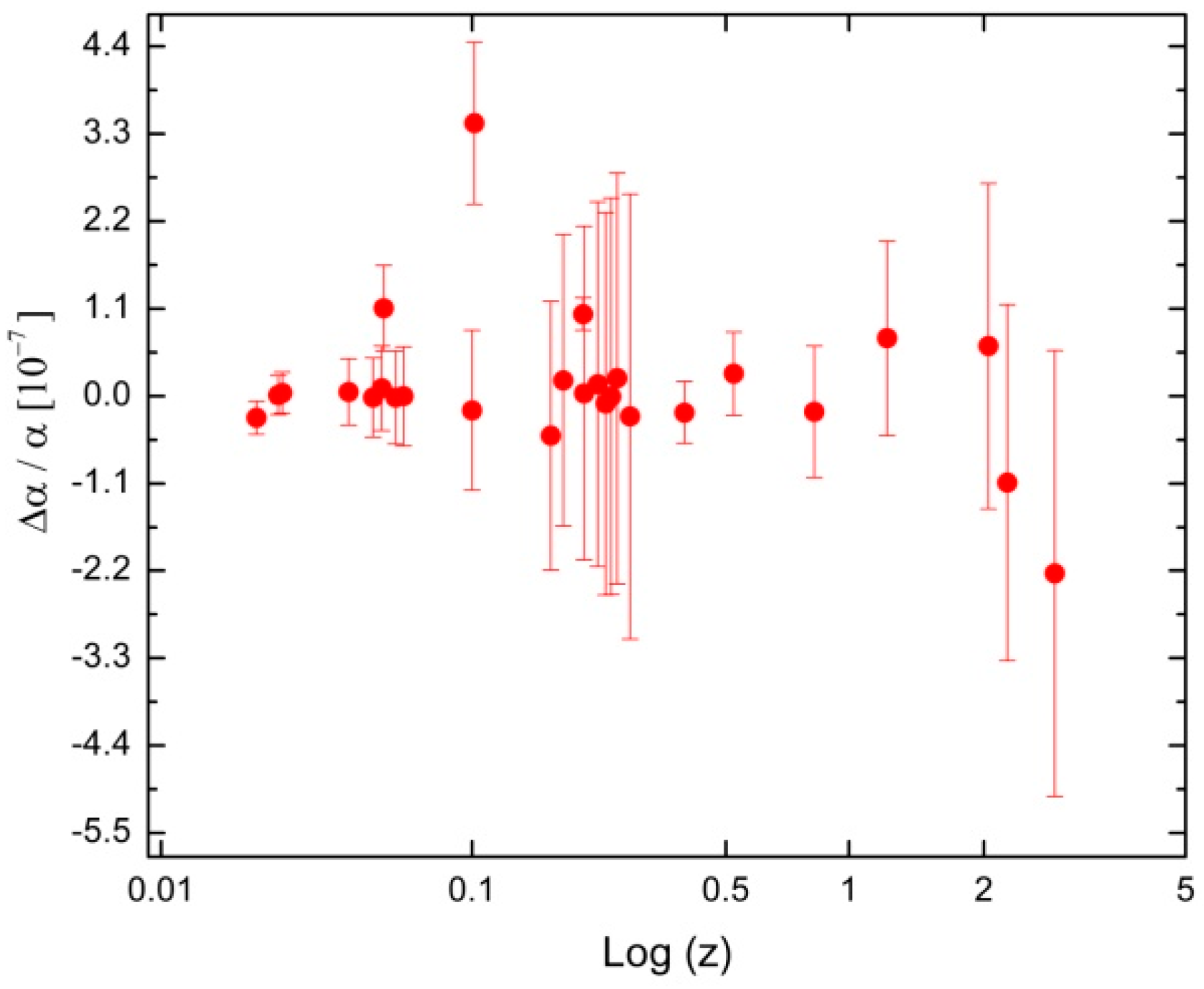
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
References
- Dirac, P.A.M. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Milne, E.A. Kinematics, dynamics, and the scale of time. Proc. R. Soc. A 1937, 158, 324–348. [Google Scholar] [CrossRef]
- Savedoff, M.D. Physical constants in extra-galactic nebulae. Nature 1995, 178, 688–689. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Schmidt, M. Does the fine-structure constant vary with cosmic time? Phys. Rev. Lett. 1967, 19, 1294–1295. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Steinhardt, C.L.; Schlegel, D. Does the fine-structure constant vary with cosmological epoch? Astrophys. J. 2004, 600, 520–543. [Google Scholar] [CrossRef]
- Grupe, D.; Pradhan, A.; Frank, S. Studying the variation of the fine-structure constant using emission-line multiplets. Astron. J. 2005, 130, 355–366. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Webb, J.K. Calculations of the relativistic effects in many-electron atoms and space-time variation of fundamental constants. Phy. Rev. A. 1999, 59, 230–237. [Google Scholar] [CrossRef]
- Webb, J.K.; Flambaum, V.V.; Christopher, W.; Drinkwater, M.J.; Barrow, J.D. Search for time variation of the fine structure constant. Phy. Rev. Lett. 1999, 82, 888–891. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Safronova, U.I.; Johnson, W.R. Energy levels and lifetimes of Nd IV, Pm IV, Sm IV, and Eu IV. Phys. Rev. A 2003, 68, 032503. [Google Scholar] [CrossRef]
- Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Dzuba, V.A.; Barrow, J.K.; Churchill, C.W.; Prochaska, J.X.; Wolfe, A.M. Further evidence for cosmological evolution of the fine structure constant. Phys. Rev. Lett. 2001, 87, 091301. [Google Scholar] [CrossRef]
- Murphy, M.T.; Webb, J.K.; Flambaum, V.V. Further evidence for a variable fine structure constant from Keck/HIRES QSO absorption spectra. Mon. Not. R. Soc. 2003, 245, 609–638. [Google Scholar] [CrossRef]
- Murphy, M.T.; Webb, J.K.; Flambaum, V.V.; Curran, S.J. Time evolution of the fine structure constant. arXiv, 2002; arXiv:astro-ph/0209488. [Google Scholar]
- Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Curran, S.J. Does the fine structure constant vary? A third quasar absorption sample consistent with varying α. Astrophys. Space Sci. 2003, 283, 565–575. [Google Scholar] [CrossRef]
- Reimers, D.; Hagen, H.; Rodriguez, P.; Wisotzki, L. Detection of further UV-bright high-redshift QSOs. Astron. Astrophys. 1998, 334, 96–98. [Google Scholar]
- Quast, R.; Reimers, D.; Levshakov, S.A. Probing the variability of the fine-structure constant with the VLT/UVES. Astron. Astrophys. 2004, 415, L7–L11. [Google Scholar] [CrossRef]
- Chand, H.; Srianand, R.; Petitjean, P.; Aracil, B.; Quast, R.; Reimers, D. Variation of the fine-structure constant: Very high resolution spectrum of QSO HE 0515-4414. Astron. Astrophys. 2006, 451, 45–56. [Google Scholar] [CrossRef]
- Levshakov, S.A.; Centurión, M.; D’Odorico, S.; Reimers, D.; Quast, R.; Pollmann, M. Most precise single redshift bound to Δα/α. Astron. Astrophys. 2006, 449, 879–889. [Google Scholar] [CrossRef]
- Levshakov, S.A.; Molaro, P.; Lopez, S.; D’Odorico, S.; Centurión, M.; Bonifacio, P.; Agafonova, I.I.; Reimers, D. A new measure of Δα/α at redshift z = 1.84 from very high resolution spectra of Q 1101–264. Astron. Astrophys. 2007, 446, 1077–1082. [Google Scholar] [CrossRef]
- Levshakov, S.A.; Reimers, D.; Kozlov, M.G.; Porsev, S.G.; Molaro, P. A new approach for testing variations of fundamental constants over cosmic epochs using FIR fine-structure lines. Astron. Astrophys. 2008, 479, 719–723. [Google Scholar] [CrossRef]
- Porsev, S.G.; Koshelev, K.V.; Tupitsyn, I.I.; Kozlov, M.G.; Reimers, D.; Levshakov, S.A. Transition frequency shifts with fine-structure-constant variation for Fe II: Breit and core-valence correlation corrections. Phys. Rev. A 2007, 76, 052507. [Google Scholar] [CrossRef]
- Agafonova, I.I.; Molaro, P.; Levshakov, S.A.; Hou, J.L. First measurement of Mg isotope abundances at high redshifts and accurate estimate of Δα/α. Astron. Astrophys. 2011, A28, 529. [Google Scholar] [CrossRef]
- Griest, K.; Whitmore, J.B.; Wolfe, M.; Prochaska, J.X.; Howk, J.C.; Marcy, G.W. Wavelength Accuracy of the Keck Hires Spectrograph and Measuring Changes in the Fine Structure Constant. Astrophys. J. 2010, 708, 158–170. [Google Scholar] [CrossRef]
- Martinez, A.F.; Vladiloand, F.G.; Bonifacio, P. Search for alpha variation in UVES spectra: Analysis of C IV and Si IV doublets towards QSO 1101-264. arXiv, 2003; arXiv:astro-ph/0312270. [Google Scholar]
- Levshakov, S.A.; Centurión, M.; Molaro, P.; D’Odorico, S. VLT/UVES constraints on the cosmological variability of the fine-structure constant. Astron. Astrophys. 2005, 434, 827–838. [Google Scholar] [CrossRef]
- Molaro, P.; Levshakov, S.A.; Monsai, S.; Centurión, M.; Bonifacio, S.; D’Odorico, S.; Monaco, L. UVES radial velocity accuracy from asteroid observations I. Implications for fine structure constant variability. Astron. Astrophys. 2008, 481, 559–569. [Google Scholar] [CrossRef]
- Gutierrez, C.M.; Lopez-Corredoira, M. The value of the fine structure constant over cosmological times. Astrophys. J. 2010, 713, 46–51. [Google Scholar] [CrossRef]
- Murphy, M.T.; Flambaum, V.V.; Muller, S.; Henkel, C. Strong limit on a variable proton-to-electron mass ratio from molecules in the distant universe. Science 2008, 320, 16111613. [Google Scholar] [CrossRef] [PubMed]
- Le, T.D. A Stringent Limit on Variation of the Fine-Structure Constant Using Absorption Line Multiplets in the Early Universe. Astrophys. 2016, 59, 285–291. [Google Scholar] [CrossRef]
- Aldenius, M.; Johansson, S.; Murphy, M.T. Accurate laboratory ultraviolet wavelengths for quasar absorption-line constraints on varying fundamental constants. Mon. Not. R. Soc. 2006, 370, 444–452. [Google Scholar] [CrossRef]
- Nave, G.; Sansonetti, C.J. Wavelengths of the 3d6(5D)4s a6D−3d6(5D)4py6P multiplet of Fe II (UV 8). Opt. Soc. Am. 2011, B28, 737–745. [Google Scholar] [CrossRef]
- Nave, G. Wavelengths of Fe II lines for studies of time variation of the fine-structure constant. Mon. Not. R. Soc. 2012, 420, 1570–1574. [Google Scholar] [CrossRef]
- Pickering, J.C.; Thorne, A.P.; Murray, J.E.; Litzén, U.; Johansson, S. Accurate laboratory wavelengths of some ultraviolet lines of Cr, Zn and Ni relevant to time variations of the fine structure constant. Mon. Not. R. Soc. 2000, 319, 163–167. [Google Scholar] [CrossRef]
- Pickering, J.C.; Donnelly, M.; Nilsson, H.; Hibbert, A.; Johansson, S. The FERRUM Project: Experimental oscillator strengths of the UV 8 multiplet and other UV transitions from the y6P levels of Fe II. Astron. Astrophys. 2002, 396, 715–722. [Google Scholar] [CrossRef]
- Murphy, M.T.; Berengut, J.C. Laboratory atomic transition data for precise optical quasar absorption spectroscopy. Mon. Not. R. Soc. 2014, 438, 388–411. [Google Scholar] [CrossRef]
- Welty, D.E.; Hobbs, L.M.; Kulkarni, V.P. A high-resolution survey of interstellar NA I D1 lines. Astrophys. J. 1994, 436, 152–175. [Google Scholar] [CrossRef]
- Welty, D.E.; Morton, D.C.; Hobbs, L.M. A High-Resolution Survey of Interstellar Ca II Absorption. Astrophys. J. 1996, 106, 533–562. [Google Scholar] [CrossRef]
- Wendt, M.; Molaro, P. Robust limit on a varying proton-to-electron mass ratio from a single H2 system. Astron. Astrophys. 2011, A96, 526. [Google Scholar]
- Murphy, M.T.; Webb, J.K.; Flambaum, V.V.; Dzuba, V.A.; Churchill, C.W.; Prochaska, J.X. Possible evidence for a variable fine-structure constant from QSO absorption lines: Motivations, analysis and results. Mon. Not. R. Soc. 2001, 327, 1223–1236. [Google Scholar] [CrossRef]
- Chand, H.; Srianand, R.; Petitjean, P.; Aracil, B. Probing the cosmological variation of the fine-structure constant: Results based on VLT-UVES sample. Astron. Astrophys. 2004, 417, 853–871. [Google Scholar] [CrossRef]
- Bainbridge, M.B.; Webb, J.K. Artificial intelligence applied to the automatic analysis of absorption spectra.Objective measurement of the fine structure constant. Mon. Not. R. Soc. 2017, 468, 1639–1670. [Google Scholar]
- Webb, J.K.; King, J.A.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B. Indications of a Spatial Variation of the Fine Structure Constant. Phys. Rev. Lett. 2011, 107, 191101. [Google Scholar] [CrossRef]
- Bagdonaite, J.; Jansen, P.; Henkel, C.; Bethlem, H.L.; Menten, K.M.; Ubachs, W. A stringent limit on a drifting proton-to-electron mass ratio from alcohol in the early universe. Science 2012, 339, 46–48. [Google Scholar] [CrossRef]
| Upper Level | Observed Wavelengths from QSO | Ritz Wavelengths from Laboratories | References |
|---|---|---|---|
| 3d6(5zD)4p6D9/2 | 2600.172 | 2600.17210(11) | [28,29,30] |
| 3d6(5zD)4p6D7/2 | 2586.649 | 2586.64934(11) | [28,29,30] |
| 3d6(5zD)4p6F11/2 | 2382.764 | 2382.76397(11) | [28,29,30] |
| 3d6(5zD)4p6F9/2 | 2374.460 | 2374.46009(11) | [28,29,30] |
| 3d6(5zD)4p6F7/2 | 2367.589 | 2367.58924(11) | [28,29,30] |
| 3d6(5zD)4p6P7/2 | 2344.212 | 2344.21276(11) | [28,29,30] |
| 3d6(5zD)4p4F9/2 | 2260.780 | 2260.77911(10) | [28,29,30] |
| 3d6(5zD)4p4D7/2 | 2249.877 | 2249.87547(10) | [28,29,30] |
| 3d6(a3yF)4p4F7/2 | 1611.200 | 1611.20037(7) | [28,29,30,31] |
| 3d5(6S)4s4p(3yP)6P7/2 | 1608.450 | 1608.45085(7) | [28,29,30,31] |
| 3d5(6S)4s4p(1xP)6P7/2 | 1260.533 | 1260.53558(6) | [28,29,30,31] |
| 3d5(4G)4s4p(3yP)6F11/ | 1144.939 | 1144.93921(5) | [28,29,30,31] |
| 3d5(4G)4s4p(3yP)6F9/2 | 1143.224 | 1143.22379(6) | [28,29,30,31] |
| 3d5(4G)4s4p(3yP)6F7/2 | 1142.366 | 1142.36568(6) | [28,29,30,31] |
| 3d5(4P)4s4p(3P)6D7/2 | 1260.533 | 1133.66526(5) | [28,29,30,31] |
| 3d6(5D)5p6D9/2 | 1127.097 | 1127.09842(5) | [28,29,30,31,32] |
| 3d6(5D)5p6D7/2 | 1125.446 | 1125.44765(5) | [28,29,30,31,32] |
| 3d5(4P)4s4p(3P)6P7/2 | 1121.975 | 1121.97473(5) | [28,29,30,31,32] |
| 3d6(5D)5p6F11/2 | 1112.047 | 1112.04833(5) | [28,29,30,31,32] |
| 3d6(5D)5p4F9/2 | 1106.362 | 1106.35952(5) | [28,29,30,31,32] |
| 3d6(5D)5p6P7/2 | 1096.877 | 1096.87689(5) | [29,30,31,32] |
| 3d5(4D)4s4p(3P)6F9/2 | 1083.419 | 1083.42027(5) | [29,30,31,32] |
| 3d5(4D)4s4p(3P)6F11/2 | 1081.874 | 1081.87528(5) | [29,30,31,32] |
| 3d5(4D)4s4p(3P)6D7/2 | 1063.971 | 1063.97182(5) | [29,30,31,32] |
| 3d5(4D)4s4p(3P)6D9/2 | 1063.176 | 1063.17688(5) | [29,30,31,32] |
| 3d5(4G)4s4p(3wP)4G9/2 | 1062.152 | 1062.1533(3) | [29,30,31,32] |
| 3d5(4D)4s4p(3P)6P7/2 | 1055.262 | 1055.26178(5) | [29,30,31,32] |
| z (10−6) | Δα/α (10−6) | σΔα/α (10−6) |
|---|---|---|
| 0.05 | −0.0194 | 0.49997 |
| 0.04197 | 0.05036 | 0.41968 |
| 0.05876 | −0.01898 | 0.58755 |
| 0.02106 | −0.27398 | 0.21057 |
| 0.52374 | 0.2802 | 0.52374 |
| 0.02559 | 0.04099 | 0.25595 |
| 0.10173 | 3.43353 | 1.01735 |
| 2.80641 | −2.23371 | 2.80641 |
| 0.39101 | −0.20865 | 0.39101 |
| 0.02487 | 0.01243 | 0.24869 |
| 2.04675 | 0.62672 | 2.04675 |
| 0.18342 | 0.19726 | 1.83416 |
| 0.20993 | 0.03515 | 2.09932 |
| 0.28012 | −0.25867 | 2.8012 |
| 0.22934 | 0.14743 | 2.29345 |
| 0.06211 | −0.00441 | 0.62106 |
| 0.05331 | 0.09425 | 0.53312 |
| 0.24065 | −0.09503 | 2.40647 |
| 0.05395 | 1.10512 | 0.53954 |
| 2.24159 | −1.08932 | 2.24159 |
| 0.10028 | −0.17914 | 1.00285 |
| 0.24921 | −0.00481 | 2.49211 |
| 0.25881 | 0.22132 | 2.5881 |
| 0.16918 | −0.49919 | 1.69177 |
| 0.82771 | −0.19849 | 0.82771 |
| 1.22393 | 0.72562 | 1.22393 |
| 0.20848 | 1.03206 | 0.20848 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.D. An Updated Constraint on Variations of the Fine-Structure Constant Using Wavelengths of Fe II Absorption Line Multiplets. Symmetry 2018, 10, 722. https://doi.org/10.3390/sym10120722
Le TD. An Updated Constraint on Variations of the Fine-Structure Constant Using Wavelengths of Fe II Absorption Line Multiplets. Symmetry. 2018; 10(12):722. https://doi.org/10.3390/sym10120722
Chicago/Turabian StyleLe, T. D. 2018. "An Updated Constraint on Variations of the Fine-Structure Constant Using Wavelengths of Fe II Absorption Line Multiplets" Symmetry 10, no. 12: 722. https://doi.org/10.3390/sym10120722
APA StyleLe, T. D. (2018). An Updated Constraint on Variations of the Fine-Structure Constant Using Wavelengths of Fe II Absorption Line Multiplets. Symmetry, 10(12), 722. https://doi.org/10.3390/sym10120722





