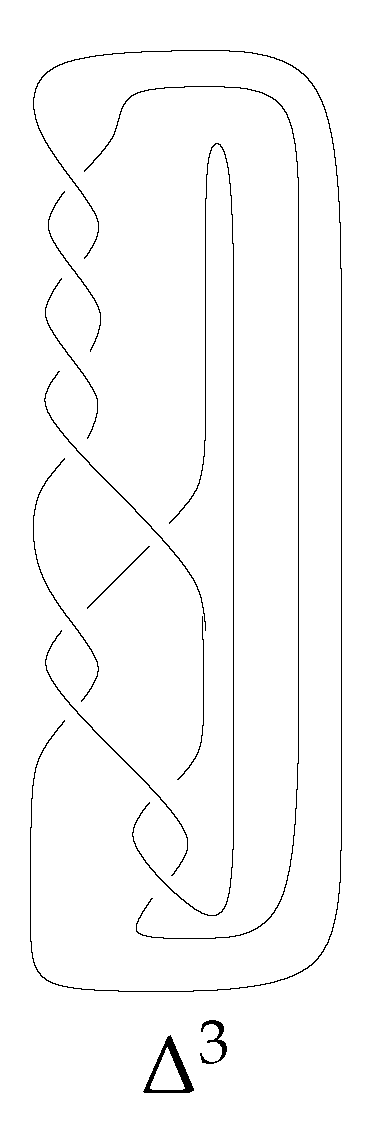
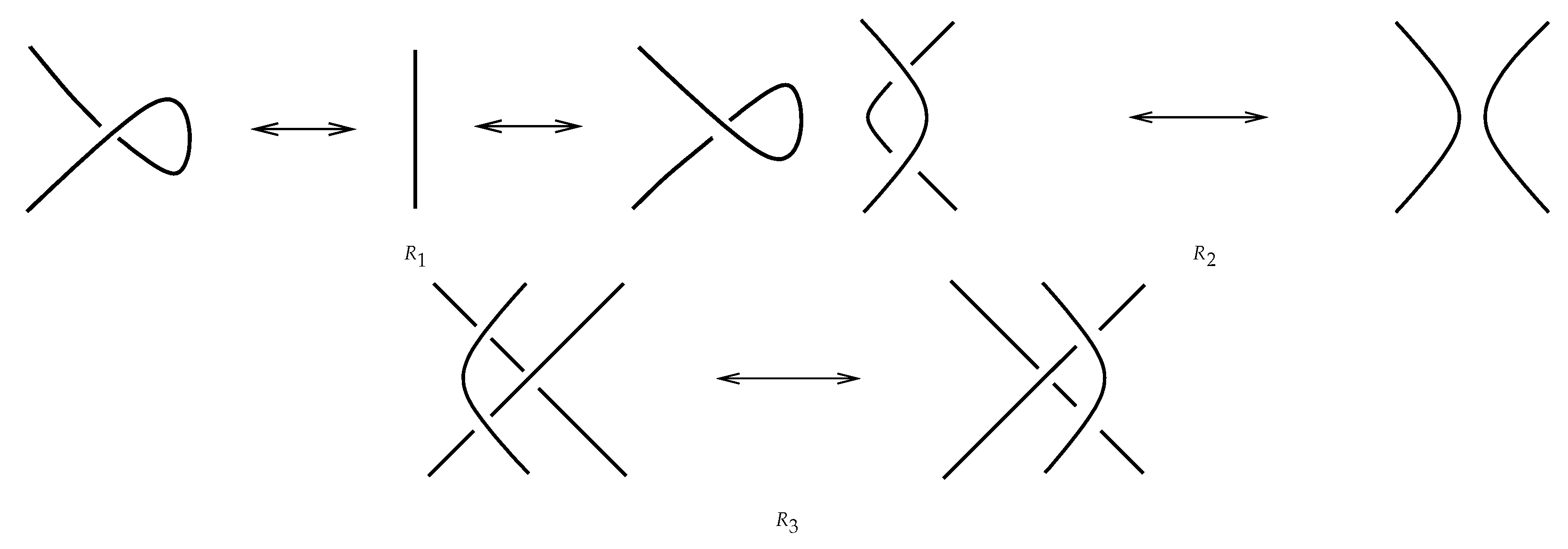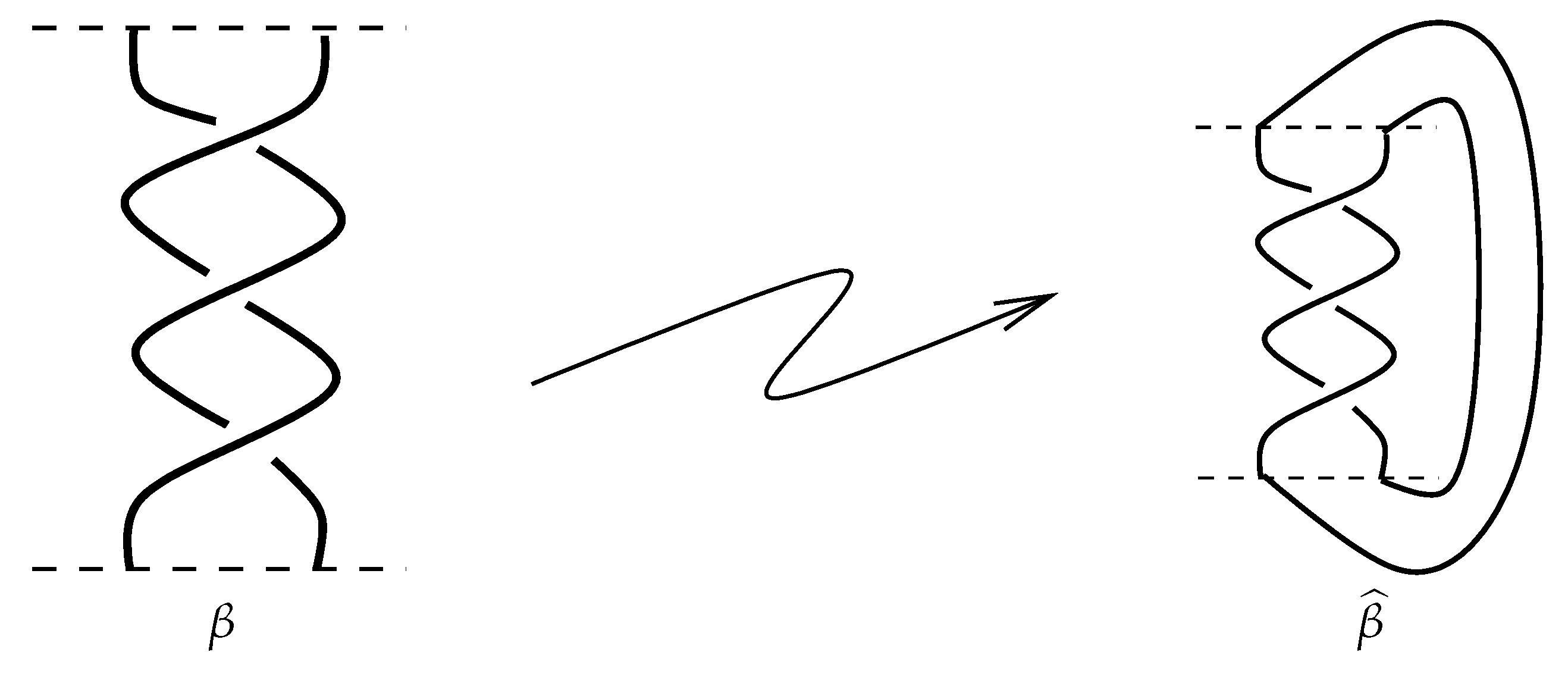1. Introduction
Khovanov homology was introduced by Mikhail Khovanov in 2000 in Reference [
1] as a categorification of the Jones polynomial, which was introduced by Jones in [
2]. His construction, using geometrical and topological objects instead of polynomials, was so interesting that it offered a completely new approach to tackle problems in low-dimensional topology.
Khovanov homology plays a vital role in developing several important results in the field of knot theory. Soon after the discovery of Khovanov homology, Bar-Natan proved in Reference [
3] that Khovanov’s invariant is stronger than the Jones polynomial. He also proved that the graded Euler characteristic of the chain complex of a link
L is the un-normalized Jones polynomial of that link. In 2005, Bar-Natan extended the Khovanov homology of links to tangles, cobordisms, and two-knots [
4]. In [
5] Bar-Natan gave a fast way of computing the Khovanov homology. In 2013, Ozsvath, Rasmussen, and Szabo introduced the odd Khovanov homology by using exterior algebra instead of symmetric algebra [
6]. Gorsky, Oblomkov, and Rasmussen gave some results on stable Khovanov homology of torus links in Reference [
7]. Putyra introduced a triply graded Khovanov homology and used it to prove that odd Khovanov homology is multiplicative with respect to disjoint unions and connected sums of links Reference [
8]. Manion gave rational Khovanov homology of three-strand pretzel links in 2011 [
9]. Nizami, Mobeen, and Ammara gave Khovanov homology of some families of braid links in Reference [
10]. Nizami, Mobeen, Sohail, and Usman gave Khovanov homology and graded Euler characteristic of 2-strand braid links in [
11].
In Reference [
12], Marko used a long exact sequence to prove that the Khovanov homology groups of the torus link
stabilize as
. A generalization of this result to the context of tangles came in the form of Reference [
13], where Lev Rozansky showed that the Khovanov chain complexes for torus braids also stabilize (up to chain homotopy) in a suitable sense to categorify the Jones–Wenzl projectors. At roughly the same time, Benjamin Cooper and Slava Krushkal gave an alternative construction for the categorified projectors in Reference [
14]. These results, along with connections between Khovanov homology, HOMFLYPT homology, Khovanov–Rozansky homology, and the representation theory of rational Cherednik algebra (see [
15]) have led to conjectures about the structure of stable Khovanov homology groups in limit
(see [
15], and results along these lines in Reference [
16]). More recently, in Reference [
17], Robert Lipshitz and Sucharit Sarkar introduced the Khovanov homotopy type of a link
L. This is a link invariant taking the form of a spectrum whose reduced cohomology is the Khovanov homology of
L.
Although computing the Khovanov homology of links is common in the literature, no general formulae have been given for all families of knots and links. In this paper, we give Khovanov homology of the three-strand braid links , , and , where is the Garside element . Particularly, we focus on the top homology groups.
2. Braid Links
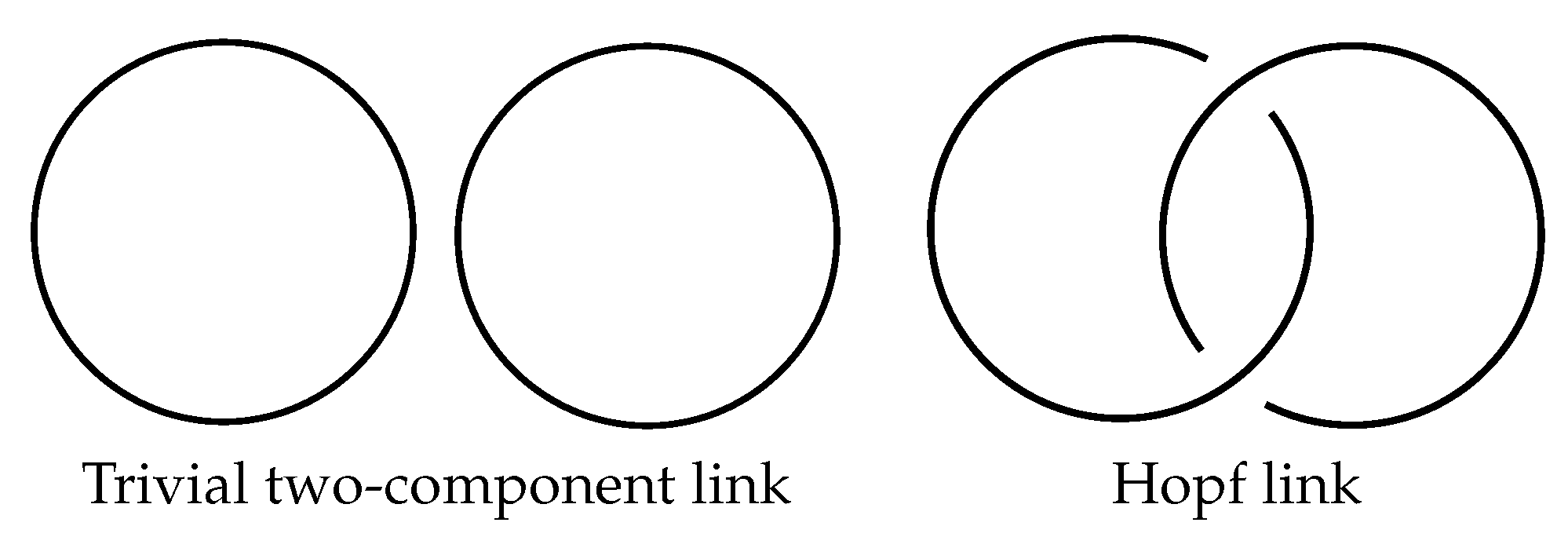
Definition 1. A knot is a simple, closed curve in the three-space. More precisely, it is the image of an injective, smooth function from the unit circle to with a nonvanishing derivative [18]. You can see some knots in Figure 1: Definition 2. An m-component link is a collection of m nonintersecting knots [18]. A trivial two-component link and the Hopf link are given in Figure 2: Definition 3. Two links and are said to be isotopic or equivalent if there is a smooth map F: , which confirms that is a link for all and that that and . Map F is called isotopy. By the isotopy class of a link L, denoted , we mean the collection of all links that are isotopic to L.
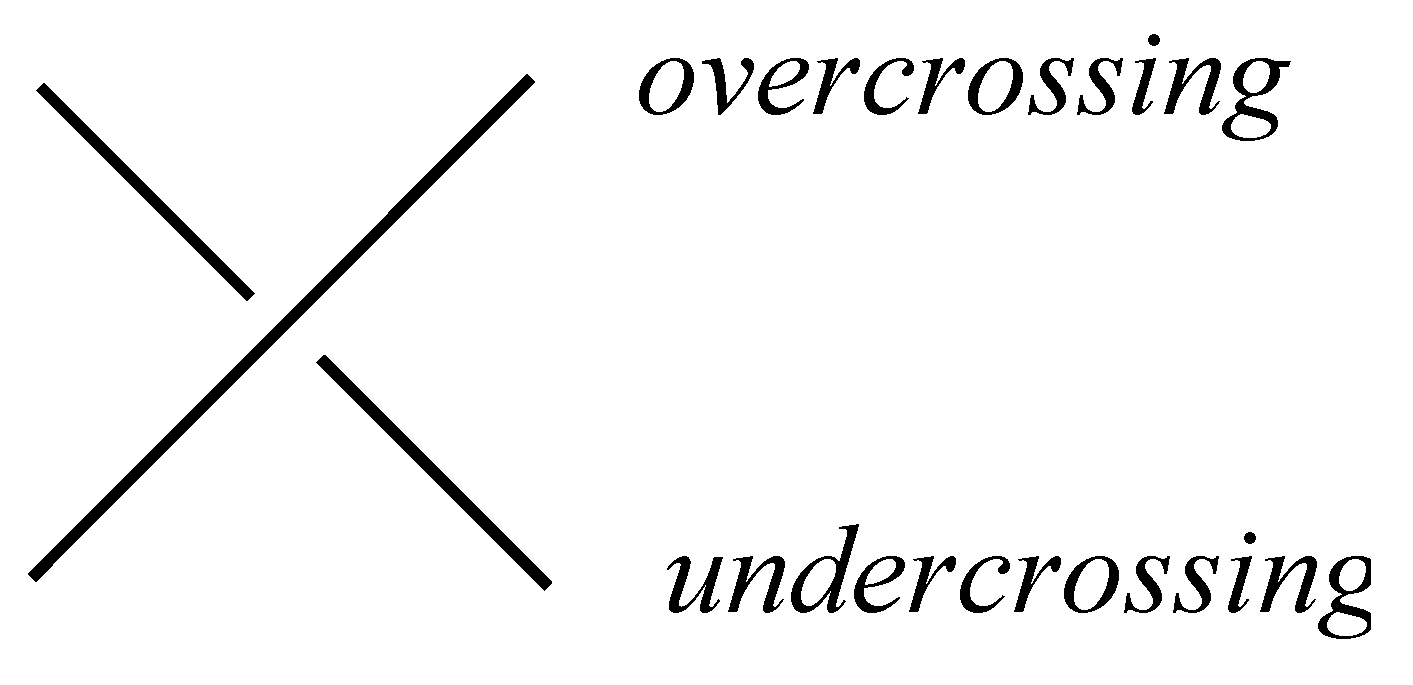
Since it is hard to work with links in
, people usually prefer working with their projections on a plane. These projections should be generic, which means that all multiple points are double points with a clear information of over- and undercrossing, as you can see in
Figure 3. Such a projection of a link is called the
diagram of the link.
Theorem 1. (Reidemeister, [19]). Let and be two diagrams of links and . Then, links and are isotopic if and only if is transformed into by planar isotopies and by a finite sequence of three local moves represented in Figure 4: Definition 4. A link invariant is a function that remains constant on all elements in an isotopy class of a link.
Remark 1. A function to qualify as a link invariant should be invariant under the Reidemeister moves.
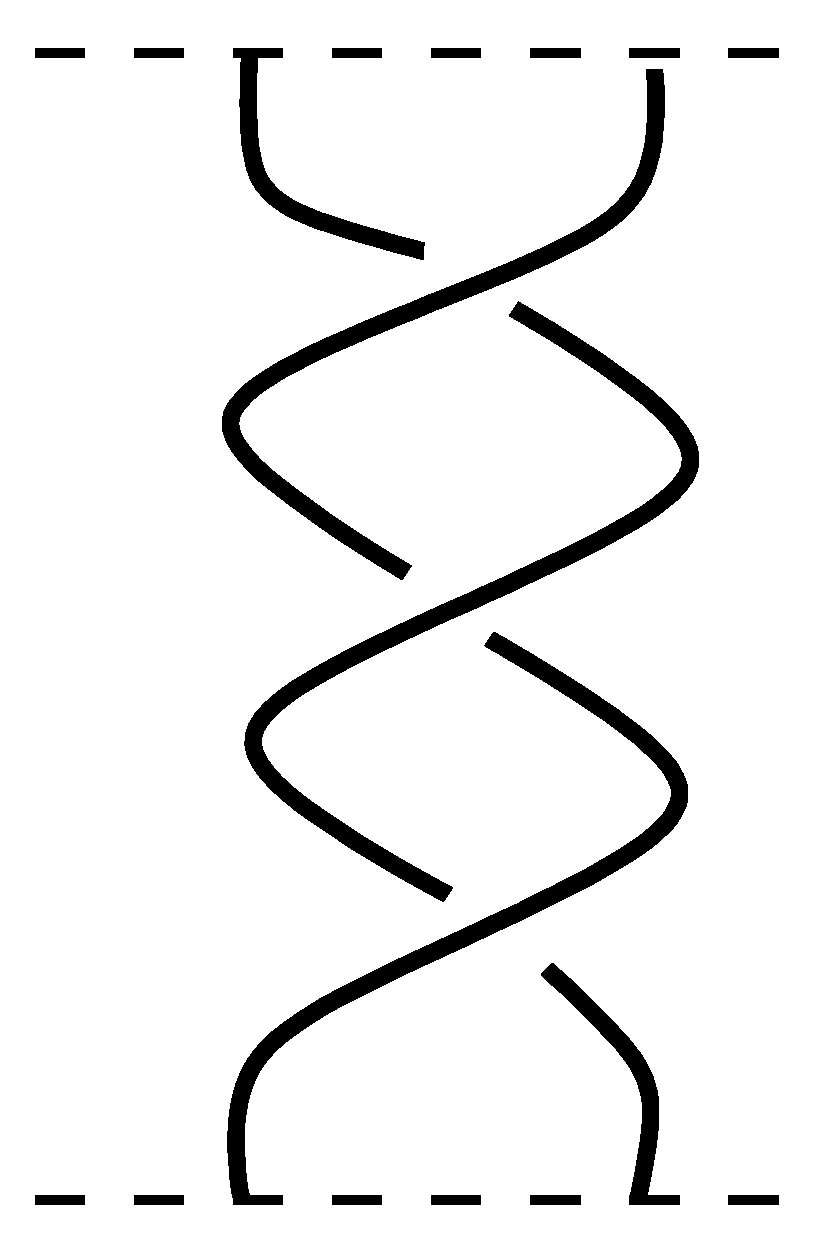
Definition 5. An n-strand braid is a collection of n nonintersecting, smooth curves joining n points on a plane to n points on another parallel plane in an arbitrary order such that any plane parallel to the given planes intersects exactly n number of curves [20]. The smooth curves are called the strands of the braid. You can see a 2-strand braid in Figure 5: Definition 6. The product of two n-strand braids α and β, denoted by , is defined by putting β below α and then gluing their common endpoints.
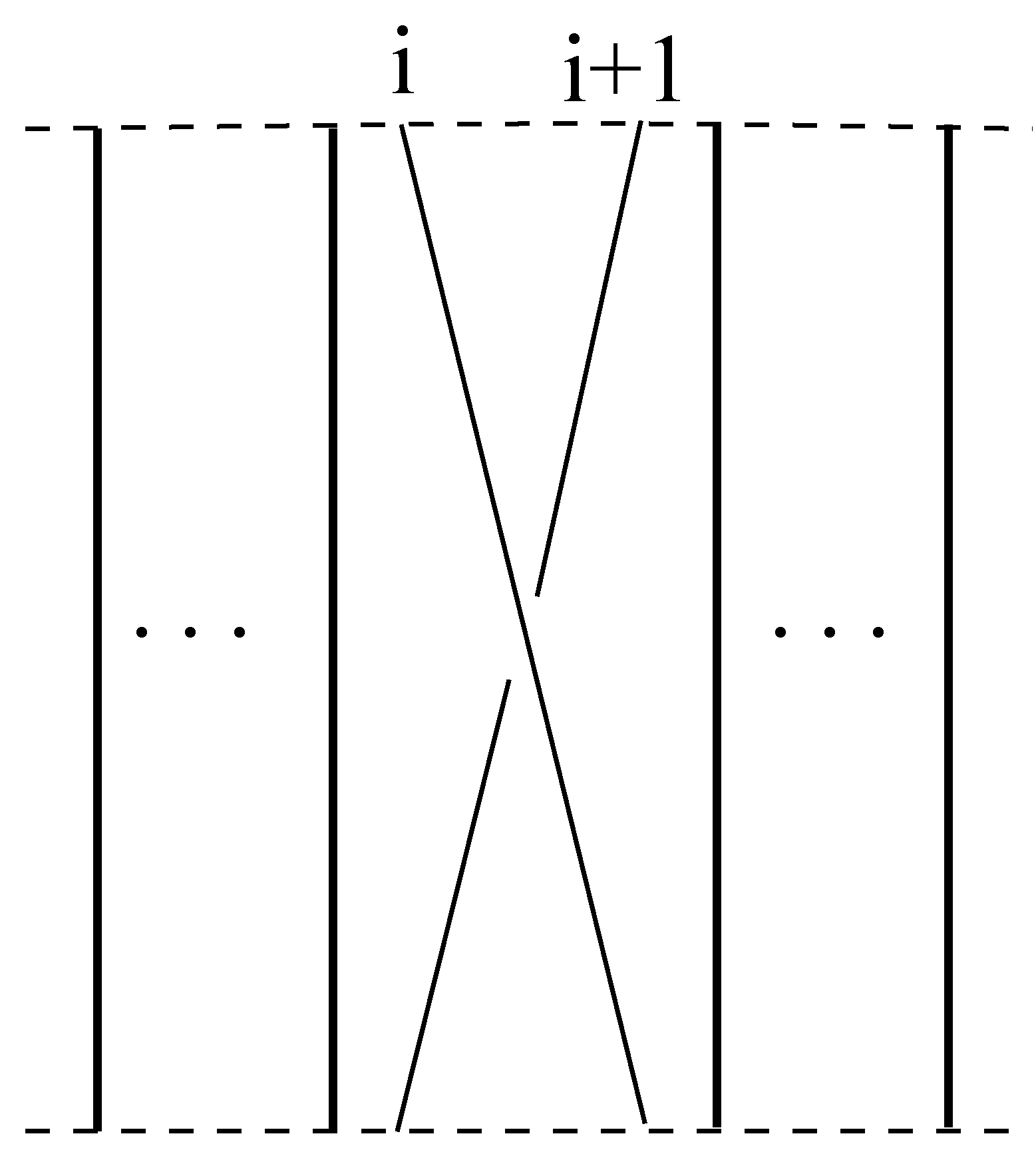
Definition 7. A braid is said to be elementary if it consists of just one crossing. The i
th elementary braid, denoted by , is given in Figure 6: Remark 2. Each braid is a product of elementary braids.
Definition 8. The closure of a braid β, denoted by , is defined by connecting its lower endpoints to its corresponding upper endpoints with smooth curves, as you can see in Figure 7. Remark 3. - 1
All braids are oriented from top to bottom.
- 2
From now onward, by braid β we mean its closure , which is actually a link.
An important result by Alexander, connecting links and braids, is:
Theorem 2. (Alexander [21]). Each link is a closure of some braid.
Definition 9. The 0- and 1-smoothings of crossing ![Symmetry 10 00720 i001 Symmetry 10 00720 i001]() are defined, respectively, by
are defined, respectively, by ![Symmetry 10 00720 i002 Symmetry 10 00720 i002]() and
and ![Symmetry 10 00720 i003 Symmetry 10 00720 i003]() .
. Definition 10. A collection of disjoint circles obtained by smoothing out all the crossings of a link L is called the Kauffman state of the link [22]. 3. Homology
Definition 11. Let be a graded vector space with homogeneous components of degree n. The graded dimension of V is the power series : .
Definition 12. The degree of the tensor product of graded vector space is the sum of the degrees of the homogeneous components of graded vector spaces and
Remark 4. In our case, the graded vector space V has the basis with degree and the q-dimension
Definition 13. The degree shift operation on a graded vector space is defined by Construction of Chain Groups: Let L be a link with n crossings, and let all crossings be labeled from 1 to n. Arrange all its Kauffman states into columns so that the rth column contains all states having r number of 1-smoothings in it. To every stat in the rth column we assign graded vector space , where m is the number of circles in . The rth chain group, denoted by , is the direct sum of all vector spaces corresponding to all states in the rth column.
Definition 14. The chain complex of graded vector spaces is defined as:such that for each r. In a system of converting the chain group into a complex, we use the maps between graded vector spaces to satisfy
For this purpose we can label the edges of the cube
by the sequence
, where
contains only one ⋆ at a time. Here, ⋆ indicates that we change a 1-smoothing to a 0-smoothing. The maps on the edges is denoted by
, the height of edges
. The direct sum of differentials in the cube along the column is
Now, we discuss the reason behind the sign of As we want from the differentials to satisfy , the maps have to anticommute on each of the vertex of the cube. A way to do this is by multiplying edges by where j is the location of ⋆ in
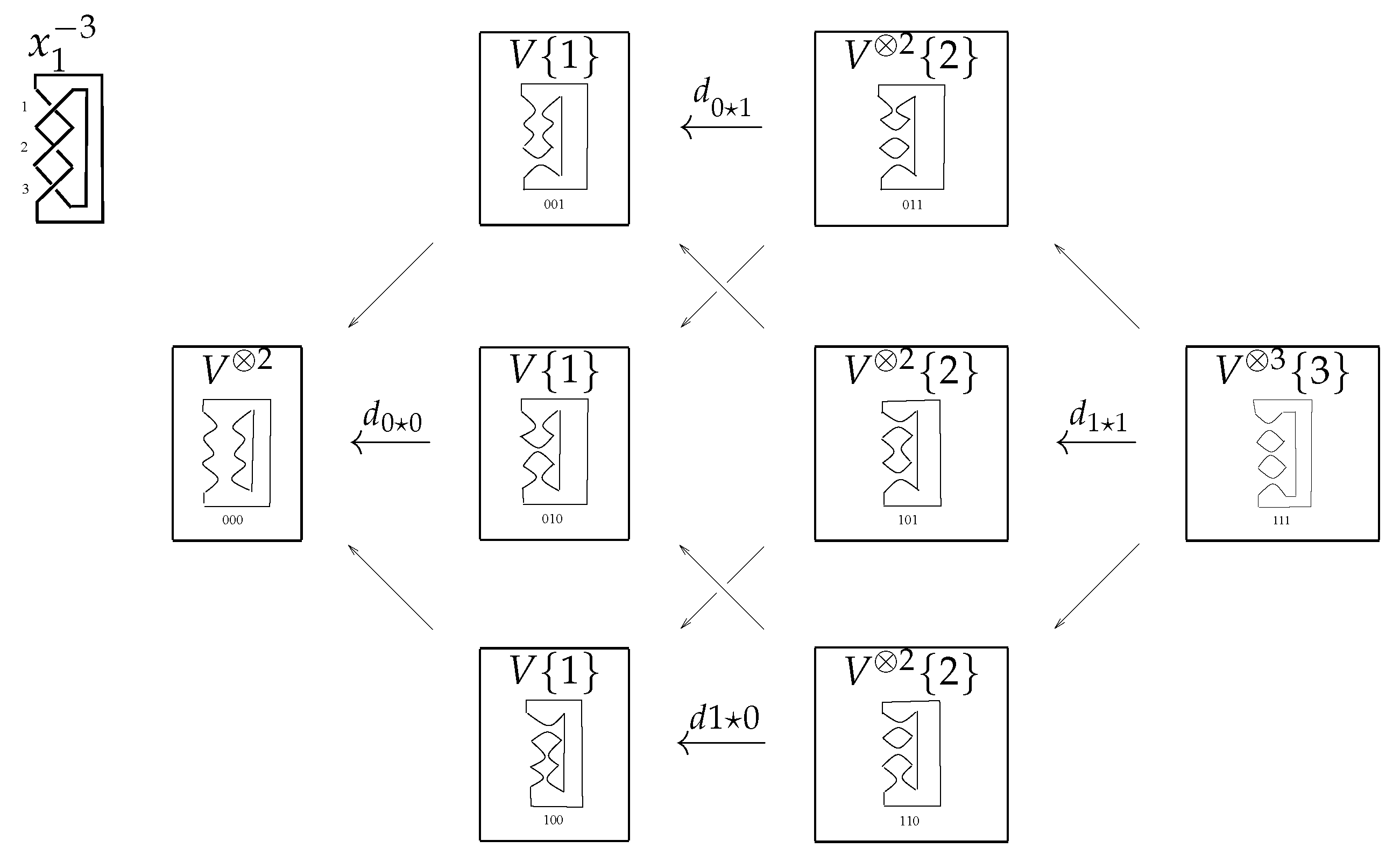
For better understanding, please see the
n-cube of trefoil knot
in
Figure 8.
It is useful to note that the ordered basis of V is and the ordered basis of is
Definition 15. Linear map that merges two circles into a single circle is defined as and
Map that divides a circle into two circles is defined as and ; see Figure 9. Definition 16. The homology group associated with the chain complex of a link L is defined as .
Definition 17. The kernel of the map , denoted by , is the set of all elements of that go to the zero element of . The elements of the kernel are called cycles, while the elements of are called boundaries.
Remark 5. Note that the image of the chain complex of is a subset of kernel as, in general,
Definition 18. The graded Poincar polynomial in variables q and t of the complex is defined as Theorem 3. (Khovanov [1]). The graded dimension of homology groups are link invariants. The graded Poincar polynomial is also a link invariant and
3.1. Homology of
Now, we give the Khovanov homology of link
![Symmetry 10 00720 i004 Symmetry 10 00720 i004]()
:
The n-cube: The 3-cube of
is given in
Figure 10:
Chain complex: The chain complex of
is
Ordered basis of the chain complex: The following are the vector spaces of the chain complex along with their ordered bases:
Differential maps in matrix form: Differential map
in terms of a matrix is:
and map
is
where
Also,
is
Khovanov Homology: On solving
or
we receive
and
So the kernel of
. Similarly, the image of
is
Thus,
To compute the homology of the next level, we first cancel out the terms that appear in both
and
, and then use a special trick: Note that the last three summands of
make up all of
, where the last three summands of
span the subspace of
generated by vectors
,
and
. Now, form a matrix whose columns are these vectors. Since the eigenvalues of this matrix are
, and 2, we can write:
Reducing the remaining matrices of kernel of
and image of
into reduced row echelon form, quotient
becomes isomorphic to
. Hence,
The range of
is
and the kernel of
is
Since
,
It is clear from the chain complex that the kernel of
is the full space
3.2. Homology of
We now compute the homology of braid link
, where
. The canonical form of this braid is
, having
factors; you can see
in
Figure 11.
The co-chain complex of the link is
We now represent the differential maps in terms of matrices. The matrix representing differential
has order
and is
Here, each matrix
, and
C has a
order:
Since
and
, the homology at this level is
Now, we go for differential map
. The matrix that represents it has an order of
and is
The order of each of the matrix
is
:
and, at the end, all rows of matrix
are zero except for the last row, which is
Here,
and
.
Since the number of spaces appear in the kernel of , it is exactly the same as the image of ,
The image of
is obvious. We just need the kernel of
. The matrix that represents
has an order of
and is
Here, the order of each
is
, and is:
Thus,
. Differential
of order
is
where
are matrices, each having an order of
Here
is the full space
and the
is
Thus, , and we finally obtain the result:
Theorem 4. The Khovanov homology of the link is The following result gives some homology groups of .
Proof. The cochain complex of link
is
Differential
having an order of
is
where
, and
C, each having an order of
, are:
Since
and
,
Now, differential
of an order of
is
where the order of each
is
and is
and
.
In this case, the kernel of and image of contain the same number of spaces. So,
Finally, the differential of
of an order of
is
where each
has an order of
and is
⋮
☐
It is evident that is full space . Moreover, is also .
We also get the Khovanov homology of braid link :
Proof. The proof is similar to the proof of Theorem 5: Obtain all states, organized them in columns, assign a graded vector space to each state, form chain groups as a direct sum of all vector spaces along a column, and form the chain complex. Then, write the differential maps in terms of matrices using the ordered bases of the chain groups, and compute their kernels and images. Finally, find the Khovanov homology groups using the relation . ☐
4. Conclusions
Although computing the Khovanov homology of links is common in the literature, no general formulae have been given for all families of knots and links. In this paper, we considered a general three-strand braid
, which, depending on the powers of Garside element
, is divided into six subclasses, and gave the Khovanov homology of
,
, and
(To learn more about these classes, see Reference [
23,
24,
25,
26].) The results particularly cover the 0th, 1st, and top homology groups of these classes, and all homology groups, in general, of link
. We hope the results will help classifying links, and in studying the important properties of these links.
 are defined, respectively, by
are defined, respectively, by  and
and 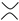 .
.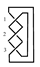 :
: