Abstract
In this paper, we compare the predictive performance of the adaptive neuro-fuzzy inference system (ANFIS) models according to the input space segmentation method. The ANFIS model can be divided into four types according to the method of dividing the input space. In general, the ANFIS1 model using grid partitioning method, ANFIS2 model using subtractive clustering (SC) method, and the ANFIS3 model using fuzzy C-means (FCM) clustering method exist. In this paper, we propose the ANFIS4 model using a context-based fuzzy C-means (CFCM) clustering method. Context-based fuzzy C-means clustering is a clustering method that considers the characteristics of the output space as well as the input space. Here, the symmetric Gaussian membership functions are obtained by the clusters produced from each context in the design of the ANFIS4. In order to evaluate the performance of the ANFIS models according to the input space segmentation method, a prediction experiment was conducted using the combined cycle power plant (CCPP) data and the auto-MPG (miles per gallon) data. As a result of the prediction experiment, we confirmed that the ANFIS4 model using the proposed input space segmentation method shows better prediction performance than the ANFIS model (ANFIS1, ANFIS2, ANFIS3) using the existing input space segmentation method.
1. Introduction
In the real world, there are active research studies on prediction in various fields such as weather, energy, communication, control, architecture, and pattern recognition. Among them, the adaptive neuro fuzzy inference system (ANFIS) model is applied to various fields as a system that combines artificial neural networks with adaptive and learning ability and fuzzy reasoning similar to the human thinking ability.
Studies that apply ANFIS models to various fields in the real world are underway. Motahari-Nezhad [1] applied ANFIS to predict the thermal contact conductance between the exhaust valve and the seat. Kaveh [2] applied ANFIS to predict the convective dryer energy consumption used to produce agricultural products. Mostafaei [3] applied ANFIS to predict cetane numbers of biodiesel fuel using a desirability function. Akib [4] applied ANFIS and linear regression (LR) to predict the depth of the insulation of sheathed file integrated bridges. Najafi [5] applied ANFIS, artificial neural networks (ANNs), and logistic methods to predict biogas production from spent mushroom compost (SMC).
Umrao [6] applied ANFIS to predict the compressive strength and elasticity of heterogeneous sedimentary rocks. Khotbehsara [7] applied ANFIS to predict SnO2 performance and ZrO2 and CaCO3 nanoparticle solution transport and self-compression characteristics. Zamani [8] applied ANFIS to predict the ratio of diesel and gas in an oil reservoir. Selimiefendigi [9] applied ANFIS to predict the convection of internal CuO–water nanofluids through the thermal cycling of a circular cylinder. Ghademejad [10] applied ANFIS to predict farmyard, multipass, and water content for clay soil compaction. Mostafaei [11] applied ANFIS to predict the characteristics of biodiesel fuel owing to fatty acid composition.
Tanrizi [12] applied ANFIS, LR, and ANN to predict body mass index. Jung [13] applied ANFIS to predict the composite index and fit index for a physical habitat simulation of freshwater fish. Vakhshouri [14] applied ANFIS to predict the compressive strength of self-compacting concrete. Zaferanlouei [15] applied ANFIS to predict the critical heat flux (CHF) to determine the economic efficiency and safety of water-cooled reactors. Zhang [16] applied ANFIS to predict the performance of a laser cutter in intelligent manufacturing mode. Najafzadeh [17] applied ANFIS to predict the debris created by the long contraction of a channel. Anusree [18] applied ANFIS, ANN, and multiple nonlinear regression (MNLR) to predict the water flow in the Karuvannur River Basin. Najafi [19] applied ANFIS and support vector machine (SVM) to predict the performance and emissions of SI (spark ignition) engines using gasoline–ethanol blended fuels.
In addition to research that applies the ANFIS model to various fields, research is being actively conducted to propose a new ANFIS model in combination with other models and methods. Pourtousi [20] proposed a bubble column hydrodynamic prediction model combining computational fluid dynamics (CFD) and ANFIS. Ali [21] proposed an ensemble-ANFIS prediction model to predict multiscalar standard precipitation indices. Liu [22] proposed a fast ensemble empirical mode decomposition (FEEMD)-ANFIS and FEEMD-MLP (Multilayer Perceptron), which is a hybrid model for wind speed prediction. Barak [23] proposed an ensemble ARIMA (auto regressive moving average) -ANFIS hybrid model for predicting energy consumption.
Zare [24] proposed a hybrid model combining wavelets and ANFIS for groundwater flow simulation prediction of the Miandarband plain. Yaseen [25] proposed a hybrid model combining the firefly algorithm and ANFIS to predict the monthly flow rate of a streamflow. Mottahedi [26] proposed an optimization model that combines particle swarm optimization (PSO) and ANFIS to predict the destruction that occurs during underground excavation. Daher [27] proposed an ANFIS model using the Parzen window membership function to predict the defects of the distillation column used in the fossil fuel process. Yadegaridehkordi [28] proposed a model combining structural equation modeling (SEM) and ANFIS to predict factors contributing to the success and development of the hotel industry in Malaysia.
Karthika [29] proposed a hybrid wavelet-ANFIS model that combines wavelets and ANFIS to predict important temperatures for agricultural production. Kassem [30] proposed an ANFIS model using a radial basis function (RBF) to predict the density of biodiesel. Thomas [31] proposed a randomized ANFIS that randomly selects the weights for earthquake prediction via ground motion parameters. Tatar [32] proposed a PSO (particle swarm optimization) -based ANFIS to predict the thermal conductivity of carbon dioxide.
In addition, performance evaluations of ANFIS models based on an input partitioning method such as the grid partitioning method and scatter partitioning method have been carried out. Vasileva-Stojanovska [33] compared the subtractive clustering (SC) method and the grid partitioning method to confirm the prediction performance according to the input space division method of the ANFIS model. Akkaya [34] compared the predictive performance of ANFIS models with input space partitioning methods to predict biomass heating prices. The input space division method used was a SC method and a fuzzy C-means (FCM) clustering method. Abdulshahed [35] compared the predictive performance of ANFIS models with input space partitioning methods to predict thermal errors in CNC (computerized numerical control) machine tools. The input space division method used is the FCM clustering method and the grid partitioning method. Mostafaei [3] predicted and compared the performance of biodiesel fuel cetane numbers using three ANFIS models using grid partitioning, subtractive clustering, and FCM clustering. Esfahanipour [36] predicted and compared the performance of the Tehran stock market using two ANFIS models using subtractive clustering and FCM clustering. Cheng [37] predicted and compared the performance of the Taiwanese stock market using two ANFIS models using subtractive clustering and FCM clustering. Malhotra [38] predicted website quality and compared performance using two ANFIS models using subtractive clustering and FCM clustering. RahimAbadi [39] estimated the condensation heat transfer coefficient and pressure drop using three ANFIS models using grid partitioning, subtractive clustering, and FCM clustering and compared their performance. The existing comparative studies of the above ANFIS models focus on influential input variable selection and the input space division method. Among them, the input space division methods generally used in comparison are the SC and FCM clustering methods of the gird partitioning and scatter partitioning methods.
In this paper, we compare and analyze the prediction performance of four ANFIS models by adding an ANFIS model based on the context-based fuzzy C-means (CFCM) clustering method, which is a new input space partitioning method. An ANFIS1 is an ANFIS model that uses the grid partitioning method, and ANFIS2 is an ANFIS model using the SC method, which is a scatter partitioning method. An ANFIS3 is an ANFIS model using the FCM clustering method, and ANFIS4 is an ANFIS model using the CFCM clustering method.
To verify the predictive performance of the four ANFIS models, experiments were conducted using a combined cycle power plant (CCPP) database and an Auto-MPG database. The CCPP database was collected from within the plant from 2006 to 2011 where the plant was set to operate at maximum load, and was used to predict the electrical energy output over time with average temperature, ambient pressure, relative humidity, and discharge vacuum time. The Auto-MPG database was used to predict the vehicle fuel consumption based on the number of cylinders, displacement, horsepower, weight, acceleration, and model year.
The composition of this paper is as follows. Section 1 describes the background of the study, and Section 2 describes the ANFIS model. Section 3 explains each ANFIS model according to the input space division method. Section 4 describes the prediction and analysis of the electric energy production of the combined power plant using the abovementioned ANFIS1, ANFIS2, ANFIS3, and ANFIS4 with the CCPP database. Finally, Section 5 contains conclusions and future research plans.
2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
Fuzzy inference [40] is effective in processing ambiguous and uncertain information by processing it in a similar way to human thinking, but it does not have learning ability. Artificial neural networks [41] have excellent learning ability, but they do not produce rule-based knowledge. A neuro-fuzzy inference system is constructed by fusing these fuzzy inferences and artificial neural networks to complement the disadvantages of each method. The neuro-fuzzy inference system generates an if-then fuzzy rule through fuzzy inference and optimizes the prediction performance by updating the parameters used in the fuzzy rule by applying the learning ability of the neural network. Because of these advantages, the neuro-fuzzy inference system is widely applied to various fields such as system control, pattern recognition, disease diagnosis, and energy efficiency prediction.
2.1. Structure of Adaptive Neuro-Fuzzy Inference System (ANFIS)
Neuro-fuzzy inference systems are classified into two types according to the combination of fuzzy inference and artificial neural network. In the first type, the artificial neural network integrates fuzzy inference, whereas in the second, fuzzy inference integrates the artificial neural network. Among the methods of the second type, fuzzy reasoning has been actively studied as a method for integrating artificial neural networks, which is classified into the Mamdani system [42] and the Takagi–Sugeno system [43,44]. The Mamdani system has the form of a fuzzy set at the conclusion of the rule, and the Takagi–Sugeno system has the form of a first-order linear equation of the input variable at the conclusion of the rule. Among them, the Takagi–Sugeno system is efficient in terms of computational ability, is adaptable to generating rules in combination with the optimization method of the artificial neural network and has the advantage of ensuring the continuity of the output space. Because of the above advantages, we choose the Takagi–Sugeno system in the ANFIS model to create and infer rules.
The ANFIS model is a type of neuro-fuzzy inference system proposed by Jang [45,46]. The ANFIS model can optimally estimate the parameters included in the membership functions and output by using the least square method (LSE) and back propagation (BP) algorithms for given input and output data. The fuzzy inference process is described briefly through a model consisting of Takagi–Sugeno rules with two inputs and one output, and the output of a first-order linear equation.
Here, and represent input variables, and and are fuzzy sets of . Similarly, and represent fuzzy sets of , and , , and represent sets of arguments set in rule . Figure 1 shows the ANFIS model, a structure of a forward network consisting of five layers with two input variables and four fuzzy rules. The nodes in each layer of the ANFIS model have different functions, which are optimized through the learning process. The connection line between the node and the node shows only the direction of flow between the nodes and does not have a weight. Next, each floor structure and procedure of the ANFIS model are explained.
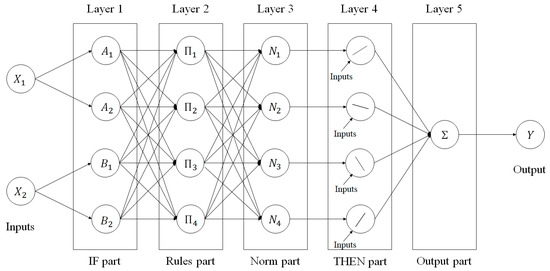
Figure 1.
Structure of an adaptive neuro-fuzzy inference system (ANFIS).
- Layer 1: In the first layer, each node can output a value belonging to a linguistic level as an output, as shown in Equation (2).The preconditioned membership function selects and uses a Gaussian membership function, as shown in Equation (3).In addition to the Gaussian membership function, various membership functions can be used, and parameter values that minimize the error are selected through the learning process.
- Layer 2: In the second layer, each node receives the membership value shown in the conditional part of the fuzzy rule, and outputs it as the weight multiplied by the rule. The output of each node represents the fitness of the fuzzy rule.
- Layer 3: In the third layer, each node calculates the ratio of the ignition forces of the th rule to the sum of all ignition forces through Equation (5). The value obtained is represented as a normalized value.
- Layer 4: In the fourth layer, each node performs an operation that multiplies the output function of the conclusion part of each rule by the standardized fitness.where is the output of Layer 3, and the parameters of the output function , , and denote the conclusion parameters.
- Layer 5: In the fifth and last layer, each node is composed of a single node. Based on all input values of the lower layer, the output value is calculated using Equation (7). The output value has a continuous-type value rather than a fuzzy set type.
2.2. Learning Method of Adaptive Neuro-Fuzzy Inference System (ANFIS)
The ANFIS model uses a hybrid learning method [45] that combines the least square method and a back propagation algorithm for learning. The hybrid learning method updates the conditional and conclusion parameters of the rule so that the error of the output can be minimized using given input and output data. The conditional parameters have a nonlinear structure, and the conclusion parameters have a linear structure. This learning method consists of forward learning and reverse learning. The forward learning process uses LSE to fix the conditional parameters and optimize the conclusion parameters. When the optimal conclusion parameter is obtained in the forward learning process, the reverse learning process is performed. The backward learning process uses the gradient descent method to optimize the parameters placed in the conditional part of the rule that defines the membership function. The above process is repeated until the error threshold of the ANFIS model is reached or when the number of repetitions specified by the user is reached. Figure 2 shows the learning process of the ANFIS model.
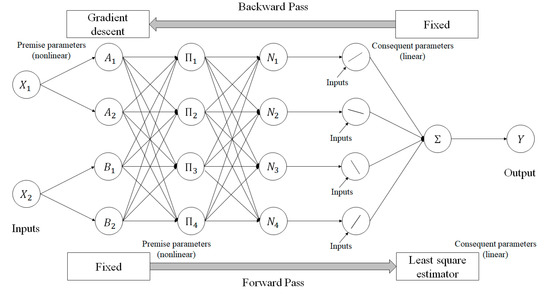
Figure 2.
Structure method of an adaptive neuro-fuzzy inference system (ANFIS).
3. Fuzzy Rule Generation Method According to Input Space Partitioning Method
In the ANFIS model, the fuzzy inference process consists of a divide-and-conquer method that divides the -dimensional input space composed of input variables into specific regions and computes the result of inference in each specific region. In other words, the conditional part of the fuzzy rule divides the input space into specific areas, and the conclusion part of the fuzzy rule has the inference result in each specific area. Thus, creating a fuzzy rule is closely related to how the input space is divided. In the ANFIS model, the grid partitioning method and scatter partitioning method are used to divide -dimensional space composed of input variables. Figure 3 shows the grid partitioning method of the input space division method. Next, ANFIS using grid partitioning (ANFIS1), ANFIS using SC (ANFIS2), ANFIS using FCM clustering (ANFIS3), and ANFIS using CFCM clustering (ANFIS4) will be described.
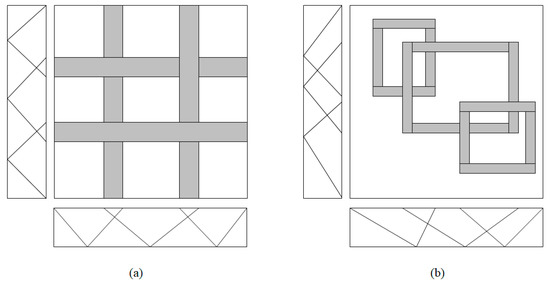
Figure 3.
Input space partitioning methods: (a) grid partitioning method and (b) scatter partitioning method.
3.1. Grid Partitioning Method
Grid partitioning [46] is a method of dividing a space into a grid-like structure so that overlapping parts do not occur in the input space. In general, when the grid partitioning method is applied, the specific partitioned area, that is, the area having the fuzzy rule, is uniformly generated so that the fuzzy rule is smoothly analyzed. Grid partitioning is the method used when the number of input variables is small, that is, when the dimension of the input space is low. For a simple example, when there are 10 input variables and each input variable is divided into two member functions, it is divided into specific areas. In other words, one rule is created for each specific area, and the total number of rules is 1024, which is a very complicated structure. Therefore, the grid partitioning method is mainly used when the number of input variables is small.
3.2. Scatter Partitioning Method
The scatter partitioning method is used to compensate the disadvantage that the number of rules increases exponentially as the input variable of the grid partitioning method described above increases. The scatter partitioning method divides the input space into clusters through a clustering algorithm. A specific area is divided by the number of clusters, and the number of each specific area is the number of fuzzy rules. Therefore, the number of rules in the scatter partitioning method is the number of clusters, and there is a strong advantage in terms of the number of input variables. The scatter partitioning method is divided into various kinds according to the clustering algorithm. In this paper, we use subtractive clustering (SC), fuzzy C-means (FCM) clustering, and context-based fuzzy C-means (CFCM) clustering.
3.2.1. Subtractive Clustering (SC)
Subtractive clustering (SC) [47,48] is a method of dividing an input space into n subdivided specific areas by analyzing n-dimensional input data to create clusters. The SC method divides the input space into appropriate clusters even if the user does not specify the number of clusters. The user sets the radius of the cluster, which is the range of influence from the center of the cluster when the input space is considered as a unit hypercube, and has a value between 0 and 1. If the radius of a cluster is set too small, the size of the cluster becomes small, so that the number of clusters increases, thus increasing the number of fuzzy rules. By contrast, if the radius of the cluster is set to be large, the size of the cluster becomes large, so that the number of clusters decreases and the number of fuzzy rules also becomes small. Figure 4 shows the SC method in which clusters are generated according to the cluster radius. The red dots represent the data, and the black dots represents the center of the cluster. Next, the procedure of the SC method will be described.
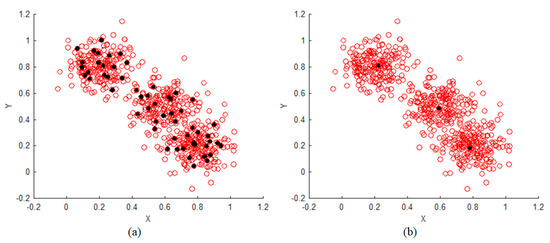
Figure 4.
Subtractive clustering method: (a) cluster radius = 0.1 and (b) cluster radius = 0.5.
- Step 1: The density of each data item in the input space is calculated using the density function of Equation (8).Here, is a positive constant and represents the radius of the cluster that the user can set.
- Step 2: Finds , which are the data having the highest density value from , and this value becomes the center value of the first cluster.
- Step 3: The center of the cluster found in Step 2 is removed by Equation (9).Here, is a constant having a positive value and represents the radius of the elimination function. represents the density measurement value of calculated in Step 2.
- Step 4: Repeat Step 2 to Step 3 until the highest density measurement value is smaller than the set value.
3.2.2. Fuzzy C-Means (FCM) Clustering
The fuzzy C-means (FCM) clustering method is based on a fuzzy set and LSE by improving the C-means clustering method proposed by Bezdek [49,50]. The FCM clustering method is a method of dividing a subdivided specific area by enumerating the values belonging to data of the cluster according to the degree of membership of each data item belonging to one cluster. The FCM clustering method divides a set of m vectors into fuzzy clusters and finds the center within each cluster as the objective function of the non-similarity measure is minimized. In existing clustering methods, arbitrary data belong to one cluster, which has a 0 or 1 degree of affiliation. However, in the FCM clustering method, there is a difference in the degree of membership of arbitrary data between 0 and 1, and they belong to clusters. The user sets the number of clusters, where the number of clusters is the number of fuzzy rules.
Figure 5 shows the FCM clustering method in which clusters are generated according to the number of clusters. The red dot represents the data, and the black dot represents the center of the cluster. Next, the procedure of the FCM clustering method will be described.
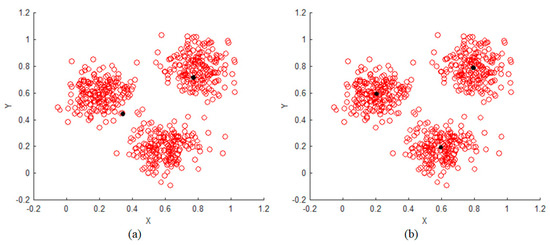
Figure 5.
Fuzzy C-means clustering method: (a) number of clusters = 2 and (b) number of clusters = 3.
- Step 1: Initialize the parameter and the membership matrix to have a random value between 0 and 1 satisfying Equation (10).Here, the distance calculation between the input data and the center of the cluster is obtained by the Euclidean norm.
- Step 2: The center value of the new cluster is calculated by the value of the input data and the previously obtained membership function .
- Step 3: Using the center value obtained in Step 2 and the input data , the membership matrix is continuously updated while increasing the number of iterations .
- Step 4: The above procedure is repeated until the error of the repeated membership matrix and is smaller than the arbitrary threshold value .
3.2.3. Context-Based Fuzzy C-Means (CFCM) Clustering
Context-based fuzzy C-means (CFCM) clustering is a method proposed by Pedrycz [51] to partition clusters by creating clusters to maintain characteristics of patterns related to the similarity of output variables as well as the data of input spaces. A typical clustering method does not take into account the pattern of output variables, but only clusters are created using the Euclidean distance between the cluster center and the input data. On the other hand, since the CFCM clustering method generates the clusters considering not only the patterns of the input data but also the patterns of the output variables, the space can be more accurately divided than in the conventional clustering method.
Figure 6 shows the difference between the FCM clustering method and the CFCM clustering method. When there is data in the input space, FCM clustering method creates two clusters because it assigns the initial center value and creates clusters using only Euclidean distance between center and data. On the other hand, the CFCM clustering method considering the output variable pattern generates three clusters considering that the data in the input space have black and white characteristics.
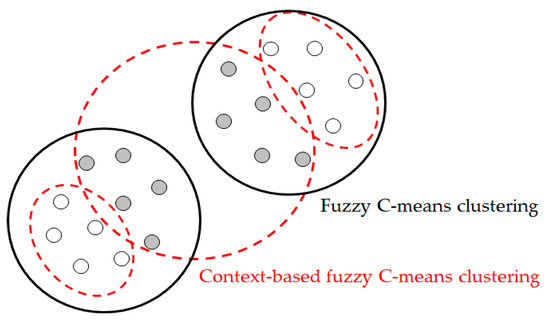
Figure 6.
Difference between FCM (fuzzy c-means) clustering method and CFCM (context-based fuzzy c-means) clustering method.
In the CFCM clustering method, the user needs to set the number of contexts and the number of clusters. As a simple example, if the number of contexts is set to six and the number of clusters to three, the number of fuzzy rules is 18. The reason is that 6 × 3 = 18 because clusters are created in each context. Figure 7 shows the CFCM clustering method in which clusters are created by setting the number of contexts (P) and the number of clusters (C) to six and three, respectively. (a) Shows the context of each triangle, and in (b), the red dot represents the data and the black dot represents the center of the cluster. Next, we explain the procedure and pseudocode of the CFCM clustering method.
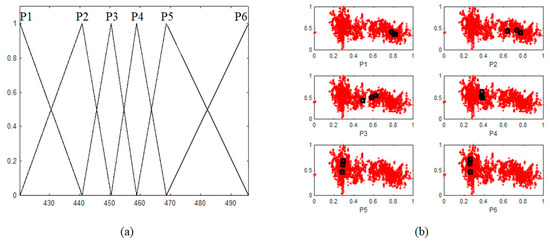
Figure 7.
Context-based fuzzy C-means clustering method: (a) contexts generated from output space, and (b) center of cluster corresponding to each context.
- Step 1: Let and the number of clusters be set.
- Step 2: Set the initial partitioning matrix and the threshold , and choose the number of iterations.
- Step 3: Compute the center of each cluster using the membership matrix and Equation (16).
- Step 4: The partitioning matrix is updated using the center value of the cluster and Equation (17).Here, represents the inclusion degree of in the generated cluster. In other words, the linguistic form defined in the output variable is expressed as a fuzzy set and computed by a fuzzy equalization algorithm. Then, can be represented by the membership value of in .
- Step 5: If is satisfied, the above procedure is stopped. If not, proceed from Step 3 again.
The CFCM clustering method described above is applied to the ANFIS model as follows. The data in the input space of layer 1 is divided into input space through CFCM clustering method which considers the pattern of output variable and outputs the belonging value. In layer 2, we take the value belonging to the previous layer, output the weights multiplied by the rule, and express the ratio of the impulse force in layer 3 as the normalized value. Multiply the normalized value at layer 4 by the output function of the conclusion, and calculate the final output using weighted average at layer 5. The following algorithm is a pseudocode of CFCM clustering.


| CFCM (context-based fuzzy c-means) Clustering Algorithm |
| Begin |
| Fixed ; |
| Fixed ; |
| Fixed ; |
| Fixed max iterations; |
| Randomly initialize ; |
| for to max iterations do |
| Update the membership matrix using Equation (12); |
| Calculate the new cluster lefts using Equation (10); |
| Calculate the new objective function using Equation (13); |
| if then |
| break; |
| else |
| ; |
| end if |
| end for |
| end |
4. Experimental Method and Result Analysis
In order to evaluate the prediction performance of the ANFIS model using each of the input space partitioning methods described in Section 3, we conducted an experiment to predict the electric energy generation of a combined power plant using the CCPP database.
4.1. Database
The CCPP database [52] is a database that was collected for six years from 2006 to 2011, when combined power plants were set to operate at full load. The database is made up of data sheet (.xls) files and has a total of five sheets. The size of one sheet is 5 × 9568. It has four input variables and one output variable. The input variables consist of the time average ambient temperature (AT), ambient pressure (AP), relative humidity (RH), and exhaust vacuum (V). The output variable represents the electrical energy (EP) generated per hour in a combined power plant. In this experiment, the data of sheet1 were used, and divided into the training data and verification data in the ratio of 50:50, by randomly selecting the data. To obtain a more uniform value, the data were normalized to values between 0 and 1 through a normalization process.
The Auto-MPG database [53] was derived for different types of automobiles with vehicle fuel consumption. It is provided in the StatLib library maintained by Carnegie Mellon University. It was first used in the American Statistical Association Exposition in 1983 and is a benchmark database frequently used in predictive experiments. The data size is 392 × 8, and it has seven input variables and one output variable. Input variables include the number of cylinders, displacement, horsepower, weight, acceleration, model year, and vehicle model name. In this experiment, six input variables were used except for the automobile model name. The output variable was the fuel consumption of the vehicle. The Auto-MPG data were also divided into learning and verification data in the ratio of 50:50, and the data were normalized to values between 0 and 1. Figure 8 shows the correlation of input variables of the CCPP data [54]. The x-axis in Figure 8 is composed of four plots, showing the time-averaged ambient temperature (AT), ambient pressure (AP), relative humidity (RH), and exhaust vacuum (V) from left to right. The y-axis consists of four plots, showing the average ambient temperature (AT), ambient pressure (AP), relative humidity (RH), and exhaust vacuum (V) over time in order from top to bottom.
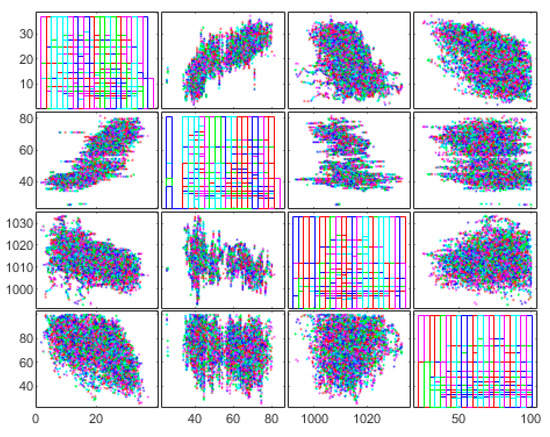
Figure 8.
Correlation of input variables of CCPP (combined cycle power plant) data.
4.2. Experiment Method
The experimental procedure is as follows. The prediction performance of each ANFIS model is compared according to four different input space division methods.
First, in the experiment using the ANFIS1 model, influential input variables were selected from the input variables, and the input variables were recombined and used in the experiment. In the input variable recombination method, the number of input variables to be used was specified, and the combination of input variables was used in which the verification RMSE (root means square error) value was the lowest. The first input combination used two influential input variables among the total input variables, the second input combination used three influential input variables among the total input variables, and finally, all the input variables were used. In the grid partitioning method, the membership function (MF) increased from 2 to 5 by 1, and the estimation performance was confirmed.
In the ANFIS2 model, the radius of the SC was increased from 0.2 to 0.9 by 0.1. In the experiment using the ANFIS3 model, the number of clusters and the fuzzification coefficient were set in the FCM clustering method. The number of clusters was increased from 5 to 50 by 5, and the fuzzification coefficient was fixed at 1.5 to confirm the prediction performance. Finally, in the experiment using the ANFIS4 model, the number of contexts (p), number of clusters (c), and the fuzzification coefficient were set in the CFCM clustering method. First, the number of contexts was fixed at 6 and 10, the number of clusters was increased from 2 to 20 by 1, and the fuzzification coefficients were fixed at 1.5. Each experiment was repeated 10 times.
The predictive performance was expressed as the root mean square error (RMSE). The RMSE can be expressed as Equation (19) as a prediction measure used to represent the difference between the estimated value or the value obtained from the prediction model and the observed value in the actual environment. The RMSE values are rounded to two decimal places.
Here, represents a result value, and represents an actual value. When , the prediction performance is 100% and the RMSE value becomes zero. Therefore, if the RMSE value is large, it indicates that the prediction performance is poor, and when it is small, it indicates that the prediction performance is good. Figure 9 shows how to select two input variables out of four input variables in the CCPP data.
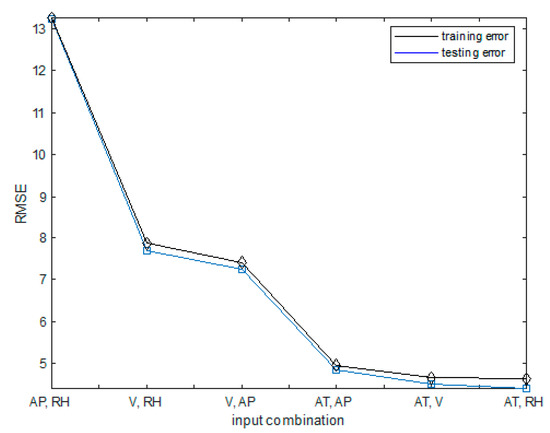
Figure 9.
Input variable recombination method.
4.3. Combined Cycle Power Plant Database
Table 1 lists the results for the ANFIS1 model using CCPP data. The two inputs of AT and RH were used when two input variables were used, and AT, V, and AP were used when three input variables were used. When three input variables were used and MF was set to 5, the model showed the best performance. Table 2 lists the results for the ANFIS2 model. The ANFIS2 model using the SC method showed the best performance when the radius of the cluster was set to 0.3.

Table 1.
Experimental results of ANFIS1 model. RMSE (root-mean square error), AT (time-averaged ambient temperature), AP (ambient pressure), RH (relative humidity), and V (exhaust vacuum), ANFIS (adaptive neuro-fuzzy inference system).

Table 2.
Experimental results of ANFIS2 model.
Figure 10 shows the RMSE values of the ANFIS1 model using the test data, and Figure 11 shows the RMSE values of the ANFIS2 model using the test data.
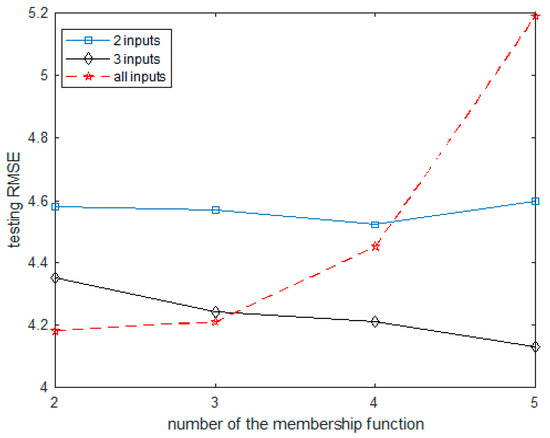
Figure 10.
The RMSE value obtained from ANFIS1 using test data.
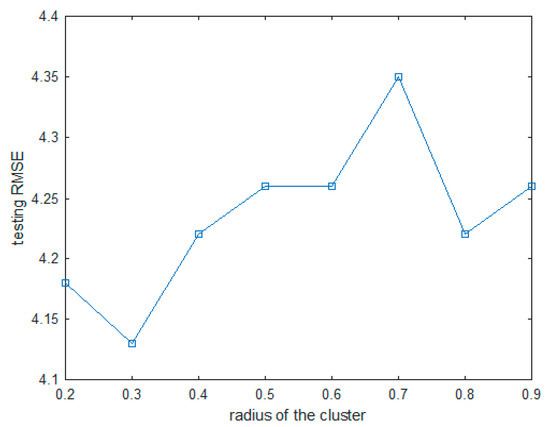
Figure 11.
The RMSE value obtained from ANFIS2 using test data.
Table 3 lists the results for the ANFIS3 model. The ANFIS3 model using the FCM clustering method showed the best performance when the number of clusters was set to 30. Table 4 lists the results for the ANFIS4 model. The ANFIS4 model performed two experiments with fixed contexts of 6 and 10. Among them, when the context was fixed to 10 and the number of clusters was set to 17, the best performance was shown. Figure 12 and Figure 13 show the RMSE values of the ANFIS3 and ANFIS4 models using the test data.

Table 3.
Experimental results of ANFIS3 model.

Table 4.
Experimental results of ANFIS4 model.
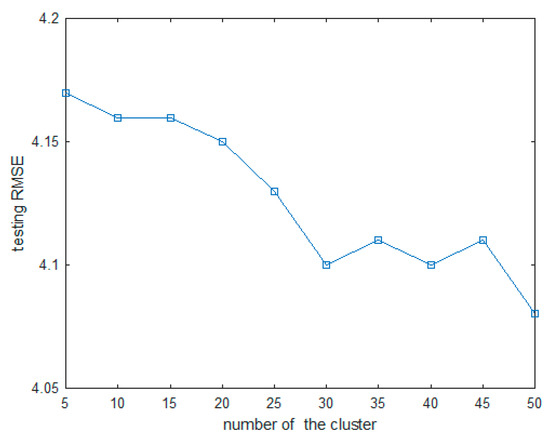
Figure 12.
The RMSEs value obtained from ANFIS3 using test data.
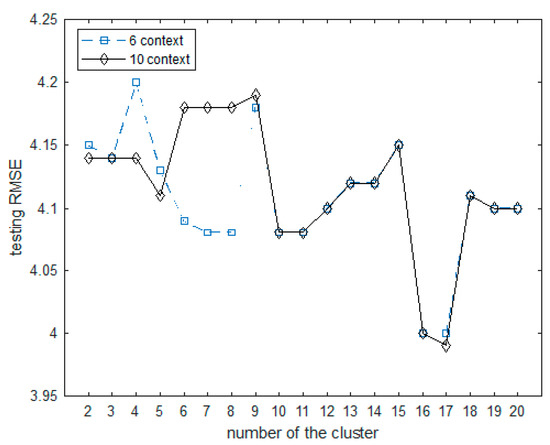
Figure 13.
RMSE values obtained from ANFIS4 using test data.
Table 5 summarizes the prediction performance of each ANFIS model. When the context of the ANFIS4 model was fixed to 10 and the number of clusters was set to 17, 170 rules were generated and the testing RMSE value was 3.99. Figure 14 shows the best prediction performance for each ANFIS model. In Figure 14, the x-axis represents the respective ANFIS models, where 1 represents the ANFIS1 model, 2 represents the ANFIS2 model, 3 represents the ANFIS3 model, and 4 represents the ANFIS4 model.

Table 5.
Analysis of prediction performance of entire ANFIS model.
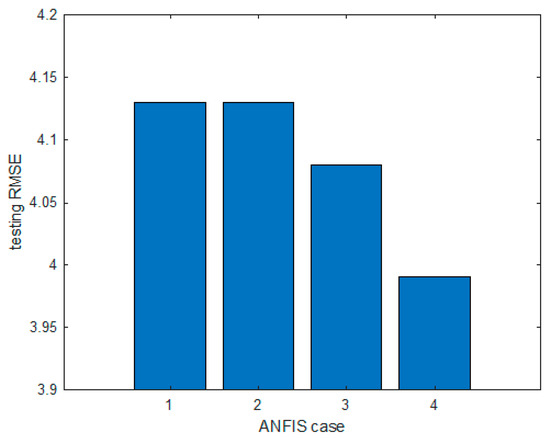
Figure 14.
The RMSE values obtained from ANFIS1, 2, 3, and 4 using testing data.
4.4. Auto-MPG Database
Table 6 lists the results for the ANFIS1 model using Auto-MPG data. We used the displacement and acceleration force when two input variables were used, and the displacement, weight, and acceleration force when three input variables were used. When four input variables were used, the displacement, horsepower, weight, and acceleration were used. When three input variables were used and MF was set to 2, the model showed the best performance. Figure 15 shows the RMSE values of the ANFIS1 model using the test data. The results of the ANFIS2 model are listed in Table 7. The ANFIS2 model using the SC method showed the best performance when the radius of the cluster was set to 0.8. Figure 16 shows the RMSE values of the ANFIS2 model using the test data.

Table 6.
Experimental results of ANFIS1 model.
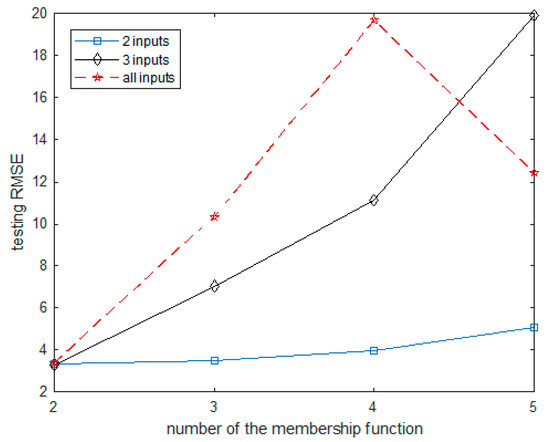
Figure 15.
The RMSE values obtained from ANFIS1 using testing data.

Table 7.
Experimental results of ANFIS2 model.
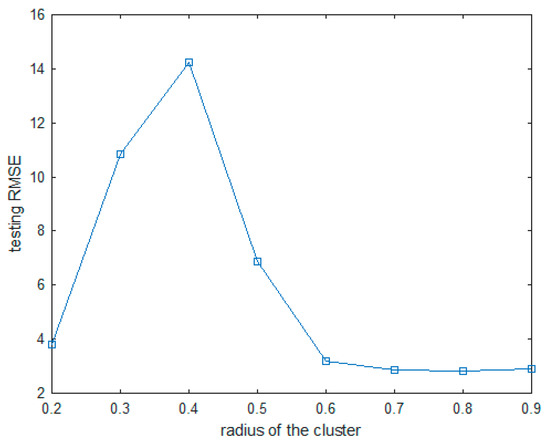
Figure 16.
The RMSE values obtained from ANFIS2 using testing data.
The results for the ANFIS3 model are listed in Table 8. The ANFIS3 model using the FCM clustering method showed the best performance when the number of clusters was set to 5. The results for the ANFIS4 model are listed in Table 9. The ANFIS4 model performed two experiments with fixed contexts of 6 and 10. Among them, when the context was fixed to 6 and the number of clusters was set to 4, the best performance was shown. Figure 17 and Figure 18 show the RMSE values of the ANFIS3 and ANFIS4 models using the test data.

Table 8.
Experimental results of the ANFIS3 model.

Table 9.
Experimental results of the ANFIS4 model.
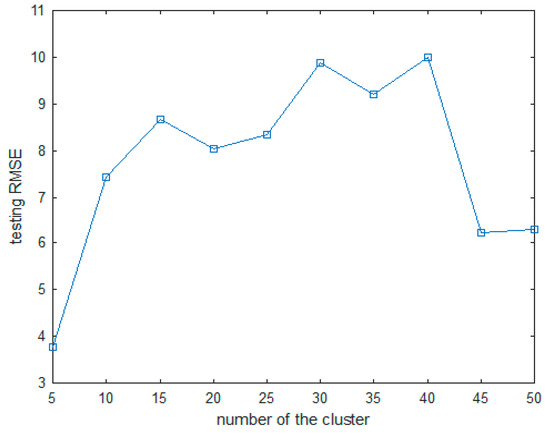
Figure 17.
The RMSE values obtained from ANFIS3 using tests data.
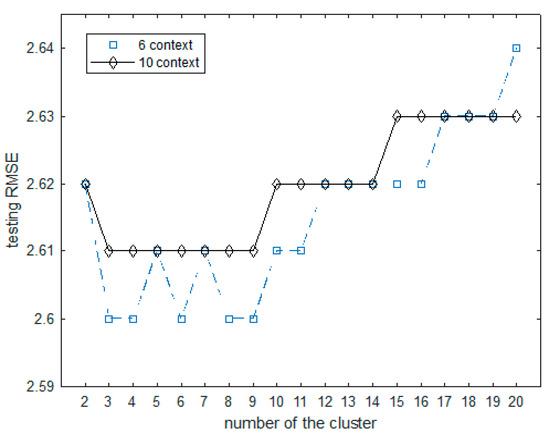
Figure 18.
RMSE values obtained from ANFIS4 using test data.
Table 10 summarizes the prediction performance of each ANFIS model. When the context of the ANFIS4 model was fixed to six and the number of clusters was set to four, 24 rules were generated and the testing RMSE value was 2.60. Figure 19 shows the best prediction performance for each ANFIS model. In Figure 19, the x-axis represents each ANFIS model, where 1 represents the ANFIS1 model, 2 represents the ANFIS2 model, 3 represents the ANFIS3 model, and 4 represents the ANFIS4 model.

Table 10.
Analysis of prediction performance of the entire ANFIS model.
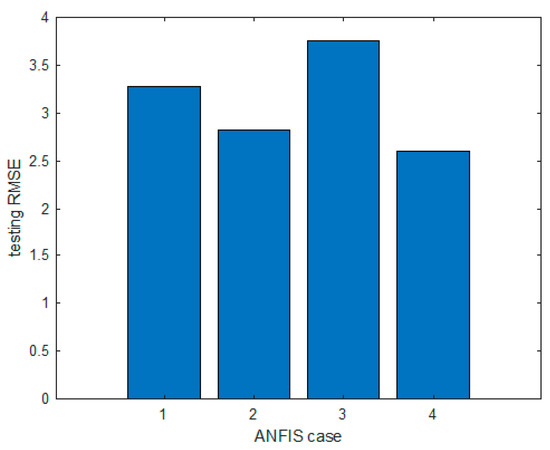
Figure 19.
The RMSE values obtained from ANFIS1, 2, 3, and 4 using testing data.
5. Conclusions
This paper compared and analyzed the prediction performance of four ANFIS models using different input space partitioning methods. As the input partitioning methods, the SC method, FCM clustering method, and CFCM clustering method were used from among the grid partitioning and scatter partitioning methods. The experimental results showed that the ANFIS4 model using the proposed CFCM clustering method exhibited a better predictive performance than the existing ANFIS models. Through this experiment, we noticed that a large number of rules was not a good thing, but an effective necessity. As a future research plan, we will study a method to improve the prediction performance by optimizing the internal parameters of the CFCM clustering method, and study a new input space division method using another clustering method.
Author Contributions
C.-U.Y. suggested the idea of the work and performed the experiments; K.-C.K. designed the experimental method; both authors wrote and critically revised the paper.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2017R1A6A1A03015496) (No. 2018R1D1A1B07044907). This work was supported by the Human Resources Program in Energy Technology of the Korea Institute of Energy Technology Evaluation and Planning (KETEP), which was granted financial resources from the Ministry of Trade, Industry, and Energy (No. 20174030201620).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Motahari-Nezhad, M.; Mazidi, M.S. An adaptive neuro-fuzzy inference system (ANFIS) model for prediction of thermal contact conductance between exhaust valve and its seat. Appl. Therm. Eng. 2016, 105, 613–621. [Google Scholar] [CrossRef]
- Kaveh, M.; Sharabiani, V.R.; Chayjan, R.A.; Taghinezhad, E.; Abbaspour-Gilandeh, Y.; Golpour, I. ANFIS and ANNs model for prediction of moisture diffusivity and specific energy consumption potato, garlic and cantaloupe drying under convective hot air dryer. Inf. Process. Agric. 2018, 5, 372–387. [Google Scholar] [CrossRef]
- Mostafaei, M. ANFIS models for prediction of biodiesel fuels cetane number using desirability function. Fuel 2018, 216, 665–672. [Google Scholar] [CrossRef]
- Akib, S.; Mohammadhassani, M.; Jahangizadeh, A. Application of ANFIS and LR in prediction of scour depth in bridges. Comput. Fluids 2014, 91, 77–86. [Google Scholar] [CrossRef]
- Najafi, B.; Ardabili, S.F. Application of ANFIS, ANN, and logistic methods in estimating biogas production from spent mushroom compost. Resour. Conserv. Recycl. 2018, 133, 169–178. [Google Scholar] [CrossRef]
- Umrao, R.K.; Sharma, L.K.; Singh, R.; Singh, T.N. Determination of strength and modulus of elasticity of heterogenous sedimentary rocks: An ANFIS predictive technique. Measurement 2018, 126, 194–201. [Google Scholar] [CrossRef]
- Khotbehsara, M.M.; Miyandehi, B.M.; Naseri, F.; Ozbakkaloglu, T.; Jafari, F.; Mohseni, E. Effect of SnO2, ZrO2, and CaCO3 nanoparticles on water transport and durability properties of self-compacting mortar containing fly ash: Experimental observations and ANFIS predictions. Constr. Build. Mater. 2018, 158, 823–834. [Google Scholar] [CrossRef]
- Zamani, H.; Rafiee-Taghanaki, S.; Karimi, M.; Arabloo, M.; Dadashi, A. Implementing ANFIS for prediction of reservoir oil solution gas–oil ratio. J. Nat. Gas Sci. Eng. 2015, 25, 325–334. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Magnetic field effects on the forced convection of CuO—Water nanofluid flow in a channel with circular cylinders and thermal predictions using ANFIS. Int. J. Mech. Sci. 2018, 146–147, 9–24. [Google Scholar] [CrossRef]
- Ghadernejad, K.; Shahgholi, G.; Mardani, A.; Chiyaneh, H.G. Prediction effect of farmyard manure, multiple passes and moisture content on clay soil compaction using adaptive neuro-fuzzy inference system. J. Terramech. 2018, 77, 49–57. [Google Scholar] [CrossRef]
- Mostafaei, M. Prediction of biodiesel fuel properties from its fatty acids composition using ANFIS approach. Fuel 2018, 229, 227–234. [Google Scholar] [CrossRef]
- Tabrizi, S.S.; Scancar, N. Prediction of body mass index: A comparative study of multiple linear regression, ANN and ANFIS models. Procedia Comput. Sci. 2017, 120, 394–401. [Google Scholar] [CrossRef]
- Jung, S.H.; Choi, S.U. Prediction of composite suitability index for physical habitat simulations using the ANFIS method. Appl. Soft Comput. 2015, 34, 502–512. [Google Scholar] [CrossRef]
- Vakhshouri, B.; Nejadi, S. Prediction of compressive strength of self-compacting concrete by ANFIS models. Neurocomputing 2018, 280, 13–22. [Google Scholar] [CrossRef]
- Zaferanlouei, S.; Rostamifard, D.; Satayeshi, S. Prediction of critical heat flux using ANFIS. Ann. Nucl. Energy 2010, 37, 813–821. [Google Scholar] [CrossRef]
- Zhang, Y.I.; Lei, J.H. Prediction of laser cutting roughness in intelligent manufacturing mode based on ANFIS. Procedia Eng. 2017, 174, 82–89. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Etemad-Shahidi, A.; Lim, S.Y. Scour prediction in long contractions using ANFIS and SVM. Ocean Eng. 2016, 111, 128–135. [Google Scholar] [CrossRef]
- Anusree, K.; Varghese, K.O. Streamflow prediction of Karuvannur River basin using ANFIS, ANN and MNLR models. Procedia Technol. 2016, 24, 101–108. [Google Scholar] [CrossRef]
- Najafi, G.; Ghobadian, B.; Moosavian, A.; Yusaf, T.; Mamat, R.; Kettner, M.; Azmi, W.H. SVM and ANFIS for prediction of performance and exhaust emissions of an SI engine with gasoline-ethanol blended fuels. Appl. Therm. Eng. 2016, 95, 186–203. [Google Scholar] [CrossRef]
- Pourtousi, M.; Sahu, J.N.; Ganesan, P.; Shamshirband, S.; Redzwan, G. A combination of computational fluid dynamics (CFD) and adaptive neuro-fuzzy system (ANFIS) for prediction of the bubble column hydrodynamics. Powder Technol. 2015, 274, 466–481. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Downs, N.J.; Maraseni, T. An ensemble—ANFIS based uncertainty assessment model for forecasting multi-scalar standardized precipitation index. Atmos. Res. 2018, 207, 155–180. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of new hybrid FEEMD–MLP. FEEMD–ANFIS, wavelet packet–MLP and wavelet—ANFIS for wind speed predictions. Energy Convers. Manag. 2015, 89, 1–11. [Google Scholar] [CrossRef]
- Barak, S.; Sadegh, S.S. Forecasting energy consumption using ensemble ARIMA-ANFIS hybrid algorithm. Int. J. Electr. Power 2016, 82, 92–104. [Google Scholar] [CrossRef]
- Zare, M.; Koch, M. Groundwater level fluctuations simulation and prediction by ANFIS- and hybrid wavelet-ANFIS/fuzzy C–means (FCM) clustering models: Application to the Miandarband plain. J. Hydro-Environ. Res. 2018, 18, 63–76. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ebtehaj, I.; Bonakdari, H.; Deo, R.C.; Mehr, A.D.; Mohtar, W.H.M.W.; Diop, L.; El-shafie, A.; Singh, V.P. Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. J. Hydrol. 2017, 554, 263–276. [Google Scholar] [CrossRef]
- Matttahedi, A.; Sereshki, F.; Ataei, M. Overbreak prediction in underground excavations using hybrid ANFIS-PSO model. Tunn. Undergr. Space Technol. 2018, 80, 1–9. [Google Scholar] [CrossRef]
- Daher, A.; Hoblos, G.; Khalil, M.; Chetouani, Y. Parzen window distribution as new membership function for ANFIS algorithm–application to a distillation column faults prediction. Chemom. Intell. Lab. Syst. 2018, 175, 1–12. [Google Scholar] [CrossRef]
- Yadegaridehkordi, E.; Nilashi, M.; Nasir, M.H.N.B.M.; Ibrahim, O. Predicting determinants of hotel success and development using structural equation modeling (SEM)–ANFIS method. Tour. Manag. 2018, 66, 364–386. [Google Scholar] [CrossRef]
- Karthika, B.S.; Deka, P.C. Prediction of air temperature by hybridized model (wavelet–ANFIS) using wavelet decomposed data. Aquatic Procedia 2015, 4, 1155–1161. [Google Scholar] [CrossRef]
- Kassem, Y.; Camur, H. Prediction of biodiesel density for extended ranges of temperature and pressure using adaptive neuro-fuzzy inference system (ANFIS) and radial basis function (RBF). Procedia Comput. Sci. 2017, 120, 311–316. [Google Scholar] [CrossRef]
- Thomas, S.; Pillai, G.N.; Pal, K.; Jagtap, P. Prediction of ground motion parameters using randomized ANFIS (RANFIS). Appl. Soft Comput. 2016, 40, 624–634. [Google Scholar] [CrossRef]
- Tatar, A.; Barati-Harooni, A.; Najafi-Marghmaleki, A.; Norouzi-Farimani, B.; Mohammadi, A.H. Predictive model based on ANFIS for estimation of thermal conductivity of carbon dioxide. J. Mol. Liquids 2016, 224, 1266–1274. [Google Scholar] [CrossRef]
- Vasileva-Stojanovska, T.; Vasileva, M.; Malinovski, T.; Trajkovik, V. An ANFIS model of quality experience prediction in education. Appl. Soft Comput. 2015, 34, 129–138. [Google Scholar] [CrossRef]
- Akkaya, E. ANFIS based prediction model for biomass heating value using proximate analysis components. Fuel 2016, 180, 687–693. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. The application of ANFIS prediction models for thermal error compensation on CNC machine tools. Appl. Soft Comput. 2015, 27, 158–168. [Google Scholar] [CrossRef]
- Esfahanipour, A.; Mardani, P. An ANFIS model for stock price prediction: The case of Tehran stock exchange. In Proceedings of the 2011 International Symposium on Innovations in Intelligent Systems and Applications, Istanbul, Turkey, 15–18 June 2011; pp. 44–49. [Google Scholar]
- Cheng, C.H.; Wei, L.Y.; Chen, Y.S. Fusion ANFIS models based on multi-stock volatility causality for TAIEX forecasting. Neurocomputing 2009, 72, 3462–3468. [Google Scholar] [CrossRef]
- Malhotra, R.; Sharma, A. A neuro-fuzzy classifier for website quality prediction. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 1274–1279. [Google Scholar]
- Abadi, S.M.A.N.R.; Mehrabi, M.; Meyer, J.P. Prediction and optimization of condensation heat transfer coefficients and pressure drops of R134a inside an inclined smooth tube. Int. J. Heat Mass Transf. 2018, 124, 953–966. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Han, M.; Sun, Y.; Fan, Y. An improved fuzzy neural network based on T.S. model. Expert Syst. Appl. 2008, 34, 2905–2920. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Sugeno, M.; Kang, G.T. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive–network–based fuzzy inference systems. IEEE SMCS 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Prentice Hall: New Dehli, India, 1997. [Google Scholar]
- Chiu, S. Fuzzy model identification based on cluster estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar]
- Yager, R.; Filev, D. Generation of fuzzy rules by mountain clustering. J. Intell. Fuzzy Syst. 1994, 2, 209–219. [Google Scholar]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum: New York, NY, USA, 1981. [Google Scholar]
- Bezdek, J.C. Fuzzy Mathematics in Pattern Classification. Ph.D. Thesis, Applied Math Center, Cornell University, Ithaca, NY, USA, 1973. [Google Scholar]
- Pedrycz, W. Conditional fuzzy C–means. Pattern Recognit. Lett. 1996, 17, 625–632. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets (accessed on 26 November 2018).
- UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/database (accessed on 26 November 2018).
- Mathworks. Available online: https://kr.mathworks.com (accessed on 26 November 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).