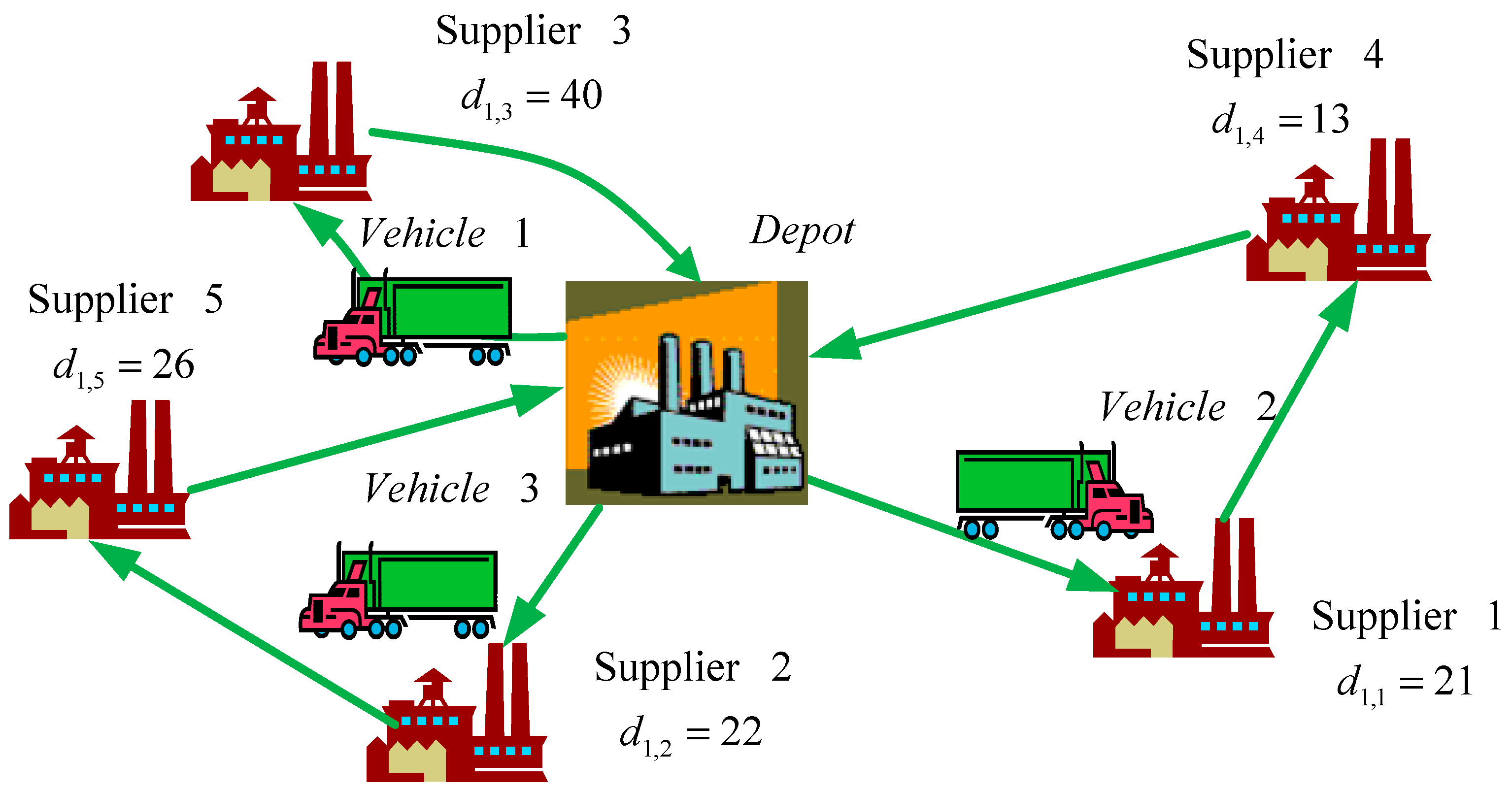
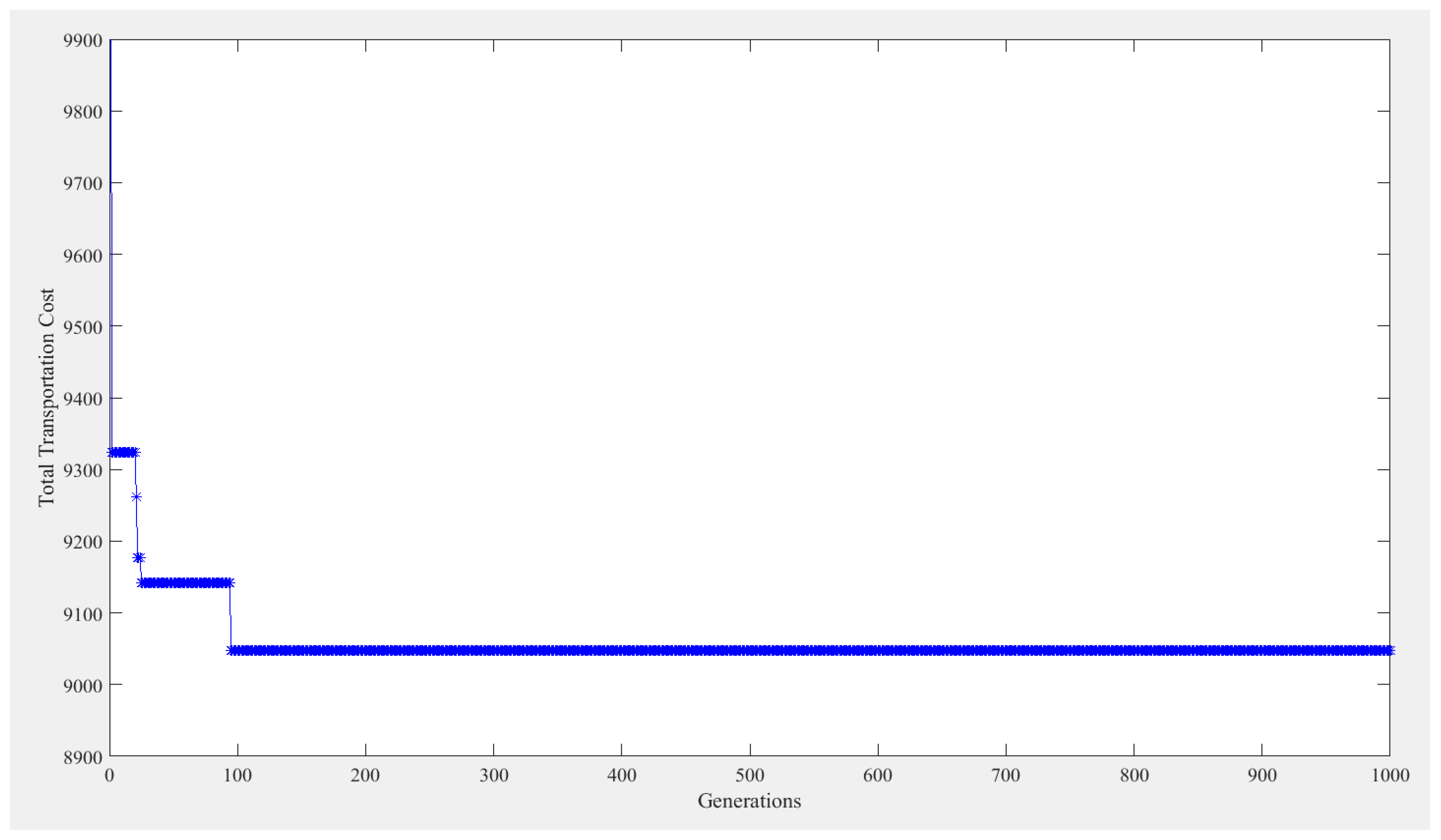
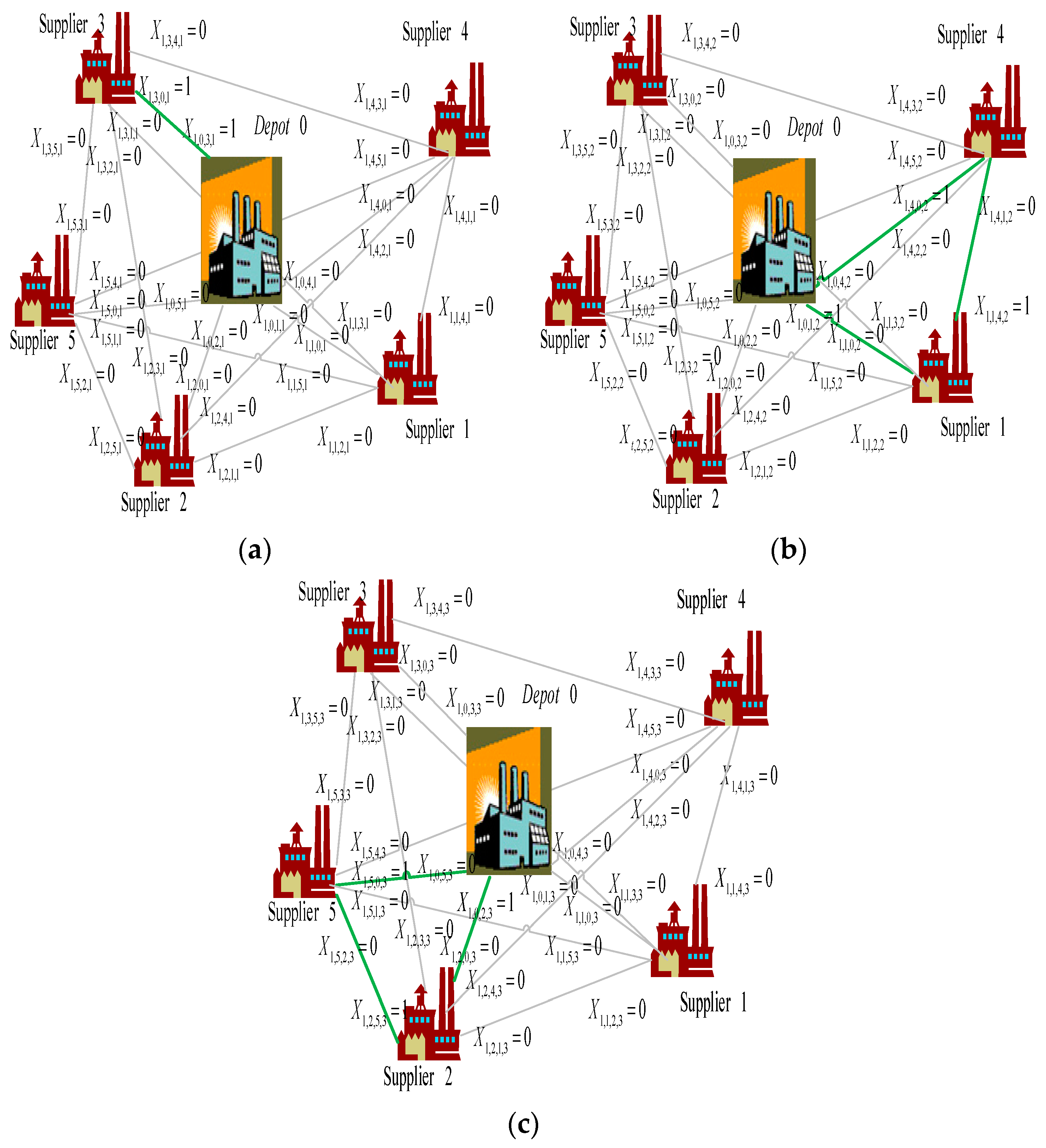
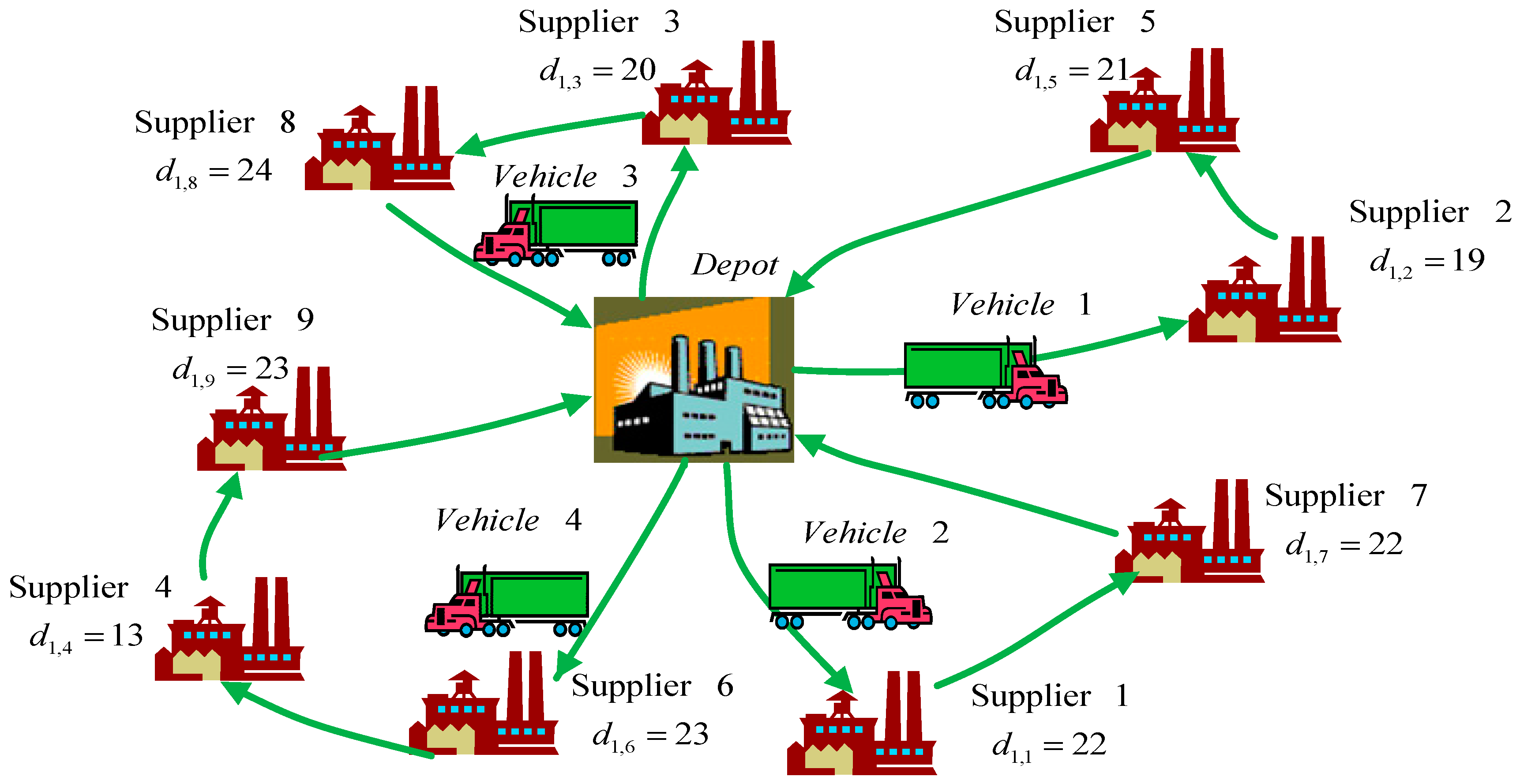
Some recent works of VRP, especially the adoption of metaheuristics, are reviewed here. Lee et al. [
17] considered a MVRP with multiple suppliers, a single depot, a fleet of identical capacity trucks, and allowing for split pick-ups. A deterministic dynamic program (DP) was proposed first, and an exact algorithm based on the shortest path search was formulated next, for simple and easy implementation. Adelzadeh et al. [
3] proposed a mathematical model, and devised a heuristic solving procedure for multi-depot VRP with a fuzzy time window and heterogeneous vehicles that have different capacities, velocities, and costs. The fuzzy concept was applied to the service levels of the time windows, and a multi-objective model was developed. A three-stage algorithm was first used to decompose the problem into some common VRPs, and a heuristic approach was developed to obtain an initial solution. A simulated annealing (SA) algorithm was proposed to improve the solutions. Duan et al. [
18] studied the stochastic time-dependent VRP and proposed two mathematical models, i.e., a robust optimal schedule time model and a minimum expected schedule time model, to ensure that all deliveries were met within the time windows. Since the robust optimal schedule time model does not need the probability distributions of the travel times, it could be transformed into a time-dependent VRP. Ant colony optimization algorithm was next applied, to improve both the initial solution and the transition probability, and as a result, to speed up the convergence. Zare-Reisabadi and Mirmohammadi [
2] studied the site-dependent VRP with soft time window, in which a fleet of vehicles must deliver goods to customers, preferably in their time windows. An integer linear programming model was proposed first. Since the problem was NP-hard, two metaheuristics algorithms were presented to obtain near-optimal solutions: an ant colony system with local searches, and a tabu search algorithm. Khaligh and MirHassani [
19] studied a VRP under endogenous uncertainty. The problem considered a single vehicle with a limited capacity need to serve customers whose demands are uncertain and that follow a known discrete probability distribution. The actual demand of a customer is known when the vehicle arrives to the customer, and the vehicle may need to return to the depot for replenishment in order to satisfy all of the demands of the customers. A multistage stochastic programming (SP) model, which could reduce the number of nonanticipativity constraints, was proposed, to find a policy to satisfy customer demand and to minimize the total expected cost. Liu et al. [
20] studied a capacitated VRP, under which the order available time was determined by the precedent order picking and packing stage in the warehouse. A tabu search algorithm was proposed to minimize the sum of vehicle completion times, and a Lagrangian relaxation algorithm was used to generate the lower bounds of the problems. Hernandez et al. [
21] considered the periodic VRP and the periodic VRP with time windows. A tactical routing plan for a time slot schedule, based on demand and service time estimates, is devised to minimize the expected cost. Two heuristics were proposed to solve the problem. The first one was a three-phase approach, i.e., solving a periodic VRP, repair, and final improvement, so that a VRP with time windows was solved for each period of the planning horizon. The second one could directly solve the entire problem at once. Khodabandeh et al. [
22] studied the VRP with time windows and a limited duration, in which each customer is visited once by one vehicle within a specific time window under the capacity constraint. The objectives were to minimize the travel time and the total number of vehicles used. A network reduction technique, by modifying the cluster-first, route-second approach by Fisher and Jaikumar [
23], was used to obtain an initial feasible solution. A simulated annealing (SA) approach was used to improve the solution. Mancini [
24] studied the VRP with time-dependent travel times, in which travel times are subject to complex variations such as speed variation, due to congestion phenomena. The goal of the model was to obtain the best routes and the best starting time for each route, and to minimize the total travel time. A two-phase heuristic approach was presented. First, a multistart random constructive heuristic was applied, to obtain promising solutions. Second, a set partitioning-based formulation was used to obtain the final solution. Yassen et al. [
25] studied the use of the harmony search algorithm in solving VRP with time windows. An adaptive harmony search algorithm that incorporated an adaptive selection mechanism was developed, to adaptively select a suitable local search algorithm, and five local search algorithms were examined. Soysal and Çimen [
26] studied the green time-dependent capacitated VRP, in which the travel speed depended on the location and the time of the day, and the fuel consumption and transportation emissions were considered. A dynamic programming model was first formulated and then used to solve small instances. A simulation-based restricted dynamic programming, which incorporated a weighted random sampling, and a restricted dynamic programming heuristic and simulation, was developed to solve large sized problems. Abdoli et al. [
5] studied the green VRP to reduce greenhouse gas emissions while considering the necessity of alternative fuel vehicles to refuel at alternative fueling stations when travelling long distances. A mixed integer programming model was presented, to show that the utilization of alternative fuel vehicles could reduce greenhouse gas emissions significantly. A simulated annealing algorithm was next developed to solve large instances with good solution quality and short computation times. Mousavi and Vahdani [
27] studied multiple vehicle location-routing problems with time windows and uncertain input data in cross-docking distribution networks. A two-phase deterministic mixed-integer linear programming (MILP) model was first presented to locate cross-docks and to schedule vehicle routing with multiple cross-docks. Next, a two-phase MILP model was presented by applying an optimization theory. Finally, a metaheuristic algorithm was proposed for solving the problems. Govindan et al. [
28] studied a two-echelon multiple-vehicle location-routing problem with time windows for a sustainable supply chain network of perishable food to meet both economical and environmental objectives. A multi-objective hybrid approach, which integrated multi-objective particle swarm optimization and adapted a multi-objective variable neighborhood search, was proposed. The results were found to outperform some genetic algorithm (GA)-based methods. Madankumar and Rajendran [
29] studied the green VRP with pickup and delivery, and used the semiconductor supply chain as an example. Three MILP models were constructed. The first model was to minimize the total routing cost and to obtain the routes and schedules for the alternative fuel vehicles while satisfying a set of requests. The second model extended the first model and considered different fuel prices at different refueling stations. The third model considered the basic pickup and delivery problem without the consideration of the green supply chain, and it was compared with the first two models. Dalmeijer and Spliet [
30] studied the time window assignment VRP, in which time windows for delivery are assigned to clients before the demand volume of clients is known. To deal with demand uncertainty, the problem assumes that the demand scenarios and their probabilities of occurrence are known. A flow formulation was presented, and a branch-and-cut algorithm was proposed, to obtain solutions quickly, and to solve large instances. Xu et al. [
31] studied a dynamic VRP and proposed an enhanced ant colony optimization model, which incorporated improved K-means and crossover operation into the traditional ant colony optimization. The improved K-means aimed to divide the region with the most reasonable distance, and the crossover operation tried to extend the search space and tried to avoid falling into a local search prematurely.
GA has been applied in solving VRP. Some works are reviewed here. Baker and Ayechew [
32] stated that unlike other heuristics, which has had considerable progress in solving VRP, GA had not made a great impact. The authors developed a conceptually straightforward GA to solve the basic VRP, and a hybrid heuristic, which incorporated a neighborhood search into the GA. A comparison with other heuristics showed that the GA was competitive in terms of computing time and solution quality. Ombuki et al. [
11] studied the VRP with hard time windows, and treated it as a multi-objective problem with two objectives: the number of vehicles and the total distance traveled. A multi-objective GA approach using the Pareto ranking technique was developed so that the weighted sum, which might cause solution bias, did not need to be applied. Alvarenga et al. [
33] studied the VRP with time windows and proposed a two-phase approach that incorporated GA and a set partitioning formulation. The objective was to minimize the travel distance, and the authors stated that the approach outperformed past heuristic methods in terms of the minimal travel distance. Vidal et al. [
34] studied three variants of VRP, the multi-depot VRP, the periodic VRP, and the multi-depot periodic VRP, under an environment of capacitated vehicles and constrained route duration. Based on the GA, the authors proposed a hybrid genetic search with an adaptive diversity control metaheuristic. Vidal et al. [
35] further proposed a hybrid genetic search with advanced diversity control to tackle four types of VRP: VRP with time windows, periodic VRP with time windows, multi-depot VRP with time windows, and site-dependent VRP with time windows. Some evaluation techniques were introduced to the GA to evaluate and prune neighborhoods, and to decompose large instances efficiently. Xiao and Konak [
36] studied the green vehicle routing and the scheduling problem, in which a fleet of heterogeneous vehicles travel within a time-varying traffic environment to minimize the total CO
2 emissions. An MIP was first proposed for small-sized problems, and an exact dynamic programming algorithm was presented next for large-sized problems. A hybrid GA, combined with the exact dynamic programming algorithm, was then developed as an efficient solution approach.