Fuzzy AHP Application for Supporting Contractors’ Bidding Decision
Abstract
1. Introduction
2. Decision Making Processes in Construction Management
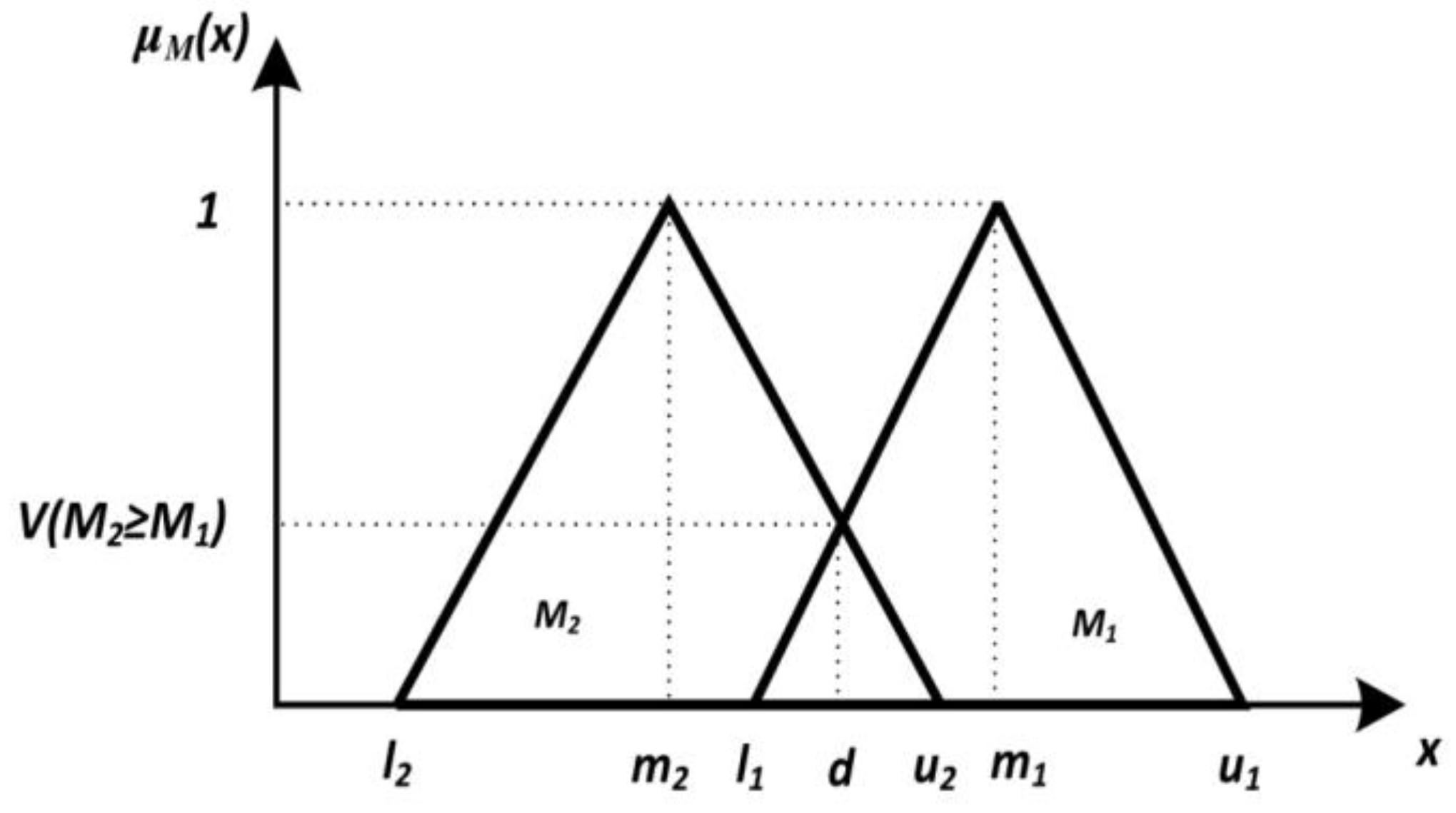
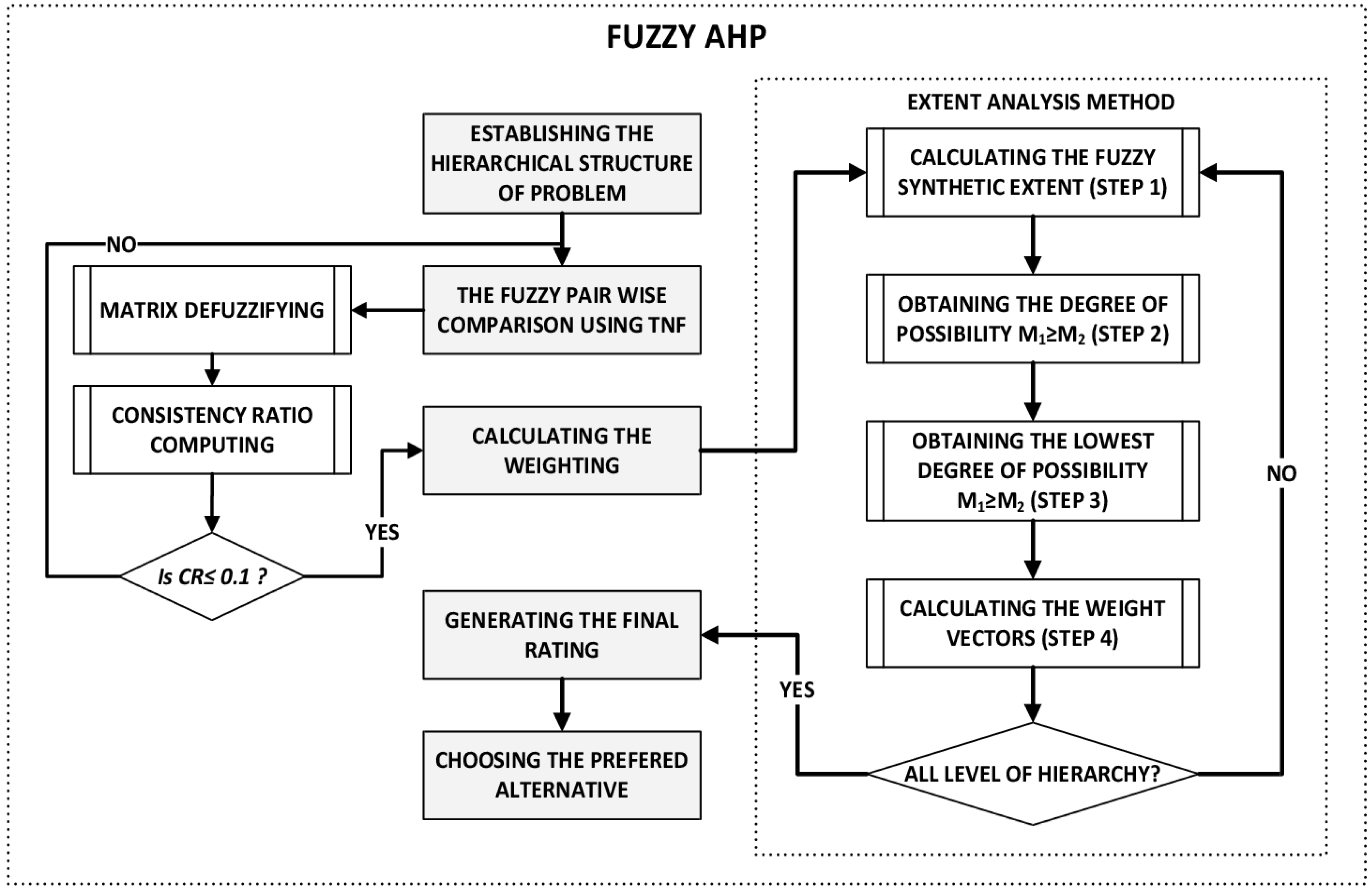
3. Bidding Decision Support Systems Based on Fuzzy AHP—Methodology
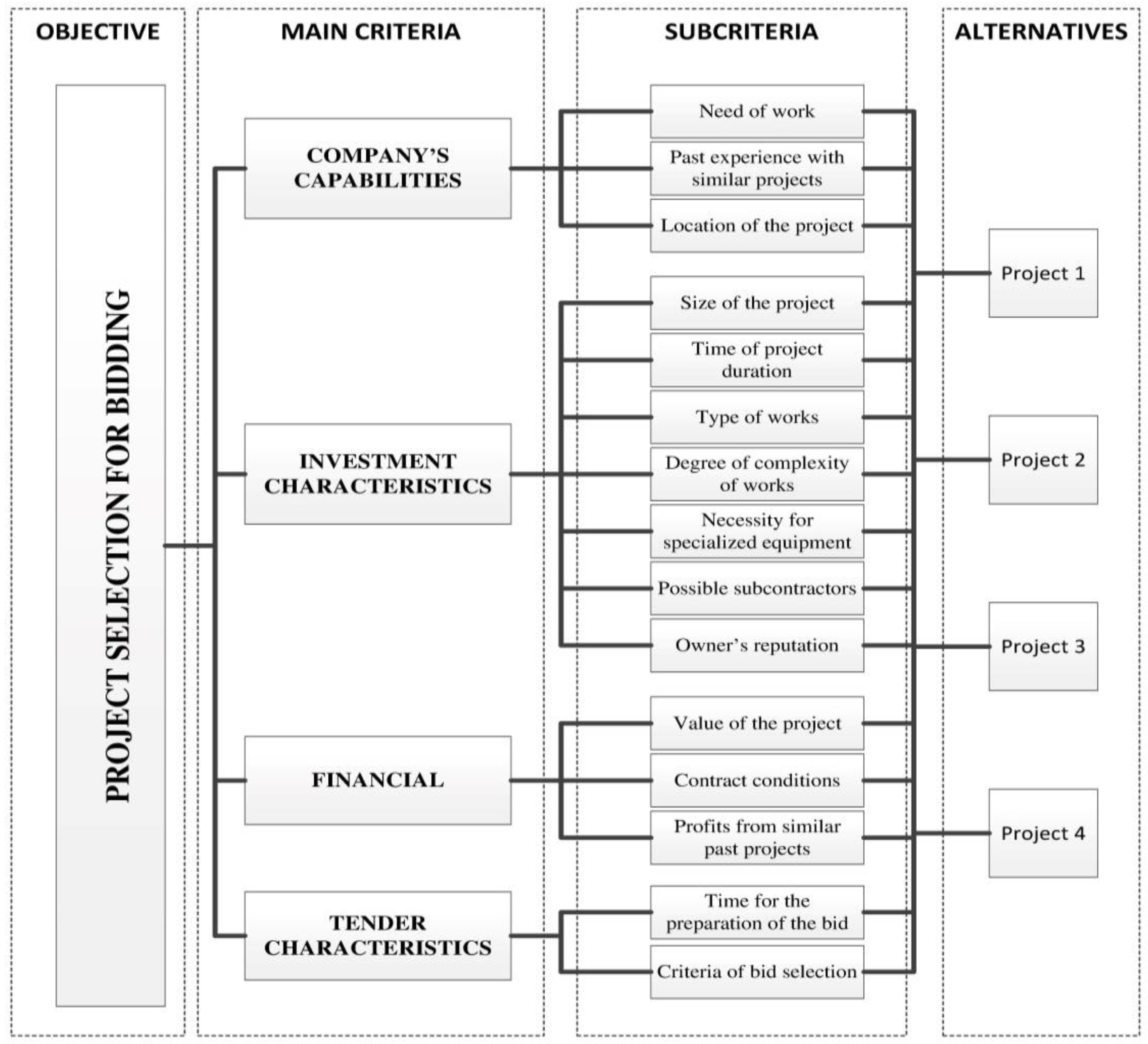
4. Project Selection for Bidding—Model Application
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shash, A.A. Factors considered in tendering decisions by top UK contractors. Constr. Manag. Econ. 1993, 11, 111–118. [Google Scholar] [CrossRef]
- Gajzler, M.; Zima, K. Evaluation of Planned Construction Projects Using Fuzzy Logic. Int. J. Civ. Eng. 2017, 15, 641–652. [Google Scholar] [CrossRef]
- Plebankiewicz, E. Modelling decision-making processes in bidding procedures with the use of the fuzzy sets theory. Int. J. Strateg. Prop. Manag. 2014, 18, 307–316. [Google Scholar] [CrossRef]
- Zima, K. The concept of investment decision support model using fuzzy set theory. In Proceedings of the 11th International Conference of Numerical Analysis and Applied Mathematics 2013 (ICNAAM 2013), Rhodes, Greece, 21–27 September 2013; pp. 1307–1311. [Google Scholar]
- Plebankiewicz, E.; Leśniak, A. Overhead costs and profit calculation by polish contractors. Technol. Econ. Dev. Econ. 2013, 19, 141–161. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antuchevičienė, J.; Kapliński, O. Multi-criteria decision making in civil engineering: Part I—A state-of-the-art survey. Eng. Struct. Technol. 2015, 7, 103–113. [Google Scholar] [CrossRef]
- Hoła, B. Identification and evaluation of processes in a construction enterprise. Arch. Civ. Mech. Eng. 2015, 15, 419–426. [Google Scholar] [CrossRef]
- Gul, P. Subcontractor selection using the integration of the AHP and PROMETHEE methods. J. Civ. Eng. Manag. 2016, 22, 1042–1054. [Google Scholar] [CrossRef]
- Yang, J.-B.; Wang, H.-H.; Wang, W.-C.; Ma, S.-M. Using data envelopment analysis to support best-value contractor selection. J. Civ. Eng. Manag. 2016, 22, 199–209. [Google Scholar] [CrossRef]
- Trinkūnienė, E.; Podvezko, V.; Zavadskas, E.K.; Jokšienė, I.; Vinogradova, I.; Trinkūnas, V. Evaluation of quality assurance in contractor contracts by multi-attribute decision-making methods. Econ. Res.-Ekon. Istraž. 2017, 30, 1152–1180. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A Dynamic Fuzzy Approach Based on the EDAS Method for Multi-Criteria Subcontractor Evaluation. Information 2018, 9, 68. [Google Scholar] [CrossRef]
- Khanzadi, M.; Turskis, Z.; Amiri, G.G.; Chalekaee, A. A model of discrete zero-sum two-person matrix games with grey numbers to solve dispute resolution problems in construction. J. Civ. Eng. Manag. 2017, 23, 824–835. [Google Scholar] [CrossRef]
- Hashemi, H.; Mousavi, S.M.; Zavadskas, E.K.; Chalekaee, A.; Turskis, Z. A New Group Decision Model Based on Grey-Intuitionistic Fuzzy-ELECTRE and VIKOR for Contractor Assessment Problem. Sustainability 2018, 10, 1635. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Selecting a Contractor by Using a Novel Method for Multiple Attribute Analysis: Weighted Aggregated Sum Product Assessment with Grey Values (WASPAS-G). Stud. Inform. Control 2015, 24, 141–150. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of Weighted Aggregated Sum Product Assessment. Electron. Electr. Eng. 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Ahmad, I. Decision-support system for modeling bid/no-bid decision problem. J. Constr. Eng. Manag. 1990, 116, 595–608. [Google Scholar] [CrossRef]
- El-Mashaleh, M.S. Empirical framework for making the bid/no-bid decision. J. Manag. Eng. 2013, 29, 200–205. [Google Scholar] [CrossRef]
- Polat, G.; Bingol, B.N.; Uysalol, E. Modeling Bid/No Bid Decision Using Adaptive Neuro Fuzzy Inference System (ANFIS): A Case Study. In Proceedings of the 2014 Construction Research Congress: Construction in a Global Network, Atlanta, GA, USA, 19–21 May 2014; pp. 1083–1092. [Google Scholar]
- Sonmez, R.; Sözgen, B. A support vector machine method for bid/no bid decision making. J. Civ. Eng. Manag. 2017, 23, 641–649. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Hsiang, C.-C.; Tsai, H.-C.; Do, H.-L. Bidding decision making for construction company using a multi-criteria prospect model. J. Civ. Eng. Manag. 2011, 17, 424–436. [Google Scholar] [CrossRef]
- Leśniak, A.; Plebankiewicz, E. Modeling the Decision-Making Process Concerning Participation in Construction Bidding. J. Manag. Eng. 2015, 31. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D.; Wang, H. Bidding strategy to support decision-making by integrating fuzzy AHP and regression-based simulation. Autom. Constr. 2013, 35, 517–527. [Google Scholar] [CrossRef]
- Leśniak, A. The simplified bidding decision model based on AHP method in ordering of investor’s supervision service. In Proceedings of the 14th GeoConference on Ecology, Economics, Education and Legislation, Multilateral Relations and Funding Opportunities, Albena, Bulgaria, 17–26 June 2014; Volume 3, pp. 501–508. [Google Scholar]
- Liu, J.B.; Hong, R.; Guo, X.J. Study on the Game Mechanism of Construction Project Bidding. In Proceedings of the International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, 11–17 July 2009; pp. 814–817. [Google Scholar]
- Leśniak, A.; Radziejowska, A. Supporting bidding decision using multi-criteria analysis methods. Procedia Eng. 2017, 208, 76–81. [Google Scholar] [CrossRef]
- Leśniak, A. Supporting contractors’ bidding decision: RBF neural network application. In Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM-2015), Rhodes, Greece, 23–29 September 2015; Volume 1738. [Google Scholar]
- Wanous, M.; Boussabaine, A.H.; Lewis, J. A neural network bid/no bid model, the case for contractors in Syria. Constr. Manag. Econ. 2003, 21, 737–744. [Google Scholar] [CrossRef]
- Ahmad, I.; Minkarah, I. Questionnaire survey on bidding in construction. J. Manag. Eng. Div. 1988, 4, 229–243. [Google Scholar] [CrossRef]
- Shash, A.A.; Abdul-Hadi, N.H. Factors affecting a contractor’s mark-up size decision in Saudi Arabia. Constr. Manag. Econ. 1992, 10, 415–429. [Google Scholar] [CrossRef]
- Bageis, A.S.; Fortune, C. Factors affecting the bid/no bid decision in the Saudi Arabian construction contractors. Constr. Manag. Econ. 2009, 27, 53–71. [Google Scholar] [CrossRef]
- Enshassi, A.; Mohamed, S.; El Karriri, A. Factors affecting the bid/no bid decision in the Palestinian construction industry. J. Financ. Manag. Prop. Constr. 2010, 15, 118–142. [Google Scholar] [CrossRef]
- Shokri-Ghasabeh, M.; Chileshe, N. Critical factors influencing the bid/no bid decision in the Australian construction industry. Constr. Innov. 2016, 16, 127–157. [Google Scholar] [CrossRef]
- Leśniak, A. Classification of the Bid/No Bid Criteria—Factor Analysis. Arch. Civ. Eng. 2015, 61, 79–90. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Ho, W. Integrated analytic hierarchy process and its applications—A literature review. Eur. J. Oper. Res. 2008, 186, 211–228. [Google Scholar] [CrossRef]
- Chang, D. Application of extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Prascevic, N.; Prascevic, Z. Application of fuzzy AHP for ranking and selection of alternatives in construction project management. J. Civ. Eng. Manag. 2017, 23, 1123–1135. [Google Scholar] [CrossRef]
- Taylana, O.; Bafail, A.O.; Abdulaala, R.M.S. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Çalik, A.; Yapici Pehlivan, N.; Kahraman, C. An integrated fuzzy AHP/DEA approach for performance evaluation of territorial units in Turkey. Technol. Econ. Dev. Econ. 2018, 24, 1280–1302. [Google Scholar] [CrossRef]
- Ucal Sari, I. Development of an integrated discounting strategy based on vendors’ expectations using FAHP and FUZZY goal programming. Technol. Econ. Dev. Econ. 2018, 24, 635–652. [Google Scholar] [CrossRef]
- Kutlu, A. Fuzzy failure modes and effects analysis by fuzzy TOPSIS-based fuzzy AHP. Experts Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Kubek, D. Multicriteria selection of the building material supplier using AHP and fuzzy AHP. J. Constr. Eng. Manag. 2015, 142, 40–57. [Google Scholar] [CrossRef]
- Report of the Public Procurement Office on the Functioning of the Public Procurement System in 2017. Available online: https://www.uzp.gov.pl/baza-wiedzy/analizy-systemowe/sprawozdania-o-funkcjonowaniu-systemu-zamowien-publicznych (accessed on 26 October 2018).
- Plebankiewicz, E.; Kozik, R. The transformation of the tender evaluation process in public procurement in Poland. IOP Conf. Ser. Mater. Sci. Eng. 2017, 251, 012042. [Google Scholar] [CrossRef]
| Method Name | Aim of Analysis | Number of Criterion Used | Source |
|---|---|---|---|
| Analytic Hierarchy Process (AHP) + PROMETHEE | subcontractor selection for main contractor | 13 | [8] |
| Data Envelopment Analysis (DEA) | subcontractor selection at short-listing stage | 5–6 selected depending on the specific tender | [9] |
| Fuzzy AHP; The method of entropy; Method of criterion impact loss (CILOS); Integrated Determination of Objective CRIteria Weights (IDOCRIW) method; The SAW method; The TOPSIS method; The COPRAS method | comparing quality assurance in different contractor contracts | 7 | [10] |
| The EDAS method | comparing quality assurance in different contractor contracts | 7 | [11] |
| hybrid MCDM model of discrete zero-sum two-person matrix games with grey numbers | delays in Design-Bid-Build projects | 8 | [12] |
| Integration of intuitionistic fuzzy sets I(FS) theory, ELECTRE and VIKOR along with Grey Relational Analysis (GRA | contractor selection problem | 20 | [13] |
| Weighted Aggregated Sum Product Assessment with Grey Values (WASPAS-G) | evaluating and selecting contractors | 6 | [14] |
| Qualitative Evaluation | Fuzzy Evaluation | AHP Equivalent |
|---|---|---|
| Extreme preference | (2; 5/2; 3) | 9 |
| Very strong preference | (3/2; 2; 5/2) | 7 |
| Strong preference | (1; 3/2; 2) | 5 |
| Moderate preference | (1; 1; 3/2) | 3 |
| Equal preference | (1; 1; 1) | 1 |
| Moderate inferiority | (2/3; 1; 1) | 1/3 |
| Strong inferiority | (1/2; 2/3; 1) | 1/5 |
| Very strong inferiority | (2/5; ½; 2/3) | 1/7 |
| Extreme inferiority | (1/3; 2/5; 1/2) | 1/9 |
| Criterion/Sub-Criterion | Name of the Criterion/Factor | Average Evaluation of Criterion/Factor * |
|---|---|---|
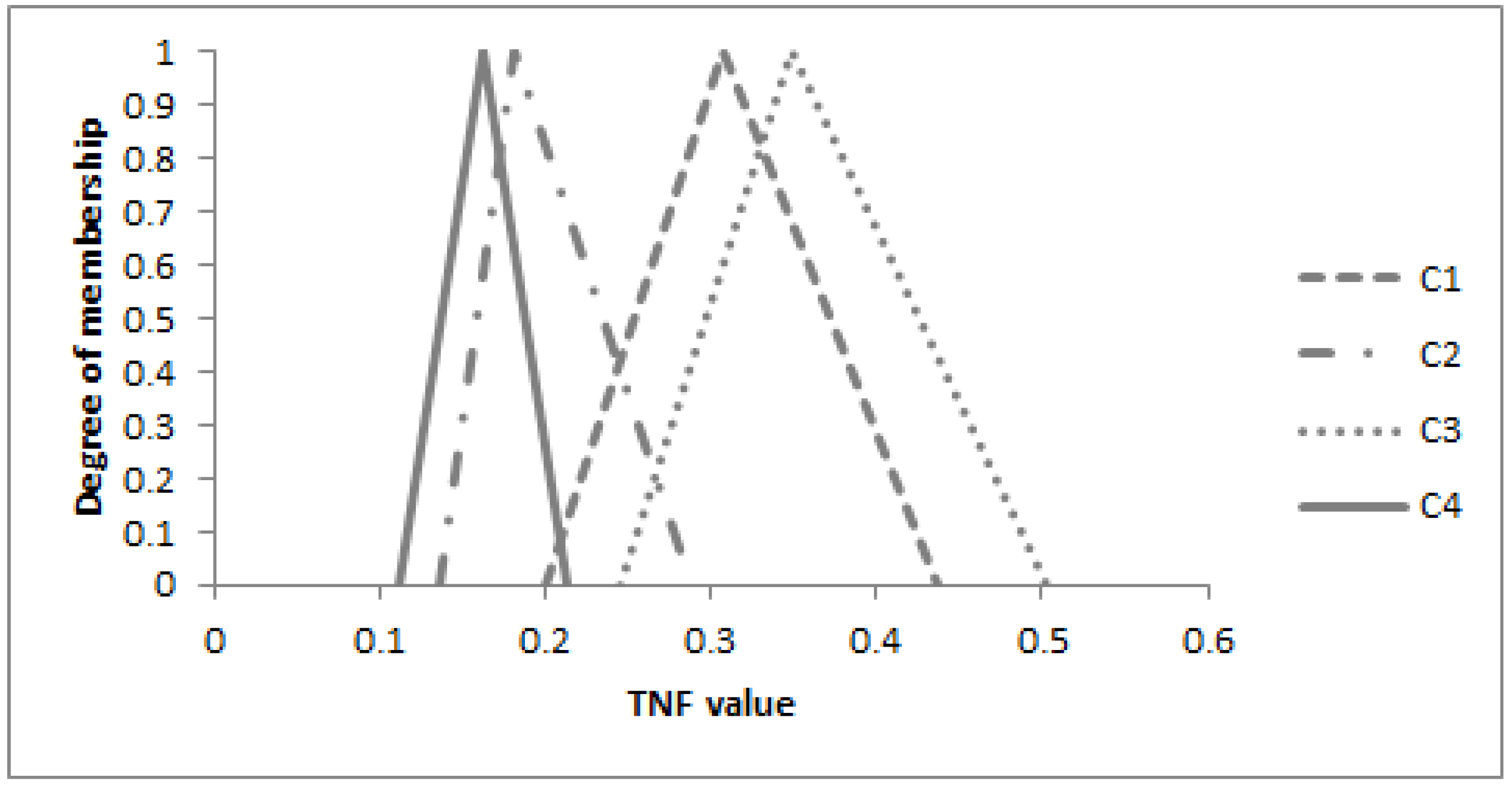
| C1 | Company’s capabilities | 5.14 |
| C1_1 | Need of work | 5.21 |
| C1_2 | Past experience with similar projects | 5.95 |
| C1_3 | Location of the project | 4.25 |
| C2 | Investment characteristics | 4.48 |
| C2_1 | Size of the project (e.g., cubic measure) | 4.95 |
| C2_2 | Time of project duration | 4.49 |
| C2_3 | Type of works | 5.98 |
| C2_4 | Degree of works complexity | 3.25 |
| C2_5 | Necessity for specialized equipment | 3.51 |
| C2_6 | Possible subcontractors | 3.87 |
| C2_7 | Owner’s reputation | 5.31 |
| C3 | Financial conditions | 5.35 |
| C3_1 | Value of the project | 5.30 |
| C3_2 | Contract conditions | 5.89 |
| C3_3 | Profits from similar past projects | 4.87 |
| C4 | Tender characteristics | 4.14 |
| C4_1 | Time for the preparation of the bid | 3.89 |
| C4_2 | Criteria of bid selection | 4.38 |
| Sub-Criterion/Factor | Project | |||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| C1_1 | 7 | 5 | 7 | 5 |
| C1_2 | 4 | 7 | 7 | 7 |
| C1_3 | 4 | 5 | 6 | 6 |
| C2_1 | 3 | 3 | 5 | 2 |
| C2_2 | 3 | 4 | 6 | 5 |
| C2_3 | 5 | 7 | 7 | 6 |
| C2_4 | 4 | 6 | 7 | 7 |
| C2_5 | 4 | 6 | 6 | 6 |
| C2_6 | 6 | 6 | 6 | 3 |
| C2_7 | 6 | 4 | 7 | 4 |
| C3_1 | 4 | 3 | 4 | 2 |
| C3_2 | 5 | 4 | 6 | 4 |
| C3_3 | 4 | 4 | 5 | 4 |
| C4_1 | 6 | 5 | 7 | 6 |
| C4_2 | 4 | 5 | 4 | 4 |
| Names | Priority Weight Vector for Each Individual Project | |||||
|---|---|---|---|---|---|---|
| Criteria | Sub-Criteria | P1 | P2 | P3 | P4 | |
| C1_1 | 0.4045 | 0.3381 | 0.5000 | 0.0000 | 0.5000 | 0.0000 |
| C1_2 | 0.6619 | 0.0000 | 0.3333 | 0.3333 | 0.3333 | |
| C1_3 | 0.0000 | 0.0309 | 0.2253 | 0.3719 | 0.3719 | |
| C2_1 | 0.1026 | 0.1990 | 0.0264 | 0.0264 | 0.9472 | 0.0000 |
| C2_2 | 0.1287 | 0.0000 | 0.1086 | 0.5586 | 0.3329 | |
| C2_3 | 0.3544 | 0.0309 | 0.3719 | 0.3719 | 0.2253 | |
| C2_4 | 0.0000 | 0.0000 | 0.1870 | 0.4065 | 0.4065 | |
| C2_5 | 0.0028 | 0.0000 | 0.3333 | 0.3333 | 0.3333 | |
| C2_6 | 0.0547 | 0.3333 | 0.3333 | 0.3333 | 0.0000 | |
| C2_7 | 0.2603 | 0.3119 | 0.0000 | 0.6881 | 0.0000 | |
| C3_1 | 0.4928 | 0.2692 | 0.3719 | 0.2253 | 0.3719 | 0.0309 |
| C3_2 | 0.7308 | 0.3694 | 0.0333 | 0.5640 | 0.0333 | |
| C3_3 | 0.0000 | 0.1688 | 0.1688 | 0.4937 | 0.1688 | |
| C4_1 | 0.0000 | 0.0000 | 0.2474 | 0.0809 | 0.4244 | 0.2474 |
| C4_2 | 1.0000 | 0.1688 | 0.4937 | 0.1688 | 0.1688 | |
| Solution | 0.2627 | 0.1486 | 0.4707 | 0.1180 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leśniak, A.; Kubek, D.; Plebankiewicz, E.; Zima, K.; Belniak, S. Fuzzy AHP Application for Supporting Contractors’ Bidding Decision. Symmetry 2018, 10, 642. https://doi.org/10.3390/sym10110642
Leśniak A, Kubek D, Plebankiewicz E, Zima K, Belniak S. Fuzzy AHP Application for Supporting Contractors’ Bidding Decision. Symmetry. 2018; 10(11):642. https://doi.org/10.3390/sym10110642
Chicago/Turabian StyleLeśniak, Agnieszka, Daniel Kubek, Edyta Plebankiewicz, Krzysztof Zima, and Stanisław Belniak. 2018. "Fuzzy AHP Application for Supporting Contractors’ Bidding Decision" Symmetry 10, no. 11: 642. https://doi.org/10.3390/sym10110642
APA StyleLeśniak, A., Kubek, D., Plebankiewicz, E., Zima, K., & Belniak, S. (2018). Fuzzy AHP Application for Supporting Contractors’ Bidding Decision. Symmetry, 10(11), 642. https://doi.org/10.3390/sym10110642








