1. Introduction
A group decision-making process, which is also called multi-person decision-making, is the problem of finding the best option accepted by the majority of decision makers among a list of possible alternatives. The basic act in the group decision-making is the process of consensus between different decision makers. Although a unanimous consensus is the ideal case, in real situations, full agreement rarely happens. Decision makers usually share and discuss their opinions about the alternatives to obtain a consensus or partial agreement for making the final decision. However, sometimes, they provide their priorities about the alternatives individually and then try to reach a consensus on them. Regardless which approach is applied, using aggregation operators is one of the most often used techniques to reach the process of consensus in group decision-making problems.
The aim of an aggregation operator of dimension K is to aggregate the K-tuple of objects into a single object by a bounded non-decreasing function
. The mean value, the median, the minimum, the maximum, the t-norms, and the t-conorms are commonly used to reach the process of consensus in group decision-making problems. To aggregate a sequence of inputs with different importance degrees, the concept of weighting vector in aggregation operators has been studied, such as the weighted minimum and the weighted maximum [
1,
2,
3]; ordered weighted average (OWA) [
4], which is calculated based on the arithmetic mean; and ordered weighted geometric (OWG) [
5], which is formulated based on the geometric mean. The main disadvantage of OWA and OWG operators, i.e., ignoring the importance of given arguments
for calculating the aggregated value, leads to definition of their extensions into the induced OWA (IOWA) operator [
6], and induced OWG (IOWG) operator [
7], respectively. However, these extensions have the inherent limitations from OWA operator and OWG operator, concerning the determination of associated weighting vector
for IOWA and IOWG operators. In practice, there is no unique strategy to find the associated weighting vector
. Usually, a quantifier function
whose definition may change from one case to another one is applied to compute the associated weighting vector
based on the formulation
for all
i [
4,
5,
8,
9].
Soft set theory (SS) [
10], characterized by a set-valued function
, is defined by a parameterization family of the universe
U. Thus, in comparison with fuzzy set theory [
11], it allows us to have a more comprehensive description of
U based on any type and number of parameters
. The concepts of fuzzy soft set (FSS) [
12] and intuitionistic fuzzy soft set (IFSS) [
13] were also studied to handle more complicated problems. Although soft set theory was originally developed to cope with the lack of parameterization tool in fuzzy sets, its flexibility to deal with set-valued functions makes it a powerful tool for providing a new methodology in decision-making problems. The first adaptivity of soft sets in decision-making was conducted by Maji et al. [
14]. However, they did not discuss the aggregation methods. Roy and Maji [
15] gave an algorithm to solve a group decision-making problem based on fuzzy soft sets. The FS minimum operator was applied for finding the consensus of multi-source parameter sets. Later, Alcantud [
16] overcame the disadvantages of Roy and Maji’s algorithm by applying FS product operator rather than FS minimum operator. Cagman et al. [
17,
18] applied FS minimum operator, FS maximum operator, and FS product operator to produce different fuzzy soft aggregation operators in a MAGDM problem. Guan et al. [
19] applied the FS intersection operator for aggregating data. Then, a new ranking system of objects, in which the rate of objects is computed based on the full unanimity of experts with respect to all parameters rather than the number of parameters that are owned by each object, was constructed to rank alternatives in a group decision problem. Zhang et al. [
20] used the IFS maximum operator to check the process of consensus in MAGDM problem. Mao et al. [
21] extended IFSOWA and IFSOWG operators for intuitionistic fuzzy soft sets under three different cases of experts’ weights called completely known, partly known, and completely unknown. Das and Kar [
22] used the IFS product and the IFS sum operators of intuitionistic fuzzy soft matrices to obtain a collective opinion among different decision makers. Zhang and Zhang [
23] utilized the FS union operation to reach the process of consensus in MAGDM problems based on trapezoidal interval type-2 fuzzy soft sets (TIT2FSSs). The TOPSIS approach was then applied to select the best option. However, recently, Pandey and Kumar [
24] modified this procedure so that the complement operation that is used by Zhang and Zhang can only be applied for TIT2FSSs in which left and right heights are equal. Tao et al. [
25] proposed four aggregation functions, including the soft maximum operator, soft minimum operator, soft average operator, and soft weighted average operator, to aggregate data in MAGDM problems. Two selection tools based on the SAW method and comparison matrix were also developed to obtain the optimal decision. Zhu and Zhan [
26] developed the new concept fuzzy parameterized fuzzy soft sets (FPFSS), where the parameters are considered as fuzzy sets and then the consensus stage proceeds by using the t-norm and t-conorm products of FPFSSs. A new choice value function is also introduced to handle the process of selection. On the other hand, some researchers attempted to develop novel aggregation methods for FSS and IFSS. For example, Zahedi et al. [
27,
28] extended the concept of fuzzy soft topology to reach the consensus based on a collective preorder relation.
Conventionally, soft-set-based aggregating tools have been developed for unipolar input data where the truth value belongs to
. Some situations require multi-polar arguments to be aggregated. To handle the problem of multi-polarity in consensus process, some studies extended the aggregation operators from unipolar scale into the bipolar scale (i.e., the interval
) [
29] and multi-polar scale (i.e., the space
where
K is a set of
m different categories) [
30,
31]. These extensions allow dealing with inputs from different categories where the output is presented by a pair
that
k shows the category of aggregated value
x. However, in many decision-making problems, the attribute set contains multi-feature or multi-polar decision parameters where the final decision should reflect the best option based on all multi-polar attributes beyond their category. For example, in the hotel booking problem, “Location” is one of the most important parameters for finding a good hotel to stay, which is a multi-feature parameter depending on how close it is to the main road, city center, tourist attractions, etc. A hotel is selected if it has the best location in terms of all features from different categories not only one. In fact, there is no ideal category
k in final solution. This issue becomes more complex when a group of people want to choose a hotel. In this case, different cases of agreement within a group including unanimous consensus and partial agreement, e.g., “almost all”, “most”, and “more than 50%”, are considered to obtain the collective view based on individuals’ opinions. Thus, an alternative aggregation operator is required to deal with multi-polar fuzzy attributes in group decision-making.
In a group decision process with multi-polar inputs, the performance of alternatives are judged by each decision maker with respect to each criterion. The main problem is to compare these judgements and reach a consensus among them. The existing aggregation methods usually consider weighted or unweighted cases under a unanimous agreement [
15,
16,
17,
18,
19,
20,
21,
22,
23]. However, besides the importance degrees of experts, the consensus degree for a fuzzy majority of the experts and different choices of experts’ judgments at a consensus level should be taken into account in the proposed alternative aggregation operator to reach more reliable methodology. Moreover, due to the extreme applicability of FSSs in MAGDM problems with multi-polar fuzzy soft input information, adaptability of the proposed aggregation operator for m-polar fuzzy soft sets should be studied. To do this, an extension of fuzzy soft sets into the m-polar fuzzy soft sets, where the values of membership functions
are extended from the unit interval
into the cubic
, needs to be developed.
Until now, weighted aggregation operators for multi-polar fuzzy soft arguments have not been considered. Thus, this study was carried out to develop some weighted m-polar aggregation operators which cover different scenarios at the consensus degree for a fuzzy majority expressed by linguistic variables, such as “most”, “much more than 70%”, and “more than half”. The main goal is to design FS-set-based algorithms for finding the best solution in group decision-making with weighted multi-polar input information according to the proposed aggregation methods. To achieve this goal, the following problems are addressed in this study: (i) how to express the multi-polarity of input data under fuzzy soft environment; (ii) how to generate an aggregation method based on the fuzzy majority concept for weighted multi-polar inputs; (iii) how to apply the proposed aggregation method for finding the solution in group decision-making problems; and (iv) how to analyze the final result obtained by the proposed algorithm. Accordingly, there are four main contributions of this research as follows: (i) to define a new concept m-polar fuzzy soft set; (ii) to introduce m-polar fuzzy soft weighted aggregation operators based on the fuzzy majority concept; (iii) to design m-polar FS-based algorithms for finding the solution in group decision-making; and (iv) to give some illustrative examples for validating and comparing the results.
The rest of this paper is organized as the following.
Section 2 represents some basic definitions and concepts from the related works.
Section 3 gives a new aggregation operator, called M-pFSMWM, for weighted m-polar fuzzy soft data. This new procedure aggregates the experts’ judgments based on their importance degrees, a linguistic or numerical consensus level between the experts, and different choices of experts’ judgments at the consensus level. Some of its desirable properties as well as special families of M-pFSMWM operator according to different values of consensus degree
and weighting vector
are studied. In
Section 4, a new score value function is developed to design an algorithm for ranking alternatives in MAGDM problems based on the M-pFSMWM operator and a new m-polar fuzzy soft preference relation. To compare the proposed M-pFSMWM operator with some existing aggregation methodologies, in
Section 5, the m-polar fuzzy soft induced ordered weighted average (M-pFSIOWA) operator and the m-polar fuzzy soft induced ordered weighted geometric (M-pFSIOWG) operator, which are the extensions of IOWA and IOWG operators, respectively, are developed and their properties are considered. We also present an algorithm to solve MAGDM problems based on M-pFSIOWA and M-pFSIOWG operators.
Section 6 focuses on the efficiency of proposed techniques by some numerical examples. Finally, in
Section 7, we discuss the advantages and limitations of our approach.
3. A New Weighted Aggregation Operator for M-pFSSs
In this section, we introduce a new weighted aggregation operator, called M-pFSMWM operator, to improve the aggregating tools for multi-polar inputs with non-negative weights under fuzzy soft environment. The advantages of this new operator is also demonstrated by some theorems and properties. To this end, we first develop the new concept of m-polar fuzzy soft sets (M-pFSS) and then introduce the M-pFSMWM operator in the domain of m-polar fuzzy soft sets.
3.1. m-Polar Fuzzy Soft Sets
Motivated by m-polar fuzzy sets given in Definition 1, the notion of m-polar fuzzy soft set is developed to model data dealing with multi-polar or multi-feature attributes. Basic operations of m-polar fuzzy soft sets are also discussed in this section.
Definition 3 (m-polar fuzzy soft set)
. Let U and P be two non-empty sets of alternatives and parameters, respectively. The pair where f is the mapping such that for any the is an m-polar fuzzy subset of U can be defined as an m-polar fuzzy soft set (M-pFSS) over U. It means, for each and any , is an m-tuple such that the , for , represents the relation between object and feature s of parameter p.
The set of all m-polar fuzzy soft sets is shown by . Furthermore, an m-polar fuzzy soft set is called a null M-pFSS, shown by , or an absolute M-pFSS, shown by , if for any , and , respectively, for all and . The complement of M-pFSS is also an M-pFSS, shown by , where for any and : for all .
Example 1. Let us suppose a person wants to rate four restaurants according to the parameters . Let he/she considers the different aspects of these parameters as follows: The location of the restaurants includes close to the main road, in green surroundings, and in shopping mall. The meal of the restaurants includes main course, appetizer (starter), and dessert. The services of the restaurants include parking lot, live music, and free Wi-Fi connectivity.
Assume that the person uses the linguistic variables “No” (0), “Yes” (1), “Very Poor” (0), “Poor” (0.1), “Medium Poor” (0.3), “Medium” (0.5), “Medium Good”(0.7), “Good” (0.9), “Very Good” (1) “Very Far” (0), “Far” (0.1), “Medium Far” (0.3), “Medium Close”(0.7), “Close” (0.9), and “Very Close” (1) shown in Table 1 for describing the performance of each alternative with respect to these parameters. Thus, a three-polar fuzzy soft set (that is shown in Table 2) can help he/she to explain his/her opinion about these four restaurants. For example, if the person considers the meal of the restaurant , then the 3-tuple (1,0,0.5) means that the main course of the restaurant is very good while the starter and the dessert are very poor and medium, respectively.
Definition 4. Let be a family of M-pFSSs over the common universe U and parameter sets . Then, for any :
- 1.
if and for all and .
- 2.
, for all .
- 3.
, for all .
Proposition 1. Let U and F be the universal sets of objects and parameters, respectively, and , and E are some subsets of F. Assume that , and are some m-polar fuzzy soft sets over U where for all , and . Then:
- 1.
, and and .
- 2.
(Idempotent) and .
- 3.
(Commutative) and .
- 4.
(Associative) and
.
- 5.
(Distributive) and
.
Proof. Trivial by Definitions 3 and 4. □
Proposition 2 (De Morgan Law)
. Let U and F be the universal sets of objects and parameters, respectively. Assume that and are two m-polar fuzzy soft sets over U where P and Q are the subsets of F and for all and . Then:
- 1.
.
- 2.
.
Proof. It is proved easily by Definitions 3 and 4. □
3.2. The M-pFSMWM Operator
In this subsection, we develop the M-pFSMWM operator in the domain of M-pFSSs. This new aggregation operator is used to reach the process of consensus in group decision-making problems with weighted m-polar fuzzy soft inputs. Additionally, we show the M-pFSMWM is a well-defined operator having the behavioral properties.
Let
be a collection of m-polar fuzzy soft sets over
U and
P, such that for all
k:
for
and
where
refers to as the multiplication of
m-times, with non-negative weights
where
. In the following, we develop a new weighted aggregation operator for m-polar fuzzy soft sets (M-pFSMWM operator) based on the weighted minimum operator given in Equation (
1) and M-pFS maximum defined in Definition 4.
Definition 5 (M-pFSMWM Operator)
. Let be a collection of m-polar fuzzy soft sets over U and P with non-negative weights such that . Let value α where be the required consensus degree. An M-pFSMWM operator of dimension K and at consensus degree α is a mapping that is defined byfor and where the sum refers to as the weighted minimum over different choices α of K, σ is the permutation operator, is the binomial coefficient, and is an indexing set, where , including lth α-combination from a set of K elements. Thus, traverses all the α-combinations of the set and represents the th element in lth α-combination of K for feature s; . In the following, the various properties of M-pFSMWM operator including idempotency, boundedness, monotonicity, and commutativity (symmetry) are discussed.
Theorem 2. Let and , for , be two collections of some m-polar fuzzy soft sets over U and P with non-negative weights that for all k: and . Let the required consensus degree α is given. Then, the M-pFSMWM operator has the following properties.
- 1.
(Idempotency) If for all k, then - 2.
- 3.
(Monotonicity) If for all k, then - 4.
- 5.
(Commutativity or Symmetry)where σ is any permutation of ;
Proof. Let for all k:
. Thus, it is clear that the distinct α-combinations of
K objects is reduced to the trivial case
K-combination of
K with
and
for all
k, i.e., the unweighted case. Thus,
since
.
First, assume for all k: . Then, by Property 1 of Theorem 2, we have . The property follows the similar way for , .
Let for all k. Then, for each : . Thus, the condition is hold since : , for any l of the possible choices of K.
Let for and : and for each . Then, for all k: where and . Hence, by Properties 1 and 3 of Theorem 2, the inequality holds.
It is trivial from Definition 5.
□
Theorem 3. Let , where , be some m-polar fuzzy soft sets over U and P such that for all k: for and , with non-negative weights where . Then, the aggregated value is still an m-polar fuzzy soft set over U.
Proof. Let
be a set of m-polar fuzzy soft arguments. Since, for each
k,
, then clearly by Theorem 2 we have
. This means that
. Now, define the function
such that for any
and
,
, given by Equation (
5), which is an m-tuple of real numbers in the unit interval
. This shows the
operator of m-polar fuzzy soft sets is still an m-polar fuzzy soft set.
Remark 1. According to Definition 5 and Theorem 3, weights in M-pFSMWM operator first re-order the position of arguments, means in the re-ordered list the first object has the biggest weight. Then, the aggregated value is computed based on the weighting vector related to the m-polar fuzzy soft sets . Thus, the weights reflect positions and importance degrees of input arguments in the aggregated value in comparison with IOWA and IOWG operators where weights only show the position of arguments. Moreover, if α shows the consensus degree, then the α-combinations of set express different scenarios of agreement among K decision makers where the decision of first, second, …, and last α individuals are checked one by one. Further, by choosing , all possible choices of agreement between K experts at consensus degree α are considered. Thus, the concept of fuzzy majority, expressed by linguistic variables such as “half plus one”, “more than 75%”, “most”, and “almost all” can be taken into account by choosing if K is an even number and if K is an odd number.
From Theorems 2 and 3, the operator degenerates to some special aggregation operators as follows.
Theorem 4. Let be a set of m-polar fuzzy soft sets over U with non-negative weights that, for all k, and . Then, the operator degenerates to some special aggregation operators as follows.
- 1.
If i.e., for and for , then - 2.
When , we havewhich is called the M-pFS weighted minimum operator. - 3.
When : if , thenwhich is the M-pFS minimum operator. - 4.
When : if ; and and for all , thenwhich is the M-pFS maximum operator. - 5.
When : If ; and and for all , then
Proof. Let
, then in any lth α-combination of
K objects involving jth element, the value of
for
and
is interpreted as the first object, i.e.,
, where
and for rest
. Thus, by using Equation (
5):
.
Let
. Then, we have
(only one trivial combination) and thus
. Hence, by Equation (
5):
When , then the resultant weighted minimum in Part 2 of Theorem 4 acts as the standard (unweighted) minimum operator. Thus, the operator is derived by the minimum operator, easily.
When and for all , then by Part 1 of Theorem 4 we have that is the largest argument since , i.e., the operator is derived by the maximum operator.
When and for all , then by Part 1 of Theorem 4 we have that is the lowest argument since , i.e., the operator is derived by the minimum operator.
□
4. Application of M-pFSMWM Operator in Group Decision-Making
In this section, the M-pFSMWM operator is applied to handle group decision-making problems with weighted m-polar fuzzy soft inputs.
In a group decision-making problem with m-polar fuzzy soft information, let and be the finite sets of alternatives and parameters, respectively, where is the weighting vector for the parameter set P such that : and . Additionally, let each be a multi-polar parameter with m different aspects or features such that is the weighting vector for the parameter where : and . Suppose that is the set of decision makers and is the weighting vector of where, for all k: and . Assume that each decision maker applies an m-polar fuzzy soft set to present the linguistic evaluation about alternatives such that and each shows the satisfaction degree of alternative about feature s of attribute . Moreover, let the required consensus degree α mean an alternative may be selected if it is acceptable for at least α individuals.
After each expert prepares a linguistic or numerical judgment of alternatives based on the parameters
, the first stage is to reach consensus among a fuzzy majority or a partial agreement of them. This step is handled through the proposed aggregation operator M-pFSMWM by Equation (
5) of the previous
Section 3. The second stage of a MAGDM problem aims to find the best option with respect to the collective view. Thus, a ranking procedure is needed to derive the optimum choice. In the following subsections, we first define a fuzzy soft preference relationship over the universe
U based on the collective view obtained by M-pFSMWM operator and then, propose a new score value function for ranking the preference order of objects.
4.1. A Fuzzy Soft Preference Relationship
The aim of this section is to define an square matrix based on a fuzzy soft preference relationship over the set of alternatives U.
Let the m-tuple
present the performance of alternative
based on parameter
and collective view obtained by M-pFSMWM operator. We define a fuzzy soft preference relationship on
U by the mapping
where for each
,
is a fuzzy preference relationship on
U which is characterized by the membership function
. For any
we define
such that
Definition 6. Suppose that is the set of alternatives and is a parameter including m different aspects . Let show the weighting vector for parameter where . If is the fuzzy preference relationship on U defined by (
6)
, then the matrix defined bywhere interprets the degree of preference of the alternative over the alternative with respect to the parameter . Moreover, for all . In Definition 6,
shows indifference between
and
based on the parameter
, which is represented by
, while
shows
is preferred to
based on the parameter
at degree
, i.e.,
. Moreover, the fuzzy soft preference relationship
can be represented by matrix
where each entry
is in fact the
matrix
. Hence, we have
Proposition 3. The fuzzy preference relationship clearly satisfies the following statements:
- 1.
- 2.
- 3.
If and , then .
for all and .
Proof. Item 1 is easily checked by Equation (6). Parts 2 and 3 are obtained by using and ( see also Theorem 1). □
Proposition 3 says that the fuzzy preference relationship satisfies the reciprocity and the restricted max-max transitivity. This means that, if and , then .
Definition 7. Let be the matrix defined in Definition 6. Then, the matrix defined bywhere is an M-polar fuzzy preference relationship on U characterized by the membership function and, for , shows the degrees of preference of the alternative over the alternative with respect to the parameter set P. For each y: if , if , and if . Clearly, for all i, each entry . For all : shows indifference between and based on parameter set P, which is represented by , while shows is preferred to () for all parameters.
Proposition 4. The following statements hold for M-polar fuzzy preference relation .
- 1.
.
- 2.
If , then .
- 3.
If and , then .
for all .
Proof. It is obtained easily by Proposition 3. □
4.2. An Approach to Group Decision-Making Based on M-pFSMWM Operator
The second stage of a group decision-making is to reach the process of selection based on an overall performance of alternatives in terms of the crisp or partial agreement among the experts. In this section, we introduce a new procedure for solving group decision-making problems based on the M-pFSMWM operator and the pairwise comparisons of alternatives that are obtained by the
matrix
defined in Equation (
8).
By using Definitions 6 and 7, a new overall score value function over the universe U is defined as below.
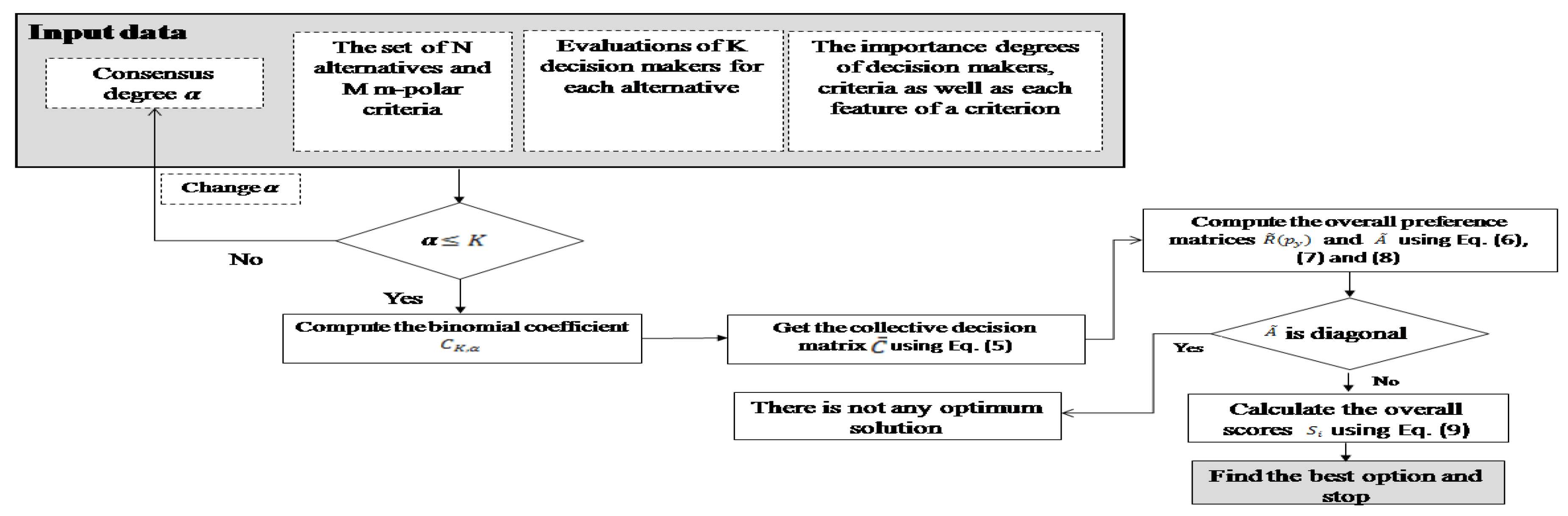
Definition 8. The mapping defined byfor is called the score value function over U where shows the importance degree of parameter and is the entry in ith row and jth column of matrix . In the following, we apply the M-pFSMWM operator for solving MAGDM problems based on m-polar fuzzy soft information (Algorithm 1).The proposed procedure uses Equation (
9) for ranking the preference order of objects. We also clarify the idea of the proposed method in Algorithm 1 by the given flowchart in
Figure 1.
| Algorithm 1. Finding the optimum solution in MAGDM problems based on M-pFSMWM operator for M-pFSSs. |
![Symmetry 10 00636 i001 Symmetry 10 00636 i001]() |
Remark 2 (Analysing Algorithm 1)
. Let K decision makers evaluate N number of alternatives based on M number of parameters where the m-polar fuzzy soft sets are applied to present their linguistic evaluations of the alternatives. According to Algorithm 1, we first utilize the M-pFSMWM operator to obtain a collective view of decision makers. The M-pFSMWM operator allows us to have not only partial agreement within a group, such as “almost all”, “most”, “more than half” etc., but also different choices for a partial agreement at the consensus degree α.
To this end, Algorithm 1 starts with finding the subsets where . This helps us to check all possible cases of agreement between K decision makers at consensus level α. In fact, the value of α shows the number of possible iterations of Algorithm 1 (). By repeating Steps 1 and 2 for different value α until , the aggregated value moves from the minimum value to the maximum value. This guaranties Algorithm 1 is convergent (please also see Theorems 2 and 4). Then, at Step 3, matrix is driven. Each entry of shows the performance of alternative based on parameter and the collective view of experts at degree α. In Step 4, the fuzzy preference relations (for ) give a comparison of objects based on the collective view of decision makers and each parameter . The information of matrices are then converted to the M-polar fuzzy soft preference relation , in Step 5, for providing comparison results where defined by if , if , otherwise . Moreover, if is an upper triangle matrix such that ; for ; and for , then we have the following descending chain on U. If is a lower triangle matrix such that ; for ; and for , then we have the ascending chain on U. However, if is a diagonal matrix, then there is no optimal option on U. In the last step of Algorithm 1, the best option is selected based on its rank in the resultant preference order. For MAGDM problems with benefit criteria, means more is better, the alternative with the highest score can be selected as the best option. However, for the problems dealing with cost criteria the counter condition should be considered.
5. The M-pFSIOWA and M-pFSIOWG Operators
To compare different m-polar fuzzy soft weighted aggregation operators with the proposed operator in
Section 3.2, in this section, we develop the m-polar fuzzy soft induced ordered weighted average (M-pFSIOWA) operator and m-polar fuzzy soft induced ordered weighted geometric (M-pFSIOWG) operator, which are the extensions of IOWA and IOWG operators, respectively. The re-ordering step of M-pFSIOWA and M-pFSIOWG operators are defined based on the weights of arguments
. Since the M-pFSIOWA and M-pFSIOWG operators are defined in the domain of M-pFSSs, these new families of IOWA and IOWG operators give more general methods for aggregating data than traditional IOWA and IOWG operators.
Motivated by development of OWA operator and OWG operator for FSs [
38,
39] and IFSSs [
21], the extensions of these two aggregation operators for M-pFSSs are defined as below.
Definition 9. - 1.
The M-pFSIOWA operator of dimension k is the mapping such that for an associated weighting vector , where and , is defined as below: - 2.
The M-pFSIOWG operator of dimension k is the mapping such that for an associated weighting vector , where and , can be defined by
where is the kth value having the jth largest of the weighting vector for M-pFSSs .
The main steps of these operations are the re-ordering step according to the weighting vector and then determining the associated weighting vector to the aggregation operators M-pFSIOWA and M-pFSIOWG. Here, for each , , and , the collection: is re-ordered as where the weighting vector shows the weights of different decision makers.
Theorem 5. Let , where , is some m-polar fuzzy soft set over U and P such that for all : for and , with non-negative weights where . Then, the aggregated value and are still an m-polar fuzzy soft set over U.
Proof. Define the function such that for any and , or . Then, the assertion is trivial from , , , and convexity of . □
The following properties are inherited to M-pFSIOWA and M-pFSIOWG operators from IOWA operator and IOWG operator, respectively.
Theorem 6. Let be some m-polar fuzzy soft sets over U and P with non-negative weights where . Let be the associated weighting vector to the M-pFSIOWA and M-pFSIOWG operators. Then,
- 1.
(Idempotency) If , thenand - 2.
(Monotonicity) If , thenand - 3.
- 4.
(Commutativity or Symmetry)andwhere σ is any permutation of .
We can also obtain some spacial cases of M-pFSIOWA and M-pFSIOWG operators by using different choices for .
Theorem 7. Let be some m-polar fuzzy soft sets over U and P with non-negative weights where . Let be the associated weighting vector to the M-pFSIOWA and M-pFSIOWG operators. Then, the M-pFSIOWA operator and M-pFSIOWG operator degenerate to some special aggregation operators as follows.
- 1.
If , thenwhich we call the m-polar fuzzy soft arithmetic average operator, andwhich we call the m-polar fuzzy soft geometric average operator. - 2.
If , thenand - 3.
If , thenand
Application of M-pFSIOWA and M-pFSIOWG Operators in Group Decision-Making
In this section, similar to Algorithm 1, we apply the M-pFSIOWA operator and M-pFSIOWG operator to propose a procedure for solving MAGDM problems with M-pFS inputs as the following Algorithm 2.
| Algorithm 2. Finding the optimum solution in MAGDM problems based on M-pFSIOWA or M-pFSIOWG operators for M-pFSSs. |
![Symmetry 10 00636 i002 Symmetry 10 00636 i002]() |
Remark 3. Note that Algorithm 2 starts with computing matrix based on M-pFSIOWA or M-pFSIOWG operators rather than the M-pFSMWM operator used in Algorithm 1. In Steps 2 and 3, the entries of the resultant matrix are used to compute the matrices and . Then, Algorithm 2 is followed similarly with Algorithm 1.
Here, by repeating Step 1 for different iteration value α until , the aggregated value computed by M-pFSIOWA operator or M-pFSIOWG operator moves between the minimum value and the maximum value (please see Theorems 6 and 7). This guarantees Algorithm 2 is also convergent.
7. Discussion
To date, various soft set-based techniques have been applied to solve decision-making problems. Some of them have proposed novel methodology to find the solution [
18,
22,
27,
28], while some authors have made effort to adapt the well-known decision-making methods, such as SAW, TOPSIS, entropy, OWA, and OWG to the soft set theory [
15,
16,
21,
40,
41]. However, a technique to solve decision-making problems based on m-polar fuzzy soft information has not been studied yet. Thus, new methodologies are proposed to handle the consensus stage and selection stage of MAGDM problem with M-pFS inputs.
For aggregating input data which take their values from
, some new m-polar aggregating methods, called M-pFSMWM operator, M-pFSIOWA operator, and M-pFSIOWG operator, are developed in
Section 3 and
Section 5. The properties comparison of these operators are summarized in
Table 9. It can be seen that the most interesting property of M-pFSMWM operator is it is sensitive for different scenarios of a partial agreement at the consensus degree α. This characteristic makes the M-pFSIOWA operator more adaptable for MAGDM problem in which not only the number of individuals satisfying an alternative is important but also the weight of decision makers who agree with this decision affect the final output. Moreover, by changing the value of consensus degree α different cases of agreement are obtained. In particular, when
, the partial agreement becomes a full agreement.
To reach the process of selection, we propose two procedures in
Section 4.2, Algorithm 1 where the consensus stage is reached based on the new M-pFSMWM operator, and
Section 5, Algorithm 2 in which the consensus stage is obtained by M-pFSIOWA or M-pFSIOWG operators are extended based on IOWA and IOWG, respectively. To reach the selection stage a new score value function, described by Equation (
9), is applied. The main advantage of the proposed formulation is to rank and compare objects based on a collective m-polar fuzzy soft preference relationship. This allows us to have a ranking system of alternatives, from the most preferred element to the least preferred element, which may include some incomparable objects because of preference relationships nature.
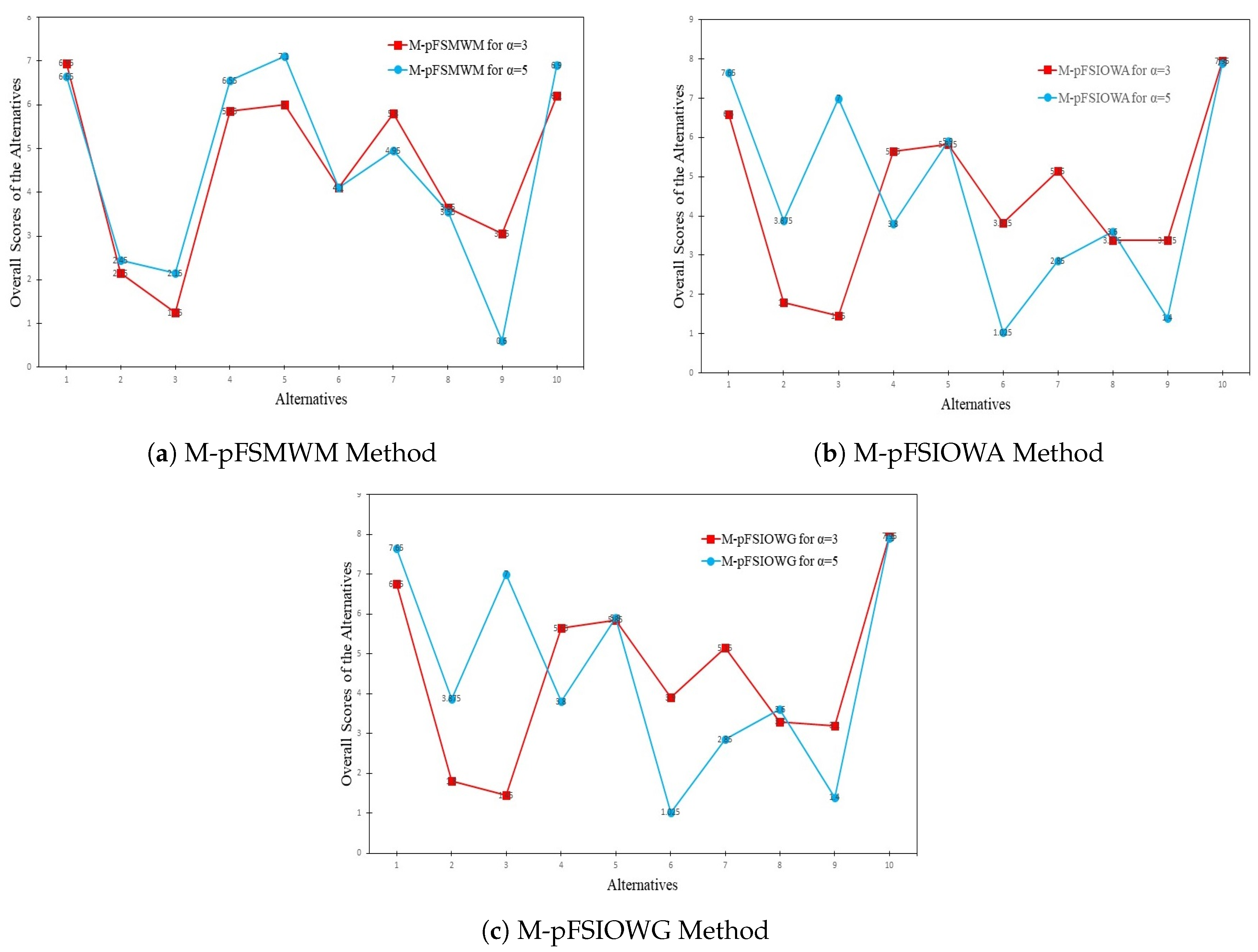
Illustrative examples, given in Examples 2 and 3, show the application of Algorithm 1 to analyze MAGDM problems with multi-polar fuzzy soft information. The obtained results are then compared with the m-polar fuzzy soft extensions of two well-known aggregation operators IOWA and IOWG, i.e., M-pFSIOWA and M-pFSIOWG, in Example 4.
Table 10 makes a comparison of the preference orders of the alternatives for methods using different aggregation operators including the new proposed M-pFSMWM method, the m-polar fuzzy soft induced ordered weighted average (M-pFSIOWA) method, and the m-polar fuzzy soft induced ordered weighted geometric (M-pFSIOWG) method. As can be seen, Hotel
is the best option for staying based on the all discussed methods except the M-pFSMWM-based method, where
is considered as the best second option for accommodation. According to final preference order obtained based on the M-pFSMWM operator, Hotel
, which has the second place based on the other methods, is the best option accepted by the majority, i.e.,
, of decision makers. Hotel
is the best place to stay in terms of all decision makers. The analysis derived in
Table 10 shows a good agreement among thees methods, however the number of computational steps in M-pFSMWM-based algorithm is
in comparison with
stages in Algorithm 2. On the other hand, the main disadvantage of M-pFSIOWA and M-pFSIOWG methods is that there is no unique approach to determine the associated weighting vector
related to the aggregation operators M-pFSIOWA and M-pFSIOWG. Finally, in
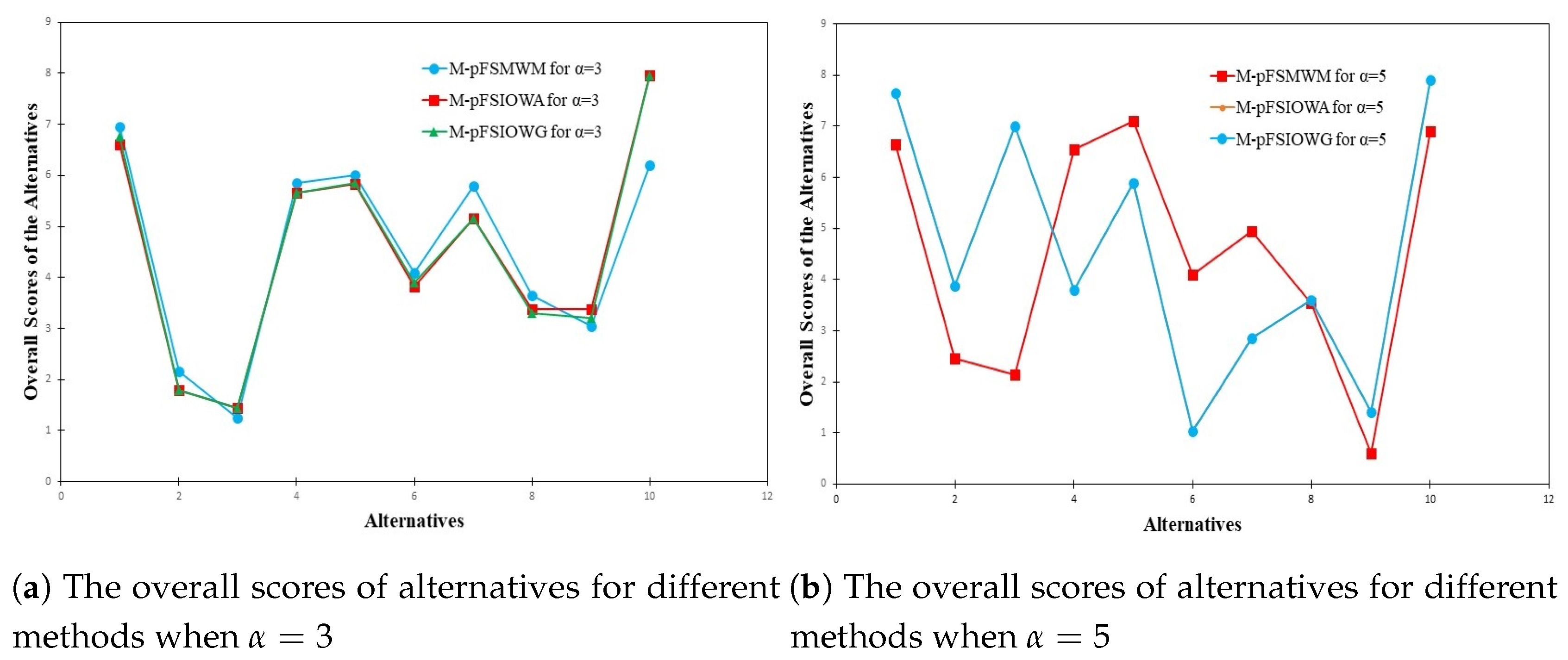
Figure 4a, the overall scores of alternatives based on the different methods for case
are shown.
Figure 4b shows the scores of alternatives obtained by using different methods for case
. Note that, using some relative preference matrices to find the scores of alternatives in all methods, leads to record a similar trend in
Figure 4b.