Detect User’s Rating Characteristics by Separate Scores for Matrix Factorization Technique
Abstract
1. Introduction
2. Related Work
3. Methods and Algorithms
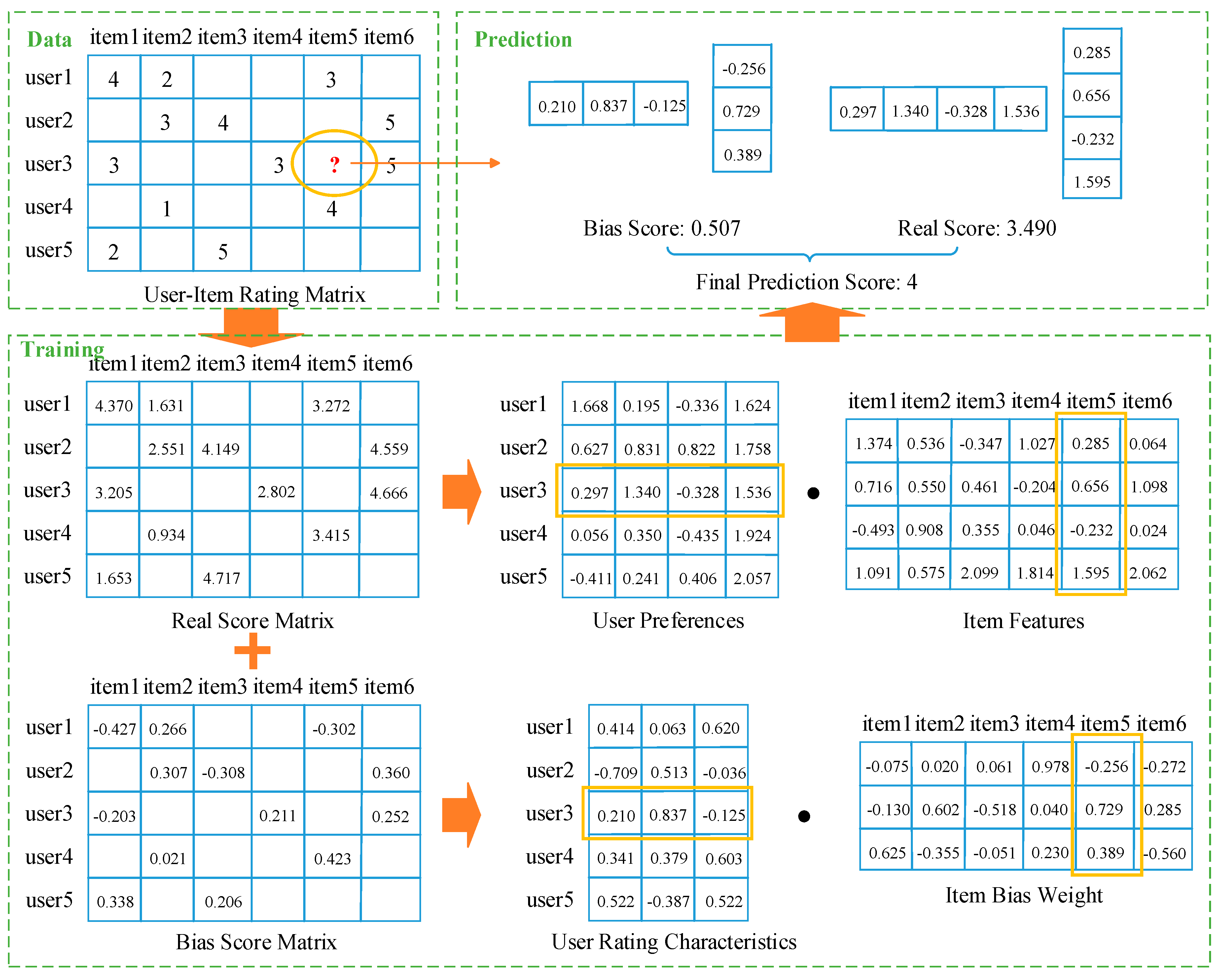
3.1. Constructing the Model
3.1.1. Real Score and Bias Score
3.1.2. User Preferences and Item Features
3.1.3. User Bias Features and Item Bias Weights
3.1.4. The Unified Model
3.2. The Solution of Our Method
- (1)
- keep and , update and ;
- (2)
- keep and , update and ;
3.2.1. The Updating Rules for and
3.2.2. The Updating Rules for and
3.2.3. Algorithm Overview
| Algorithm 1. Algorithm of Proposed Model |
| Input: User-item rating matrix Parameters , , , , , Output: Matrix , , and 1. Randomly initialize , , and ; 2. repeat 3. Compute and based on Equations (4) and (6); 4. for to do 5. Update according to Equation (15); 6. Update according to Equation (16); 7. end for 8. Go to step 3; 9. for to do 10. Update according to Equation (21); 11. Update according to Equation (22); 12. end for 13. until convergence |
4. Experimental Evaluation
4.1. Data Description
4.2. Evaluation Measures
4.3. Compared Methods
4.4. Experimental Results
- The experimental results show that the proposed method has the lowest MAE value in all rounds of tests, which means that our method has a higher prediction accuracy. Therefore, it is verified that considering the user’s rating characteristics can indeed improve the performance of the recommendation system.
- Although our algorithm has achieved the best results in all three datasets, the degree of improvement is different. By comparing with the best results of other algorithms, we reduced the MAE value by about 0.03 in MovieLens-100K, by nearly 0.04 in MovieLens-1M and by 0.02 in Epinions. By observing the statistics of the three datasets from Table 1, we believe that the reason for this difference may be due to the number of ratings per user. Because on the MovieLens-1M dataset, the average number of users’ rating times is the largest, reached about 165 times, which is very useful to get accurate user’s rating characteristics, while in Epinions, the average number of users rating times is only about 23, which brings a certain degree of difficulty to accurately get the user’s rating characteristics.
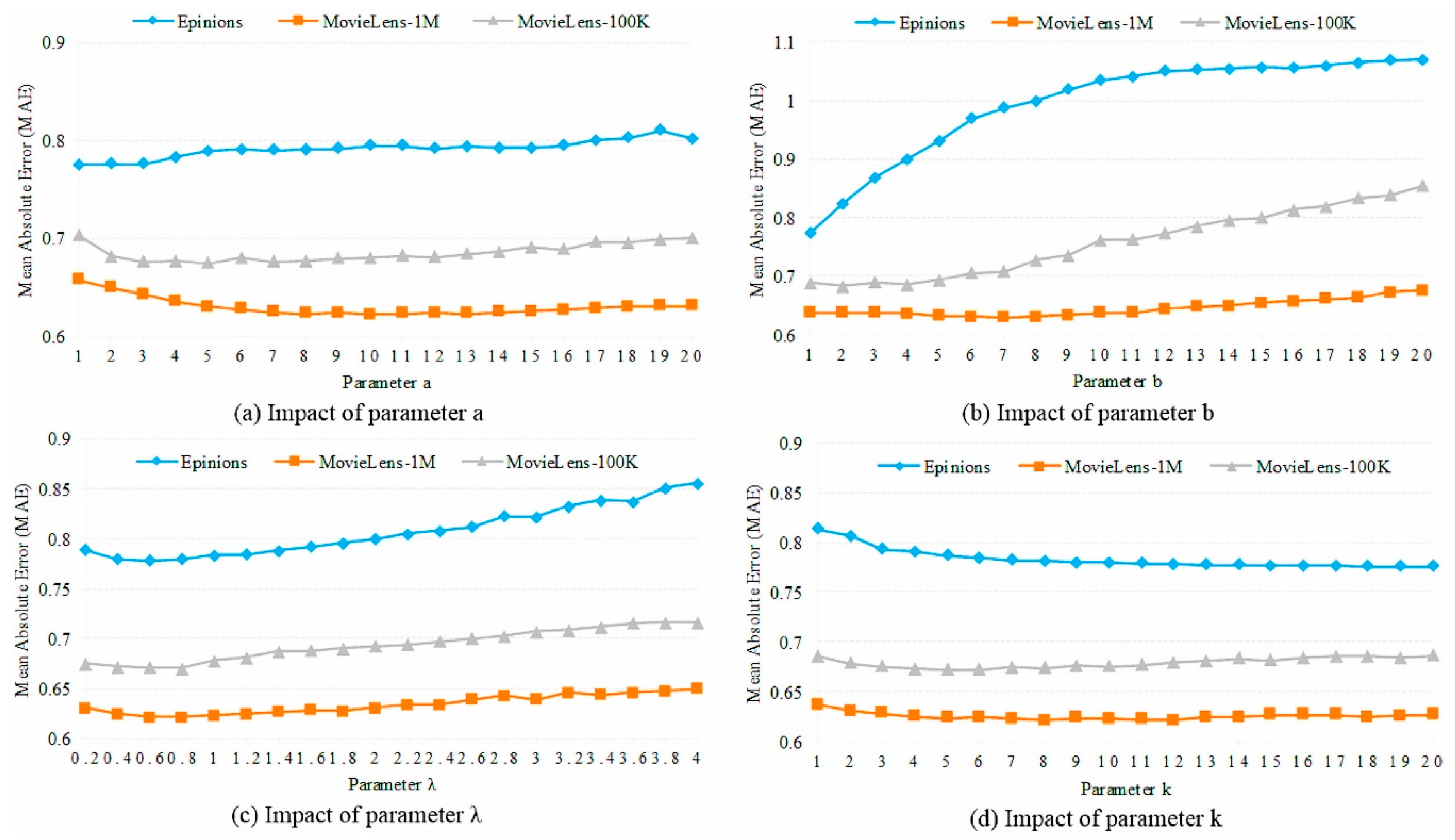
- We set different values for the parameter on the three datasets, which means that the more user rating times, the more complex the user’s rating characteristics we can get; thus, we need to use a higher dimensional vector to express bias features.
4.5. Experimental Results
4.5.1. Impact of
4.5.2. Impact of
4.5.3. Impact of and
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Felfernig, A.; Isak, K.; Szabo, K.; Zachar, P. The VITA financial services sales support environment. In Proceedings of the National Conference on Innovative Applications of Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; AAAI Press: Menlo Park, CA, USA, 2007; pp. 1692–1699. [Google Scholar]
- Petrevska, B.; Koceski, S. Tourism recommendation system: Empirical investigation. Revista De Turism Studii Si Cercetari in Turism 2012, 11, 11–18. [Google Scholar]
- Gomez-Uribe, C.A.; Hunt, N. The Netflix Recommender System. ACM Trans. Manag. Inf. Syst. 2015, 6, 1–19. [Google Scholar] [CrossRef]
- Schafer, J.B.; Dan, F.; Herlocker, J.; Sen, S. Collaborative Filtering Recommender Systems. The Adaptive Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 291–324. [Google Scholar]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 421425. [Google Scholar] [CrossRef]
- Huang, Z.; Zeng, D.; Chen, H. A comparison of collaborative-filtering recommendation algorithms for e-commerce. IEEE Intell. Syst. 2007, 22, 68–78. [Google Scholar] [CrossRef]
- Stai, E.; Kafetzoglou, S.; Tsiropoulou, E.E.; Papavassiliou, S. A holistic approach for personalization, relevance feedback & recommendation in enriched multimedia content. Multimedia Tools Appl. 2016, 77, 1–44. [Google Scholar]
- Pouli, V.; Kafetzoglou, S.; Tsiropoulou, E.E.; Dimitriou, A.; Papavassiliou, S. Personalized multimedia content retrieval through relevance feedback techniques for enhanced user experience. In Proceedings of the 13th International Conference on Telecommunications (ConTEL), Graz, Austria, 13–15 July 2015; pp. 1–8. [Google Scholar]
- Takács, G.; Pilászy, I.; Németh, B.; Tikk, D. Investigation of various matrix factorization methods for large recommender systems. In Proceedings of the 2nd KDD Workshop on Large-Scale Recommender Systems and the Netflix Prize Competition, Las Vegas, NV, USA, 24–27 August 2008; ACM: New York, NY, USA, 2008; p. 6. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 8. [Google Scholar] [CrossRef]
- Breese, J.S.; Heckerman, D.; Kadie, C. Empirical analysis of predictive algorithms for collaborative filtering. In Proceedings of the Fourteenth conference on Uncertainty in artificial intelligence, Madison, WI, USA, 24–26 July 1998; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998; pp. 43–52. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Borchers, A.; Riedl, J. An algorithmic framework for performing collaborative filtering. In Proceedings of the 22nd annual international ACM SIGIR conference on Research and development in information retrieval, Berkeley, CA, USA, 15–19 August 1999; ACM: New York, NY, USA, 1999; pp. 230–237. [Google Scholar]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th international conference on World Wide Web, Hong Kong, China, 1–5 May 2001; ACM: New York, NY, USA, 2001; pp. 285–295. [Google Scholar]
- Vucetic, S.; Obradovic, Z. Collaborative filtering using a regression-based approach. Knowl. Inf. Syst. 2005, 7, 1–22. [Google Scholar] [CrossRef]
- Xu, B.; Bu, J.; Chen, C.; Cai, D. An exploration of improving collaborative recommender systems via user-item subgroups. In Proceedings of the 21st international conference on World Wide Web, Lyon, France, 16–20 April 2012; ACM: New York, NY, USA, 2012; pp. 21–30. [Google Scholar]
- O’Connor, M.; Herlocker, J. Clustering items for collaborative filtering. In Proceedings of the ACM SIGIR workshop on recommender systems, Berkeley, CA, USA, 19 August 1999; p. 128. [Google Scholar]
- Miyahara, K.; Pazzani, M. Collaborative filtering with the simple Bayesian classifier. In PRICAI 2000 Topics in Artificial Intelligence, Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Melbourne, VIC, Australia, 28 August–1 September 2000; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1886. [Google Scholar]
- Mori, K.; Nguyen, T.; Harada, T.; Thawonmas, R. An Improvement of Matrix Factorization with Bound Constraints for Recommender Systems, Advanced Applied Informatics (IIAI-AAI). In Proceedings of the 5th IIAI International Congress on IEEE, Kumamoto, Japan, 10–14 July 2016; pp. 103–106. [Google Scholar]
- Kunaver, M.; Fajfar, I. Grammatical Evolution in a Matrix Factorization Recommender System. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 12–16 June 2016; pp. 392–400. [Google Scholar]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Application of Dimensionality Reduction in Recommender System-A Case Study; DTIC Document. Technology Report; Minnesota Univ Minneapolis Dept of Computer Science: Minneapolis, MN, USA, 2000. [Google Scholar]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2001, 556–562. [Google Scholar]
- Yu, K.; Zhu, S.; Lafferty, J.; Gong, Y. Fast nonparametric matrix factorization for large-scale collaborative filtering. In Proceedings of the 32nd international ACM SIGIR conference on Research and development in information retrieval, Boston, MA, USA, 19–23 July 2009; ACM: New York, NY, USA, 2009; pp. 211–218. [Google Scholar]
- Srebro, N.; Rennie, J.D.; Jaakkola, T.S. Maximum-margin matrix factorization. In Proceedings of the Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2004; Volume 17, pp. 1329–1336. [Google Scholar]
- Zhang, G.; He, M.; Wu, H.; Cai, G.; Ge, J. Non-negative multiple matrix factorization with social similarity for recommender systems. In Proceedings of the 3rd IEEE/ACM International Conference on Big Data Computing, Applications and Technologies, Shanghai, China, 6–9 December 2016; ACM: New York, NY, USA, 2016; pp. 280–286. [Google Scholar]
- Liang, D.; Altosaar, J.; Charlin, L.; Blei, D.M. Factorization meets the item embedding: Regularizing matrix factorization with item co-occurrence. In Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; ACM: New York, NY, USA, 2016; pp. 59–66. [Google Scholar]
- Wibowo, A.T. Generating pseudotransactions for improving sparse matrix factorization. In Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; ACM: New York, NY, USA, 2016; pp. 439–442. [Google Scholar]
- Ortega, F.; Hernando, A.; Bobadilla, J.; Kang, J.H. Recommending items to group of users using Matrix Factorization based Collaborative Filtering. Inf. Sci. 2016, 345, 313–324. [Google Scholar] [CrossRef]
- Adamopoulos, P.; Tuzhilin, A. On Unexpectedness in Recommender Systems: Or How to Better Expect the Unexpected. ACM Trans. Intell. Syst. Technol. 2014, 5, 1–32. [Google Scholar] [CrossRef]
- Wang, J.; Liu, R.; Liu, Y. Non-negative Matrix Factorization Algorithm with Bias in Recommender System. J. Chin. Comput. Syst. 2018, 39, 69–73. [Google Scholar]
- Koren, Y. Collaborative filtering with temporal dynamics. Commun. ACM 2010, 53, 89–97. [Google Scholar] [CrossRef]
- Herlocker, J.L.; Konstan, J.A.; Terveen, L.G.; Riedl, J.T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. 2004, 22, 5–53. [Google Scholar] [CrossRef]
- Bedi, P.; Gautam, A.; Sharma, C. Using novelty score of unseen items to handle popularity bias in recommender systems. In Proceedings of the International Conference on Contemporary Computing and Informatics, Mysore, India, 27–29 November 2014; pp. 934–939. [Google Scholar]
- Abdollahpouri, H.; Burke, R.; Mobasher, B. Controlling Popularity Bias in Learning-to-Rank Recommendation. In Proceedings of the Eleventh ACM Conference on Recommender Systems, Como, Italy, 27–31 August 2017; ACM: New York, NY, USA. [Google Scholar]
- Collins, A.; Tkaczyk, D.; Aizawa, A.; Beel, J. Position Bias in Recommender Systems for Digital Libraries. In Transforming Digital Worlds, Proceedings of the Transforming Digital Worlds Conference, Sheffield, UK, 25–28 March 2018; Chowdhury, G., McLeod, J., Gillet, V., Willett, P., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Salakhutdinov, R.; Mnih, A. Probabilistic Matrix Factorization. NIPS 2007, 1, 1–2. [Google Scholar]
- Liu, J.; Jiang, Y.; Li, Z.; Lu, H. Domain-sensitive recommendation with user-item subgroup analysis. IEEE Trans. Knowl. Data Eng. 2016, 28, 939–950. [Google Scholar] [CrossRef]
- Kumar, V.; Pujari, A.K.; Sahu, S.K.; Kagita, V.R.; Padmanabhan, V. Proximal maximum margin matrix factorization for collaborative filtering. Pattern Recognit. Lett. 2017, 86, 62–67. [Google Scholar] [CrossRef]
- Hernando, A.; Bobadilla, J.; Ortega, F. A non-negative matrix factorization for collaborative filtering recommender systems based on a Bayesian probabilistic model. Knowl. Based Syst. 2016, 97, 188–202. [Google Scholar] [CrossRef]
- Liao, C.L.; Lee, S.J. A clustering based approach to improving the efficiency of collaborative filtering recommendation. Electron. Commer. Res. Appl. 2016, 18, 1–9. [Google Scholar] [CrossRef]
- Cai, Y.; Leung, H.; Li, Q.; Min, H.; Tang, J.; Li, J. Typicality-based collaborative filtering recommendation. IEEE Trans. Knowl. Data Eng. 2014, 26, 766–779. [Google Scholar] [CrossRef]
| MovieLens-100K | MovieLens-1M | Epinions | |
|---|---|---|---|
| # of users | 943 | 6040 | 15,687 |
| # of items | 1682 | 3952 | 11,657 |
| # of ratings | 100,000 | 1,000,209 | 354,857 |
| # of ratings per user | 106.4 | 165.60 | 22.62 |
| # of ratings per item | 59.45 | 253.09 | 30.44 |
| Rating Sparsity | 93.70% | 95.81% | 99.81% |
| IB | SVD | PMF | MCoC | DsRec | PMMMF | Hern | SCC | TyCo | Our | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.7325 | 0.7412 | 0.7248 | 0.7024 | 0.7105 | 0.7221 | 0.7068 | 0.7589 | 0.7356 | 0.6820 |
| 2 | 0.7290 | 0.7335 | 0.7213 | 0.7210 | 0.7098 | 0.7104 | 0.7087 | 0.7546 | 0.7247 | 0.6713 |
| 3 | 0.7329 | 0.7401 | 0.7205 | 0.7138 | 0.7122 | 0.7156 | 0.7080 | 0.7574 | 0.7289 | 0.6753 |
| 4 | 0.7432 | 0.7388 | 0.7280 | 0.7189 | 0.7201 | 0.7166 | 0.7133 | 0.7621 | 0.7301 | 0.6894 |
| 5 | 0.7405 | 0.7342 | 0.7235 | 0.7242 | 0.7164 | 0.7190 | 0.7064 | 0.7608 | 0.7298 | 0.6818 |
| avg | 0.7356 | 0.7376 | 0.7236 | 0.7197 | 0.7138 | 0.7167 | 0.7086 | 0.7588 | 0.7298 | 0.6800 |
| IB | SVD | PMF | MCoC | DsRec | PMMMF | Hern | SCC | TyCo | Our | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.7012 | 0.6956 | 0.6923 | 0.6824 | 0.6795 | 0.6745 | 0.6689 | 0.6913 | 0.6643 | 0.6247 |
| 2 | 0.6946 | 0.6915 | 0.6886 | 0.6836 | 0.6823 | 0.6757 | 0.6675 | 0.6874 | 0.6613 | 0.6231 |
| 3 | 0.7088 | 0.7013 | 0.6894 | 0.6876 | 0.6804 | 0.6742 | 0.6681 | 0.6902 | 0.6620 | 0.6221 |
| 4 | 0.6985 | 0.6950 | 0.6902 | 0.6824 | 0.6794 | 0.6750 | 0.6692 | 0.6895 | 0.6637 | 0.6222 |
| 5 | 0.7023 | 0.6968 | 0.6911 | 0.6853 | 0.6811 | 0.6762 | 0.6684 | 0.6908 | 0.6640 | 0.6264 |
| avg | 0.7011 | 0.6960 | 0.6903 | 0.6843 | 0.6805 | 0.6751 | 0.6684 | 0.6898 | 0.6631 | 0.6237 |
| IB | SVD | PMF | MCoC | DsRec | PMMMF | Hern | SCC | TyCo | Our | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.8622 | 0.8594 | 0.8574 | 0.8489 | 0.8122 | 0.8019 | 0.7984 | 0.8067 | 0.8011 | 0.7748 |
| 2 | 0.8678 | 0.8612 | 0.8591 | 0.8502 | 0.8094 | 0.8024 | 0.8012 | 0.8071 | 0.8042 | 0.7789 |
| 3 | 0.8712 | 0.8577 | 0.8563 | 0.8491 | 0.8130 | 0.8003 | 0.7990 | 0.8058 | 0.8037 | 0.7801 |
| 4 | 0.8638 | 0.8584 | 0.8575 | 0.8480 | 0.8105 | 0.8047 | 0.8005 | 0.8074 | 0.8020 | 0.7764 |
| 5 | 0.8694 | 0.8569 | 0.8579 | 0.8496 | 0.8117 | 0.8033 | 0.7991 | 0.8062 | 0.8041 | 0.7813 |
| avg | 0.8669 | 0.8578 | 0.8576 | 0.8492 | 0.8114 | 0.8025 | 0.7996 | 0.8066 | 0.8030 | 0.7783 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Sun, G. Detect User’s Rating Characteristics by Separate Scores for Matrix Factorization Technique. Symmetry 2018, 10, 616. https://doi.org/10.3390/sym10110616
Zhao J, Sun G. Detect User’s Rating Characteristics by Separate Scores for Matrix Factorization Technique. Symmetry. 2018; 10(11):616. https://doi.org/10.3390/sym10110616
Chicago/Turabian StyleZhao, Jia, and Gang Sun. 2018. "Detect User’s Rating Characteristics by Separate Scores for Matrix Factorization Technique" Symmetry 10, no. 11: 616. https://doi.org/10.3390/sym10110616
APA StyleZhao, J., & Sun, G. (2018). Detect User’s Rating Characteristics by Separate Scores for Matrix Factorization Technique. Symmetry, 10(11), 616. https://doi.org/10.3390/sym10110616




