Abstract
In the algebra of single-valued structures, cyclicity is one of the fundamental properties of groups. Therefore, it is natural to study it also in the algebra of multivalued structures (algebraic hyperstructure theory). However, when one considers the nature of generalizing this property, at least two (or rather three) approaches seem natural. Historically, all of these had been introduced and studied by 1990. However, since most of the results had originally been published in journals without proper international impact and later—without the possibility to include proper background and context-synthetized in books, the current way of treating the concept of cyclicity in the algebraic hyperstructure theory is often rather confusing. Therefore, we start our paper with a rather long introduction giving an overview and motivation of existing approaches to the cyclicity in algebraic hyperstructures. In the second part of our paper, we relate these to -hyperstructures, a broad class of algebraic hyperstructures constructed from (pre)ordered (semi)groups, which were defined and started to be studied much later than sources discussed in the introduction were published.
1. Introduction, Preliminaries and Historical Context
The notion of cyclicity in group theory is one of the first notions that all university students learn in their introductory courses of algebra. Usually, the additive group of integers serves as an example of an infinite cyclic group while its decomposition modulo n serves as an example of a finite cyclic group. In the algebraic hyperstructure theory, which was initiated by Marty [1], the notion of cyclicity was one of the very first topics to be noticed. In fact, only three years after Marty (or rather a year and a half; see “Received” date), Wall touched this problem in one of the concluding remarks of his paper [2]. His definition uses plain words yet the mathematization of his idea is an obvious analogy of group cyclicity. After Wall, the notion of cyclicity was studied only by a small number of authors (to a great depth, though). Until the 1990s, we can observe two schools which picked up this topic: an Italian one represented by De Salvo, Freni, Corsini and Bonansinga and a Greek one represented by Vougiouklis, Konguetsof, Kessoglides and Spartalis.
1.1. The Origins by Wall
Prior to including Wall’s definition, we recall the well-known definition of the (algebraic) hypergroup.
Definition 1.
By a hypergroupoid, we mean a pair , where “*” is a mapping , where is the set of all non-empty subsets of H. By a hypergroup, we mean a hypergroupoid which is associative, i.e., for all , there is , and reproductive, i.e., for all , there is . An associative hypergroupoid is called semihypergroup; a reproductive hypergroupoid is called quasihypergroup.
Definition 2
([2], p. 96). If a hypergroup H is generated by a single element a of H, then H will be called a cyclic hypergroup.
After defining cyclic hypergroups, Wall observed that: “In a cyclic hypergroup the commutative law does not necessarily hold. We may write
and clearly . It is evident that the set of elements generated by a single element of a hypergroup is closed, …, but I am unable to say whether or not it forms a hypergroup”, and then he sought some analogy of the representation of a cyclic group as the group of rotations of a regular polygon.
1.2. The Original Approach of De Salvo and Freni
The Italian school linked the concept of cyclicity to the concept of completeness in hypergroups—see, e.g., De Salvo and Freni [3]—because complete hypergroups were being studied by Freni, Corsini, De Salvo, Romeo and others [3,4,5,6] at around that time. It is important to notice that the first papers of the Italian school concerning cyclicity such as Freni [7] or De Salvo and Freni [3,8] do not mention Wall’s paper at all. Also worth mentioning is the fact that most of the papers of the Italian school were written in Italian (and published in Italian university journals) and some in French. Unlike Wall, the Italian school studied the notion of cyclicity not only for hypergroups, but also for semihypergroups De Salvo and Freni [8] and later even for hypergroupoids Freni [9].
Even though not mentioning Wall, the Italian school originally viewed cyclicity in hypergroups in the same way as he did: a (hyper)group (or, rather, a semihypergroup in their case) is called cyclic, if we obtain the whole (hyper)group when a (hyper)operation is repeatedly applied on a certain element called a generator.
Definition 3
([3,8]). We call , , a cyclic part of a semihypergroup H if there exists an element such that, for all , there exists such that . The element is called generator of P. If H is a cyclic part, we call H a cyclic semihypergroup.
Notice that this need not be the same for all , which becomes important when one considers the below Definition 5. Of course, when considering cyclic (hyper)structures, it is useful to consider the concept of cyclicity of an element. This can be found already in De Salvo and Freni [3,8].
Definition 4
([3,8]). Let H be a cyclic semihypergroup with generator h. We call cyclicity (Italian: ciclicità) of an element the minimum such that ; we write . We call cyclicity of Hand denote .
1.3. The Approach of Vougiouklis
Not knowing of the Italian school, Vougiouklis [10] picked up the original Wall’s definition and—in a paper published in English at around the same time as Freni [7], De Salvo and Freni [3,8] and other notable papers of the Italian school—he initiated the study of P-cyclic hypergroups, or rather cyclicity in hypergroups related to P–hyperoperations. The definition of Vougiouklis is rather wide in order to describe as many types of cyclicity as possible. In the same way as Wall (and unlike the Italians who started from semihypergroups), Vougiouklis considered cyclicity in hypergroups. However, one can see that the Italian Definition 3 is, for hypergroups, a special case of his definition. Moreover, notice that the concept of period n is different from . Indeed, if two generators of a cyclic hypergroup H have a different period, then H has no period, yet its cyclicity can be determined.
Definition 5
([10]). A hypergroup is called cyclic if, for some , there is
where and . If there exists such that Formula (1) is finite, we say that H is a cyclic hypergroup with finite period; otherwise, H is a cyclic hypergroup with infinite period. The element in Formula (1) is called generator of H, the smallest power n for which Formula (1) is valid is called period of h. If all generators of H have the same period n, then H is called cyclic with period n. If, for a given generator h, Formula (1) is valid but no such n exists (i.e., Formula (1) cannot be finite), then H is called cyclic with infinite period. If we can, for some , write
Then, the hypergroup H is called single-power cyclic with a generator h. If Formula (1) is valid and for all and, for a fixed , there is
then we say that H is a single-power cyclic hypergroup with an infinite period for h.
By a P–hyperoperation, Vougiouklis means a hypergroupoid constructed from a commutative group and its arbitrary subset P using the hyperoperation
defined for all , where e is the unit element of . In [10], Vougiouklis shows that is a hypergroup which is—if we start with a cyclic group–cyclic in the sense of Definition 5. Later in the paper and also in Konguetsof et al. [11] or Vougiouklis [12], some criteria for elements of H and its generators are established; a great number of other results in this direction can be found in the PhD thesis of Vougiouklis defended in 1980 and called “Cyclicity of hypergroups”.
1.4. An Alternative Approach of the Italian School
In a series of papers published mainly in Italian between 1980 and 1986 (notice that many of the Italian papers were written simultaneously or their “in print” versions are cross referenced), members of the Italian school, which apart from De Salvo and Freni included also Corsini, Romeo or Bonansinga, provided (under the influence of Koskas, Mittas and Sureau) a great number of results on notions such as completeness of hypergroups, complete closures, complete parts, subhypergroups generated by some elements of a hypergroup, etc. In [13] (published in 1986 but cited already in De Salvo [14], which was received in 1984), De Salvo and Freni studied subhypergroups generated by one element, where by “generating” we mean the intersection of all subhypergroups which are complete parts and contain the element in question. They called such hypergroups strongly cyclic (“fortemente ciclici”) and observed that there exists a connection between this kind of generating and the property of cyclicity of the group , where is the fundamental relation of H. The way of finding this well-known relation of the algebraic hyperstructure theory is described in Antampoufis and Hošková-Mayerová [15], where also a thorough discussion on two possible approaches to this topic is given.
Definition 6
([15,16]). Let be a (semi)hypergroup and a natural number. We define relation as follows:
and define , where is the diagonal relation on H. We denote the transitive closure of β and call it the fundamental relation on H. The quotient is called the fundamental (semi)group. The mapping is called canonical projection. On hypergroups, the set , where 1 is the identity of the group , is called the heart of the hypergroup H. Finally, by we denote the set of elements which are in relation with .
Before we proceed, it is to be noted that one of the well established facts of the algebraic hyperstructure theory is that, in a hypergroup, (see Freni [17]). The following is a reworded remark from De Salvo and Freni [13], which—in a form of definition—can be found in Corsini [18] and Corsini and Leoreanu [19].
Theorem 1
([13], Osservazione 1.3). A hypergroup H is strongly cyclic, generated by x, if and only if is a cyclic group generated by .
Definition 7
([18], p. 276). A hypergroup H is called cyclic with a generator x if is a cyclic group generated from .
1.5. Corsini’s Book: A Synthesis of Approaches
In 1986, Corsini published (in Italian) his book on hyperstructure theory, which first appeared in English in 1993 as [18]. It is important to notice that, in his book, he mentions that Vougiouklis encouraged him to write it. In other words, what we see in [18] is a synthesis of the approaches existing so far.
Now, in order to distinguish between the original definition of De Salvo and Freni on one hand and the definition using the canonical projection (i.e., strong cyclicity), Corsini [18] called the original approach, in the case of hypergroups, where the names would overlap, s-cyclic while, in the case of semihypergroup, where no overlapping was possible (because Definition 7 is based on hypergroups), he left in use the original name; notice that the first part of Definition 8 is equivalent to Definition 3 of De Salvo and Freni [3,8]. Moreover, strong cyclicity of De Salvo and Freni [13] is referred to as cyclicity; see the above Definition 7.
Definition 8
([18], p. 278). A semihypergroup H is called cyclic if there exists such that, for all , there exists such that . We call h the s–generator of H. A hypergroup is calleds-cyclic if it is a cyclic semihypergroup.
The relation between cyclic (= strongly cyclic) and s-cyclic hypergroups is the following.
Theorem 2
([18], p. 281). Every hypergroup H, if it is s-cyclic, is cyclic, and is generated by its s–generator h.
Notice that the Theorem 2 originated in De Salvo and Freni [13] as Proposizione 2.5, where the result is given using the original terminology (“if a hypergroup is cyclic, then it is strongly cyclic”).
The following theorem is valid both for “cyclic” in the sense of canonical projection and for s-cyclicity (in this case even for semihypergroups as follows from [8], Proposizione 1). Notice that, while all cyclic groups are commutative, it was already Wall [2] who observed that commutativity is not always granted for cyclic hypergroups.
Theorem 3
([19], p. 18). If H is a cyclic and complete hypergroup, then it is commutative.
If we realize that only one definition of cyclicity in semihypergroups exists, no confusion can arise from the following theorem.
Theorem 4
([19], p. 18). A cyclic and complete semihypergroup is a join space.
1.6. Current State of the Art
Even though a great many important results have been achieved by the Italian and the Greek schools, the concept of cyclicity in the algebraic hyperstructure theory is not a “closed issue”. Recently, single power cyclicity has been especially studied. Al Tahan and Davvaz [20] studied some properties of single power cyclic hypergroups and links of these to regular relations. They also applied their results in the study of braid groups (which have important applications in knot theory). Moreover, in [21], Al Tahan and Davvaz implicitly use the idea of –hyperstructures (i.e., hyperstructures that we discuss further on) to construct a cyclic hypergroup of an arbitrary braid group of n strands. Finally, e.g., Karimian and Davvaz [22] recently studied γ-cyclic hypergroups, which are based on Freni’s [23] relation γ, which is a generalization of the β relation used throughout this paper.
1.7. A Remark Concluding the Introduction
Regardless of the evolution of terminology, one can observe the following:
- There exist two main approaches towards cyclicity in the hyperstructure theory: through the fact that we get a hypergroup by repeatedly applying the hyperoperation on a generator, or through the canonical projection. Both were introduced by the Italian school. The former was independently introduced by Vougiouklis and is related to the original Wall’s definition. The latter is related to the notion of completeness and the results of Koskas.
- Vougiouklis defined numerous cases of cyclicity and periods such as single power (one generator only) and finite/infinite period. The purpose of his definition was to study a specific class of cyclic hypergroups, those based on P–hyperoperations.
- The original definition of Wall, the definition of Vougiouklis and the definition using canonical projection were provided for hypergroups. The original definition of De Salvo and Freni was provided for semihypergroups.
- Cyclicity of a (semi)hypergroup (defined by the Italian schools) and period of a hypergroup (defined by Vougiouklis) are, in a general case, different.
Finally, let us point out that the class of cyclic hypergroups, i.e., the one using canonical projection, is the broadest one. Some cyclic hypergroups are s-cyclic and some s-cyclic hypergroups are single power cyclic; see Figure 1.
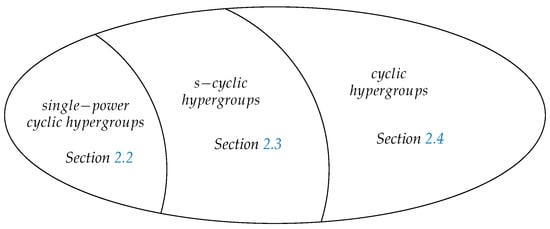
Figure 1.
Various notions of cyclicity in hypergroups and their relations; from the most special case (single-power cyclic hypergroups) to the most general one (cyclic hypergroups).
Notation.
From now on, we are going to use only the following names: cyclic, s-cyclic and single power cyclic.
2. Examples
Unfortunately, the papers of both the Italian and the Greek schools contain examples only very occasionally (if at all). Therefore, in this section, we try to demonstrate various notions of cyclicity using as many various examples as possible.
2.1. Theoretical Background
Before including some examples of cyclic hypergroups, recall three very useful lemmas. Notice that, in the following definition, the name “extensive” is used e.g., by Chvalina [24,25] while e.g., Massouros [26] uses a geometrically motivated name “closed”.
Definition 9.
A hyperoperation “*” on H is called extensive (or closed ) if for all there is . A hypergroupoid with an extensive hyperoperation is called an extensive hypergroupoid.
Lemma 1.
Every extensive semihypergroup is a hypergroup.
Proof.
Obvious because and “*” is extensive. ☐
Lemma 2.
Let be an extensive semihypergroup (i.e., by Lemma 1 a hypergroup). Then, relation β is a total relation, and, as a result, is a one-element group.
Proof.
Obvious because in this case . ☐
In other words, since every one-element group is cyclic, every hypergroup such that is a one-element group, is cyclic, which—as included e.g., in [20] is the case of all single power cyclic hypergroups.
Lemma 3
([20]). Every single power cyclic hypergroup has a trivial fundamental group .
Most of the examples included below are based upon what is known as “Ends lemma”, which was proved by Chvalina [25] and studied by Novák [27,28], later with Cristea [29] and Křehlík [30,31] and Chvalina [32]. Semihypergroups of the below type are called –semihypergroups. Notice that Novák or Chvalina have actually not “invented” the concept of –hyperstructures as they have rather provided a name for a concept implicitely present in a number of papers dated as early as (to our best knowledge) Pickett [33] (1967) or even—if preordering is considered—Marty [1]. In addition, by Remark 1, most such results are valid for preordered semigroups, i.e., also in the context of equivalence relations. For some further reading on this topic, see Novák [34].
Lemma 4
([25], Theorem 1.3, p. 146). Let be a partially ordered semigroup. Binary hyperoperation defined by
is associative. The semihypergroup is commutative if and only if the semigroup is commutative.
Lemma 5
([25], Theorem 1.4, p. 147). Let be a partially ordered semigroup. The following conditions are equivalent:
- For any pair , there exists a pair such that and .
- The semi-hypergroup defined by Formula (6) is a hypergroup.
Remark 1.
In groups, condition of Lemma 5 holds trivially as it is sufficient to put and . In addition, when one verifies the proofs, one can see that downgrading from partially ordered (semi)groups to preordered ones is possible for all implications except for “commutativity of `*’ implies commutativity of `·’.
2.2. Single Power Cyclic Hypergroups
The following example presents a class of single power cyclic hypergroups with infinite periods, i.e., hypergroups which are also s-cyclic and cyclic. With respect to single power cyclicity and s-cyclicity, only some of its elements are generators while, with respect to cyclicity, each of its elements is a generator.
Example 1.
Suppose , with the usual addition and ordering of integers. Since is a partially ordered group, , where is a hypergroup. Let us examine its cyclicity with respect to the different approaches mentioned above.
In the context of Definition 5 of Vougiouklis, we can see that, for an arbitrary negative and , we have , i.e., and is a single-power cyclic hypergroup with infinite periods for infinitely many generators (yet not all because only negative integers generate it).
In order to relate this hypergroup to the Definition 7 of Corsini, we first need to establish the relation β and the canonical projection φ. However, by Lemma 3, we know that is a one-element set, i.e., a trivial cyclic group; it is easy to show that , i.e., for all . Thus, is a cyclic hypergroup.
As regards generators, by Theorem 2, any negative integer, i.e., any s–generator of , is a generator. However, if we regard Definition 7, every integer is a generator.
In the following example, we again have a single power cyclic hypergroup with infinite period. However, in this case, an arbitrary element is a generator under all definitions.
Example 2.
Regard multiplication on the open interval . Then , where , is a semihypergroup, which—due to extensivity—is a hypergroup. Now, for an arbitrary there is and, obviously, is a single power cyclic hypergroup with infinite period for an arbitrary .
In the following example we have a class of single power cyclic hypergroups with finite period and only one generator. As was the case in Example 1, the set of generators will be different under cyclicity because the hyperoperation is extensive.
Example 3.
Regard , where “gcd” stands for the greatest common divisor of natural numbers and “|” is the divisibility relation. Since is a partially ordered semigroup, , where , for all , is a semihypergroup. Since for all , is, by Lemma 1, a hypergroup.
Now, obviously . Thus, is single power cyclic with period 2 and one generator 1. Of course, instead of , we can regard the set of divisors of an arbitrary and get a class of finite single power cyclic hypergroups with period 2.
2.3. s–Cyclic Hypergroups Which Are Not Single Power Cyclic
Now, we present an example of classes of hypergroups which are s-cyclic, i.e., also cyclic, yet not single power cyclic. For reasons of clarity, we choose a set of a small cardinality.
Example 4.
Denote the group of permutations of three elements, i.e.,
Obviously, and . Now, since, for an arbitrary pair of permutations there is , where “∘” is the usual operation of composition of permutations, it is easy to verify that if we set whenever , we get that is a preordered group. Therefore, if we define a hyperoperation on by
for all , then is an –hypergroup which is not extensive. Now, in order to construct the canonical projection, we construct the (commutative) Cayley table of the hyperoperation. In it, we will use the following notation: “+” will stand for the set , i.e., the set of permutations with positive parity, and “−” will stand for the set , i.e., the set of permutations with negative parity.
| * | e | |||||
| e | + | − | − | − | + | + |
| + | + | + | − | − | ||
| + | + | − | − | |||
| + | − | − | ||||
| + | + | |||||
| + |
Thus, we can see that “ whenever there exist permutations such that ” means that and . In addition, since e.g., , we never obtain a cross-combination between sets denoted “+” and “−”. Therefore, e.g., and e.g., and we have that
which is isomorphic to the cyclic group generated by . Therefore, is cyclic with generators .
Obviously, and (and likewise for and ), we get that is s-cyclic with period 3 (because ); . However, since for no element of there exists any such that (notice that for all —and likewise for ), is not single power cyclic.
2.4. Cyclic Hypergroups Which Are Not s–Cyclic
Finally, we include an example of cylic hypergroups which are not s-cyclic, i.e., which cannot be single power cyclic either. Notice that the hyperoperation is again not extensive, yet we get that is a total relation.
Example 5.
Let be a hypergroup, where “*” is defined by the following table.
| * | 1 | 2 | 3 | 4 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
Now, it is easy to see that for all , for all and for all . Therefore, is neither s-cyclic nor single power cyclic. However, since for all , i.e., β is a total relation, we have that is a one-element group (which is trivially–cyclic), i.e., is a cyclic hypergroup.
3. New Results
In this section, we present several new results concerning various kind of cyclicity, especially with respect to –hyperstructures. We choose this class of hyperstructures because the papers of both the Italian and the Greek schools contain a great many results on various types of cyclicity, yet none of them are specifically linked to –hyperstructures—for the simple reason that this concept was defined several years later.
First of all, if we rewrite Definition 5 (or rather, Definition 3) in the context of the –hyperoperation Formula (6), we immediately have the following. (Notice that, as has been pointed out above, in the case of hypergroups, “cyclic” of Definition 5 is “s-cyclic” of Definition 3.)
Theorem 5.
Let be the –semihypergroup of a partially-ordered semigroup . Then, is a cyclic semihypergroup (i.e., in case of hypergroups, an s-cyclic hypergroup) if and only if there exists an element such that all minimal elements of H can be expressed as for some . In such a case, h is a generator of and is the greatest of these exponents.
Example 6.
Denote . Define addition of the pairs component-wise and the relation “≤” in such a way that whenever and . Obviously, is a partially-ordered semigroup which has infinitely many minimal elements—pairs , where . All of these elements can be expressed as powers of the pair , which makes this pair a generator of this cyclic semihypergroup. However, cyclicity of is infinite.
In the “Ends lemma”, we often regard idempotent operations such as “min”, “max”, “∪”, “∩”, etc. For these, the following corollary can be given.
Corollary 1.
Let be an –semihypergroup constructed from a partially ordered semigroup such that “*” is extensive and “·” is idempotent. Then, has at most one generator—the smallest element of . Moreover, in this case, is a single power cyclic hypergroup with period (and cyclicity) 2.
Proof.
In the case described in Theorem 5, we get, for an arbitrary and arbitrary ,
which means that the only chance that Formula (1) becomes valid is in case that (notice that, due to reflexivity of “≤”, there is always ). In other words, if is a hypergroup (and, by Lemma 1, extensivity of the hyperoperation turns the semihypergroup into a hypergroup), then H is single power cyclic with period 2. Of course, the only generator of H is the smallest element of H. □
The following example can be compared to De Salvo and Freni [8], Proposizione 12 and Corollario 4; notice that, in our example, and “*” is extensive. In addition, see Example 3.
Example 7.
Regard the preordered semigroup and its –hypergroup , where for all . Since , we get that and 1 is the only generator of the single power cyclic hypergroup with period 2. (or 0 instead of 1 if we consider ). If we change to , we get that the hypergroup is not single power cyclic because has no smallest element, i.e., there is no integer such that .
The following lemma is obvious yet very useful in our future considerations; notice that, by , we mean a lower bound of a and b.
Lemma 6.
Let be an –hypergroup of a partially ordered group and arbitrary.
- If , then , i.e., .
- If are such that exists, then , i.e., .
Proof.
If , then obviously also , i.e., also , i.e., . In other words, . If are such that exists, then, since and , we have that . In other words, . □
Thus, we can see, as an immediate corollary, that:
Theorem 6.
Suppose that is an –hypergroup of a partially ordered group such that has the smallest element or is well ordered. Then, is a one-element group.
Corollary 2.
Let be an –hypergroup of a partially ordered group . If there are at least two distinct minimal elements in , then is not trivial.
Proof.
Obvious because the relation “≤” is reflexive. Thus, if are minimal, then , and , . Therefore, we can never find two (or more) elements such that . Thus, , i.e., . ☐
In the following example, we have no minimal elements, yet is again not trivial. Notice that in this way we can get cyclic hypergroups, which are not s-cyclic. Also worth mentioning is the fact that all infinite cyclic groups are isomorphic to the cyclic group .
Example 8.
Regard the additive group of “selected complex numbers”, i.e., with the usual component wise addition. Obviously, is a group with the neutral element such that the opposite of is . Now, say that whenever and . Obviously, “≤” is compatible with the addition. Thus, we set and know that is a hypergroup.
Now, regard e.g., and . In this case, while and we will never be able to find such that both and belong to because the sum of imaginary parts is always unique. In other words, for an arbitrary and , we have that , i.e., . Thus, it can be easily observed that , which is isomorphic to the cyclic group . Therefore, by Definition 7, is a cyclic hypergroup with generators , where , i.e., infinitely many generators which could be grouped as , . In contrast to Example 5, the fundamental group is not trivial, though. Obviously, is not s-cyclic because we are not able to get the whole of H from any by means of uniting powers of a because—in contrast to cyclicity in groups—only positive powers of generators are available.
Finally, what does it mean that elements of , “generate” ? As has been mentioned in Section 1.4, H must be the intersection of all subhypergroups which are complete parts and contain the generator. For a generator h, we denote this . In [13], Osservazione 1.4, De Salvo and Freni show that all subhypergroups of a cyclic hypergroup are complete parts, i.e., it is enough to consider the intersection of subhypergroups. Now, what are the subhypergroups of which contain e.g., the generator belonging to ? Since for an arbitrary , we have that every subhypergroup G of H containing an element from must (in order to provide for ) contain , where K is a suitable subset of . However, this is not enough for the reproductive axiom, i.e., for all , to hold because the sum of non-negative imaginary parts is always greater than the parts themselves and . Therefore, we need also (all) negative imaginary parts. The same reasoning holds for real parts. Thus, , where is arbitrary, equals H, which is in accordance with Theorem 1 (the same holds also for generators from the set ).
Remark 2.
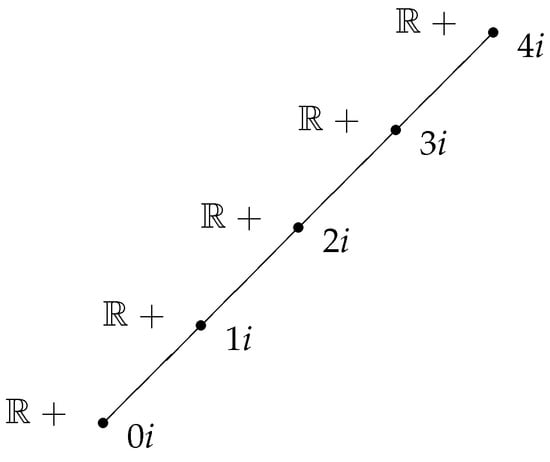
Obviously, if , then H is cyclic because and is a cyclic group. See also Figure 2.

Figure 2.
Related to Example 8 and Remark 2 when . Elements are in relation based on the imaginary part and within the same class based on the real part.
Given Remark 2, we know that we can construct cyclic –hypergroups such that their fundamental group has any cardinality we choose (given Example 8 including infinity). Thus, there arises an obvious question: “How can this be done?”
First of all, in a finite case, the notion of a partially ordered cyclic group is absurd because antisymmetry of the relation conflicts with the compatibility of the relation and the group operation. Therefore, if we insist on the fact that the relation “≤” used in the construction of –hyperstructures is a partial order, we cannot start with a finite cyclic group (such as, e.g., groups of n elements, where n is prime). However, we can take any cyclic group and “expand” it by “attaching” copies of some (finite or infinite) set to each of its elements—as has been done in Example 8.
4. Conclusions and Future Work
The aim of this paper has been to clarify one of the fundamental properties of hypergroups, cyclicity. We have pointed out two approaches to this concept: via the fundamental relation and the canonical projection, or by repeatedly applying the hyperoperation on the generator. Thus, we were able to link the three existing concepts of cyclicity: the class of single power cyclic hypergroups, which is included (not strictly) in the class of s-cyclic hypergroups, which is included (again, not strictly) in the class of cyclic hypergroups—see Figure 1. As a tool to show this, we have chosen the concept of –hyperstructures. It is to be noted that, even though numerous properties of –hyperstructures have already been studied, the important issue of cyclicity in this class of hyperstructures constructed from partially ordered (semi)groups has been neglected so far.
We intend to continue our study of cyclicity in hypergroups by linking it to the concept of reducibility. The notion of reduced hypergroups was introduced by Jantosciak [35], when he noticed that the elements of a non-empty set H can play interchangeable roles with respect to a hyperoperation defined on it, and explained this property by means of three equivalencies on H, called fundamental relations, that identify the elements with the same properties. To be more precise, two elements of a hypergroup are called
- operationally equivalent if and , for all ,
- inseparable if for we have if and only if ,
- essentially indistinguishable if they are operationally equivalent and inseparable.
Then, a hypergroup is called reduced if the equivalence class of each element of H with respect to the essentially indistinguishable relation is a singleton.
Based on this, we intend to find out based on which assumptions the various types of cyclic hypergroups presented in this paper are reduced hypergroups.
Author Contributions
Investigation, Writing-Original Draft Preparation, Writing-Review and Editing: M.N., Š.K. and I.C. (equal contribution).
Funding
The first author was supported by the FEKT-S-17-4225 grant of Brno University of Technology. The second author acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0285).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marty, F. Sur une généralisation de la notion de groupe. IV Congrès des Mathématiciens Scandinaves 1934, 45–49. [Google Scholar]
- Wall, H.S. Hypergroups. Am. J. Math. 1934, 59, 77–98. [Google Scholar] [CrossRef]
- De Salvo, M.; Freni, D. Sugli ipergruppi ciclici e completi. Matematiche (Catania) 1980, 35, 211–226. [Google Scholar]
- Corsini, P. Sur les semi-hypergroupes complètes et les groupoides. Atti Soc. Pel. Sci. Fis. Mat. Nat. 1980, 26, 391–398. [Google Scholar]
- Corsini, P.; Romeo, G. Hypergroupes complètes et T–groupoids; Atti Convegno su “Sistemi binari e loro applicazioni”: Taormina, Italy, 1978; pp. 129–146. [Google Scholar]
- De Salvo, M. Sugli ipergruppi completi finiti. Riv. Mat. Univ. Parma 1982, 8, 269–280, (submitted 1980). [Google Scholar]
- Freni, D. Ipergruppi ciclici e torsione negli ipergruppi. Matematiche (Catania) 1980, 35, 270–286. [Google Scholar]
- De Salvo, M.; Freni, D. Semi-ipergruppi e ipergruppi ciclici. Atti Sem. Mat. Fis. Univ. Modena 1981, 30, 44–59. [Google Scholar]
- Freni, D. Una nota su gli ipergruppoidi ciclici. Ratio Mathematica 1995, 9, 101–111. [Google Scholar]
- Vougiouklis, T. Cyclicity in a special class of hypergroups. Acta Univ. Carolinae Math. Phys. 1981, 22, 3–6. [Google Scholar]
- Konguetsof, L.; Vougiouklis, T.; Kessoglides, M.; Spartalis, S. On cyclic hypergroups with period. Acta Univ. Carolinae Math. Phys. 1987, 28, 3–7. [Google Scholar]
- Vougioulis, T. Isomorphisms on P–hypergroups and cyclicity. Ars Combinatoria 1990, 29A, 241–245. [Google Scholar]
- De Salvo, M.; Freni, D. Ipergruppi finitamente generati. Riv. Mat. Univ. Parma 1986, 12, 177–186. [Google Scholar]
- De Salvo, M. Su le potenze ad esponente intero in un ipergruppo e gli r–ipergruppi. Riv. Mat. Univ. Parma 1985, 4, 409–421. [Google Scholar]
- Antampoufis, N.; Hošková-Mayerová, Š. A brief survey on the two different approaches of fundamental equivalence relations on hyperstructures. Ratio Math. 2017, 33, 47–60. [Google Scholar]
- Koskas, M. Groupoids, demi-hypergroupes et hypergroupes. J. Math. Pure Appl. 1970, 48, 155–192. [Google Scholar]
- Freni, D. A note on the core of a hypergroup and the transitive closure β⋆ of β. Riv. Mat. Pura Appl. 1991, 8, 153–156. [Google Scholar]
- Corsini, P. Prolegomena of Hypergroup Theory; Aviani Editore: Tricesimo, Italy, 1993. [Google Scholar]
- Corsini, P.; Leoreanu, V. Applications of Hyperstructure Theory; Kluwer Academic Publishers: Dodrecht, The Netherlands; Boston, MA, USA; London, UK, 2003. [Google Scholar]
- Al Tahan, M.; Davvaz, B. On some properties of single power cyclic hypergroups and regular relations. J. Algebra Appl. 2017, 16, 1750214. [Google Scholar] [CrossRef]
- Al Tahan, M.; Davvaz, B. On a special single-power cyclic hypergroup and its automorphisms. Discrete Math. Algorithm. Appl. 2016, 8, 1650059. [Google Scholar] [CrossRef]
- Karimian, M.; Davvaz, B. On the γ-cyclic hypergroups. Commun. Algebra 2006, 34, 4579–4589. [Google Scholar] [CrossRef]
- Freni, D. A new characterization of the derived hypergroup via strongly regular equivalencies. Commun. Algebra 2002, 30, 3977–3989. [Google Scholar] [CrossRef]
- Chvalina, J. Commutative hypergroups in the sense of Marty and ordered sets. In General Algebra and Ordered Sets, Proceedings of the International Conference Olomouc; Verlag Johannes Heyn: Olomouc, Czech Republic, 1994; pp. 19–30. [Google Scholar]
- Chvalina, J. Functional Graphs, Quasi-Ordered Sets and Commutative Hypergroups; Masaryk University: Brno, Czech Republic, 1995. (In Czech) [Google Scholar]
- Massouros, C.G. On path hypercompositions in graphs and automata. MATEC Web Conf. 2016, 41, 05003. [Google Scholar] [CrossRef]
- Novák, M. On EL–semihypergroups. Eur. J. Combin. 2015, 44 Pt B, 274–286. [Google Scholar] [CrossRef]
- Novák, M. Some basic properties of EL–hyperstructures. Eur. J. Combin. 2013, 34, 446–459. [Google Scholar] [CrossRef]
- Novák, M.; Cristea, I. Composition in EL–hyperstructures. Hacet. J. Math. Stat. 2018, in press. [Google Scholar]
- Křehlík, Š.; Novák, M. From lattices to Hv–matrices. An. Şt. Univ. Ovidius Constanţa 2016, 24, 209–222. [Google Scholar] [CrossRef]
- Novák, M.; Křehlík, Š. EL–hyperstructures revisited. Soft Comput. 2018, 22, 7269–7280. [Google Scholar] [CrossRef]
- Chvalina, J.; Křehlík, Š.; Novák, M. Cartesian composition and the problem of generalising the MAC condition to quasi-multiautomata. An. Şt. Univ. Ovidius Constanţa 2016, 24, 79–100. [Google Scholar]
- Pickett, H.E. Homomorphisms and subalgebras of multialgebras. Pac. J. Math. 1967, 21, 327–342. [Google Scholar] [CrossRef]
- Novák, M. EL–semihypergroups in which the quasi-ordering is not antisymmetric. In Mathematics, Information Technologies and Applied Sciences 2017: Post-Conference Proceedings of Extended Versions of Selected Papers; University of Defence: Brno, Czech Republic, 2017; pp. 183–192. [Google Scholar]
- Jantosciak, J. Reduced hypergroups. In Algebraic Hyperstructures and Applications, Proceedings of the Fourth International Congress, Xanthi, Greece, 1990; Vougiouklis, T., Ed.; World Scientific: Singapore, 1991; pp. 119–122. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).