Local and Holistic Feature Fusion for Occlusion-Robust 3D Ear Recognition
Abstract
1. Introduction
2. Related Work and Contribution
2.1. Automatic 2D Ear Detection
2.2. Automatic 3D Ear Recognition
2.3. Deep-Learning-Based Recognition
2.4. Noncooperative Game Theory (NGT)-Based Recognition
2.5. Contributions
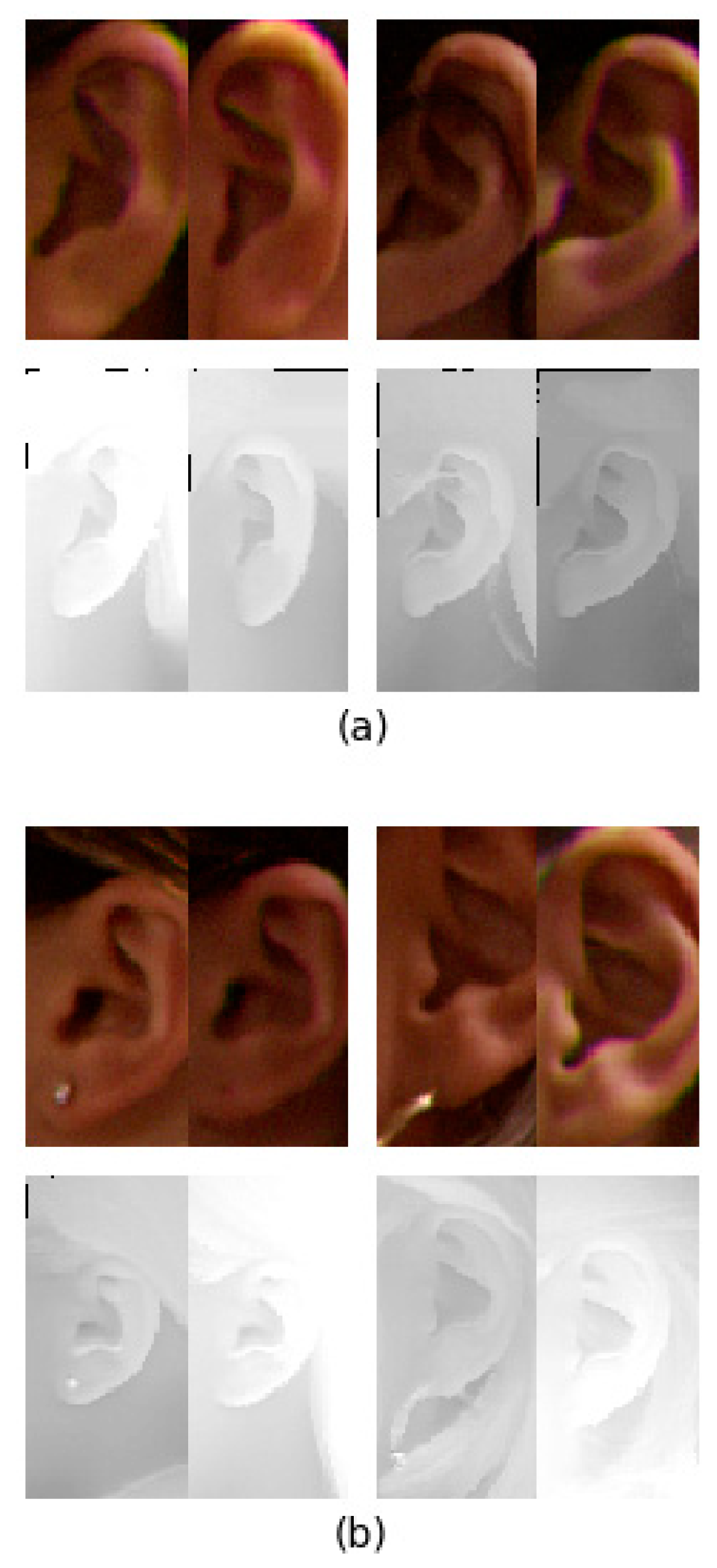
3. Ear Data Detection
4. Local Feature Representation
4.1. Definition of Features
4.2. Keypoint Selection
4.3. Local Feature Representation
4.4. Two-Step NGT-Based Method for the Local Surface Matching Engine
| Algorithm 1 Two-step NGT-based method for two images alignment |
| 1: Build the initial set of strategies 2: Generate a set of keypoint correspondences maintaining a rigid constraint |
5. Holistic Feature Extraction
5.1. Preprocessing
5.2. Holistic Representation
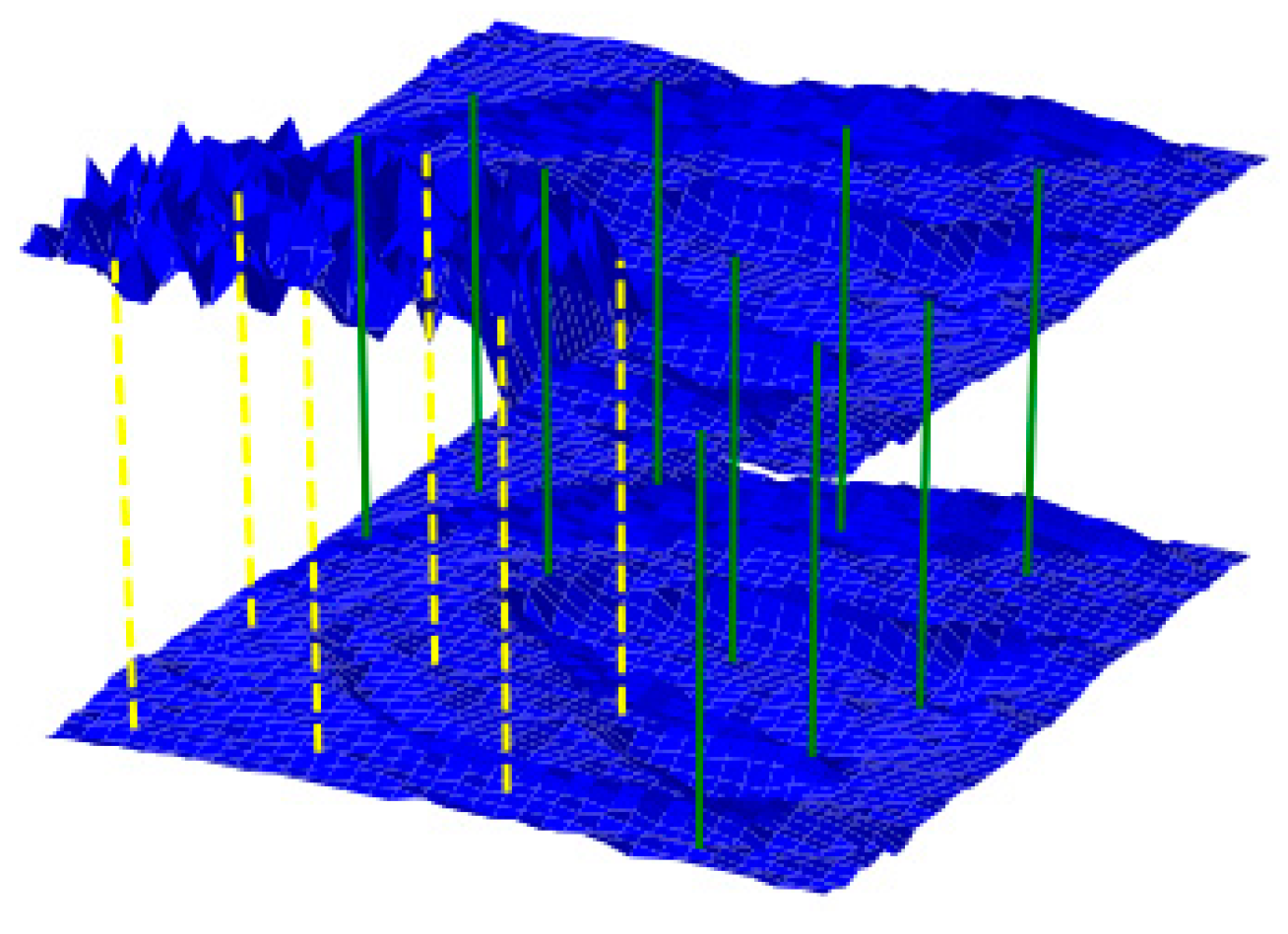
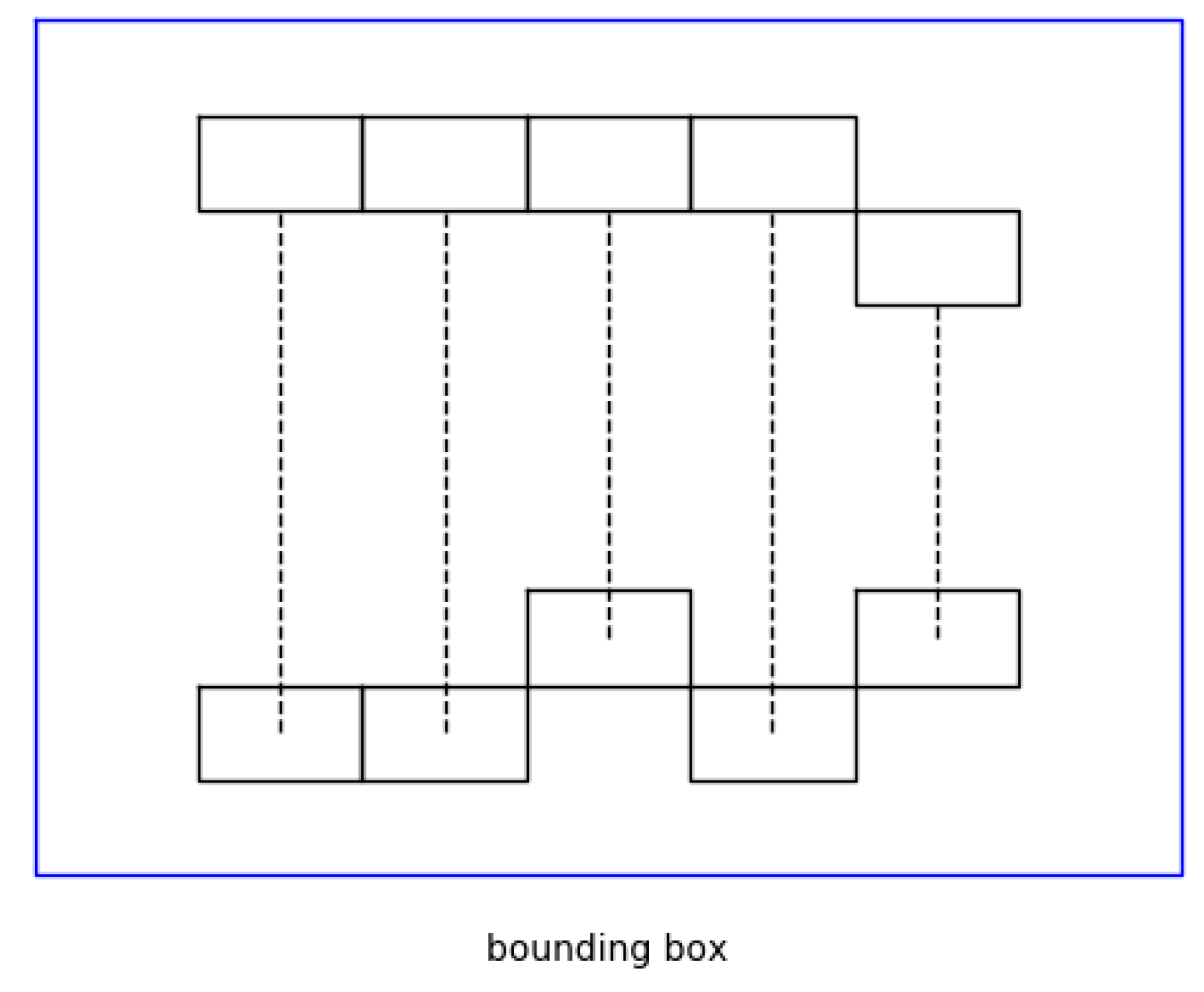
5.3. Holistic Feature Matching Engine
| Algorithm 2 Variant of breed voxelized surface matching |
| In the offline enrollment stage: 1: Denote the normal direction of the gallery model 2: Construct a bounding box enclosing the gallery model, where the bottom of the bounding box is perpendicular to . 3: Voxelize the gallery model using a voxel grid constructed from the bounding box enclosing the gallery model [11]. In the online stage: 1: Calculate the joint spatial extent of the registered probe-model and gallery-model bounding boxes and the voxel grid enclosing the bounding box [11]. 2: Choose the corresponding voxels between the registered probe and gallery models within the bounding boxes by proposing a “normal projection” matching strategy 2.1: Determine the set of gallery voxels and a set of centers of gallery voxels , where is the center of . 2.2: For , do the following. 2.3: Draw a straight line through ; its direction is the same as . 2.4: Find the voxel that intersects in the corresponding probe model . Assign and as a pair. 2.5: End for. 3: Remove the abnormal pairs of voxels. 4: Perform voxelized subject vectorization; the vectors and correspond to the probe and gallery models 5: Calculate the registration error of the two models using Equation (11). |
6. Fusion
7. Experimental Results and Discussion
7.1. Training of the Data Fusion Parameters
7.2. Ear Recognition with Natural Occlusion
7.3. Ear Recognition with Random Occlusion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Emeršič, Ž.; Meden, B.; Peer, P.; Štruc, V. Evaluation and analysis of ear recognition models: Performance, complexity and resource requirements. In Neural Computing and Applications; Springer: Berlin, Germany, 2018; pp. 1–16. [Google Scholar]
- Emeršič, Ž.; Štruc, V.; Peer, P. Ear recognition: More than a survey. Neurocomputing 2017, 255, 26–39. [Google Scholar] [CrossRef]
- Ganapathi, I.I.; Prakash, S. 3D ear recognition using global and local features. IET Biom. 2018, 7, 232–241. [Google Scholar] [CrossRef]
- Prakash, S. False mapped feature removal in spin images based 3D ear recognition. In Proceedings of the 2016 3rd International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 11–12 February 2016; pp. 620–623. [Google Scholar]
- Krotewicz, P. Novel ear-assisted 3D face recognition under expression variations. Int. J. Biom. 2016, 8, 65–81. [Google Scholar] [CrossRef]
- Chen, H.; Bhanu, B.; Wang, R. Performance evaluation and prediction for 3D ear recognition. In Proceedings of the International Conference on Audio- and Video-Based Biometric, Rye Brook, NY, USA, 20–22 July 2005; pp. 748–757. [Google Scholar]
- Maity, S.; Abdel-Mottaleb, M. 3D ear segmentation and classification through indexing. IEEE Trans. Inf. Forensics Secur. 2015, 10, 423–435. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, Z.; Yuan, L.; Zeng, H.; Chen, L. 3D Ear Normalization and Recognition Based on Local Surface Variation. Appl. Sci. 2017, 7, 104. [Google Scholar] [CrossRef]
- Albarelli, A.; Rodola, E.; Bergamasco, F.; Torsello, A. A non-cooperative game for 3d object recognition in cluttered scenes. In Proceedings of the 2011 International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission, Hangzhou, China, 16–19 May 2011; pp. 252–259. [Google Scholar]
- Rodolà, E.; Albarelli, A.; Bergamasco, F.; Torsello, A. A scale independent selection process for 3d object recognition in cluttered scenes. Int. J. Comput. Vis. 2013, 102, 129–145. [Google Scholar] [CrossRef]
- Zhou, J.; Cadavid, S.; Abdel-Mottaleb, M. An efficient 3-D ear recognition system employing local and holistic features, IEEE Trans. Inf. Forensics Secur. 2012, 7, 978–991. [Google Scholar] [CrossRef]
- Ansari, S.; Gupta, P. Localization of ear using outer helix curve of the ear. In Proceedings of the International Conference on Computing: Theory and Applications, Kolkata, India, 5–7 March 2007; pp. 688–692. [Google Scholar]
- Sarangi, P.P.; Panda, M.; Mishra, B.P.; Dehuri, S. An automated ear localization technique based on modified Hausdorff distance. In Proceedings of the International Conference on Computer Vision and Image Processing, Roorkee, India, 9–12 September 2017; pp. 229–240. [Google Scholar]
- Zhang, Y.; Mu, Z. Ear Detection under Uncontrolled Conditions with Multiple Scale Faster Region-Based Convolutional Neural Networks. Symmetry 2017, 9, 53. [Google Scholar] [CrossRef]
- Hurley, D.J.; Nixon, M.S.; Carter, J.N. Force field energy functionals for image feature extraction. Image Vis. Comput. 2002, 20, 311–317. [Google Scholar] [CrossRef]
- Yuan, L.; Mu, Z.C. Ear detection based on skin-color and contour information. In Proceedings of the International Conference on Machine Learning and Cybernetics, Qingdao, China, 11–14 July 2010; pp. 2213–2217. [Google Scholar]
- Arbab-Zavar, B.; Nixon, M.S. On shape-mediated enrolment in ear biometrics. In Advances in Visual Computing; Springer: Berlin/Heidelberg, Germany, 2007; pp. 549–558. [Google Scholar]
- Cummings, A.H.; Nixon, M.S.; Carter, J.N. A novel ray analogy for enrolment of ear biometrics. In Proceedings of the 2010 Fourth IEEE International Conference on Biometrics: Theory Applications and Systems (BTAS), Washington, DC, USA, 27–29 September 2010; pp. 1–6. [Google Scholar]
- Prakash, S.; Gupta, P. An efficient ear localization technique. Image Vis. Comput. 2012, 30, 38–50. [Google Scholar] [CrossRef]
- Yan, P.; Bowyer, K.W. Biometric recognition using 3D ear shape. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 29, 1297–1308. [Google Scholar] [CrossRef] [PubMed]
- Deepak, R.; Nayak, A.V.; Manikantan, K. Ear detection using active contour model. In Proceedings of the International Conference on Emerging Trends in Engineering, Technology and Science, Pudukkottai, India, 24–26 February 2016; pp. 1–7. [Google Scholar]
- Ganesh, M.R.; Krishna, R.; Manikantan, K.; Ramachandran, S. Entropy based Binary Particle Swarm Optimization and classification for ear detection. Eng. Appl. Artif. Intell. 2014, 27, 115–128. [Google Scholar] [CrossRef]
- Halawani, A.; Li, H. Human ear localization: A template-based approach. In Proceedings of the International Workshop on Pattern Recognition (ICOPR 2015), Dubai, UAE, 4–5 May 2015; pp. 4–5. [Google Scholar]
- Islam, S.M.; Bennamoun, M.; Davies, R. Fast and fully automatic ear detection using cascaded adaboost. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Copper Mountain, CO, USA, 7–9 January 2008; pp. 1–6. [Google Scholar]
- Shih, H.C.; Ho, C.C.; Chang, H.T.; Wu, C.S. Ear detection based on arc-masking extraction and AdaBoost polling verification. In Proceedings of the International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP 2009), Kyoto, Japan, 12–14 September 2009; pp. 669–672. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Machine Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Cintas, C.; Quinto-Sánchez, M.; Acuña, V.; Paschetta, C.; De Azevedo, S.; de Cerqueira, C.C.S.; Canizales-Quinteros, S. Automatic ear detection and feature extraction using geometric morphometrics and convolutional neural networks. IET Biom. 2016, 6, 211–223. [Google Scholar] [CrossRef]
- Emersic, Z.; Gabriel, L.; Struc, V.; Peer, P. Convolutional Encoder-Decoder Networks for Pixel-wise Ear Detection and Segmentation. IET Biom. 2018. [Google Scholar] [CrossRef]
- Chen, H.; Bhanu, B. Human ear recognition in 3D. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 718–737. [Google Scholar] [CrossRef] [PubMed]
- Cadavid, S.; Abdel-Mottaleb, M. 3-D ear modeling and recognition from video sequences using shape from shading. IEEE Trans. Inform. Forensics Secur. 2018, 3, 709–718. [Google Scholar] [CrossRef]
- Islam, S.M.; Davies, R.; Bennamoun, M.; Mian, A.S. Efficient detection and recognition of 3D ears. Int. J. Comput. Vis. 2011, 95, 52–73. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, Z.; Li, H.; Shen, Y. 3D ear identification based on sparse representation. PLoS ONE 2014, 9, e95506. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Cadavid, S.; Abdel-Mottaleb, M. A computationally efficient approach to 3d ear recognition employing local and holistic features. In Proceedings of the 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Colorado Springs, CO, USA, 20–25 June 2011; pp. 98–105. [Google Scholar]
- Liu, Y.; Zhang, B.; Lu, G.; Zhang, D. Online 3D Ear Recognition by Combining Global and Local Features. PLoS ONE, 2016, 11, e0166204. [Google Scholar] [CrossRef] [PubMed]
- Ganapathi, I.I.; Ali, S.S.; Prakash, S. Geometric statistics-based descriptor for 3D ear recognition. In The Visual Computer; Springer: Berlin, Germany, 2018; pp. 1–13. [Google Scholar]
- Tian, L.; Mu, Z. Ear recognition based on deep convolutional network. In Proceedings of the International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Datong, China, 15–17 October 2016; pp. 437–441. [Google Scholar]
- Chowdhury, M.; Islam, R.; Gao, J. Robust ear biometric recognition using neural network. In Proceedings of the 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 1855–1859. [Google Scholar]
- Omara, I.; Wu, X.; Zhang, H.; Du, Y.; Zuo, W. Learning pairwise SVM on deep features for ear recognition. In Proceedings of the IEEE/ACIS 16th International Conference on Computer and Information Science (ICIS), Wuhan, China, 24–26 May 2017; pp. 341–346. [Google Scholar]
- Emeršič, Ž.; Štepec, D.; Štruc, V.; Peer, P. Training convolutional neural networks with limited training data for ear recognition in the wild. In Proceedings of the 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG), Washington, DC, USA, 30 May–3 June 2017; pp. 987–994. [Google Scholar]
- Almisreb, A.A.; Jamil, N.; Din, N.M. Utilizing AlexNet Deep Transfer Learning for Ear Recognition. In Proceedings of the Fourth International Conference on Information Retrieval and Knowledge Management (CAMP), Kota Kinabalu, Malaysia, 26–28 March 2018; pp. 1–5. [Google Scholar]
- Zhang, Y.; Mu, Z.; Yuan, L.; Yu, C. Ear verification under uncontrolled conditions with convolutional neural networks. IET Biom. 2018, 7, 185–198. [Google Scholar] [CrossRef]
- Hansley, E.E.; Segundo, M.P.; Sarkar, S. Employing fusion of learned and handcrafted features for unconstrained ear recognition. IET Biom. 2018, 7, 215–223. [Google Scholar] [CrossRef]
- Ying, T.; Shining, W.; Wanxiang, L. Human ear recognition based on deep convolutional neural network. In Proceedings of the Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1830–1835. [Google Scholar]
- Yaman, D.; Eyiokur, F.I.; Sezgin, N.; Ekenel, H.K. Age and Gender Classification from Ear Images. In Proceedings of the International Workshop on Biometrics and Forensics (IWBF), Sassari, Italy, 7–8 June 2018; pp. 1–7. [Google Scholar]
- Fan, T.Y.; Mu, Z.C.; Yang, R.Y. Multi-modality recognition of human face and ear based on deep learning. In Proceedings of the International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Ningbo, China, 9–12 July 2017; pp. 38–42. [Google Scholar]
- Garcia-Garcia, A.; Gomez-Donoso, F.; Garcia-Rodriguez, J.; Orts-Escolano, S.; Cazorla, M.; Azorin-Lopez, J. Pointnet: A 3D convolutional neural network for real-time object class recognition. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1578–1584. [Google Scholar]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and multi-view cnns for object classification on 3D data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas Valley, NV, USA, 26 June–1 July 2016; pp. 5648–5656. [Google Scholar]
- Xu, X.; Corrigan, D.; Dehghani, A.; Caulfield, S.; Moloney, D. 3D Object Recognition Based on Volumetric Representation Using Convolutional Neural Networks. In Proceedings of the International Conference on Articulated Motion and Deformable Objects, Palma de Mallorca, Spain, 13–15 July 2016; pp. 147–156. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from cells: Deep kdnetworks for the recognition of 3D point cloud models. In Proceedings of the IEEE International Conference on Computer Vision, Copenhagen, Denmark, 7 September–11 August 2017; pp. 863–872. [Google Scholar]
- Feng, Y.; Zhang, Z.; Zhao, X.; Ji, R.; Gao, Y. GVCNN: Group-View Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 264–272. [Google Scholar]
- Chen, L.; Mu, Z. Partial data ear recognition from one sample per person. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 799–809. [Google Scholar] [CrossRef]
- Koenderink, J.J.; Van Doorn, A.J. Surface shape and curvature scales. Image Vis. Comput. 1992, 10, 557–564. [Google Scholar] [CrossRef]
- Dorai, C.; Jain, A.K. COSMOS-A representation scheme for 3D free-form objects. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 1115–1130. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bulò, S.R.; Bomze, I.M. Infection and immunization: A new class of evolutionary game dynamics. Games Econ. Behav. 2011, 71, 193–211. [Google Scholar] [CrossRef]
- Turk, G.; Levoy, M. Zippered polygon meshes from range images. In Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 24–29 July 1994; pp. 311–318. [Google Scholar]
- Albarelli, A.; Rodola, E.; Torsello, A. A game-theoretic approach to fine surface registration without initial motion estimation. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 430–437. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Cappelli, R.; Maio, D.; Maltoni, D. Combining fingerprint classifiers. In Proceedings of the International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 351–361. [Google Scholar]

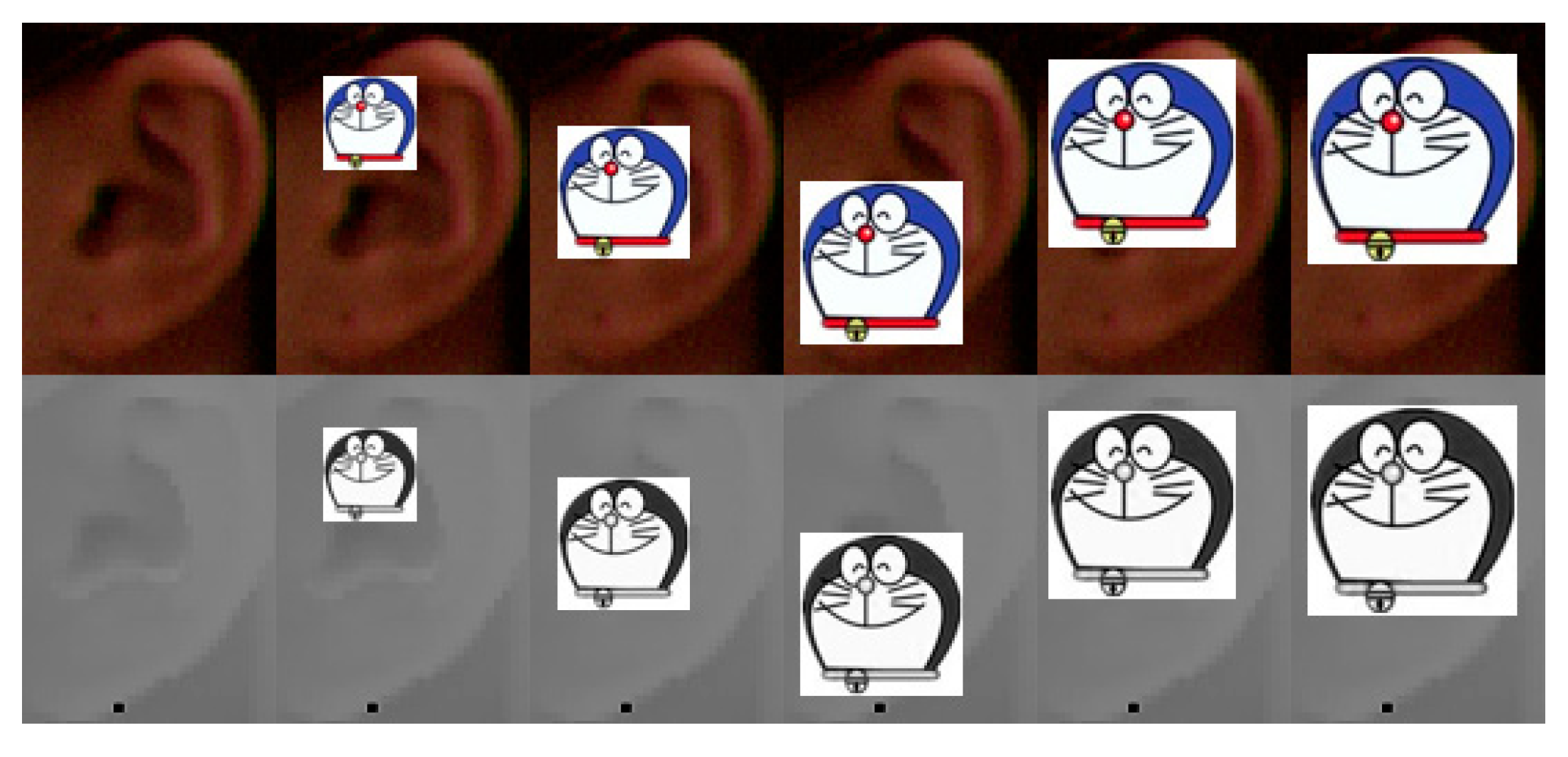




| Number of Images in Dataset | Occlusion Rate (%) | Precision (%) | Recall (%) | Accuracy (%) | F1 Score (%) |
|---|---|---|---|---|---|
| 1800 | 0 | 100 | 100 | 100 | 100 |
| 1800 | 10 | 100 | 100 | 100 | 100 |
| 1800 | 20 | 100 | 100 | 100 | 100 |
| 1800 | 30 | 99.9 | 100 | 99.9 | 99.9 |
| 1800 | 40 | 99.9 | 99.6 | 99.6 | 99.7 |
| 1800 | 50 | 99.5 | 98.9 | 98.6 | 99.2 |
| SPHIS + Two-Step NGT | A Variant of Breed Surface Voxelization | Our Proposed Method | |
|---|---|---|---|
| H vs. Single1 | 97.1% | 94.3% | 97.1% |
| E vs. Single2 | 97.6% | 97.6% | 97.6% |
| Method | Gallery | Probe | Rank 1 |
|---|---|---|---|
| Our proposed method | Single1 | H | 97.1% |
| SPHIS + two-step NGT | Single1 | H | 97.1% |
| SPHIS + NGT [9] | Single1 | H | 94.3% |
| Method | Gallery | Probe | Rank 1 |
|---|---|---|---|
| Our proposed method | Single2 | E | 97.6% |
| SPHIS + two-step NGT | Single2 | E | 97.6% |
| SPHIS + NGT [9] | Single2 | E | 95.2% |
| Technique | Percentage of Occlusion | |||||
|---|---|---|---|---|---|---|
| 0% | 10% | 20% | 30% | 40% | 50% | |
| Yan and Bowyer [20] | 97.8% | 73.5% | 45.1% | 25.8% | 8.9% | 1.4% |
| Zhang et al. [8] | 98.6% | 74.2% | 46.0% | 26.7% | 9.9% | 2.4% |
| Zhou et al. [11] | 98.3% | 95.9% | 90.1% | 65.1% | 40.5% | 18.8% |
| Our proposed method | 98.8% | 98.3% | 94.2% | 80.5% | 64.6% | 44.8% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Mu, Z. Local and Holistic Feature Fusion for Occlusion-Robust 3D Ear Recognition. Symmetry 2018, 10, 565. https://doi.org/10.3390/sym10110565
Zhu Q, Mu Z. Local and Holistic Feature Fusion for Occlusion-Robust 3D Ear Recognition. Symmetry. 2018; 10(11):565. https://doi.org/10.3390/sym10110565
Chicago/Turabian StyleZhu, Qinping, and Zhichun Mu. 2018. "Local and Holistic Feature Fusion for Occlusion-Robust 3D Ear Recognition" Symmetry 10, no. 11: 565. https://doi.org/10.3390/sym10110565
APA StyleZhu, Q., & Mu, Z. (2018). Local and Holistic Feature Fusion for Occlusion-Robust 3D Ear Recognition. Symmetry, 10(11), 565. https://doi.org/10.3390/sym10110565





