Abstract
Because of the efficient tradeoff in area–time complexities, digit-serial systolic multiplier over has gained substantial attention in the research community for possible application in current/emerging cryptosystems. In general, this type of multiplier is designed to be applicable to one certain field-size, which in fact determines the actual security level of the cryptosystem and thus limits the flexibility of the operation of cryptographic applications. Based on this consideration, in this paper, we propose a novel hybrid-size digit-serial systolic multiplier which not only offers flexibility to operate in either pentanomial- or trinomial-based multiplications, but also has low-complexity implementation performance. Overall, we have made two interdependent efforts to carry out the proposed work. First, a novel algorithm is derived to formulate the mathematical idea of the hybrid-size realization. Then, a novel digit-serial structure is obtained after efficient mapping from the proposed algorithm. Finally, the complexity analysis and comparison are given to demonstrate the efficiency of the proposed multiplier, e.g., the proposed one has less area-delay product (ADP) than the best existing trinomial-based design. The proposed multiplier can be used as a standard intellectual property (IP) core in many cryptographic applications for flexible operation.
1. Introduction
Finite field multipliers have gained substantial attentions recently due to their critical roles in many cryptosystems such as elliptic curve cryptography (ECC), especially on hardware platforms [1]. Typically, there are three types of structuring related to the finite field multipliers, namely the bit-serial, bit-parallel, and digit-serial. Because of the efficient tradeoff in area–time complexities, digit-serial structures usually are more widely preferred than the other two in many applications [2].
Along with the recent advance in artificial intelligence technology, systolic structure has becoming more and more attracting in high-performance hardware platforms [3]. Accordingly, digit-serial systolization of finite field multipliers have the potential to be applied in high-performance cryptosystems due to their superior features such as high-throughput rate and regularity and modularity. Thus far, several efforts have been made on efficient implementation of digit-serial systolic finite field multipliers: (i) an efficient systolic finite field multiplier is presented in [3], where its complexity is significantly reduced compared with the previous reported one; (ii) a systolic-like digit-serial multiplier is reported in [4] and it is found that the systolic structure proposed is specifically suitable for Reed–Solomon Codec; (iii) an efficient digit-serial systolic multiplier is presented in [5]; (iv) the same authors reported a unified digit-serial systolic multiplier based on trinomials and all-one-polynomials [6]; (v) a low-complexity systolic multiplier is given in [7], where its complexity is optimized to be minimal; (vi) an efficient resource-sharing technique is employed in another digit-serial systolic multiplier to achieve low critical-path and high-performance operation [8]; and (vii) an efficient systolic digit-serial multipliers is reported in [9], where the complexity is so far the least in the literature. These designs, undoubtedly, represent the major advance in the field of systolic digit-serial multipliers.
On the other side, however, the existing digit-serial systolic finite field multipliers, more or less, still have some drawbacks to be overcome: (i) although the digit-serial systolic multipliers have relatively few processing elements (PEs), the register-complexity of the multipliers is still large; and (ii) the current digit-serial multipliers are designed to be fixed field-size, and thus cannot provide enough flexibility to meet the current technology trend, i.e., one cryptosystem can meet different security level (field-size) need and the designers have to finalize different field-size multipliers with respect to different application requirement, which is some sort of inefficient in integrated chip (IC) design. Facing with these two challenges, in this paper, we have proposed a novel hybrid-size digit-serial systolic multiplier with low-complexity implementation. The proposed work is carried out through a combination of two coherent interdependent stages’ efforts: (i) a novel hybrid-size digit-serial systolic multiplication algorithm is proposed which provides enough flexibility to both pentanomial- and trinomial-based multipliers; and (ii) the proposed algorithm is then mapped into a novel systolic structure through a series of optimization techniques. Thorough complexity analysis and detailed comparison have also been made to confirm the efficiency of the proposed design, i.e., it not only offers flexibility to be switched from one field-size to another one, but also has smaller area–time complexities compared with the existing single field-size digit-serial systolic multipliers. The proposed design can not only be used as a standard intellectual property (IP) core for various field-size cryptosystem, but also can be employed as a core computation unit in reconfigurable cryptographic processor (where demands flexible field-size choice).
The rest of the paper is organized as follows: Section 2 presents the mathematical formulation of the proposed digit-serial multiplication algorithm. Section 3 shows the detailed steps of the proposed systolic structure mapped from the algorithm. The analysis and comparison are provided in Section 4. The conclusion is given in Section 5.
2. Mathematical Formulation of the Proposed Multiplication Algorithm
Let the three elements A, B, and C and let the polynomial basis be the , where x is the root of ( determines the field) [1]. Suppose for two field-sizes with and , and , we can first define that
and
where , , and and it is clear that in both and are the same (for ), and the same applies to and .
Suppose in the field-size of , let be the product of and (corresponding field polynomial is ), we can have
where and . Similarly, for the field-size of , we can have as the product of and (the field polynomial is ):
where, similarly, we have and . One can then have
Then, after comparing Equation (3) with Equation (5), we can have
where or 2 according to Equations (3) and (5), respectively, and
Then, we can have the following definitions:
For any integer of , we have (meanwhile, one can have ); then, we can define
Similarly, we can have
where we assume .
It is clear that we can now transfer Equation (6) into
where works for terms only when and
where we can see that Equation (10) can be used to perform two field-size finite field multiplications if we select the control signal properly.
The above equations can thus be summarized as Algorithm 1.
| Algorithm 1. Proposed multiplication algorithm for hybrid field-size-based implementation |
| Inputs: and (also and ) are the pair of elements (polynomial basis representation) in for |
| field-size of and , respectively |
| Output: for and is the field polynomial |
| 1. Initialization step |
| 1.1 Define , , …, for according to (8) 1.2 Define , , …, for according to (9) 1.3 Define |
| 2. Multiplication step |
| 2.1 According to the field-size selection signal, determine the value of j 2.2 For 2.3 2.4 End for |
| 3. Final step |
| 3.1 Get |
The detailed processes of Steps 2.2 and 2.4 are the key multiplication processes.
Note that, due to the difference of the field polynomial , the process of deriving from is slightly different from each other. For instance, assume
where we can have
when is a trinomial of . While, for pentanomial , we can have
Besides that, one has to note that the National Institute of Standards and Technology (NIST) has recommended five irreducible polynomials for ECC implementation [10,11] (three pentanomials and two trinomials). Without loss of generality, we can assume is a pentanomial and is a trinomial. The corresponding structure presented below is also based on this assumption.
3. Proposed Hybrid-Size Digit-Serial Systolic Multiplier
In this section, we propose several optimization technique to successfully map the corresponding algorithm into desired systolic structure. Specifically:
3.1. Novel Input Data Broadcasting Scheme
One major component of the register-complexity of a systolic finite field multiplier comes from the input data broadcasting. In this subsection, we propose a novel input data broadcasting that the main inputs to each PE are fed independent from each other and thus the relation of these data between the PEs is reduced to minimum, which can significantly reduce the related register-complexity among systolic array. In Figure 1, the proposed input data broadcasting technique is employed.
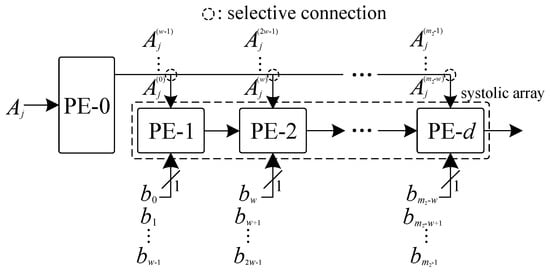
Figure 1.
The proposed input data broadcasting technique.
As shown in Figure 1, according to Step 2.3 of Algorithm 1, each PE in the systolic array is fed with two inputs, namely the and the corresponding . The output of each PE is then transferred to the next PE on its right. The complete output can be delivered after cycles, with the help of an extra accumulation cell. Since differences exist among all the , we have used the selective connection to rightly connect each PE according to Algorithm 1. Because only one signal pipelining to the next PE is used, the register-complexity of the systolic array is significantly reduced. The details of the internal structures of these PEs are shown below. Note that, due to the simple internal structure of the PEs, i.e., critical-path of the PE is quite small, the proposed broadcasting technique has very limited influence on the overall time complexity.
3.2. Proper Arrangement on the Input Data Delivery
The two inputs, i.e., and , must be properly arranged to meet the data dependence requirement for hybrid-size operation. For , according to Algorithm 1, all bits are delivered in a grouped-sequential way, which can be realized by the structure, as shown in Figure 2. One can see that the shift-register is producing the required output bits to each PE of Figure 1 based on Algorithm 1, while the hybrid-size selection is done by the inserting of an extra MUX (MUX is short for multiplexer) in the shifting path such that the shift-register can be working under the field-size of either or through the proper control of the MUX (control signal).
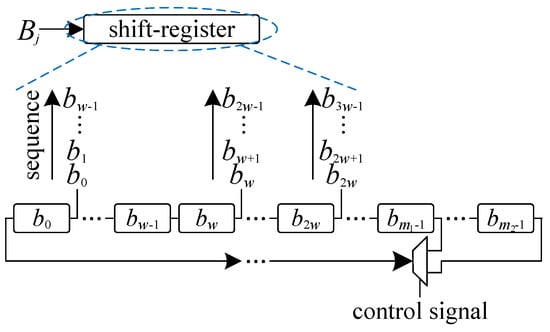
Figure 2.
The proposed shift-register to deliver input data .
The operand , through the help of PE-0, delivers the correct output bits to each PE according to Algorithm 1, which requires a more sophisticated structure, as shown in Figure 3a. From Equations (13) and (14), one can observe that there are one XOR gate involved when obtaining from (trinomial-based multiplication) while it requires three XOR gates when deriving from . Thus, according to the data dependence requirement of Algorithm 1, one can find that there are d number of operands being delivered from PE-0 at the same cycle period, i.e., . These operands, in fact, involve multiple identical bits between each other and thus can be shared. For simplicity of discussion, let assume and , we can have (, , for , and for )
and
where we can see that the identical bits, e.g., , can be shared among these (), as shown by the example in Figure 3b (where we have shown how the MUXes are located to obtain hybrid-size implementation). Since other bits cannot be shared, we just use the MUX to connect with the two bits at the same position (according to Equations (8) and (9)) such that, through the proper working of these MUXes, the correct signals can be produced to the corresponding PE.
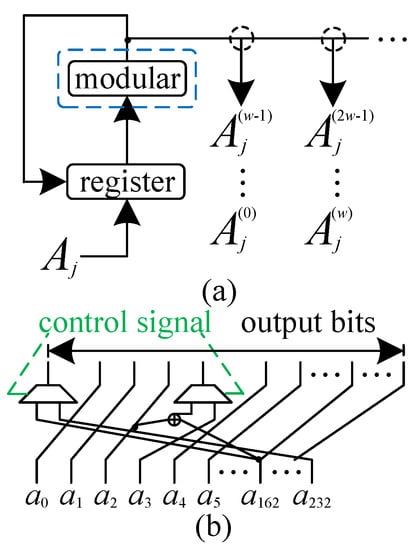
Figure 3.
The internal structure of PE-0 to deliver input data : (a) internal structure; and (b) an example of how the MUXes are inserted to obtain hybrid-size implementation for the modular cell in PE-0.
One can also notice that, according to Equations (9), (13), and (14), with the help of a modular operation (done by the modular cell in Figure 3), the PE-0 delivers the corresponding output to each PE, i.e., obtaining from (for ), which needs a delay time of ( is the delay time of an XOR gate, and it takes for trinomial-based multiplier and for pentanomial-based one [9]). Besides that, one has to note that all the in one specific can be obtained through the sharing of identical bits, as represented by the selective connection in Figure 1 and Figure 3. Following this arrangement, the proposed hybrid-size structure operates in an ordered form according to Algorithm 1.
3.3. Hybrid Accumulation
The accumulation of the digit-serial operation also needs adjustment when compared with the conventional ones. As shown in Figure 4, where we have used a -bit MUX cell to obtain the hybrid-size accumulation (where the accumulation cell is realized through the XOR cell connected with the register cell in a back-loop style). Note that these bit-level MUXes connect with the -bit output of PE-, while the remaining bits of PE-d are directly connected with the accumulation cell. According to Equations (8) and (9), and Algorithm 1, we can let the MUX determine the multiplier is working under the condition of field-size of either bits or bits. Besides that, the number of output bits is also selected according to the specific chosen field-size, as shown in Figure 4, i.e., after designated number of cycle periods, the output is produced based on the value of the control signal.
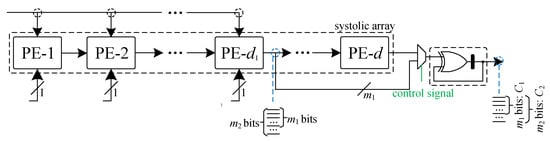
Figure 4.
The detailed arrangement of how the accumulation cell operate to realize the hybrid-size implementation (only bit-level MUXes are employed and the remaining bits of the output of PE-d are directly connected with the accumulation cell), where the black box in the accumulation cell denotes the register cell.
3.4. Final Structure
The internal structure of each PE is shown in Figure 5b, where it mainly consists of an AND cell, an XOR cell, and a register cell. With the combination of all the optimization techniques introduced above, we have presented the finalized proposed hybrid-size digit-serial structure, as shown in Figure 5a. All the control signals connected with the inserted MUXes collaborate together to switch the finite field multiplier from operating in one field-size to another. After designated cycle periods of accumulation, the multiplier delivers the desired output.
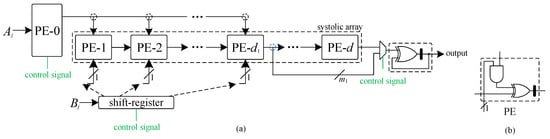
Figure 5.
The final structure: (a) the proposed structure; and (b) the internal structure of a regular PE.
4. Complexity and Comparison
For simplicity of discussion, we just follow the assumption in Section 3 that comes from a pentanomial while is the field-size of a trinomial. The detailed complexity of the proposed multiplier is: (i) Systolic array: The systolic array has d number of PEs, where each PE has AND gates, XOR gates, and registers. (ii) Shift-register: The shift-register for requires registers and one MUX. (iii) Accumulation cell: The accumulation cell requires MUXes, XORs, and registers. (iv) PE-0: There are in total XOR gates, MUXes, and registers involved. Moreover, the proposed structure has a critical-path of ( is the delay time of an MUX), and it takes cycles to produce the desired output for hybrid-size operation. Overall, the complexity of the proposed design is listed along with the existing digit-serial multipliers (trinomial- or pentanomial-based designs) in Table 1 in terms of logic gates number, register number, latency (number of cycle periods), and critical-path. Note that the designs of [5,6] are based on all-one-polynomials (or used all-one-polynomials as a computation core), we thus do not list them in Table 1, just for a fair comparison. As shown in Table 1, one can see that the proposed hybrid-size digit-serial multiplier has relatively better area–time complexities than the existing ones, especially when considering that the proposed one can offer hybrid field-size operation (the existing ones are all single field-size based). To have a detailed comparison, we have also used the NanGate’s Library Creator and the 45-nm FreePDK Base Kit from North Carolina State University (NCSU) [12] to estimate the area and time complexities of all the designs for , , and . The obtained area, delay (latency time), power, area-delay product (ADP), and power-delay product (PDP) are listed in Table 2 for a comparison. Again, we can observe that the proposed one has better performance than the existing ones, e.g., it has at least 7.3% less ADP than the best trinomial one of [8], while it offers the flexibility to execute the pentanomial-based multiplier. Compared with the existing pentanomial ones, the proposed one still has better ADP when considering the scaling of the field-size. The proposed one also has 41.5% less ADP and 34.6% less PDP than the conventional hybrid field-size implementation (we have combined the best existing ones of [8,9] together to realize it).

Table 1.
Comparison of Area–Time Complexities of Various Digit-Serial Systolic Multipliers.

Table 2.
Comparison of Area–Time Complexities of Various Digit-Serial Systolic Multipliers.
The proposed hybrid-size digit-serial systolic multiplier, undoubtedly, can be extended as a standard IP core in various cryptosystems that demand different security levels. On the other hand, due to the low-complexity of the proposed design, it can also be used in cryptosystem for flexible operation, in the case the user of that cryptosystem needs to change/upgrade the system. Moreover, it is worth mentioning that the proposed hybrid field-size strategy can also be extended to multiple filed-size implementation.
5. Conclusions
This paper presents a novel implementation of a hybrid field-size digit-serial systolic multiplier over . A novel digit-serial multiplication algorithm suitable for hybrid field-size realization is proposed first. Then, through a series of optimization techniques, the proposed algorithm is successfully mapped into a high-performance digit-serial systolic multiplier. The complexity analysis and detailed comparison have been given to confirm the efficiency of the proposed design. Future work may focus on the application of the proposed design in various cryptosystems.
Author Contributions
Resources, Z.H.; Writing—Review & Editing, J.X.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IP | Intellectual property |
| ECC | Elliptic curve cryptography |
| PE | Processing elements |
| IC | Integrated chip |
| NCSU | North Carolina State University |
References
- Blake, I.; Seroussi, G.; Smart, N.P. Elliptic Curves in Cryptography; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Xie, J.; Meher, P.K.; He, J. Low-latency area-delay-efficient systolic multiplier over GF(2m) for a wider class of trinomials using parallel register sharing. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012; pp. 89–92. [Google Scholar]
- Systolic Array. Available online: https://en.wikipedia.org/wiki/Systolic-array (accessed on 25 September 2018).
- Kim, C.H.; Hong, C.P.; Kwon, S. A digit-serial multiplier for finite field GF(2m). IEEE Trans. Very Large Scale Integr. Syst. 2005, 13, 476–483. [Google Scholar]
- Meher, P.K. Systolic and non-systolic scalable modular designs of finite field multipliers for Reed-Solomon Codec. IEEE Trans. Very Large Scale Integr. Syst. 2009, 17, 747–757. [Google Scholar] [CrossRef]
- Talapatra, S.; Rahaman, H.; Mathew, J. Low complexity digit serial systolic montgomery multipliers for special class of GF(2m). IEEE Trans. Very Large Scale Integr. Syst. 2010, 18, 847–852. [Google Scholar] [CrossRef]
- Talapatra, S.; Rahaman, H.; Saha, S.K. Unified digit serial systolic montgomery multiplication architecture for special classes of polynomials over. In Proceedings of the 13th Euromicro Conference on Digital System Design: Architectures, Methods and Tools, Lille, France, 1–3 September 2010; pp. 427–432. [Google Scholar]
- Pan, J.-S.; Lee, C.-Y.; Meher, P.K. Low-latency digit-serial and digit-parallel systolic multipliers for large binary extension fields. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3195–3204. [Google Scholar] [CrossRef]
- Xie, J.; Meher, P.K.; Mao, Z. High-throughput digit-level systolic multiplier over GF(2m) based on irreducible trinomials. IEEE Trans. Circuits Syst. II 2015, 62, 481–485. [Google Scholar] [CrossRef]
- Xie, J.; Meher, P.K.; Mao, Z.-H. Low-latency high-throughput systolic multipliers over GF(2m) for NIST recommended pentanomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 881–890. [Google Scholar] [CrossRef]
- NIST. Boulder, CO, USA. Available online: http://www.csrc.nist.gov/publications (accessed on 25 September 2018).
- Nangate Standard Cell Library. Available online: http://www.si2.org/openeda.si2.org/projects/nangatelib (accessed on 25 September 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).