Modified Kudryashov Method to Solve Generalized Kuramoto-Sivashinsky Equation
Abstract
:1. Introduction
2. Analysis of the Modified Kudryashov Method
- Step 1.
- Consider the given NLPDE of the following form .
- Step 2.
- Apply the wave transformation in Equation (2), where:Here, is the wave variable and is the velocity; both are non-zero constants. Hence, Equation (2) transforms to the following ODE:where the prime represents the derivative with respect to .
- Step 3.
- Let the initial solution guess of Equation (4) be,where N is a non-zero and positive constant calculated by the principle of homogeneous balancing of Equation (4), are unknowns to be calculated and is the solution of the following auxiliary ODE:given by,where D is the integral constant and we assume .
- Step 4.
- Step 5.
3. MKM Application to Solve the Generalized Kuramoto–Sivashinsky Equation
- Case 1.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 2.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 3.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 4.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and , the second set of unknown coefficients are given by,
- Case 5.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 6.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 7.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 8.
- For and in Equation (1), the unknown coefficients are given by,Further, for the same and value, the second set of unknown coefficients are given by,
- Case 9.
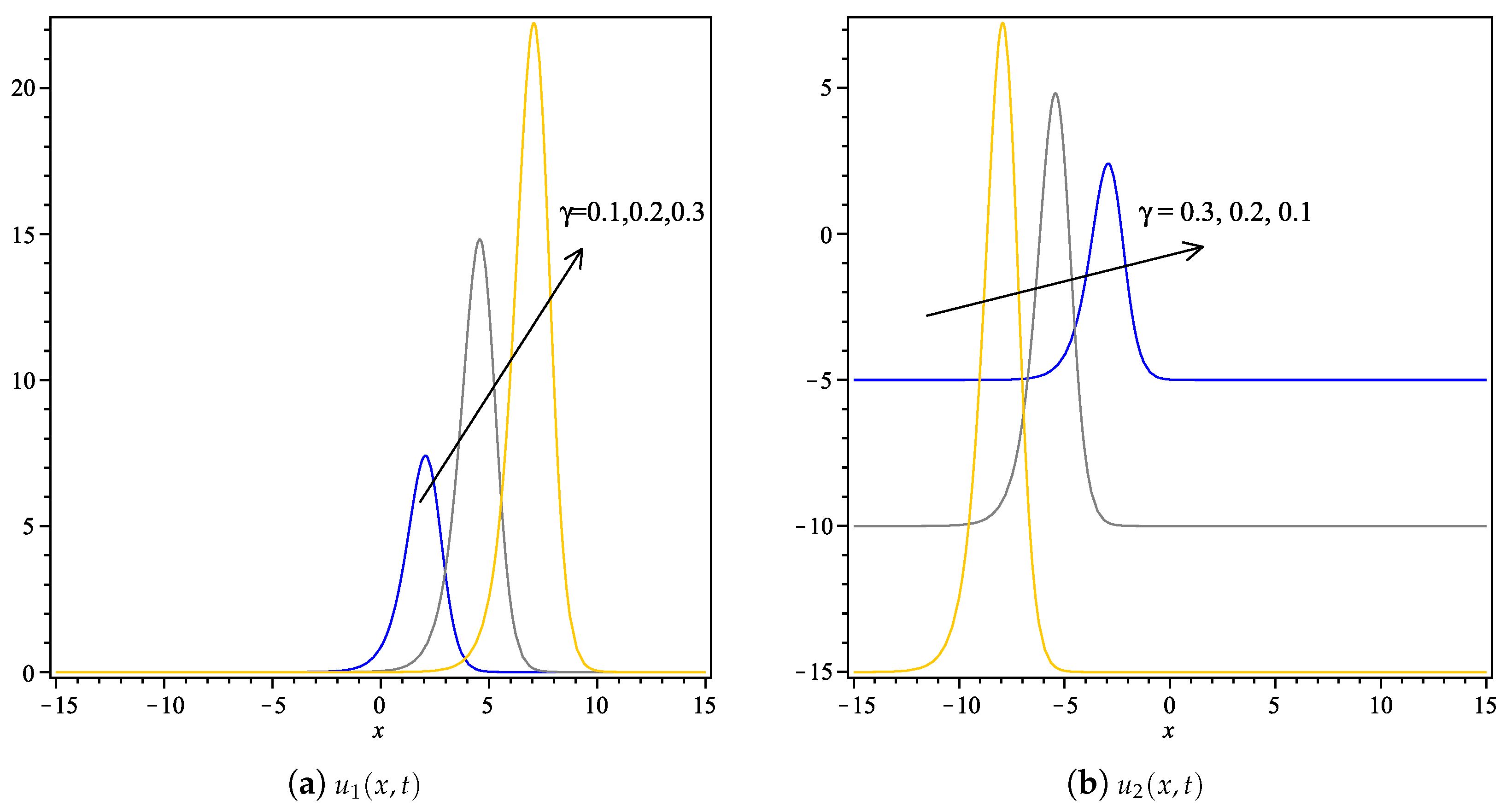
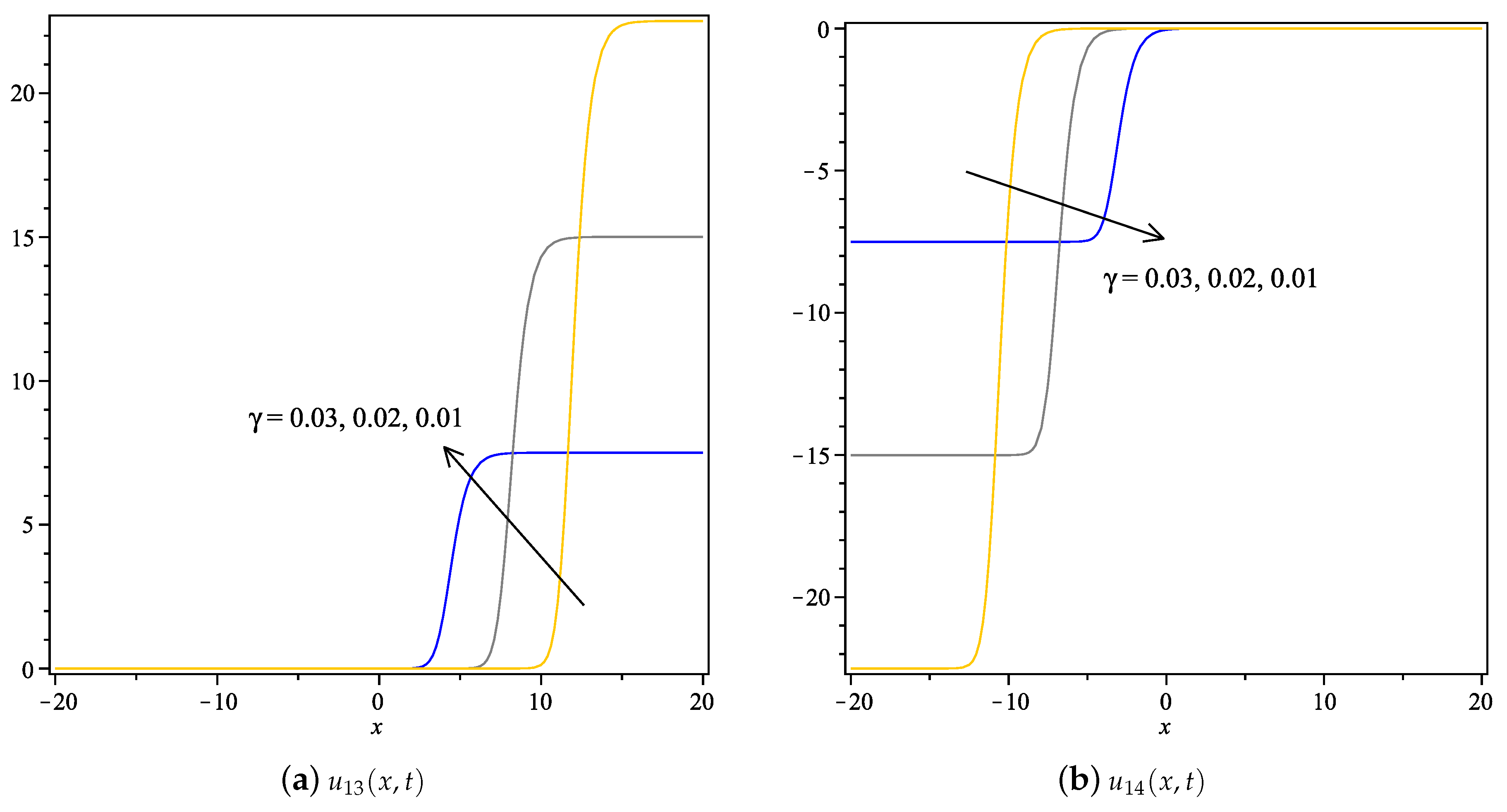
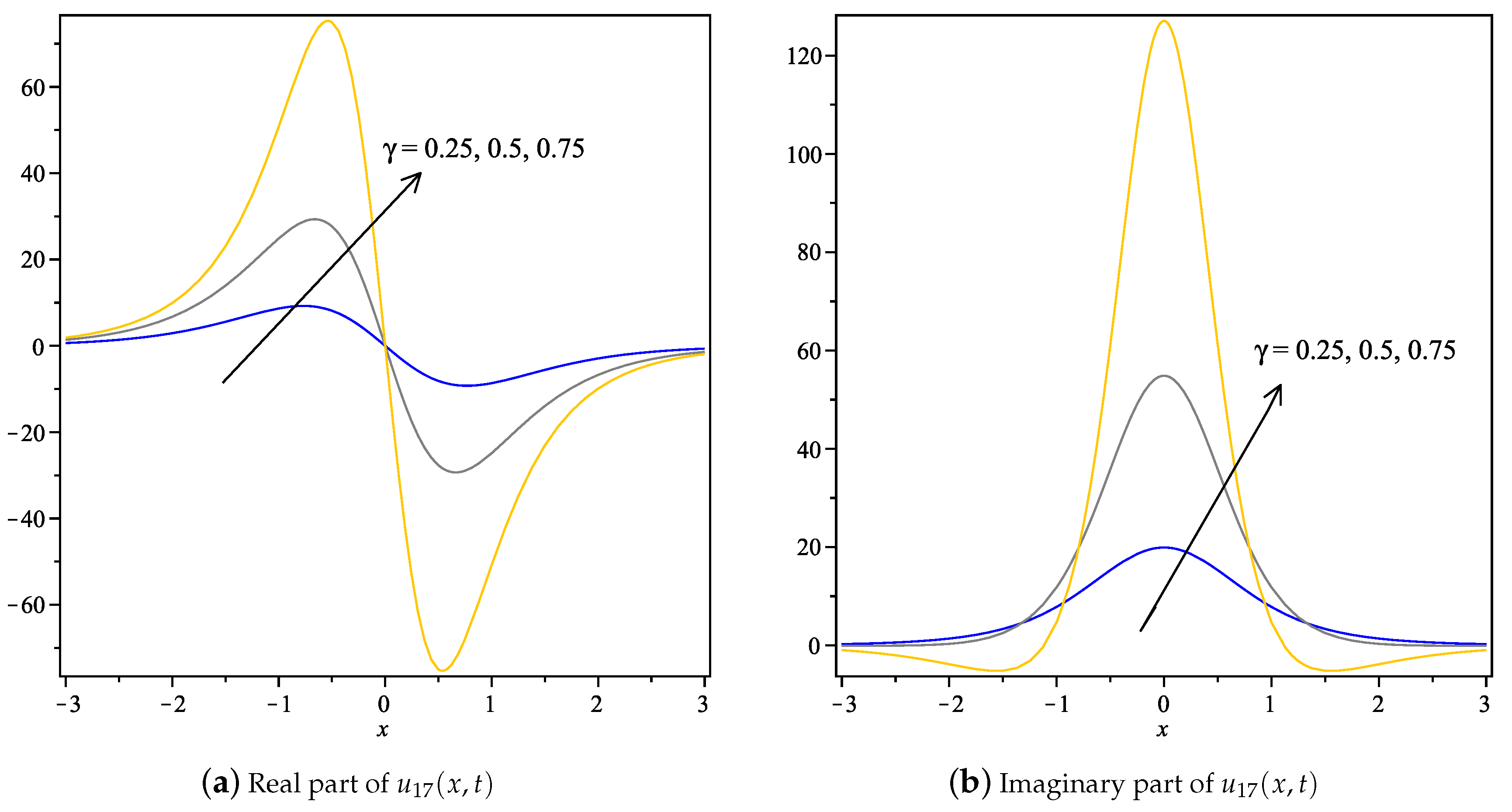
- For and in Equation (1), the unknown coefficients are given by,Therefore, the exact complex solution of Equation (1) is given by,The 2D graph of real and imaginary parts of are drawn in Figure 9.Further, for the same and value, the second set of unknown coefficients are given by,
- Case 10.
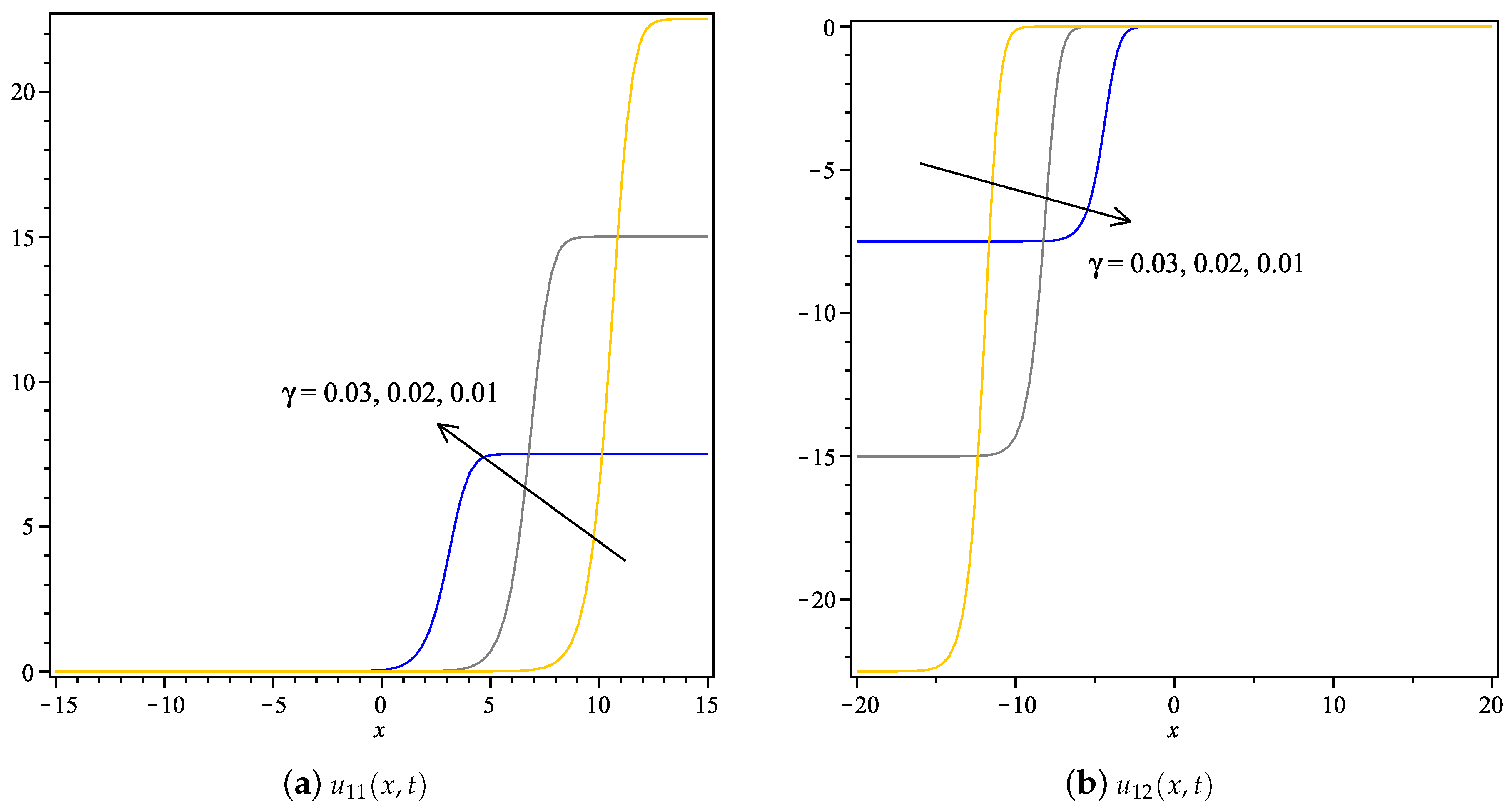
- For and in Equation (1), the unknown coefficients are given by,Therefore, the exact complex solution of Equation (1) is given by,The 2D graphs of real and imaginary parts of are drawn in Figure 11.Further, for the same and value, the second set of unknown coefficients are given by,
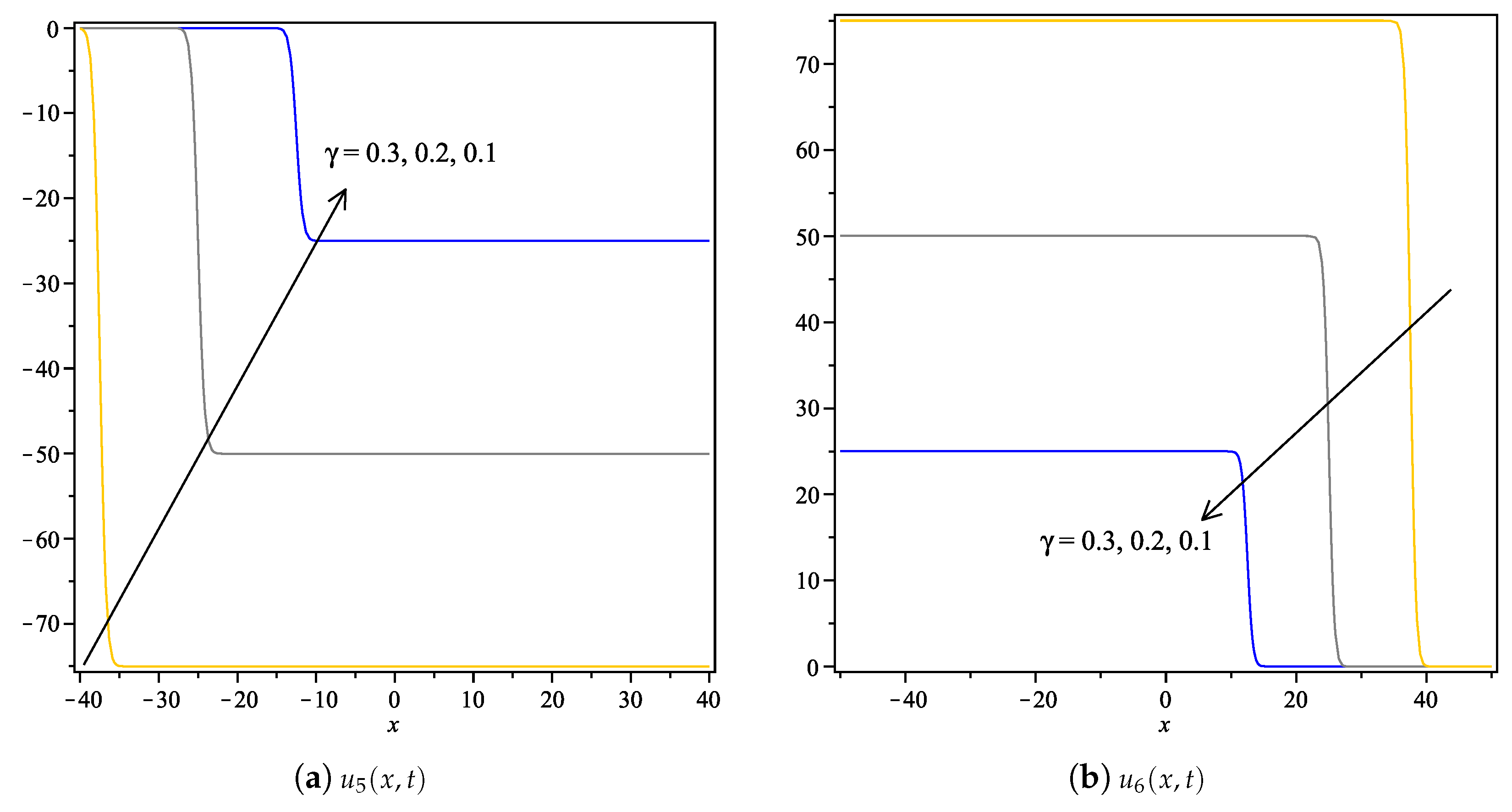
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. GKSE in the Previous Studies
Appendix B. Studying GKSE by GKM and SGEEM
- For solving Equation (1) by the generalized Kudryashov method [22,23,24], the homogeneous balancing of Equation (8) gives , which has infinite solutions. For the value , this gives . Therefore,where is the solution of , Applying these equations to Equation (8) leads to the polynomial in and its powers. Collecting the coefficients of and attempting to solve the overdetermined equations results in the continuous execution of Maple. Hence, we conclude that Equation (1) cannot be solved by the generalized Kudryashov method.
- Next, for solving Equation (1) by the sine-Gordon equation expansion method [26], the homogeneous balancing is the same as the MKM given by . Thus,Substituting the above equation in Equation (8) and following the steps in [26] lead to the polynomials in , , their products and powers. Collecting the coefficients, equating them to zero and solving in Maple result in the continuous execution. Thus, we conclude that Equation (1) cannot be solved by the sine-Gordon equation expansion method either.
References
- Kudryashov, N.A. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys. Lett. A 1990, 147, 287–290. [Google Scholar] [CrossRef]
- Parkes, E.J.; Duffy, B.R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations. Comput. Phys. Commun. 1996, 98, 288–300. [Google Scholar] [CrossRef]
- Hamid, B.A. An exact solution to the Kuramoto-Sivashinsky equation. Phys. Lett. A 1999, 263, 338–340. [Google Scholar] [CrossRef]
- Baldwin, D.; Göktas, Ü.; Hereman, W.; Hong, L.; Martino, R.S.; Miller, J.C. Symbolic computation of exact solutions expressible in hyperbolic and elliptic functions for nonlinear PDEs. J. Symb. Comput. 2004, 37, 669–705. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Zhao, S. Exact travelling wave solutions to the generalized Kuramoto-Sivashinsky equation. Latin Am. Appl. Res. 2004, 34, 65–68. [Google Scholar]
- Kudryashov, N.A. Solitary and Periodic Solutions of the Generalized Kuramoto-Sivashinsky Equation. Regul. Chaotic Dyn. 2008, 13, 234–238. [Google Scholar] [CrossRef]
- Khater, A.H.; Temsah, R.S. Numerical solutions of the generalized Kuramoto-Sivashinsky equation by Chebyshev spectral collocation methods. Comput. Math. Appl. 2008, 56, 1465–1472. [Google Scholar] [CrossRef]
- Porshokouhi, M.G.; Ghanbari, B. Application of He’s variational iteration method for solution of the family of Kuramoto-Sivashinsky equations. J. King Saud Univ.-Sci. 2011, 23, 407–411. [Google Scholar] [CrossRef]
- Khalique, C.M. Exact Solutions of the Generalized Kuramoto-Sivashinsky Equation. Caspian J. Math. Sci. 2012, 1, 109–116. [Google Scholar]
- Feng, D. Exact Solutions of Kuramoto-Sivashinsky Equation. Int. J. Educ. Manag. Eng. 2012, 6, 61–66. [Google Scholar] [CrossRef]
- Lakestani, M.; Dehghan, M. Numerical solutions of the generalized Kuramoto-Sivashinsky equation using B-spline functions. Appl. Math. Model. 2012, 36, 605–617. [Google Scholar] [CrossRef]
- Yang, J.; Lu, X.; Tang, X. Exact travelling wave solutions for the generalized Kuramoto-Sivashinsky equation. J. Math. Sci. Adv. Appl. 2015, 31, 1–13. [Google Scholar]
- Rashidinia, J.; Jokar, M. Polynomial scaling functions for numerical solution of generalized Kuramoto-Sivashinsky equation. Appl. Anal. 2015, 10, 1–10. [Google Scholar] [CrossRef]
- Acan, O.; Keskin, Y. Approximate solution of Kuramoto-Sivashinsky equation using reduced differential transform method. AIP Conf. Proc. 2015, 1648, 470003-1–470003-4. [Google Scholar]
- Foroutan, M.; Manafian, J.; Taghipour-Farshi, H. Exact solutions for Fitzhugh-Nagumo model of nerve excitation via Kudryashov method. Opt. Quantum Electron. 2017, 49, 352. [Google Scholar] [CrossRef]
- Ali, K.K.; Nuruddeen, R.I.; Hadhoud, A.R. New exact solitary wave solutions for the extended (3 + 1)-dimensional Jimbo-Miwa equations. Results Phys. 2018, 9, 12–16. [Google Scholar] [CrossRef]
- Hosseini, K.; Mayeli, P.; Ansari, R. Modified Kudryashov method for solving the conformable time-fractional Klein-Gordon equations with quadratic and cubic nonlinearities. Optik 2017, 130, 737–742. [Google Scholar] [CrossRef]
- Hosseini, K.; Ansari, R. New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Med. 2017, 27, 628–636. [Google Scholar] [CrossRef]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Joardar, A.K.; Kumar, D.; al Woadud, K.M.A. New exact solutions of the combined and double combined sinh-cosh-Gordon equations via modified Kudryashov method. Int. J. Phys. Res. 2018, 1, 25–30. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Kumar, D.; Hosseini, K.; Samadani, F. The system of equations for the ion sound and Langmuir waves and its new exact solutions. Results Phys. 2018, 9, 1631–1634. [Google Scholar]
- Mahmud, F.; Samsuzzoha, M.; Akbar, M.A. The generalized Kudryashov method to obtain exact traveling wave solutions of the PHI-four equation and the Fisher equation. Results Phys. 2017, 7, 4296–4302. [Google Scholar] [CrossRef]
- Demiray, S.T.; Pandir, Y.; Bulut, H. Generalized Kudryashov Method for Time-Fractional Differential Equations. Abstract Appl. Anal. 2014, 2014, 901540. [Google Scholar]
- Bibi, S.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T. Some new exact solitary wave solutions of the van der Waals model arising in nature. Results Phys. 2018, 9, 648–655. [Google Scholar] [CrossRef]
- Raslan, K.R.; L-Danaf, T.S.E.; Ali, K.K. New exact solutions of coupled generalized regularized long wave equations. J. Egypt. Math. Soc. 2017, 25, 400–405. [Google Scholar] [CrossRef]
- Bulut, H.; Sulaiman, T.A.; Baskonus, H.M.; Sandulyak, A.A. New solitary and optical wave structures to the (1 + 1)-dimensional combined KdV-mKdV equation. Optik 2017, 135, 327–336. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. Dark, bright and other optical solitons to the decoupled nonlinear Schrödinger equation arising in dual-core optical fibers. Opt. Quantum Electron. 2018, 50, 165. [Google Scholar] [CrossRef]
- Yang, X.-L.; Tang, J.-S. Travelling Wave Solutions for Konopelchenko-Dubrovsky Equation Using an Extended sinh-Gordon Equation Expansion Method. Commun. Theor. Phys. 2008, 50, 1047–1051. [Google Scholar]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the space-time fractional (1+1)-dimensional coupled nonlinear Schrödinger equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Gepreel, K.A. Extended trial equation method for nonlinear coupled Schrodinger Boussinesq partial differential equations. J. Egypt. Math. Soc. 2016, 24, 381–391. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y.; Misirli, E. The Extended Trial Equation Method for Some Time Fractional Differential Equations. Discret. Dyn. Nat. Soc. 2013, 2013, 491359. [Google Scholar] [CrossRef]
- Gurefe, Y.; Misirli, E.; Sonmezoglu, A.; Ekici, M. Extended trial equation method to generalized nonlinear partial differential equations. Appl. Math. Comput. 2013, 219, 5253–5260. [Google Scholar] [CrossRef]
- Ravi, L.K.; Ray, S.S.; Sahoo, S. New exact solutions of coupled Boussinesq-Burgers equations by Exp-function method. J. Ocean Eng. Sci. 2017, 2, 34–46. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Lu, D.; Khater, M.M.A. Solitary wave solutions for the generalized Zakharov-Kuznetsov-Benjamin-Bona-Mahony nonlinear evolution equation. J. Ocean Eng. Sci. 2017, 2, 137–142. [Google Scholar] [CrossRef]
- Alam, M.N.; Alam, M.M. An analytical method for solving exact solutions of a nonlinear evolution equation describing the dynamics of ionic currents along microtubules. J. Taibah Univ. Sci. 2017, 11, 939–948. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Ebaid, A.; Aly, E.H. Exact solutions for the transformed reduced Ostrovsky equation via the F-expansion method in terms of Weierstrass-elliptic and Jacobian-elliptic functions. Wave Motion 2012, 49, 296–308. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Joudi, S. Applications of an Extended G′/G-Expansion Method to Find Exact Solutions of Nonlinear PDEs in Mathematical Physics. Math. Probl. Eng. 2010, 2010, 768573. [Google Scholar] [CrossRef]

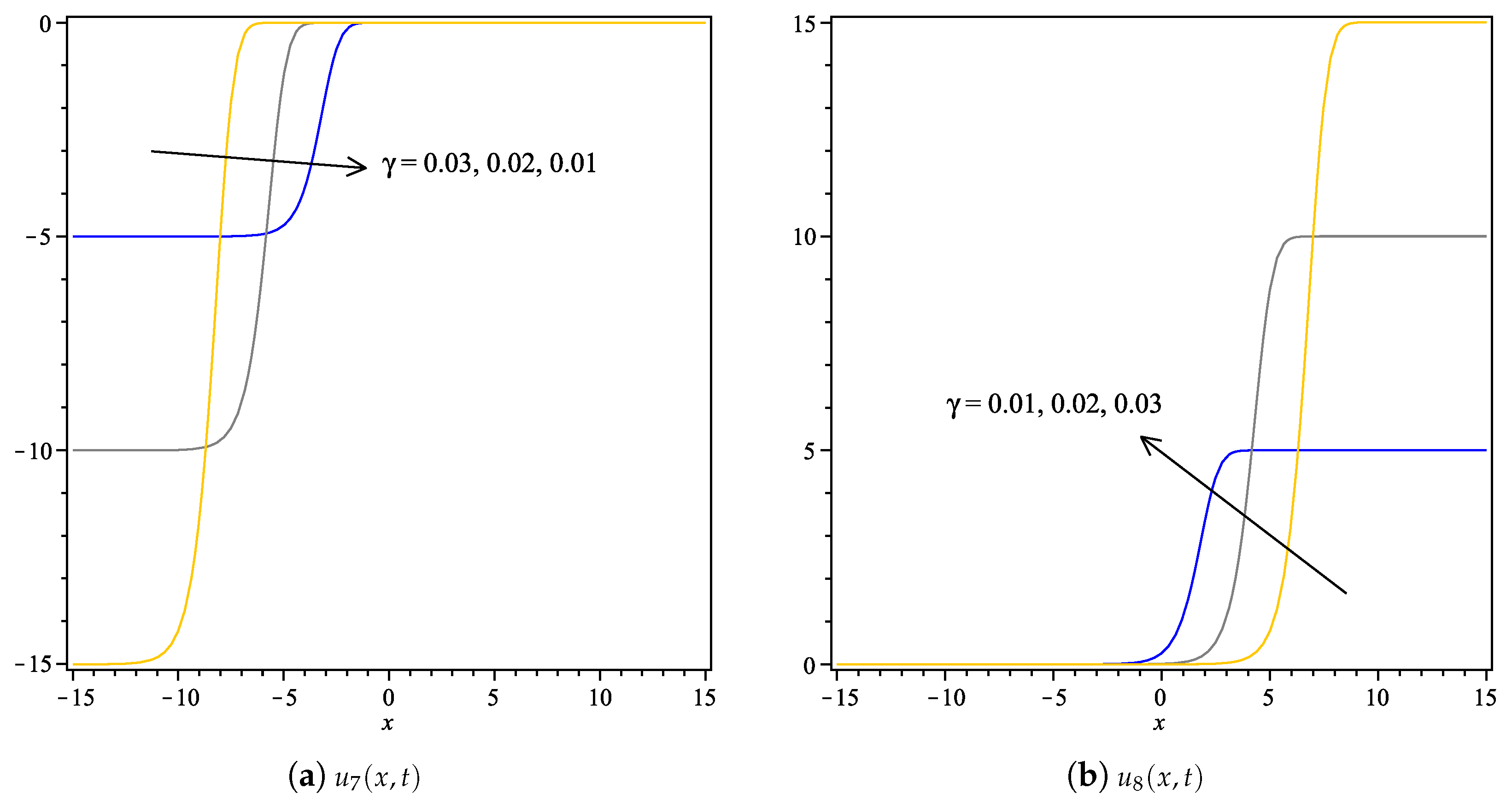





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilicman, A.; Silambarasan, R. Modified Kudryashov Method to Solve Generalized Kuramoto-Sivashinsky Equation. Symmetry 2018, 10, 527. https://doi.org/10.3390/sym10100527
Kilicman A, Silambarasan R. Modified Kudryashov Method to Solve Generalized Kuramoto-Sivashinsky Equation. Symmetry. 2018; 10(10):527. https://doi.org/10.3390/sym10100527
Chicago/Turabian StyleKilicman, Adem, and Rathinavel Silambarasan. 2018. "Modified Kudryashov Method to Solve Generalized Kuramoto-Sivashinsky Equation" Symmetry 10, no. 10: 527. https://doi.org/10.3390/sym10100527
APA StyleKilicman, A., & Silambarasan, R. (2018). Modified Kudryashov Method to Solve Generalized Kuramoto-Sivashinsky Equation. Symmetry, 10(10), 527. https://doi.org/10.3390/sym10100527





