A Review and Mathematical Treatment of Infinity on the Smith Chart, 3D Smith Chart and Hyperbolic Smith Chart
Abstract
1. Introduction
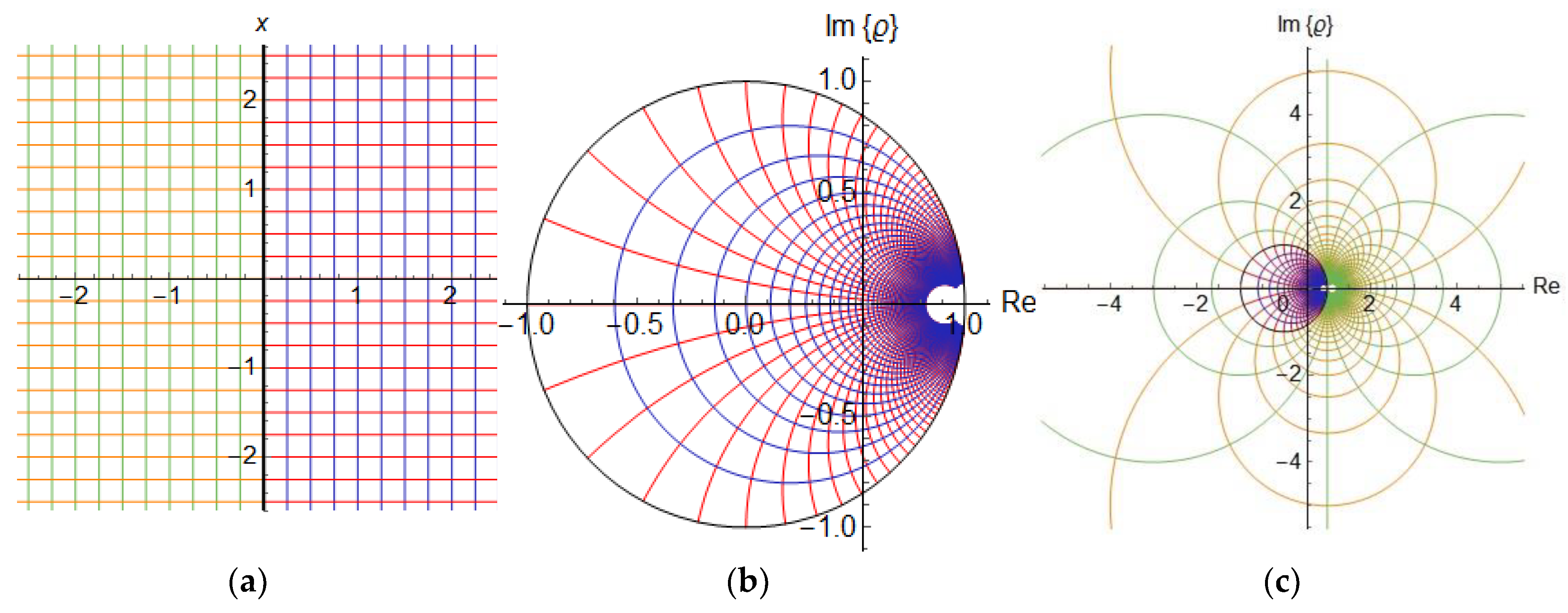
2. Planar Smith Chart and Möbius Transformations
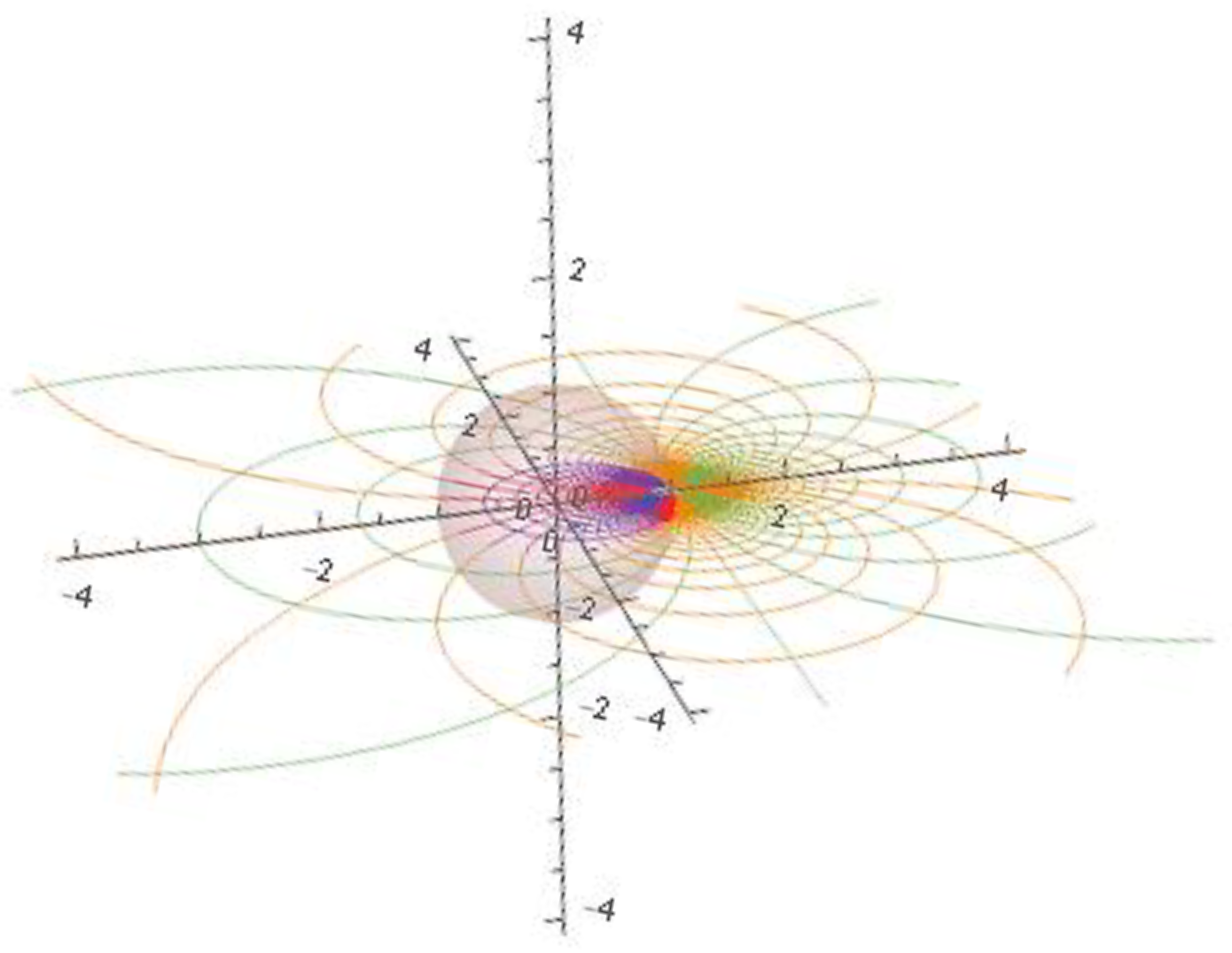
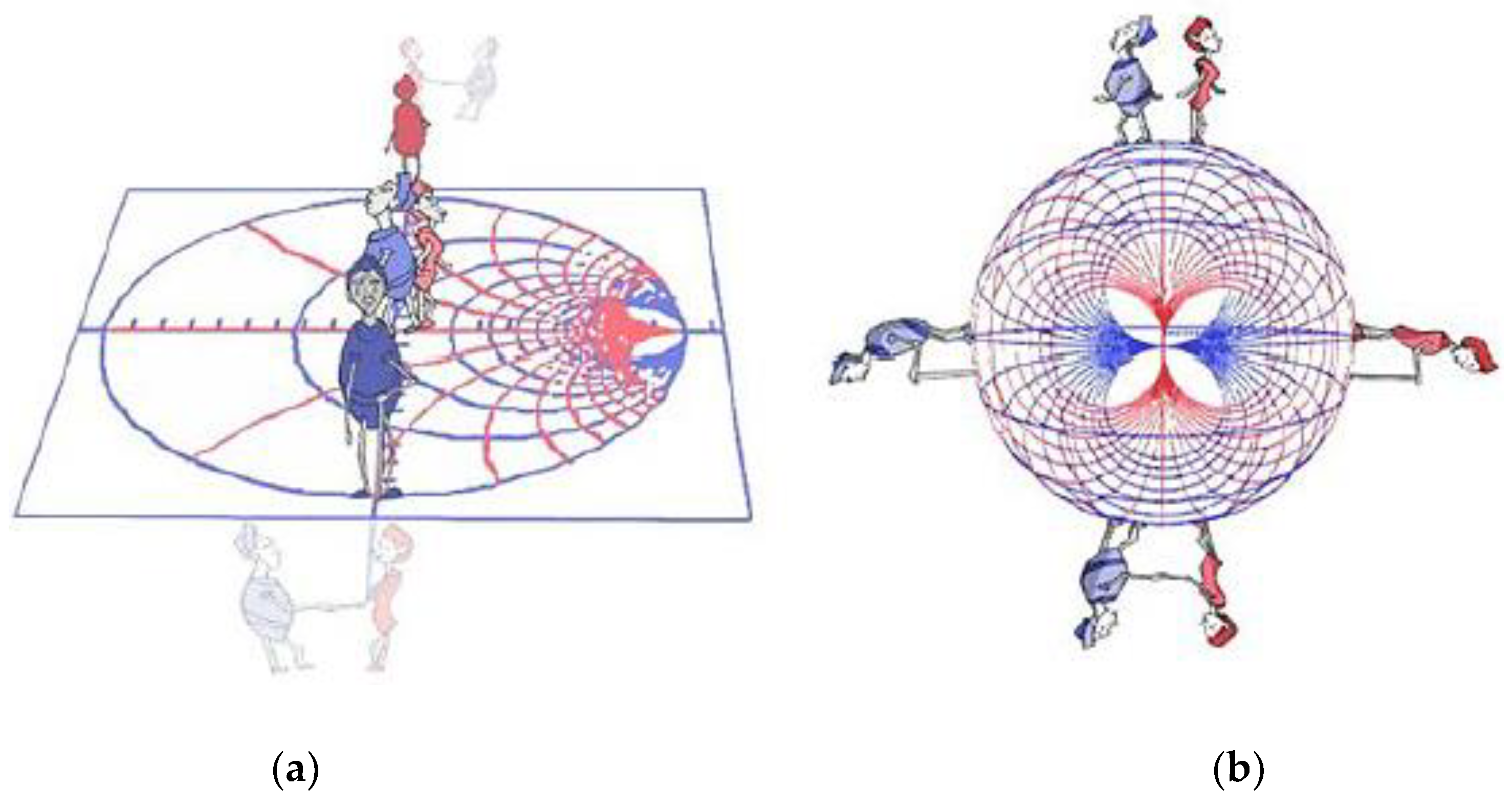
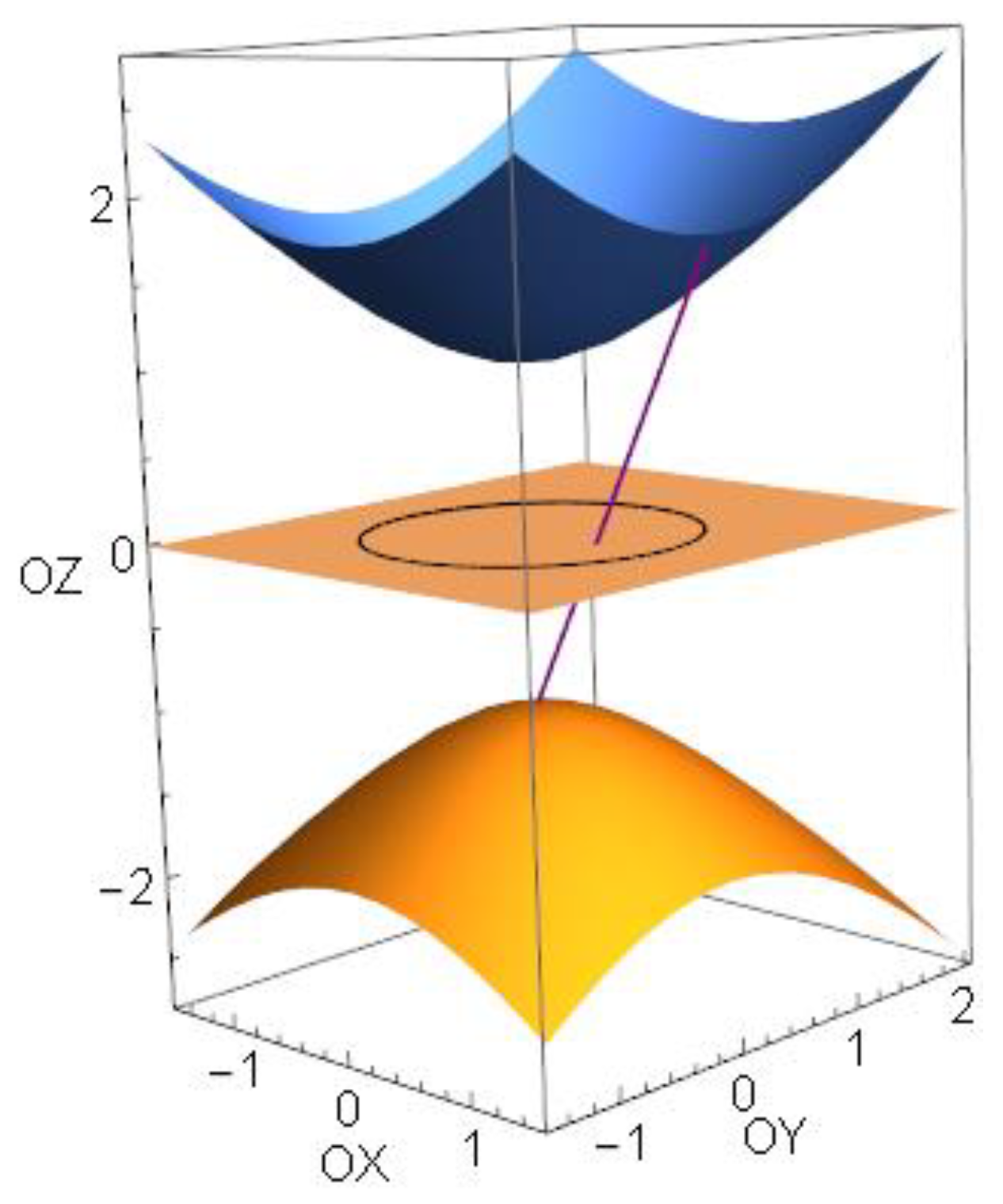
3D Smith Chart and Infinity
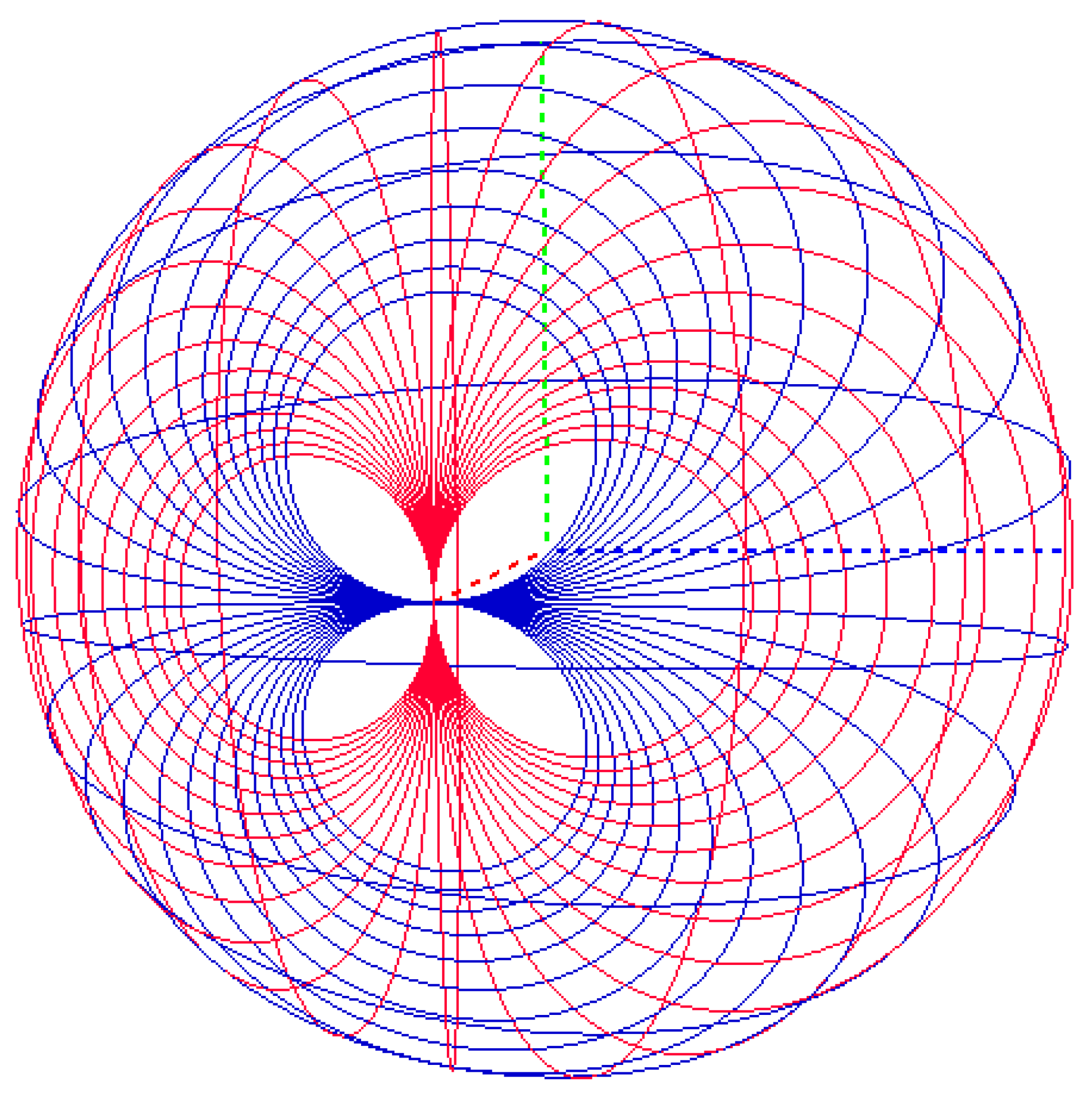
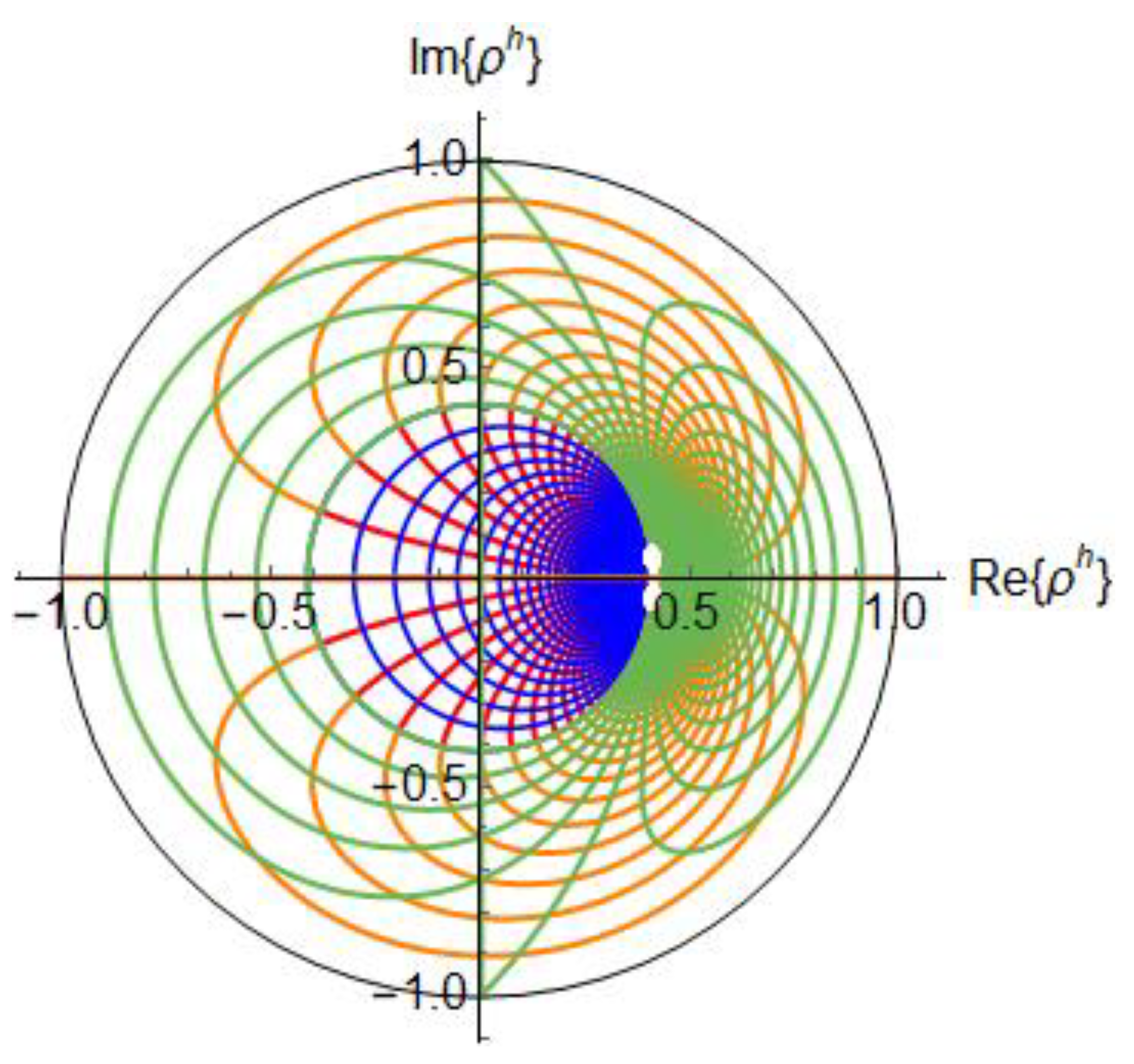
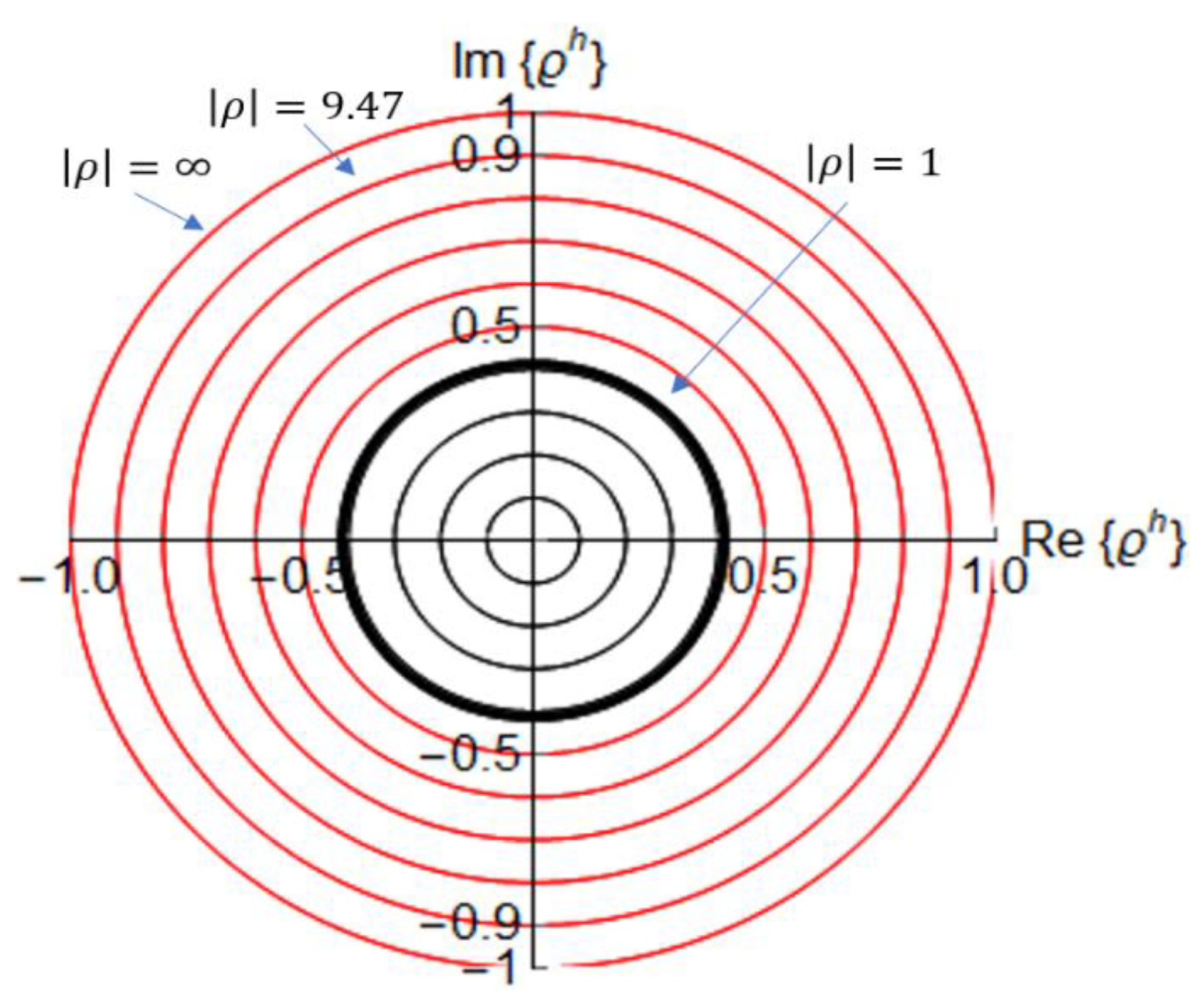
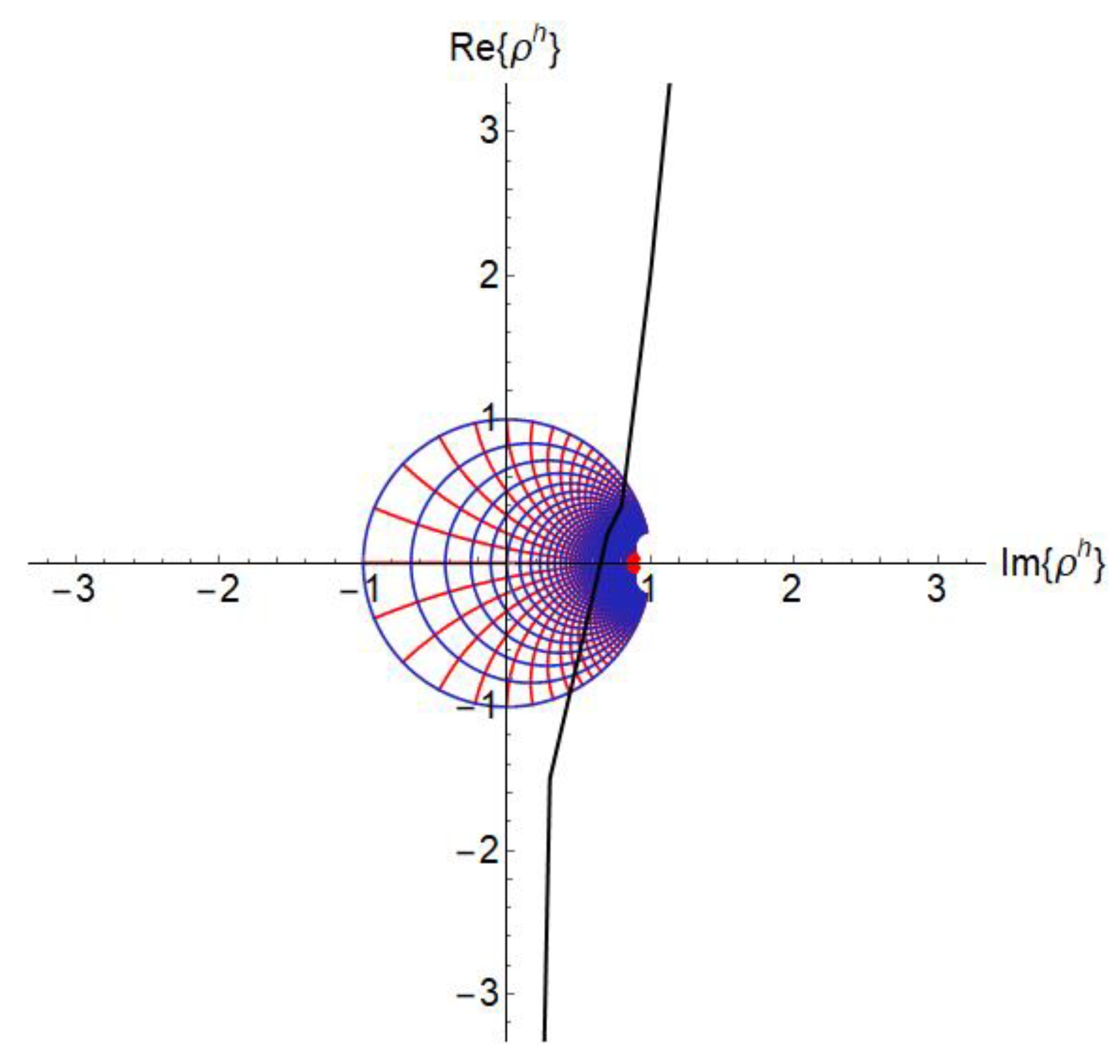
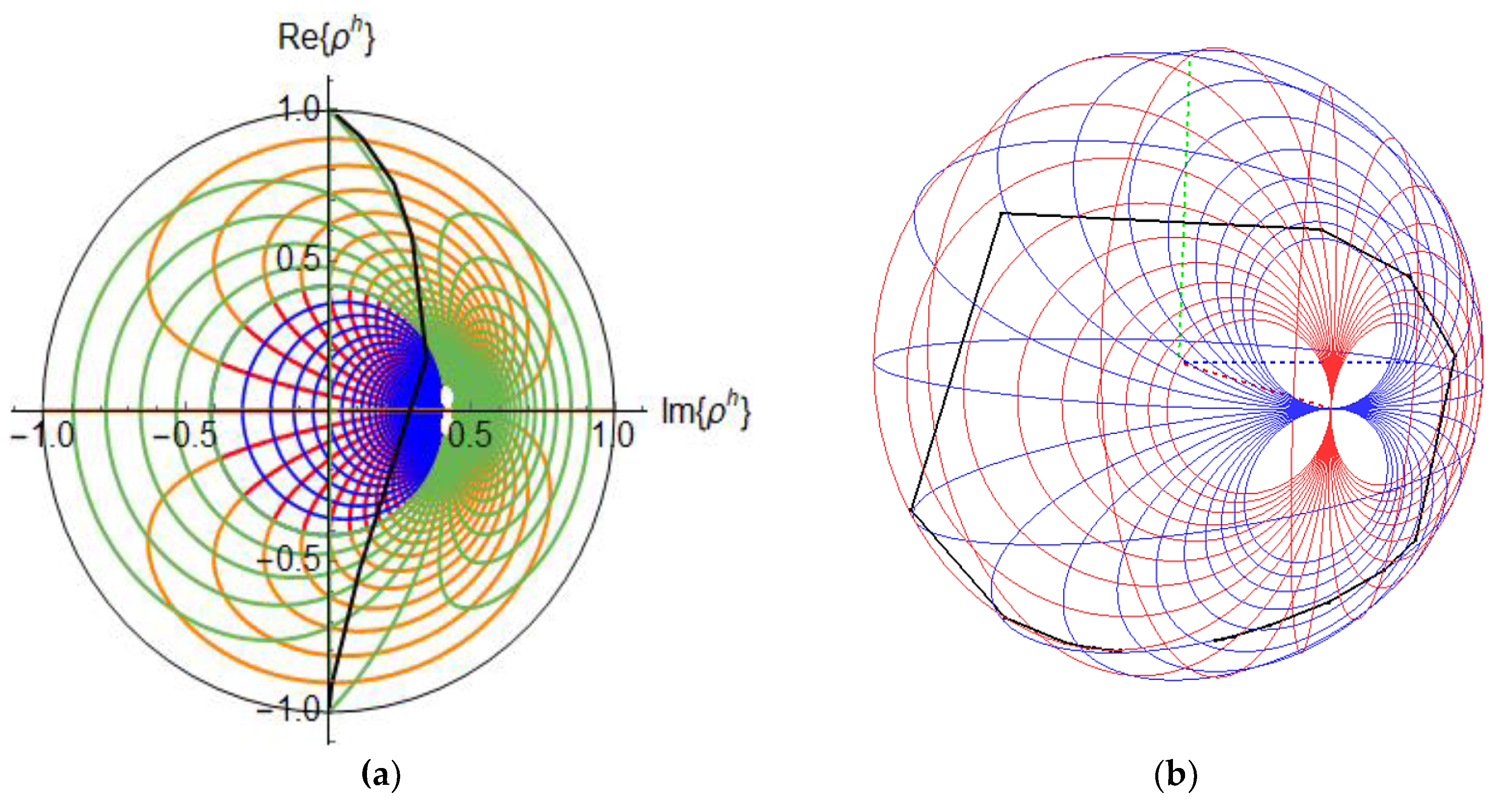
3. A Hyperbolic Smith Chart
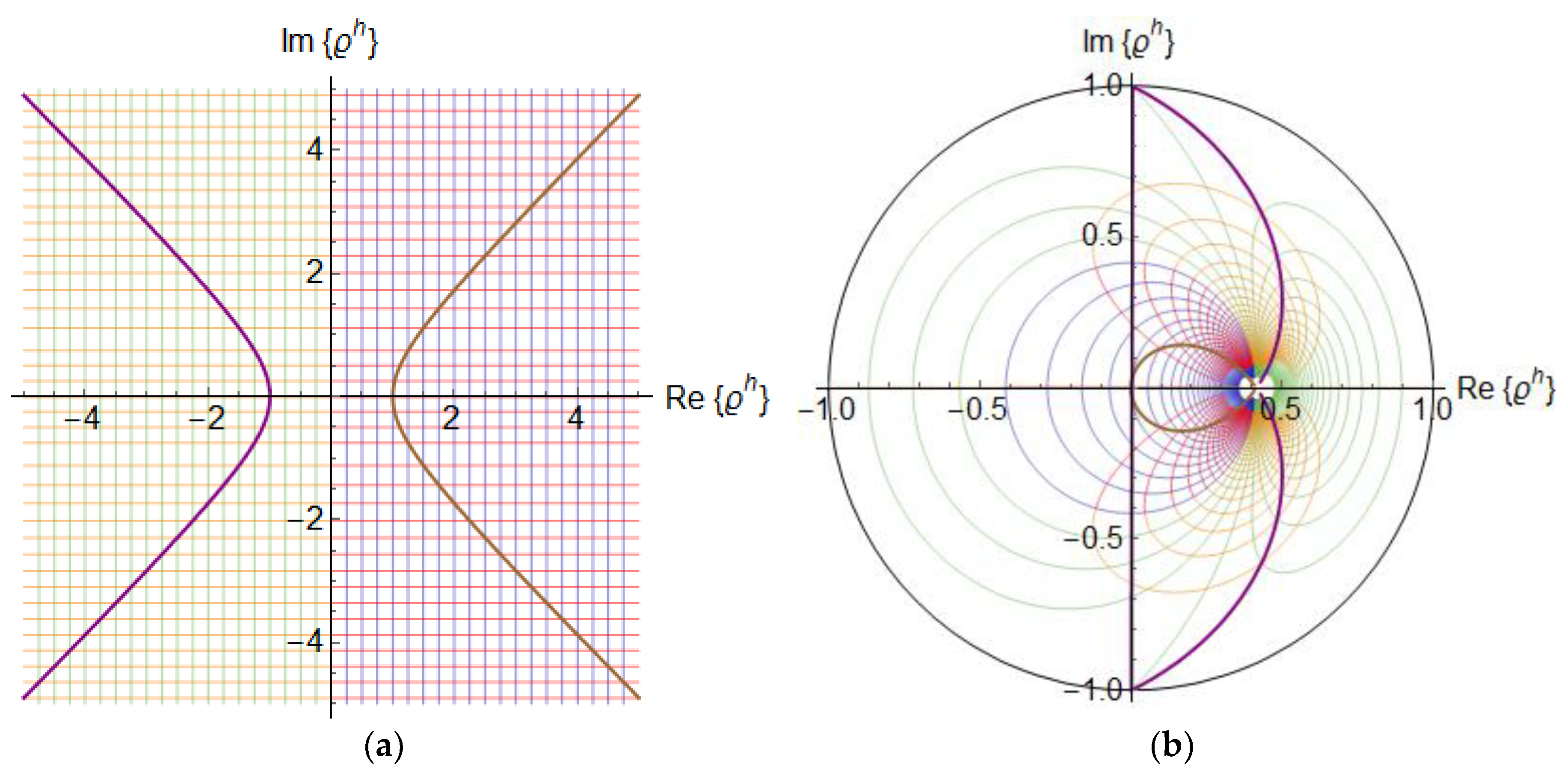
4. Properties
5. Application Example and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smith, P.H. Transmission-line calculator. Electronics 1939, 12, 29–31. [Google Scholar]
- Smith, P.H. Electronic Applications of the Smith Chart; McGraw-Hill Book Company: New York, NY, USA, 1969. [Google Scholar]
- Fikioris, G. Analytical studies supplementing the Smith Chart. IEEE Trans. Educ. 2004, 47, 261–268. [Google Scholar] [CrossRef]
- Trueman, C.W. Interactive transmission line computer program for undergraduate teaching. IEEE Trans. Educ. 2000, 43, 1–14. [Google Scholar] [CrossRef]
- Huang, C.L.; Pang, Y.H.; Tsai, K.L. Web-based Smith Chart learning helper. A guessing game for quarter-wavelength transformer. In Proceedings of the 2013 IEEE International Conference on Teaching, Assessment and Learning for Engineering (TALE), Bali Dynasty Resort, Kuta, Indonesia, 26–29 August 2013; pp. 410–413. [Google Scholar]
- Graham, P.J.; Distler, R.J. Use of the Smith Chart with complex characteristic impedance. IEEE Trans. Educ. 1968, 11, 144–146. [Google Scholar] [CrossRef]
- Muller, A.A.; Soto, P.; Dascalu, D.; Neculoiu, D.; Boria, V.E. A 3-D Smith Chart based on the riemann sphere for active and passive microwave circuits. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 286–288. [Google Scholar] [CrossRef]
- Muller, A.A.; Soto, P.; Dascalu, D.; Neculoiu, D.; Boria, V.E. The 3D Smith Chart and its practical applications. Microw. J. 2012, 5, 64–74. [Google Scholar]
- Muller, A.A.; Sanabria-Codesal, E.; Moldoveanu, A.; Asavei, V.; Soto, P.; Boria, V.E.; Lucyszyn, S. Apollonius unilateral transducer constant power gain circles on 3D Smith charts. Electron. Lett. 2014, 50, 1531–1533. [Google Scholar] [CrossRef]
- Muller, A.A.; Sanabria-Codesal, E.; Moldoveanu, A.; Asavei, V.; Lucyszyn, S. Extended capabilities of the 3-D Smith Chart with group delay and resonator quality factor. IEEE Trans. Microw. Theory Tech. 2017, 65, 10–19. [Google Scholar] [CrossRef]
- Bocher, M. Infinite regions of various geometries. Bull. Am. Math. Soc. 1913, 20, 185–200. [Google Scholar] [CrossRef]
- Gupta, M. Escher’s art, Smith chart, and hyperbolic geometry. IEEE Microw. Mag. 2006, 7, 66–76. [Google Scholar] [CrossRef]
- Muller, A.A.; Sanabria-Codesal, E. A hyperbolic compact generalized Smith Chart. Microw. J. 2016, 59, 90–94. [Google Scholar]
- Muller, A.A.; Sanabria-Codesal, E.; Moldoveanu, A.; Asavei, V.; Dascalu, D. Two compact Smith Charts: The 3D Smith Chart and a hyperbolic disc model of the generalized infinite Smith Chart. Rom. J. Inf. Sci. Technol. 2016, 19, 166–174. [Google Scholar]
- Brannan, D.A.; Esplen, M.F.; Gray, J.J. Geometry; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Iversen, B. Hyperbolic Geometry, London Mathematical Society Student Texts 25; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Hvidsten, M. Exploring Geometry; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Poincare, H. Science and Hypothesis; Dover Publications: New York, NY, USA, 1912. [Google Scholar]
- White, J.F. High Frequency Techniques: An Introduction to RF and Microwave Engineering; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- 3D Smith Chart. Available online: http://www.3dsmithchart.com (accessed on 3 September 2018).
- Casu, E.A.; Muller, A.A.; Fernandez-Bolanos, M.; Fumarola, A.; Krammer, A.; Schuler, A.; Ionescu, A.M. Vanadium oxide bandstop tunable filter for Ka Frequency Bands based on a novel reconfigurable spiral shape defected ground plane CPW. IEEE Access 2018, 6, 12206–12212. [Google Scholar] [CrossRef]
- Phase Change H2020 Project. Available online: https://phasechange-switch.org/ (accessed on 3 September 2018).


| Comparative Capabilities | Smith Chart | 3D Smith Chart |
|---|---|---|
| Positive resistance | Interior of unity circle | North hemisphere |
| Negative resistance ) | NO (towards infinity) | South hemisphere |
| Perfect match | Origin | North pole |
| NO | South pole | |
| Inductive | Above the abscissa | East |
| Capacitive | Below the abscissa | West |
| r,x,g,b constant | Circles, circle arcs, 1 line | Circles |
| Purely resistive | Abscissa | Greenwich meridian |
| Power levels/group delays | NO | 3D space(Exterior > 0, Interior < 0) |
| Comparative Capabilities | Hyperbolic Smith Chart |
|---|---|
| Positive resistance | Inside the 0.414 radius circle |
| Negative resistance | Between the 0.414 radius circle and unit circle |
| Perfect match | Origin |
| Unit circle | |
| Inductive | Above axes |
| Capacitive | Bellow axes |
| constant | Quartic curves and 0.414 radius circle circumference |
| Purely resistive | O axes |
| Chart | Geometry | |
|---|---|---|
| Smith Chart | 2D Euclidean | Not usable |
| Extended 2 Smith chart | 2D Euclidean | unending |
| 3D Smith chart | Inversive, spherical | South pole |
| Hyperbolic Smith chart | hyperbolic | Contour of the unit circle |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Peñalver, M.J.; Sanabria-Codesal, E.; Moldoveanu, F.; Moldoveanu, A.; Asavei, V.; A. Muller, A.; Ionescu, A. A Review and Mathematical Treatment of Infinity on the Smith Chart, 3D Smith Chart and Hyperbolic Smith Chart. Symmetry 2018, 10, 458. https://doi.org/10.3390/sym10100458
Pérez-Peñalver MJ, Sanabria-Codesal E, Moldoveanu F, Moldoveanu A, Asavei V, A. Muller A, Ionescu A. A Review and Mathematical Treatment of Infinity on the Smith Chart, 3D Smith Chart and Hyperbolic Smith Chart. Symmetry. 2018; 10(10):458. https://doi.org/10.3390/sym10100458
Chicago/Turabian StylePérez-Peñalver, María Jose, Esther Sanabria-Codesal, Florica Moldoveanu, Alin Moldoveanu, Victor Asavei, Andrei A. Muller, and Adrian Ionescu. 2018. "A Review and Mathematical Treatment of Infinity on the Smith Chart, 3D Smith Chart and Hyperbolic Smith Chart" Symmetry 10, no. 10: 458. https://doi.org/10.3390/sym10100458
APA StylePérez-Peñalver, M. J., Sanabria-Codesal, E., Moldoveanu, F., Moldoveanu, A., Asavei, V., A. Muller, A., & Ionescu, A. (2018). A Review and Mathematical Treatment of Infinity on the Smith Chart, 3D Smith Chart and Hyperbolic Smith Chart. Symmetry, 10(10), 458. https://doi.org/10.3390/sym10100458






