An Automatic Algorithm to Generate a Reachability Tree for Large-Scale Fuzzy Petri Net by And/Or Graph

Abstract

Fuzzy Petri net (FPN) is widely used to repre sent, model and analyse knowledge-based systems (KBSs). Meanwhile, a reachability tree is an important tool to fully represent the flow relationship of FPN and is widely applied to implement inference in industrial areas. However, the traditional reachability ignores recording the dependence relationships (‘and/or’ relationship) among the places in the neighbouring layers. This paper develops a modified reachability tree based on an and/or graph and presents a three-phase generation algorithm to model the reachability tree for the corresponding FPN automatically via fuzzy production rules (FPRs). Four cases are used to verify the correctness and feasibility of the proposed algorithm from different viewpoints, such as general FPRs, FPRs with a condition-sharing situation, FPRs with a conclusion-sharing situation, and FPRs with multi-conclusions. Simulation results reveal that the proposed approach has the ability to automatically generate the reachability tree for the corresponding FPN correctly.

1. Introduction

The fuzzy Petri net (FPN), a kind of backward extension high-level Petri net (HLPN), has been widely applied to model and analyse uncertainty systems or knowledge-based systems (KBSs) [1]. Due to two unique features of FPN-structural store representation for fuzzy information and visualization description for uncertainty reasoning, FPN has been widely applied in various industrial areas, such as robotics [2,3], intelligent manufacturing systems [4,5], traffic control [6,7], semantic network [8,9], etc.

According to the above two characteristics of FPN, the main mechanisms of a FPN model’s application could be classified into two types, a reasoning algorithm using the reachability tree and a reasoning algorithm using the algebra form [10,11].

The reachability tree is an equivalent model of FPN to record the reasoning path(s) among places intuitively. Chen et al. proposed various reasoning algorithms to implement fault diagnosis based on the corresponding reachability tree of a FPN model utilizing the immediate reachable set (IRS) and reachable set (RS), such as forward-reasoning algorithm [12], backward-reasoning method [13] and weighted fuzzy reasoning [14]. Manoj et al. extended Chen et al.’s research and proposed a hierarchical FPN for all types of data abstraction based on a reachability tree model [15]. In industrial applications, the reachability tree method is also widely applied to implement special tasks. Wu et al. proposed a hybrid method to analyze the reliability of the solar array by employing fault tree analysis and a fuzzy reasoning Petri net. The simulation results reveal that the top two factors to cause the solar array fault are harsh thermal environment and impact caused by particles in space array [16]. Chiang et al. presented a model to evaluate sleep quality by combing the fast Fourier transform and fuzzy Petri net. Compared with other existing data mining approaches, the proposed electroencephalogram (EEG)-based sleep quality detection model is able to increase the assessment accuracy to 82.4% [17]. Reference [18,19,20] also demonstrate some typically applications of inference by using reachability tree in various industrial areas, such as micro distribution, risk evaluation, et al.

Based on the literature mentioned above, it is easy to find that reachability tree is a powerful tool to fully represent the flow relationships among places and transitions of the entire FPN model and to implement inference operations based on a visible method. According to the above highlights of the reachability tree, various reasoning mechanisms based on the reachability tree mechanism were widely discussed in different industrial areas. However, with the rapidly increasing complexity of real industrial systems, the scale of the corresponding FPN model is also raised. The state-explosion issue hinders the further application of the inference mechanism using a reachability tree in industrial areas. The drawbacks of the reachability tree under the state-explosion issue could be summarized into two aspects:

• It difficult to directly describe the dependence relationships (‘and’ or ‘or’ relationship) among the places in the neighbouring layers;
• It difficult to generate automatically a large reachability tree for a rather complex expert system.

To overcome the shortcomings mentioned above, the goal of this manuscript is to propose an algorithm to automatically generate a reachability tree for a corresponding large-scale FPN model with complex flow-relationships among places and transitions. To fulfil this goal, this paper includes three main phases. First, a modified reachability tree based on an and/or graph model [21], decision tree theory [22] and fuzzy relations [23] is presented to fully record the flow-relationship among places and describe the dependence relationships among places in the neighbouring layers. Furthermore, an automatic generation algorithm is proposed in this manuscript to the reachability tree for the corresponding large-scale FPN model for solving the state-explosion issue. Finally, four groups of cases are employed to test the feasibility of the proposed generation algorithm.

The organization of the remaining parts is as follows: the modified reachability is illustrated in Section 2 after discussing the general definition of FPN, fuzzy production rule (FPR) and and/or graph. Section 3 demonstrates the entire flowchart and reveals the algorithm complexity of the presented generation algorithm of the modified reachability tree. A series of examples are given to prove the validity and feasibility of the presented algorithm in Section 4. Section 5 summarises and gives a brief conclusion.

2. Modified Reachability Tree for Different Fuzzy Petri Net (FPN) Models

FPN and FPR are the two main formal ways to fulfil the KBS requirements. Meanwhile, the reachability tree is a stronger tool to fully represent flow-relationship among places of FPN. This section first introduces the basic concepts both of FPN, FPR. Then, the corresponding modified reachability trees of different types of FPN models are generated after introducing the improved thinking of the reachability tree utilizing the and/or graph.

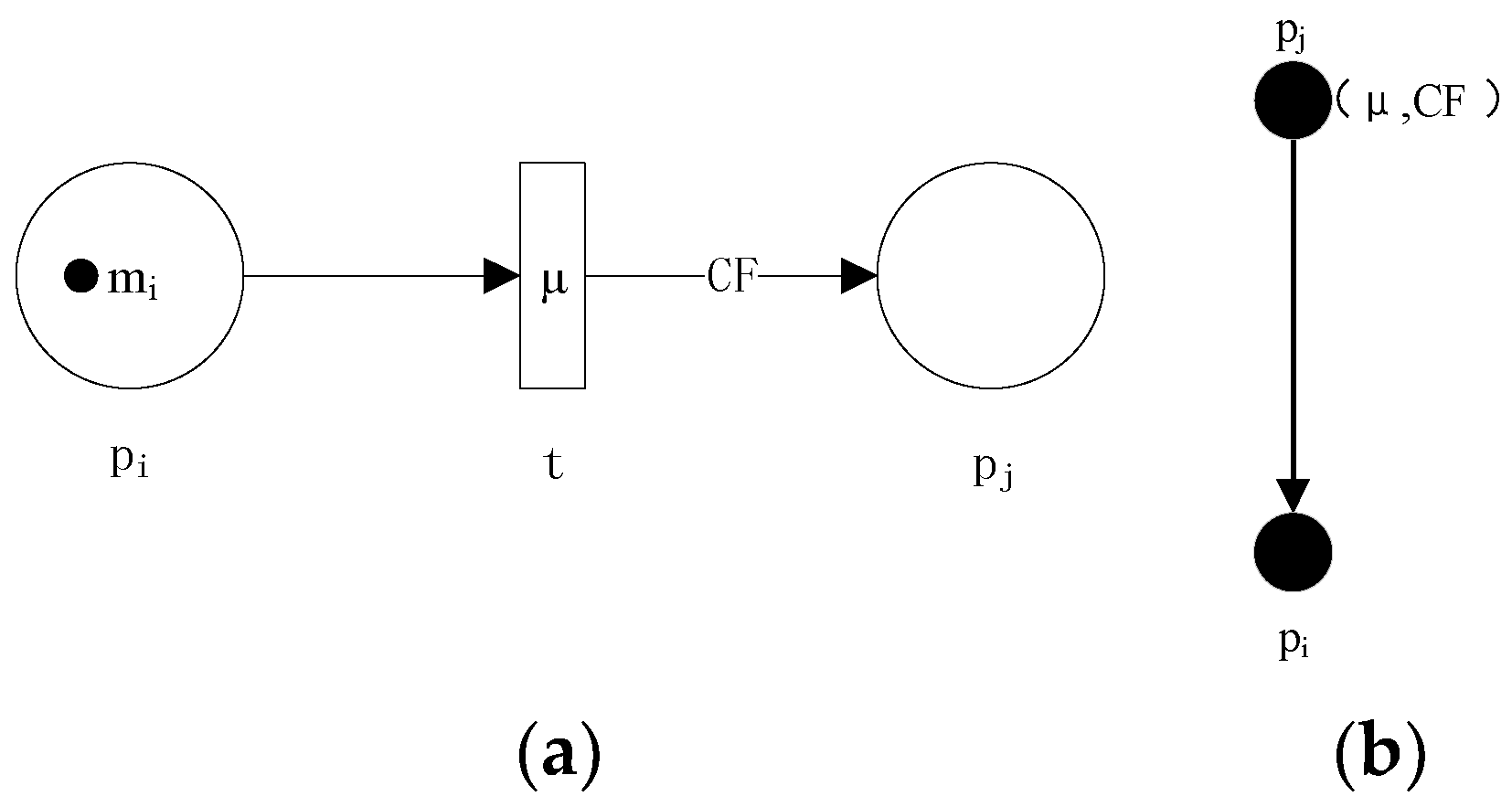
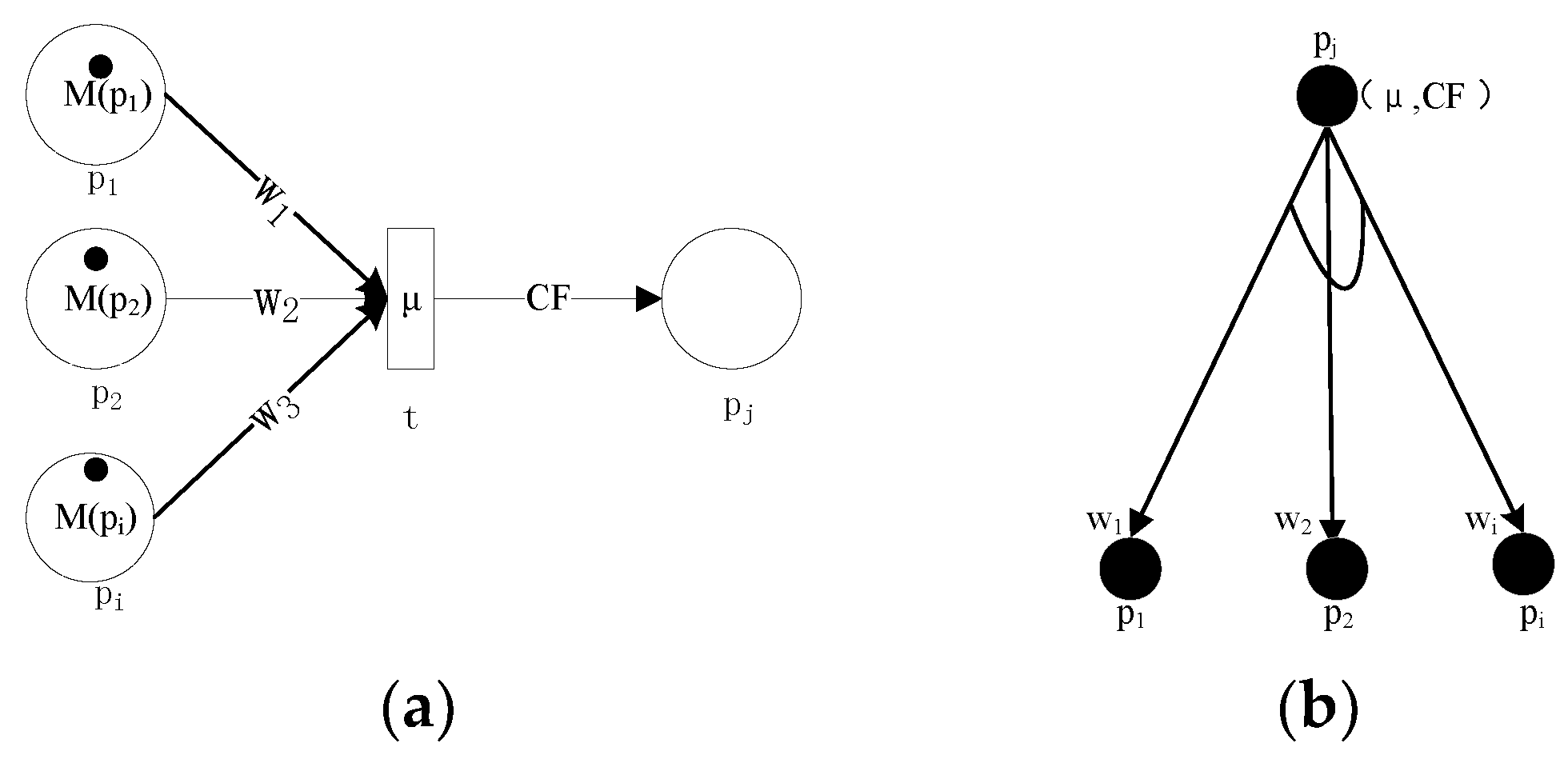
2.1. FPN and Fuzzy Production Rule (FPR)

FPN is generally defined as the following 8-tuple formalism.

$$\begin{array}{cc}FPN& \sum =(P,T,I,O,M,\mu ,W,CF)\end{array}$$

where, $P=\{p_1,p_2,\cdots ,p_n\}$ represents a finite set of places; n represents the number of places in the rule; $T=\{t_1,t_2,\cdots ,t_m\}$ represents a finite set of transitions; m represents the number of transitions in the rule;$I(O)$ is the input (output) function, i.e., the mapping relation between places and transitions; $M={(m_1,m_2,\cdots ,m_n)}^T$ indicates the identity of places; $w_i$ indicates the weight of places $p_i$, i.e., the support degree for the rule establishment by preconditions $p_i$; $C{F}_j$ indicates the credibility, i.e., the true extent of the conclusion after transitions $t_j$ fired; and $\mu :\mu \to (0,1]$, ${\mu }_i$ is the threshold of transitions $t_j$.

FPR is commonly used to represent the uncertainties in expert systems [20,21,22]. General FPRs are formalized and described as follows.

$$\begin{array}{ccccc}if& D(\lambda )& then& Q& (CF,\mu ,w)\end{array}$$

where, $D$ is a limited set of preconditions; $D=\{D_1,D_2,\cdots D_n\}$; $Q$ is a limited set of conclusions; $Q=\{Q_1,Q_2,\cdots Q_m\}$; $\lambda$ is the true extent of each precondition; $\lambda \in [0,1]$; $CF$ is the credibility of the rule; $CF\in (0,1]$ is the credibility of the conclusion obtained after the rule is executed; $\mu$ is the threshold of the rule, $\mu \in (0,1]$; and $w$ is the weight of each precondition, $w\in (0,1]$.

Moreover, FPRs can be divided into three main types, which are ‘simple’, ‘or’, and ‘and’ rules according to the different relationship among conditions.

Type 1: Simple rule

$$\begin{array}{ccccc}if& D(\lambda )& then& Q& (w=1,\mu ,CF)\end{array}$$

Type 2: And rule

$$\begin{array}{cccccccc}if& D_1({\lambda }_1)& and& D_2({\lambda }_2)& and& \cdots & and& \begin{array}{cccc}{D}_n({\lambda }_n)& then& Q& ({\displaystyle \sum _{i=1}^n{w}_i=1},\mu ,CF)\end{array}\end{array}$$

Type 3: Or rule

$$\begin{array}{cccccccc}if& D_1({\lambda }_1)& or& D_2({\lambda }_2)& or& \cdots & or& \begin{array}{cccc}{D}_n({\lambda }_n)& then& Q& (w_i=1,{\mu }_i,C{F}_i)\end{array}\end{array}$$

2.2. A Modified Reachability Tree Based on And/Or Graph

The reachability tree was the main method to implement the inference process using FPN’s capability for graphic description during the 20th century. According to [13], the reachability tree could be generated by the immediate reachability set (IRS) and reachability set (RS). Although the traditional reachability tree can fully represent the flow relationship among places, the logical relationship such as ‘and’ and ‘or’ among the connected places is ignored in the current version. Hence, a modified reachability tree is proposed in this section based on the and/or graph

If the original problem can only be solved when solutions of multiple simple problems are simultaneously established, the relationship among these simple problems is an ‘and’ relation; if the original problem can be solved when multiple simple problems are established, the relationship among these simple problems is an ‘or’ relation; if the original problem can be solved when any simple problem is established, the relationship is called ‘Simple’ elation. The problem that can no longer be resolved is called the original problem [21].

Based on the characteristics of the and/or graph mentioned above, the differences between the traditional reachability tree and the modified reachability tree could be summarized into the following three aspects:

• The symbol ‘︶’ is used to mark the ‘and’ relation for the ‘and’ type FPR in the modified reachability tree.
• All parameters’ values are marked in the modified reachability tree.
• The modified reachability reverse records the flow relationship between the input place(s) and the output place(s) to aid in decomposition and reasoning operations.

According to the logic relations among conditions of FPRs, there are three types of FPR, which are the ‘simple’, ‘or’, and ‘and’ rules. Furthermore, the corresponding FPN model and the equivalent modified reachability tree of each type of FPR are drawn in Figure 1, Figure 2 and Figure 3, respectively.

3. Generation Algorithm of Reachability Tree for FPN

3.1. Introduction to Breadth-First Search (BFS)

Breadth-first search (BFS) is one of the classical algorithms to seek a tree or graph. The entire implementation of BFS starts at the tree root or some arbitrary node of a graph. Then, it moves on the nodes at the next depth level and executes the same operations once all the neighbouring nodes at the present prior depth are analyzed. The queue data structure is often used because of the non-recursive mechanism of BFS [24].

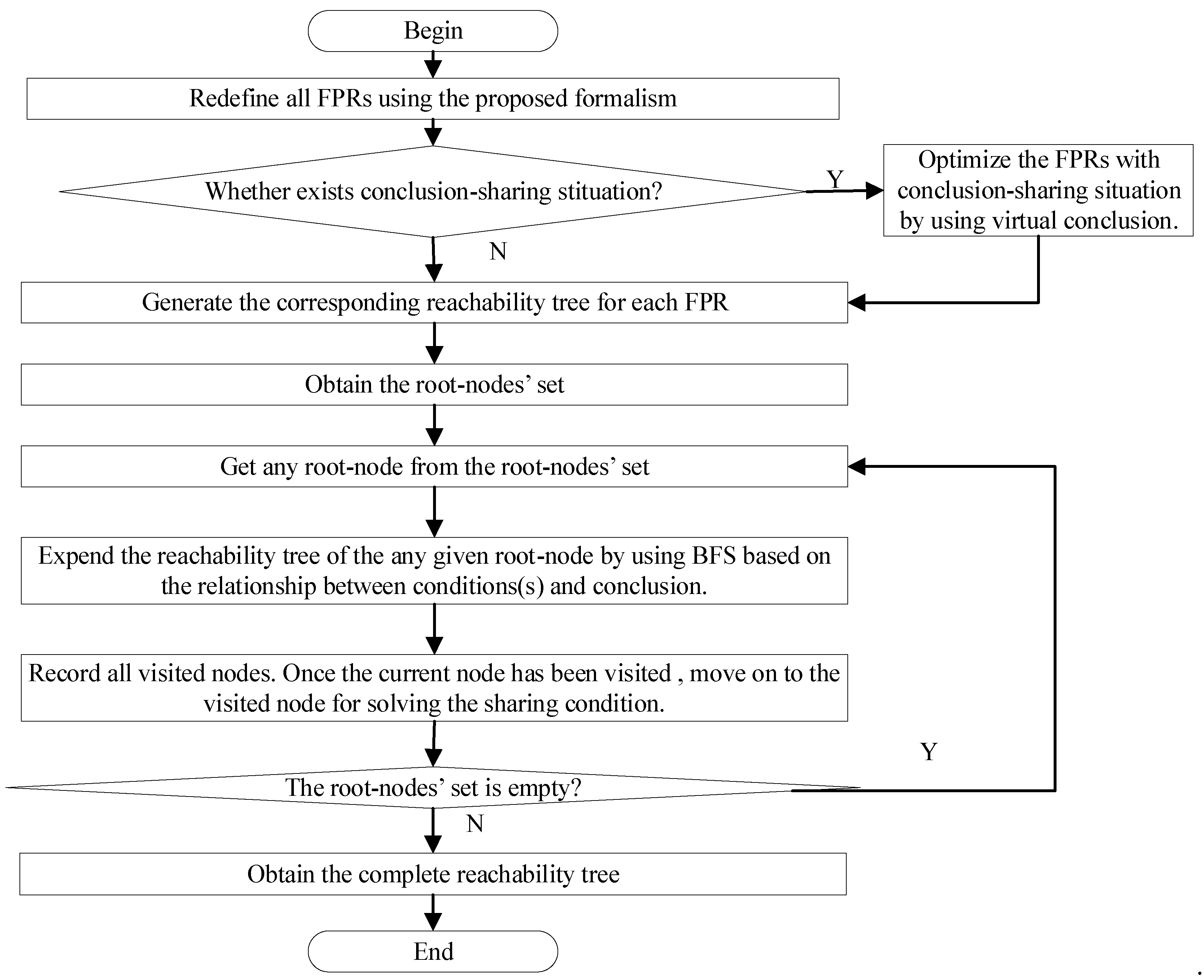
3.2. Algorithm to Generate the Reachability Tree for FPN

The proposed generation algorithm owns the capability to build the corresponding reachability tree for a large-scale FPN model. The main thinking of the presented algorithm includes three phases, which are:

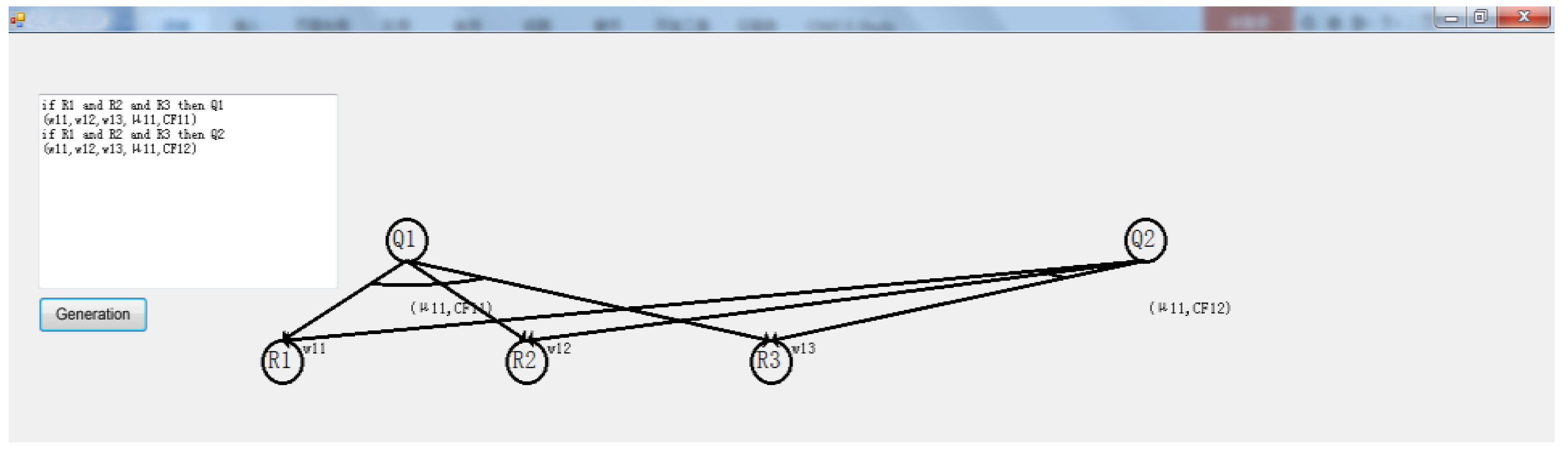
• Phase 1 is used to redefine and optimize the FPRs, which includes two operations. First, redefine all FPRs based on the following formalism one by one:

  $$<type(simple,or,and?),\{condition(s)\},conclusion,\left\{parameters\right\}>$$
  Then, settle the conclusion-sharing case in KBS. In KBS, a common situation that exists is that many FPRs could obtain the same conclusion. The conclusion-sharing situation will lead to chaotic and complex flow-relationships in the reachability tree. Hence, in this algorithm, the conclusion-sharing situations will be checked first and the FPRs with the conclusion-sharing situations will be divided into two FPRs by using a virtual conclusion as follows.

  $$<type(simple,or,and?),\{condition(s)\},\begin{array}{cc}virtual& conclusion\end{array},\left\{parameters\right\}>$$

  (1)

  $$<type(simple,or,and?),\{\begin{array}{cc}virtual& conclusion\end{array}(s)\},\begin{array}{cc}previous& conclusion\end{array},\left\{parameters\right\}>$$

  (2)
• Phase 2 is used to generate all reachability trees for each FPR and to calculate the number of all root-nodes.
• Phase 3 is to expand the reachability tree of an any given root-node from the root-nodes’ set by using the BFS mechanism repeatedly until the final completed reachability tree is gained, and to execute the BFS operation for each root-node.

The flowchart of the generation algorithm is illustrated as shown in Figure 4.

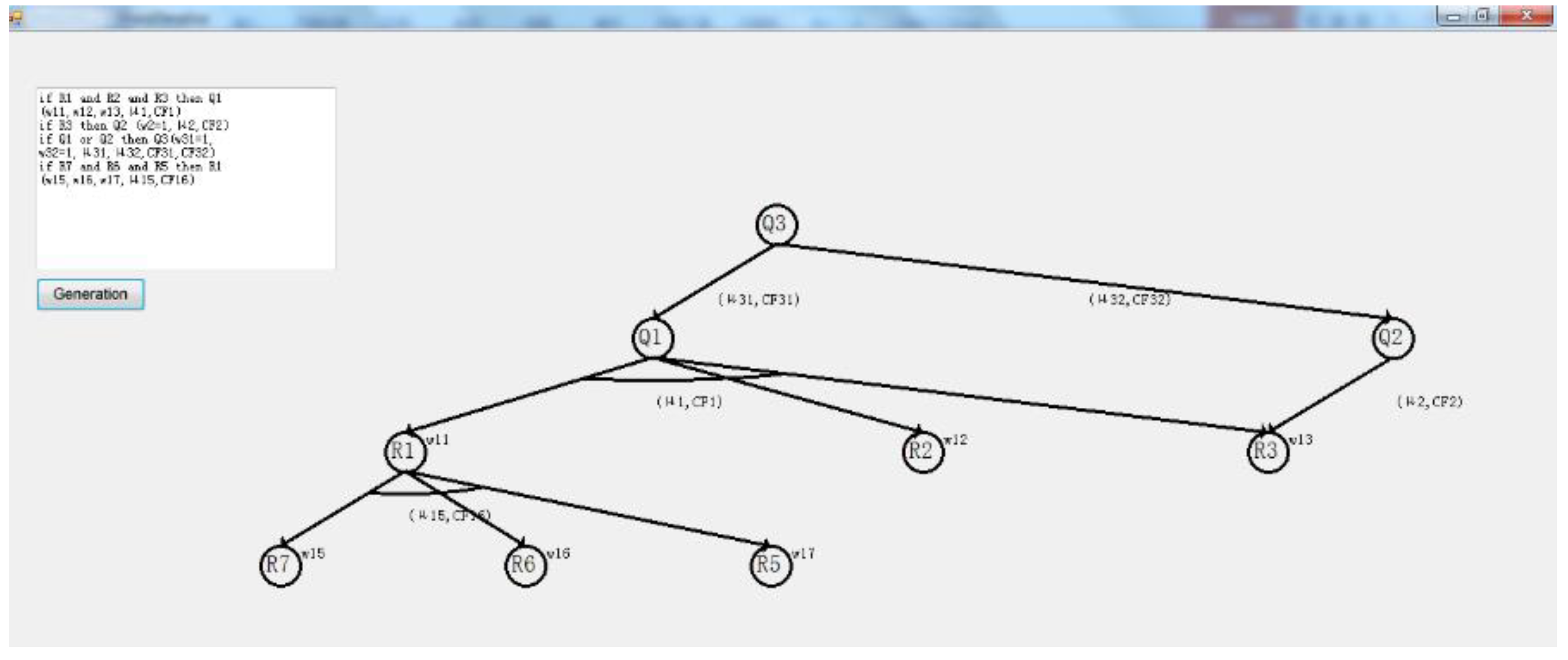
4. Experiments and Related Analysis

In this section, four groups of FPRs with different characteristics are used to test the feasibility of the proposed algorithm., which are:

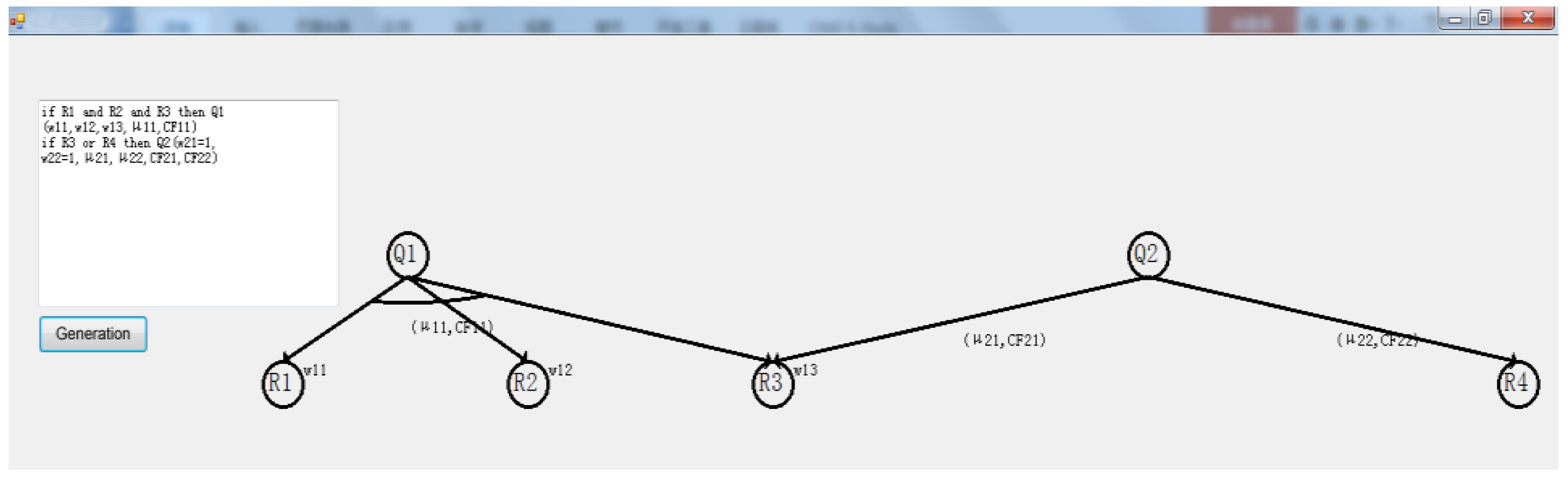
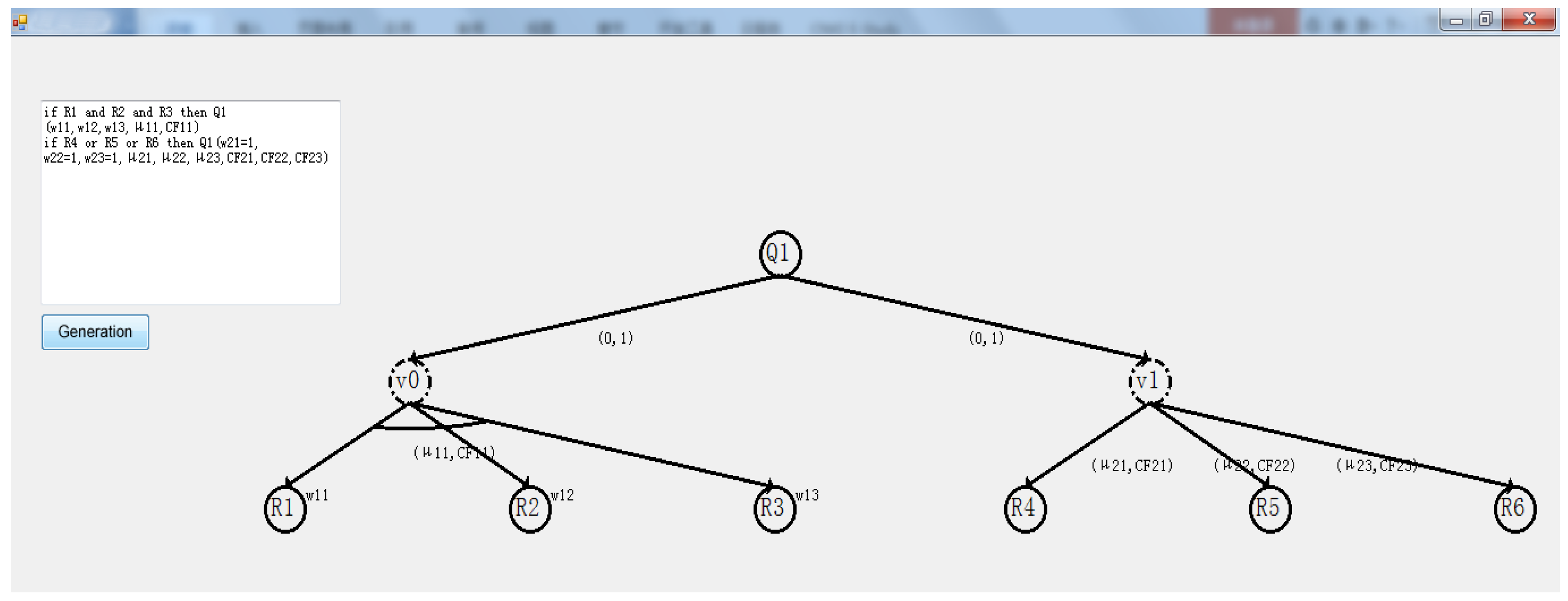
• FPRs with ‘and’ and ‘or’ relationships;
• FPRs with sharing condition situation;
• FPRs with sharing conclusion situation;
• FPR with multi-conclusions.

4.1. Experimental Data and Simulation Results

Experiment one: in this experiment, four FPRs, includes one simple type, two ‘and’ rules and a ‘or’ rule, are used to generate the corresponding reachability tree. The FPRs are listed in

Table 1. Four fuzzy production rules (FPRs) in a knowledge-based system (KBS).

No	FPR
Rule 1	$\begin{array}{ccccccccc}if& R_1& and& R_2& and& R_3& then& Q_1& (w_{11},w_{12},w_{13},{\mu }_1,C{F}_1)\end{array}$
Rule 2	$\begin{array}{ccccc}if& R_3& then& Q_2& (w_2=1,{\mu }_2,C{F}_2)\end{array}$
Rule 3	$\begin{array}{ccccccc}if& Q_1& or& Q_2& then& Q_3& (w_{31}=1,w_{32}=1,{\mu }_{31},{\mu }_{32},C{F}_{31},C{F}_{32})\end{array}$
Rule 4	$\begin{array}{ccccccccc}if& R_7& and& R_6& and& R_5& then& R_1& \begin{array}{ccccccc}if& Q_1& or& Q_2& then& Q_3& (w_{15},w_{16},w_{17},{\mu }_{15},C{F}_{16})\end{array}\end{array}$

and the simulation result is demonstrated in Figure 5.

Experiment two: in this experiment, two FPRs with sharing conditions are used to generate the corresponding reachability tree. The FPRs are listed in

Table 2. Two FPRs in a KBS.

No	FPR
Rule 1	$\begin{array}{ccccccccc}if& R_1& and& R_2& and& R_3& then& Q_1& (w_{11},w_{12},w_{13},{\mu }_{11},C{F}_{11})\end{array}$
Rule 2	$\begin{array}{ccccccc}if& R_1& or& R_2& then& Q_2& (w_{21}=1,w_{22}=1,{\mu }_{21},{\mu }_{22},C{F}_{21},C{F}_{22})\end{array}$

and the simulation result is demonstrated in Figure 6.

Experiment three: in this experiment, a FPR with multi-conclusions is used to generate the corresponding reachability tree. The FPRs are listed in

Table 3. Two FPRs in a KBS.

No	FPR
Rule 1	$\begin{array}{ccccccccc}if& R_1& and& R_2& and& R_3& then& Q_1& (w_{11},w_{12},w_{13},{\mu }_{11},C{F}_{11})\end{array}$
Rule 2	$\begin{array}{ccccccccc}if& R_1& or& R_2& or& R_3& then& Q_1& (w_{21}=1,w_{22}=1,w_{23}=1,{\mu }_{21},{\mu }_{22},{\mu }_{23},C{F}_{21},C{F}_{22},C{F}_{23})\end{array}$

and the simulation result is demonstrated in Figure 7.

Experiment Four: in this experiment, two FPRs with a sharing conclusion are used to generate the corresponding reachability tree. The FPRs are listed in

Table 4. FPR with multi-conclusions.

No	FPR
Rule 1	$\begin{array}{ccccccccc}if& R_1& and& R_2& and& R_3& then& \begin{array}{ccc}{Q}_1& and& Q_2\end{array}& (w_{11},w_{12},w_{13},{\mu }_{11},C{F}_{11},C{F}_{12})\end{array}$

and the simulation result is demonstrated in Figure 8.

4.2. Analysis of Simulation Results

The above four experiments test how feasible is the automatic reachability tree generation ability in the proposed algorithm from four aspects, which are generally FPRs, FPRs with sharing conditions, FPRs with sharing conclusion and FPR with multi-conclusions.

The simulation result of experiment 1 shows that the algorithm generates the correct reachability tree for simple FPRs. Then, experiment two reveals that the proposed algorithm owns the capability to find and merge the sharing conditions among FPRs. Based on experiments one and two, the condition-sharing situation and conclusion-sharing situation are both included in experiment three to verify the correctness of the proposed algorithm. For the conclusion-sharing case in experiment three, a virtual node is automatically added to represent the flow relationship among FPRs. Finally, the FPR with multi-conclusions is used to test the algorithm from the viewpoint of multi-input and multi-output cases in experiment four. The four simulation results reveal that the proposed algorithm can generate the corresponding reachability for the FPN model correctly.

5. Conclusions

The current method neglects to record the dependence relationships (‘and’ or ‘or’ relationships) among the places in the neighbouring layers. Focusing on this issue, a modified reachability tree is proposed in this manuscript based on the and/or graph. Furthermore, an automatic generation algorithm is proposed to execute the modelling operation from FPN to the corresponding reachability tree. Four experiments from different cases are employed to test the feasibility of the proposed algorithm. Simulation results show that the proposed algorithm possesses the capability to generate the corresponding reachability tree for the large-scale FPN model automatically.