Path Planning for the Mobile Robot: A Review
Abstract
:1. Introduction
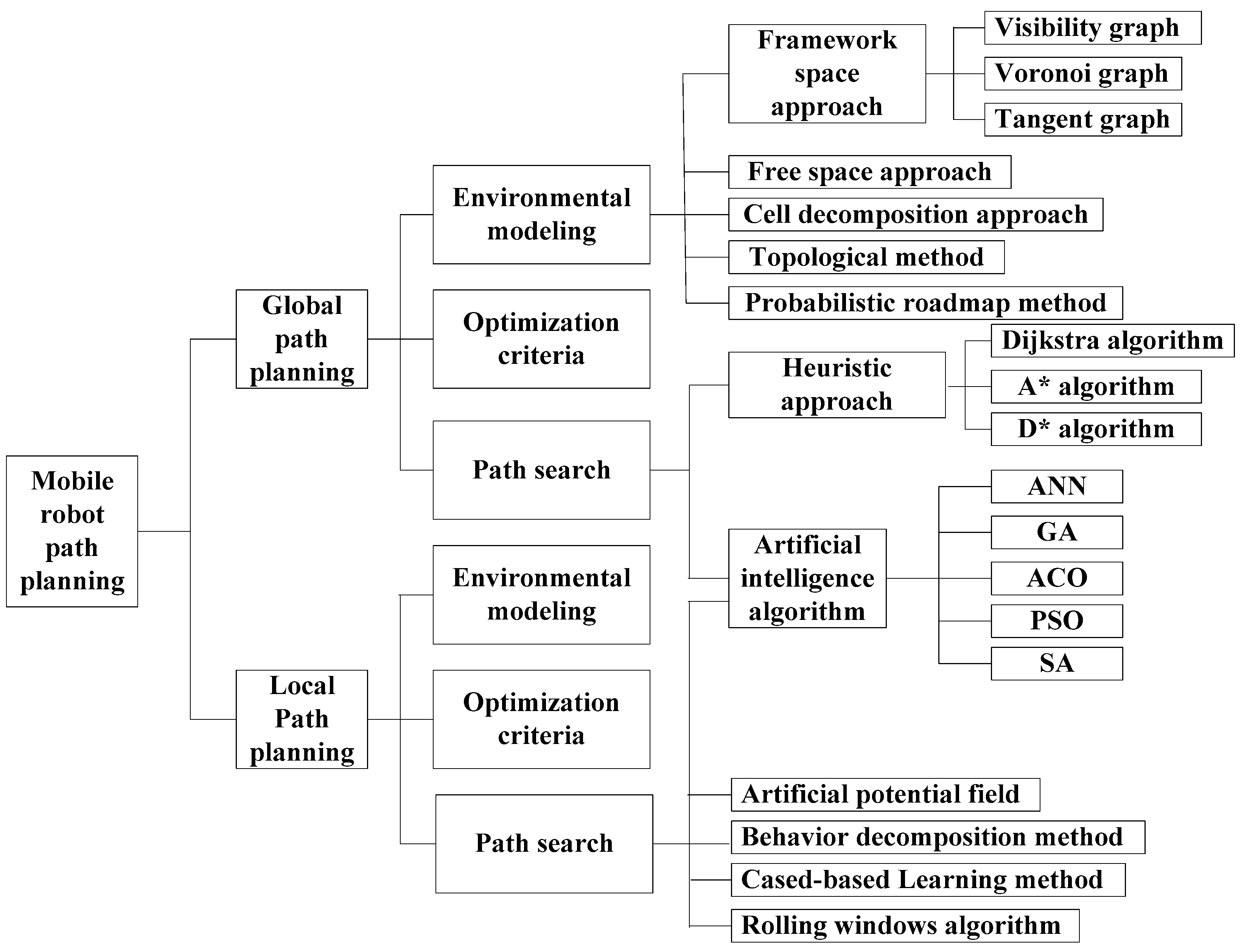
2. Review of Global Path Planning
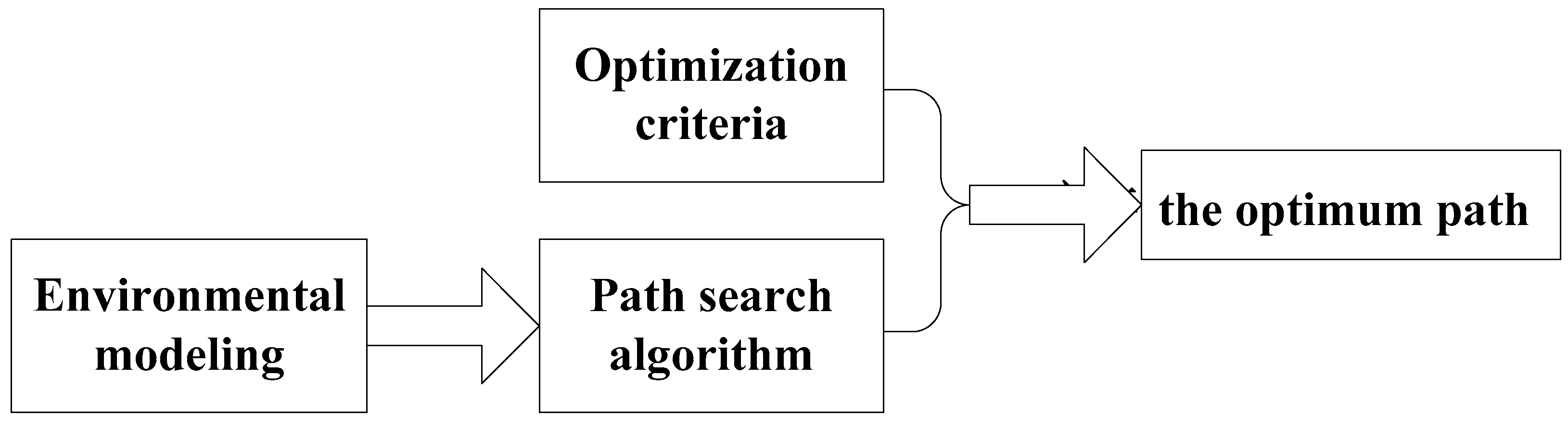
2.1. Environmental Modeling
2.1.1. Framework Space Approach
Visibility Graph
Voronoi Graph
Tangent Graph
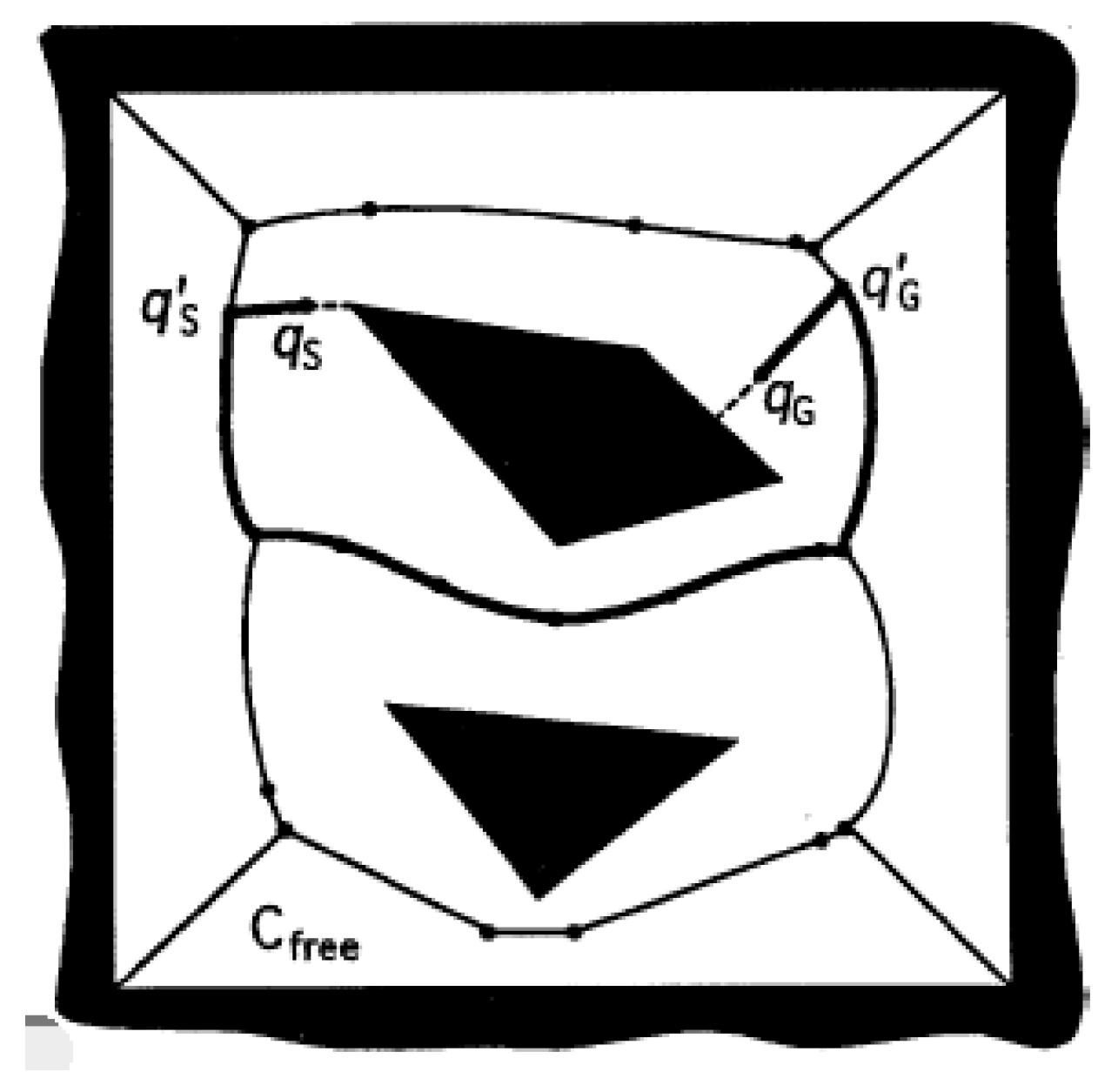
2.1.2. Free Space Approach
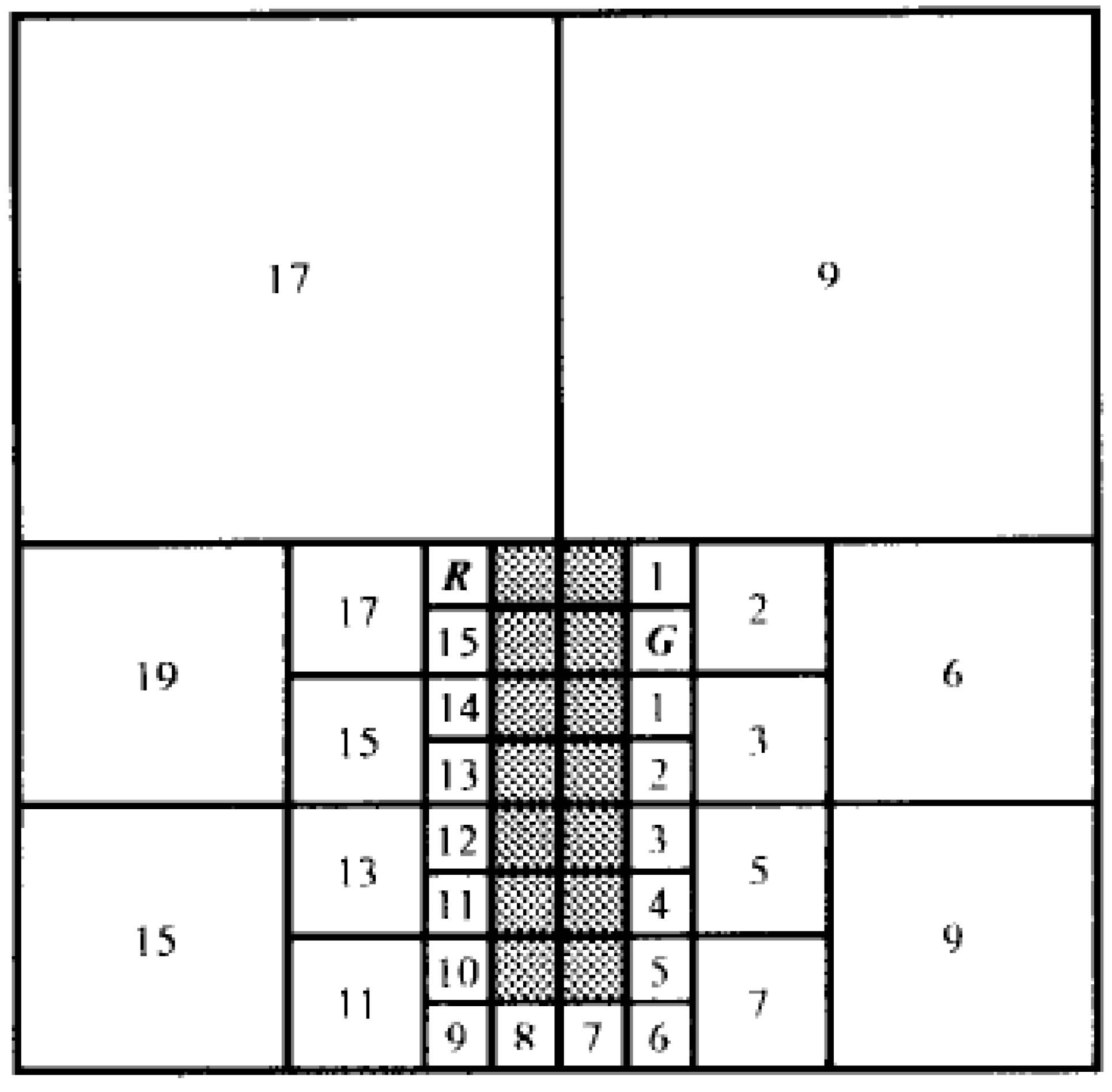
2.1.3. Cell Decomposition Approach
2.1.4. Topological Method
2.1.5. Probabilistic Roadmap Method
2.2. Optimization Criteria
2.2.1. Path Length
2.2.2. Smoothness
2.2.3. Safety Degree
2.3. Path Search Algorithm
2.3.1. Heuristic Approach
Dijkstra Algorithm
A* Algorithm
D* Algorithm
2.3.2. Artificial Intelligence Algorithm
ANN
GA
ACO
PSO
SA
3. Review of Local Path Planning
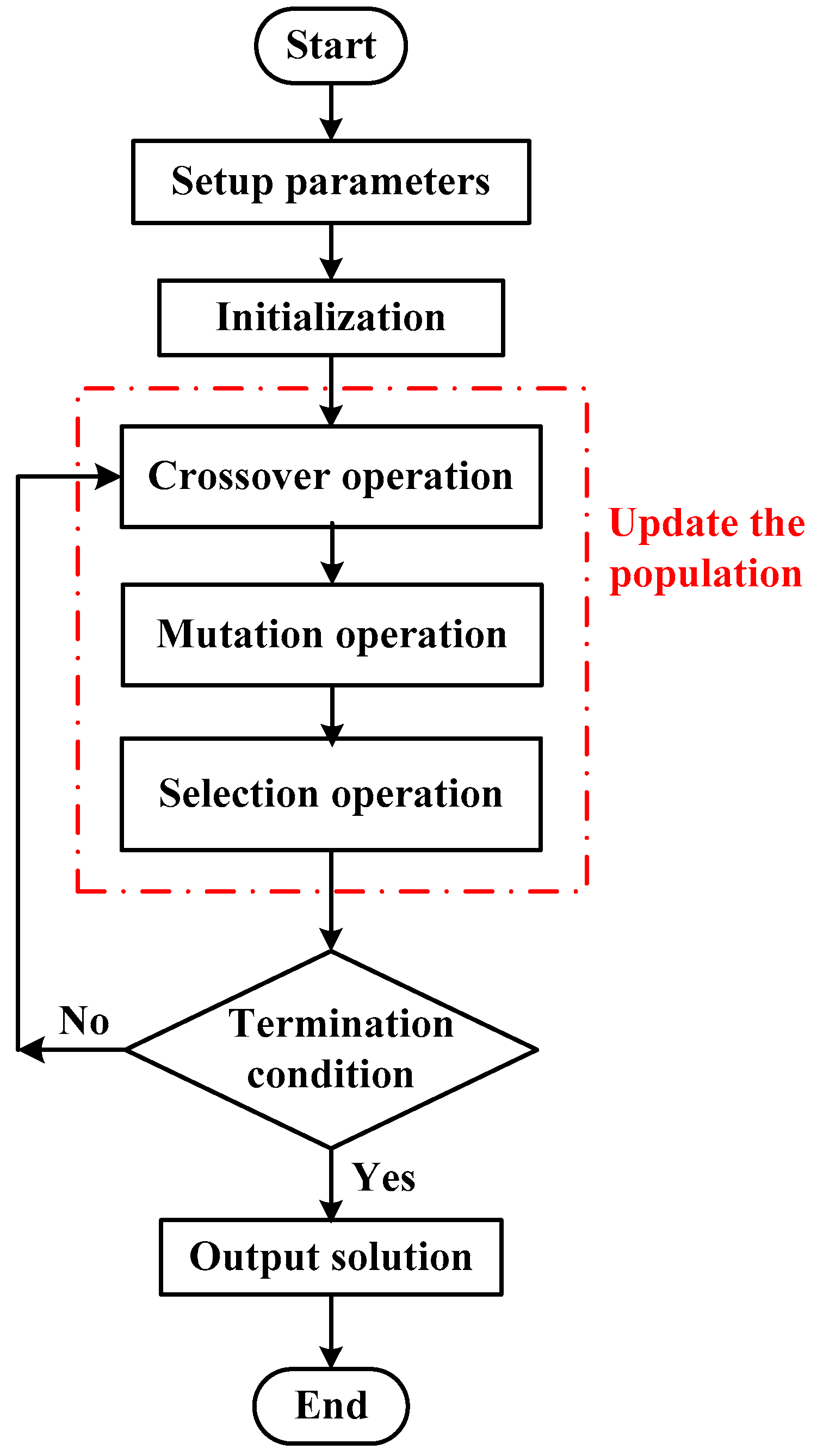
3.1. Artificial Potential Field
3.2. Behavior Decomposition Method
3.3. Cased-Based Learning Method
3.4. Rolling Windows Algorithm
3.5. Artificial Intelligence Algorithm
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, B.W.; Zhu, Z.X.; Luo, J.J. Hybridizing Particle Swarm Optimization and Differential Evolution for the Mobile Robot Global Path Planning. Int. J. Adv. Robot. Syst. 2016, 13, 1–17. [Google Scholar] [CrossRef]
- Zhuang, Y.; Sun, Y.L.; Wang, W. Mobile robot hybrid path planning in an obstacle-cluttered environment based on steering control and improved distance propagating. Int. J. Innov. Comput. Inf. Control 2012, 8, 4095–4109. [Google Scholar]
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328. [Google Scholar] [CrossRef]
- Li, P.; Huang, X.H.; Wang, M. A novel hybrid method for mobile robot path planning in unknown dynamic environment based on hybrid DSm model grid map. J. Exp. Theor. Artif. Intell. 2011, 23, 5–22. [Google Scholar] [CrossRef]
- Goerzen, C.; Kong, Z.; Mettler, B. A survey of motion planning algorithms from the perspective of autonomous UAV guidance. J. Intell. Robot. Syst. Theory Appl. 2010, 57, 65–100. [Google Scholar] [CrossRef]
- Hoang, H.V.; Sang, H.A.; Tae, C.C. Dyna-Q-based vector direction for path planning problem of autonomous mobile robots in unknown environments. Adv. Robot. 2013, 27, 159–173. [Google Scholar]
- Liu, Y.; Arimoto, S. Proposal of tangent graph and extended tangent graph for path planning of mobile robots. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 312–317. [Google Scholar]
- Henrich, D. Fast motion planning by parallel processing—A review. J. Intell. Robot. Syst. Theory Appl. 1997, 20, 45–69. [Google Scholar] [CrossRef]
- Habib, M.K.; Asama, H. Efficient method to generate collision free paths for an autonomous mobile robot based on new free space structuring approach. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems (IROS’91), Osaka, Japan, 3–5 November 1991; pp. 563–567. [Google Scholar]
- Chen, D.Z.; Szczerba, R.J.; Uhran, J.J. Framed-quadtree approach for determining Euclidean shortest paths in a 2-D. environment. IEEE Trans. Robot. Autom. 1997, 13, 668–681. [Google Scholar] [CrossRef]
- Liang, W.J. Research on Robot Path Planning for Dynamic Environment and Cooperation. Master’s Thesis, Zhejiang University, Hangzhou, China, 2010. [Google Scholar]
- Kavraki, L.; Latombe, J. Randomized preprocessing of configuration space for fast path planning. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 2138–2145. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]
- Hsu, D.; Latombe, J.; Kurniawati, H. On the probabilistic foundations of probabilistic roadmap planning. Int. J. Robot. Res. 2006, 25, 627–643. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, G.X.; Zhao, J.B.; Rong, H.; Ipate, F.; Lefticaru, R. A Modified Membrane-Inspired Algorithm Based on Particle Swarm Optimization for Mobile Robot Path Planning. Int. J. Comput. Commun. Control 2015, 10, 732–745. [Google Scholar] [CrossRef]
- Hidalgo-Paniagua, A.; Vega-Rodriguez, M.A.; Ferruz, J.; Pavón, N. MOSFLA-MRPP, Multi-Objective Shuffled Frog-Leaping Algorithm applied to Mobile Robot Path Planning. Eng. Appl. Artif. Intell. 2015, 44, 123–136. [Google Scholar] [CrossRef]
- Dijkstra, E. A note on two problems in connexion with graphs. Numer. Math. 1959, 4, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths in graphs. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3310–3317. [Google Scholar] [Green Version]
- Ferguson, D.; Stentz, A. Using interpolation to improve path planning the field D* algorithm. J. Field Robot. 2006, 23, 79–101. [Google Scholar] [CrossRef]
- Nash, A.; Daniel, K.; Koenig, S.; Felner, A. Theta*, Any-angle path planning on grids. J. Artif. Intell. Res. 2010, 39, 533–579. [Google Scholar]
- Xiao, K.; Gao, C.; Hu, X.; Pan, H.W. Improved Theta*, Improved any-angle path planning on girds. J. Comput. Inf. Syst. 2014, 10, 8881–8890. [Google Scholar]
- Martin, P.; Del Pobil, A.P. Application of artificial neural networks to the robot path planning problem. In Proceedings of the Ninth International Conference on Applications of Artificial Intelligence in Engineering, Pennsylvania, PA, USA, 19–21 July 1994; pp. 73–80. [Google Scholar]
- Mulder, E.; Mastebroek, H.A.K. Construction of an interactive and competitive artificial neural network for the solution of path planning problems. In Proceedings of the European Symposium on Artificial Neural Networks, Bruges, Belgium, 22–24 April 1998; pp. 407–412. [Google Scholar]
- Li, C.H.; Zhang, J.Y.; Li, Y.B. Application of artificial neural network based on Q-learning for mobile robot path planning. In Proceedings of the 2006 IEEE International Conference on Information Acquisition, Weihai, China, 20–23 August 2006; pp. 978–982. [Google Scholar]
- Raza, S.; Haider, S. Path planning in RoboCup soccer simulation 3D using evolutionary artificial neural network. In Proceedings of the Advances in Swarm Intelligence 4th International Conference, Harbin, China, 12–15 June 2013; pp. 342–350. [Google Scholar]
- Contreras-Gonzalez, A.; Hernandez-Vega, J.; Hernandez-Santos, C.; Palomares-Gorham, D.G. A method to verify a path planning by a back-propagation artificial neural network. In Proceedings of the 10th Latin American Workshop on Logic/Languages, Algorithms and New Methods of Reasoning, Puebla, Mexico, 15 August 2016; pp. 98–105. [Google Scholar]
- Min, Z.; Ansari, N.; Hou, E.S.H. Mobile manipulator path planning by a genetic algorithm. J. Robot. Syst. 1994, 11, 143–153. [Google Scholar]
- Liu, Y.F.; Qiu, Y.H. Robot path planning based on genetic algorithms with two-layer encoding. Control Theory Appl. 2000, 17, 429–432. [Google Scholar]
- Pehlivanoglu, Y.V.; Baysal, O.; Hacioglu, A. Path planning for autonomous UAV via vibrational genetic algorithm. Aircr. Eng. Aerosp. Technol. 2007, 79, 352–359. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, S. UAV path planning based on adaptive genetic algorithm. J. Syst. Simul. 2008, 20, 5411–5414. [Google Scholar]
- Tsai, C.; Huang, H.; Chan, C. Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation. IEEE Trans. Ind. Electron. 2011, 58, 4813–4821. [Google Scholar] [CrossRef]
- Tuncer, A.; Yildirim, M. Dynamic path planning of mobile robots with improved genetic algorithm. Comput. Electr. Eng. 2012, 38, 1564–1572. [Google Scholar] [CrossRef]
- Qu, H.; Xing, K.; Alexander, T. An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots. Neurocomputing 2013, 120, 509–517. [Google Scholar] [CrossRef]
- Liu, F.; Liang, S.; Xian, X.D. Optimal Path Planning for Mobile Robot Using Tailored Genetic Algorithm. IAES TELKOMNIKA Indones. J. Electr. Eng. 2014, 12, 1–9. [Google Scholar] [CrossRef]
- Shorakaei, H.; Vahdani, M.; Imani, B.; Gholami, A. Optimal cooperative path planning of unmanned aerial vehicles by a parallel genetic algorithm. Robotica 2016, 34, 823–836. [Google Scholar] [CrossRef]
- Wen, Z.Q.; Cai, Z.X. Global path planning approach based on ant colony optimization algorithm. J. Cent. South Univ. Technol. 2006, 13, 707–712. [Google Scholar] [CrossRef]
- Wang, H.J.; Xiong, W. Research on global path planning based on ant colony optimization for AUV. J. Mar. Sci. Appl. 2009, 8, 58–64. [Google Scholar] [CrossRef]
- Zhu, X.; Han, Q.; Wang, Z. The application of an improved ant colony algorithm in mobile robot path planning. Key Eng. Mater. 2011, 467–469, 222–225. [Google Scholar] [CrossRef]
- Zhao, J.; Fu, X. Improved ant colony optimization algorithm and its application on path planning of mobile robot. J. Comput. 2012, 7, 2055–2062. [Google Scholar] [CrossRef]
- Gao, M.K.; Chen, Y.M.; Liu, Q.; Huang, C.; Li, Z.; Zhang, D. Three-dimensional path planning and guidance of leg vascular based on improved ant colony algorithm in augmented reality. J. Med. Syst. 2015, 39, 111–133. [Google Scholar] [CrossRef] [PubMed]
- You, X.; Liu, K.; Liu, S. A chaotic ant colony system for path planning of mobile robot. Int. J. Hybrid Inf. Technol. 2016, 9, 329–338. [Google Scholar] [CrossRef]
- Zhang, Q.R.; Li, S.H. Path planning based on improved particle swarm optimization for a mobile robot. WSEAS Trans. Syst. Control 2007, 2, 347–352. [Google Scholar]
- Gong, D.W.; Zhang, J.H.; Zhang, Y. Multi-objective Particle Swarm Optimization for Robot Path Planning in Environment with Danger Sources. J. Comput. 2011, 6, 1554–1561. [Google Scholar] [CrossRef]
- Cheng, Z.; Tang, Y.X.; Liu, Y.L. 3-D Path Planning for UAV Based on Chaos Particle Swarm Optimization. Appl. Mech. Mater. 2012, 232, 625–630. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wu, L.N.; Wang, S.H. UCAV Path Planning by Fitness-scaling Adaptive Chaotic Particle Swarm Optimization. Math. Probl. Eng. 2013, 2013, 705238. [Google Scholar] [CrossRef]
- Liu, Y.K.; Li, M.K.; Xie, C.L.; Peng, M.; Xie, F. Path-planning research in radioactive environment based on particle swarm algorithm. Prog. Nucl. Energy 2014, 74, 184–192. [Google Scholar] [CrossRef]
- Yusof, T.S.T.; Toha, S.F.; Yusof, H. Path Planning for Visually Impaired People in an Unfamiliar Environment Using Particle Swarm Optimization. Procedia Comput. Sci. 2015, 76, 80–86. [Google Scholar] [CrossRef]
- Martinez-Alfaro, H.; Flugrad, D.R. Collision-free path planning for mobile robots and/or AGVs using simulated annealing. In Proceedings of the 1994 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 2–5 October 1994. [Google Scholar]
- Vougioukas, S.; Ippolito, M.; Cugini, U. Path planning based on accelerated simulated annealing. In Proceedings of the 1996 Research Workshop on ERNET—European Robotics Network, Darmstadt, Germany, 9–10 September 1996; pp. 259–268. [Google Scholar]
- Miao, H.; Tian, Y.C. Robot path planning in dynamic environments using a simulated annealing based approach. In Proceedings of the 2008 10th International Conference on Control, Automation, Robotics and Vision, Hanoi, Vietnam, 17–20 December 2008; pp. 1253–1258. [Google Scholar]
- Chou, M.C. Path-planning for an autonomous robot using a simulating annealing. J. Inf. Optim. Sci. 2011, 32, 297–314. [Google Scholar] [CrossRef]
- Miao, H.; Tian, Y.C. Dynamic robot path planning using an enhanced simulated annealing approach. Appl. Math. Comput. 2013, 222, 420–437. [Google Scholar] [CrossRef] [Green Version]
- Behnck, L.P.; Doering, D.; Pereira, C.E.; Rettberg, A. A modified simulated annealing algorithm for SUAVs path planning. IFAC-PapersOnLine 2015, 48, 63–68. [Google Scholar] [CrossRef]
- Vadakkepat, P.; Tan, K.C.; Wang, M.L. Evolutionary Artificial Potential Fields and their application in real time robot path planning. In Proceedings of the 2000 Congress on Evolutionary Computation, LA Jolla, CA, USA, 16–19 July 2000; pp. 256–263. [Google Scholar]
- Park, M.G.; Lee, M.C. Artificial potential field based path planning for mobile robots using a virtual obstacle concept. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Kobe, Japan, 20–24 July 2003; pp. 735–740. [Google Scholar]
- Cao, Q.X.; Huang, Y.W.; Zhou, J.L. An evolutionary artificial potential field algorithm for dynamic path planning of mobile robot. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3331–3336. [Google Scholar]
- Zhang, Q.S.; Chen, D.D.; Chen, T. An obstacle avoidance method of soccer robot based on evolutionary artificial potential field. Energy Procedia 2012, 16, 1792–1798. [Google Scholar] [CrossRef]
- Zhou, L.; Li, W. Adaptive Artificial Potential Field Approach for Obstacle Avoidance Path Planning. In Proceedings of the 7th International Symposium on Computational Intelligence and Design, Hangzhou, China, 13–14 December 2014; pp. 429–432. [Google Scholar]
- Whitbrook, A.M.; Aickelin, U.; Garibaldi, J.M. Idiotypic immune networks in mobile-robot control. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2007, 37, 1581–1598. [Google Scholar] [CrossRef]
- Huq, R.; Mann, G.K.I.; Gosine, R.G. Mobile robot navigation using motor schema and fuzzy context dependent behavior modulation. Appl. Soft Comput. J. 2008, 8, 422–436. [Google Scholar] [CrossRef]
- Fernandez-Leon, J.A.; Acosta, G.G.; Mayosky, M.A. Behavioral control through evolutionary neurocontrollers for autonomous mobile robot navigation. Robot. Auton. Syst. 2009, 57, 411–419. [Google Scholar] [CrossRef]
- Shi, C.X.; Wang, Y.Q.; Yang, J.Y. A local obstacle avoidance method for mobile robots in partially known environment. Robot. Auton. Syst. 2010, 58, 425–434. [Google Scholar] [CrossRef]
- Toibero, J.M.; Roberti, F.; Carelli, R.; Fiorini, P. Switching control approach for stable navigation of mobile robots in unknown environments. Robot. Comput. Integr. Manuf. 2011, 27, 558–568. [Google Scholar] [CrossRef]
- Marefat, M.; Britanik, J. Case-based process planning using an object-oriented model representation. Robot. Comput. Integr. Manuf. 1997, 13, 229–251. [Google Scholar] [CrossRef]
- Zhang, X.C.; Ji, G.; Shao, G.F.; Wei, J.; Li, Z.S. Research on soccer robot learning based on cases. J. Harbin Inst. Technol. 2004, 36, 905–907. [Google Scholar]
- Zhang, P.Y.; Lu, T.S.; Song, L.B. The Case-Based Learning of Mot ion Planning and Its SVR Implementation for Volleyball Robot. J. Shanghai Jiaotong Univ. 2006, 40, 461–465. [Google Scholar]
- Weng, M.; Du, Q.Y.; Qu, R.; Cai, Z. A Path Planning Algorithm Based on Typical Case Reasoning. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 1263–1266. [Google Scholar] [CrossRef]
- Zhong, X.Y.; Peng, X.F.; Miao, M.L. Planning of robot paths through environment modelling and adaptive window. J. Huazhong Univ. Sci. Technol. 2010, 38, 107–111. [Google Scholar]
- Liu, C.M.; Li, Z.B.; Huang, Z.H.; Zuo, L.; Wu, J.; Xu, X. A reactive navigation method of mobile robots based on LSPI and rolling windows. J. Cent. South Univ. Sci. Technol. 2013, 44, 970–977. [Google Scholar]
- Chou, C.C.; Lian, F.L.; Wang, C.C. Characterizing Indoor Environment for Robot Navigation Using Velocity Space Approach with Region Analysis and Look-Ahead Verification. IEEE Trans. Instrum. Meas. 2011, 60, 442–451. [Google Scholar] [CrossRef]
- Zhang, H.Y. An improved immune algorithm for simple assembly line balancing problem of type 1. J. Algorithms Comput. Technol. 2017, 11, 317–326. [Google Scholar] [CrossRef]
- Khari, M.; Kumar, P.; Burgos, D.; Crespo, R.G. Optimized test suites for automated testing using different optimization techniques. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. An Effective Hybrid Butterfly Optimization Algorithm with Artificial Bee Colony for Numerical Optimization. Int. J. Interact. Multimedia Artif. Intell. 2017, 4, 14–21. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.-y.; Lin, W.-m.; Chen, A.-x. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. https://doi.org/10.3390/sym10100450
Zhang H-y, Lin W-m, Chen A-x. Path Planning for the Mobile Robot: A Review. Symmetry. 2018; 10(10):450. https://doi.org/10.3390/sym10100450
Chicago/Turabian StyleZhang, Han-ye, Wei-ming Lin, and Ai-xia Chen. 2018. "Path Planning for the Mobile Robot: A Review" Symmetry 10, no. 10: 450. https://doi.org/10.3390/sym10100450




