A Novel Similarity Measure for Interval-Valued Intuitionistic Fuzzy Sets and Its Applications
Abstract
:1. Introduction
2. Preliminary
- (1):
- iff and and and
- (2):
- (3):
- (4):
- iff and and and .
- (5):
- (S1):
- (S2):
- if and only if
- (S3):
- (S4):
- If , then , and .
3. Some Existing Similarity Measures
4. A New Similarity Measure between Interval-Valued Intuitionistic Fuzzy Sets
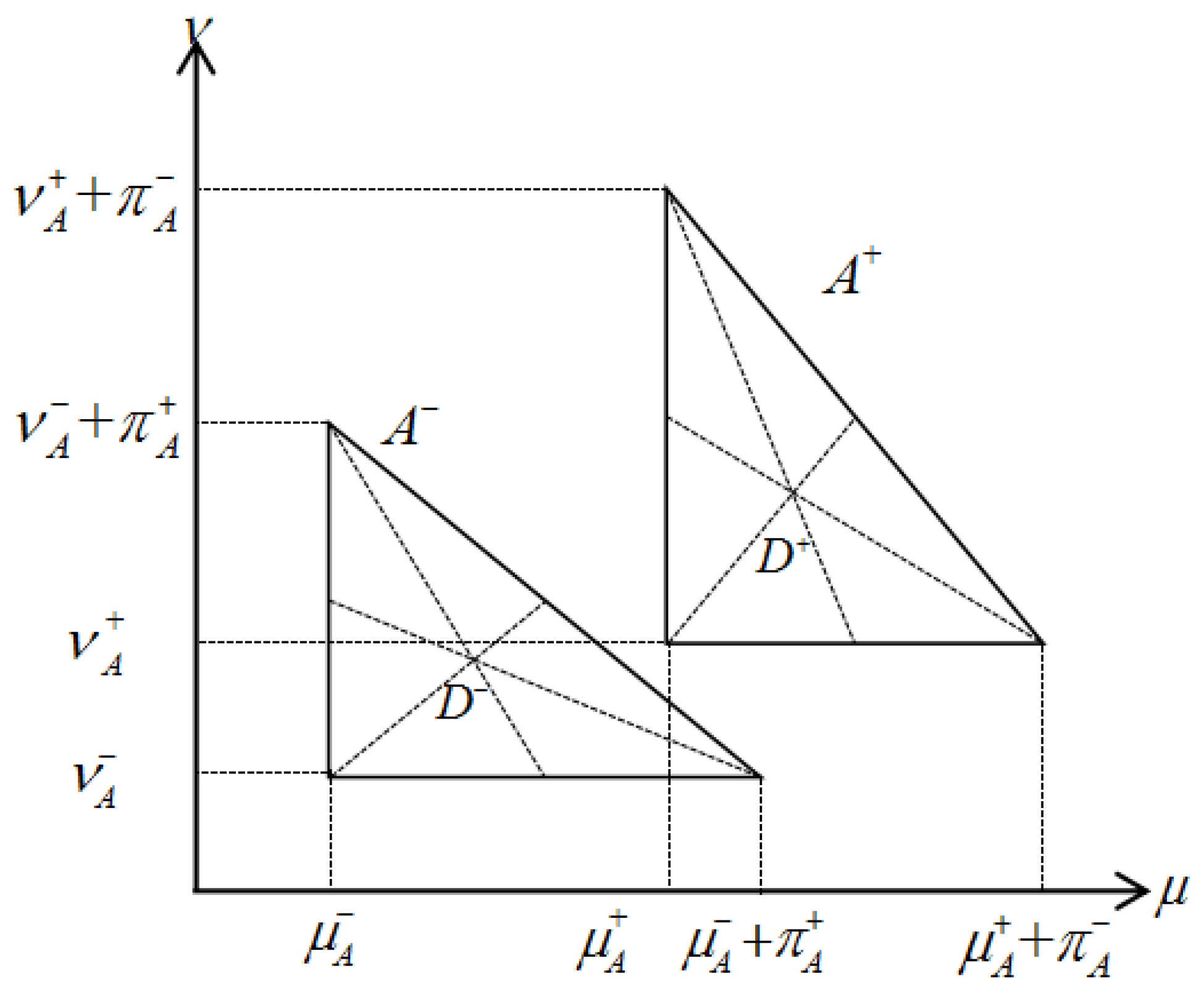
5. Geometric Interpretation of the Novel Similarity Measure
6. Applications
6.1. Pattern Recognition
6.1.1. Algorithms for Pattern Recognition
6.1.2. Applications for Pattern Recognition
6.2. Applications for Medical Diagnosis
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T.; Rangasamy, P. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Gau, W.L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifiying Field in Logics: Neutrosophic Logic, Neutrosophy, Neutrosophic Set, Neutrosophic Probability; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Zhang, X.H.; Smarandache, F.; Liang, X.L. Neutrosophic duplet semi-group and cancellable neutrosophic triplet groups. Symmetry 2017, 9, 275. [Google Scholar] [CrossRef]
- Zhang, X.H.; Bo, C.X.; Smarandache, F.; Park, C. New operations of totally dependent- neutrosophic sets and totally dependent-neutrosophic soft sets. Symmetry 2018, 10, 187. [Google Scholar] [CrossRef]
- Chen, S.M. Similarity measures between vague sets and between elements. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1997, 27, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Hong, D.H.; Kim, C. A note on similarity measures between vague sets and between elements. Inf. Sci. 1999, 115, 83–96. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Wang, W.Q.; Xin, X.L. Distance measure between intuitionistic fuzzy sets. Pattern Recognit. Lett. 2005, 26, 2063–2069. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric. Fuzzy Sets Syst. 2004, 148, 319–328. [Google Scholar] [CrossRef]
- Chen, T.Y. A note on distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric. Fuzzy Sets Syst. 2007, 158, 2523–2525. [Google Scholar] [CrossRef]
- Li, D.F.; Cheng, C. New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit. Lett. 2002, 23, 221–225. [Google Scholar] [CrossRef]
- Mitchell, H.B. On the Dengfeng-Chuntian similarity measure and its application to pattern recognition. Pattern Recognit. Lett. 2003, 24, 3101–3104. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Shi, P. Similarity measures on intuitionistic fuzzy sets. Pattern Recognit. Lett. 2003, 24, 2687–2693. [Google Scholar] [CrossRef]
- Ye, J. Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math. Comput. Model. 2011, 53, 91–97. [Google Scholar] [CrossRef]
- Xu, Z.S. Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making. Fuzzy Optim. Decis. Mak. 2007, 6, 109–121. [Google Scholar] [CrossRef]
- Boran, F.E.; Akay, D. A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition. Inf. Sci. 2014, 255, 45–57. [Google Scholar] [CrossRef]
- Zhang, H.M.; Yu, L.Y. New distance measures between intuitionistic fuzzy sets and interval-valued fuzzy sets. Inf. Sci. 2013, 245, 181–196. [Google Scholar] [CrossRef]
- Luo, M.X.; Zhao, R.R. A distance measure between intuitionistic fuzzy sets and its application in medical diagnosis. Artif. Intell. Med. 2018, 89, 34–39. [Google Scholar] [CrossRef] [PubMed]
- Atanassov, K.T.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Liu, X.D.; Zheng, S.H.; Xiong, F.L. Entropy and subsethood for general interval-valued intuitionistic fuzzy sets. Int. Conf. Fuzzy Syst. Knowl. Discov. 2005, 42–52. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. An overview of distance and simiarity measures of intuitionistic fuzzy sets. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2008, 16, 529–555. [Google Scholar] [CrossRef]
- Wei, C.P.; Wang, P.; Zhang, Y.Z. Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf. Sci. 2011, 181, 4273–4286. [Google Scholar] [CrossRef]
- Singh, P. A New Method on Measure of Similarity between Interval-Valued Intuitionistic Fuzzy Sets for Pattern Recognition. J. Appl. Comput. Math. 2012, 1. [Google Scholar] [CrossRef]
- Khalaf, M. Medical diagnosis via interval valued intuitionistic fuzzy sets. Ann. Fuzzy Math. Inf. 2013, 6, 245–249. [Google Scholar]
- Dhivya, J.; Sridevi, B. Similarity measure between interval-valued intuitionistic fzzy sets and their applications to medical diagnosis and pattern recognition. Int. J. Math. Arch. 2018, 9, 58–65. [Google Scholar]
- Meng, F.Y.; Chen, X. Entropy and similarity measure for Atannasov’s interval-valued intuitionistic fuzzy sets and their application. Fuzzy Optim. Decis. Mak. 2015, 15, 75–101. [Google Scholar] [CrossRef]
- Xu, Z.S. On similarity measures of interval-valued intuitionistic fuzzy sets and their application to pattern recognitions. J. Southeast Univ. 2007, 23, 027. [Google Scholar]
- Mathew, T.J.; Sherly, E.; Alcantud, J.C.R. A multimodal adaptive approach on soft set based diagnostic risk prediction system. J. Intell. Fuzzy Syst. 2018, 34, 1609–1618. [Google Scholar] [CrossRef]
- Celik, Y.; Yamak, S. Fuzzy soft set theory applied to medical diagnosis using fuzzy arithmetic operations. J. Inequal. Appl. 2013, 1, 82. [Google Scholar] [CrossRef]
- De, S.K.; Biswas, R.; Roy, A.R. An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets Syst. 2001, 117, 209–213. [Google Scholar] [CrossRef]
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| [24] | 0.90 | 0.90 | 0.90 | 0.95 |
| [24] | 0.90 | 0.90 | 0.90 | 0.90 |
| [28] | 1.00 | 0.98 | 0.95 | 0.94 |
| 0.95 | 0.90 | 0.80 | 0.94 |
| Feature1 | Feature2 | Feature3 | Feature4 | |
|---|---|---|---|---|
| B |
| Classification Results | |||||
|---|---|---|---|---|---|
| [24] | 0.87 | 0.87 | 0.86 | 0.87 | N.A. |
| [24] | 0.75 | 0.76 | 0.79 | 0.76 | |
| [25] | 0.78 | 0.79 | 0.78 | 0.79 | N.A. |
| [28] | 0.82 | 0.86 | 0.88 | 0.88 | N.A. |
| 0.82 | 0.81 | 0.88 | 0.75 |
| Recognition Results | |||||
|---|---|---|---|---|---|
| [24] | 0.59 | 0.58 | 0.81 | 0.97 | |
| [24] | 0.53 | 0.53 | 0.79 | 0.94 | |
| [25] | 0.48 | 0.47 | 0.74 | 0.94 | |
| [28] | 0.64 | 0.56 | 0.83 | 0.98 | |
| 0.60 | 0.58 | 0.85 | 0.97 |
| (Temperature) | (Cough) | (Headache) | (Stomach Pain) | |
|---|---|---|---|---|
| (Viral fever) | ||||
| (Typhoid) | ||||
| (Pneumonia) | ||||
| (Stomach problem) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, M.; Liang, J. A Novel Similarity Measure for Interval-Valued Intuitionistic Fuzzy Sets and Its Applications. Symmetry 2018, 10, 441. https://doi.org/10.3390/sym10100441
Luo M, Liang J. A Novel Similarity Measure for Interval-Valued Intuitionistic Fuzzy Sets and Its Applications. Symmetry. 2018; 10(10):441. https://doi.org/10.3390/sym10100441
Chicago/Turabian StyleLuo, Minxia, and Jingjing Liang. 2018. "A Novel Similarity Measure for Interval-Valued Intuitionistic Fuzzy Sets and Its Applications" Symmetry 10, no. 10: 441. https://doi.org/10.3390/sym10100441
APA StyleLuo, M., & Liang, J. (2018). A Novel Similarity Measure for Interval-Valued Intuitionistic Fuzzy Sets and Its Applications. Symmetry, 10(10), 441. https://doi.org/10.3390/sym10100441





