4. Secure Resolving Dimension for Special Classes of Graphs
Observation 1. Let order of G ≥ 3. Suppose sdim (G) = 1. Then, dim (G) = (since sdim(G) ≥ dim(G)). Therefore, G = Pn. However, sdim(Pn) = 2, which is a contradiction. Therefore, sdim(G) ≥ 2.
Observation 2. sdim(G) = 1 if and only if G = P1or P2.
Theorem 1. sdim(G) = 2, G is a tree if and only if G = Pn (n ≥ 3).
Proof. If G = Pn (n ≥ 3), then sdim(G) = 2.
Conversely, suppose n ≥ 4. Suppose there are two pendant vertices v1, v2 adjacent with w of G. Take a vertex t, which is adjacent to w (t ≠ v1, v2). {v1, w} is not a resolving set, since t and v2 will not have distinct codes with respect to {v1, w}. Assume that {v1, v2} is a resolving set of G. Then, it is not secure, since {v1, w} and {v2, w} are not resolving sets. Suppose {v1, t} is resolving. Then, it is not secure (since {v1, w}, {w, t} are not resolving sets of G). Let {a, b} be a resolving set of G. a, b ∉ {v1, v2, w}. Then, {a, b} is not secure, since neither {w, b} nor {w, a} is a resolving set of Pn (since d(v1, a) = d(w, a) + 1 = d(v2, a)). Therefore, no vertex of G supports two or more pendant vertices. Suppose that w is a vertex of G that supports one pendant vertex and there exists at least two neighbors of w having degrees greater than or equal to two. Then, we will not get any resolving set with cardinality two containing w. Therefore, any vertex of G with a pendant neighbor has at most one neighbor of degree greater than or equal to two. Therefore, G is a path. Suppose that n = 3. Since G is acyclic and connected, G = P3. □
Theorem 2. sdim(Cn) = dim(Cn) = 2.
Proof. Let V(Cn) = {m1, m2, …, mn}.
Let M = {m1, m2}. Then, M is a resolving set of Cn. It can be verified that {m1, mi} is a resolving set where 3 ≤ i ≤ n.
Then, m1 and mk are diametrically opposite vertices. Let M = {m1, m2}. Clearly, {m1, m2} is a resolving set of Cn. It can be substantiated that {m1, mi} is resolving when 3 ≤ i ≤ n, i ≠ k. Also, {mk, m2} is a resolving set of Cn. Therefore, sdim (G) = 2 = dim(G).
Remark 3. sdim(G) ≤ 1 + dim(G).
Proof. sdim(G)≥ dim(G). Suppose that dim(G) < sdim(G). Let T= {u1, u2, …., uk} be a basis of G. Let W = {u1, u2, …, uk, v}. Then, W is a SR set of G. Therefore, sdim(G) ≤ k + 1. However, sdim(G) > dim(G) = k. Therefore, sdim(G) ≤ 1 + dim(G). Hence the remark. □
Theorem 3. sdim(G) = n − 1 if and only if G = Kn or K1, n −1.
Proof. Let
G = Kn or
K1,n − 1. Then,
sdim(G) = n − 1. Suppose that
sdim(G) = n − 1. Then,
dim(G) is
n − 1 or
n − 2. If
dim(G) =
n − 1, then
G = Kn. Suppose that
dim(G) is n − 2. Then,
G = Ka, b (a, b≥ 1), (b ≥ 2
, a ≥ 1), Ka + (K1 ∪ Kb) (b, a ≥ 1
). Suppose that
G = Ka,b (a, b ≥ 2
), sdim(G) = dim(G) = a + b − 2 [
1]. Suppose that
G = (b ≥ 2
, a ≥ 1
), then
dim(G) = a + b − 2. If
a = 1, then
=
K1,b. In this case,
sdim(G) = b and
dim(G) = b − 1. If
a ≥ 2, then
sdim(G) = a + b − 2 =
dim(G).
Let G = Ka + (K1∪ Kb), (a, b ≥ 1). When a = 1 and b = 1, G = P3 and sdim(P3) = 2 and dim(P3) = 1. Clearly, G is a star. When a = 1 and b ≥ 2, sdim(G) = a + b − 1 = dim(G). Suppose that a > 1 and b = 1. Then, sdim(G) = a = dim(G). Suppose that a, b > 1. Then, sdim(G) = a + b − 1= dim(G). Except when G is a star, sdim(G) = dim(G) = n − 2. Therefore, G = K1, n − 1. □
Theorem 3. Let T be a connected graph. Let G = TK2. Then, sdim(T) ≤ sdim(TK2) ≤ sdim(T) + 1.
Proof. Refer to Theorem 7 [
1]. Let
G = T K2, T1, and
T2 be the transcripts of
T in
G. Let
X be a basis of
T, and let
X1 = {
x1, x2, …, xk} and
X2 = {
y1, y2, …, yk} be the basis of
T1 and
T2 respectively, corresponding to
X. Let
S = X1 ∪ {
y1}. Then,
S is a SR set of
G. Therefore,
sdim(G) ≤ sdim(T) + 1. Let V
1, V
2 be the vertex sets of
T1 and
T2 respectively
. Then,
V(G)
= V1 ∪ V2. Let
X be a secure basis of
G. Let
X1 = X ∩ V1, X2 = X ∩ V2. Let
S1 ⊆
V (T1) be the union of
X1 and the set
X’2 consisting of those vertices of
V1 corresponding to
X2. Then,
S1 is a SR set of
T1. Therefore,
sdim(T) = sdim(T1) ≤ | S1| = |X1 ∪ X’2| ≤ |X1| + | X’2| = |X| = sdim(G). Hence, the theorem. □
Corollary 1. Letϵ> 0. Then, where T is a connected induced subgraph of G.
Proof. Let
T = K1, 2n + 1. sdim(T) = 2
n + 1. Let
G = T K2. Then, we get a graph
G containing
T as an induced subgraph [
1]. Further,
sdim(G) ≤ 2
n. Therefore,
as
n → 0. Hence, the corollary. □
6. Secure Resolving Domination Number for Some Well-known Graphs
γsr(Kn) = n − 1, n ≥ 2.
γsr (K1, n – 1) = n − 1, n ≥ 2.
where (Km(a1, a2, …, am)) is the multi-star graph formed by joining ai ≥ 1 (1 ≤ i ≤ m) pendant vertices to each vertex xi of a complete graph Km with V(Km) = {x1, x2, …, xm}.
Illustration 2. Consider the following graph K3(1, 1, 1).![Symmetry 10 00439 i002]()
let
N = {u1, u2, u3}. Then
N is a secure, dominating, and resolving set of
K3(1, 1, 1
). It can be easily seen that
. γsr (K
3(1, 1, 1)) = 3.
Proposition 1. Let γs be the minimum cardinality of a secure dominating set of G. Then, max {γs(G), dim(G), γr(G)} ≤ γsr(G) ≤ γs(G) + dim(G).
Proof. Let L be a minimum secure dominating set of G and W be a basis of G. Then, L ∪ W is a SRD set of G. Hence, γsr(G) ≤ γs(G) + dim(G). The first inequality is obvious. □
Remark 5. P ∪ {u} is a SRD set of G, P is a minimum resolving dominating set of G.
Illustration 3. Consider the given graph G.
![Symmetry 10 00439 i003]()
Here, γ(G) = 2 and dim(G) = 3 (since {u1, u4} is a minimum dominating set, {u5, u7, u8} is a minimum resolving set of G). γr(G) = 4 (since {u1, u5, u7, u8} is a minimum resolving dominating set of G. {u1, u4, u5, u7, u8} is a SRD set of G. Let S be a minimum SRD set of G. Consequently, γsr(G) ≤ 5. Since S is resolving, S must contain two of the pendant vertices. If S contains u2, then u6 and the remaining pendant vertices are not resolved. If S contains u6, then u2 and the remaining pendant vertices are not resolved. If S contains u4, then u5 and u3 are not resolved. Therefore, either S contains u5 and two of the pendant vertices or u3 and two of the pendant vertices. If S contains u5 and two of the pendant vertices, then the remaining pendant vertex is not resolved. Therefore, the resolving dominating set contains u1. Therefore, the possibilities of the resolving dominating sets are {u1, u5, u7, u8}, {u1, u5, u8, u9}, {u1, u5, u7, u9}, {u1, u3, u7, u8}, {u1, u3, u8, u9}, and {u1, u3, u7, u9}. None of these is secure, since u2 and u6 cannot be replaced in all of these sets. Therefore, γsr(G) ≥ 5. Hence, γsr(G) = 5. Thus, γ(G) < dim(G) < γr(G) < γsr(G). Also, γsr(G) = γ(G) + dim(G). γs(G) = 3, since G has no secure dominating set with two vertices, and {u1, u4, u3} is a secure dominating set. Therefore, γsr(G) = 5 < γs(G) + dim(G) = 6 and max {γs(G), dim(G), γr(G)} = 4 < γsr(G) = 5.
Remark 6. When G = Kn, γ(G) = 1, γs(G) = 1, dim(G) = n − 1, γr(G) = n − 1, γsr(G) = n − 1. Therefore, max {γs(G), dim(G), γr(G)} = γsr(G).
Observation 3. γsr(G) ≥ g(m, d), where g(m, d) = min,
d is a diameter of G, the order of G is m ≥ 2, and d and m are positive integers with d < m. This follows from proposition 2.1 [6] and that γsr(G) ≥ γr(G). Observation 4. For every positive integer k, there are only finitely many connected graphs with secure resolving domination number k.
Proof. Consider a graph
G with order
m ≥ 2 and
γsr(G) = k. From corollary 2.2 [
6]
.
γ(G) ≤ γsr(G ) = k. Therefore, the diameter of
G is not more than
3k − 1. Therefore,
. Therefore, there are only finitely many connected graphs with
γsr(G) = k. □
Remark 7. Suppose that γsr(G) = 2. Then, the number of connected graphs with γsr(G) = 2 has an order of at most 11.
Proof. By the above observation,
In fact, the above bound for n can be improved. □
Observation 5. For any G with γsr(G) = 2, the order of G is not more than 4.
Proof. Let γsr(G) = 2. Let X = {p, q} be a γsr—set of G. If d(p, q) ≥ 4, then p and q cannot dominate the point at a distance 2 from p in the shortest path joining p and q. Therefore, d(p, q) ≤ 3. □
Case (i): Distance between p and q is 1.
As every single vertex in
V (G) − X is adjacent with either both
p and
q or one of them, the distances of the vertices in
V (G) − X from
p and
q are (1, 2), (2, 1), and (1, 1). Then,
G is as follows:
![Symmetry 10 00439 i004]()
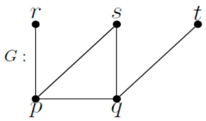
Here, s cannot enter X by removing a vertex of X, since such a resulting set is not a dominating set. Therefore, G = P4. If both pendants r and t are removed, then the resulting set is K3, for which γsr(G) = 2. That is, G = K3.
If
r, s, and
t are present and
r is adjacent with
s, then the graph is:
![Symmetry 10 00439 i005]()
Here, r cannot enter X, since resolving fails.
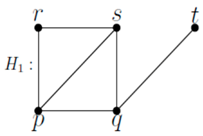
If
r, s, and
t are existing,
r and
t are adjacent with
s, then the graph is:
![Symmetry 10 00439 i006]()
Here, s cannot enter X, since resolution fails.
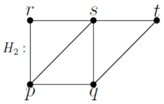
If
r and
t are adjacent, then the graph
H3 is as follows:
![Symmetry 10 00439 i007]()
In
H3,
s cannot enter
X, since domination fails. If
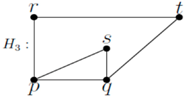
r, s, and
t are mutually adjacent, then the graph
H4 is as follows:
![Symmetry 10 00439 i008]()
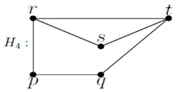
In the above graph, s cannot enter X, since resolution fails. The remaining cases are: (i) s is not present, and r and t are non-adjacent. In this case, G = P4. (ii) r and t are available, s is not present and r and t are adjacent. We get G = C4. (iii) r and s are alone present and r and s adjacent. We get C4 with a diagonal. (iv) r and s are alone and present, and they are not adjacent. We get K3 with a pendant vertex. Thus, in this case, G = P3, P4, C4, C4 with a diagonal and K3 with a pendant vertex.
Since every vertex in
V(G) − X is adjacent with at least one of
p and
q, the distances of the vertices 3 in
V(G) − X from
p and
q are (1, 3), (3, 1), (1, 2), (2, 1), and (1, 1). Therefore, the graph is as follows:
![Symmetry 10 00439 i009]()
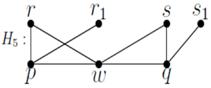
For security in
H5,
r1 cannot enter {
p,
q} by removing
p or
q, since domination fails. Therefore, only one of
r and
r1 can be present. Similarly, one of
s and
s1 can be present. Therefore, the graphs are as follows:
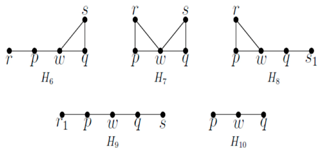
![Symmetry 10 00439 i010]()
![Symmetry 10 00439 i011]()
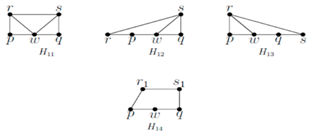
In graph H9, w cannot enter X = {p, q}. In H6, if w enters X by removing p or q, then the resulting set is not resolving, although it is dominating. In graph H7, if w enters X, then for domination, q should be replaced by w. However, the resulting set is not resolving. Same is the graph H8. In graphs H11, H12, and H13, w cannot enter X, since resolution fails. In graph H14, w cannot enter X, since domination fails.
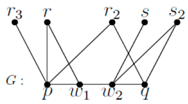
Since vertices in V(G) − X are adjacent with one of p and q, the distances of the vertices in V (G) − X from p and q are (1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), and (4, 1).
Only one of r, r2, and r3 can be present, since {p, q} is an SRD set. Similarly, only one of s and s2 can be present. If any number of edges among the vertices r3, r, x2, s, and s2 are inserted, then w1 cannot enter X by replacing p or q, since domination fails.
Subcase (i): r3 is present.
In this case, w1 cannot enter X by replacing p, q, since domination fails.
Subcase (ii): s2 is exist.
In this case, w2 cannot enter X by replacing p, q. (since domination fails).
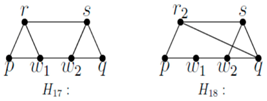
Subcase (iii): One of r, r2, and s is present.
Then, the graphs are as follows:
![Symmetry 10 00439 i013]()
In H15, either w1 or w2 cannot enter X by replacing p, q, since resolution fails. In H16, w1 cannot enter X, since domination fails.
In H17, w1 cannot enter X, since resolution fails. In H18, w1 cannot enter X, since domination fails.
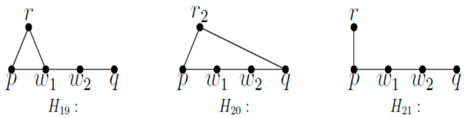
Subcase (iv): Only one of r, r2 is present, and none of s, s2 is present.
Then, the graphs are as follows:
![Symmetry 10 00439 i015]()
In H19, w1 cannot enter X, since resolution fails. In H20, w2 cannot enter X, since domination fails. In H21, w1 cannot enter X, since domination fails. Similarly, if only one of s and s2 is present, and none of r, r1, and r2 is present, then w2 cannot enter X. Therefore, G = P4.
Subcase (v): None of x, x2, x3, y, and y2is present. Then, G = P4. □
Corollary 2. γsr(G) = 2 if and only if G = P4, P3, C3, C4, and K3with a pendant vertex and K4− {e}.
Proposition 2. Let l ≥ 1, m ≥ 2, and n = l + m be three integers. Then, there exists G with γ(G) = l, dim(G) = q and γsr(G) = n.
Proof. We follow the proof given in proposition 3.1 [
6]. Construct a graph G from the path
P3l − 1: v1, v2, …, v3l − 1 of order
3l − 1. Join
m—pairs of vertices
xj, yj, 1 ≤ j ≤ m and join
xj and
yj for each
j. Consider,
Fj—a copy of the path
P2: xj yj. Join the vertex of
Fj, 1 ≤ j ≤ m to the vertex
v3t − 1. For
l = m = 2, the graph is as follows:
![Symmetry 10 00439 i016]()
Let V = {v1, v2, …, v3l-1}, T = {x1, x2, …, xm}, and W = {y1, y2, …, ym}. Then, γ(G) = l and dim(G) = m (since {v2, v5, …, v3l − 1} is dominating, and T is a basis of G. Each resolving set of G has at least one vertex from each set, {xj, yj}, 1 ≤ j ≤ m. All of the vertices xj, yj, and v3l − 1 are dominated by them. We need at least = l vertices to dominate V-{v3l − 1}. As a result, γr(G) ≥ l + m. However, K = {v2, v5, …, v3l − 1} ∪ X is a resolving dominating set for G. Hence, γr(G) ≤|K| = l + m. Therefore, γr(G) = l + m. Clearly, K is a SRD set of G. Therefore, γsr(G) ≤ l + m. However, γsr(G) ≥ γr(G) = l + m. Therefore, γsr(G) = l + m = n. □
Theorem 4. Let G be a graph of order n ≥ 2. γsr(G) = n − 1 if and only if G = Kn or K1, n − 1.
Proof. γsr(G) = n − 1. Consequently, no (n − 2) subset of V(G) is a SRD set of G. Suppose that there exists an (n − 2) resolving subset S of V (G) that is not a secure dominating set of G. Let V (G) − S = {u, v}. Suppose that S is not a dominating set of G. Since G is connected, exactly one of u and v is not dominated by S, say u. Clearly, u is a pendant of v. □
Claim: v is adjacent with every vertex of S.
Suppose that v is not adjacent with a vertex w of S. Let T’ = (S − {w})∪{v} = V (G) − {u, w}. Since G is connected and w is not adjacent with u and v, w is adjacent with some vertex of S. T’ is a dominating set of G. Therefore, there exists an (n − 2) subset that is a resolving and dominating set of G.
S1= (T’∪ {u}) − {v} is a dominating set of G. Clearly, S is a resolving set, since d (u, v) = 1, d(u, w) ≥ 2. Therefore, S1 is a secure resolving domination set of G. Therefore, γsr(G) ≤ n − 2, which is a contradiction. w is adjacent with some vertex x in S. Therefore, S2 = (S ∪ {w}) − {x} is a dominating set of G. d(u, v) ≥ 2 and d(x, w) = 1. Therefore, S2 is a secure resolving domination set of G. Therefore, γsr(G) ≤ n − 2, which is a contradiction. Suppose that S is a dominating set of G, but not a secure dominating set of G. Suppose that u cannot enter S by replacing a vertex of S. Then, any neighbor of u is either an isolate of S or has private neighbor v. Suppose that every neighbor x of u is an isolate of S. In this case, if u is not adjacent with v, then G is disconnected, which is a contradiction. If u is adjacent with v, then (S − N[u]) ∪ {v} is connected. Then, (S − {x}) ∪ {u} is a dominating set of G.
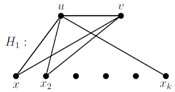
Suppose that
(S − N(u)) = φ. Then, either
G is a star or
G is of the form:
![Symmetry 10 00439 i017]()
where
v is adjacent with some or all of
x1, x2, …, xk. If
G is a star, then
γsr(G) = n − 1. If
G is not a star, then the above graph has
γsr(G) ≤ n − 2, which is a contradiction.
Suppose that (S − N(u)) ≠ φ. Then, v is adjacent with at least one vertex, say z of (S − N(u)). d(v,z) = 1, d(xi, z) ≠ 1. Therefore, (S − {xi}) ∪ {u} is resolving. Therefore, there exists an (n − 2) SRD set of G, which is a contradiction.
Suppose that there exists a neighbor x of u which has private neighbor v. Let x be an isolate of S. Then, G is of the form H1 or of the form H2, where u and v are made adjacent in H1. However, H1 and H2 have an (n − 2) secure dominating set of G, which is a contradiction.
If x is not an isolate of S, then either G is complete, or G has (n − 2) SRD set of G, which is a contradiction. Similarly, v can enter S by replacing a vertex of S. Therefore, any (n − 2) resolving subset of V (G) is a secure dominating set of G, provided that G is not a star or G is not Kn.
Therefore, the theorem follows.
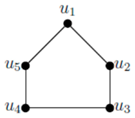 let H = {u1, u3}. Then, H is resolving, and for any u ∈ V − H, there exists v ∈ H such that (H − {v}) ∪ {u}) is a resolving set of C5. It can be easily seen that sdim(G) = 2.
let H = {u1, u3}. Then, H is resolving, and for any u ∈ V − H, there exists v ∈ H such that (H − {v}) ∪ {u}) is a resolving set of C5. It can be easily seen that sdim(G) = 2.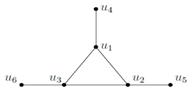 let N = {u1, u2, u3}. Then N is a secure, dominating, and resolving set of K3(1, 1, 1). It can be easily seen that. γsr (K3(1, 1, 1)) = 3.
let N = {u1, u2, u3}. Then N is a secure, dominating, and resolving set of K3(1, 1, 1). It can be easily seen that. γsr (K3(1, 1, 1)) = 3.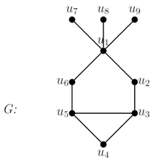

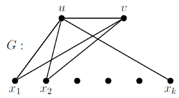 where v is adjacent with some or all of x1, x2, …, xk. If G is a star, then γsr(G) = n − 1. If G is not a star, then the above graph has γsr(G) ≤ n − 2, which is a contradiction.
where v is adjacent with some or all of x1, x2, …, xk. If G is a star, then γsr(G) = n − 1. If G is not a star, then the above graph has γsr(G) ≤ n − 2, which is a contradiction.