Gröbner-Shirshov Bases for Temperley-Lieb Algebras of Complex Reflection Groups
Abstract
:1. Introduction
- (1)
- In the first part of this paper, extending the result for type in [16], we construct a Gröbner-Shirshov basis for the Temperley-Lieb algebra of the complex reflection group of type and compute the dimension of , by enumerating the standard monomials which are in bijection with the fully commutative elements.
- (2)
- In the second part of this paper, we try to understand some combinatorial aspects on the dimension of the Temperley-Lieb algebra .
2. Preliminaries
Gröbner-Shirshov Basis
- (a)
- S is closed under composition.
- (b)
- For each , a normal form of p with respect to S is unique.
- (c)
- The set of S-standard monomials forms a linear basis of the algebra defined by S.
3. Temperley-Lieb Algebras of Types and
3.1. Temperley-Lieb Algebra of Type
3.2. Temperley-Lieb Algebra of Type

4. Gröbner-Shirshov Bases for Temperley-Lieb Algebras of the Complex Reflection Group of Type

- First, consider the compositions between and another relation.
- -
- -
- -
- Next, we take the relation and another relation.
- -
- -
- -
- -
- -
- -
- Calculate for the relation and another relation.
- -
- -
- -
- -
- -
- -
- -
- Check for the relation and another relation.
- -
- -
- -
- -
- Finally, consider and another relation.
- -
- -
- -
- -
- -
5. Combinatorial Aspects—Connections to Fully Commutative Elements and Dyck Paths
- The -packet is the set of collections labeled by prefixes of the form
- The -packet, , is the set of collections labeled by or prefixes of the form
- The -packet contains only the collection labeled by or .
- The -packet contains only the collection labeled by the empty prefix .
- The -packet is the set of collections labeled by prefixes of the form
- The -packet, , is the set of collections labeled by or prefixes of the form
- The -packet contains only the collections labeled by or .
- The -packet contains only the collection labeled by the empty prefix . These elements cover the elements of .
- Every collection in the packet has elements.
- The size of the packet is
6. Temperley-Lieb Algebras of Types and
- The subalgebra is a subalgebra of , whose -basis consists ofWe remark thatIn particular, for , we recover the same formula as we had in [16]:
- More generally, the subalgebra ( and ) is a subalgebra of , whose -basis consists ofWe remark that
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Temperley, H.N.V.; Lieb, E.H. Relations between percolation and colouring problems and other graph theoretical problems associated with regular planar lattices: Some exact results for the percolation problem. Proc. R. Soc. Lond. Ser. A 1971, 322, 251–280. [Google Scholar] [CrossRef]
- Jones, V.F.R. Hecke algebra representations of braid groups and link polynomials. Ann. Math. 1987, 126, 335–388. [Google Scholar] [CrossRef]
- Shirshov, A.I. Some algorithmic problems for Lie algebras. Sibirk. Math. Z. 1962, 3, 292–296. (In Russian)Translated in ACM SIGSAM Bull. Commun. Comput. Algebra 1999, 33, 3–6 [Google Scholar]
- Buchberger, B. An Algorithm for Finding the Basis Elements of the Residue Class Ring of a Zero Dimensional Polynomial Ideal. Ph.D. Thesis, University of Innsbruck, Innsbruck, Austria, 1965. (In German) Translated in J. Symb. Comput. 2006, 41, 475–511. [Google Scholar]
- Bokut, L.A. Imbedding into simple associative algebras. Algebra Logic 1976, 15, 117–142. [Google Scholar] [CrossRef]
- Bergman, G.M. The diamond lemma for ring theory. Adv. Math. 1978, 29, 178–218. [Google Scholar] [CrossRef]
- Bokut, L.A.; Shiao, L.-S. Gröbner-Shirshov bases for Coxeter groups. Comm. Algebra 2001, 29, 4305–4319. [Google Scholar] [CrossRef]
- Lee, D. Gröbner-Shirshov bases and normal forms for the Coxeter groups E6 and E7. In Advances in Algebra and Combinatorics; World Scientific Pub.: Singapore, 2008; pp. 243–255. [Google Scholar]
- Svechkarenko, O. Gröbner-Shirshov Bases for the Coxeter Group E8. Master’s Thesis, Novosibirsk State University, Novosibirsk, Russia, 2007. [Google Scholar]
- Lee, D.-I. Standard monomials for the Weyl group F4. J. Algebra Appl. 2016, 15, 1650146. [Google Scholar] [CrossRef]
- Lee, D.-I.; Lee, J.-Y. Gröbner-Shirshov bases for non-crystallographic Coxeter groups. arXiv, 2018; arXiv:1809.08419. [Google Scholar]
- Kang, S.-J.; Lee, I.-S.; Lee, K.-H.; Oh, H. Hecke algebras, Specht modules and Gröbner-Shirshov bases. J. Algebra 2002, 252, 258–292. [Google Scholar] [CrossRef]
- Kang, S.-J.; Lee, I.-S.; Lee, K.-H.; Oh, H. Representations of Ariki-Koike algebras and Gröbner-Shirshov bases. Proc. Lond. Math. Soc. 2004, 89, 54–70. [Google Scholar] [CrossRef]
- Lee, D.-I. Cyclotomic Hecke algebras of G(r, p, n). Algebr. Represent. Theory 2010, 13, 705–718. [Google Scholar] [CrossRef]
- Dattoil, G.; Ricci, P.E.; Cesarano, C. Beyond the monomiality: The monumbrality principle. J. Comput. Anal. Appl. 2004, 6, 77–83. [Google Scholar]
- Kim, S.; Lee, D.-I. Gröbner-Shirshov bases for Temperley-Lieb algebras of types B and D. arXiv, 2017; arXiv:1808.05026. [Google Scholar]
- Lee, K.-H.; Oh, S.-J. Catalan triangle numbers and binomial coefficients. Contemp. Math. 2018, 713, 165–185. [Google Scholar]
- Stembridge, J.R. Some combinatorial aspects of reduced words in finite Coxeter groups. Trans. Am. Math. Soc. 1997, 349, 1285–1332. [Google Scholar] [CrossRef]
- Kleshchev, A.; Ram, A. Homogeneous representations of Khovanov-Lauda algebras. J. Eur. Math. Soc. 2010, 12, 1293–1306. [Google Scholar] [CrossRef]
- Kleshchev, A.; Ram, A. Representations of Khovanov-Lauda-Rouquier algebras and combinatorics of Lyndon words. Math. Ann. 2011, 349, 943–975. [Google Scholar] [CrossRef]
- Fan, C.K. A Hecke Algebra quotient and some combinatorial applications. J. Algebraic Combin. 1996, 5, 175–189. [Google Scholar] [CrossRef]
- Stembridge, J.R. On the fully commutative elements of Coxeter groups. J. Algebraic Combin. 1996, 5, 353–385. [Google Scholar] [CrossRef] [Green Version]
- Feinberg, G.; Lee, K.-H. Fully commutative elements of type D and homogeneous representations of KLR-algebras. J. Comb. 2015, 6, 535–557. [Google Scholar] [CrossRef]
- Feinberg, G.; Lee, K.-H. Homogeneous representations of type A KLR-algebras and Dyck paths. Sém. Lothar. Combin. 2016, 75, Art. B75b. [Google Scholar]
- Feinberg, G.; Kim, S.; Lee, K.-H.; Oh, S.-J. Fully commutative elements of the complex reflection groups. arXiv, 2018; arXiv:1808.04269. [Google Scholar]

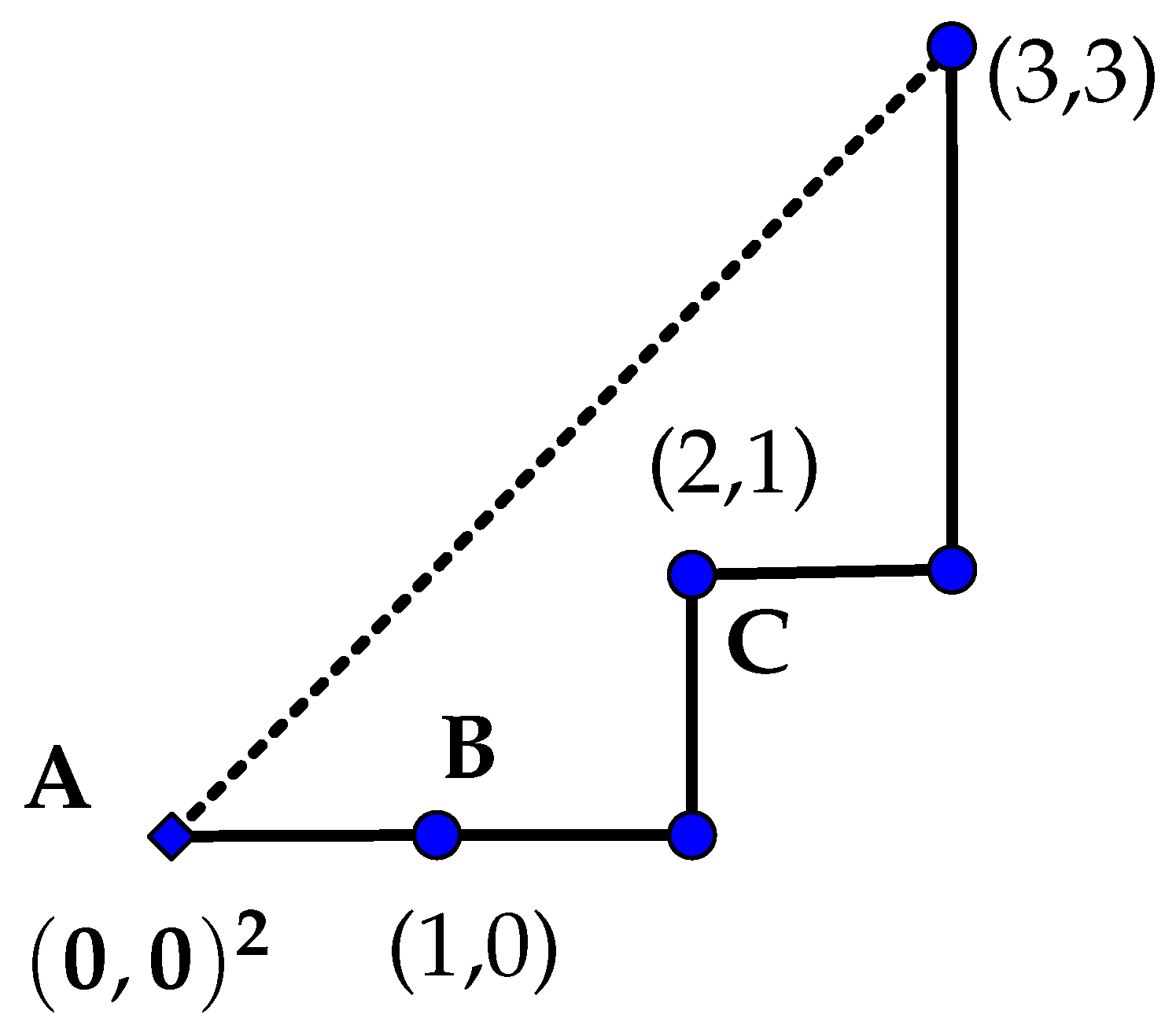
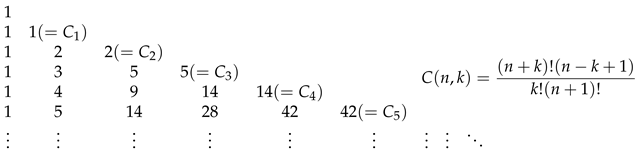
| Standard Monomials | Fully Commutative Elements | |
|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-Y.; Lee, D.-i.; Kim, S. Gröbner-Shirshov Bases for Temperley-Lieb Algebras of Complex Reflection Groups. Symmetry 2018, 10, 438. https://doi.org/10.3390/sym10100438
Lee J-Y, Lee D-i, Kim S. Gröbner-Shirshov Bases for Temperley-Lieb Algebras of Complex Reflection Groups. Symmetry. 2018; 10(10):438. https://doi.org/10.3390/sym10100438
Chicago/Turabian StyleLee, Jeong-Yup, Dong-il Lee, and SungSoon Kim. 2018. "Gröbner-Shirshov Bases for Temperley-Lieb Algebras of Complex Reflection Groups" Symmetry 10, no. 10: 438. https://doi.org/10.3390/sym10100438
APA StyleLee, J.-Y., Lee, D.-i., & Kim, S. (2018). Gröbner-Shirshov Bases for Temperley-Lieb Algebras of Complex Reflection Groups. Symmetry, 10(10), 438. https://doi.org/10.3390/sym10100438





