Phase Diffusion of a q-Deformed Oscillator
Abstract
:1. Introduction
2. The q-Deformed Algebra
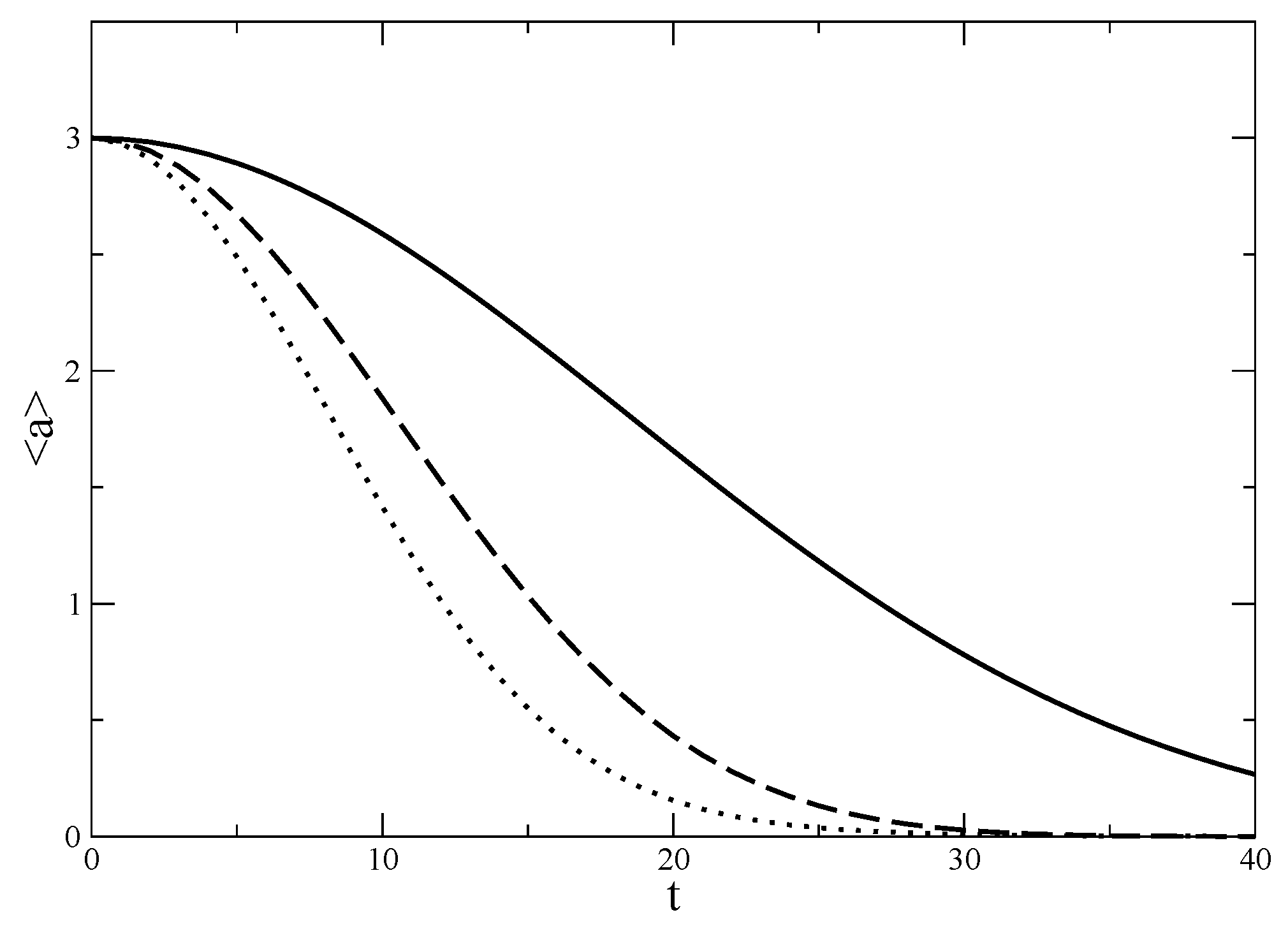
3. Phase Collapse in a Bosonic System
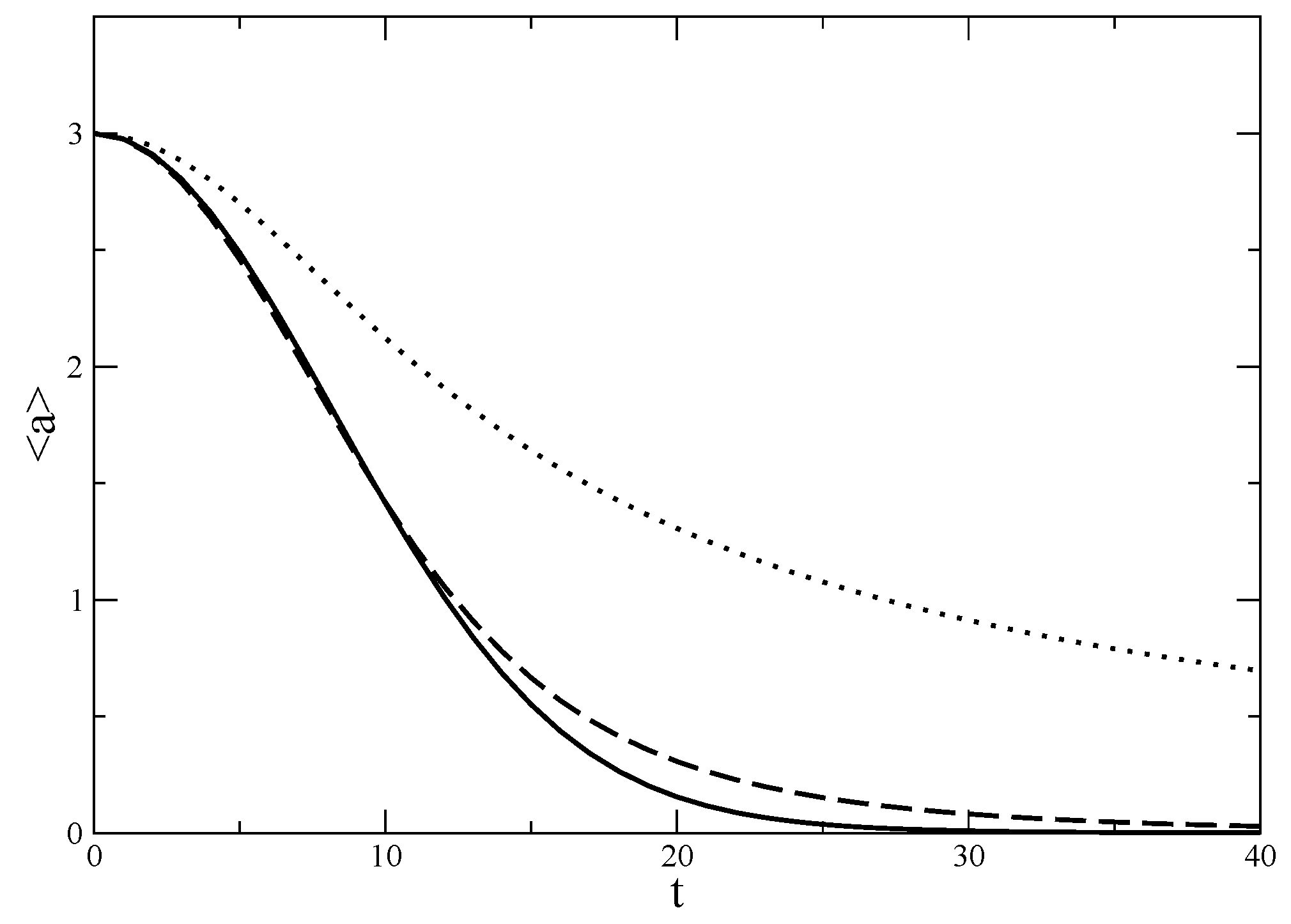
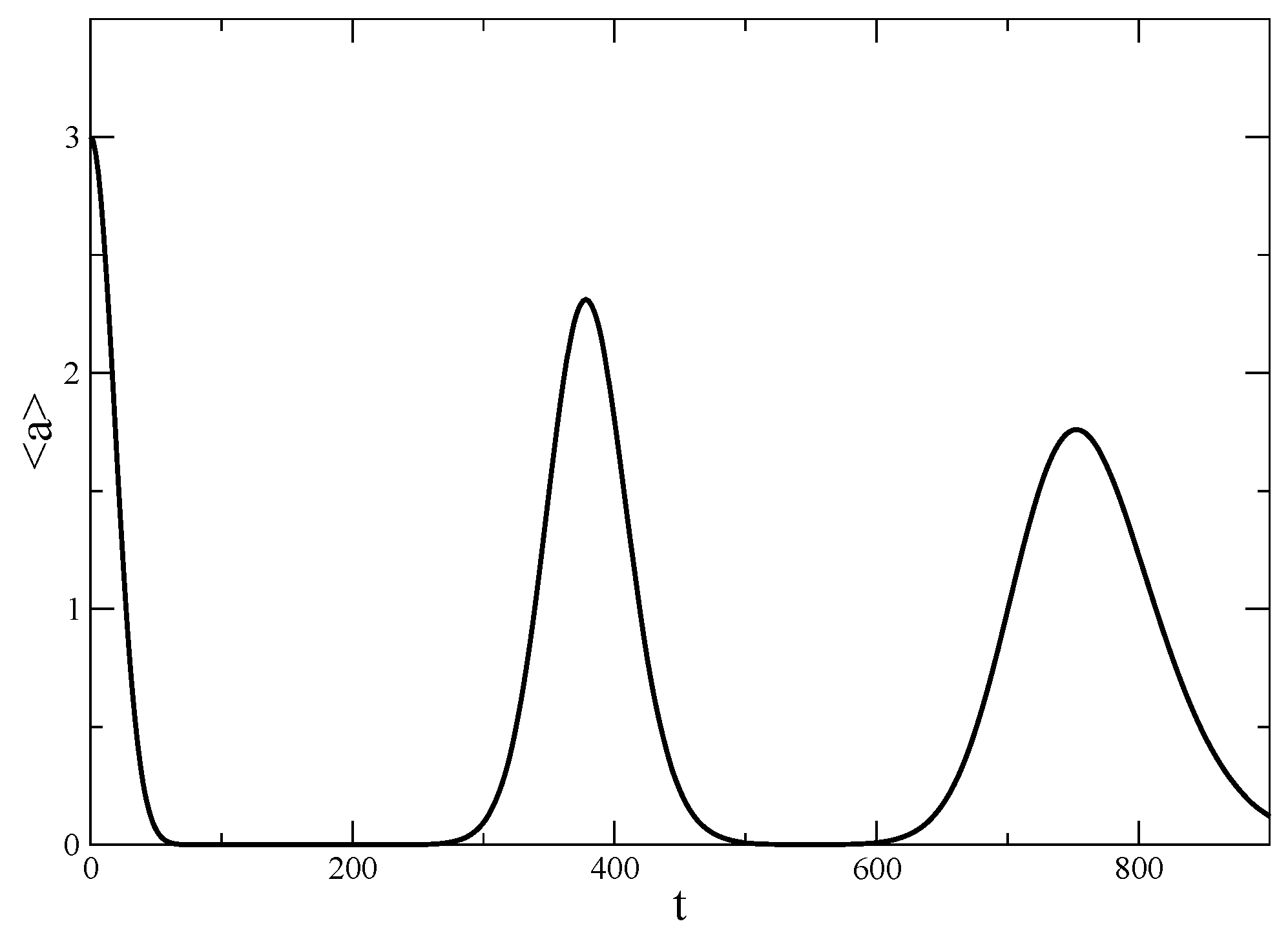
4. Time Evolution of a Coherent State in a Deformed Algebra
5. Conclusions
References
- Macfarlane, A.J. On q-analogues of the quantum harmonic oscillator and the quantum group SU(2)q. J. Phys. A: Math. Gen. 1989, 22, 4581–4588. [Google Scholar] [CrossRef]
- Biedenharn, L.C. The quantum group SUq(2) and a q-analogue of the boson operators. J. Phys. A: Math. Gen. 1989, 22, L873–L878. [Google Scholar] [CrossRef]
- Kulish, P.P.; Damaskinsky, E.V. On the q oscillator and the quantum algebra suq(1,1). J. Phys. A: Math. Gen. 1990, 23, L415–L419. [Google Scholar] [CrossRef]
- Johal, R.S.; Gupta, R.K. Two parameter quantum deformation of U(2) ⊃ U(1) dynamical symmetry and the vibrational spectra of diatomic molecules. Int. J. Mod. Phys. E 1998, 7, 553–557. [Google Scholar] [CrossRef]
- Chang, Z.; Yan, H. Diatomic-molecular spectrum in view of quantum group theory. Phys. Rev. A 1991, 44, 7405–7413. [Google Scholar] [CrossRef] [PubMed]
- Bonatsos, D.; Daskaloyannis, C.; Kolokotronis, P. Coupled q-oscillators as a model for vibrations of polyatomic molecules. J. Chem. Phys. 1997, 106, 605–609. [Google Scholar] [CrossRef]
- Xie, M.; Hou, X.W.; Ma, Z.Q. q-Deformed harmonic oscillators applied to the vibrational spectrum of methane. Chem. Phys. Lett. 1996, 262, 1–7. [Google Scholar] [CrossRef]
- Bonatsos, D.; Drenska, S.B.; Raychev, P.P.; Russev, R.P.; Smirnov, Y.F. Description of superdeformed bands by the quantum algebra SUq(2). J. Phys. G: Nucl. Part. Phys. 1991, 17, L67–L74. [Google Scholar] [CrossRef]
- Raychev, P.P.; Roussev, R.P.; Smirnov, Y.F. The quantum algebra SUq(2) and rotational spectra of deformed nuclei. J. Phys. G: Nucl. Part. Phys. 1990, 16, L137–L141. [Google Scholar] [CrossRef]
- Barbier, R.; Meyer, J.; Kibler, M. A Uqp(u2) model for rotational bands of nuclei. J. Phys. G: Nucl. Part. Phys. 1994, 20, L13–L19. [Google Scholar] [CrossRef]
- Sklyanin, E.K. Some algebraic structures connected with the YangBaxter equation. Funct. Anal. Appl+ 1982, 16, 263–270. [Google Scholar] [CrossRef]
- Daoud, M.; Kibler, M. Statistical mechanics of qp-bosons in D dimensions. Phys. Lett. A 1995, 206, 13–17. [Google Scholar] [CrossRef]
- Lee, C.R.; Yu, J.P. On q-analogues of the statistical distribution. Phys. Lett. A 1990, 150, 63–66. [Google Scholar] [CrossRef]
- The specific heat and equation of state for the q-analogue of the harmonic lattice. Phys. Lett. A 1995, 202, 18–23. [CrossRef]
- Negadi, T.; Kibler, M. A q-deformed Aufbau Prinzip. J. Phys. A: Math. Gen. 1992, 25, L157–L160. [Google Scholar] [CrossRef]
- Kibler, M.; Negadi, T. On the q-analogue of the hydrogen atom. J. Phys. A: Math. Gen. 1991, 24, 5283–5289. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Swamy, P.N. An interacting particles system revisited in the framework of the q-deformed algebra. J. Phys. A: Math. Theor. 2008, 41, 275211:1–275211:11. [Google Scholar] [CrossRef]
- Liu, Y.X.; Sun, C.P.; Yu, S.X.; Zhou, D.L. Semiconductor-cavity QED in high-Q regimes with q-deformed bosons. Phys. Rev. A 2001, 63, 023802. [Google Scholar] [CrossRef]
- Aneva, B. Deformed coherent and squeezed states of multiparticle processes. Eur. Phys. J. C 2003, 31, 403–414. [Google Scholar] [CrossRef]
- Naderi, M.H.; Soltanolkotabi, M.; Roknizadeh, R. Dynamical properties of a two-level atom in three variants of the two-photon q-deformed Jaynes–Cummings model. J. Phys. Soc. Jpn. 2004, 73, 2413–2423. [Google Scholar] [CrossRef]
- Črnugelj, J.; Martinis, M.; Mikuta-Martinis, V. Properties of a deformed Jaynes-Cummings model. Phys. Rev. A 1994, 50, 1785–1791. [Google Scholar] [CrossRef] [PubMed]
- Chaturvedi, S.; Srinivasan, V. Para-Bose oscillator as a deformed Bose oscillator. Phys. Rev. A 1991, 44, 8024–8026. [Google Scholar] [CrossRef] [PubMed]
- Harouni, M.B.; Roknizadeh, R.; Naderi, M.H. Q-deformed description of excitons and associated physical results. J. Phys. B: At. Mol. Opt. Phys. 2009, 42, 095501:1–095501:8. [Google Scholar] [CrossRef]
- Young, C.A.S. q-Deformed supersymmetry and dynamic magnon representations. J. Phys. A: Math. Theor. 2007, 40, 9165–9176. [Google Scholar] [CrossRef]
- Sharma, S.S.; Sharma, N.K.; Zamick, L. An Interacting Particles System Revisited in the Framework of the q-Deformed Algebra. 1995; arXiv:quant-ph/9506036.arXiv.org e-Print archive. http://arxiv.org/abs/quant-ph/9506036v1 (accessed December 17, 2009). [Google Scholar]
- Gardiner, C.W. Particle-number-conserving Bogoliubov method which demonstrates the validity of the time-dependent Gross-Pitaevskii equation for a highly condensed Bose gas. Phys. Rev. A 1997, 56, 1414–1423. [Google Scholar] [CrossRef]
- Girardeau, M.; Arnowitt, R. Theory of many-Boson systems: Pair Theory. Phys. Rev. 1959, 113, 755–761. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E. Ueber das Paulische Aquivalenzverbot. Z. Phys. 1928, 47, 631. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 1940, 58, 1098–1113. [Google Scholar] [CrossRef]
- Lewenstein, M.; You, L. Quantum phase diffusion of a Bose-Einstein condensate. Phys. Rev. Lett. 1996, 77, 3489–3493. [Google Scholar] [CrossRef] [PubMed]
- Blaizot, J.P.; Ripka, G. Quantum Theory of Finite Systems; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Imamoḡlu, A.; Lewenstein, M.; You, L. Inhibition of coherence in trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 78, 2511–2514. [Google Scholar] [CrossRef]
- Villain, P.; Lewenstein, M.; Dum, R.; Castin, Y.; You, L.; Imamoglu, A.; Kennedy, T.A.B. Quantum dynamics of the phase of a Bose ± Einstein condensate. J. Mod. Opt. 1997, 44, 1775. [Google Scholar] [CrossRef]
- Birol, T.; Dereli, T.; Müstecaplioğlu, O.E.; You, L. Coherence lifetimes of excitations in an atomic condensate due to the thin spectrum. Phys. Rev. A: At. Mol. Opt. Phys. 2007, 76, 043616. [Google Scholar] [CrossRef]
- Birol, T.; Müstecaplioğlu, O.E. Effects of zero mode and thin spectrum on the life time of atomic Bose Einstein condensates. Eur. Phys. J. Special Topics 2008, 160, 11–22. [Google Scholar] [CrossRef]
- van Wezel, J.; van den Brink, J.; Zaanen, J. An intrinsic limit to quantum coherence due to spontaneous symmetry Breaking. Phys. Rev. Lett. 2005, 94, 230401. [Google Scholar] [CrossRef] [PubMed]
- van Wezel, J.; van den Brink, J. Spontaneous symmetry breaking in quantum mechanics. Am. J. Phys. 2007, 75, 635–638. [Google Scholar] [CrossRef]
- van Wezel, J.; van den Brink, J. Limit to manipulation of qubits due to spontaneous symmetry breaking. J. Magn. Magn. Mater. 2007, 310, e503–e505. [Google Scholar] [CrossRef]
- Arik, M.; Coon, D.D. Hilbert spaces of analytic functions and generalized coherent states. J. Math. Phys. 1976, 17, 524–527. [Google Scholar] [CrossRef]
- McDermott, R.J.; Solomon, A.I. Squeezed states parametrized by elements of noncommutative algebras. Czech. J. Phys. 1996, 46, 235–241. [Google Scholar] [CrossRef]
- Jaynes, E.; Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Gentile, G. Osservazioni sopra le statistiche intermedie. Nuovo Cim. 1940, 17, 493. [Google Scholar] [CrossRef]
- Gentile, G. Le statistiche intermedie e le proprietà dell’elio liquido. Nuovo Cim. 1942, 19, 109. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Sanchez-Mondragon, J.J. Periodic spontaneous collapse and revival in a simple quantum model. Phys. Rev. Lett. 1980, 44, 1323–1326. [Google Scholar] [CrossRef]

© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Birol, T.; Müstecaplıoğlu, Ö.E. Phase Diffusion of a q-Deformed Oscillator. Symmetry 2009, 1, 240-251. https://doi.org/10.3390/sym1020240
Birol T, Müstecaplıoğlu ÖE. Phase Diffusion of a q-Deformed Oscillator. Symmetry. 2009; 1(2):240-251. https://doi.org/10.3390/sym1020240
Chicago/Turabian StyleBirol, Turan, and Özgür Esat Müstecaplıoğlu. 2009. "Phase Diffusion of a q-Deformed Oscillator" Symmetry 1, no. 2: 240-251. https://doi.org/10.3390/sym1020240
APA StyleBirol, T., & Müstecaplıoğlu, Ö. E. (2009). Phase Diffusion of a q-Deformed Oscillator. Symmetry, 1(2), 240-251. https://doi.org/10.3390/sym1020240



