Abstract
We examine the problem of phase diffusion rate in a U(1) global phase symmetry broken system, from the perspective of q-deformed oscillators where the deformation parameter represents the anharmonicity. It is shown that broken phase symmetry states, described by deformed coherent states, suffer phase diffusion at a rate determined by the deformation parameter. Analytical discussions are given for the case of weak deformations, while detailed numerical results are presented when strong anharmonicity is present in the system.
1. Introduction
For a long time, deformations of Lie algebras and studies of associated quantum groups [1,2,3] had been considered to be a mere mathematical curiosity that may only be useful for developing exactly solvable toy models, especially for statistical and many body physics, where exactly solvable models are rare. In few cases, deformation parameter (q) is treated as a phenomenological fitting parameter to explain some molecular spectral anomalies [4,5,6,7]. A wide literature concerning deformed algebras has developed in the last few decades in different fields of physics. Many studies of nuclear physics involving q-deformations are presented. For instance, rotational spectra of deformed nuclei is calculated [8,9,10] using algebra, which is the q-analogue of the [11]. Statistical mechanics of deformed systems are considered in various contexts too. Examples include the statistical properties of qp-bosons in different dimensions [12], statistical distribution of a gas of q-bosons [13], and specific heat of a q-deformed lattice [14]. Finally, some research in the field of chemical physics have focused quantum groups [15], and the q-analogue of Hydrogen atom is studied in [16]. Quantum groups allow for particles with intermediate statistics, between bosons and fermions, and as such is hardly accepted for an interpretation of a physical event. On the other hand, recent efforts illuminate the link between nonlinear interactions and parastatistical behavior of deformed particles [17,18].
As the status of deformation parameters changed from being phenomenological to microscopical, one intriguing question is how to characterize the life time of such deformed particles and to comprehend how their life time depends on their intermediate quantum statistics. The answer of these questions can be illuminating for efficient manipulations these particles.
We specifically focus on the case of deformed bosons, which are quanta of q-deformed harmonic oscillators [19,20,21,22]. Various physical systems, such as excitons [23], magnons [24], trapped ions [25], or colliding atoms in Bose-Einstein condensates (BECs) [26,27] can be considered to be represented by q-deformed oscillators. In these systems, deformation parameter depends on the microscopical parameters of the system. For example in the case of Frenkel excitons, q depends on the excitation density. As the mean spacing of excitons in the low dimensional, finite size, semiconductor gets smaller relative to the Bohr radius of the excitons, exciton-exciton collisions, or bi-exciton processes, become significant. This attributes to fermionic character to otherwise bosonic excitons. Similar deformation happens to a Bose gas when it falls into Tonks-Girerdau regime where the cold bosonic atoms statistically transmute to demonstrate fermionic behavior.
Without resorting to any quantum group studies, statistical transmutation of bosonic particles can be formulated by various statistics changing transformations, typically Jordan-Wigner map [28] or Holstein-Primakoff [29]. q-Deformed description however is beyond such mathematical tools and has deeper fundamental significance. Deformation parameter is related to the total number of particles or total angular momentum, which are conserved quantities associated with the symmetries of the many body system. Usual treatments of many-body systems violates such conservation rules and thus are symmetry breaking approaches. Violation of a conservation rule leads to quantum fluctuations. Particle number or angular momentum are conjugate to angular variables and thus, recovery of the symmetry can be traced via phase diffusion times. Representing nonlinear interactions via q-deformations can therefore be viewed to be a symmetry recovering approach. q-Deformation and the q-parameter can be compared to the rise of the Goldstone modes with inertial parameters, characterizing the time scales of the recovery of the lost symmetry.
The phase diffusion of interacting bosons is studied in [30] for atomic BECs (Also see [31]). A toy model [32,33] of the phase dynamics in the condensate mode is used for analyzing dephasing rates of coherent, squeezed and thermal-coherent condensates [34,35], together with another dephasing mechanism, the so called thin spectrum [36,37,38].
In this paper we aim to examine the problem of phase diffusion in a more general setting. We assume an arbitrary nonlinear interaction among the particles in a system, that can be described as a q-deformation on a phase symmetry breaking state of the system. We particularly consider a deformed coherent state [39] and our analysis characterize the phase diffusion rate as a function of the strength of anharmonicity. Similar coherent states, as well as squeezed states [19,40], are also studied under Jaynes-Cummings model [41] to investigate the interaction of a deformed radiation field with a two level atom [20,21] or to study emission spectra of excitons in quantum dots [23]. Our analysis, on the other hand, focus on the quantum phase diffusion of a deformed bosonic field per se, due to recovery of a broken symmetry, via self interactions of the field particles.
The paper is organized as follows: In Section 2, we introduce the particular q-deformed algebra we are going to use. In Section 3, the phase diffusion of a coherent state due to interactions is reviewed, using a toy model that reveals the essential physical mechanism of the phase collapse. In Section 4, we calculate the phase diffusion rate of a deformed coherent state. Finally, we conclude in Section 5.
2. The q-Deformed Algebra
A limiting case of the q-deformed algebras present in the literature is the one originally used to introduce the deformed coherent states in [39], which has the q-commutation relation
between the deformed creation and annihilation operators and . Here, right hand side is simply taken to be unity but in general it could be a q dependent operator as well. This more general consideration is not expected give a qualitatively different result for our purpose. Deformation parameter is taken as . For an arbitrary value of q, the eigenvalues of the operator are seen not to be integers (except for 0 and 1), and the following relations hold for its normalized eigenstates:
with
where n is an integer.
The deformed operator can be thought to be obtained from the undeformed operator a, which satisfies , via
where and f is the nonlinearity function. Note that , . The deformed commutation relations discussed above can be obtained by substituting
One interesting fact is that even though the Hilbert space is infinite dimensional, i.e., there are a countable infinity number of eigenstates corresponding to every nonnegative integer n, the eigenvalues are bounded from above, as
except for , when one has the undeformed bosonic harmonic oscillator algebra. This finite upper bound is describing Gentile parastatistical character of the q-bosons [42,43].
Emphasizing the connection between the q parameter and the nonlinear interactions, alternate forms of deformed coherent states can be considered. Analogous to quantum optical generation of squeezed states and sub-Poissonian distributions via nonlinear optical systems, it is possible to deform coherent states to get squeezed states or states with deformed Poisson distributions. A deformed coherent state is introduced as the right eigenstate of the annihilation operator, so
for a complex number. It has the expansion
where
and the q-exponential function is
The deformed coherent state has the deformed-poisson distribution. In the limit ; and , so the distribution reduces to Poisson distribution. This is clearly seen in Figure 1.
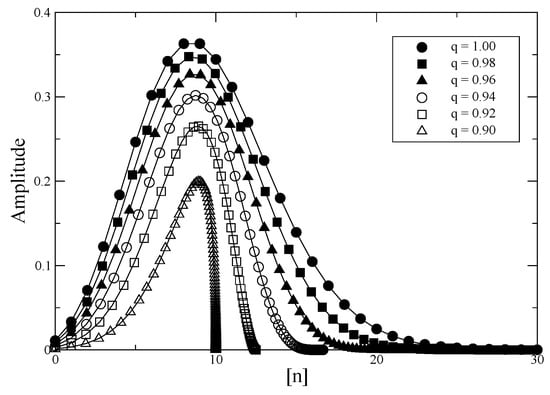
Figure 1.
The (normalized) amplitudes of number states in the coherent state , for different values of the deformation parameter. Note that the horizontal axis is , not n, and each value of n corresponds to a data point in the plot.
For the maximum possible value of is , so the distribution of the amplitudes still looks symmetric. (The deformed Poisson distribution is not significantly different from the undeformed one.) However, for , the maximum possible value of is , and a clear asymmetry is seen because of this upper limit. In this limit the variance is decreasing rapidly with decreasing q.
3. Phase Collapse in a Bosonic System
In this section we consider a bosonic system
in order to see the phase collapse in the context of a toy model [33]. In this (bosonic) limit, we get the ordinary coherent state:
Note that we denote the eigenstates of the number operator by instead of in order to emphasize that we are studying bosons. The time evolution of the harmonic state under the effect of a harmonic Hamiltonian
is trivial to solve, and is well known to give another coherent state, i.e.,
up to an overall phase factor. However, if the Hamiltonian is anharmonic this will not be the case. In order to see this, consider the simplest Hamiltonian
The time dependent expectation value of the annihilation operator a is given by
For small times t, this gives
so the state loses its coherent character at a time scale . However, due to the fact that energy levels have constant spacing, time evolution is periodic and this expectation value will revive after a time . Note that in the thermodynamic limit, where the number of particles , the ratio of revival time to collapse times diverges.
The nonlinearity in the starting Hamiltonian could be represented by a deformation in the form
with . To the first order, nonlinear interaction coefficient is found to be . This suggests that for small values of , can be interpreted as perturbed about the bosonic character. A similar (perturbative) character is observed in [18] for Frenkel excitons for large system sizes. In principle, an actual system may contain additional nonlinear interactions beyond simple two body collisions, which is similar to a Kerr type nonlinearity in optics. Kerr nonlinearity is used to generate optical squeezed states, and higher order nonlinear processes would cause more non-trivial deformations of Poisson distribution. As in the case of phase-number squeezing, one would expect further changes in the phase and number fluctuations, and thus related phase diffusion behavior depending on the amount of deformation or nonlinearity present in the physical system. In the subsequent discussions, more general q-deformation picture will be treated.
4. Time Evolution of a Coherent State in a Deformed Algebra
We now consider the time evolution of a coherent state for under the effect of a harmonic Hamiltonian,
for a bosonic deformation which satisfies
The time dependent annihilation operator in Heisenberg picture is
so its time dependent expectation value is:
Although it is not possible to give an analytical form to this function, we can expand it for small values of get an estimate about its time evolution. Substituting
and
one gets
The form of this lowest nontrivial order terms look familiar to the corresponding ones for interacting bosons. Roughly terms will contribute to the sum. The spacing between frequencies of each term is . So, for small time scales, the expectation value of the order parameter will decay with a rate proportional to the reciprocal of a collapse time . Of course this is a very crude approximation, and the simple small t expansion used in the previous section does not apply as it requires us to include higher order terms in .
Nevertheless, it is shown that the coherent states, which are defined as the right eigenstates of the annihilation operator, do not stay coherent under time evolution due to a simple harmonic Hamiltonian for a general value of q. The decay rate depends on the simplest parameters, the variance of the undeformed Poisson distribution , Planck constant ℏ, the energy scale in the Hamiltonian , and the parameter which, in a way, quantifies how much the commutation relations are deformed. (Here, is the expectation value of the number operator for the coherent state.) We give numerical plots of time evolution in Figure 2 and Figure 3 to show how with increasing values of the collapse gets faster, and for larger values when higher order terms become important this no longer is the case. This happens at values of where the the second order term in the difference (which is present in the exponential for the expression of ) becomes important, i.e., around . For the plots, we have used a relatively small number of atoms, , so that the ratio of revival and collapse times is small enough to see the long time behavior clearly on one plot. In this particular case higher order terms become important at at the order of . In Figure 2 increasing values of correspond to larger nonlinearity and hence faster decay. However, in Figure 3 it is seen that for even larger values of this is not the case. Even though larger corresponds to larger nonlinearity, the variation of decreases with increasing as clearly seen in Figure 1. In this range this decrease dominates and decay gets slower for larger .
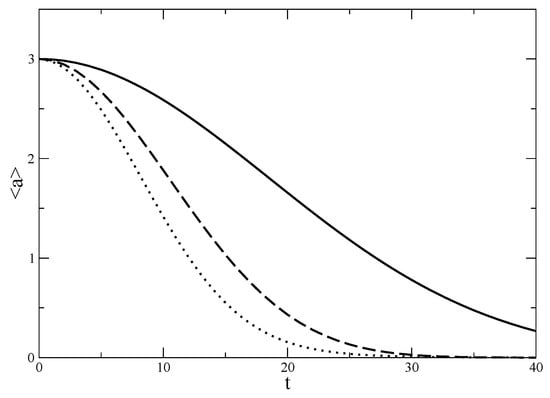
Figure 2.
Expectation value of the annihilation operator versus time in units of , where the initial state is a coherent state with . Value of is for solid, for dashed and for dotted line.
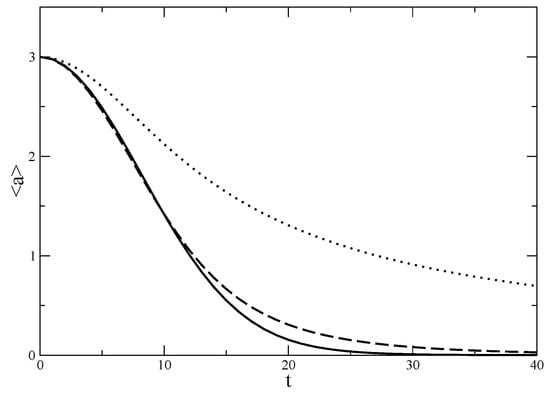
Figure 3.
Expectation value of the annihilation operator versus time in units of , where the initial state is a coherent state with . Value of is for solid, for dashed and for dotted line.
Two distinct behaviors of the coherence time with the deformation parameter observed here indicate a nontrivial effect of nonlinearities and some beautiful physics. The nonlinearity in the Hamiltonian helps to recover the broken symmetry. As deformation increases, higher order nonlinear processes also influence the transfer of quantum fluctuations between the amplitude and the phase. It is necessary to examine them separately to assess their roles in quantum noise redistribution more clearly. However, the effect we see here is more strongly related to the initial noise distribution. For a larger deformation, the system we examine starts with more phase broadened initial state to evolve under nonlinear Hamiltonian. Kerr type interaction is more forgiving for those less phase coherent states and allows them to be longer lived. This observation reveals that with increasing deformation we have two competing effects. One is the increase of efficiency of Kerr type squeezing of number fluctuations, or the quicker recovery of broken symmetry, while the other is to prepare an initial state less prone to life shortening effects of phase diffusion.
Finally, Figure 4 is plotted in order to show that even though there is some revival, it is not exact. The simple reason for this is that the energy difference between the levels is different and monotonously goes to zero as . One common example to this lossless but irreversible behavior is observed in the Jaynes Cummings Model [44], which is intrinsically and strongly anharmonic. Our interpretation of q-deformation with intrinsic nonlinearities shines some light on the irreversible dynamics and eventual fate of the broken symmetry, which is the recovery of it. Though the system enjoys some brief moments of revivals, it can be seen that these are progressively lower in amplitude and broader. That means, only partial recovery of the initial phase coherence is possible, and longer lifetime of the revived states occurs progressively.
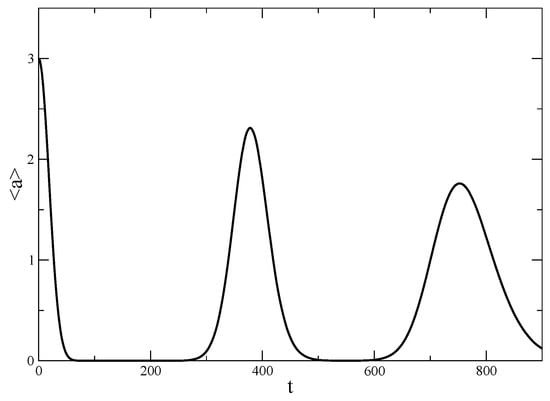
Figure 4.
Expectation value of the annihilation operator versus time in units of , where the initial state is a coherent state with and , for larger times. Revival is observed, but it is not exact so that the expectation value does not go up to its initial value.
5. Conclusions
Coherent states, which are considered as variational ground states in many different contexts, do not respect the phase symmetry of Hamiltonians they are used for. In bosonic systems, any anharmonicity causes the loss of the coherent nature in a time scale inversely proportional to the strength of the anharmonicity. A q-deformed harmonic oscillator, though seemingly harmonic, necessarily has an underlying anharmonicity quantified by the deviation of the parameter q from 1. Therefore deformed coherent state must undergo phase diffusion even though the deformed Hamiltonian involves no terms other than . We have shown that this indeed is the case, and the collapse time of the expectation value of the annihilation operator, which is nonzero for coherent states, is inversely proportional to .
References
- Macfarlane, A.J. On q-analogues of the quantum harmonic oscillator and the quantum group SU(2)q. J. Phys. A: Math. Gen. 1989, 22, 4581–4588. [Google Scholar] [CrossRef]
- Biedenharn, L.C. The quantum group SUq(2) and a q-analogue of the boson operators. J. Phys. A: Math. Gen. 1989, 22, L873–L878. [Google Scholar] [CrossRef]
- Kulish, P.P.; Damaskinsky, E.V. On the q oscillator and the quantum algebra suq(1,1). J. Phys. A: Math. Gen. 1990, 23, L415–L419. [Google Scholar] [CrossRef]
- Johal, R.S.; Gupta, R.K. Two parameter quantum deformation of U(2) ⊃ U(1) dynamical symmetry and the vibrational spectra of diatomic molecules. Int. J. Mod. Phys. E 1998, 7, 553–557. [Google Scholar] [CrossRef]
- Chang, Z.; Yan, H. Diatomic-molecular spectrum in view of quantum group theory. Phys. Rev. A 1991, 44, 7405–7413. [Google Scholar] [CrossRef] [PubMed]
- Bonatsos, D.; Daskaloyannis, C.; Kolokotronis, P. Coupled q-oscillators as a model for vibrations of polyatomic molecules. J. Chem. Phys. 1997, 106, 605–609. [Google Scholar] [CrossRef]
- Xie, M.; Hou, X.W.; Ma, Z.Q. q-Deformed harmonic oscillators applied to the vibrational spectrum of methane. Chem. Phys. Lett. 1996, 262, 1–7. [Google Scholar] [CrossRef]
- Bonatsos, D.; Drenska, S.B.; Raychev, P.P.; Russev, R.P.; Smirnov, Y.F. Description of superdeformed bands by the quantum algebra SUq(2). J. Phys. G: Nucl. Part. Phys. 1991, 17, L67–L74. [Google Scholar] [CrossRef]
- Raychev, P.P.; Roussev, R.P.; Smirnov, Y.F. The quantum algebra SUq(2) and rotational spectra of deformed nuclei. J. Phys. G: Nucl. Part. Phys. 1990, 16, L137–L141. [Google Scholar] [CrossRef]
- Barbier, R.; Meyer, J.; Kibler, M. A Uqp(u2) model for rotational bands of nuclei. J. Phys. G: Nucl. Part. Phys. 1994, 20, L13–L19. [Google Scholar] [CrossRef]
- Sklyanin, E.K. Some algebraic structures connected with the YangBaxter equation. Funct. Anal. Appl+ 1982, 16, 263–270. [Google Scholar] [CrossRef]
- Daoud, M.; Kibler, M. Statistical mechanics of qp-bosons in D dimensions. Phys. Lett. A 1995, 206, 13–17. [Google Scholar] [CrossRef]
- Lee, C.R.; Yu, J.P. On q-analogues of the statistical distribution. Phys. Lett. A 1990, 150, 63–66. [Google Scholar] [CrossRef]
- The specific heat and equation of state for the q-analogue of the harmonic lattice. Phys. Lett. A 1995, 202, 18–23. [CrossRef]
- Negadi, T.; Kibler, M. A q-deformed Aufbau Prinzip. J. Phys. A: Math. Gen. 1992, 25, L157–L160. [Google Scholar] [CrossRef]
- Kibler, M.; Negadi, T. On the q-analogue of the hydrogen atom. J. Phys. A: Math. Gen. 1991, 24, 5283–5289. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Swamy, P.N. An interacting particles system revisited in the framework of the q-deformed algebra. J. Phys. A: Math. Theor. 2008, 41, 275211:1–275211:11. [Google Scholar] [CrossRef]
- Liu, Y.X.; Sun, C.P.; Yu, S.X.; Zhou, D.L. Semiconductor-cavity QED in high-Q regimes with q-deformed bosons. Phys. Rev. A 2001, 63, 023802. [Google Scholar] [CrossRef]
- Aneva, B. Deformed coherent and squeezed states of multiparticle processes. Eur. Phys. J. C 2003, 31, 403–414. [Google Scholar] [CrossRef]
- Naderi, M.H.; Soltanolkotabi, M.; Roknizadeh, R. Dynamical properties of a two-level atom in three variants of the two-photon q-deformed Jaynes–Cummings model. J. Phys. Soc. Jpn. 2004, 73, 2413–2423. [Google Scholar] [CrossRef]
- Črnugelj, J.; Martinis, M.; Mikuta-Martinis, V. Properties of a deformed Jaynes-Cummings model. Phys. Rev. A 1994, 50, 1785–1791. [Google Scholar] [CrossRef] [PubMed]
- Chaturvedi, S.; Srinivasan, V. Para-Bose oscillator as a deformed Bose oscillator. Phys. Rev. A 1991, 44, 8024–8026. [Google Scholar] [CrossRef] [PubMed]
- Harouni, M.B.; Roknizadeh, R.; Naderi, M.H. Q-deformed description of excitons and associated physical results. J. Phys. B: At. Mol. Opt. Phys. 2009, 42, 095501:1–095501:8. [Google Scholar] [CrossRef]
- Young, C.A.S. q-Deformed supersymmetry and dynamic magnon representations. J. Phys. A: Math. Theor. 2007, 40, 9165–9176. [Google Scholar] [CrossRef]
- Sharma, S.S.; Sharma, N.K.; Zamick, L. An Interacting Particles System Revisited in the Framework of the q-Deformed Algebra. 1995; arXiv:quant-ph/9506036.arXiv.org e-Print archive. http://arxiv.org/abs/quant-ph/9506036v1 (accessed December 17, 2009). [Google Scholar]
- Gardiner, C.W. Particle-number-conserving Bogoliubov method which demonstrates the validity of the time-dependent Gross-Pitaevskii equation for a highly condensed Bose gas. Phys. Rev. A 1997, 56, 1414–1423. [Google Scholar] [CrossRef]
- Girardeau, M.; Arnowitt, R. Theory of many-Boson systems: Pair Theory. Phys. Rev. 1959, 113, 755–761. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E. Ueber das Paulische Aquivalenzverbot. Z. Phys. 1928, 47, 631. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 1940, 58, 1098–1113. [Google Scholar] [CrossRef]
- Lewenstein, M.; You, L. Quantum phase diffusion of a Bose-Einstein condensate. Phys. Rev. Lett. 1996, 77, 3489–3493. [Google Scholar] [CrossRef] [PubMed]
- Blaizot, J.P.; Ripka, G. Quantum Theory of Finite Systems; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Imamoḡlu, A.; Lewenstein, M.; You, L. Inhibition of coherence in trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 78, 2511–2514. [Google Scholar] [CrossRef]
- Villain, P.; Lewenstein, M.; Dum, R.; Castin, Y.; You, L.; Imamoglu, A.; Kennedy, T.A.B. Quantum dynamics of the phase of a Bose ± Einstein condensate. J. Mod. Opt. 1997, 44, 1775. [Google Scholar] [CrossRef]
- Birol, T.; Dereli, T.; Müstecaplioğlu, O.E.; You, L. Coherence lifetimes of excitations in an atomic condensate due to the thin spectrum. Phys. Rev. A: At. Mol. Opt. Phys. 2007, 76, 043616. [Google Scholar] [CrossRef]
- Birol, T.; Müstecaplioğlu, O.E. Effects of zero mode and thin spectrum on the life time of atomic Bose Einstein condensates. Eur. Phys. J. Special Topics 2008, 160, 11–22. [Google Scholar] [CrossRef]
- van Wezel, J.; van den Brink, J.; Zaanen, J. An intrinsic limit to quantum coherence due to spontaneous symmetry Breaking. Phys. Rev. Lett. 2005, 94, 230401. [Google Scholar] [CrossRef] [PubMed]
- van Wezel, J.; van den Brink, J. Spontaneous symmetry breaking in quantum mechanics. Am. J. Phys. 2007, 75, 635–638. [Google Scholar] [CrossRef]
- van Wezel, J.; van den Brink, J. Limit to manipulation of qubits due to spontaneous symmetry breaking. J. Magn. Magn. Mater. 2007, 310, e503–e505. [Google Scholar] [CrossRef]
- Arik, M.; Coon, D.D. Hilbert spaces of analytic functions and generalized coherent states. J. Math. Phys. 1976, 17, 524–527. [Google Scholar] [CrossRef]
- McDermott, R.J.; Solomon, A.I. Squeezed states parametrized by elements of noncommutative algebras. Czech. J. Phys. 1996, 46, 235–241. [Google Scholar] [CrossRef]
- Jaynes, E.; Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Gentile, G. Osservazioni sopra le statistiche intermedie. Nuovo Cim. 1940, 17, 493. [Google Scholar] [CrossRef]
- Gentile, G. Le statistiche intermedie e le proprietà dell’elio liquido. Nuovo Cim. 1942, 19, 109. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Sanchez-Mondragon, J.J. Periodic spontaneous collapse and revival in a simple quantum model. Phys. Rev. Lett. 1980, 44, 1323–1326. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.