Abstract
We analyse in a common framework the properties of the Voronoi tessellations resulting from regular 2D and 3D crystals and those of tessellations generated by Poisson distributions of points, thus joining on symmetry breaking processes and the approach to uniform random distributions of seeds. We perturb crystalline structures in 2D and 3D with a spatial Gaussian noise whose adimensional strength is α and analyse the statistical properties of the cells of the resulting Voronoi tessellations using an ensemble approach. In 2D we consider triangular, square and hexagonal regular lattices, resulting into hexagonal, square and triangular tessellations, respectively. In 3D we consider the simple cubic (SC), body-centred cubic (BCC), and face-centred cubic (FCC) crystals, whose corresponding Voronoi cells are the cube, the truncated octahedron, and the rhombic dodecahedron, respectively. In 2D, for all values α>0, hexagons constitute the most common class of cells. Noise destroys the triangular and square tessellations, which are structurally unstable, as their topological properties are discontinuous in α=0. On the contrary, the honeycomb hexagonal tessellation is topologically stable and, experimentally, all Voronoi cells are hexagonal for small but finite noise with α<0.12. Basically, the same happens in the 3D case, where only the tessellation of the BCC crystal is topologically stable even against noise of small but finite intensity. In both 2D and 3D cases, already for a moderate amount of Gaussian noise (α>0.5), memory of the specific initial unperturbed state is lost, because the statistical properties of the three perturbed regular tessellations are indistinguishable. When α>2, results converge to those of Poisson-Voronoi tessellations. In 2D, while the isoperimetric ratio increases with noise for the perturbed hexagonal tessellation, for the perturbed triangular and square tessellations it is optimised for specific value of noise intensity. The same applies in 3D, where noise degrades the isoperimetric ratio for perturbed FCC and BCC lattices, whereas the opposite holds for perturbed SCC lattices. This allows for formulating a weaker form of the Kelvin conjecture. By analysing jointly the statistical properties of the area and of the volume of the cells, we discover that also the cells shape heavily fluctuates when noise is introduced in the system. In 2D, the geometrical properties of n-sided cells change with α until the Poisson-Voronoi limit is reached for α>2; in this limit the Desch law for perimeters is shown to be not valid and a square root dependence on n is established, which agrees with exact asymptotic results. Anomalous scaling relations are observed between the perimeter and the area in the 2D and between the areas and the volumes of the cells in 3D: except for the hexagonal (2D) and FCC structure (3D), this applies also for infinitesimal noise. In the Poisson-Voronoi limit, the anomalous exponent is about 0.17 in both the 2D and 3D case. A positive anomaly in the scaling indicates that large cells preferentially feature large isoperimetric quotients. As the number of faces is strongly correlated with the sphericity (cells with more faces are bulkier), in 3D it is shown that the anomalous scaling is heavily reduced when we perform power law fits separately on cells with a specific number of faces.
Keywords:
Voronoi tessellation; numerical simulations; random geometry; symmetry break; topological stability; Poisson point process; Desch law; Lewis law; cubic crystals; simple cubic; face-centred cubic; body-centred cubic; Gaussian noise; anomalous scaling; isoperimetric quotient; fluctuations; Kelvin's conjecture; Kepler's conjecture; Kendall’s conjecture 1. Introduction
A Voronoi tessellation [1,2] is a partitioning of an Euclidean N-dimensional space defined in terms of a given discrete set of points . For almost any point there is one specific point which is closest to a. Some point a may be equally distant from two or more points of X. If X contains only two points, x1 and x2, then the set of all points with the same distance from x1 and x2 is a hyperplane, which has codimension 1. The hyperplane bisects perpendicularly the segment from x1 and x2. In general, the set of all points closer to a point than to any other point , is the interior of a convex (N-1)-polytope usually called the Voronoi cell for xi. The set of the (N-1)-polytopes Πi, each corresponding to - and containing - one point , is the Voronoi tessellation corresponding to X. Extensions to the case of non-Euclidean spaces have also been presented [3,4].
Since Voronoi tessellations boil up to being optimal partitionings of the space resulting from a set of generating points, they define a natural discrete mathematical measure, and have long been considered for applications in several research areas, such as telecommunications [5], biology [6], astronomy [7], forestry [8], atomic physics [9], metallurgy [10], polymer science [11], materials science [12,13], and biophysics [14]. In condensed matter physics, the Voronoi cell of the lattice point of a crystal is known as the Wigner-Seitz cell, whereas the Voronoi cell of the reciprocal lattice point is the Brillouin zone [15,16]. Voronoi tessellations have been used for performing structure analysis for crystalline solids and supercooled liquids [17,18], for detecting glass transitions [19], for emphasizing the geometrical effects underlying the vibrations in the glass [20], and for performing detailed and efficient electronic calculations [21,22] Moreover, a connection has been recently established between the Rayleigh-Bènard convective cells and Voronoi cells, with the hot spots (locations featuring the strongest upward motion of hot fluid) of the former basically coinciding with the points generating the Voronoi cells, and the locations of downward motion of cooled fluid coinciding with the sides of the Voronoi cells [23]. Finally, Voronoi tessellations are a formidable tool for performing arbitrary space integration of sparse data, without adopting the typical procedure of adding spurious information, as in the case of linear or splines interpolations. In particular, in a geophysical context, Voronoi tessellations have been widely used to analyse spatially distributed observational or model output data [24,25,26]. Actually, in was in this context that Thiessen and Alter, with the purpose of computing river basins water balance from irregular and sparse rain observations, discovered independently for the 2D case the tessellation introduced by Voronoi just few years earlier [27].
The theoretical investigation of the statistical properties of general N-dimensional Voronoi tessellations has proved to be a rather hard task, so that direct numerical simulation is the most extensively adopted investigative approach. The quest for achieving low computational cost for actually evaluating the Voronoi tessellation of a given discrete set of points X is ongoing and involves an extensive research performed within various scientific communities [28,29,30,31,32].
A great deal of theoretical and computational work has focused on the more specific and tractable problem of studying the statistical properties of Poisson-Voronoi tessellations. These are Voronoi tessellations obtained starting from a random set of points X generated as output of a homogeneous Poisson point process. This problem has a great relevance at practical level because it corresponds, e.g., to studying crystal aggregates with random nucleation sites and uniform growth rates. Exact results concerning the mean statistical properties of the interface area, inner area, number of vertices, etc. of the Poisson-Voronoi tessellations have been obtained for Euclidean spaces [33,34,35,36,37,38,39]; an especially impressive account is given in [40]. Moreover, the Kendall’s conjecture has recently been proved, i.e. large cells, asymptotically, tend have to a spherical shape [41,42,43]. Several computational studies on 2D and 3D spaces have confirmed the theoretical findings, and, moreover, have shown that both 2-parameter [44] and 3-parameter [45] gamma distributions fit up to a high degree of accuracy the empirical probability distribution functiona (pdfs) of several geometrical characteristics of the cells [46,47]. The ab-initio derivation of the pdf of the geometrical properties of Poisson-Voronoi tessellations have not been yet obtained, except in asymptotic regimes [48], which are, surprisingly, not compatible with the gamma distributions family.
In recent years, various studies have focused on the geometrical properties of Voronoi tessellations resulting from non strictly Poissonian random processes. In particular, given the obvious relevance in terms of applications, such as for packing problems, a great deal of attention has been directed towards tessellations resulting from points which are randomly distributed in the space and are subjected to a minimal point-to-point distance δ - a sort of hard-core nuclei hypothesis [46,49]. Whereas the δ=0 case corresponds to the Poisson-Voronoi situation, it is observed that by increasing δ the degree of randomness of the tessellation is decreased - the pdfs of the statistical properties of the geometrical characteristics become more and more peaked - until for a certain critical δ-value a regular tessellation, which in the 2D case is the hexagonal honeycomb one, is obtained. In any case, it is found that the gamma distributions provide excellent fits for a very large range of values of δ [46].
In this paper we approach the problem of understanding general properties of the Voronoi tessellations by joining on the two extreme situations of perfectly deterministic, regular tessellation, to the tessellation resulting from a set of points X generated with a Poisson point process.
We first consider three regular polygonal tessellations of the plane, the honeycomb hexagonal, the square, and triangular tessellations. They are obtained by setting the points xi as vertices of regular triangles, squares, and hexagons, respectively. Hexagonal tessellation is optimal both in terms of perimeter-to-area ratio and in terms of cost [50,51]. The extremal properties of such a tessellation are clearly highlighted in [52], where it is noted that a Gibbs system of repulsive charges in 2D arranges spontaneously for low temperatures (freezes) as a regular hexagonal crystal. Moreover, the fact that Rayleigh-Bènard convective cells may generate an hexagonal tessellation [23] is related to the fact that, under specific parameters ranges, the stationary solutions of the 2D Swift-Hohemberg equation generate naturally hexagonal tessellations [53].
Moreover, we analyse three cubic crystals covering the 3D Euclidean space, namely the simple cubic (SC), the face-centred cubic (FCC) and the body-centred cubic (BCC) lattices [15]. The corresponding space-filling Voronoi cells of such crystals are the cube, the rhombic dodecahedron, and the truncated octahedron. The cubic crystal system is one of the most common crystal systems found in elemental metals, and naturally occurring crystals and minerals. These crystals feature truly extraordinary geometrical properties. The cube is the only space-filling regular solid. The FCC (together with the Hexagonal Close Packed structure) features the largest possible packing fraction: the related 1611 Kepler’s conjecture has been recently proved by [54] The Voronoi cell of BCC has been conjectured by Kelvin in 1887 as being the space-filling cell with the smallest surface to volume ratio, and only recently two counter-examples have been given in [55] and [56]. Interestingly, Gabbrielli [56] found a novel space-filling cell by imaginatively looking at the patterns generated as stationary solution of the 3D Swift-Hohenberg equation, thus methodologically mimicking the more usual 2D case. Finally, the truncated octahedron is conjectured to have the lowest cost among all 3D space-filling cells [51]. These mathematical properties correspond to very important physical features. Because of its low density, basically due to the low packing faction, the SC system has a high energy structure and is rare in nature, and it is found only in the alpha-form of Po. The BCC is a more compact system and have a low energy structure, is therefore more common in nature. Examples of BCC structures include Fe, Cr, W, and Nb. Finally, thanks to its extremal properties in terms of packing fraction and the resulting high density, FCC crystals are fairly common and specific examples include Pb, Al, Cu, Au and Ag.
The extremal properties in terms of surface–to-area ratio of the hexagonal (in 2D) and truncated octahedral (in 3D) tessellations imply that they may serve as optimal tool for achieving data compression [57]. Another similarity of these two tessellations is related to their topologically stability with respect to infinitesimal perturbations to the position of the lattice points [58].
Using an ensemble-based approach, we study the break-up of the symmetry of the 2D and 3D crystals and quantitatively evaluate how the statistical properties of the resulting Voronoi cells change when we perturb the positions of the lattice points xi, with a spatially homogeneous Gaussian noise of parametrically controlled strength. The strength of considered perturbation ranges up to the point where typical displacements become larger than the lattice unit vector, which basically leads to the limiting case of the Poisson-Voronoi process.
Our paper is organized as follows. In Section 2 we discuss some basic properties of the Voronoi tessellations in 2D and in 3D, present some exact results, and describe the strategy and the concepts behind the numerical simulations. In Section 3 we review extensively the main results presented in [59] for 2D systems and in [60] for 3D systems, and propose some novel findings and concepts. In Section 4 we summarize and discuss our findings and present some perspectives for future work.
2. Data and Methods
2.a. Scaling Properties of Voronoi tessellations
In this paper we consider perfect crystals, crystals with random dislocations, and sparse points resulting from a spatially homogeneous Poisson process. Perfect crystals are obtained when the pdf of the random point process can be expressed as a sum of Dirac masses obeying a discrete translational symmetry. Crystals with random dislocations are periodical in the statistical sense since the pdf of the point-process is a non-singular Lebesgue measurable function obeying discrete translational symmetry. Finally, the pdf of the homogeneous Poisson point process is constant in space. In general, we then consider a random point process characterized by a spatially homogeneous coarse-grained intensity , such that the expectation value of the number of points xi in a generic region Γ∈Pn is , where is the Lebesgue n-measure of Γ, whereas the fluctuations in the number of points are . If , we are in the thermodynamic limit and boundary effects are negligible, so that the number of cells of the Voronoi tessellation resulting from the set of points xi and contained inside Γ is .
Using scaling arguments [59,60], one obtains that in all cases considered the statistical properties of the Voronoi tessellation are intensive, so that the point density can be scaled to unity, or, alternatively, the domain can be scaled to the Cartesian n-cube . We will stick to the second approach. We then define () as the mean value (standard deviation) of the variable Y over the cells for the single realization of the random process, whereas the expression (), indicates the ensemble mean (standard deviation) of the random variable E.
We have that , where V is the n-volume of the Voronoi cell, , where A is the n-surface area of the Voronoi cell. The proportionality constants depend of the specific random point process considered. Therefore, by multiplying the ensemble mean estimators of the mean and standard deviation of the various geometrical properties of the Voronoi cells times the appropriate power of , we obtain universal functions.
In the 2D case, we analyse n, P, and A, corresponding to the number of sides, the perimeter and the area of each Voronoi cell, respectively. In the 3D case, we focus our interest on f, A, and V, corresponding to the number of faces, the surface area and the volume of each Voronoi cell, respectively.
2.b. Some Exact Results
2.b.1. 2D Tessellations
If we consider a regular square grid of points xi with sides , the Voronoi cell Πi corresponding to xi is given by the square centred in xi with the same side length and orientation as the xi grid, so that the grid of the vertices yi of the tessellation is translated with respect to the xi grid by l/2 in both orthogonal directions (the verse is not relevant). Therefore, the vertices of the Voronoi tessellation resulting from the points yi are nothing but the initial points xi. If , we will have points – and corresponding square Voronoi cells - in . Similarly, a regular hexagonal honeycomb tessellation featuring points and corresponding regular Voronoi cells in is obtained by using a grid of points xi set as regular triangles with sides , where the angle between and is 60°. Finally, the regular triangular tessellation featuring a density of Voronoi cells derives from a regular grid of points xi set as hexagons with sides , again with an angle of 60° between the and . Therefore, the regular hexagonal and the regular triangular tessellation are conjugate via Voronoi tessellation.
In the case of these crystalline structures, all cells are alike, and given the deterministic nature of the tessellation, there are no fluctuations within the ensemble, so that taking ensemble averages is immaterial. It is easy to deduce the properties of the Voronoi cells from basic Euclidean geometry:
- for square tessellation, we have , ;for honeycomb tessellation, we have and ,
- for triangular tessellation, we have and .
The standard isoperimetric ratio , which is unity for circles, is , , , for square, honeycomb and triangular tessellation, respectively.
On the other end of the “spectrum of randomness”, when considering Poisson-Voronoi tessellations, we have that the ensemble mean – where the statistics is computed over all realizations of the random process – of the number of sides of the Voronoi cells inside Γ is , which agrees with the general Euler theorem on planar graphs with trivalent vertices. Additionally, one obtains that [40]. Note that the regular square and triangular tessellations do not obey the Euler theorem, as they feature non-generic tetravalent and hexavalent vertices. Moreover, it can be proved that the ensemble mean of the average perimeter of a Voronoi cell is and the ensemble mean of its standard deviation is . Finally, whereas by definition we have , direct numerical calculations show that the ensemble mean of the standard deviation of the area of the cells is [40].
2.b.2. 3D Tessellations
Since each Voronoi cell is, by construction, convex, its vertices (v), edges (e), and faces (f) are connected by the simplified Euler-Poincare formula for 3D polyhedra . Moreover, in a generic solid vertices are trivalent (i.e. given by the intersection of three edges), so that , which implies that , so that the knowledge of the number of vertices of a cell provides a rather complete information about the polyhedron. Another general result is that in each cell the average number (n) of sides of each face is , which marks a clear difference with respect to the plane case, where the Euler theorem applies. For the detailed description of how geometrically construct the SC, BCC, and FCC cubic crystals, we refer the reader to [15]. Since we impose a total of lattice points per unit volume and corresponding Voronoi cells in , the length of the side of the cubes of the SC, BCC, and FCC crystals are , , and , respectively. Basic Euclidean geometry allows us to fully analyse these structures. The cells of the Voronoi tessellation of the SC crystal are cubes (having 12 edges, six faces, eight trivalent vertices) of side length and total surface area . The cells of the Voronoi tessellation of the BCC crystal are truncated octahedra (having 36 edges, 14 faces, 24 trivalent vertices) of side length and total surface area . The cells of the Voronoi tessellation of the FCC crystal are rhombic dodecahedra (having 24 edges, 12 faces, six trivalent vertices, eight tetravalent vertices) of side length and total surface area . The standard isoperimetric quotient , which measures in non-dimensional units the surface-to-volume ratio of a solid (Q = 1 for a sphere), is 0.5236, 0.7534, and 0.7405 for the SC, BCC, and FCC structures, respectively.
Exact results have been obtained on Poisson-Voronoi tessellations using rather cumbersome analytical tools. We report some of the results discussed in [40]:
- the average number of vertices is and its standard deviation is ; exploiting the Euler-Poincare relation plus the genericity property, we obtain , , , and ;
- the average surface area is (with here indicating the usual Gamma function), and its standard deviation is ;
- the average volume is, by definition, , whereas its standard deviation is .
2.c. Simulations
For all 2D and 3D crystals we introduce a symmetry-breaking homogeneous ε-Gaussian noise, which randomises the position of the points xi about their deterministic positions with a spatial variance . We define , thus expressing the mean squared displacement as a fraction of the natural squared length scale, where in the 2D case and in the 3D case. When ensembles are considered, the probability distribution of the points xi is still periodic. The parameter can be loosely interpreted as a normalized temperature of the lattice. By definition, if we are in the deterministic case. We study how the statistical properties of the resulting Voronoi cells change with α, covering the whole range going from the symmetry breaking, occurring when α becomes positive, up to the progressively more and more uniform distribution of xi, obtained when , so that the distributions of nearby points xi overlap more and more significantly. The actual simulations are performed by applying, within a customised routine, the MATLAB7.0® functions voronoin.m and convhulln.m, which implement the algorithm introduced in [31], to a set of points xi generated according to the considered random process. The function voronoin.m associates to each point the vertices of the corresponding Voronoi cell and its volume, whereas the function convhulln.m is used to generate the convex hull of the cell.
In the 2D case, we actually perform our statistical analyses by considering M=1,000 members of the ensemble of Voronoi tessellations generated for each value of α ranging from 0 to 5 with step 0.01, plus additional values aimed at checking the weak- and high-noise limits. Tessellation has been performed starting from points xi () belonging to the square , but only the cells belonging to have been considered for evaluating the statistical properties. Since the external shell having a thickness of 0.2 comprises about 20 layers of cells, boundary effects due to one-step Brownian diffusion of the points nearby the boundaries, which, in the case of large values of α, cause depletion, become negligible. Another set of simulations is performed by computing an ensemble of 1,000 Poisson-Voronoi tessellations generated starting from a set of uniformly randomly distributed points per unit volume.
In the 3D case, the statistical analysis is performed over M=100 ensemble members of Voronoi tessellations with ρ0 = 1,000,000 generated for all values of ranging from 0 to 2 with step 0.01, plus additional values aimed at checking the weak- and high-noise limits, and the Poisson-Voronoi case. Similarly to the 2D case, tessellation has been performed starting from points xi belonging to the square , but only the cells belonging to have been considered.
A serious complication arises for the 3D case, where the convex hull is given in terms of 2-simplices, i.e. triangles. Whereas this information is sufficient for computing the total surface area of the cell, an additional step is needed in order to define the topological properties of the cell. In fact, in order to determine the actual number of faces of the cell and define exactly what polygon each face is, we need to explore whether neighbouring simplices are coplanar, and thus constitute higher order polygons. This is accomplished by computing the unit vector orthogonal to each simplex and computing the matrix of the scalar products for all the simplices of the cell. When the scalar products , with , of unit vectors orthogonal to n neighbouring simplices with are close to 1 - within a specified tolerance , corresponding to a tolerance of about in the angle between the unit vector - we have that is a polygon with n+2 sides. We have consistently verified that when choosing any tolerance smaller than we obtain basically the same results.
3. Results
3.a. Two-dimensional case
3.a.1. Number of sides of the cells
In the case of the regular square tessellation, the introduction of a minimal amount of symmetry-breaking noise induces a transition in the statistics of and , since and are discontinuous in . In Figure 1a)-Figure 1b) we plot the functions and ; the half-width of the error bars are twice the corresponding values of and , whereas the Poisson-Voronoi values are indicated for reference. We have that , where by we mean the limit for infinitesimal noise of the quantity , practically obtained by considering very small positive values of the parameter . The regular square tessellation results to be structurally unstable, as the introduction of noise breaks the special quadrivalent nature of the vertices of the Voronoi cells and drives the system to the generic behaviour described by Euler’s theorem. Moreover, , which shows that the width of the distribution of the number of sides is finite also for infinitesimal noise. The ensemble fluctuations and are discontinuous functions in , since they reach a finite positive value as soon as the noise is switched on. Considering larger values of α, we have that is almost constant (within few percents) up to , where its value begins to quickly increase before reaching the asymptotic value for , which essentially coincides with what obtained in the Poisson-Voronoi case. The function is, in agreement with Euler’s law, constant within few permils around the value of 6 for all , so that the mean topological charge is zero. These results suggest that, topologically speaking, the route to randomness from the square regular tessellation to the Poisson-Voronoi case goes through a finite range , where the statistical properties of the topology of the cells are rather stable. This corresponds to the linear perturbation regime [58]. Moreover, in this range, hexagons dominate and their fraction is almost constant (within few percents), whereas for larger values of the fraction of hexagons declines but is still dominant (not shown).
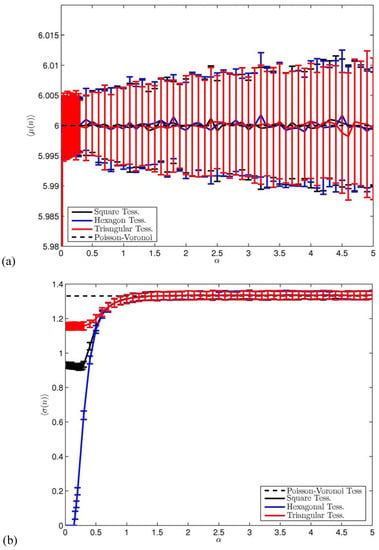
Figure 1.
Ensemble mean of the mean - (a) - and of the standard deviation - (b) - of the number of sides (n) of the Voronoi cells. Note that in (a) the number of sides of all cells is 4 (3) - out of scale - for α=0 in the case of regular square (triangular) tessellation. Half-width of the error bars is twice the standard deviation computed over the ensemble. Poisson-Voronoi limit is indicated.
Similarly, the triangular tessellation results to be unstable: we have that and , and again the ensemble fluctuations and are discontinuous functions in . As expected, for all values , with hexagons being the dominant class of polygons. The introduction of an infinitesimal noise destroys the peculiar hexavalent vertices of the Voronoi cells and makes the system obey the Euler’s theorem. Also in this case, we find a finite range - slightly wider than for the square tessellation - such that and the fraction of hexagons, are numerically almost constant. This property seems to define robustly a topologically quasi-stable weakly perturbed state.
When considering the regular hexagon honeycomb tessellation, the impact of introducing noise in the position of the points xi is quite different from what previously observed. Results are also shown in Figure 1a)-Figure 1b). The first feature is that an infinitesimal noise does not affect at all the tessellation, in the sense that all cells remain hexagons. Moreover, even finite-size noise basically does not distort cells in such a way that figures other than hexagons are created. We have not observed non n=6 cells for up to in any member of the ensemble. This has been confirmed also considering larger densities (e.g. ρ0 = 1,000,000). It is more precise, though, to frame the structural stability of the hexagon tessellation in probabilistic terms: the creation of non-hexagons is very unlikely for the considered range. Since the presence of a Gaussian noise induces for each point xi a probability distribution with – an unrealistic- non-compact support, it is possible to have low-probability outliers that, at local level, can distort heavily the tessellation. Anyway, for all values of we have that within a few permils, as imposed by the Euler’s theorem. For , is positive and increases monotonically with ; this is accompanied by a monotonic decrease with of the fraction of hexagons, which are nevertheless dominant for all values of . For the value of is not distinguishable from what obtained for perturbed square and triangular tessellations. This implies that, from a statistical point of view, the variable n loses memory of its unperturbed state already for a rather low amount of Gaussian noise, well before becoming undistinguishable from the random Poisson case.
3.a.2. Area and Perimeter of the cells
For all of the perturbed regular tessellations considered in this study, the parametric dependence on of the statistical properties of the area of the Voronoi cells is more regular than for the case of the number of sides. Results are shown in Figure 2a)-Figure 2b).
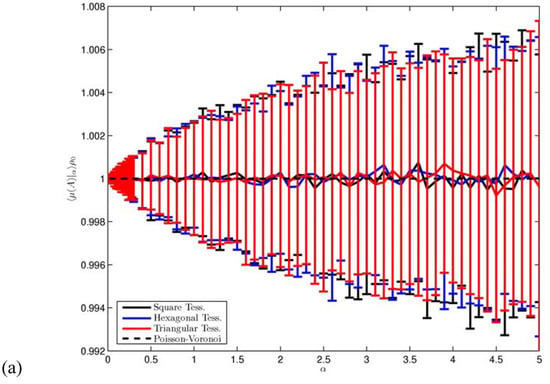
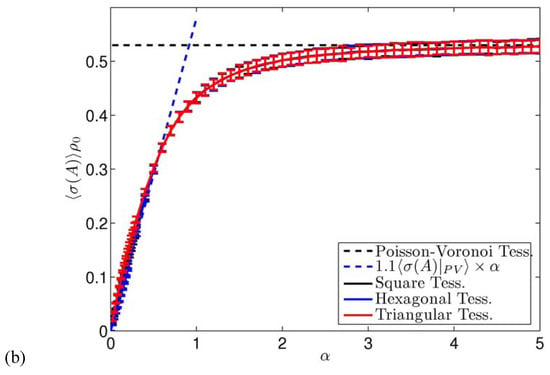
Figure 2.
Ensemble mean of the mean - (a) - and of the standard deviation - (b) - of the area (A) of the Voronoi cells. Half-width of the error bars is twice the standard deviation computed over the ensemble. Poisson-Voronoi limit is indicated. In (b), linear approximation for small values of α is also shown. Values are multiplied times the appropriate power of the density in order to obtain universal functions.
In general, the ensemble mean value of the area of the Voronoi cells is, basically by definition, constrained to be for all values of , whereas for all perturbed tessellations the size of fluctuations increases with and reaches for an asymptotic value, coinciding with that observed in the Poisson-Voronoi case. The -dependence of is more interesting. We first note that the functions computed from the three perturbed tessellation are very similar, and the same occurs for . This implies that the impact of adding noise in the system in the variability of the area of the cells is quite general and does not depend on the unperturbed patterns. We can be confident of the generality of this result also because for relatively small values of (say, ), has a specific functional form reminding of symmetry breaking behaviour: in such a range we have that . The agreement with a linear approximation is worse for the triangular tessellation case. For , is almost indistinguishable from the Poisson-Voronoi value, so that we can estimate an asymptotic value .
Results for the statistical estimators of the perimeter of the Voronoi cells are shown in Figure 3a)-Figure 3b). When considering the perturbed square tessellation, basically coincides with that of the Poisson-Voronoi case for . Note that also , which also agrees with the asymptotic Poisson-Voronoi limit. Anyway, is a function with some interesting structure: for features a distinct minimum , whereas for a maximum for is realized, with .
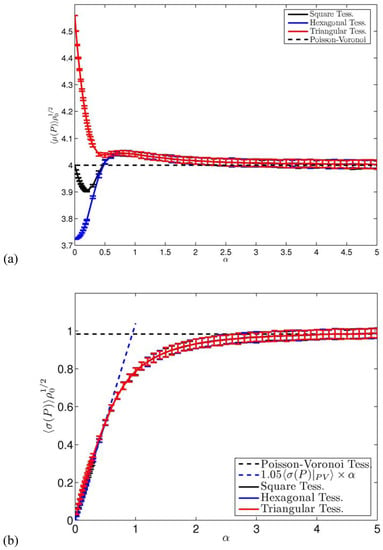
Figure 3.
Ensemble mean of the mean - (a) - and of the standard deviation - (b) - of the perimeter (P) of the Voronoi cells. Half-width of the error bars is twice the standard deviation computed over the ensemble. Poisson-Voronoi limit is indicated. In (b), linear approximation for small values of α is also shown. Values are multiplied times the appropriate power of the density in order to obtain universal functions.
The unperturbed honeycomb hexagonal tessellation is optimal in the sense of perimeter-to-area ratio, and, when noise is added, the corresponding function increases quadratically (not shown) with for , whereas for its value coincides with what obtained starting from the regular square tessellation. Finally, in the case of triangular tessellation, the unperturbed case features the largest perimeter-to-area ratio, which is strongly reduced as soon as the noise is switched on, so that a relative minimum is then obtained again for , with . For the value of the function basically coincides with those resulting from the two other tessellations. We deduce that there is, counter-intuitively, a specific amount of noise which optimises the mean perimeter-to-area ratio for the two unstable regular tessellation – corresponding to for the square one and to for the triangular one - whereas, for the opposite is realized for all tessellations. When considering the functions , we are in a similar situation as for the statistics of mean cells area: the result of the impact of noise is the same for all tessellations. For , is proportional to , with ; also in this case the triangular tessellation has a worse agreement with this low-noise approximation. Moreover, for , becomes undistinguishable from the asymptotic value realized for Poisson-Voronoi process, given by .
3.a.3. Area and perimeter of n-sided cells
A subject of intense investigation has been the characterization of the geometrical properties of n-sided cells; see [39] and references therein for a detailed discussion. We have then computed for the considered range of the quantities , , , and , obtained by stratifying the outputs of the ensemble of simulations with respect to the number of sides n of the resulting cells. The 2-standard deviation confidence interval centred around the ensemble mean is shown in Figure 4a)-Figure 4b) for the area and the perimeter of the cells, respectively, for selected values of . Note that for larger values of n the error bar is larger because the number of n-sided cells is small. The results of the three perturbed regular tessellations basically agree for , thus confirming what shown previously. In particular, for , the results coincide with what resulting from the Poisson-Voronoi case. In this regime, we verify the Lewis law [61], i.e. . Our data give , which is slightly less than what resulting from an asymptotic computation [48], where obtained a linear coefficient of 0.25 is reported. Secondly, and more interestingly, we confirm that Desch’s law [62] is violated, i.e. , as shown, e.g., in [46]. Nevertheless, instead of a polynomial dependence on n, we find that a square root law can be established, i.e. . Our data give , again slightly less than the asymptotic computation [48], where is obtained. We note that the Lewis law and such a law allow the establishment of a weakly n-dependent relationship such as , which seems to fit properly with a well-defined 2D isoperimentric ratio . Moreover, this agrees with the asymptotic result for large n, , which derives from the fact that cells with many sides tend to have a circular shape, or, in other terms, their isoperimetric ratio tends to unity [48]. In the next section we will analyse more in detail the problem of relating perimeters and areas of the cells and quantify how the typical shape of the cells varies when cells of different perimeters are considered. In the intermediate range (), we have that the Lewis law and the square root law are not verified, and, quite naturally, the functions and get more and more similar to their Poisson-Voronoi counterparts as increases.
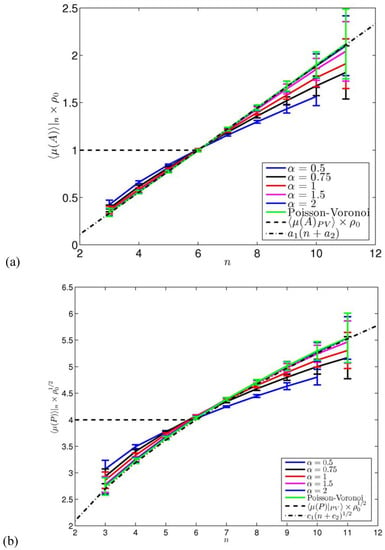
Figure 4.
Ensemble mean of A - (a) - and of P - (b) - of n-sided Voronoi cells. Half-width of the error bars is twice the ensemble standard deviation. Full ensemble mean is indicated. Linear (a) and square root (b) fits of the Poisson-Voronoi limit results as a function of n is shown. Values are multiplied times the appropriate power of the density in order to obtain universal functions.
An interesting result is that, for , agrees within statistical uncertainty of few permils with . This implies that . Similarly, for , constitutes an excellent approximation within 1% to , whose value, as shown in Figure 3a), is rather close to 4 for , but agreement within statistical uncertainty is basically not found, except, marginally, for very large values of . This implies that . The ensemble mean estimators restricted to the non-hexagonal polygons are instead heavily biased (positive bias for n>6 and negative bias for n<6). The fact that the ensemble mean of the area and perimeter of the Voronoi cells is so accurately approximated when selecting only the most probable state from a topological point of view - hexagons - is surely striking, also because in the considered range hexagons are dominant but other polygons are also well-represented. In fact, for, e.g., , the density of hexagons is smaller than the sum of the densities of pentagons and heptagons.
3.a.4. Anomalous Scaling
We define the constant such that for each cell indexed by j we have , where in general . The first inequality excludes the possibility of fractal objects and the second inequality implies that no cells can have an isoperimetric ratio larger than circles. As we have seen, in the considered Voronoi tessellations cells having a larger number of sides are associated to larger areas and perimeters. In order to quantify how their shape changes, we consider the possibility of a scaling law approximating the (statistical) relationship between the area and the perimeter of the cells of the form with , which corresponds to expressing . Therefore, if , is monotonically increasing with P. Note also that, since the Voronoi tessellation is not a fractal with non-integer dimension, the proposed scaling law makes sense at most in the limited range . We then take the ensemble average for the exponent among the equivalent tessellations. In the Poisson-Voronoi limit (Figure 5), which suggests the occurrence of a 7/3 exponent.
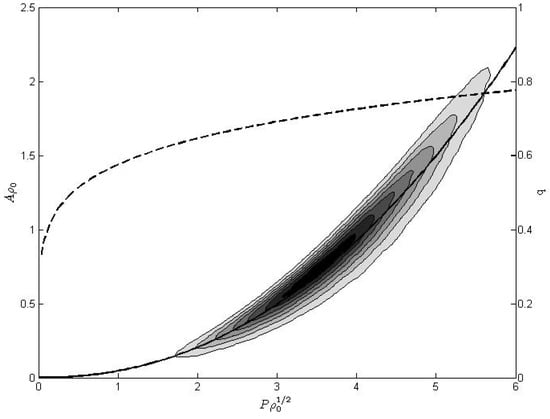
Figure 5.
Joint distribution of the perimeter and of the area of the Voronoi cells in the Poisson-Voronoi tessellation limit in 2D. The black solid line indicates the best log-log least squares fit, with ensemble mean of the exponent . The dashed black line reports the fit of isoperimetric quotient (see right vertical axis), which scales with the area with exponent . The effective range of applicability of the scaling law is between 1.5 and 6 in units of normalized area. Correspondingly, q ranges between 0.65 and 0.78, and ε between 0.052 and 0.062. Details in the text.
If is larger than zero, we have that, typically, a cell with a larger volume has a relatively smaller surface, and, in other terms, a larger isoperimetric quotient (which increases ) The values of the best estimates of for the perturbed triangular, square, and hexagonal tessellations are shown in Figure 6 as a function of . In all cases we find that is larger than 2, with typical uncertainties of the order of at most . With infinitesimal noise, anomalous scaling is observed for the perturbed square and triangular tessellations. In the former case, , the exponent has a local minimum for the same value of which optimises the mean perimeter-to-area ratio. In the latter case, the simple logarithmic fit applies reasonably well only for values of slightly larger than zero, and anomalous scaling is observed in all cases. When considering the perturbed hexagonal tessellation, anomalous scaling is observed for all finite values of noise, but, interestingly, , which implies that for infinitesimal noise anomalous scaling is not observed. Therefore, in the limit of vanishing noise large cells tend to have a larger isoperimetric quotient in the perturbed triangular and square tessellations, whereas, in the perturbed hexagonal case, such a selection does not take place: cell shape are better preserved. In all cases, the value of the scaling exponent becomes undistinguishable from the Poisson-Voronoi limit for , with rather small discrepancies already for .
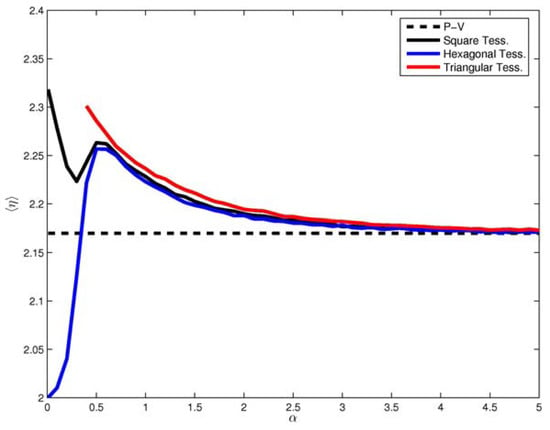
Figure 6.
Ensemble mean of the scaling exponent fitting the power-law relation for the perturbed square, hexagonal and triangular Voronoi tessellations. The anomalous scaling () is apparent. The error bars, whose half-width is twice the ensemble standard deviation, are too small to be plotted. The Poisson-Voronoi limit (see Figure 5) is indicated. Details in the text.
3.b. Three-dimensional case
3.b.1. Faces, Edges, Vertices
If , we deal with actual SC, BCC, and FCC lattices. When spatial noise is present in the system, the resulting Voronoi cells are generic polyhedra, so that degenerate quadrivalent vertices, such as those present in the rhombic dodecahedron [58] are removed with probability 1. Therefore, we expect that , , , and . These relations have been verified up to a very high degree of accuracy in our simulations, so that, in order to describe the topology of the cell, it is sufficient to present the statistical properties of just one among e, f, and v. In Figure 7 we present our results relative to the number of faces of the Voronoi cells.
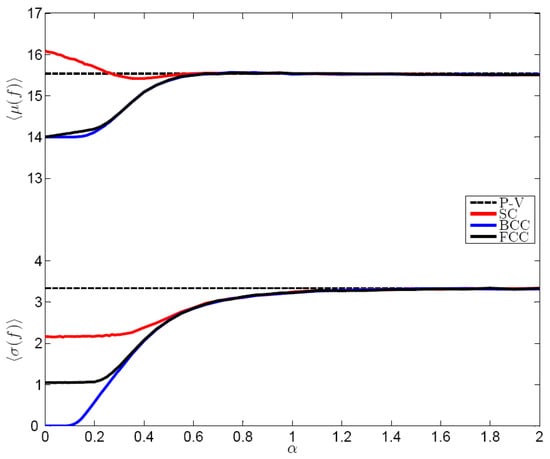
Figure 7.
Ensemble mean of the mean and of the standard deviation of the number of faces of the Voronoi cells for perturbed SC, BCC and FCC cubic crystals. The error bars, whose half-width is twice the standard deviation computed over the ensemble, are too small to be plotted. The Poisson-Voronoi limit is indicated.
In the case of the SC and FCC crystals, a minimal amount of symmetry-breaking noise impacts as a singular perturbation the statistical properties of and , since and are discontinuous in . In the SC case, the average number of faces jumps from 8 to slightly above 16, whereas, as shown in [58], the disappearance of the quadrivalent vertices in the rhombic dodecahedron case (FCC crystal) causes an increase of two units (up to exactly 14) in the average number of faces. Near , for both SC and FCC perturbed crystals, depends linearly on as . The proportionality constant has opposite sign in the two cases, with for the SC case and for the FCC case.
Moreover, the introduction of noise generates the sudden appearance of a finite standard deviation in the number of faces in each cell , which is larger for SC crystals. In the case of FCC crystals, in [58] a theoretical value is proposed, whereas our numerical estimate is about 10% lower, actually in good agreement with the numerical results presented in [58]. Somewhat surprisingly, the is almost constant for a finite range near ranging up to about for the SC crystal and for the FCC crystal, thus defining an intrinsic width of the distribution of faces for a – well-defined - “weakly perturbed” state. In the case of the perturbed FCC crystals, in such a range of weak noise we only observe cells having 12 up to 18 faces: this defines the range of applicability of the weak noise linear perturbation analysis [58].
When considering the BCC crystal, the impact of introducing noise in the position of the points xi is rather different. Results are also shown in Figure 7. Infinitesimal noise does not affect at all the tessellation, in the sense that all Voronoi cells are 14-faceted (as in the unperturbed state). Moreover, even finite-size noise basically does not distort cells in such a way that other polyhedra are created. We have not observed – also going to higher densities - any non-14 faceted polyhedron for up to in any member of the ensemble, so that and in a finite range. However, since the Gaussian noise induces for each point xi a pdf with a non-compact support, as discussed in Section 3.a.1, we may have extreme fluctuations distorting heavily the tessellation. Therefore, we should interpret this result as that finding non 14-faceted cells is highly – in some sense, exponentially - unlikely.
In Figure 7 the Poisson-Voronoi limiting case is indicated; our simulations provide results in perfect agreement with analytical results [63]. For the values of and of the Voronoi tessellations of the three perturbed crystals asymptotically converge to what resulting from the Poisson-Voronoi tessellation, as expected. We should note, though, that in the 2D case the asymptotic convergence has been shown to be much slower [59] so that spatial noise in 3D seems to mix things up much more efficiently. Similarly to the 2D case, the perturbed tessellations are statistically undistinguishable – especially those resulting from the BCC and FCC distorted lattices – well before converging to the Poisson-Voronoi case, thus pointing at some general behavior.
Additional statistical properties of the distribution of the number of faces in the Voronoi tessellation need to be mentioned. The mode of the distribution is quite interesting since the number of faces is, obviously, integer. In the FC and BCC cases, up to the mode is 14, whereas for larger values of 15-faceted polyhedra are the most common ones. Also the Voronoi tessellations of medium-to – highly perturbed SC crystals are dominated by 15-faceted polyhedra, whereas 16-faceted polyhedra dominate up to .
3.b.2. Area and Volume of the cells
The statistical properties of the area and of the volume of the Voronoi tessellations of the perturbed cubic crystals have a less pathological behavior with respect to what previously described when noise is turned on, as all properties are continuous and differentiable in . Still, some rather interesting features can be observed.
As mentioned above, the ensemble mean of the mean volume of the cells is set to in all cases, so that we discuss the properties of the ensemble mean , shown in Figure 8. We first observe that for all cubic structures the standard deviation converges to zero with vanishing noise, thus meaning that small variations in the position in the lattice points do not create dramatic rearrangements in the cells when their volumes are considered. Moreover, for , a well-defined linear behavior is observed for all SC, BCC, and FCC structures. The proportionality constant X is not distinguishable between the BCC and the FCC perturbed crystals, and actually , where the pedix refers to the asymptotic Poisson-Voronoi value; the SC curve is somewhat steeper near the origin. The three curves become undistinguishable for , so when the noise is moderately intense and reticules are still relatively organized. As previously observed, this seems to be a rather general and robust feature. It is also interesting to note that the attainment of the Poisson-Voronoi limit is quite slow, as compared to the case of the statistical properties of the number of faces of the cell, and a comparable agreement is obtained only for (not shown).
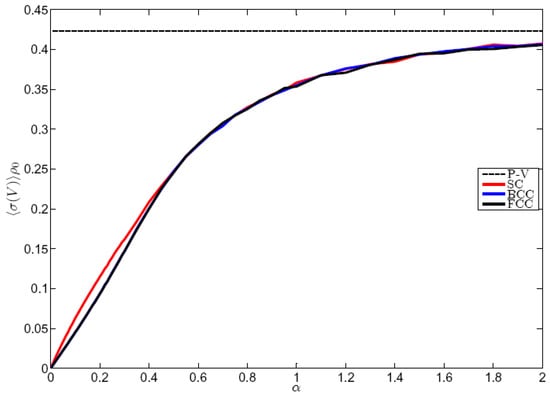
Figure 8.
Ensemble mean of the standard deviation of the volume (V) of the Voronoi cells for perturbed SC, BCC and FCC cubic crystal. The ensemble mean of the mean is set to the inverse of the density. Values are multiplied times the appropriate power of the density in order to obtain universal functions. The error bars, whose half-width is twice the standard deviation computed over the ensemble, are too small to be plotted. The Poisson-Voronoi limit is indicated.
When considering the area of the cells (Figure 9), further interesting properties can be highlighted. First, the behaviour of the ensemble mean is rather similar to what just discussed for . Nevertheless, in this case the agreement between the three perturbed structure is more precisely verified – the three curves are barely distinguishable for all values of . Moreover, we again observe a linear behavior like , which suggests that the systems closely “align” towards Poisson-like randomness for small values of . This closely mirrors what observed in the 2D case for the expectation value of the standard deviation of the perimeter and of the area of the Voronoi cells [59].
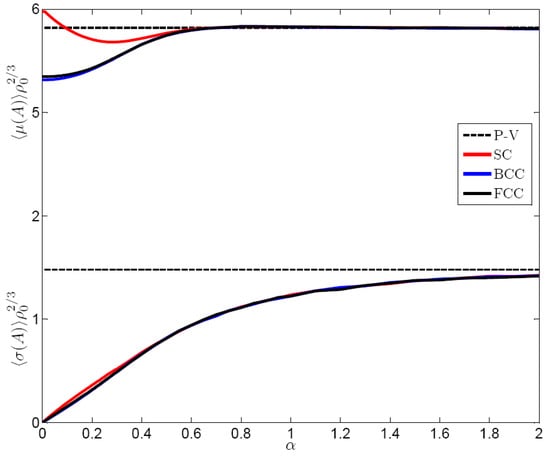
Figure 9.
Ensemble mean of the mean and of the standard deviation of the area (A) of the Voronoi cells for perturbed SC, BCC and FCC cubic crystals. Values are multiplied times the appropriate power of the density in order to obtain universal functions. The error bars, whose half-width is twice the standard deviation computed over the ensemble, are too small to be plotted. The Poisson-Voronoi limit is indicated.
The properties of for the perturbed crystal structures are also shown in Figure 9. A striking feature is that, similarly to what noted in the case of triangular and square tessellations of the plane, there is a specific amount of noise that optimises the mean surface for the perturbed SC crystals. We see that the mean area of the cells decreases by about 8% when is increased from 0 to about 0.3, where a (quadratic) minimum is attained. For stronger noise, the mean area of the Voronoi cells of the perturbed SC crystals decreases, and, for , the asymptotic value of the Poisson-Voronoi tessellation is reached. In terms of cell surface minimization, the unperturbed cubic tessellation is about 3% worse than the “most random” tessellation.
The dependence of with respect to is very interesting also for the perturbed BCC and FCC cubic crystals. In both cases, the mean area increases quadratically (with very similar coefficient) for small values of , which shows that the Voronoi tessellations of the BCC and FCC cubic crystals are local minima for the mean surface in the set of space-filling tessellations. We know that neither the truncated octahedron nor the rhombic dodecahedron are global minima, since (at least) the Weaire-Phelan [55] and the Gabbrielli [56] structures have a smaller surface. It is reasonable to expect that a similar quadratic increase of the average surface should be observed when perturbing with spatial gaussian noise the crystalline structure corresponding to the Weaire-Phelan and Gabbrielli cells. For , the values of for perturbed BCC and FCC crystals basically coincide, and for the Poisson-Voronoi limit is reached within a high accuracy.
3.b.3. Shape of the cells
The analysis of the properties of the joint area-volume pdf for the Voronoi cells of the considered tessellations sheds light on the statistics of fluctuations of these quantities. A first interesting statistical property where the joint cells area-volume pdf has to be considered is the isoperimetric quotient . The quantity Q is strictly positive and smaller than 1 for 3D objects, where 1 is realized in the optimal case given by the sphere. Instead, Q is zero for any object with Hausdorff dimension smaller than 3. When evaluating the expectation value of the mean isoperimetric quotient of an ensemble of Voronoi tessellation, we have:
The presence of fluctuations implies that testing the average sphericity – which is basically what Q measures - of a random tessellation is a slightly different problem from testing the average surface for a given average volume, which is what Figure 9 refers to, whereas in regular tessellations the two problems are equivalent. In Figure 10 we present our results for the three perturbed crystal structures. In agreement with what observed in Figure 9, we have that by optimally tuning the intensity of the noise () perturbing the SC crystal, reaches a maximum, whereas the isoperimetric quotient of the perturbed FCC and BCC crystals has a local maximum for vanishing noise and is monotonically decreasing with . For , the value of basically coincides for the three perturbed crystalline structures, so that agreement is obtained well before the Poisson-Voronoi limit is attained. It is notable, and counterintuitive, that in the case of the regular SC crystal the isoperimetric quotient is lower than the value of obtained in the Poisson-Voronoi limit.
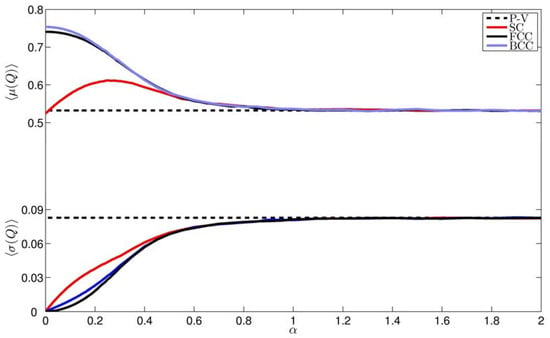
Figure 10.
Ensemble mean of the mean and of the standard deviation (see the different scales) of the isoperimetric quotient of the Voronoi cells for perturbed SC, BCC and FCC cubic crystals The error bars, whose half-width is twice the standard deviation computed over the ensemble, are too small to be plotted. The Poisson-Voronoi limit is indicated. Details in the text.
In order to analyse the variability of shape of the cells, we have also analysed . Results are also depicted in Figure 10. We observe that for all perturbed crystalline structures the variability of the isoperimetric quotient increases with the intensity of noise, as suggested by intuition. This does not tell us much more than what could be derived from the inspection of Figure 8 and Figure 9.
More interesting features appear when considering specifically the weak noise limit of . For all of the three perturbed crystals, , again, consistently with what shown in Figure 8 and Figure 9. Nevertheless the way such limit is approached varies considerably. In the SC and BCC case, for small values of , a well-defined linear behavior is observed, with a much larger coefficient for the SC case than in the BCC case, where . Instead, in the FCC case, the approach to 0 of is quadratic, so that for small values of we have that . Therefore, the FCC structure preserves the shape of its cells much more efficiently when noise is introduced. Note that what observed in the weak noise limit is confirmed qualitatively for all values of , as we always have .
For the results for the SC, FCC and BCC crystals basically agree and converge to the Poisson-Voronoi limit for . Therefore, whereas the Voronoi tessellation of the BCC crystal is the most stable against noise when the topological properties of the cells are considered (see Figure 7), when analyzing the shape of the cells from a metrical point of view, the FCC crystal is actually the most stable.
In order to further clarify the variability of the shapes of the cells, we take advantage of a strategy of investigation commonly adopted for studying Voronoi tessellations, i.e. the stratification of the expectation values of the geometrical properties with respect to classes defined by the number of sides of the cells [46,48,59,60]. In the present case, it would be profitable to study quantities such as and , where the pedix indicates that the averages are performed only on cells with f faces. It is readily observed that, in all cases, both and increase with f (not shown), for the basic and intuitive reason that cells with a larger number of faces are typically larger in volume and have larger areas.
Moreover, and this is a more interesting point, (typically large) cells with a large number of faces have typically a large isoperimetric quotient Q, which makes sense in the context of Kendall’s conjecture [41,42,43,48]. In Figure 11(a), Figure 11(b), and Figure 11(c) we present the expectation value of the isoperimetric quotient as a function of for the three perturbed cubic crystals.
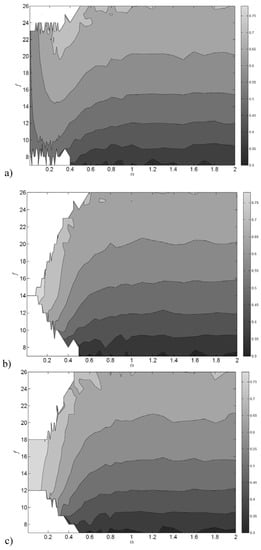
Figure 11.
Ensemble mean of the isoperimetric quotient of the Voronoi cells for perturbed SC (a), BCC (b) and FCC(c) cubic crystals, where averages are taken over cells having f faces. A white shading indicates that the corresponding ensemble is empty. More faceted cells are typically bulkier.
We observe that, in all cases, for a given value of , increases significantly with f, thus confirming the geometrical intuition. Moreover, whereas in the BCC and FCC case for a given f decreases monotonically with , in the SC perturbed crystal for all values of f we have an increase of with up to . For the results of the three perturbed crystals tend to converge to the Poisson-Voronoi limit. Therefore, in all considered cases the kind of dependence of the average isoperimetric quotient with respect to noise observed in Figure 10 is realized also in each class of cells as defined by the f label. At any rate, the main additional information contained in Figure 11 is that for all perturbed crystal structures the number of faces acts as a very good proxy variable for the isoperimetric quotient, and for the shape of the cells.
3.b.4. Fluctuations and Anomalous Scaling
As discussed above, the areas and the volumes of the Voronoi cells resulting from a random tessellations cells are highly variable. See Figure 12 for the joint cells area-volume distribution in the case of Poisson-Voronoi tessellation. All considered perturbed crystal structures give qualitatively similar results, but feature, as obvious from the previous discussion, more peaked distributions. We follow the same approach outlined in Section 3.a.4.
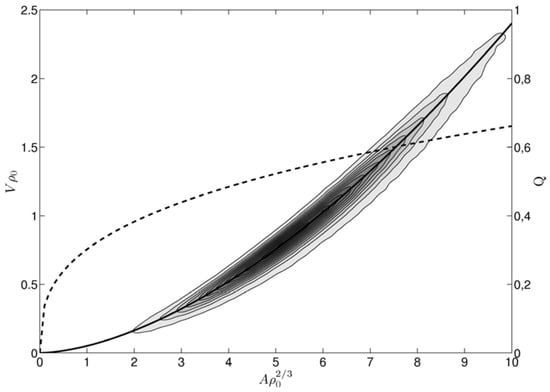
Figure 12.
Joint distribution of the area and of the volume of the Voronoi cells in the Poisson-Voronoi tessellation limit. The black solid line indicates the best log-log least squares fit, with ensemble mean of the exponent . The dashed black line reports the corresponding fit of isoperimetric quotient (see right vertical axis), which scales with the area with exponent . The effective range of applicability of the scaling law is between 2 and 10 in units of normalized area. Correspondingly, Q ranges between 0.35 and 0.65, and ε between 0.056 and 0.076. Details in the text.
If the space is tessellated with finite-size cells which are geometrically similar, their shape determines Q and, consequently, the constant such that for each cell indexed by j we have , where in general , where the first inequality excludes the possibility of fractal objects and the second inequality implies that no tessellations can beat spheres. As we have seen, in the considered Voronoi tessellations the cells are definitely not similar, with larger (and more faceted) cells associated to larger isoperimetric quotients. In order to quantify this, we take the following approach. We consider the possibility of a scaling law approximating the (statistical) relationship between the volume and the area of the cells of the form with , so that, if , is monotonically increasing with A, It should be mentioned that this parameterization of amounts to defining Q as . Note also for all values of A the constraint holds, so that the proposed (anomalous) scaling law makes sense at most in the limited range .
Therefore, in each generated tessellation we attempt a power law fit between the area and the volume of the individual cells as with , by performing a linear regression between the logarithm of the volume and of the area of cells. Therefore, given how weight is calculated in the regression, we implicitly define an effective limited range where scaling applies, which corresponds to the interval of A values corresponding to the bulk of the statistics of the cells. Such an interval is, by definition, always included within the largest possible interval . A corresponding range of values of and of is then obtained. We then take the ensemble average for the exponent among the equivalent tessellations. The values of the best fit for for the perturbed SC, BCC, and FCC crystals are shown in Figure 13 as a function of . In all cases we find that is larger than 3/2, with typical uncertainties of the order of at most . Therefore, is always larger than zero: such an anomalous scaling implies that, typically, a cell with a larger volume has a relatively smaller surface, and, in other terms, a larger isoperimetric quotient (which increases ).
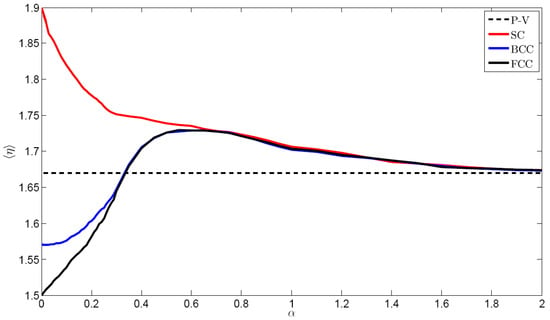
Figure 13.
Ensemble mean of the scaling exponent fitting the power-law relation for the Voronoi cells of perturbed SC, BCC and FCC cubic crystals. The presence of an anomalous scaling () due to the fluctuations in the shape of the cells is apparent. The error bars, whose half-width is twice the standard deviation computed over the ensemble, are too small to be plotted. The Poisson-Voronoi limit (see Figure 12) is indicated. Details in the text.
In particular, in the Poisson-Voronoi limit - black line in Figure 12 - which suggests the occurrence of a 5/3 exponent. It is also remarkable that, as soon as noise is turned on, anomalous scaling due to is observed in for the SC and BCC cubic crystals. In the SC case, , the exponent is monotonically decreasing for all values of , and becomes undistinguishable from the Poisson-Voronoi limit for . In the BCC case, as opposed to what one could expect given the structural stability of the crystal, , which implies that a (modest) anomalous scaling is observed also for infinitesimal noise. The exponent increases for small values of , overshoots the Poisson-Voronoi limit, and for its value basically coincides with what obtained in the SC case. When considering the FCC perturbed crystal, an anomalous scaling is observed for all finite values of noise, but, quite notably, , which means that for infinitesimal noise anomalous scaling is not observed. So, in this regard, the FCC crystal seems to be more robust than the BCC one. In other terms, in the limit of vanishing noise (and of vanishing variability in the statistics of the areas and volumes of the cells) large cells tend to have a larger isoperimetric quotient in the perturbed SC and BCC crystals. Instead, in the perturbed FCC crystal such a selection does not take place: in this sense, shapes are better preserved.
As mentioned before, the number of faces provides a good proxy indicator for the shape of the cell, or, more precisely, of its isoperimetric quotient. In order to find a robust confirmation of the interpretation proposed for the presence of the anomalous exponent depicted in Figure 13, we then attempt a power-law fit separately for each class of cells, each labelled with the number of faces. Therefore, for each value of the noise applied to the SC, FCC and BCC crystals, we obtain via best fit and ensemble averaging the estimate of the exponent pertaining to the subset of cells having f faces. We find that for all cases considered results to be lower than the corresponding “global” , so that we basically always have (with typical uncertainties of the order of ), including when weak perturbation to the SC crystals are considered. We do not plot as a function of and f for the three perturbed crystals, since what is obtained is just a plateau with no structure along the or f directions. We then have that since shape fluctuations are greatly reduced within each class of the f-faceted cells, the anomalous scaling is greatly suppressed.
4. Summary and Conclusions
In this paper we have summarized and extended the main findings presented in [59,60]; the goal has been to perform a numerical study aimed at bridging the properties of regular tessellations in 2D and 3D, generated by crystalline structures, to those resulting from Poisson point processes, thus analyzing in a common framework symmetry breaking processes and the approach to uniformly random distributions. This is achieved by resorting to a simple parametric form of random perturbations driven by a Gaussian noise to the positions of the points around which the Voronoi tessellation is created. The standard deviation of the position of the points induced by the Gaussian noise is expressed as (n indicating the dimensionality of the space), where is the control parameter, is the coarse-grained density of tessellation generating points, and is the natural length scale. As 2D unperturbed crystalline structures, we consider triangular, square and hexagonal regular lattices, corresponding to hexagonal, square and triangular tessellations, respectively. In 3D we consider the simple cubic (SC), body-centred cubic (BCC), and face-centred cubic (FCC) crystals, whose corresponding Voronoi cells are the cube, the truncated octahedron, and the rhombic dodecahedron, respectively. By increasing , we explore the transition from perfect crystals to less and less regular structures, until the limit of uniformly random distribution of points is attained. Note that, for all values of , the pdf of the lattice points is periodic. For each value of , we have performed a set of simulations, in order to create an ensemble of Voronoi tessellations in the unit cube, and have computed the statistical properties of the cells.
The first notable result is that spatial noise “reveals” the topological instability of the Voronoi tessellations corresponding to the square and hexagonal lattice in 2D and to the SC and FCC lattices in 3D. As soon as noise is turned on, their degeneracies – to be intended as non-generic properties of their vertices – are removed: ensemble mean of the mean and of the standard deviation have discontinuities, and finite ensemble fluctuations appear. Instead, the topological properties of the Voronoi cells of the triangular crystals in 2D and BCC crystal in 3D (which are non-degenerate) are stable against infinitesimal noise, as well known from linear theory, so that the zero-noise limit of the Voronoi tessellation of their perturbed structure is coincident with the unperturbed case. As a new result, we have that the topology of these tessellations is robust also against small but finite noise. For strong noise, the statistical properties of the tessellations of the perturbed crystals converge to those of the Poisson-Voronoi limit, but, quite notably, the memory of the specific initial unperturbed state is lost already for moderate noise, since the statistical properties of the perturbed tessellations are typically indistinguishable for .
In the case of perturbed square (triangular) tessellation, for a specific intensity of the noise determined by (), it is possible to minimise the mean isoperimetric ratio of the Voronoi cells, whereas by choosing we obtain a relative maximum for perimeter-to-area ratio for all perturbed tessellations. Similarly, the mean area of the perturbed SC structure has a local minimum for . So, counter-intuitively, both in 2D and 3D noise can act as an “optimiser”. As in the case of the perimeter for 2D hexagonal tessellations, for perturbed BCC and FCC structures the mean area increases only quadratically with for weak noise, thus suggesting that the unperturbed Voronoi tessellations are local minima for the interface area.
The observation that the truncated octahedron is a “large” local maximum for the isoperimetric ratio in 3D for space-filling tessellations suggests a weak re-formulation of the Kelvin conjecture of global optimality of the truncated octahedron, which has been proved false [55,56]. For large values of (e.g. , quite expectedly, the statistical properties of the perturbed regular tessellations converge, both in terms of ensemble mean and fluctuations, to those of the Poisson Voronoi process with the same intensity.
The cells shape can also be investigated by analysing what kind of scaling exists between their n-measure and the n-1 measure of their boundaries. Practically, we attempt power law fits between the perimeters and the areas of the 2D cells, and between the surface areas and the volumes of the 3D cells. We obtain with a very high degree of precision, for all perturbed tessellations, and for any intensity of noise, a positive anomalous scaling, so that (in n-dimensional space). In particular, we have and in the Poisson-Voronoi limit in 2D and 3D, respectively. A positive anomaly is observed also for infinitesimal noise, except in the case of the perturbed triangular crystal (with hexagonal tessellation) in 2D and of the perturbed FCC crystal in 3D. These crystals feature the smallest anomaly in the exponent for all values of . The anomaly shows how large and small cells of the tessellation differ in their shape, since indicates that large cells preferentially feature large isoperimetric quotients (the bigger, the bulkier). Therefore, this suggests that in 3D the Voronoi tessellation of the FCC crystal is the most stable in preserving the cells’ shape, even if it is topologically unstable. This marks a difference with the 2D case, where the hexagonal tessellation is stable both topologically and metrically. Note also that, basically because the isoperimetric quotient is strictly larger than zero (Voronoi tessellation is not a fractal) and strictly lower than one (no cells can beat n-spheres), these scaling relations make sense only within a finite range of values and should be taken as descriptive of the bulk statistical properties of the cells.
In 2D, the geometrical properties of n-sided cells change with until the Poisson-Voronoi limit is reached for ; in this limit the Desch law for perimeters is confirmed to be not valid and a square root dependence on n, which allows an easy link to the Lewis law for areas, is established. Moreover, the ensemble mean of the cells area and perimeter restricted to the hexagonal cells provides a striking approximation to the full ensemble mean for ; this reinforces the idea that hexagons, apart from their bare numerical prominence, can be taken as typical polygons in 2D Voronoi tessellations.
In 3D we also find that the number of faces of a cell is a good proxy for its isoperimetric quotient: cells with a larger number of faces are typically bulkier. A further indication that the fluctuations in the shape determine the anomalous scaling between the areas and the volumes of the cells lies in the fact that the anomaly is almost suppressed when we classify the cells according to the number of their faces and attempt the power law fit class by class.
This work clearly defines a way of connecting, with a simple parametric control of spatial noise, crystal structure to uniformly random distribution of points, thus also defining the range of applicability of the weak noise linear perturbation analysis as developed in [58] Such a procedure can be in principle applied for describing the “dissolution” of any crystalline structure. The results here described may be useful in understanding the physical properties of graphene, which has recently received a great deal of attention as first example of truly atomic 2D crystalline matter [64]. In fact, in graphene atoms are positioned in a regular hexagonal honeycomb structure and therefore the Voronoi tessellation is given, as explained in Section 2, by regular triangles. We have shown in this work that such tessellation is rather peculiar as it maximises the perimeter-to-area ratio of the Voronoi cells and its topology is unstable with respect to infinitesimal dislocations of the initial points, thus being affected by vibrational motions and defects. In 3D, it would be important to analyse the impact of spatial noise on other relevant crystalline structures, such as the lattice whose Voronoi cell is the Weaire-Phelan and Gabbrielli structures. Moreover, since the perfect Hexagonal Close Packed (HCP) and FCC crystals are in close correspondence and agreement is found also when infinitesimal perturbations to the position of the points are considered [58], it would be interesting to compare extensively their statistical properties as finite noise of increasing amplitude is considered. Note that this analysis may provide some useful information regarding the well-known phase transition between white tin (HCP) and grey tin (FCC).
The impact of noise on higher order statistical properties, such those of neighboring cells [49], should be seriously addressed. This matter is especially worth exploring given the recent explanation of the violation of the Aboav’s law for Poisson-Voronoi tessellations in 2D [39] and the recent investigations on higher dimensional space [65]. Finally, two additional important issues should be taken care of. First, some effort should be put on the understanding of why 2-parameter gamma distributions do such an amazing job in describing the pdfs of several geometrical properties of the Voronoi cells [66] Moreover, whereas most analyses aim at understanding the bulk statistical properties of the cells, it may be worthy changing the point of view and studying the statistical properties of the extreme cells by taking advantage of the approach based on Gnedenko’s theorem [67].
Acknowledgements
The author wishes to thank C.T.J. Dodson and four anonymous reviewers for useful comments.
References
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier Mémoire: Sur quelques propriétées des formes quadritiques positives parfaites. J. Reine Angew. Math. 1907, 133, 97–178. [Google Scholar]
- Voronoi, G. Nouvelles Applications des Parametres Continus a la Theorie des Formes Quadratiques. Duesieme Memoire: Recherches sur les Paralleloderes Primitifs. J. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar]
- Isokawa, Y. Poisson-Voronoi tessellations in three-dimensional hyperbolic spaces. Adv. Appl. Probl. 2000, 32, 648–662. [Google Scholar] [CrossRef]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S. N. Spatial Tessellations - Concepts and Applications of Voronoi Diagrams, 2nd ed.; Wiley: London, UK, 2000. [Google Scholar]
- Sortais, M.; Hermann, S.; Wolisz, A. Analytical Investigation of Intersection-Based Range-Free Localization Information Gain. In Proceedings of the European Wireless 2007, Paris, France, April 2007. [Google Scholar]
- Finney, J. L. Volume occupation, environment and. accessibility in proteins. The problem of the protein surface. J. Mol. Biol. 1975, 96, 721–732. [Google Scholar] [CrossRef]
- Icke, V. Particles, space and time. Astrophys. Space Sci. 1996, 244, 293–312. [Google Scholar] [CrossRef]
- Barrett, T. M. Voronoi tessellation methods to delineate harvest units for spatial forest planning. Can. J. For. Res. 1997, 27, 903–910. [Google Scholar] [CrossRef]
- Goede, A.; Preissner, R.; Frömmel, C. Voronoi cell: New method for allocation of space among atoms: Elimination of avoidable errors in calculation of atomic volume and density. J. Comp. Chem. 1997, 18, 1113–1118. [Google Scholar] [CrossRef]
- Weaire, D.; Kermode, J.P.; Wejchert, J. On the distribution of cell areas in a Voronoi network. Phil. Mag. B 1986, 53, L101–L105. [Google Scholar] [CrossRef]
- Dotera, T. Cell Crystals: Kelvin’s Polyhedra in Block Copolymer Melts. Phys. Rev. Lett. 1999, 82, 105–108. [Google Scholar] [CrossRef]
- Bennett, L. H.; Kuriyama, M.; Long, G. G.; Melamud, M.; Watson, R. E.; Weinert, M. Local atomic environments in periodic and aperiodic Al-Mn alloys. Phys. Rev. B 1986, 34, 8270–8272. [Google Scholar] [CrossRef]
- Li, S.; Wongsto, A. Unit cells for micromechanical analyses of particle-reinforced composites. Mechanics of Materials 2004, 36, 543–572. [Google Scholar] [CrossRef]
- Soyer, A.; Chomilier, J.; Mornon, J.P.; Jullien, R.; Sadoc, J.F. Voronoi tessellation reveals the condensed matter character of folded proteins. Phys. Rev. Lett. 2000, 85, 3532–3535. [Google Scholar] [CrossRef] [PubMed]
- Bassani, F.; Pastori-Parravicini, G. Electronic States and Optical Transitions in Solids; Pergamon: Oxford, UK, 1975. [Google Scholar]
- Ashcroft, N. W.; Mermin, N. D. Solid State Physics; Saunders: Philadelphia, USA, 1976. [Google Scholar]
- Tsumuraya, K.; Ishibashi, K.; Kusunoki, K. Statistics of Voronoi polyhedra in a model silicon glass. Phys. Rev. B 1993, 47, 8552. [Google Scholar] [CrossRef]
- Yu, D.-Q.; Chen, M.; Han, X.-J. Structure analysis methods for crystalline solids and supercooled liquids. Phys. Rev. E 2005, 72, 051202. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, H. G. E.; Ilyin, V.; Makedonska, N.; Procaccia, I.; Schupper, N. Statistical mechanics of the glass transition as revealed by a Voronoi tessellation. Phys. Rev. E 2007, 75, 50404(R). [Google Scholar] [CrossRef] [PubMed]
- Luchnikov, V. A.; Medvedev, N. N.; Naberukhin, Yu. I.; Schober, H. R. Voronoi-Delaunay analysis of normal modes in a simple model glass. Phys. Rev. B 2000, 62, 3181. [Google Scholar] [CrossRef]
- Averill, F. W.; Painter, G. S. Pseudospherical integration scheme for electronic-structure calculations. Phys. Rev. B 1989, 39, 8115. [Google Scholar] [CrossRef]
- Rapcewicz, K.; Chen, B.; Yakobson, B.; Bernholc, J. Consistent methodology for calculating surface and interface energies. Phys. Rev. B 1998, 57, 007281. [Google Scholar] [CrossRef]
- Rapaport, D. C. Hexagonal convection patterns in atomistically simulated fluids. Phys. Rev. E 2006, 73, 025301. [Google Scholar] [CrossRef]
- Tsai F., T.-C.; Sun, N.-Z.; Yeh W., W.-G. Geophysical parameterization and parameter structure identification using natural neighbors in groundwater inverse problems. J. Hydrology 2004, 308, 269–283. [Google Scholar] [CrossRef]
- Lucarini, V.; Danihlik, E.; Kriegerova, I.; Speranza, A. Does the Danube exist? Versions of reality given by various regional climate models and climatological data sets. J. Geophys. Res. 2007, 112, D13103. [Google Scholar] [CrossRef]
- Lucarini, V.; Danihlik, R.; Kriegerova, I.; Speranza, A. Hydrological Cycle in the Danube basin in present-day and XXII century simulations by IPCCAR4 global climate models. J. Geophys. Res. 2008, 113, D09107. [Google Scholar] [CrossRef]
- Thiessen, A. H.; Alter, J. C. Climatological Data for July, 1911: District No. 10, Great Basin. Monthly Weather Review 1911, 1082–1089. [Google Scholar]
- Bowyer, A. Computing Dirichlet tessellations. Computer J. 1981, 24, 162–166. [Google Scholar] [CrossRef]
- Watson, D. F. Computing the n-dimensional tessellation with application to Voronoi polytopes. Computer J. 1981, 24, 167–172. [Google Scholar] [CrossRef]
- Tanemura, M.; Ogawa, T.; Ogita, N. A new algorithm for three-dimensional Voronoi tessellation. J. Compu. Phys. 1983, 51, 191–207. [Google Scholar] [CrossRef]
- Barber, C. B.; Dobkin, D. P.; Huhdanpaa, H.T. The Quickhull Algorithm for Convex Hulls. ACM TOMS 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Han, D.; Bray, M. Automated Thiessen polygon generation. Water Resour. Res. 2006, 42, W11502. [Google Scholar] [CrossRef]
- Meijering, J. L. Interface area, edge length, and number of vertices in crystal aggregates with random nucleation: Phillips Research Reports. Philips Res. Rep. 1953, 8, 270–290. [Google Scholar]
- Christ, N. H.; Friedberg, R.; Lee, T. D. Random lattice field theory: General formulation. Nuclear Physics B 1982, 202, 89–125. [Google Scholar] [CrossRef]
- Drouffe, J. M.; Itzykson, C. Random geometry and the statistics of two-dimensional cells. Nucl. Phys. B 1984, 235, 45–53. [Google Scholar] [CrossRef]
- Miles, R. E. A synopsis of Poisson Flats In Euclidean Spaces. In Stochastic Geometry; Harding, E. F., Kendall, D. G., Eds.; Wiley: London, UK, 1974; pp. 202–227. [Google Scholar]
- Møller, J. Random tessellations in Rd. Adv. Appl. Prob. 1989, 21, 37–73. [Google Scholar] [CrossRef]
- Calka, P. Precise formulae for the distributions of the principal geometric characteristics of the typical cells of a two-dimensional Poisson Voronoi tessellation and a Poisson line process. Adv. Appl. Probab. 2003, 35, 551–562. [Google Scholar] [CrossRef]
- Hilhorst, H. J. Planar Voronoi cells: the violation of Aboav’s law explained. J. Phys. A: Math. Gen. 2006, 39, 7227–7243. [Google Scholar] [CrossRef]
- Finch, S. R. unpublished. Available on http://algo.inria.fr/csolve/vi.pdf. Addendum to Finch S. R.; Mathematical Constants; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kovalenko, I. N. Proof of David Kendall’s conjecture concerning the shape of large random polygons. Cybernetics and Systems Analysis 1997, 33, 461–467. [Google Scholar] [CrossRef]
- Hug, D.; Schneider, R. Typical cells in Poisson hyperplane tessellations. Discr. Comput. Geom. 2007, 38, 305–319. [Google Scholar] [CrossRef]
- Hug, D.; Reitzner, M.; Schneider, R. The limit shape of the zero cell in a stationary Poisson hyperplane tessellation. Ann. Probab. 2004, 32, 1140–1167. [Google Scholar]
- Kumar, S.; Kurtz, S. K.; Banavar, J. R.; Sharma, M. G. Properties of a three-dimensional Poisson-Voronoi tessellation: a Monte Carlo study. Journal of Statistical Physics 1992, 67, 523–551. [Google Scholar] [CrossRef]
- Hinde, A. L.; Miles, R. E. Monte Carlo estimates of the distributions of the random polygons of the Voronoi tessellation with respect to a Poisson process. Journal of Statistical Computation and Simulation 1980, 10, 205–223. [Google Scholar] [CrossRef]
- Zhu, H. X.; Thorpe, S. M.; Windle, A. H. The geometrical properties of irregular two-dimensional Voronoi tessellations. Philosophical Magazine A 2001, 81, 2765–2783. [Google Scholar] [CrossRef]
- Tanemura, M. Statistical distributions of Poisson-Voronoi cells in two and three Dimensions. Forma 2003, 18, 221–247. [Google Scholar]
- Hilhorst, H. J. Asymptotic statistics of the n-sided planar Poisson–Voronoi cell: I. Exact results. J. Stat. Mech. 2005, P09005. [Google Scholar] [CrossRef]
- Kumar, V. S.; Kumaran, V. Voronoi neighbor statistics of hard-disks and hard-spheres. J. Chem. Phys. 2005, 123, 074502. [Google Scholar] [CrossRef] [PubMed]
- Newman, D. The Hexagon Theorem. IEEE Trans. Inform. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Du, Q.; Wang, D. The Optimal Centroidal Voronoi Tessellations and the Gersho’s Conjecture in the Three Dimensional Space. Comput. Math. Appl. 2005, 49, 1355–1373. [Google Scholar] [CrossRef]
- Karch, R.; Neumann, M.; Neumann, F.; Ullrich, R.; Neumüller, J.; Schreiner, W. A Gibbs point field model for the spatial pattern of coronary capillaries. Physica A 2006, 369, 599–611. [Google Scholar] [CrossRef]
- Swift, J.; Hohenberg, P.C. Hydrodynamic fluctuations at the convective instability. Phys. Rev. A 1977, 15, 319–328. [Google Scholar] [CrossRef]
- Hales, T. C. A Proof of the Kepler Conjecture. Ann. Math. 2005, 162, 1065–1185. [Google Scholar] [CrossRef]
- Weaire, D.; Phelan, R. A Counter-Example to Kelvin’s Conjecture on Minimal Surfaces. Philos. Mag. Lett. 1994, 69, 107–110. [Google Scholar] [CrossRef]
- Gabbrielli, R. A new counter-example to Kelvin’s conjecture on minimal surfaces. Phil. Mag. Lett. 2009, 89. [Google Scholar] [CrossRef]
- Entezari, A.; van de Ville, D.; Möller, T. Practical Box Splines for Reconstruction on the Body Centered Cubic Lattice. IEEE T. Vis. Comput. Gr. 2008, 14, 313–328. [Google Scholar] [CrossRef] [PubMed]
- Troadec, J. P.; Gervois, A.; Oger, L. Statistics of Voronoi cells of slightly perturbed face-centered cubic and hexagonal close-packed lattices. Europhy. Lett. 1998, 42, 167–172. [Google Scholar] [CrossRef]
- Lucarini, V. From Symmetry Breaking to Poisson Point Process in 2D Voronoi Tessellations: the Generic Nature of Hexagons. J. Stat. Phys. 2008, 130, 1047–1062. [Google Scholar] [CrossRef]
- Lucarini, V. Three-Dimensional Random Voronoi Tessellations: From Cubic Crystal Lattices to Poisson Point Processes. J. Stat. Phys. 2009, 134, 185–206. [Google Scholar] [CrossRef]
- Lewis, F. T. The correlation between cell division and the shapes and sizes of prismatic cells in the epidermis of Cucumis. Anat. Rec. 1928, 38, 341–376. [Google Scholar] [CrossRef]
- Desch, C. H. The solidification of metals from the liquid state. J. Inst. Metals 1919, 22, 241. [Google Scholar]
- Finch, S. R. Mathematical Constants; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Geim, A. K.; Novoselov, K. S. The rise of grapheme. Nature Materials 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Hilhorst, H. J. Heuristic theory for many-faced d-dimensional Poisson-Voronoi cells, 2009; arXiv:cond-mat/0906.4449v1.
- Dodson, C. T. J. On the entropy flows to disorder. 2008; arXiv:math-ph /0811.4318v2. [Google Scholar]
- Coles, S. G. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).