OptMAVEn-2.0: De novo Design of Variable Antibody Regions against Targeted Antigen Epitopes
Abstract
1. Introduction
2. Methods
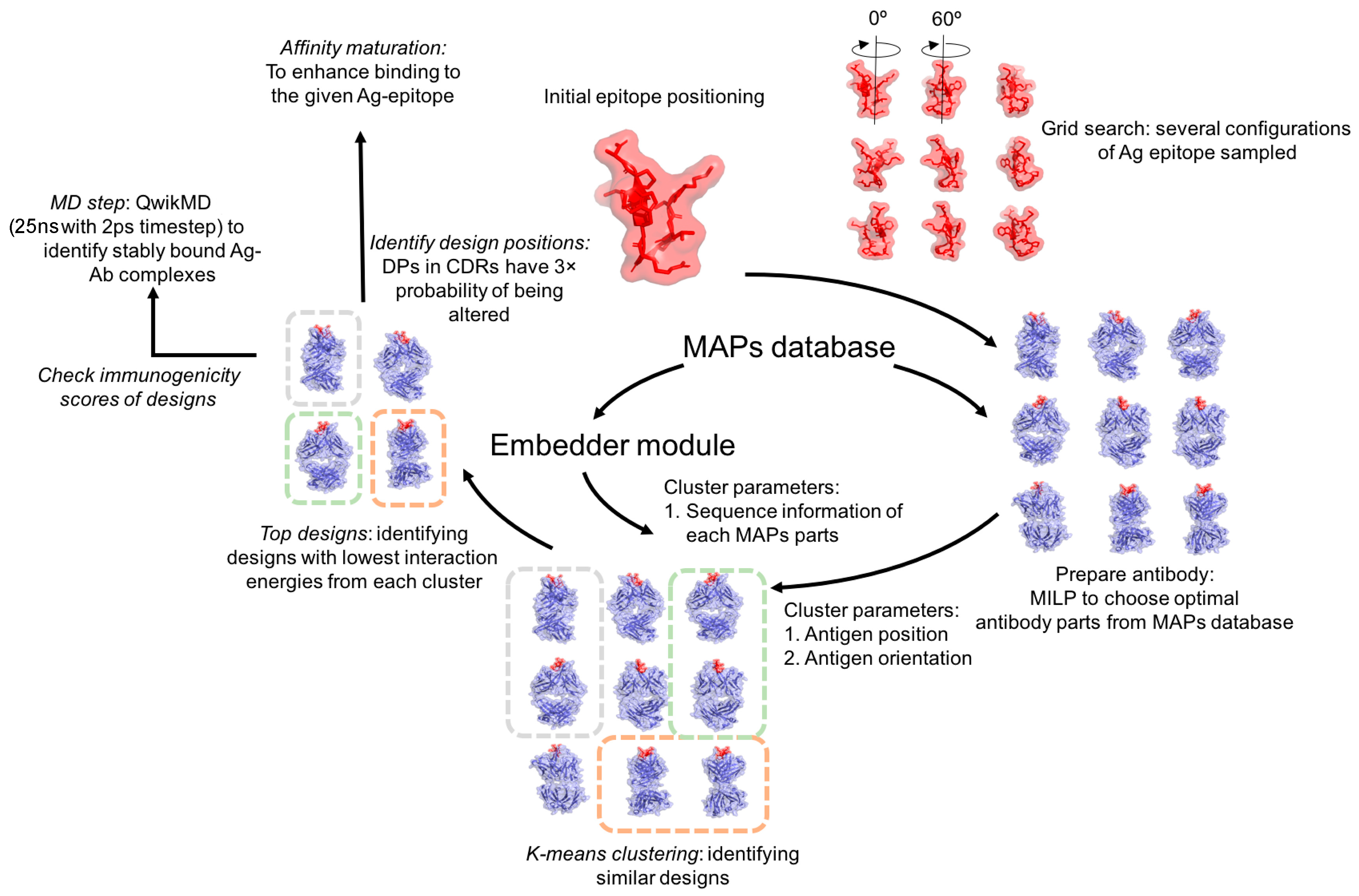
2.1. Overview
2.2. Design and Implementation
2.3. Starting an Experiment
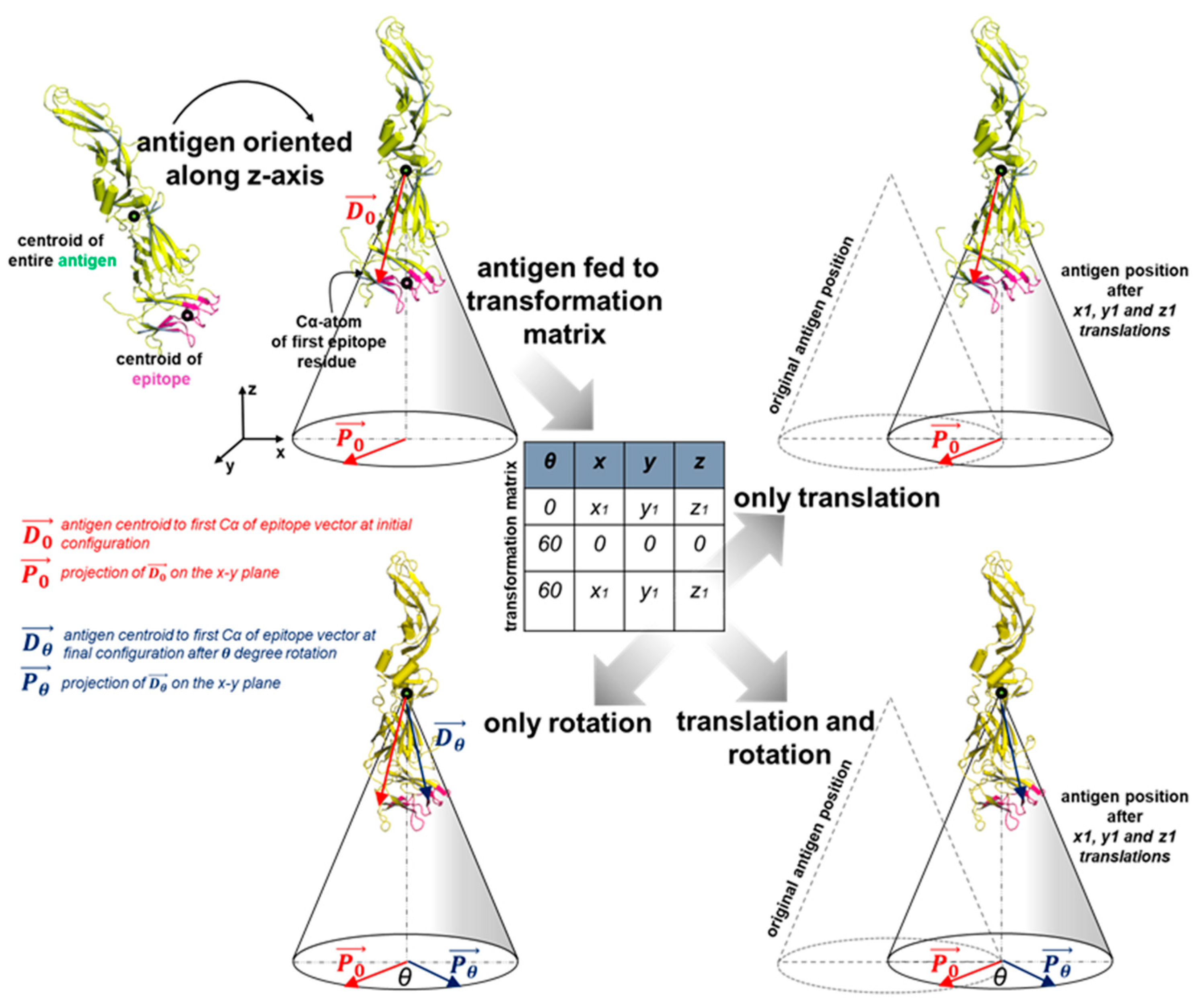
2.4. Antigen Positioning
2.5. MAPs Interaction Energy Calculations
2.6. Optimal Selection of MAPs Parts
2.7. Antibody Assembly
2.8. Clustering the Antibody Designs
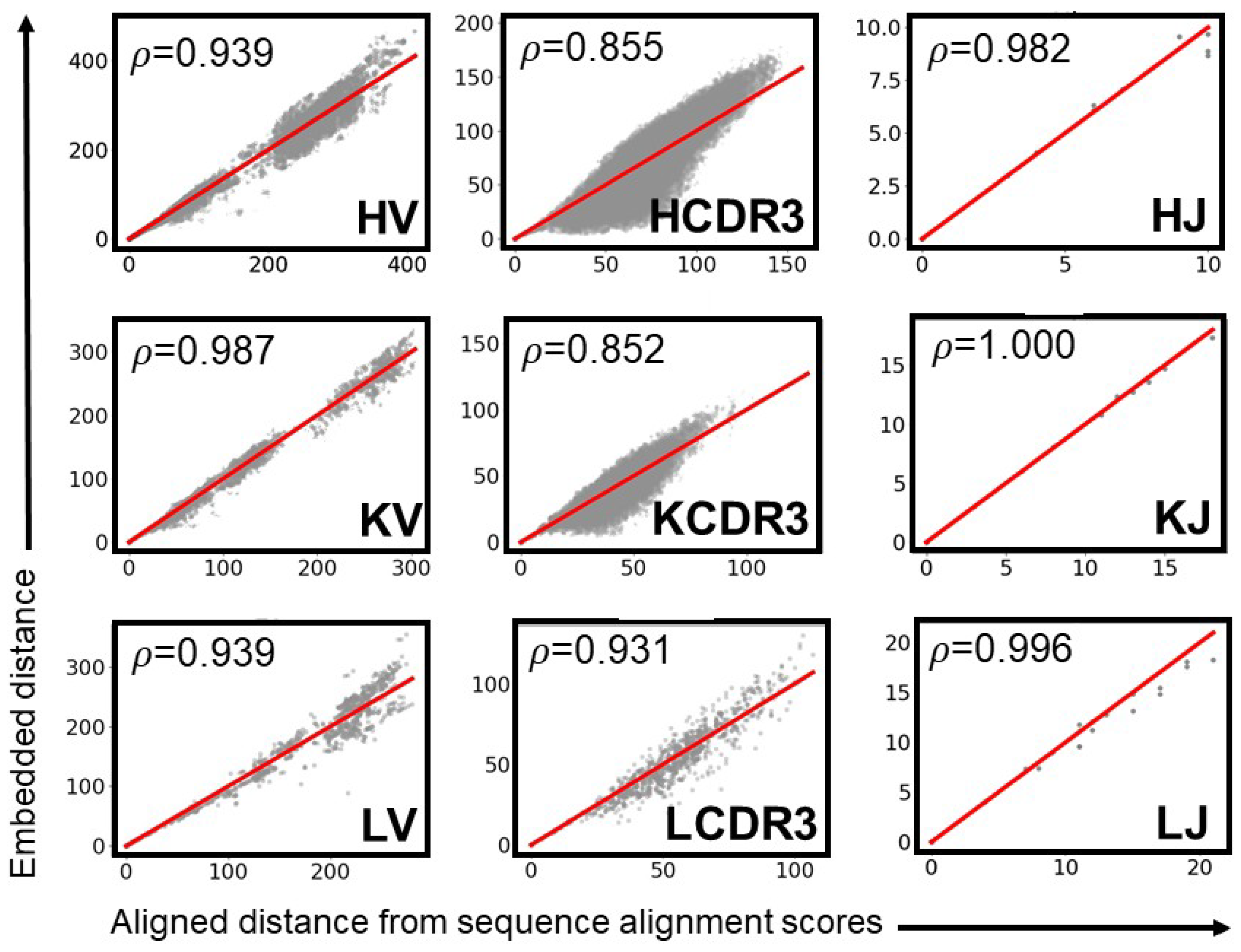
2.8.1. Pre-Processing Step
2.8.2. k-means Clustering
2.9. Ranking the Antibody Designs
3. Results
3.1. Computational Benchmarking of OptMAVEn and OptMAVEn-2.0 on 10 Antigens
OptMAVEn-2.0 Reduces Time and Disk Requirements by 74% and 84%, Respectively
3.2. Test of OptMAVEn-2.0 on 54 Additional Antigens Reveals Sub-Linear Scaling
3.3. Test Cases on Zika E Protein
3.3.1. Setup for the Test Cases on Zika E Protein
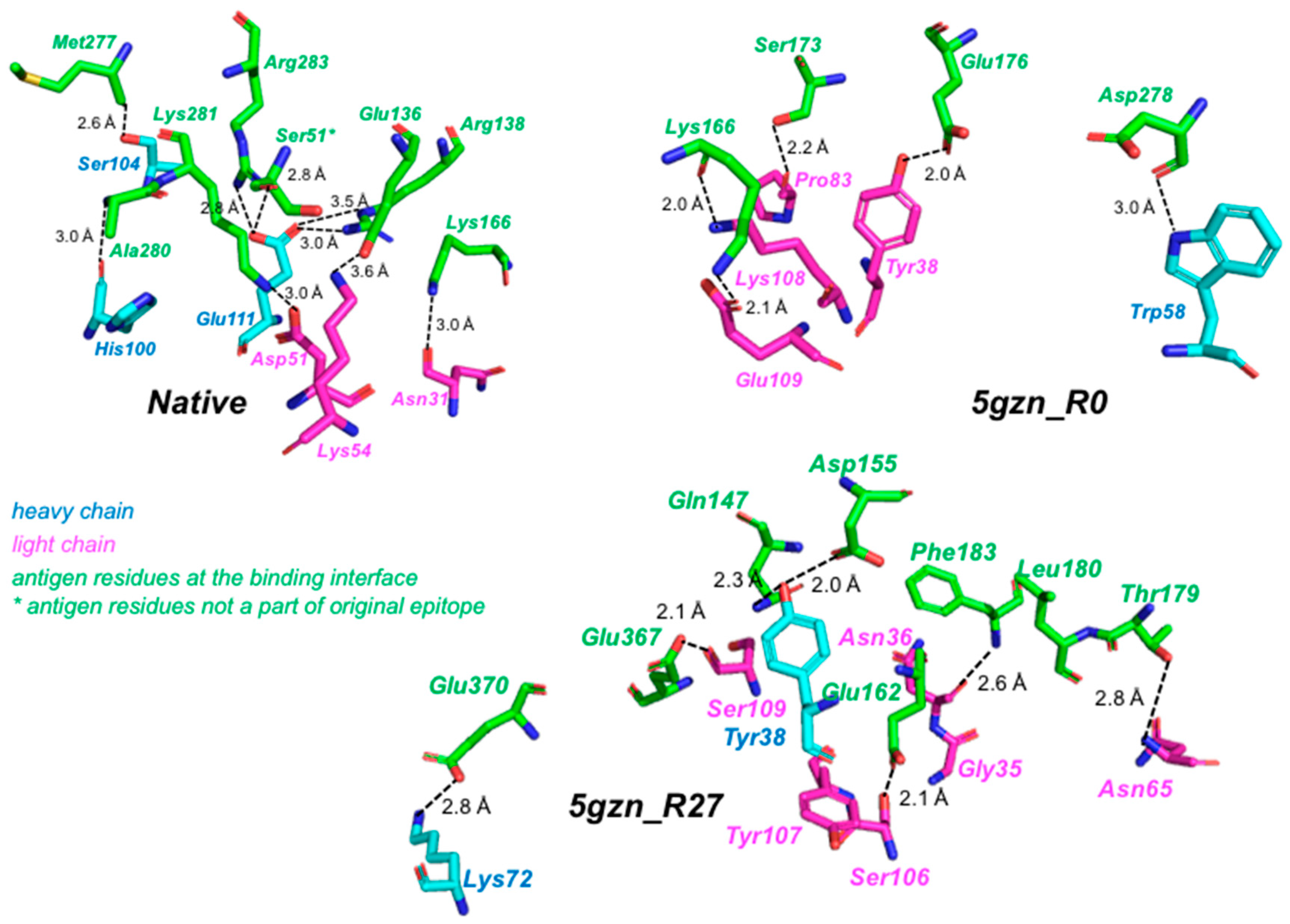
3.3.2. Recovery of Native Residues in the Test Cases on Zika E Protein
3.3.3. Humanization Scores in the Test Cases on Zika E Protein
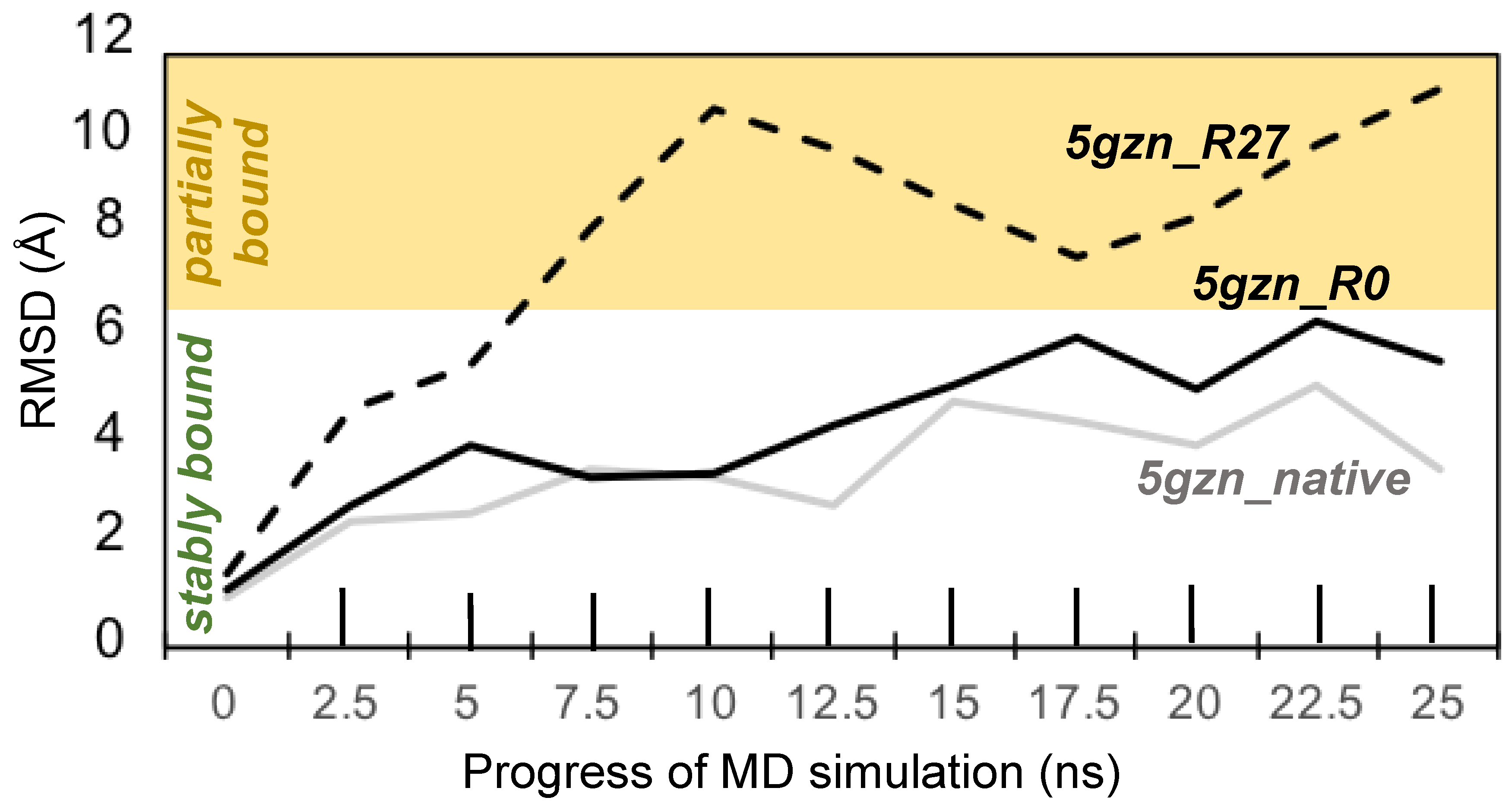
3.3.4. Molecular Dynamics Simulations
3.4. Test Cases on Hen Egg White Lysozyme
3.4.1. Setup for the Test Cases on Lysozyme
3.4.2. Recovery of Native Residues and Contacts in the Test Cases on Lysozyme
4. Summary and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ecker, D.M.; Jones, S.D.; Levine, H.L. The therapeutic monoclonal antibody market. mAbs 2015, 7, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Mahmuda, A.; Bande, F.; Al-Zihiry, K.J.K.; Abdulhaleem, N.; Majid, R.A.; Hamat, R.A.; Abdullah, W.O.; Unyah, Z. Monoclonal antibodies: A review of therapeutic applications and future prospects. Trop. J. Pharm. Res. 2017, 16, 713–722. [Google Scholar] [CrossRef]
- Shepard, H.M.; Phillips, G.L.; Thanos, C.D.; Feldmann, M. Developments in therapy with monoclonal antibodies and related proteins. Clin. Med. J. R. Coll. Physicians 2017, 17, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Schirrmann, T.; Meyer, T.; Schütte, M.; Frenzel, A.; Hust, M. Phage display for the generation of antibodies for proteome research, diagnostics and therapy. Molecules 2011, 16, 412–426. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.; Conroy, P.J.; Whisstock, J.C.; O’Kennedy, R.J. A tale of two specificities: Bispecific antibodies for therapeutic and diagnostic applications. Trends Biotechnol. 2013, 31, 621–632. [Google Scholar] [CrossRef] [PubMed]
- Weiner, G.J. Building better monoclonal antibody-based therapeutics. Nat. Rev. Cancer 2015, 15, 361–370. [Google Scholar] [CrossRef] [PubMed]
- Weiner, L.M.; Surana, R.; Wang, S. Monoclonal antibodies: Versatile platforms for cancer immunotherapy. Nat. Rev. Immunol. 2010, 10, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Rudnick, S.I.; Adams, G.P. Affinity and Avidity in Antibody-Based Tumor Targeting. Cancer Biother. Radiopharm. 2009, 24, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Irani, V.; Guy, A.J.; Andrew, D.; Beeson, J.G.; Ramsland, P.A.; Richards, J.S. Molecular properties of human IgG subclasses and their implications for designing therapeutic monoclonal antibodies against infectious diseases. Mol. Immunol. 2015, 67, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Simpson, E.L.; Bieber, T.; Guttman-Yassky, E.; Beck, L.A.; Blauvelt, A.; Cork, M.J.; Silverberg, J.I.; Deleuran, M.; Kataoka, Y.; Lacour, J.-P.; et al. Two Phase 3 Trials of Dupilumab versus Placebo in Atopic Dermatitis. N. Engl. J. Med. 2016, 375, 2335–2348. [Google Scholar] [CrossRef] [PubMed]
- Saper, C.B. A guide to the perplexed on the specificity of antibodies. J. Histochem. Cytochem. 2009, 57, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Shriver, Z.; Trevejo, J.M.; Sasisekharan, R. Antibody-based strategies to prevent and treat influenza. Front. Immunol. 2015, 6, 315. [Google Scholar] [CrossRef] [PubMed]
- Saeed, A.F.; Wang, R.; Ling, S.; Wang, S. Antibody engineering for pursuing a healthier future. Front. Microbiol. 2017, 8, 495. [Google Scholar] [CrossRef] [PubMed]
- Boder, E.T.; Raeeszadeh-Sarmazdeh, M.; Price, J.V. Engineering antibodies by yeast display. Arch. Biochem. Biophys. 2012, 526, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Leenaars, M.; Hendriksen, C.F.M. Critical steps in the production of polyclonal and monoclonal antibodies: Evaluation and recommendations. ILAR J. 2005, 46, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Pantazes, R.J.; Maranas, C.D. OptMAVEn—A new framework for the de novo design of antibody variable region models targeting specific antigen epitopes. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Pantazes, R.J.; Maranas, C.D. OptCDR: A general computational method for the design of antibody complementarity determining regions for targeted epitope binding. Protein Eng. Des. Sel. 2010, 23, 849–858. [Google Scholar] [CrossRef] [PubMed]
- Lapidoth, G.D.; Baran, D.; Pszolla, G.M.; Norn, C.; Alon, A.; Tyka, M.D.; Fleishman, S.J. AbDesign: An algorithm for combinatorial backbone design guided by natural conformations and sequences. Proteins Struct. Funct. Bioinform. 2015, 83, 1385–1406. [Google Scholar] [CrossRef] [PubMed]
- Adolf-Bryfogle, J.; Kalyuzhniy, O.; Kubitz, M.; Weitzner, B.D.; Hu, X.; Adachi, Y.; Schief, W.R.; Dunbrack, R.L., Jr. Rosetta Antibody Design (RAbD): A General Framework for Computational Antibody Design. PLoS Comput. Biol. 2018, 14, e1006112. [Google Scholar] [CrossRef] [PubMed]
- Lazar, G.A.; Desjarlais, J.R.; Jacinto, J.; Karki, S.; Hammond, P.W. A molecular immunology approach to antibody humanization and functional optimization. Mol. Immunol. 2007, 44, 1996–2008. [Google Scholar] [CrossRef] [PubMed]
- De Groot, A.S.; McMurry, J.; Moise, L. Prediction of immunogenicity: In silico paradigms, ex vivo and in vivo correlates. Curr. Opin. Pharmacol. 2008, 8, 620–626. [Google Scholar] [CrossRef] [PubMed]
- Chennamsetty, N.; Voynov, V.; Kayser, V.; Helk, B.; Trout, B.L. Design of therapeutic proteins with enhanced stability. Proc. Natl. Acad. Sci. USA 2009, 106, 11937–11942. [Google Scholar] [CrossRef] [PubMed]
- Miklos, A.E.; Kluwe, C.; Der, B.S.; Pai, S.; Sircar, A.; Hughes, R.A.; Berrondo, M.; Xu, J.; Codrea, V.; Buckley, P.E.; et al. Structure-based design of supercharged, highly thermoresistant antibodies. Chem. Biol. 2012, 19, 449–455. [Google Scholar] [CrossRef] [PubMed]
- Der, B.S.; Kluwe, C.; Miklos, A.E.; Jacak, R.; Lyskov, S.; Gray, J.J.; Georgiou, G.; Ellington, A.D.; Kuhlman, B. Alternative Computational Protocols for Supercharging Protein Surfaces for Reversible Unfolding and Retention of Stability. PLoS ONE 2013, 8, e64363. [Google Scholar] [CrossRef] [PubMed]
- Pantazes, R.J.; Maranas, C.D. MAPs: A database of modular antibody parts for predicting tertiary structures and designing affinity matured antibodies. BMC Bioinform. 2013, 14, 168. [Google Scholar] [CrossRef] [PubMed]
- Stojmirovic, A. Quasi-metric spaces with measure. Topol. Proc. 2004, 28, 655–671. [Google Scholar]
- Moré, J.J.; Wu, Z. Distance Geometry Optimization for Protein Structures. J. Glob. Optim. 1999, 15, 219–234. [Google Scholar] [CrossRef]
- Stojmirovic, A.; Yu, Y. Information channels in protein interaction networks. arXiv, 2009; arXiv:0901.0287. [Google Scholar]
- Ribeiro, J.V.; Bernardi, R.C.; Rudack, T.; Stone, J.E.; Phillips, J.C.; Freddolino, P.L.; Schulten, K. QwikMD—Integrative Molecular Dynamics Toolkit for Novices and Experts. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Pantazes, R.J.; Grisewood, M.J.; Li, T.; Gifford, N.P.; Maranas, C.D. The Iterative Protein Redesign and Optimization (IPRO) suite of programs. J. Comput. Chem. 2015, 36, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Python Software Foundation. Python Language Reference, version 2.7; Python Software Foundation: Wilmington, DE, USA, 2013. [Google Scholar]
- Community, N. NumPy Reference. 2011. Available online: https://docs.scipy.org/doc/numpy-1.13.0/reference/ (accessed on 20 May 2018).
- Oliphant, T.E. SciPy: Open source scientific tools for Python. Comput. Sci. Eng. 2007. [Google Scholar] [CrossRef]
- Cock, P.J.A.; Antao, T.; Chang, J.T.; Chapman, B.A.; Cox, C.J.; Dalke, A.; Friedberg, I.; Hamelryck, T.; Kauff, F.; Wilczynski, B.; et al. Biopython: Freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 2009, 25, 1422–1423. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Lefranc, M.-P. IMGT Unique Numbering for the Variable (V), Constant (C), and Groove (G) Domains of IG, TR, MH, IgSF, and MhSF. Cold Spring Harb. Protoc. 2011, 2011, 633–642. [Google Scholar] [CrossRef] [PubMed]
- Henikoff, S.; Henikoff, J.G. Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA 1992, 89, 10915–10919. [Google Scholar] [CrossRef] [PubMed]
- Havel, T.; Kuntz, I.; Crippen, G. The theory and practice of distance geometry. Bull. Math. Biol. 1983, 45, 665–720. [Google Scholar] [CrossRef]
- Mucherino, A.; Liberti, L.; Lavor, C. MD-jeep: An implementation of a Branch and Prune algorithm for distance geometry problems. In Mathematical Software—ICMS 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 186–197. [Google Scholar]
- Schwieters, C.D.; Kuszewski, J.J.; Tjandra, N.; Clore, G.M. The Xplor-NIH NMR molecular structure determination package. J. Magn. Reson. 2003, 160, 65–73. [Google Scholar] [CrossRef]
- Pappu, R.V.; Hart, R.K.; Ponder, J.W. Tinker: A package for molecular dynamics simulation. J. Phys. Chem. B 1988, 102, 9725–9742. [Google Scholar] [CrossRef]
- Marimont, R.B.; Shapiro, M.B. Nearest neighbour searches and the curse of dimensionality. IMA J. Appl. Math. 1979, 24, 59–70. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, H.; Liu, X.; Dai, L.; Ma, T.; Qi, J.; Wong, G.; Peng, R.; Liu, S.; Li, J. Molecular determinants of human neutralizing antibodies isolated from a patient infected with Zika virus. Sci. Transl. Med. 2016, 8. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Fernandez, E.; Dowd, K.A.; Speer, S.D.; Platt, D.J.; Gorman, M.J.; Govero, J.; Nelson, C.A.; Pierson, T.C.; Diamond, M.S. Structural Basis of Zika Virus-Specific Antibody Protection. Cell 2016. [Google Scholar] [CrossRef] [PubMed]
- Holmes, M.A.; Buss, T.N.; Foote, J. Conformational correction mechanisms aiding antigen recognition by a humanized antibody. J. Exp. Med. 1998, 187, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Wensley, B. Structure of a Lysozyme Antibody Complex. Available online: https://www.rcsb.org/structure/4TSB (accessed on 20 May 2018).
- Rouet, R.; Dudgeon, K.; Christie, M.; Langley, D.; Christ, D. Fully human VH single domains that rival the stability and cleft recognition of camelid antibodies. J. Biol. Chem. 2015. [Google Scholar] [CrossRef] [PubMed]
- Soria-Guerra, R.E.; Nieto-Gomez, R.; Govea-Alonso, D.O.; Rosales-Mendoza, S. An overview of bioinformatics tools for epitope prediction: Implications on vaccine development. J. Biomed. Inform. 2015, 53, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Rice, P.; Longden, L.; Bleasby, A. EMBOSS: The European Molecular Biology Open Software Suite. Trends Genet. 2000. [Google Scholar] [CrossRef]
- Poosarla, V.G.; Li, T.; Goh, B.C.; Schulten, K.; Wood, T.K.; Maranas, C.D. Computational de novo design of antibodies binding to a peptide with high affinity. Biotechnol. Bioeng. 2017, 114, 1331–1342. [Google Scholar] [CrossRef] [PubMed]
- Foote, J.; Eisen, H.N. Kinetic and affinity limits on antibodies produced during immune responses. Proc. Natl. Acad. Sci. USA 1995, 92, 1254–1256. [Google Scholar] [CrossRef] [PubMed]
- Fellouse, F.A.; Esaki, K.; Birtalan, S.; Raptis, D.; Cancasci, V.J.; Koide, A.; Jhurani, P.; Vasser, M.; Wiesmann, C.; Kossiakoff, A.A.; et al. High-throughput Generation of Synthetic Antibodies from Highly Functional Minimalist Phage-displayed Libraries. J. Mol. Biol. 2007. [Google Scholar] [CrossRef] [PubMed]
- Entzminger, K.C.; Hyun, J.M.; Pantazes, R.J.; Patterson-Orazem, A.C.; Qerqez, A.N.; Frye, Z.P.; Hughes, R.A.; Ellington, A.D.; Lieberman, R.L.; Maranas, C.D.; et al. De novo design of antibody complementarity determining regions binding a FLAG tetra-peptide. Sci. Rep. 2017, 7, 10295. [Google Scholar] [CrossRef] [PubMed]
- Checa, A.; Ortiz, A.R.; De Pascual-Teresa, B.; Gago, F. Assessment of solvation effects on calculated binding affinity differences: Trypsin inhibition by flavonoids as a model system for congeneric series. J. Med. Chem. 1997, 40, 4136–4145. [Google Scholar] [CrossRef] [PubMed]
- Lazaridis, T.; Karplus, M. Effective energy function for proteins in solution. Proteins 1999, 35, 133–152. [Google Scholar] [CrossRef]
- Choi, H.; Kang, H.; Park, H. New solvation free energy function comprising intermolecular solvation and intramolecular self-solvation terms. J. Cheminform. 2013, 5, 8. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Liu, X.; Zhang, J.Z.H. Interaction Entropy: A New Paradigm for Highly Efficient and Reliable Computation of Protein-Ligand Binding Free Energy. J. Am. Chem. Soc. 2016, 138, 5722–5728. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Singh, S.K.; Wang, X.; Rup, B.; Gill, D. Coupling of aggregation and immunogenicity in biotherapeutics: T- and B-cell immune epitopes may contain aggregation-prone regions. Pharm. Res. 2011, 28, 949–961. [Google Scholar] [CrossRef] [PubMed]

| Category | Criterion | Gap Penalty (g) | ||||
|---|---|---|---|---|---|---|
| Rank 1 | Rank 2 | Rank 3 | Rank 4 | Rank 5 | ||
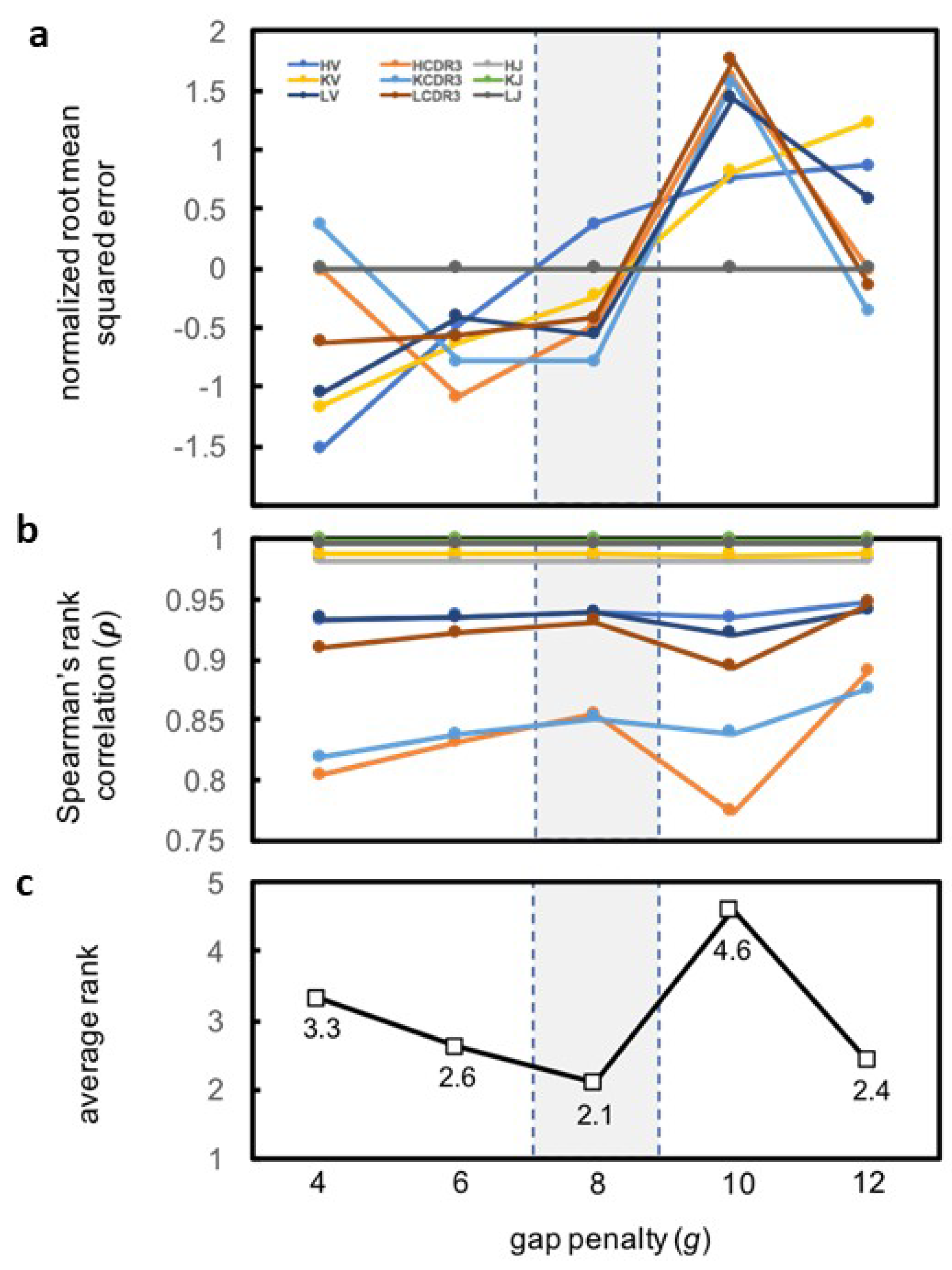
| HV | ρ | 12 | 8 | 6 | 10 | 4 |
| HCDR3 | ρ | 12 | 8 | 6 | 4 | 10 |
| KV | ρ | 12 | 8 | 6 | 4 | 10 |
| KCDR3 | ρ | 12 | 8 | 10 | 6 | 4 |
| LV | ρ | 12 | 8 | 6 | 4 | 10 |
| LCDR3 | ρ | 12 | 8 | 6 | 4 | 10 |
| HV | RMSE | 4 | 6 | 8 | 10 | 12 |
| HCDR3 | RMSE | 6 | 8 | 12 | 4 | 10 |
| KV | RMSE | 4 | 8 | 6 | 12 | 10 |
| KCDR3 | RMSE | 8 | 6 | 12 | 4 | 10 |
| LV | RMSE | 4 | 8 | 6 | 12 | 10 |
| LCDR3 | RMSE | 4 | 6 | 8 | 12 | 10 |
| Antigen | Tpos | Tener | TMILP | TCPU | Dmax | Emin | Npos |
|---|---|---|---|---|---|---|---|
| 1NSN | 32.7 | 214.2 | 26.8 | 273.7 | 1004 | −658.7 | 2428 |
| 2IGF | 2.1 | 20.0 | 26.4 | 48.4 | 820 | −76.4 | 3023 |
| 2R0W | 2.0 | 17.8 | 20.2 | 40.0 | 779 | −277.0 * | 2955 |
| 2VXQ | 26.1 | 174.4 | 19.6 | 220.1 | 970 | −174.5 | 2711 |
| 2ZUQ | 41.6 | 290.9 | 18.8 | 351.4 | 1094 | −346.0 | 2645 |
| 3BKY | 5.0 | 54.8 | 33.7 | 93.5 | 824 | −216.1 | 3035 |
| 3FFD | 5.3 | 35.0 | 19.5 | 59.8 | 657 | +576.6 | 2347 |
| 3G5V | 22.0 | 33.1 | 20.8 | 75.9 | 808 | −309.9 | 2976 |
| 3L5W | 29.6 | 173.9 | 24.4 | 227.9 | 1008 | −281.4 | 2798 |
| 3MLS | 5.8 | 53.0 | 21.9 | 80.7 | 809 | −249.6 | 2903 |
| Antigen | Tpos | Tener | TMILP | TCPU | Dmax | Emin | Npos |
|---|---|---|---|---|---|---|---|
| 1NSN | 0.036 | 22.3 | 1.8 | 24.2 | 142.4 | −438.1 | 442 |
| 2IGF | 0.009 | 26.1 | 5.6 | 31.7 | 169.7 | −118.5 | 1374 |
| 2R0W | 0.010 | 22.4 | 4.9 | 27.4 | 152.9 | −127.9 * | 1204 |
| 2VXQ | 0.033 | 33.7 | 3.6 | 37.4 | 135.4 | −235.3 | 893 |
| 2ZUQ | 0.046 | 40.4 | 3.2 | 43.6 | 167.3 | −131.3 | 774 |
| 3BKY | 0.011 | 33.9 | 6.7 | 40.6 | 197.4 | −208.4 | 1647 |
| 3FFD | 0.014 | 10.9 | 2.0 | 13.0 | 83.8 | +92.6 | 492 |
| 3G5V | 0.012 | 21.0 | 4.2 | 25.2 | 137.6 | −458.5 | 1035 |
| 3L5W | 0.033 | 36.4 | 3.8 | 40.2 | 144.7 | −394.0 | 910 |
| 3MLS | 0.009 | 18.0 | 3.3 | 21.3 | 114.7 | −171.2 | 807 |
| Antigen | Tpos | Tener | TMILP | TCPU | Dmax | Emin | Npos |
|---|---|---|---|---|---|---|---|
| 1NSN | −2.96 | −0.982 | −1.162 | −1.053 | −0.848 | +220.6 | −0.740 |
| 2IGF | −2.35 | +0.116 | −0.674 | −0.184 | −0.684 | −42.1 | −0.342 |
| 2R0W | −2.29 | +0.102 | −0.613 | −0.165 | −0.707 | +149.1 * | −0.390 |
| 2VXQ | −2.90 | −0.714 | −0.732 | −0.770 | −0.855 | −60.8 | −0.482 |
| 2ZUQ | −2.95 | −0.857 | −0.774 | −0.906 | −0.815 | +214.6 | −0.534 |
| 3BKY | −2.65 | −0.208 | −0.700 | −0.362 | −0.620 | +7.7 | −0.265 |
| 3FFD | −2.58 | −0.505 | −0.984 | −0.663 | −0.895 | −484.0 | −0.679 |
| 3G5V | −3.27 | −0.198 | −0.698 | −0.479 | −0.769 | −148.6 | −0.459 |
| 3L5W | −2.95 | −0.680 | −0.806 | −0.753 | −0.843 | −112.6 | −0.488 |
| 3MLS | −2.80 | −0.469 | −0.823 | −0.578 | −0.848 | +78.4 | −0.556 |
| Shapiro P | 6.0 × 10−1 | 5.8 × 10−1 | 1.0 × 10−1 | 8.2 × 10−1 | 1.8 × 10−1 | 3.6 × 10−1 | 9.4 × 10−1 |
| mean | −2.77 | −0.440 | −0.797 | −0.591 | −0.788 | −36.3 | −0.494 |
| s. d. | 0.303 | 0.383 | 0.164 | 0.296 | 0.090 | 213.2 | 0.145 |
| p-value | 3.5 × 10−10 | 5.5 × 10−3 | 9.2 × 10−8 | 1.4 × 10−4 | 5.0 × 10−10 | 6.2 × 10−1 | 1.9 × 10−6 |
| mean (ratio) | 0.002 | 0.363 | 0.160 | 0.256 | 0.163 | n/a | 0.321 |
| % reduction | 99.8 | 63.7 | 84.0 | 74.4 | 83.7 | n/a | 67.9 |
| Antigen | Nres | Natom | Npos | TCPU | Dmax | Emin |
|---|---|---|---|---|---|---|
| 1ACY | 10 | 156 | 1558 | 40.9 | 188.3 | −370.6 |
| 1CE1 | 8 | 93 | 1694 | 44.3 | 200.9 | −513.3 |
| 1CFT | 5 | 84 | 1554 | 38.9 | 187.9 | −253.5 |
| 1DZB | 129 | 1958 | 749 | 42.2 | 136.3 | −775.8 |
| 1EGJ | 101 | 1643 | 650 | 34.1 | 106.9 | −618.6 |
| 1F90 | 9 | 156 | 1328 | 35.0 | 165.8 | −377.5 |
| 1FPT | 11 | 162 | 1478 | 38.4 | 180.0 | −455.6 |
| 1HH6 | 11 | 159 | 718 | 20.8 | 104.6 | −385.5 |
| 1I8I | 9 | 142 | 1480 | 38.4 | 179.7 | −350.8 |
| 1JHL | 129 | 1962 | 985 | 53.7 | 132.3 | −766.6 |
| 1JRH | 95 | 1491 | 397 | 21.9 | 99.6 | −541.4 |
| 1KC5 | 8 | 119 | 1299 | 36.8 | 162.1 | −376.1 |
| 1KIQ | 129 | 1968 | 730 | 41.4 | 119.1 | −750.1 |
| 1MLC | 129 | 1968 | 618 | 35.9 | 111.2 | −752.0 |
| 1N64 | 16 | 241 | 990 | 28.1 | 132.9 | −386.6 |
| 1NAK | 10 | 166 | 1192 | 41.5 | 154.1 | −393.3 |
| 1OBE | 13 | 195 | 417 | 13.5 | 77.9 | −397.0 |
| 1ORS | 132 | 2146 | 1001 | 55.7 | 162.4 | −625.5 |
| 1PZ5 | 8 | 124 | 1348 | 34.1 | 167.4 | −419.5 |
| 1QNZ | 18 | 301 | 575 | 18.5 | 91.4 | −367.3 |
| 1SM3 | 9 | 126 | 1354 | 34.8 | 167.9 | −454.2 |
| 1TQB | 102 | 1659 | 489 | 26.8 | 104.1 | −534.6 |
| 1V7M | 145 | 2258 | 588 | 37.5 | 115.4 | −561.0 |
| 1XGY | 6 | 85 | 1811 | 45.4 | 212.8 | −293.1 |
| 1ZA3 | 91 | 1346 | 71 | 7.5 | 91.8 | −758.7 |
| 2A6I | 9 | 136 | 1093 | 29.1 | 141.8 | −365.2 |
| 2BDN | 68 | 1106 | 810 | 35.2 | 115.1 | −740.6 |
| 2DQJ | 129 | 1968 | 590 | 34.0 | 111.6 | −852.4 |
| 2FJH | 98 | 1565 | 312 | 18.4 | 99.7 | −528.8 |
| 2H1P | 11 | 182 | 561 | 17.0 | 90.4 | −355.0 |
| 2HH0 | 9 | 151 | 1062 | 28.6 | 140.0 | −282.7 |
| 2HRP | 10 | 177 | 1013 | 27.9 | 135.4 | −366.5 |
| 2IFF | 129 | 1966 | 595 | 33.9 | 126.7 | −594.4 |
| 2JEL | 85 | 1293 | 596 | 28.1 | 101.9 | −539.5 |
| 2OR9 | 11 | 181 | 734 | 21.1 | 106.7 | −387.8 |
| 2QHR | 11 | 185 | 761 | 20.3 | 111.3 | −340.2 |
| 2R29 | 97 | 1553 | 641 | 33.2 | 105.3 | −698.4 |
| 3AB0 | 136 | 1955 | 380 | 23.9 | 107.8 | −765.0 |
| 3BDY | 95 | 1521 | 779 | 36.3 | 133.9 | −439.7 |
| 3CVH | 8 | 142 | 1168 | 30.7 | 149.6 | −333.7 |
| 3D85 | 133 | 2074 | 441 | 27.9 | 109.8 | −717.0 |
| 3E8U | 11 | 136 | 1481 | 38.1 | 180.8 | −431.4 |
| 3ETB | 144 | 2332 | 296 | 21.8 | 111.3 | −898.6 |
| 3F58 | 11 | 136 | 1317 | 34.6 | 168.5 | −322.6 |
| 3G6D | 106 | 1667 | 418 | 24.2 | 103.2 | −876.8 |
| 3GHB | 10 | 146 | 1341 | 33.5 | 166.7 | −383.4 |
| 3GHE | 15 | 255 | 773 | 26.9 | 112.2 | −430.1 |
| 3HR5 | 9 | 142 | 1340 | 38.4 | 166.5 | −478.7 |
| 3KS0 | 92 | 1443 | 1148 | 54.3 | 148.0 | −578.5 |
| 3MLX | 14 | 235 | 621 | 20.5 | 94.7 | −367.7 |
| 3NFP | 124 | 1909 | 292 | 19.7 | 104.5 | −771.6 |
| 3P30 | 84 | 1437 | 32 | 4.7 | 65.2 | −714.9 |
| 3QG6 | 6 | 105 | 1425 | 36.1 | 175.2 | −362.4 |
| 3RKD | 146 | 2185 | 776 | 46.1 | 124.5 | −793.7 |
| Accession | Antibody Name (from Paper) | Native Heavy Chain HScore | Designed Heavy Chain HScores | Native Light Chain HScore | Designed Light Chain HScores |
|---|---|---|---|---|---|
| 5GZN | Z3L1 | 52 | 17–36 | 4 | 16–41 |
| 5KVD | ZV-2 | 152 | 6–59 | 56 | 0–31 |
| 5KVE | ZV-48 | 128 | 21–68 | 59 | 1–27 |
| 5KVF | ZV-64 | 107 | 21–44 | 22 | 22–30 |
| 5KVG | ZV-67 | 133 | 10–39 | 111 | 10–25 |
| Accession | Native Heavy Chain HScore | Designed Heavy Chain HScores | Native Light Chain HScore | Designed Light Chain HScores |
|---|---|---|---|---|
| 1BVK | 85 | 10–37 | 57 | 7–27 |
| 4TSB | 26 | 12–32 | 21 | 16–38 |
| 4PGJ | 87 | 20–49 | N/A | 5–39 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, R.; Allan, M.F.; Maranas, C.D. OptMAVEn-2.0: De novo Design of Variable Antibody Regions against Targeted Antigen Epitopes. Antibodies 2018, 7, 23. https://doi.org/10.3390/antib7030023
Chowdhury R, Allan MF, Maranas CD. OptMAVEn-2.0: De novo Design of Variable Antibody Regions against Targeted Antigen Epitopes. Antibodies. 2018; 7(3):23. https://doi.org/10.3390/antib7030023
Chicago/Turabian StyleChowdhury, Ratul, Matthew F. Allan, and Costas D. Maranas. 2018. "OptMAVEn-2.0: De novo Design of Variable Antibody Regions against Targeted Antigen Epitopes" Antibodies 7, no. 3: 23. https://doi.org/10.3390/antib7030023
APA StyleChowdhury, R., Allan, M. F., & Maranas, C. D. (2018). OptMAVEn-2.0: De novo Design of Variable Antibody Regions against Targeted Antigen Epitopes. Antibodies, 7(3), 23. https://doi.org/10.3390/antib7030023





