Model-Based Comparison of Antibody Dimerization in Continuous and Batch-Wise Downstream Processing
Abstract
:1. Introduction
2. Theory
2.1. Downstream Processing Platform
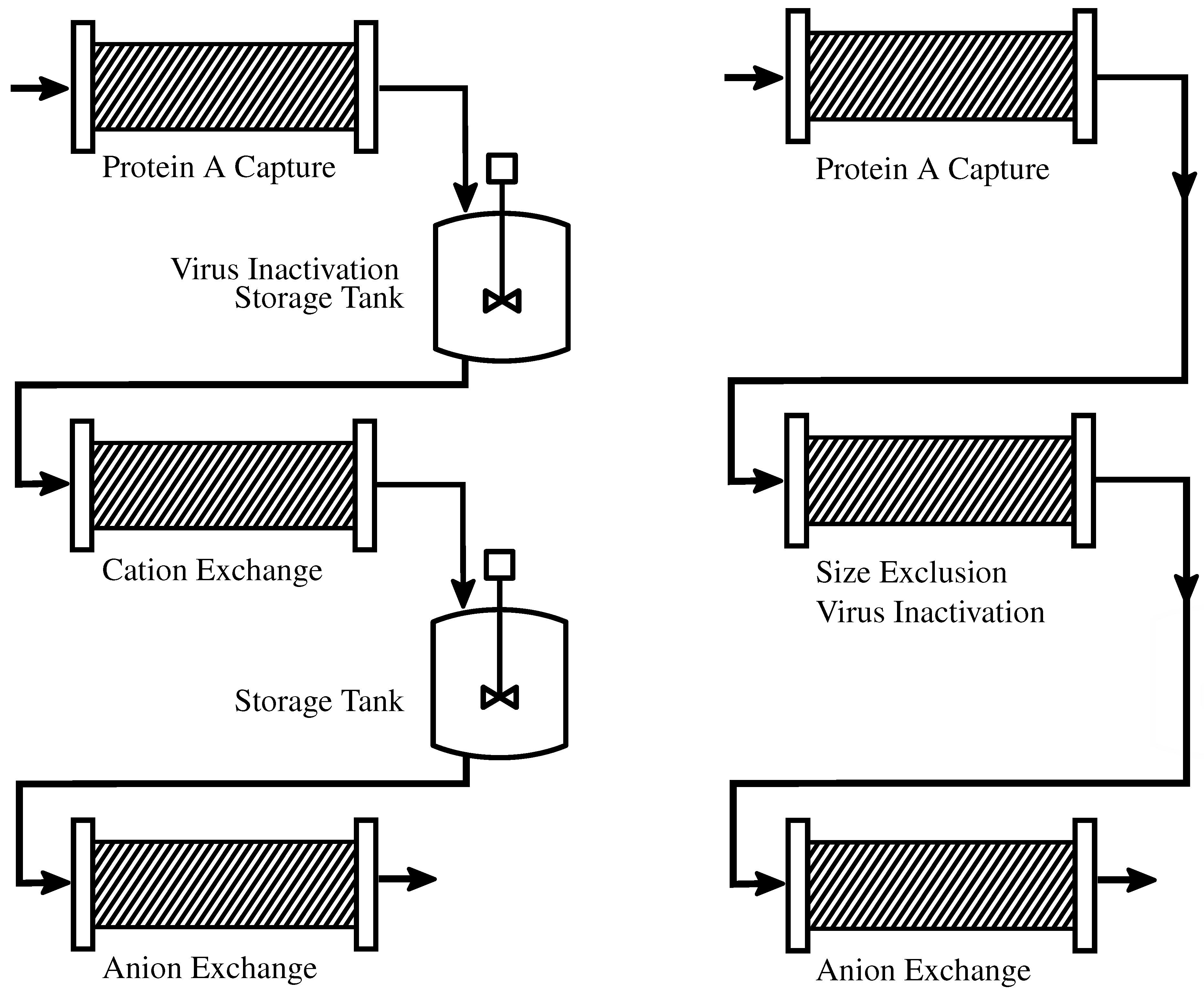
2.1.1. Batch-Wise Processes
2.1.2. Continuous Processes
2.2. Aggregation Model
2.3. Column Models
2.3.1. Protein A Column Model
2.3.2. IEX and SEC Column Models
2.4. Boundary Conditions and Initial Values
2.5. Simulation
3. Results and Discussion
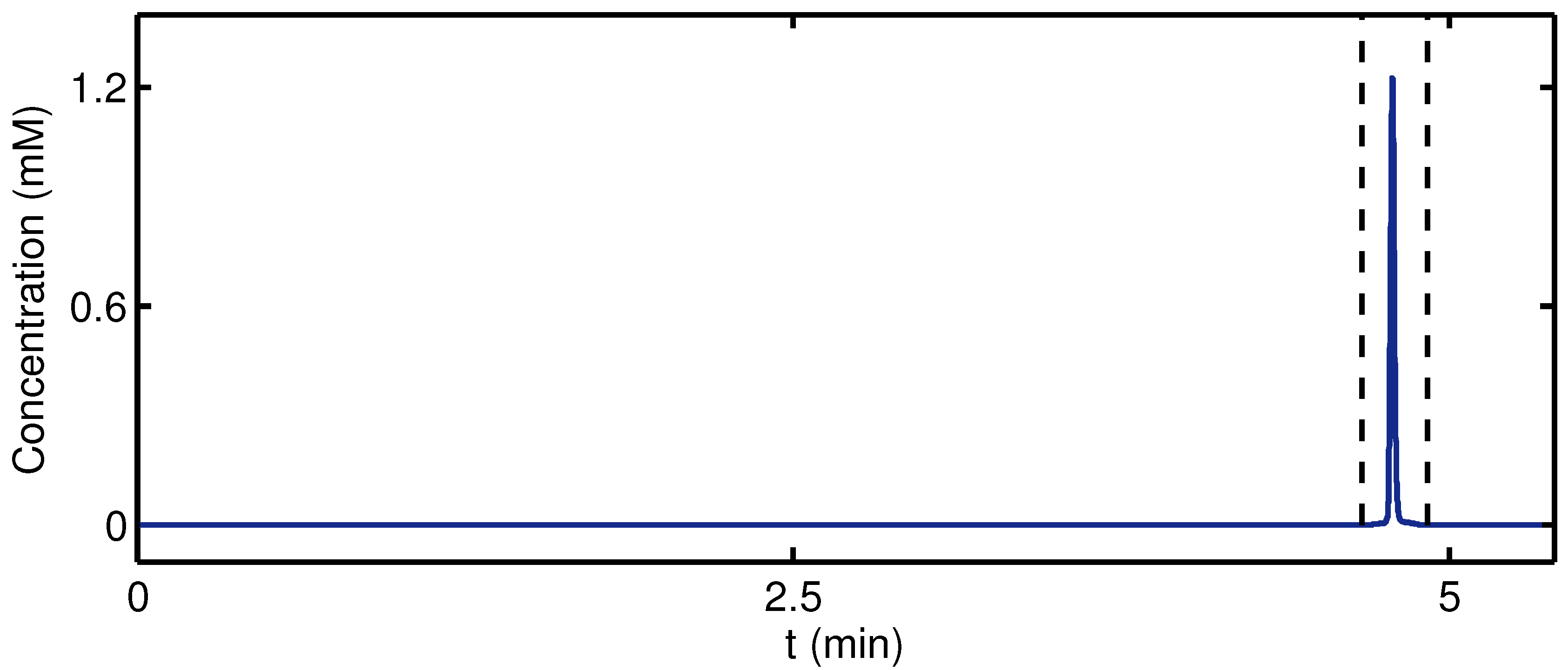
| Fraction of Dimer, | |||
|---|---|---|---|
| Batch | Continuous | ||
| Protein A Feed | |||
| Protein A Elute | |||
| End of Virus Inactivation | |||
| End of Storage | |||
| CIEX Elute | |||
| SEC Elute | |||
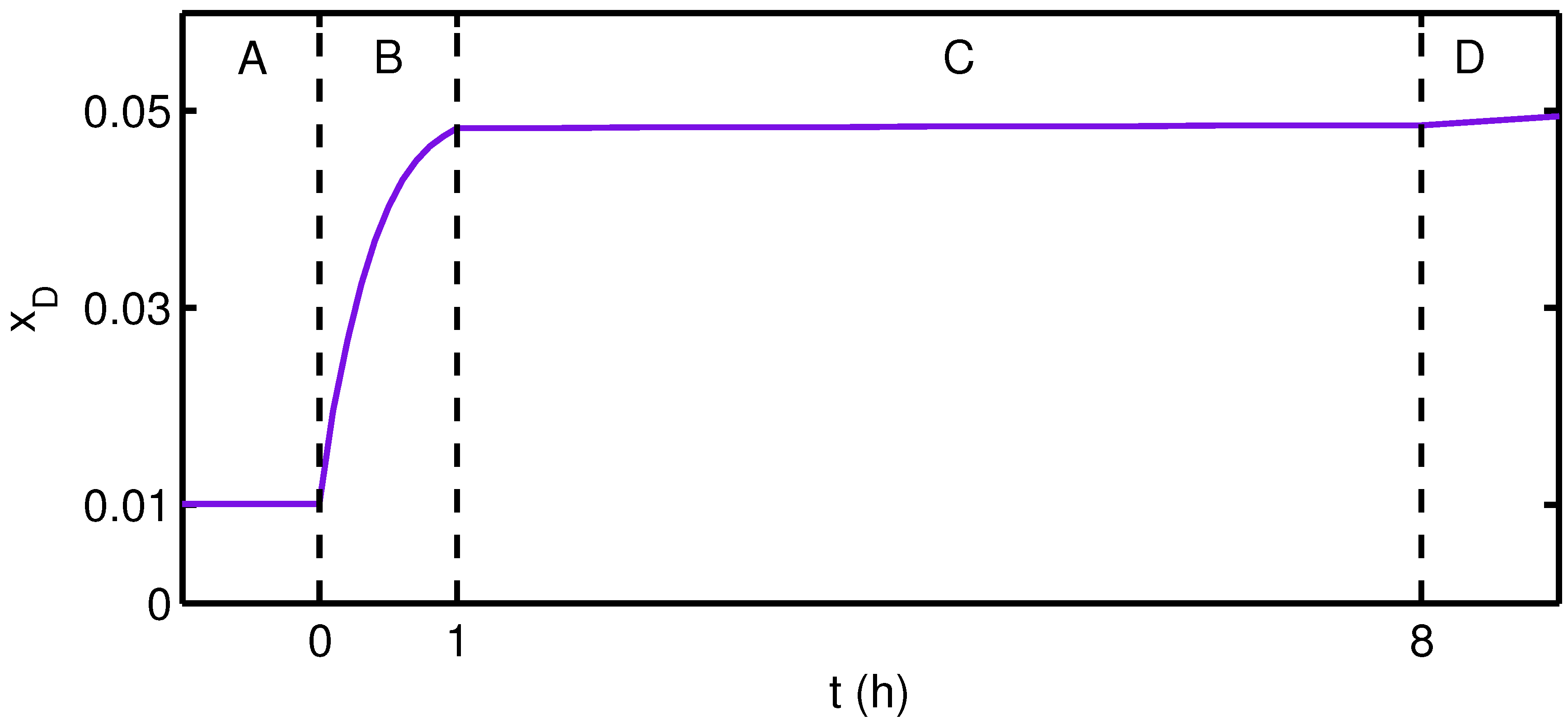
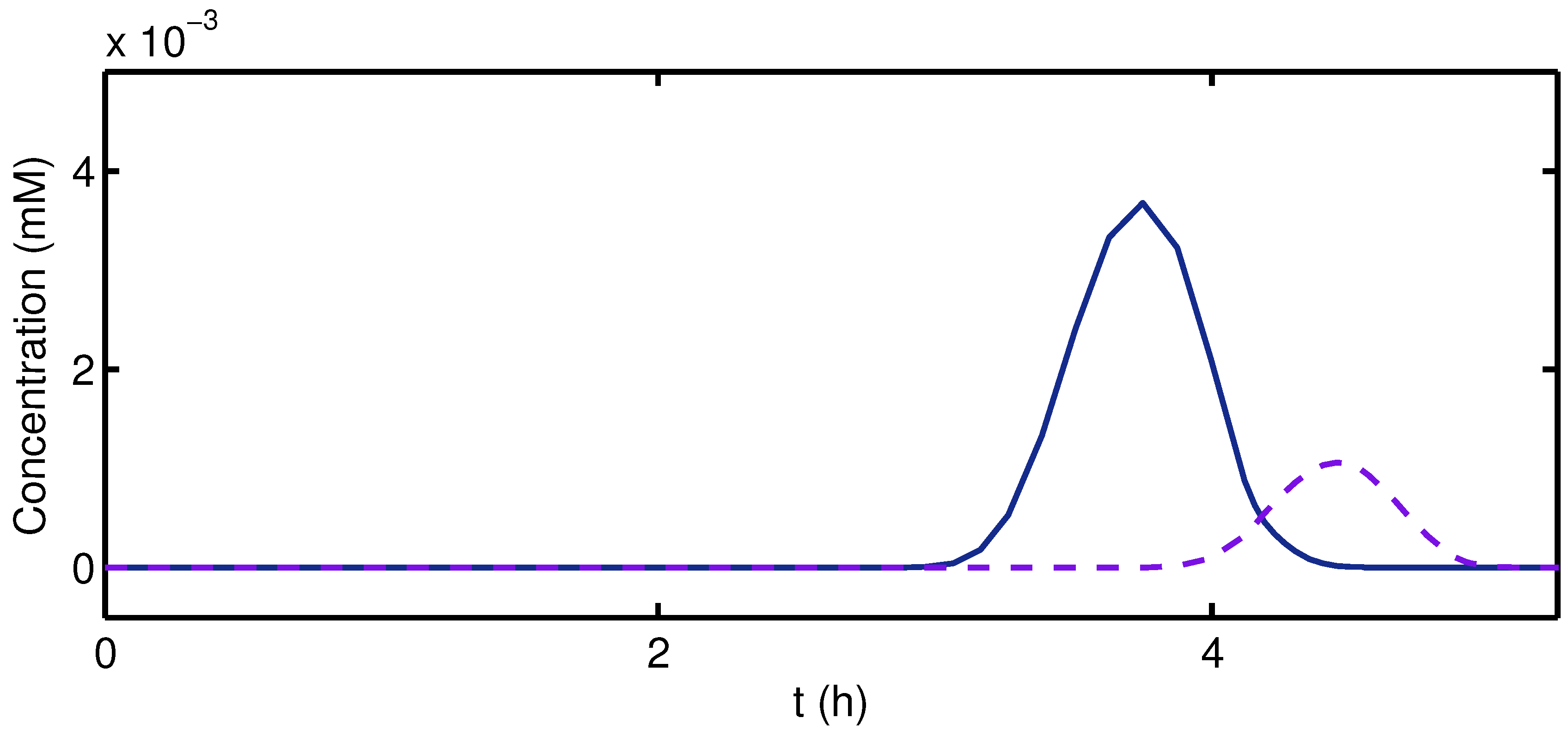

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hagel, L.; Jagschies, G.; Sofer, G. Biopharmaceuticals Today. In Handbook of Process Chromatography, 2nd ed.; Sofer, L., Ed.; Academic Press: Amsterdam, The Netherlands, 2008; pp. 1–22. [Google Scholar]
- Marichal-Gallardo, P.A.; Álvarez, M.M. State-of-the-art in downstream processing of monoclonal antibodies: Process trends in design and validation. Biotechnol. Prog. 2012, 28, 899–916. [Google Scholar] [CrossRef] [PubMed]
- Westerberg, K. Modeling for Quality and Safety in Biopharmaceutical Production Processes. PhD Thesis, Lund University, Lund, Scania, Sweden, 2012. [Google Scholar]
- Shukla, A.A.; Hubbard, B.; Tressel, T.; Guhan, S.; Low, D. Downstream processing of monoclonal antibodies—Application of platform approaches. J. Chromatogr. B 2007, 848, 28–39. [Google Scholar] [CrossRef] [PubMed]
- Perez-Almodovar, E.X.; Carta, G. IgG adsorption on a new protein A adsorbent based on macroporous hydrophilic polymers. I. Adsorption equilibrium and kinetics. J. Chromatogr. A 2009, 1216, 8339–8347. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.K.; Osuna-Sanchez, H.; Valéry, E.; Sørensen, E.; Bracewell, D.G. Design of high productivity antibody capture by protein A chromatography using an integrated experimental and modeling approach. J. Chromatogr. B 2012, 899, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Borg, N.; Brodsky, Y.; Moscariello, J.; Vunnum, S.; Vedantham, G.; Westerberg, K.; Nilsson, B. Modeling and robust pooling design of a preparative cation-exchange chromatography step for purification of monoclonal antibody monomer from aggregates. J. Chromatogr. A 2014, 1359, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhang, S.; Carta, G. Unfolding and aggregation of a glycosylated monoclonal antibody on a cation exchange column. Part I. Chromatographic elution and batch adsorption behavior. J. Chromatogr. A 2014, 1356, 117–128. [Google Scholar] [PubMed]
- Ojala, F.; Degerman, M.; Hansen, T.B.; Broberg Hansen, E.; Nilsson, B. Prediction of IgG1 aggregation in solution. Biotechnol. J. 2014, 9, 800–804. [Google Scholar] [CrossRef] [PubMed]
- Arosio, P.; Barolo, G.; Müller-Späth, T.; Wu, H.; Morbidelli, M. Aggregation stability of a monoclonal antibody during downstream processing. Pharm. Res. 2011, 28, 1884–1894. [Google Scholar] [CrossRef] [PubMed]
- Lumry, R.; Eyring, H. Conformation changes of proteins. J. Phys. Chem. 1954, 58, 110–120. [Google Scholar] [CrossRef]
- Chi, E.Y.; Krishnan, S.; Randolph, T.W.; Carpenter, J.F. Physical stability of proteins in aqueous solution: Mechanism and driving forces in nonnative protein aggregation. Pharm. Res 2003, 20, 1325–1336. [Google Scholar] [CrossRef] [PubMed]
- Kelley, B. Very large scale monoclonal antibody purification: The case for conventional unit operations. Biotechnol. Progr. 2007, 23, 995–1008. [Google Scholar] [CrossRef] [PubMed]
- Deisenhofer, J. Crystallographic refinement and atomic models of a human Fc fragment and its complex with fragment B of protein A from Staphylococcus aureus at 2.9 and 2.8 ANG. resolution. Biochemistry 1981, 20, 2361–2370. [Google Scholar] [CrossRef]
- Kelley, B.; Tobler, S.A.; Brown, P.; Coffman, J.L.; Godavarti, R.; Iskra, T.; Switzer, M.; Vunnum, S. Weak partitioning chromatography for anion exchange purification of monoclonal antibodies. Biotechnol. Bioeng. 2008, 101, 553–566. [Google Scholar] [CrossRef] [PubMed]
- Ojala, F. Modeling Antibody Aggregation in Downstream Processing. PhD Thesis, Lund University, Lund, Scania, Sweden, 2015. [Google Scholar]
- Brooks, C.A.; Cramer, S.M. Steric mass-action ion exchange: Displacement profiles and induced salt gradients. AIChE J. 1992, 38, 1969–1978. [Google Scholar] [CrossRef]
- Karlsson, D.; Jakobsson, N.; Brink, K.J.; Axelsson, A.; Nilsson, B. Methodologies for model calibration to assist the design of a preparative ion-exchange step for antibody purification. J. Chromatogr. A 2004, 1033, 71–82. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.E. Numerical methods and modeling for chemical engineers; John Wiley & Sons: New York, NY, 1984. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002; Volume 31. [Google Scholar]
- Shu, C.W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws; Springer: Berlin, Germany; Heidelberg, Germany, 1998. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The matlab ode suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Voitl, A.; Butté, A.; Morbidelli, M. Behavior of human serum albumin on strong cation exchange resins: I. Experimental analysis. J. Chromatogr. A 2010, 1217, 5484–5491. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, R.; Nguyen, T.; Macneil, S.; Jones, L.; Crampton, S.; Vunnum, S. Cation exchange surface-mediated denaturation of an aglycosylated immunoglobulin (IgG1). J. Chromatogr. A 2012, 1251, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Marek, W.; Muca, R.; Woś, S.; Piątkowski, W.; Antos, D. Isolation of monoclonal antibody from a Chinese hamster ovary supernatant. II: Dynamics of the integrated separation on ion exchange and hydrophobic interaction chromatography media. J. Chromatogr. A 2013, 1305, 64–75. [Google Scholar] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sellberg, A.; Ojala, F.; Nilsson, B. Model-Based Comparison of Antibody Dimerization in Continuous and Batch-Wise Downstream Processing. Antibodies 2015, 4, 157-169. https://doi.org/10.3390/antib4030157
Sellberg A, Ojala F, Nilsson B. Model-Based Comparison of Antibody Dimerization in Continuous and Batch-Wise Downstream Processing. Antibodies. 2015; 4(3):157-169. https://doi.org/10.3390/antib4030157
Chicago/Turabian StyleSellberg, Anton, Frida Ojala, and Bernt Nilsson. 2015. "Model-Based Comparison of Antibody Dimerization in Continuous and Batch-Wise Downstream Processing" Antibodies 4, no. 3: 157-169. https://doi.org/10.3390/antib4030157
APA StyleSellberg, A., Ojala, F., & Nilsson, B. (2015). Model-Based Comparison of Antibody Dimerization in Continuous and Batch-Wise Downstream Processing. Antibodies, 4(3), 157-169. https://doi.org/10.3390/antib4030157





