Impacts of Future Crop Tree Release Treatments on Forest Carbon as REDD+ Mitigation Benefits
Abstract
1. Introduction
2. Materials and Methods
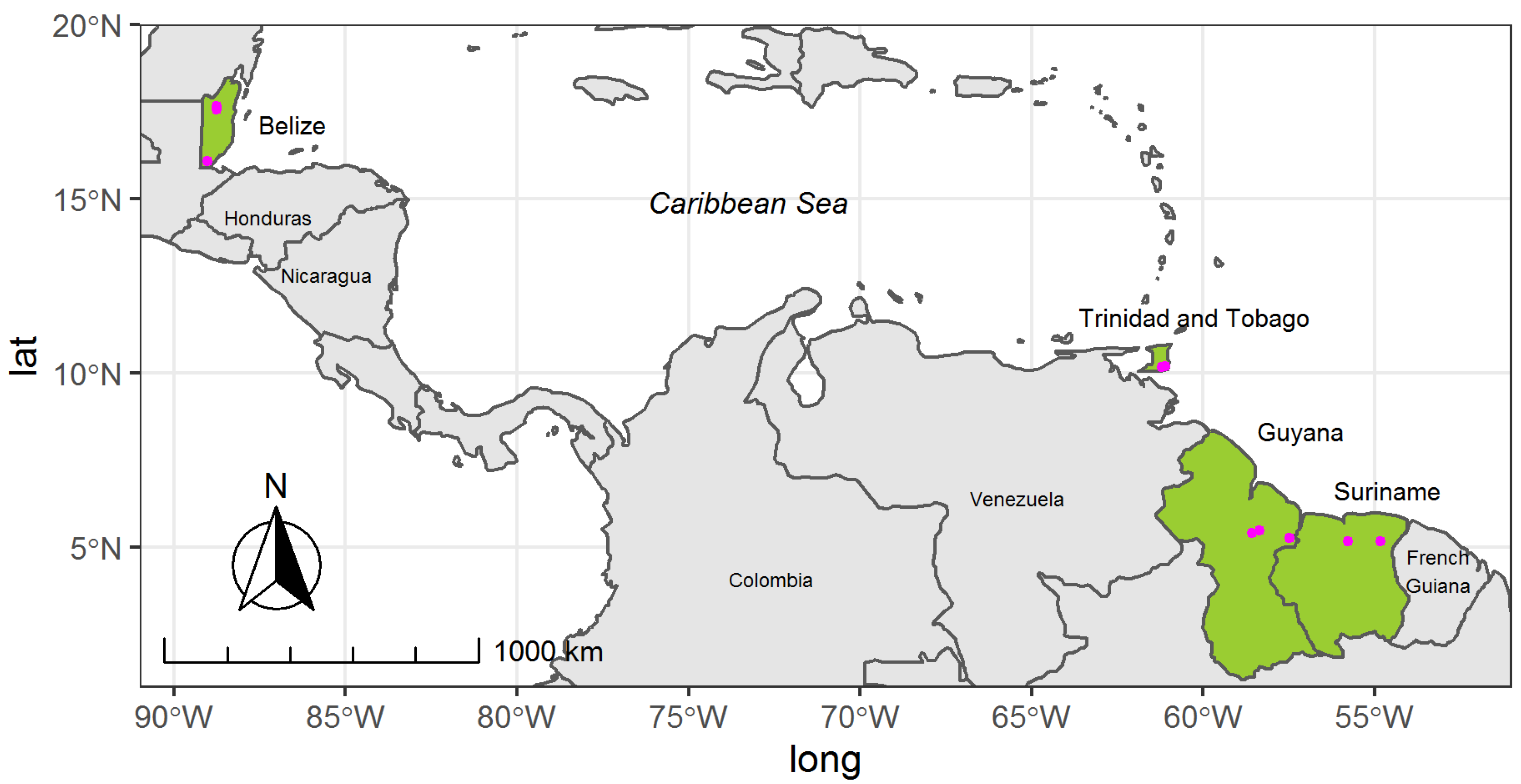
2.1. Study Sites
2.2. Pre-Harvest Iinventory
2.3. Silvicultural Treatment
2.4. Time Study
2.5. Descriptive Statistics
2.6. Treatment Costs
2.6.1. Costs of Labor
2.6.2. Machinery Costs
2.7. Carbon Analysis
2.7.1. Above Ground Biomass Growth Simulation
2.7.2. Carbon Prices
2.7.3. Discount Rate
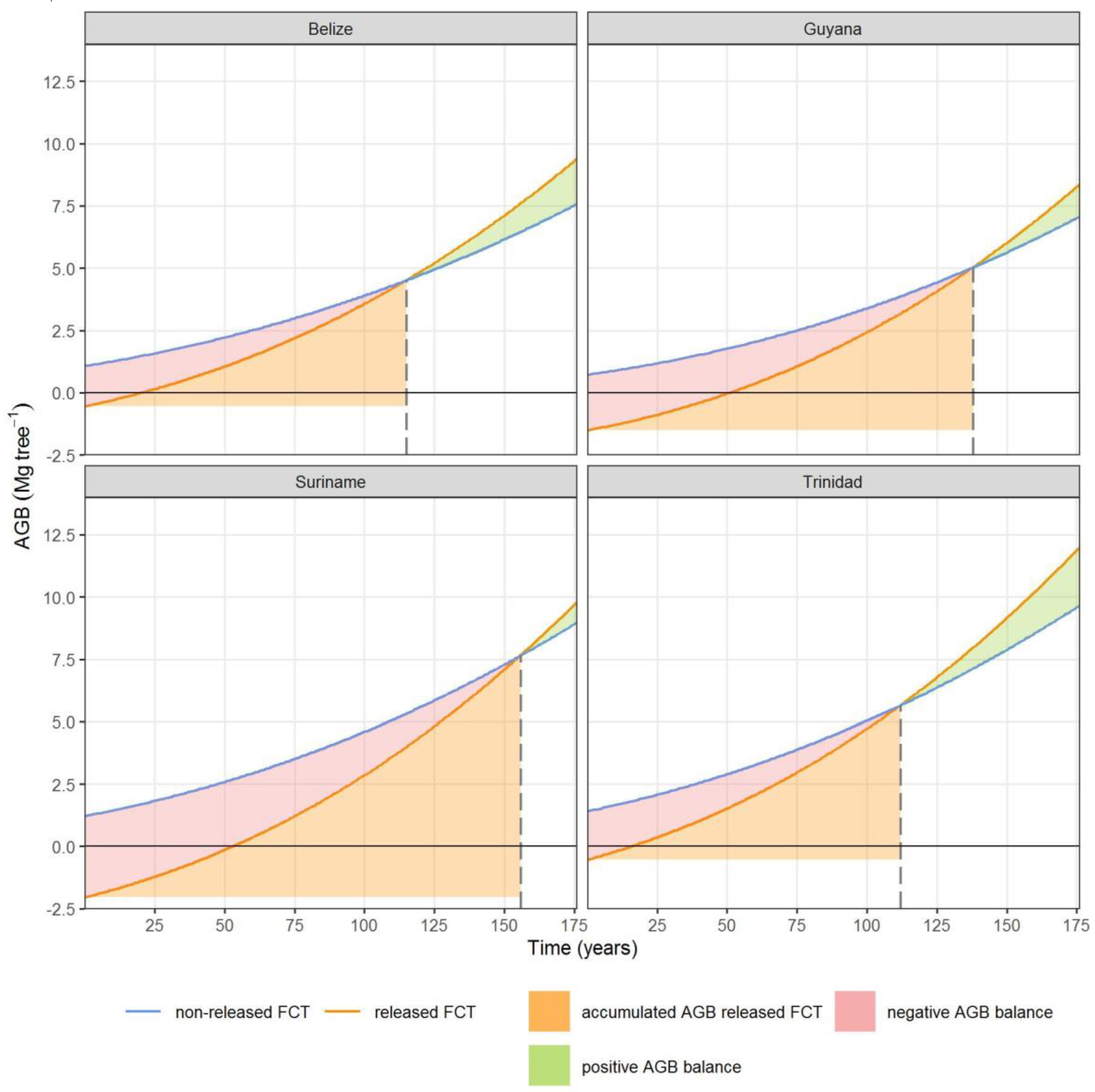
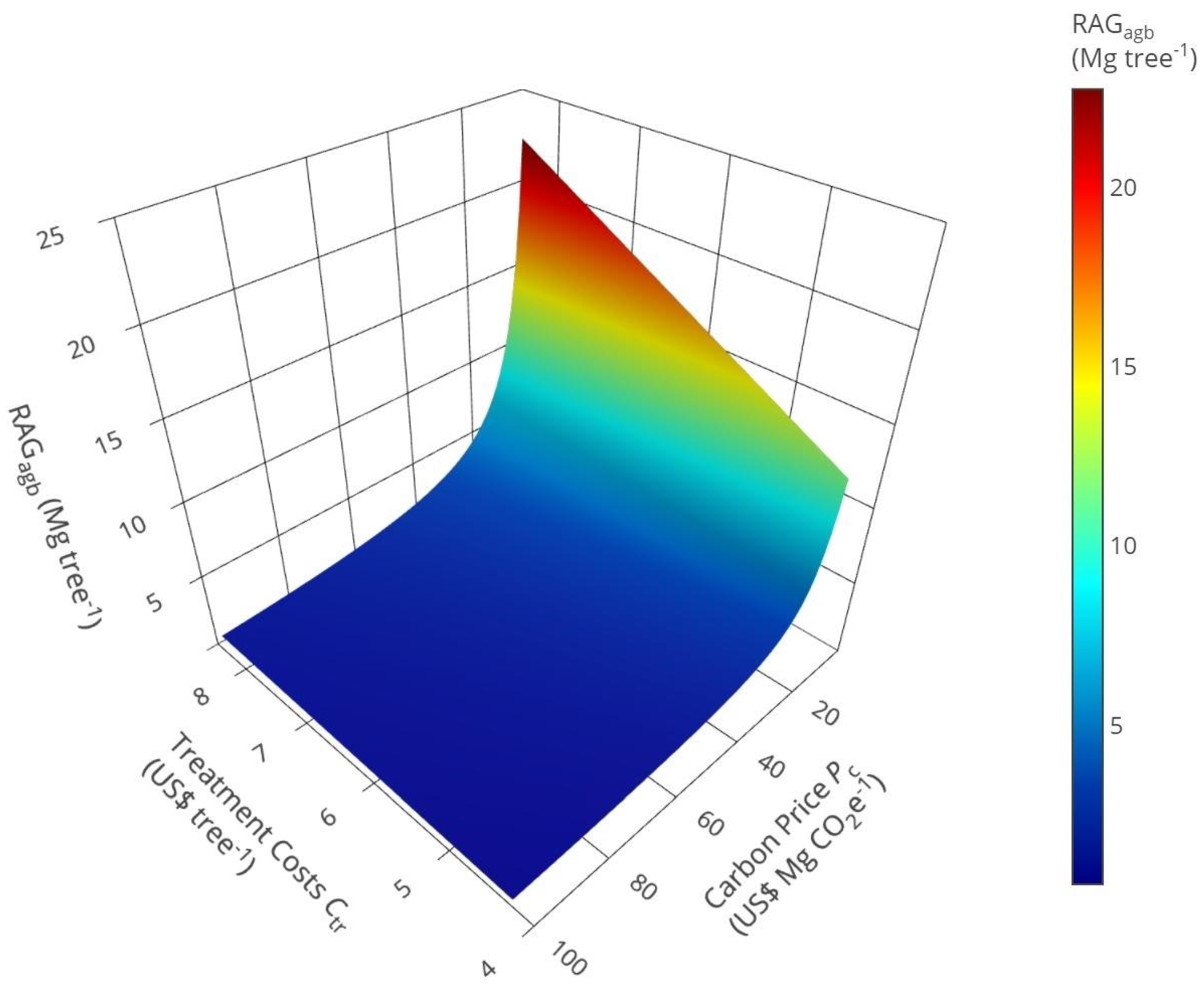
2.7.4. Required Additional Growth
3. Results
3.1. Effects of Selective Logging and FCTR Treatment
3.2. Carbon Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO. Global Forest Resources Assessment 2020; FAO: Rome, Italy, 2020; ISBN 978-92-5-132581-0. [Google Scholar]
- Mackey, B.; Kormos, C.F.; Keith, H.; Moomaw, W.R.; Houghton, R.A.; Mittermeier, R.A.; Hole, D.; Hugh, S. Understanding the importance of primary tropical forest protection as a mitigation strategy. Mitig Adapt. Strat. Glob. Chang. 2020, 25, 763–787. [Google Scholar] [CrossRef]
- Lugo, A.E.; Brown, S. Tropical forests as sinks of atmospheric carbon. For. Ecol. Manag. 1992, 54, 239–255. [Google Scholar] [CrossRef]
- Soepadmo, E. Tropical rain forests as carbon sinks. Chemosphere 1993, 27, 1025–1039. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Baccini, A.; Walker, W.; Carvalho, L.; Farina, M.; Sulla-Menashe, D.; Houghton, R.A. Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 2017, 358, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Pearson, T.R.H.; Brown, S.; Casarim, F.M. Carbon emissions from tropical forest degradation caused by logging. Environ. Res. Lett. 2014, 9, 34017. [Google Scholar] [CrossRef]
- Pearson, T.R.H.; Brown, S.; Murray, L.; Sidman, G. Greenhouse gas emissions from tropical forest degradation: An underestimated source. Carbon Balance Manag. 2017, 12, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Knapp, D.E.; Broadbent, E.N.; Oliveira, P.J.C.; Keller, M.; Silva, J.N. Selective logging in the Brazilian Amazon. Science 2005, 310, 480–482. [Google Scholar] [CrossRef]
- Putz, F.E.; Zuidema, P.A.; Pinard, M.A.; Boot, R.G.A.; Sayer, J.A.; Sheil, D.; Sist, P.; Vanclay, J.K. Improved tropical forest management for carbon retention. PLoS Biol. 2008, 6, e166. [Google Scholar] [CrossRef]
- Nasi, R.; Putz, F.; Pacheco, P.; Wunder, S.; Anta, S. Sustainable Forest Management and Carbon in Tropical Latin America: The Case for REDD+. Forests 2011, 2, 200–217. [Google Scholar] [CrossRef]
- West, T.A.; Vidal, E.; Putz, F.E. Forest biomass recovery after conventional and reduced-impact logging in Amazonian Brazil. For. Ecol. Manag. 2014, 314, 59–63. [Google Scholar] [CrossRef]
- Vidal, E.; West, T.A.P.; Putz, F.E. Recovery of biomass and merchantable timber volumes twenty years after conventional and reduced-impact logging in Amazonian Brazil. For. Ecol. Manag. 2016, 376, 1–8. [Google Scholar] [CrossRef]
- Neupane, P.R.; Wiati, C.B.; Angi, E.M.; Köhl, M.; Butarbutar, T.; Reonaldus Gauli, A. How REDD+ and FLEGT-VPA processes are contributing towards SFM in Indonesia–the specialists’ viewpoint. Int. For. Rev. 2019, 21, 460–485. [Google Scholar] [CrossRef]
- Sufo Kankeu, R.; Sonwa, D.J.; Eba’a Atyi, R.; Moankang Nkal, N.M. Quantifying post logging biomass loss using satellite images and ground measurements in Southeast Cameroon. J. Res. 2016, 27, 1415–1426. [Google Scholar] [CrossRef]
- Galante, M.V.; Dutschke, M.; Patenaude, G.; Vickers, B. Climate Change Mitigation through Reduced-Impact Logging and the Hierarchy of Production Forest Management. Forests 2012, 3, 59–74. [Google Scholar] [CrossRef]
- Lamprecht, H. Silviculture in the Tropics. Tropical Forest Ecosystems and Their Tree Species, Possibilities and Methods for Their Long-Term Utilization; Deutsche Gesellschaft für Technische Zusammenarbeit GmbH: Eschborn, Germany, 1989; ISBN 388085422X. [Google Scholar]
- Hu, J.; Herbohn, J.; Chazdon, R.L.; Baynes, J.; Vancley, J. Silvicultural treatment effects on commercial timber volume and functional composition of a selectively logged Australian tropical forest over 48 years. For. Ecol. Manag. 2020, 457, 117690. [Google Scholar] [CrossRef]
- Wadsworth, F.H.; Zweede, J.C. Liberation: Acceptable production of tropical forest timber. For. Ecol. Manag. 2006, 233, 45–51. [Google Scholar] [CrossRef]
- Villegas, Z.; Peña-Claros, M.; Mostacedo, B.; Alarcón, A.; Licona, J.C.; Leaño, C.; Pariona, W.; Choque, U. Silvicultural treatments enhance growth rates of future crop trees in a tropical dry forest. For. Ecol. Manag. 2009, 258, 971–977. [Google Scholar] [CrossRef]
- Peña-Claros, M.; Fredericksen, T.S.; Alarcón, A.; Blate, G.M.; Choque, U.; Leaño, C.; Licona, J.C.; Mostacedo, B.; Pariona, W.; Villegas, Z.; et al. Beyond reduced-impact logging: Silvicultural treatments to increase growth rates of tropical trees. For. Ecol. Manag. 2008, 256, 1458–1467. [Google Scholar] [CrossRef]
- Verwer, C.; Peña-Claros, M.; van der Staak, D.; Ohlson-Kiehn, K.; Sterck, F.J. Silviculture enhances the recovery of overexploited mahogany Swietenia macrophylla. J. Appl. Ecol. 2008, 45, 1770–1779. [Google Scholar] [CrossRef]
- Abetz, P. Müssen wir in der waldbaulichen Behandlung der Fichte wieder umdenken? Eur. J. For. Res. 1990, 109, 79–85. [Google Scholar] [CrossRef]
- Abetz, P.; Klädtke, J. The Target Tree Management System. Die Z-Baum-Kontrollmethode. Forstw. Cbl. 2002, 121, 73–82. [Google Scholar] [CrossRef]
- Burschel, P.; Huss, J. Grundriss des Waldbaus. Ein Leitfaden für Studium und Praxis: 207 Tabellen, 3., unveränd. Aufl.; Ulmer: Stuttgart, Germany, 2003; ISBN 3800145707. [Google Scholar]
- Hein, S.; Lenk, E.; Klädtke, J.; Kohnle, U. Z-Baum orientierte Auslesedurchforstung in Buche [Fagus sylvatica L.]: Auswirkungen auf Qualität, Sortenstruktur und Wertleistung. Allg. Forst Und Jagdztg. 2007, 179, 8–20. [Google Scholar]
- Hein, S.; Herbstritt, S.; Kohnle, U. Auswirkung der Z-Baum-Auslesedurchforstung auf Wachstum, Sortenertrag und Wertleistung im europäischen Fichten-Stammzahlversuch (Picea abies [L.] Karst.) in Südwestdeutschland. Allg. Forst Und Jagdztg. 2007, 179, 192–201. [Google Scholar]
- Hein, S.; Herbstritt, S.; Kohnle, U. The European Stem Number Experiment in Norway Spruce (Picea abies [L.] Karst.): Effect of Crop Tree Thinning on Growth, Timber Assortment and Economic Results. Allg. Forst Und Jagdztg. 2008, 179, 192–201. [Google Scholar]
- Herbstritt, S.; Kohnle, U.; Abetz, P.; Kenk, G. The European Stem Number Experiment in Norway Spruce (Picea abies (L.) Karst.). 3. Report; Berichte Freiburger Forstliche Forschung No. 66; Forstliche Versuchs- und Forschungsanstalt Baden-Württemberg: Freiburg, Germany, 2006. [Google Scholar]
- Mäkinen, H.; Isomäki, A. Thinning intensity and growth of Norway spruce stands in Finland. Forestry 2004, 77, 349–364. [Google Scholar] [CrossRef]
- Graaf, N.R.; Poels, R.L.H.; Van Rompaey, R.S.A.R. Effect of silvicultural treatment on growth and mortality of rainforest in Surinam over long periods. For. Ecol. Manag. 1999, 124, 123–135. [Google Scholar] [CrossRef]
- David, H.C.; Carvalho, J.O.; Pires, I.P.; Santos, L.S.; Barbosa, E.S.; Braga, N.S. A 20-year tree liberation experiment in the Amazon: Highlights for diameter growth rates and species-specific management. For. Ecol. Manag. 2019, 453, 117584. [Google Scholar] [CrossRef]
- Kuusipalo, J.; Jafarsidik, Y.; Ådjers, G.; Tuomela, K. Population dynamics of tree seedlings in a mixed dipterocarp rainforest before and after logging and crown liberation. For. Ecol. Manag. 1996, 81, 85–94. [Google Scholar] [CrossRef]
- Kuusipalo, J.; Hadengganan, S.; Ådjers, G.; Sagala, A.S. Effect of gap liberation on the performance and growth of dipterocarp trees in a logged-over rainforest. For. Ecol. Manag. 1997, 92, 209–219. [Google Scholar] [CrossRef]
- Gräfe, S.; Eckelmann, C.-M.; Playfair, M.; Oatham, M.P.; Pacheco, R.; Bremner, Q.; Köhl, M. Future crop tree release treatments in neotropical forests—An empirical study on the sensitivity of the economic profitability. For. Policy Econ. 2020, 121, 102329. [Google Scholar] [CrossRef]
- Gräfe, S.; Eckelmann, C.-M.; Playfair, M.; Oatham, M.P.; Pacheco, R.; Bremner, Q.; Köhl, M. Recovery Times and Sustainability in Logged-Over Natural Forests in the Caribbean. Forests 2020, 11, 256. [Google Scholar] [CrossRef]
- Nurmohamed, R.; Naipal, S.; Becker, C. Rainfall variability in Suriname and its relationship with the tropical Pacific ENSO SST anomalies and the Atlantic SST anomalies. Int. J. Clim. 2007, 27, 249–256. [Google Scholar] [CrossRef]
- Giannini, A.; Kushnir, Y.; Cane, M.A. Interannual Variability of Caribbean Rainfall, ENSO, and the Atlantic Ocean*. J. Clim. 2000, 13, 297–311. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. National Forest Monitoring and Assessment. Manual for Integrated Field Data Collection; National Forest Monitoring and Assessment Working Paper NFMA 37/E; 2008; Available online: http://www.fao.org/forestry/14727-072b68bcfa49334202f1586889517ce24.pdf (accessed on 24 April 2020).
- Nyland, R.D. Silviculture: Concepts and Applications, 3rd ed.; WAVELAND Press: Long Grove, IL, USA, 2016; ISBN 978-1478627142. [Google Scholar]
- Alder, D. An Assessment of Broadleaf Forest Resources and Sustainable Yield in Belize; Belize Forest Planning and Management Project Consultancy Report No. 11; 1993; Available online: https://mayaforestbelize.files.wordpress.com/2016/11/alder-forest-resources-1993.pdf. (accessed on 9 December 2016).
- GFC. Forest Sector Information Report–Annual Review 2016; Guyana Forestry Commission: Georgetown, Guyana, 2016. [Google Scholar]
- SBB. Production, Export and Import of Timber and Timber Products in 2012; Foundation for Forest Management and Production Control: Paramaribo, Suriname, 2013. [Google Scholar]
- SBB. Suriname Forestry Sector 2013; Foundation for Forest Management and Production Control: Paramaribo, Suriname, 2014. [Google Scholar]
- Ramnarine, S.; Jhilmit, S.; John, K. Manual for the Establishment and Management of Periodic Blocks in Trinidad; Ministry of Public Utilities and the Environment: Port of Spain, Trinidad and Tobago, 2002. [Google Scholar]
- Abetz, P. Eine Entscheidungshilfe für die Durchforstung von Fichtenbeständen. Allg. Forstz. 1975, 666–667. [Google Scholar]
- Friard, O.; Gamba, M. BORIS: A free, versatile open-source event-logging software for video/audio coding and live observations. Methods Ecol. Evol. 2016, 7, 1325–1330. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org (accessed on 3 December 2019).
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. J. R. Stat. Soc. Ser. A 1972, 135, 370. [Google Scholar] [CrossRef]
- Alaimo, V.; Bosch, M.; Gualavisí, M.; Villa, J.M. Measuring the Cost of Salaried Labor in Latin America and the Caribbean; IDB Technical Note No. 1291; Inter-American Development Bank: Washington, DC, USA, 2017. [Google Scholar]
- Whiteman, A. A Roundwood Production Cost Model. For. Suriname: Model. Description and User Guide. Project GCP/SUR/001/NET. Forestry Advisory Assistance to the Ministry of Natural Resources in Suriname; Ministry of Natural Resources Suriname; Food and Agriculture Organization of the United Nations: Rome, Italy, 1999; Available online: http://www.fao.org/3/X6826E/X6826E00.htm (accessed on 21 February 2020).
- Whiteman, A. Economic Data and Information About the Forest Sector in Suriname. Project GCP/SUR/001/NET.Forestry Advisory Assistance to the Ministry of Natural Resources in Suriname; Ministry of Natural Resources Suriname; Food and Agriculture Organization of the United Nations: Rome, Italy, 1999. [Google Scholar]
- KWF; DLG; ENTAM. Prüfbericht Motorsäge STIHL MS 880; Kuratorium für Waldarbeit und Forsttechnik (KWF); Deutsche Landwirtschafts Gesellschaft (DLG); European Network for Testing of Agricultural Machines (ENTAM): Groß-Umstadt, Germany, 2009. [Google Scholar]
- Richardson Saw & Lawnmower. Available online: https://www.richardsonsaw.com (accessed on 21 February 2020).
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Tanguy, A.; Piponiot, C.; Chave, J.; Hérault, B. Biomass: An r package for estimating above-ground biomass and its uncertainty in tropical forests. Methods Ecol. Evol. 2017, 8, 1163–1167. [Google Scholar] [CrossRef]
- Zanne, A.E.; Lopez-Gonzalez, G.; Coomes, D.A.; Ilic, J.; Jansen, S.; Lewis, S.L.; Miller, R.B.; Swenson, N.G.; Wiemann, M.C.; Chave, J. Data from: Towards a Worldwide Wood Economics Spectrum. 2009. Available online: https://datadryad.org/stash/dataset/doi:10.5061/dryad.234 (accessed on 27 April 2020).
- Herault, B.; Ouallet, J.; Blanc, L.; Wagner, F.; Baraloto, C. Growth responses of neotropical trees to logging gaps. J. Appl. Ecol. 2010, 47, 821–831. [Google Scholar] [CrossRef]
- Jonkers, W.B.J.; Tjon, K.; Wirjosentono, J. Long-term effects of logging in a Neotropical rain forest in Suriname. In International Expert Meeting on the Development and Implementation of National Codes of Practice for Forest Harvesting: Issues and Options; International Forestry Cooperation Office, Ed.: Tokyo, Japan, 2003; pp. 157–166. [Google Scholar]
- Lieberman, D.; Lieberman, M.; Hartshorn, G.; Peralta, R. Growth rates and age-size relationships of tropical wet forest trees in Costa Rica. J. Trop. Ecol. 1985, 1, 97–109. [Google Scholar] [CrossRef]
- Vieira, S.; de Camargo, P.B.; Selhorst, D.; da Silva, R.; Hutyra, L.; Chambers, J.Q.; Brown, I.F.; Higuchi, N.; dos Santos, J.; Wofsy, S.C.; et al. Forest structure and carbon dynamics in Amazonian tropical rain forests. Oecologia 2004, 140, 468–479. [Google Scholar] [CrossRef]
- Werger, M.J.A. Sustainable Management of Tropical Rainforests. The CELOS Management System; Tropenbos International: Paramaribo, Suriname, 2011. [Google Scholar]
- Ramstein, C.; Dominioni, G.; Ettehad, S.; Lam, L.; Quant, M.; Zhang, J.; Mark, L.; Nierop, S.; Berg, T.; Leuschner, P.; et al. State and Trends of Carbon Pricing 2019; The World Bank: Washington, DC, USA, 2019; ISBN 978-1-4648-1435-8. [Google Scholar]
- Arnold, T. How Net Present Value Is Implemented. In A Pragmatic Guide to Real Options; Arnold, T., Ed.; Palgrave Macmillan: New York, NY, USA, 2014; pp. 1–13. ISBN 978-1-137-39116-2. [Google Scholar]
- Remer, D.S.; Nieto, A.P. A compendium and comparison of 25 project evaluation techniques. Part 1: Net present value and rate of return methods. Int. J. Prod. Econ. 1995, 42, 79–96. [Google Scholar] [CrossRef]
- Karsenty, A. Economic Instruments for Tropical Forests. The Congo Basin Case; International Institute for Environment and Development: London, UK, 2000; ISBN 2876143763. [Google Scholar]
- Cubbage, F.; Davis, R.; Frey, G.; Behr, D.C.; Sills, E. Financial and Economic Evaluation Guidelines for International Forestry Projects. In Tropical Forestry Handbook; Pancel, L., Köhl, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–17. ISBN 978-3-642-41554-8. [Google Scholar]
- Clark, D.A.; Brown, S.; Kicklighter, D.W.; Chambers, J.Q.; Thomlinson, J.R.; Ni, J.; Holland, E.A. Net primary production in tropical forests: An evaluation and synthesis of existing field data. Ecol. Appl. 2001, 11, 371–384. [Google Scholar] [CrossRef]
- Salas Macías, C.A.; Alegre Orihuela, J.C.; Iglesias Abad, S. Estimation of above--ground live biomass and carbon stocks in different plant formations and in the soil of dry forests of the Ecuadorian coast. Food Energy Secur. 2017, 6. [Google Scholar] [CrossRef]
- Malhi, Y.; Baker, T.R.; Phillips, O.L.; Almeida, S.; Alvarez, E.; Arroyo, L.; Chave, J.; Czimczik, C.I.; Di Fiore, A.; Higuchi, N.; et al. The above-ground coarse wood productivity of 104 Neotropical forest plots. Glob. Chang. Biol. 2004, 10, 563–591. [Google Scholar] [CrossRef]
- Eggleston, S. IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies (IGES): Hayama, Japan, 2006; ISBN 4-88788-032-4. [Google Scholar]
- Rutishauser, E.; Hérault, B.; Baraloto, C.; Blanc, L.; Descroix, L.; Sotta, E.D.; Ferreira, J.; Kanashiro, M.; Mazzei, L.; d’Oliveira, M.V.N.; et al. Rapid tree carbon stock recovery in managed Amazonian forests. Curr. Biol. 2015, 25, R787–R788. [Google Scholar] [CrossRef]
- Keller, M.; Asner, G.P.; Blate, G.; McGlocklin, J.; Merry, F.; Peña-Claros, M.; Zweede, J. Timber production in selectively logged tropical forests in South America. Front. Ecol. Environ. 2007, 5, 213–216. [Google Scholar] [CrossRef]
- Zimmerman, B.L.; Kormos, C.F. Prospects for Sustainable Logging in Tropical Forests. BioScience 2012, 62, 479–487. [Google Scholar] [CrossRef]
- Piponiot, C.; Sist, P.; Mazzei, L.; Peña-Claros, M.; Putz, F.E.; Rutishauser, E.; Shenkin, A.; Ascarrunz, N.; de Azevedo, C.P.; Baraloto, C.; et al. Carbon recovery dynamics following disturbance by selective logging in Amazonian forests. Elife 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Köhl, M.; Neupane, P.R.; Lotfiomran, N.; Delzon, S. The impact of tree age on biomass growth and carbon accumulation capacity: A retrospective analysis using tree ring data of three tropical tree species grown in natural forests of Suriname. PLoS ONE 2017, 12, e0181187. [Google Scholar] [CrossRef]
- Newbery, D.M.; Ridsdale, C.E. Neighbourhood abundance and small--tree survival in a lowland Bornean rainforest. Ecol. Res. 2016, 31, 353–366. [Google Scholar] [CrossRef]
- UNFCC. Report of the Conference of the Parties on its 16th session, held in Cancun, 29 November–10 December 2010. Addendum. Part two: Action taken by the Conference of the Parties at its sixteenth session. FCCC/CP/2010/7/Add.1; UNFCC: Bonn, Germany, 2011; Available online: https://unfccc.int/documents/6527 (accessed on 29 September 2020).
| Criteria | Description |
|---|---|
| Species | The species of FCTs should achieve a high commercial value in the relevant timber markets. All project countries applied a species classification system (see above). FCTs should have been listed within either the highest or higher value species class since they are the future value drivers of the stand. |
| Crown class | Future crop trees must be able to compete successfully after the release. So they were selected from trees whose canopies are already located in the dominant, co-dominant or strong intermediate crown class. |
| Log grade | FCTs should have log grades requiring straight logs free of defects or visible diseases (log grade 1). |
| Vitality | FCTs should be of good health and vitality without low forks. |
| Age | Trees could qualify as FCTs at any age as long as they are expected to survive long enough to reach the next cutting cycle. |
| Distribution | FCTs should not all be concentrated in the “good quality” area of the forest stand. FCTs should have been evenly distributed across the forest stand but their relative quality may differ, e.g., the “good quality” area of the stand may have FCTs with 10 m log length while the “poorer quality” area may have FCTs with 5 m log length. |
| Quantity | There was no defined number of trees to be identified as FCTs. |
| No. | Work Element | Definition | Category |
|---|---|---|---|
| 1 | Searching | searching and identification of the target tree, including walking to the next tree | Production |
| 2 | Preparation | felling preparation, e.g., liana cutting, clean up, determination of felling direction and rescue ways | |
| 3 | Felling | tree felling starts from the chainsaw engine start until the tree lies on the ground | |
| 4 | Maintenance | maintenance of the chainsaw, e.g., sharpen the chain, refuel | |
| 5 | Break | resting break | No production |
| 6 | Other | other activities which do not fit into the work elements 1–6 |
| Chainsaw type | Stihl MS 880 + 90cm Bar |
| Purchase cost (Cp) | US$ 1900 |
| Fuel consumption (Kgas) | 4 L hr−1 (3.7–4.3 L hr−1) |
| Oil/grease consumption (Koil) | 0.99 L hr−1 (0.36–1.62 L hr−1) |
| Effective machine hours per year (Temh) | 241 |
| Expected life time (Tel) | 5 y |
| AGB (Mg ha−1) | N (Trees ha−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean | SE | 95% CI | Mean | SE | 95% CI | |||
| Lower | Upper | Lower | Upper | |||||
| Selective logging | ||||||||
| Belize | 15.1 | 3.41 | 6.8 | 23.5 | 5.2 | 0.7 | 3.5 | 6.9 |
| Guyana | 7.5 | 3.41 | 0 | 15.8 | 3.7 | 0.7 | 2 | 5.4 |
| Suriname | 35.4 | 4.15 | 25.2 | 45.6 | 7.6 | 0.8 | 5.5 | 9.6 |
| Trinidad | 26.3 | 4.15 | 16.1 | 36.5 | 4.3 | 0.8 | 2.2 | 6.3 |
| FCTs | ||||||||
| Belize | 2.8 | 0.8 | 0.7 | 4.9 | 2.6 | 0.8 | 0.6 | 4.6 |
| Guyana | 0.3 | 0.8 | 0 | 2.4 | 0.4 | 0.8 | 0 | 2.4 |
| Suriname | 3.9 | 1 | 1.3 | 6.4 | 3.2 | 1 | 0.7 | 5.6 |
| Trinidad | 4.8 | 1 | 2.2 | 7.3 | 3.4 | 1 | 1 | 5.8 |
| Competitors | ||||||||
| Belize | 4.2 | 1.6 | 0.3 | 8.1 | 4.1 | 1.3 | 1 | 7.2 |
| Guyana | 0.9 | 1.6 | 0 | 4.8 | 0.5 | 1.3 | 0 | 3.6 |
| Suriname | 10.3 | 2 | 5.5 | 15.2 | 4.8 | 1.6 | 0.9 | 8.6 |
| Trinidad | 6.6 | 2 | 1.8 | 11.4 | 4.3 | 1.6 | 0.4 | 8.1 |
| Residual trees | ||||||||
| Belize | 97.8 | 23.6 | 40 | 156 | 82.2 | 12.3 | 52.2 | 112 |
| Guyana | 151.5 | 23.6 | 93.7 | 209 | 106.8 | 12.3 | 76.7 | 137 |
| Suriname | 181 | 28.9 | 110.2 | 252 | 105.5 | 15 | 68.8 | 142 |
| Trinidad | 176.3 | 28.9 | 105.5 | 247 | 87 | 15 | 50.3 | 124 |
| Total stand | ||||||||
| Belize | 124 | 31.8 | 46.7 | 202 | 97.5 | 14.6 | 61.9 | 133 |
| Guyana | 163 | 31.8 | 85.1 | 241 | 115.2 | 14.6 | 79.5 | 151 |
| Suriname | 235 | 38.9 | 140.2 | 331 | 124.8 | 17.8 | 81.1 | 169 |
| Trinidad | 237 | 38.9 | 141.7 | 332 | 117.9 | 17.9 | 74.2 | 162 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gräfe, S.; Köhl, M. Impacts of Future Crop Tree Release Treatments on Forest Carbon as REDD+ Mitigation Benefits. Land 2020, 9, 394. https://doi.org/10.3390/land9100394
Gräfe S, Köhl M. Impacts of Future Crop Tree Release Treatments on Forest Carbon as REDD+ Mitigation Benefits. Land. 2020; 9(10):394. https://doi.org/10.3390/land9100394
Chicago/Turabian StyleGräfe, Sebastian, and Michael Köhl. 2020. "Impacts of Future Crop Tree Release Treatments on Forest Carbon as REDD+ Mitigation Benefits" Land 9, no. 10: 394. https://doi.org/10.3390/land9100394
APA StyleGräfe, S., & Köhl, M. (2020). Impacts of Future Crop Tree Release Treatments on Forest Carbon as REDD+ Mitigation Benefits. Land, 9(10), 394. https://doi.org/10.3390/land9100394






