Comparison of Statistical Approaches for Modelling Land-Use Change
Abstract
1. Introduction
2. Materials and Methods
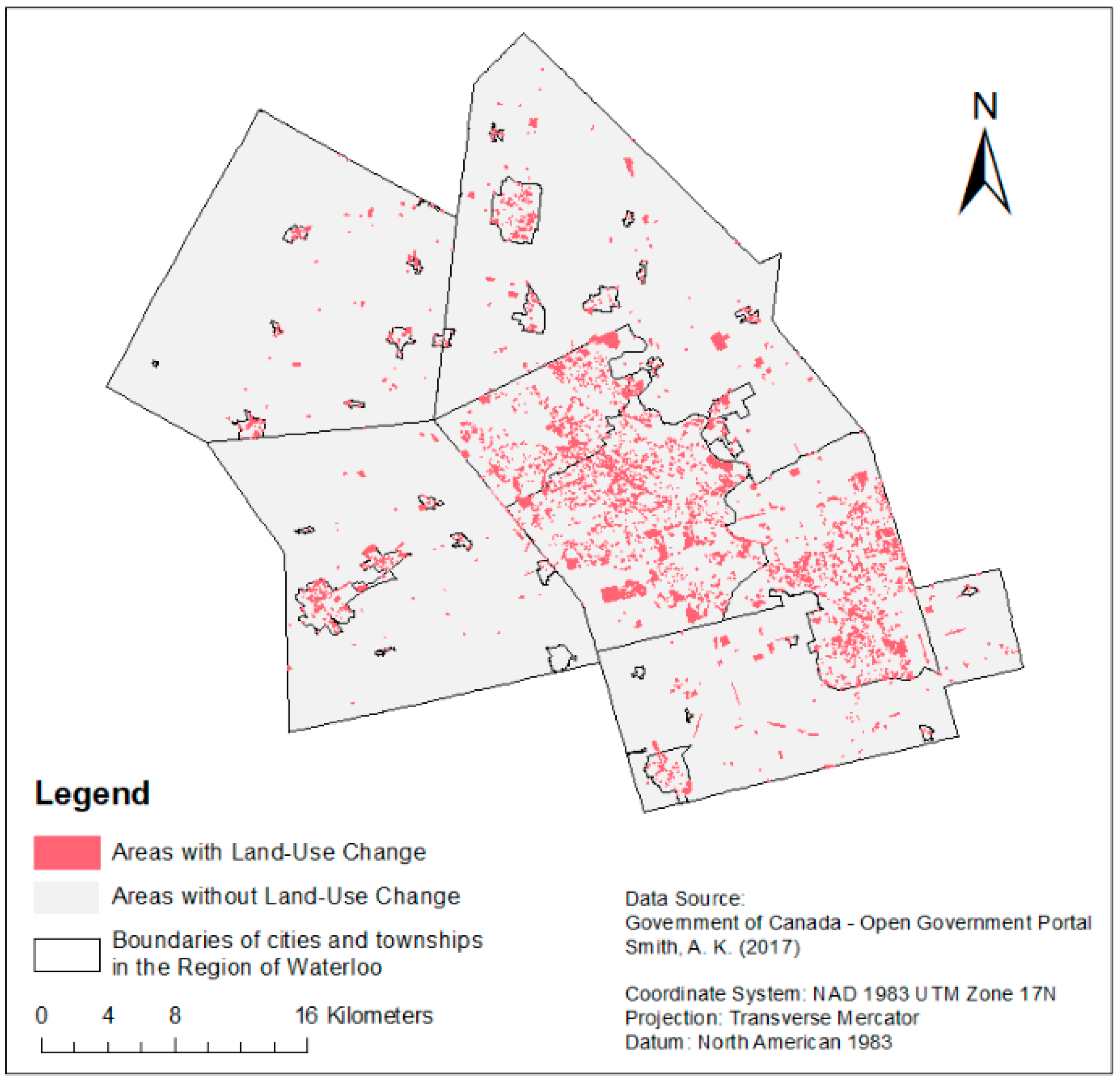
2.1. Study Area
2.2. Data
2.3. Statistical Modelling Approaches
2.3.1. Markov Chain
2.3.2. Logistic Regression
2.3.3. Generalized Additive Model
2.3.4. Survival Analysis
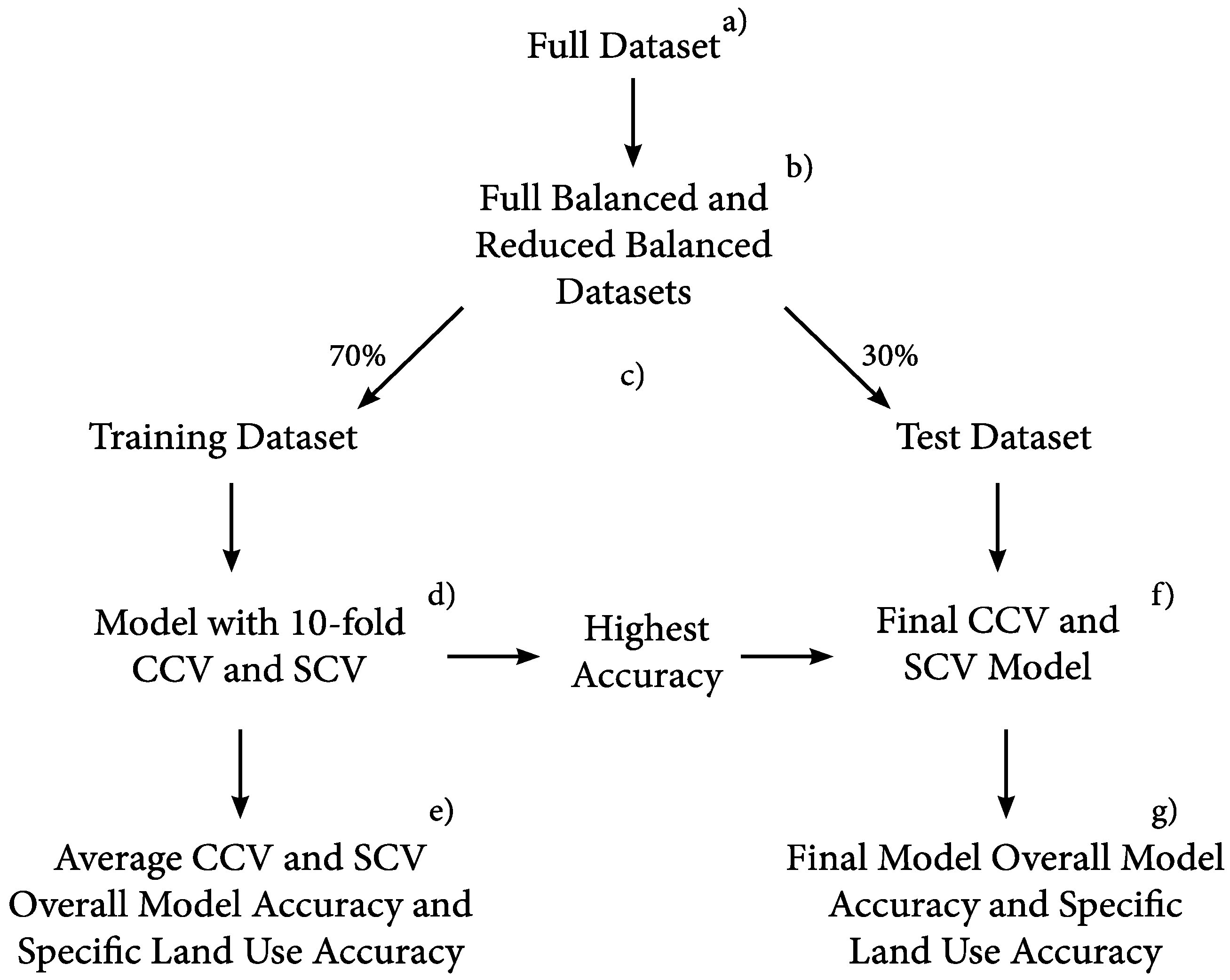
2.4. Analysis
2.5. Implementation of Statistical Approaches
3. Results
3.1. Conventional Cross-Validation and Final Models
3.2. Spatial Cross-Validation and Final Models
3.3. The Combination of Statistical Methods
4. Discussion
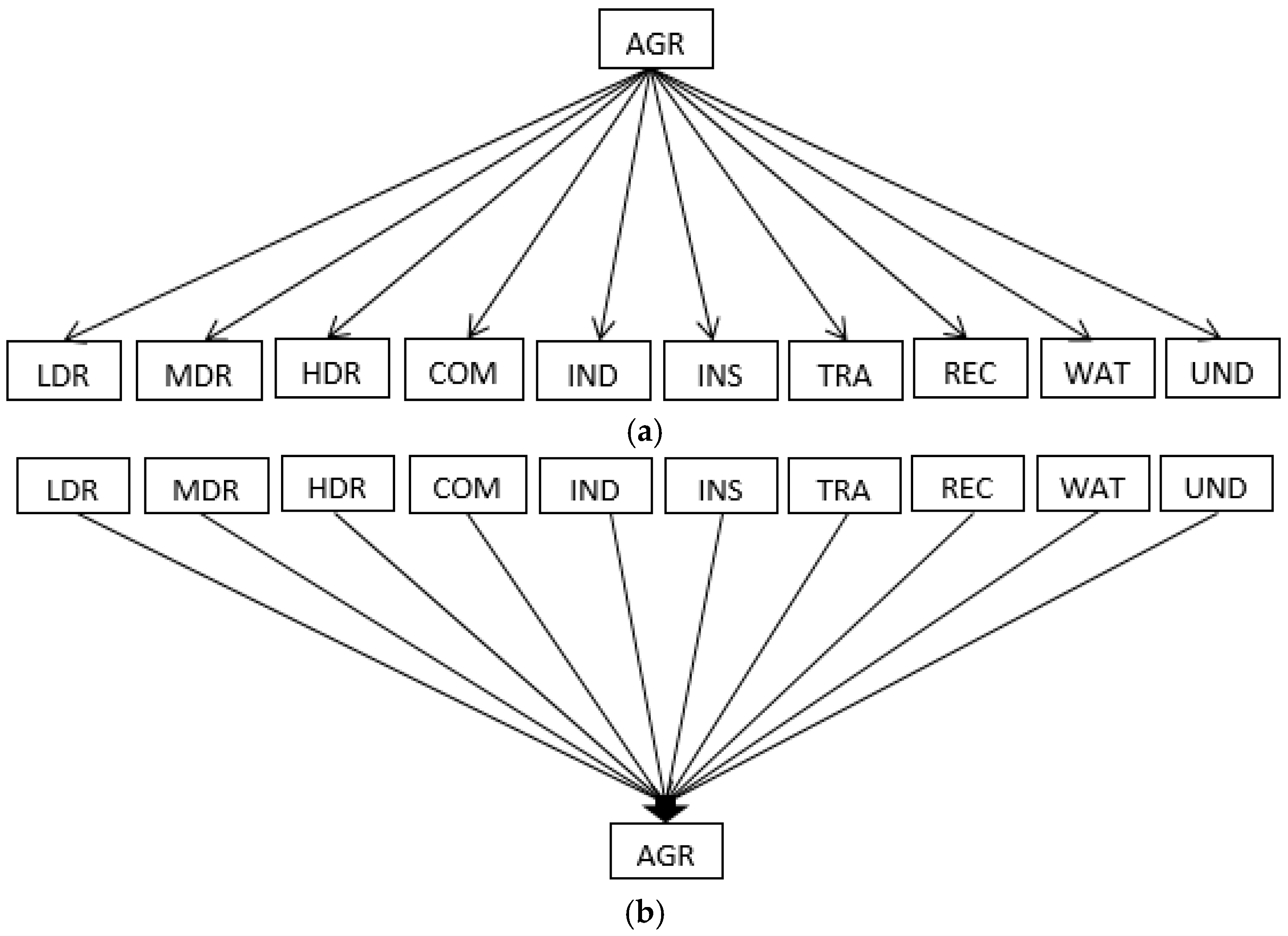
4.1. Modelling One-to-One Land-use Change versus Many-to-One Land-Use Change
4.2. Operationalizing the Combined Statistical Model
4.3. Future Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Name | Description (Unit) |
|---|---|
| lu2015 | 2015 land-use of a parcel in the Region of Waterloo |
| lu2010 | 2010 land-use of a parcel in the Region of Waterloo |
| lu2006 | 2006 land-use of a parcel in the Region of Waterloo |
| lc2010 | 2010 land-cover of a parcel in the Region of Waterloo |
| lc2006 | 2006 land-cover of a parcel in the Region of Waterloo |
| DA_Area | Area of a DA (km2) |
| Parcel_Area | Area of a parcel (km2) |
| MeanDEM | Mean elevation of a parcel (km above sea level) |
| MeanSlope | Mean slope of a parcel (degree) |
| Ramp_dist | Distance from the centroid of a parcel to the nearest highway ramp (km) |
| River_dist | Distance from the centroid of a parcel to the nearest river (km) |
| Water_dist | Distance from the centroid of a parcel to the nearest water body (km) |
| Wood_dist | Distance from the centroid of a parcel nearest wooded area (km) |
| Lroad_dist | Distance from the centroid of a parcel to the nearest local road (km) |
| Mroad_dist | Distance from the centroid of a parcel to the nearest main road (km) |
| lu4_dist | Distance from the centroid of a parcel to the nearest commercial parcel (km) |
| lu5_dist | Distance from the centroid of a parcel to the nearest industrial parcel (km) |
| lu8_dist | Distance from the centroid of a parcel to the nearest protected area/recreational parcel (km) |
| lu9_dist | Distance from the centroid of a parcel to the nearest agricultural parcel (km) |
| DA_population_density | Population density in a DA (population in DA/DA area) in 2010 (person/km2) |
| Residential_population_density | Residential population density in a DA (population in DA/total residential areas in DA) in 2010 (person/km2) |
| Change_Population | The rate of change of population from 2006 to 2011 based on the DA a parcel resides |
| Change_AveIncome | The rate of change of average income from 2006 to 2011 based on the DA a parcel resides |
| F_lu1 | Proportion of low-density residential parcels around a parcel |
| F_lu2 | Proportion of median-density residential parcels around a parcel |
| F_lu3 | Proportion of high-density residential parcels around a parcel |
| F_lu4 | Proportion of commercial parcels around a parcel |
| F_lu5 | Proportion of industrial parcels around a parcel |
| F_lu6 | Proportion of institution parcels around a parcel |
| F_lu7 | Proportion of transportation parcels around a parcel |
| F_lu8 | Proportion of protected area/recreation parcels around a parcel |
| F_lu9 | Proportion of agricultural parcels around a parcel |
| F_lu10 | Proportion of water parcels around a parcel |
| F_lu11 | Proportion of developing parcels around a parcel |
Appendix C
| # | Name | Classification Description Based on Perceived Uses and Services |
|---|---|---|
| 1 | Low-Density Residential | Parcels that appear to contain a single dwelling for a single family on a large property. These parcels typically appear outside the urban core in suburbs or rural areas. While houses tend to be larger than medium density residential, it is not a requirement for the classification. |
| 2 | Medium-Density Residential | Average sized parcels containing a single dwelling for a single family, which may or may not be attached to adjacent dwellings. This class contains the majority of residential parcels within subdivisions and the urban core. In most parcels, the house and driveway cover most or all of the width of the parcels, with yards in the front and back. Townhouses are usually classified as medium-density residential. * |
| 3 | High-Density Residential | Parcels containing buildings with multiple dwellings or units, and therefore multiple families within the parcel. Typically in two forms, apartment or condo buildings, and townhouses where one parcel contains multiple units. Parcels may contain green space and parking lots in addition to the buildings. |
| 4 | Commercial | Parcels containing business where customers visit to obtain products and services, or office buildings which may not receive customers. Larger parcels, such as malls or box stores, will contain large parking lots for customers. These parcels do not contain large outdoor storage areas, although garden and home improvement stores may have some outdoor storage. |
| 5 | Industrial | Parcels which contain a business with an outdoor storage area such as a factory or a car scrapyard. These business typically do not receive customers although there may be parking lots for employees and areas for incoming materials and outgoing products. |
| 6 | Institutional | Manually classified parcels for schools (private and public) and hospitals. Schools and hospitals can appear as a variety of classes but provide different services from these misclassifications (e.g., Commercial or Protected Areas and Recreation). Manually classifying these parcels allows for them to be included in the landscape without large amounts of misclassification. |
| 7 | Transportation | Parcels which represent roads and railways. These parcels often include the boulevard and sidewalks. Highway interchange parcels include all the land which is owned and managed by the managing government. |
| 8 | Protected Areas and Recreation | Areas which have a primary purpose of recreation, such as parks, or protected areas such as forests. Commercial forests and private forests are included in this class as they appear very similar, or even identical to the natural forests. |
| 9 | Agriculture | Parcels which are primarily used for raw food production. This includes fields for crops and pastures. Some parcels will have barns and/or a farm house, while others may have neither. Parcels may also include a portion which is forested, sometimes referred to as “the back forty”. |
| 10 | Water | Parcels which have a main purpose of outlining waterbodies such as rivers. Lakes are included when the lake occupies a majority of the parcel. The rest of the parcel may include sections which would otherwise be classified as Protected Areas and Recreation. |
| 11 | Under Development | Properties where construction has not been completed and no residents or business has moved in. These parcels may become many different classes when complete, but the class cannot be guaranteed at the time of the imagery. Depending on the progress of a development project, residential areas and big box stores or shopping complexes may appear similar as the area is represented by only a single parcel. |
| First Class | Second Class | Problem | Solution |
|---|---|---|---|
| Low-Density Residential | Medium-Density Residential | Parcel size is a continuous variable and it is difficult to define the exact separation between the two classes. | In many cases where there is confusion, the house is the same size as the surrounding properties which are either low or medium density and is a similar distance from the road. The parcel in question will usually have its additional size added through its backyard. If the backyard visually occupies two thirds of the property, it can be easily called low density, if less, medium density. If the parcel has a backyard smaller than two thirds, but the front yard and house are large, then it can also be classified as low density. If an absolute value of size is needed, 2000 m2 should be used as the minimum size for Low Density Residential. |
| Low-Density Residential | Protected Area and Recreation | Household in a large parcel is surrounded by forest or green land with no appearance of backyard/garden. Sometimes the parcel could contain a small portion of backyard/garden relative to the total of the parcel. * | Even the size of the house and the maintained portion of the property is very small compared to the area of the forest, the parcel should be classified as low-density residential. * |
| Medium-Density Residential | Under Development | A house is visible in the parcel that is under development | If there is a completed house with grass on the property it should be considered complete and classified as Medium Density Residential. If the house does not appear complete or there is no grass where there should be, it should be classified as Under Development. |
| Example | Class | Reasoning |
|---|---|---|
| Airport | Commercial | Airports provide services similar to Commercial parcels, where people are constantly visiting the parcel. Visually they are similar as they both include large paved areas such as parking lots and a large building. |
| Fire station | Commercial | Although functionally different from Commercial parcels, they are very similar in the imagery. |
| Graveyard | Protected Areas and Recreation | Graveyards and cemeteries are visually similar to parks, where there are paths for people to walk and grass fields. The only visual difference is that there are pieces of stone (headstones) scattered across the fields and there is no sports equipment. |
| Water Tower | Protected Areas and Recreation | Water towers can be visually similar to parks as they can have large grassy areas surrounding the tower. If the water tower is in a parcel without much grassed area, it may be classified as Commercial instead. |
| Commercial Forest –Post-Harvest | Various | If the harvested forest appears to be converted into agriculture, classify as Agriculture. If it shows signs of urban development, it should be classified as Under Development. If it appears to be replanted and is still being used as a commercial forest, classify as Protected Areas and Recreation. |
| Catwalk | Transportation | The paths between houses, or catwalks, are similar to roads, although a little smaller. A path through a park or green space would not be considered transportation. |
| Walking paths | Protected Areas and Recreation | Walking paths in the area can often be found under large electrical transmission lines. The transmission lines and towers account for a small portion of the parcel, and therefore simply appear as grassy corridors through subdivisions, similar to parks. |
| Church | Commercial | Churches are visibly similar to Commercial parcels because they are a building which has a parking lot and some property. Functionally they are also similar as people will visit a church for a relatively short period of time, similar to a business. |
| Artifacts | N/A | The parcel data is not perfect and has artifacts from either previous versions, or mistakes during creation. Some artifacts have little impact on the data, while others have large impacts. The most frequent example is a single parcel being divided into multiple parcels by the artifacts. |
| Artifacts–Splits | N/A | When a parcel is divided by artifacts all segments should be classified as the original type if suitable. If a segment can clearly be classified as another land use type it should be done. For example, if a Low Density Residential parcel is divided into three pieces, two covering the house and one covering a forest at the back of the property, the two on the house should be Low Density Residential and the one on the forest should be Protected Areas and Recreation. |
| Artifacts–Slivers | N/A | Another form of artifact is a sliver. These sliver parcels are very thin and long. Examples can be a few centimeters wide but almost a kilometer long. Sliver parcels should be ignored and not classified if noticed. |
| Mixed Parcels | N/A | Occasionally parcels will contain multiple land use types other than the previously mentioned scenarios. For example a parcel may contain a house and land on one half and part of a waterbody on the other half. In these scenarios where there is no clear majority of land use type the following order of priority should be used: Medium Density Residential > High Density Residential > Low Density Residential > Commercial > Industrial > Institution > Transportation > Under Development > Agriculture > Protected Areas and Recreation > Water |
| Future Development | N/A | In the scenarios where parcels have been created but no development has begun, classify the parcel based on the currently present land use type. If the imagery shows evidence of development, then classify as Under Development. |
Appendix D
| Method | MC | LR | GAM | SA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Land-Use Change | FB | RB | FB | RB | FB | RB | FB | RB | |
| Low-density residential | n/a | n/a | 2.93 | 2.93 | 152.06 | 152.06 | 1.14 | 1.14 | |
| Medium-density residential | n/a | n/a | 6.21 | 3.56 | 2468.95 | 2816.7 | 4.56 | 1.24 | |
| High-density residential | n/a | n/a | 2.92 | 1.02 | 282.7 | 199.04 | 1.41 | 1.2 | |
| Commercial | n/a | n/a | 1.55 | 1.03 | 1127.83 | 3408.59 | 2 | 1.27 | |
| Industrial | n/a | n/a | 0.83 | 0.83 | 5 | 5 | 1.16 | 1.16 | |
| Institution | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | |
| Transportation | n/a | n/a | 1.07 | 0.98 | 311.44 | 229.72 | 1.5 | 1.25 | |
| Protected area and recreation | n/a | n/a | 0.89 | 0.89 | 17.28 | 17.28 | 1.14 | 1.14 | |
| Agriculture | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | |
| Water | n/a | n/a | 0.65 | 0.65 | 4.42 | 4.42 | 0.79 | 0.79 | |
| Under development | n/a | n/a | 1.06 | 1.03 | 779.71 | 434.11 | 1.47 | 1.24 | |
| Total | 17.42 | 8.7 | 18.11 | 12.92 | 5149.39 | 7266.92 | 15.17 | 10.43 | |
| Method | MC | LR | GAM | SA | |
|---|---|---|---|---|---|
| Land-Use Change | |||||
| Low-density residential | 11.11 | 0 | 0 | 0 | |
| Medium-density residential | 36.77 | 1.18 | 5.04 | 0.38 | |
| High-density residential | 3.60 | 1.22 | 6.98 | 1.38 | |
| Commercial | 5.30 | 0.91 | 1.75 | 2.20 | |
| Industrial | 4.73 | 0 | 0 | 0 | |
| Institution | 20.00 | n/a | n/a | n/a | |
| Transportation | 0.04 | 3.53 | 3.36 | 3.05 | |
| Protected area and recreation | 17.58 | 0 | 0 | 0 | |
| Agriculture | 0.91 | n/a | n/a | n/a | |
| Water | 1.29 | n/a | n/a | n/a | |
| Under development | 19.45 | 0.80 | 5.10 | 1.97 | |
| Overall | 3.63 | 0.73 | 2.78 | 1.12 | |
| Method | LR | GAM | SA | |
|---|---|---|---|---|
| Land-Use Change | ||||
| Low-density residential | 0 | 0 | 0 | |
| Medium-density residential | 2.20 | 4.48 | 0.11 | |
| High-density residential | 1.89 | 1.57 | 0.68 | |
| Commercial | 4.85 | 1.98 | 1.55 | |
| Industrial | 0 | 0 | 0 | |
| Institution | n/a | n/a | n/a | |
| Transportation | 2.83 | 3.98 | 2.11 | |
| Protected area and recreation | 0 | 0 | 0 | |
| Agriculture | n/a | n/a | n/a | |
| Water | n/a | n/a | n/a | |
| Under development | 1.53 | 3.87 | 5.38 | |
| Overall | 0.02 | 1.98 | 0.84 | |
| Method | MC | LR | GAM | SA | |
|---|---|---|---|---|---|
| Land-Use Change | |||||
| Low-density residential | 15.39 | 0 | 0 | 0 | |
| Medium-density residential | 40.15 | 0.29 | 6.09 | 1.10 | |
| High-density residential | 0.29 | 2.78 | 4.27 | 3.17 | |
| Commercial | 2.95 | 0.90 | 9.70 | 1.29 | |
| Industrial | 0.01 | 0 | 0 | 0 | |
| Institution | 0 | n/a | n/a | n/a | |
| Transportation | 2.5 | 0.14 | 3.72 | 2.86 | |
| Protected area and recreation | 17.79 | 0 | 0 | 0 | |
| Agriculture | 6.65 | n/a | n/a | n/a | |
| Water | 22.13 | n/a | n/a | n/a | |
| Under development | 17.39 | 1.89 | 0.34 | 1.36 | |
| Overall | 0.01 | 0.53 | 1.86 | 0.19 | |
| Method | LR | GAM | SA | |
|---|---|---|---|---|
| Land-Use Change | ||||
| Low-density residential | 0 | 0 | 0 | |
| Medium-density residential | 1.47 | 0.73 | 0.11 | |
| High-density residential | 2.28 | 1.68 | 2.67 | |
| Commercial | 1.06 | 8.43 | 0.95 | |
| Industrial | 0 | 0 | 0 | |
| Institution | n/a | n/a | n/a | |
| Transportation | 2.58 | 0.65 | 1.70 | |
| Protected area and recreation | 0 | 0 | 0 | |
| Agriculture | n/a | n/a | n/a | |
| Water | n/a | n/a | n/a | |
| Under development | 0.63 | 3.08 | 0.72 | |
| Overall | 0.64 | 1.40 | 0.56 | |
Appendix E
| Method | Final LR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 1.21 | −4.43 | 2.71 | 3.37 | |||||
| lu2006_3 | 2.63 | −2.59 | −1.49 | ||||||
| lu2006_4 | 1.11 | −2.93 | −0.52 | −2.47 | 1.78 | ||||
| lu2006_5 | −1.27 | −3.69 | |||||||
| lu2006_7 | −1.81 | −1.29 | −3.55 | ||||||
| lu2006_8 | 1.53 | −2.80 | |||||||
| lu2006_9 | 1.75 | −2.18 | |||||||
| lu2006_11 | −2.07 | −1.05 | −3.39 | ||||||
| lc2006_2 | 1.82 | −1.65 | |||||||
| lc2006_3 | −1.50 | ||||||||
| lc2006_4 | −1.17 | ||||||||
| lc2006_5 | −1.56 | ||||||||
| lc2006_6 | −2.16 | ||||||||
| lc2006_7 | −1.92 | ||||||||
| lc2006_8 | 2.32 | −1.52 | −1.74 | ||||||
| lc2010_2 | 0.78 | 2.06 | |||||||
| lc2010_3 | 2.39 | −0.98 | −1.85 | −0.90 | |||||
| lc2010_5 | 1.06 | 1.97 | 0.61 | 0.52 | 4.40 | −1.47 | |||
| lc2010_6 | −1.05 | 4.45 | |||||||
| lc2010_7 | 2.62 | 3.91 | 0.61 | 6.51 | −2.86 | ||||
| lc2010_8 | 2.89 | 1.21 | 2.09 | 1.51 | |||||
| ParcelArea | −0.01 | −48.91 | −40.99 | −41.70 | 5.19 | ||||
| DA_Area | −28.73 | ||||||||
| MeanSlope | −3.52 | ||||||||
| MeanDEM | −3.54 | 5.94 | −9.62 | −9.18 | |||||
| Wood_dist | 0.33 | −0.70 | −0.72 | ||||||
| River_dist | 2.11 | ||||||||
| Water_dist | 0.32 | 0.52 | |||||||
| LRoad_dist | 6.47 | −9.23 | 2.41 | ||||||
| MRoad_dist | 0.68 | 1.26 | |||||||
| Ramp_dist | 0.08 | ||||||||
| lu4_dist | −0.41 | −10.42 | −2.78 | 8.69 | −0.86 | −1.33 | |||
| lu5_dist | |||||||||
| lu8_dist | 2.03 | −1.71 | 1.05 | −3.80 | 15.49 | ||||
| lu9_dist | −0.22 | 0.18 | |||||||
| Residential_ Popn_Density | −0.04 | −0.04 | 0.03 | ||||||
| DA_Popn_ Density | −1.31 × 10−4 | −1.49 × 10−4 | 2.74 × 10−4 | ||||||
| F_lu1 | 2.48 | ||||||||
| F_lu2 | 1.46 | ||||||||
| F_lu7 | 0.83 | 1.25 | |||||||
| F_lu8 | 3.94 | 3.00 | |||||||
| F_lu9 | 2.30 | ||||||||
| F_lu11 | 0.84 | 0.76 | |||||||
| Method | Final LR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 1.21 | 4.04 | 3.37 | ||||||
| lu2006_3 | 2.63 | −1.36 | |||||||
| lu2006_4 | 1.11 | −2.51 | |||||||
| lu2006_5 | −1.13 | −3.57 | |||||||
| lu2006_7 | −2.71 | ||||||||
| lu2006_8 | 1.53 | 2.75 | −1.96 | ||||||
| lu2006_9 | −2.07 | ||||||||
| lu2006_11 | −3.24 | ||||||||
| lc2006_2 | 1.82 | −4.23 | |||||||
| lc2006_3 | −2.99 | ||||||||
| lc2006_5 | −3.74 | ||||||||
| lc2006_6 | −5.08 | ||||||||
| lc2006_7 | −3.77 | ||||||||
| lc2006_8 | 2.32 | −2.74 | |||||||
| lc2010_2 | 1.69 | −1.42 | 1.47 | ||||||
| lc2010_3 | 3.47 | −1.28 | −1.03 | ||||||
| lc2010_5 | 1.06 | 2.33 | 0.97 | 4.40 | |||||
| lc2010_6 | 4.45 | ||||||||
| lc2010_7 | 2.62 | 5.01 | 6.51 | −2.65 | |||||
| lc2010_8 | 2.89 | 1.91 | 2.39 | ||||||
| ParcelArea | −48.15 | −209.63 | −17.55 | −41.70 | 12.70 | ||||
| DA_Area | −54.93 | ||||||||
| MeanSlope | −0.59 | ||||||||
| Wood_dist | −0.69 | −0.67 | |||||||
| River_dist | 2.11 | ||||||||
| LRoad_dist | 9.73 | −6.63 | |||||||
| MRoad_dist | 0.67 | −1.42 | |||||||
| Ramp_dist | 0.17 | ||||||||
| lu4_dist | −0.41 | −6.01 | −2.72 | 19.15 | −1.16 | −3.04 | |||
| lu5_dist | |||||||||
| lu8_dist | 2.03 | −3.44 | 15.49 | ||||||
| lu9_dist | −0.27 | ||||||||
| Residential_ Popn_Density | 0.03 | ||||||||
| DA_Popn_ Density | −1.43 × 10−4 | 2.42 × 10−4 | |||||||
| Change_ AveIncome | −1.02 | ||||||||
| F_lu1 | 3.10 | ||||||||
| F_lu2 | −1.37 | ||||||||
| F_lu7 | −2.56 | ||||||||
| F_lu9 | −2.69 | ||||||||
| F_lu11 | −1.77 | ||||||||
| Method | Final GAM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 1.22 | −3.76 | −1.24 | 2.08 | |||||
| lu2006_3 | 2.67 | −2.66 | −1.65 | ||||||
| lu2006_4 | 0.98 | −2.74 | −1.05 | −4.51 | |||||
| lu2006_5 | −1.81 | −3.68 | |||||||
| lu2006_7 | −1.46 | −2.00 | −3.99 | ||||||
| lu2006_8 | 1.54 | −3.54 | |||||||
| lu2006_9 | −3.44 | −3.52 | |||||||
| lu2006_11 | −1.32 | −2.00 | −4.41 | ||||||
| lc2006_2 | 1.76 | −2.11 | |||||||
| lc2006_3 | −1.94 | ||||||||
| lc2006_4 | −1.87 | ||||||||
| lc2006_5 | −1.88 | ||||||||
| lc2006_7 | 0.66 | −1.93 | |||||||
| lc2006_8 | 2.61 | −1.92 | |||||||
| lc2010_2 | −0.41 | −2.23 | 2.28 | ||||||
| lc2010_3 | 1.17 | −1.09 | 1.09 | −0.98 | −2.53 | ||||
| lc2010_5 | 0.96 | 1.90 | 1.18 | 0.82 | −2.63 | ||||
| lc2010_7 | 2.66 | 4.32 | 2.65 | 0.88 | −4.76 | ||||
| lc2010_8 | 2.37 | −1.20 | 2.59 | 1.61 | |||||
| ParcelArea | −6.83 | S | S | S | |||||
| MeanSlope | S | ||||||||
| MeanDEM | S | S | S | ||||||
| Wood_dist | S | S | S | ||||||
| River_dist | S | ||||||||
| Water_dist | S | S | |||||||
| LRoad_dist | S | S | S | S | |||||
| MRoad_dist | S | S | S | S | |||||
| Ramp_dist | S | S | S | ||||||
| lu4_dist | S | S | S | S | S | ||||
| lu5_dist | S | ||||||||
| lu8_dist | S | S | S | ||||||
| lu9_dist | S | S | |||||||
| Residential_Popn_Density | S | S | |||||||
| DA_Popn_Density | S | S | |||||||
| Change_AveIncome | S | S | |||||||
| Change_Popn | S | S | |||||||
| F_lu2 | S | ||||||||
| F_lu11 | 0.69 | ||||||||
| Method | Final GAM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 1.22 | 4.56 | 2.16 | ||||||
| lu2006_3 | 2.67 | −1.52 | |||||||
| lu2006_4 | 0.98 | −0.84 | −3.79 | ||||||
| lu2006_5 | −1.51 | ||||||||
| lu2006_8 | 1.54 | ||||||||
| lu2006_9 | −1.39 | ||||||||
| lu2006_11 | −2.07 | ||||||||
| lc2006_2 | 1.76 | 2.48 | |||||||
| lc2006_3 | 3.54 | ||||||||
| lc2006_5 | 2.59 | ||||||||
| lc2006_7 | 0.66 | 2.18 | |||||||
| lc2006_8 | 2.61 | 2.28 | |||||||
| lc2010_2 | −2.18 | 4.85 | |||||||
| lc2010_3 | 3.28 | −2.05 | 3.80 | −2.41 | |||||
| lc2010_5 | 0.96 | 2.85 | −0.82 | 3.52 | 1.45 | −1.25 | |||
| lc2010_6 | 2.14 | ||||||||
| lc2010_7 | 2.66 | 4.51 | 5.52 | 1.76 | −3.69 | ||||
| lc2010_8 | 2.37 | −2.34 | 4.51 | ||||||
| ParcelArea | S | S | S | S | |||||
| DA_Area | S | S | |||||||
| MeanSlope | S | ||||||||
| MeanDEM | S | S | |||||||
| Wood_dist | S | S | |||||||
| River_dist | S | ||||||||
| LRoad_dist | S | −9.98 | S | ||||||
| MRoad_dist | S | S | S | ||||||
| Ramp_dist | S | ||||||||
| lu4_dist | S | S | S | S | S | ||||
| lu5_dist | S | ||||||||
| lu8_dist | S | S | |||||||
| Residential_Popn_Density | S | S | S | S | |||||
| DA_Popn_Density | S | ||||||||
| F_lu2 | −1.81 | −1.14 | |||||||
| F_lu11 | −2.09 | ||||||||
| Method | Final SA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 0.72 | −1.91 | 1.87 | −0.85 | |||||
| lu2006_3 | 1.38 | −0.60 | −0.81 | ||||||
| lu2006_4 | 0.64 | −0.72 | −1.34 | −0.81 | |||||
| lu2006_5 | −0.76 | −2.37 | |||||||
| lu2006_7 | 2.58 | −1.05 | 1.30 | −2.26 | |||||
| lu2006_8 | 0.84 | −1.79 | |||||||
| lu2006_9 | 1.58 | 0.53 | 1.01 | −1.02 | |||||
| lu2006_10 | −0.52 | ||||||||
| lu2006_11 | 0.70 | −0.35 | −1.91 | ||||||
| lc2006_2 | 1.01 | −0.60 | 2.71 | ||||||
| lc2006_3 | −0.36 | 2.38 | |||||||
| lc2006_4 | −1.49 | ||||||||
| lc2006_5 | −0.49 | 2.26 | −1.48 | −1.28 | |||||
| lc2006_6 | −0.91 | −2.06 | |||||||
| lc2006_7 | −0.63 | −1.16 | |||||||
| lc2006_8 | 0.76 | −0.35 | −1.42 | −1.23 | |||||
| lc2010_2 | 0.75 | −1.26 | |||||||
| lc2010_3 | 1.63 | −0.57 | −1.02 | −0.74 | |||||
| lc2010_5 | 0.59 | 1.53 | 0.35 | 0.31 | 2.43 | −0.69 | |||
| lc2010_6 | −0.97 | 1.88 | |||||||
| lc2010_7 | 1.05 | 1.83 | 0.35 | −1.42 | 3.25 | −1.99 | |||
| lc2010_8 | 1.02 | 1.19 | 0.59 | ||||||
| ParcelArea | −75.41 | −16.84 | −20.50 | −19.21 | 2.05 | ||||
| DA_Area | −25.10 | ||||||||
| MeanSlope | −0.19 | ||||||||
| MeanDEM | −2.24 | 2.62 | −4.61 | ||||||
| Wood_dist | 0.29 | −0.45 | |||||||
| River_dist | 0.88 | ||||||||
| Water_dist | −0.15 | ||||||||
| LRoad_dist | 0.73 | −2.72 | |||||||
| MRoad_dist | −0.28 | −0.63 | |||||||
| Ramp_dist | 0.03 | 0.05 | |||||||
| lu4_dist | −4.80 | −1.90 | 1.49 | −24.46 | |||||
| lu5_dist | |||||||||
| lu8_dist | 0.53 | −0.58 | −1.85 | 3.07 | |||||
| lu9_dist | |||||||||
| Residential_Popn _Density | −0.02 | −0.02 | 0.02 | ||||||
| DA_Popn_Density | −0.60 × 10−4 | −1.16 × 10−4 | 1.07 × 10−4 | ||||||
| Change_AveIncome | −0.20 | ||||||||
| Change_Popn | −0.03 | −0.61 | |||||||
| F_lu1 | 0.79 | ||||||||
| F_lu2 | 0.42 | ||||||||
| F_lu3 | |||||||||
| F_lu7 | 0.54 | 0.52 | 1.40 | ||||||
| F_lu9 | 0.97 | ||||||||
| F_lu11 | |||||||||
| Method | Final SA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 0.72 | −2.09 | 0.91 | 1.87 | −0.67 | ||||
| lu2006_3 | 1.38 | −0.85 | |||||||
| lu2006_4 | 0.64 | −1.04 | −1.16 | ||||||
| lu2006_5 | −1.08 | −2.58 | |||||||
| lu2006_7 | 0.88 | 2.58 | −0.99 | 1.30 | |||||
| lu2006_8 | 0.84 | 0.92 | −0.66 | ||||||
| lu2006_9 | 1.59 | 1.01 | −2.11 | ||||||
| lu2006_11 | 0.70 | −1.96 | |||||||
| lc2006_2 | 1.01 | 2.71 | |||||||
| lc2006_3 | 2.38 | ||||||||
| lc2006_5 | 2.26 | −1.48 | |||||||
| lc2006_6 | −1.63 | ||||||||
| lc2006_7 | −1.16 | ||||||||
| lc2006_8 | 0.76 | −1.42 | |||||||
| lc2010_2 | 1.42 | −1.19 | |||||||
| lc2010_3 | 2.42 | −0.71 | −0.76 | −0.62 | |||||
| lc2010_4 | |||||||||
| lc2010_5 | 0.59 | 1.86 | 0.62 | 2.43 | |||||
| lc2010_6 | 1.88 | ||||||||
| lc2010_7 | 1.06 | 2.12 | −1.42 | 3.25 | −0.91 | ||||
| lc2010_8 | 1.02 | 0.96 | −1.00 | 0.57 | |||||
| ParcelArea | −49.28 | −105.50 | −19.21 | ||||||
| MeanSlope | −0.13 | ||||||||
| MeanDEM | −3.85 | ||||||||
| Wood_dist | −0.35 | ||||||||
| River_dist | −0.42 | 0.88 | |||||||
| MRoad_dist | −1.16 | ||||||||
| Ramp_dist | 0.03 | ||||||||
| lu4_dist | −3.13 | −1.22 | 2.00 | −24.46 | −1.10 | 0.47 | |||
| lu5_dist | 0.81 | ||||||||
| lu8_dist | 0.53 | −1.36 | 3.07 | ||||||
| lu9_dist | −0.27 | ||||||||
| Residential_Popn _Density | −0.02 | ||||||||
| DA_Popn_Density | 1.21 × 10−4 | ||||||||
| Change_Popn | −0.61 | ||||||||
| Change_AveIncome | −0.46 | ||||||||
| F_lu7 | 1.40 | 0.81 | |||||||
| F_lu9 | 0.97 | ||||||||
| Method | Final LR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 1.49 | −4.36 | −1.54 | 2.89 | 3.51 | ||||
| lu2006_3 | 3.87 | −2.43 | −0.62 | 1.90 | |||||
| lu2006_4 | 1.74 | −2.80 | −1.14 | −2.43 | |||||
| lu2006_5 | −4.07 | ||||||||
| lu2006_7 | −1.55 | −1.27 | −3.75 | ||||||
| lu2006_8 | 1.57 | −3.08 | |||||||
| lu2006_9 | 2.23 | −1.81 | |||||||
| lu2006_11 | 1.49 | −2.00 | −1.17 | 1.66 | −3.68 | ||||
| lc2006_2 | −1.65 | 1.41 | |||||||
| lc2006_3 | −1.42 | ||||||||
| lc2006_4 | −1.11 | ||||||||
| lc2006_5 | −1.50 | ||||||||
| lc2006_6 | 4.35 | ||||||||
| lc2006_7 | −1.82 | 4.37 | |||||||
| lc2006_8 | 1.06 | −1.38 | 6.39 | ||||||
| lc2010_2 | 0.81 | 2.00 | |||||||
| lc2010_3 | 2.48 | −0.98 | −1.84 | −3.88 | −0.90 | ||||
| lc2010_5 | 0.77 | 2.04 | 0.54 | 0.53 | −1.47 | ||||
| lc2010_6 | 0.59 | −1.00 | 1.90 | ||||||
| lc2010_7 | 1.08 | 3.88 | 0.61 | −2.69 | |||||
| lc2010_8 | 1.67 | 1.33 | 2.16 | 2.30 | 1.12 | ||||
| ParcelArea | −110.10 | −60.91 | −43.29 | 5.03 | |||||
| DA_Area | 24.30 | −30.89 | 30.50 | ||||||
| MeanSlope | −0.21 | −0.34 | |||||||
| MeanDEM | −9.38 | −10.43 | |||||||
| Wood_dist | 0.37 | −0.86 | 15.36 | −1.12 | |||||
| Water_dist | −0.42 | 0.72 | |||||||
| LRoad_dist | 6.21 | −1.00 | 2.67 | ||||||
| MRoad_dist | 0.76 | 1.38 | |||||||
| Ramp_dist | 0.07 | ||||||||
| lu4_dist | −0.42 | −10.28 | −3.07 | 10.34 | −38.12 | −1.14 | |||
| lu5_dist | 0.45 | 24.05 | |||||||
| lu8_dist | −1.79 | 1.46 | −3.90 | ||||||
| lu9_dist | 0.26 | 0.54 | |||||||
| Residential_ Popn_Density | −0.03 | −0.03 | 0.03 | ||||||
| DA_Popn_ Density | −1.32 × 10−4 | −1.62 × 10−4 | 2.40 × 10−4 | ||||||
| Change_Popn | −0.18 | ||||||||
| F_lu1 | −0.77 | 1.77 | |||||||
| F_lu2 | 1.24 | ||||||||
| F_lu7 | 0.78 | ||||||||
| F_lu8 | −4.02 | 2.79 | |||||||
| F_lu11 | 0.94 | ||||||||
| Method | Final LR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 1.49 | −3.45 | 3.51 | ||||||
| lu2006_3 | 3.87 | −1.30 | |||||||
| lu2006_4 | 1.74 | −2.73 | |||||||
| lu2006_5 | −1.11 | −3.21 | |||||||
| lu2006_7 | −2.50 | ||||||||
| lu2006_8 | 1.57 | −1.89 | |||||||
| lu2006_9 | −2.00 | ||||||||
| lu2006_11 | 1.49 | 1.66 | −2.89 | ||||||
| lc2006_6 | −4.75 | ||||||||
| lc2006_8 | 1.06 | ||||||||
| lc2010_2 | 1.34 | −1.49 | 1.10 | 1.39 | |||||
| lc2010_3 | 3.49 | −1.16 | |||||||
| lc2010_5 | 0.77 | 1.89 | 4.35 | ||||||
| lc2010_6 | 0.59 | 4.37 | |||||||
| lc2010_7 | 1.08 | 3.56 | 0.93 | 6.39 | −2.72 | ||||
| lc2010_8 | 1.67 | 1.39 | 2.41 | ||||||
| ParcelArea | 24.30 | −46.73 | −45.64 | −3.88 | 12.38 | ||||
| MeanSlope | −0.21 | 0.41 | −0.63 | ||||||
| MeanDEM | 9.70 | ||||||||
| Wood_dist | −0.92 | ||||||||
| River_dist | 2.30 | ||||||||
| LRoad_dist | −7.23 | ||||||||
| MRoad_dist | 0.76 | ||||||||
| lu4_dist | −0.42 | −4.87 | −3.02 | 13.83 | −38.12 | −2.05 | −3.27 | ||
| lu5_dist | 24.05 | ||||||||
| lu8_dist | −3.06 | 15.36 | |||||||
| lu9_dist | 0.33 | ||||||||
| Residential_ Popn_Density | −0.04 | ||||||||
| DA_Popn_ Density | −1.64 × 10−4 | 2.44 × 10−4 | |||||||
| Change_ AveIncome | −1.19 | ||||||||
| F_lu1 | 3.91 | ||||||||
| F_lu2 | −1.52 | ||||||||
| F_lu8 | −3.91 | ||||||||
| F_lu11 | −1.85 | ||||||||
| Method | Final GAM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | −3.96 | −1.87 | −1.54 | ||||||
| lu2006_3 | 2.90 | −3.13 | −1.19 | ||||||
| lu2006_4 | 1.00 | −2.91 | −1.98 | −4.79 | |||||
| lu2006_5 | −2.87 | ||||||||
| lu2006_7 | −2.77 | −3.32 | |||||||
| lu2006_8 | 1.74 | −2.28 | |||||||
| lu2006_9 | −3.52 | −2.42 | |||||||
| lu2006_11 | 1.41 | −2.06 | −2.32 | −3.03 | |||||
| lc2006_2 | 1.50 | −1.86 | |||||||
| lc2006_3 | 1.46 | −1.58 | |||||||
| lc2006_4 | 0.91 | −1.55 | |||||||
| lc2006_5 | −1.64 | ||||||||
| lc2006_7 | −1.70 | ||||||||
| lc2006_8 | 1.28 | −1.60 | |||||||
| lc2010_2 | −0.69 | 2.43 | |||||||
| lc2010_3 | 0.90 | 1.11 | −1.02 | −2.31 | |||||
| lc2010_5 | 0.92 | 1.80 | 1.17 | 0.78 | −2.38 | ||||
| lc2010_7 | 0.58 | 4.11 | 2.59 | 0.78 | −3.98 | ||||
| lc2010_8 | 1.11 | −0.63 | −1.22 | 2.75 | 1.58 | ||||
| ParcelArea | −73.74 | S | S | ||||||
| DA_Area | 35.23 | S | |||||||
| MeanSlope | S | ||||||||
| MeanDEM | S | ||||||||
| Wood_dist | S | S | S | S | |||||
| Water_dist | S | ||||||||
| LRoad_dist | S | S | S | S | S | ||||
| MRoad_dist | S | S | S | S | |||||
| Ramp_dist | S | ||||||||
| lu4_dist | −0.39 | S | S | S | S | S | |||
| lu5_dist | S | ||||||||
| lu8_dist | S | S | S | ||||||
| lu9_dist | S | ||||||||
| Residential_Popn_Density | S | S | |||||||
| DA_Popn_Density | S | S | |||||||
| Change_AveIncome | S | S | |||||||
| Change_Popn | S | S | S | ||||||
| F_lu2 | S | ||||||||
| Method | Final GAM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | −4.56 | −1.45 | 5.00 | ||||||
| lu2006_3 | 2.90 | −0.89 | |||||||
| lu2006_4 | 1.00 | −4.81 | −1.51 | −3.95 | |||||
| lu2006_5 | −3.36 | ||||||||
| lu2006_7 | −2.44 | ||||||||
| lu2006_8 | 1.74 | -2.50 | |||||||
| lu2006_9 | −2.55 | ||||||||
| lu2006_11 | 1.41 | −3.38 | |||||||
| lc2006_2 | 1.50 | ||||||||
| lc2006_3 | 1.46 | ||||||||
| lc2006_4 | |||||||||
| lc2006_5 | 0.91 | ||||||||
| lc2006_6 | −5.49 | ||||||||
| lc2006_7 | |||||||||
| lc2006_8 | 1.28 | ||||||||
| lc2010_2 | −2.06 | 3.08 | |||||||
| lc2010_3 | 2.68 | −1.98 | 1.46 | ||||||
| lc2010_5 | 0.92 | 2.18 | −0.68 | 1.63 | −1.83 | ||||
| lc2010_6 | 0.58 | −1.08 | |||||||
| lc2010_7 | 1.11 | 4.27 | 2.66 | 1.96 | −3.49 | ||||
| lc2010_8 | 3.12 | 2.89 | 2.18 | ||||||
| ParcelArea | S | S | S | ||||||
| DA_Area | 35.23 | S | |||||||
| MeanSlope | −0.64 | ||||||||
| MeanDEM | S | ||||||||
| Wood_dist | −2.01 | ||||||||
| River_dist | S | ||||||||
| Water_dist | S | S | |||||||
| LRoad_dist | S | S | |||||||
| MRoad_dist | S | S | |||||||
| Ramp_dist | |||||||||
| lu4_dist | −0.39 | S | S | S | S | ||||
| lu5_dist | |||||||||
| lu8_dist | S | S | S | ||||||
| lu9_dist | |||||||||
| Residential_Popn_Density | S | S | S | ||||||
| DA_Popn_Density | S | ||||||||
| Change_AveIncome | S | ||||||||
| Change_Popn | |||||||||
| F_lu1 | S | ||||||||
| F_lu2 | |||||||||
| F_lu11 | |||||||||
| Method | Final SA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 0.90 | −1.92 | −0.84 | 2.36 | 1.91 | −1.16 | |||
| lu2006_3 | 1.33 | −0.60 | −0.25 | −1.15 | |||||
| lu2006_4 | 0.55 | −0.73 | −0.76 | −1.37 | −2.56 | ||||
| lu2006_5 | 1.30 | −2.62 | |||||||
| lu2006_6 | 7.33 | −1.96 | |||||||
| lu2006_7 | 2.99 | −1.17 | 1.36 | −0.99 | |||||
| lu2006_8 | 0.63 | −2.08 | |||||||
| lu2006_9 | 1.56 | 0.51 | 1.66 | 1.07 | |||||
| lu2006_10 | −0.46 | ||||||||
| lu2006_11 | 0.48 | −0.34 | 0.80 | ||||||
| lc2006_2 | 1.28 | −0.64 | 2.83 | −1.72 | |||||
| lc2006_3 | 0.96 | −0.40 | 2.44 | −1.35 | |||||
| lc2006_5 | −0.52 | 2.23 | −1.58 | ||||||
| lc2006_6 | −0.92 | −1.90 | |||||||
| lc2006_7 | 0.45 | −0.68 | −1.25 | ||||||
| lc2006_8 | 0.87 | −0.38 | 2.03 | −1.57 | |||||
| lc2010_2 | 0.80 | −1.42 | |||||||
| lc2010_3 | 1.66 | −0.68 | −1.01 | 3.75 | −0.71 | ||||
| lc2010_5 | 0.67 | 1.56 | 0.34 | 2.37 | −0.66 | ||||
| lc2010_6 | −0.50 | −1.07 | 1.83 | ||||||
| lc2010_7 | 1.24 | 1.85 | −0.31 | 0.24 | −1.10 | 3.22 | −1.88 | ||
| lc2010_8 | 1.18 | 1.22 | −0.75 | 0.63 | |||||
| ParcelArea | 8.13 | −6.77 | −20.99 | 6.73 | −24.66 | −20.11 | |||
| DA_Area | 1.56 | −21.53 | |||||||
| MeanSlope | −0.18 | ||||||||
| MeanDEM | −2.13 | ||||||||
| Wood_dist | 0.28 | −0.51 | 0.92 | ||||||
| River_dist | 0.91 | ||||||||
| Water_dist | −0.15 | ||||||||
| LRoad_dist | 0.58 | −3.73 | 1.45 | ||||||
| MRoad_dist | 0.23 | −0.26 | 0.43 | −0.62 | |||||
| Ramp_dist | 0.04 | ||||||||
| lu4_dist | −0.35 | −4.65 | −2.35 | 2.53 | −25.33 | −0.52 | |||
| lu5_dist | 0.48 | ||||||||
| lu8_dist | 0.77 | −0.59 | −0.85 | −1.69 | −1.96 | 2.68 | 0.81 | ||
| lu9_dist | 0.14 | ||||||||
| Residential_Popn _Density | −0.02 | -0.02 | 0.02 | ||||||
| DA_Popn_Density | −0.65 × 10−4 | −1.05 × 10−4 | 9.30 × 10 −5 | ||||||
| Change_AveIncome | 0.20 | ||||||||
| Change_Popn | −0.03 | ||||||||
| F_lu2 | −0.39 | 0.31 | |||||||
| F_lu3 | 1.07 | ||||||||
| F_lu7 | 1.00 | ||||||||
| F_lu11 | −0.82 | 0.37 | |||||||
| Method | Final SA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | LDR | MDR | HDR | COM | IND | TRA | REC | UND | |
| lu2006_2 | 0.90 | −2.09 | 2.36 | 1.05 | 1.91 | ||||
| lu2006_3 | 1.33 | −0.75 | |||||||
| lu2006_4 | 0.55 | −1.04 | −1.29 | ||||||
| lu2006_5 | 1.30 | −1.88 | |||||||
| lu2006_6 | 7.33 | ||||||||
| lu2006_7 | 1.10 | 2.99 | −0.88 | 1.36 | −1.47 | ||||
| lu2006_8 | 0.63 | 1.78 | −1.00 | ||||||
| lu2006_9 | 1.56 | 3.04 | 1.66 | 1.07 | −1.13 | ||||
| lu2006_11 | 0.48 | 0.80 | −1.47 | ||||||
| lc2006_2 | 1.28 | 2.83 | −1.72 | ||||||
| lc2006_3 | 0.96 | 2.44 | −1.35 | ||||||
| lc2006_5 | 2.23 | −1.58 | |||||||
| lc2006_7 | 0.45 | −1.25 | |||||||
| lc2006_8 | 0.87 | 2.03 | −1.57 | ||||||
| lc2010_2 | 1.42 | −1.04 | |||||||
| lc2010_3 | 2.42 | −0.77 | −0.73 | 3.75 | −0.49 | ||||
| lc2010_5 | 0.67 | 1.86 | 0.60 | 2.37 | −0.39 | ||||
| lc2010_6 | −0.50 | 1.83 | |||||||
| lc2010_7 | 1.24 | 2.12 | −1.10 | 3.22 | −1.82 | ||||
| lc2010_8 | 1.18 | 0.96 | |||||||
| ParcelArea | 8.13 | −39.48 | −101.00 | 6.73 | −20.11 | 6.14 | |||
| DA_Area | 1.56 | ||||||||
| MeanSlope | −0.20 | ||||||||
| Wood_dist | −0.60 | 0.92 | |||||||
| Water_dist | 0.26 | ||||||||
| River_dist | −0.42 | 0.91 | |||||||
| LRoad_dist | 0.84 | ||||||||
| MRoad_dist | 0.23 | −0.79 | |||||||
| lu4_dist | −0.35 | −3.13 | −2.20 | 2.06 | −25.33 | −1.46 | −1.29 | ||
| lu5_dist | 0.53 | 0.48 | −1.18 | ||||||
| lu8_dist | 0.77 | −1.69 | −1.14 | 2.68 | |||||
| DA_Popn_Density | −1.21 × 10−4 | ||||||||
| F_lu1 | −1.70 | ||||||||
| F_lu2 | −0.39 | ||||||||
| F_lu7 | 1.00 | ||||||||
| F_lu11 | −2.10 | ||||||||
References
- Verburg, P.; van Berkel, D.; van Doorn, A.; van Eupen, M.; van den Heiligenberg, H. Trajectories of land use change in Europe: A model-based exploration of rural futures. Landsc. Ecol. 2010, 25, 217–232. [Google Scholar] [CrossRef]
- Marshall, E.; Randhir, T. Spatial modeling of land cover change and watershed response using Markovian cellular automata and simulation. Water Resour. Res. 2008, 44, 1–11. [Google Scholar] [CrossRef]
- Robinson, D.; Brown, D. Evaluating the effects of land-use development policies on ex-urban forest cover: An integrated agent-based GIS approach. Int. J. Geogr. Inf. Sci. 2009, 23, 1211–1232. [Google Scholar] [CrossRef]
- Serneels, S.; Lambin, E.F. Proximate causes of land-use change in Narok District, Kenya: A spatial statistical model. Agric. Ecosyst. Environ. 2001, 85, 65–81. [Google Scholar] [CrossRef]
- Rutherford, G.; Bebi, P.; Edwards, P.; Zimmermann, N. Assessing land-use statistics to model land cover change in a mountainous landscape in the European Alps. Ecol. Model. 2008, 212, 460–471. [Google Scholar] [CrossRef]
- An, L.; Brown, D.G. Survival Analysis in Land Change Science: Integrating with GIScience to Address Temporal Complexities. Ann. Assoc. Am. Geogr. 2008, 98, 1–22. [Google Scholar] [CrossRef]
- Pontius, R.; Boersma, W.; Castella, J.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Aspinall, R. Modelling land use change with generalized linear models—A multi-model analysis of change between 1860 and 2000 in Gallatin Valley, Montana. J. Environ. Manag. 2004, 72, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Arsanjani, J.J.; Helbich, M.; Kainz, W.; Boloorani, A.D. Integration of logistic regression, Markov chain and cellular automata models to simulate urban expansion. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 265–275. [Google Scholar] [CrossRef]
- Huang, J.; Wu, Y.; Gao, T.; Zhan, Y.; Cui, W. An Integrated Approach based on Markov Chain and Cellular Automata to Simulation of Urban Land Use Changes. Appl. Math. Inf. Sci. 2015, 775, 769–775. [Google Scholar]
- Ebrahimipour, A.; Saadat, M.; Farshchin, A. Prediction of urban growth through cellular automata-Markov chain. Bull. Soc. R. Sci. Liège 2016, 85, 824–839. [Google Scholar]
- Tang, J.; Wang, L.; Yao, Z. Spatio-temporal urban landscape change analysis using the Markov chain model and a modified genetic algorithm. Int. J. Remote Sens. 2007, 28, 3255–3271. [Google Scholar] [CrossRef]
- Bell, A.; Robinson, D.; Malik, A.; Dewal, S. Modular ABM development for improved dissemination and training. Environ. Model. Softw. 2015, 73, 189–200. [Google Scholar] [CrossRef]
- Rounsevell, M.; Robinson, D.; Murray-Rust, D. From actors to agents in socio-ecological systems models. Philos. Trans. R. Soc. B 2012, 367, 259–269. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Brown, D.G.; An, L.; Yang, S.; Ligmann-Zielinska, A. Comparative performance of logistic regression and survival analysis for detecting spatial predictors of land-use change. Int. J. Geogr. Inf. Sci. 2013, 27, 1960–1982. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Muñoz, J.; Felicísimo, A.M. Comparison of statistical methods commonly used in predictive modelling. J. Veg. Sci. 2004, 15, 285–292. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Maier, H. Chapter 2: Pavement Selection Strategies in Long-life Concrete Pavements in Europe and Canada. Available online: https://international.fhwa.dot.gov/pubs/pl07027/llcp_07_02.cfm (accessed on 30 January 2018).
- Yeandle, M. The Global Financial Centres Index 22. Long Finance. 2017. Available online: http://www.luxembourgforfinance.com/sites/luxembourgforfinance/files/files/GFCI22_Report.pdf (accessed on 13 January 2018).
- Census Bulletin 2016: Population, Age and Sex. Region of Waterloo. 2016. Available online: https://www.regionofwaterloo.ca/en/resources/Census/Census-Bulletin-1-Population-Age-and-Sex-access.pdf (accessed on 7 September 2018).
- Smith, A.K. An Evaluation of High-Resolution Land Cover and Land Use Classification Accuracy by Thematic, Spatial, and Algorithm Parameters. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2017. [Google Scholar]
- Lambin, E.F.; Turner, B.L.; Geist, H.J.; Agbola, S.B.; Angelsen, A.; Bruce, J.W.; Coomes, O.T.; Dirzo, R.; Fischer, G.; Folke, C.; et al. The causes of land-use and land-cover change: Moving beyond the myths. Glob. Environ. Chang. 2001, 11, 261–269. [Google Scholar] [CrossRef]
- Hettig, E.; Lay, J.; Sipangule, K. Drivers of Households’ Land-Use Decisions: A Critical Review of Micro-Level Studies in Tropical Regions. Land 2016, 5, 32. [Google Scholar] [CrossRef]
- Schneider, L.C.; Pontius, R.G., Jr. Modeling land-use change in the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 83–94. [Google Scholar] [CrossRef]
- Lo, C.P.; Yang, X. Drivers of Land-Use/Land-Cover Changes and Dynamic Modeling for the Atlanta, Georgia Metropolitan Area. Photogramm. Eng. Remote Sens. 2002, 68, 1073–1082. [Google Scholar]
- Wood, E.C.; Tappan, G.G.; Hadj, A. Understanding the drivers of agricultural land use change in south-central Senegal. J. Arid Environ. 2004, 59, 565–582. [Google Scholar] [CrossRef]
- Verburg, P.H.; Veldkamp, T.A.; Bouma, J. Land use change under conditions of high population pressure: The case of Java. Glob. Environ. Chang. 1999, 9, 303–312. [Google Scholar] [CrossRef]
- Census Profile. Statistics Canada, 2011. Available online: https://www12.statcan.gc.ca/census-recensement/2011/dp-pd/prof/index.cfm?Lang=E (accessed on 13 January 2018).
- Maser, S.; Riker, W.; Rosett, R. The effects of zoning and externalities on the price of land: An empirical analysis of Monroe County, New York. J. Law Econ. 1977, 20, 111–132. [Google Scholar] [CrossRef]
- Cohen, J. A Constitutional Safety Valve: The Variance in Zoning and Land-Use Based Environmental Controls. Boston Coll. Environ. Aff. Law Rev. 1994, 22, 307–364. [Google Scholar]
- Stokey, E.; Zeckhauser, R. A Primer for Policy Analysis; W. W. Norton: New York, NY, USA, 1978; ISBN 0-393-05688-0. [Google Scholar]
- Trexler, J.C.; Travis, J. Nontraditional regression analyses. Ecology 1993, 74, 1629–1637. [Google Scholar] [CrossRef]
- Müller, D.; Zeller, M. Land use dynamics in the central highlands of Vietnam: A spatial model combining village survey data with satellite imagery interpretation. Agric. Econ. 2002, 27, 33–354. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Routledge: Abingdon-on-Thames, UK, 1990; ISBN 0412343908. [Google Scholar]
- Brown, D.G. Predicting vegetation types at treeline using topography and biophysical disturbance variables. J. Veg. Sci. 1994, 5, 641–656. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B Methodol. 1972, 34, 187–220. [Google Scholar]
- Batista, G.; Prati, R.; Monard, M. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Int. Jt. Conf. Artif. Intell. 1995, 14, 1137–1145. [Google Scholar]
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; Wiley: New York, NY, USA, 1975; ISBN 0-471-35645-X. [Google Scholar]
- R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 12 August 2016).
- Kuhn, M. Caret: Classification and Regression Training. Available online: https://CRAN.R-project.org/package=caret (accessed on 17 December 2016).
- Wood, S.N. Thin-plate regression splines. J. R. Stat. Soc. Ser. B 2003, 65, 95–114. [Google Scholar] [CrossRef]
- Wood, S.N. Stable and efficient multiple smoothing parameter estimation for generalized additive models. J. Am. Stat. Assoc. 2004, 99, 673–686. [Google Scholar] [CrossRef]
- Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B 2011, 73, 3–36. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017; ISBN 978-1-4987-2834-8. [Google Scholar]
- Wood, S.N.; Pya, N.; Säfken, B. Smoothing parameter and model selection for general smooth models. J. Am. Stat. Assoc. 2016, 111, 1548–1563. [Google Scholar] [CrossRef]
- Therneau, T. Survival Analysis. 2018. Available online: https://cran.r-project.org/web/packages/survival/survival.pdf (accessed on 31 October 2018).
- Pontius, R.G., Jr.; Spencer, J. Uncertainty in extrapolations of predictive land-change models. Environ. Plan. B Plan. Des. 2005, 32, 211–230. [Google Scholar] [CrossRef]
- Clark, W. Markov chain analysis in geography: An application to the movement of rental housing areas. Ann. Assoc. Am. Geogr. 1965, 55, 351–359. [Google Scholar] [CrossRef]
- Iacono, M.; Levinson, D.; El-Geneidy, A.; Wasfi, R. A Markov chain model of land use change. Tema J. Land Use Mobil. Environ. 2015, 8, 263–276. [Google Scholar] [CrossRef]
- Braimoh, A.K.; Onishi, T. Spatial determinants of urban land use change in Lagos, Nigeria. Land Use Policy 2007, 24, 502–515. [Google Scholar] [CrossRef]
- Brown, D.G.; Groovaerts, P.; Burnicki, A.; Meng-Ying, L. Stochastic Simulation of Land-Cover Change Using Geostatistics and Generalized Additive Models. Photogramm. Eng. Remote Sens. 2002, 68, 1051–1061. [Google Scholar]
- Verburg, P.; Overmars, K. Dynamic simulation of land-use change trajectories with the CLUE-s model. In Modelling Land-Use Chang; The GeoJournal Library; Springer: Dordrecht, The Netherlands, 2007; Volume 90, pp. 321–337. [Google Scholar]
- Meiyappan, P.; Dalton, M.; O’neill, B.C.; Jain, A.K. Spatial modeling of agricultural land use change at global scale. Ecol. Model. 2014, 291, 152–174. [Google Scholar] [CrossRef]
- Evans, T.; Robinson, D.T.; Schmitt-Harsh, M. Limitations, challenges, and solutions to integrating carbon dynamics with land-use models. In Land Use and the Carbon Cycle: Advances in Integrated Science, Management, and Policy; Cambridge University Press: Cambridge, UK, 2013; pp. 178–208. ISBN 978-0-511-89482-4. [Google Scholar]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000; ISBN 0-387-98957-9. [Google Scholar]
- Liaw, A.; Matthew, W. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Ghimire, B.; Bogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Q.; Gong, J.; Zhou, J.; Li, Y. Land-cover classification of the Yellow River Delta wetland based on multiple end-member spectral mixture analysis and a Random Forest classifier. Int. J. Remote Sens. 2016, 37, 1845–1867. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.S.; Townshend, J.R.G. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Vanegas, C.A.; Kelly, T.; Weber, B.; Halatsch, J.; Aliaga, D.G.; Müller, P. Procedural generation of parcels in urban modeling. Comput. Graph. Forum 2012, 31, 681–690. [Google Scholar] [CrossRef]
- Matthews, R.; Gilbert, N.; Roach, A.; Polhil, J.; Gotts, N. Agent-based land-use models: A review of applications. Landsc. Ecol. 2007, 22, 1447–1459. [Google Scholar] [CrossRef]
- Huigen, M. Agent Based Modeling in Land-Use and Land-Cover Change Studies; IR-03-044; IIASA: Laxenburg, Austria, 2003. [Google Scholar]
- Flake, G.W. The Computational Beauty of Nature: Computer Explorations of Fractals, Chaos, Complex Systems, and Adaptation; MIT Press: Cambridge, MA, USA, 1998; ISBN 0-262-06200-3. [Google Scholar]
- Robinson, D.T.; Murray-Rust, D.; Rieser, V.; Milicic, V.; Rounsevell, M. Modelling the impacts of land system dynamics on human well-being: Using an agent-based approach to cope with data limitations in Koper, Slovenia. Comput. Environ. Urban Syst. 2012, 36, 164–176. [Google Scholar] [CrossRef]
- Murray-Rust, D.; Rieser, V.; Robinson, D.T.; Miličič, V.; Rounsevell, M. Agent-based modelling of land use dynamics and residential quality of life for future scenarios. Environ. Model. Softw. 2013, 46, 75–89. [Google Scholar] [CrossRef]
- Brown, D.G.; Robinson, D. Effects of Heterogeneity in Residential Preferences on an Agent-Based Model of Urban Sprawl. Ecol. Soc. 2006, 11, 1. [Google Scholar] [CrossRef]
- Fontaine, C.; Rounsevell, M. An agent-based approach to model future residential pressure on a regional landscape. Landsc. Ecol. 2009, 24, 1237–1254. [Google Scholar] [CrossRef]
- Orsi, F. Centrally located yet close to nature: A prescriptive agent-based model for urban design. Comput. Environ. Urban Syst. 2019, 73, 157–170. [Google Scholar] [CrossRef]
- Murray-Rust, D.; Brown, C.; van Vliet, J.; Alam, S.J.; Robinson, D.T.; Verburg, P.H.; Rounsevell, M. Combining Agent Functional Types, capitals and services to model land use dynamics. Environ. Model. Softw. 2014, 59, 187–201. [Google Scholar] [CrossRef]
- Robinson, D.T. Modelling feedbacks between human and natural processes in the land system. Earth Syst. Dyn. 2018, 9, 895–914. [Google Scholar] [CrossRef]
| Land-Use Change | Full-Balanced | Reduced-Balanced |
|---|---|---|
| Low-Density Residential | 870 | 870 |
| Medium-Density Residential | 10,816 | 1000 |
| High-Density Residential | 1698 | 1000 |
| Commercial | 3320 | 1000 |
| Industrial | 530 | 530 |
| Institution | 10 | 10 |
| Transportation | 1892 | 1000 |
| Protected Area and Recreation | 520 | 520 |
| Agriculture | 500 * | 500 * |
| Water | 72 | 72 |
| Under Development | 1484 | 1000 |
| Method | MC | LR | GAM | SA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Land-Use Change | FB | RB | FB | RB | FB | RB | FB | RB | |
| Low-Density Residential | 35.79 | 46.90 | 68.62 | 68.62 | 65.85 | 65.85 | 70.95 | 70.95 | |
| Medium-Density Residential | 67.46 | 30.69 | 89.62 | 88.44 | 93.98 | 87.00 | 89.56 | 89.18 | |
| High-Density Residential | 42.79 | 39.19 | 71.10 | 69.88 | 79.46 | 77.71 | 71.64 | 70.26 | |
| Commercial | 24.62 | 29.92 | 80.89 | 81.80 | 91.61 | 86.53 | 78.45 | 76.25 | |
| Industrial | 45.58 | 50.31 | 90.05 | 90.05 | 89.95 | 89.95 | 88.84 | 88.84 | |
| Institution | 60.00 | 80.00 | n/a | n/a | n/a | n/a | n/a | n/a | |
| Transportation | 56.12 | 56.08 | 79.68 | 76.15 | 83.08 | 79.72 | 79.76 | 76.71 | |
| Protected Area and Recreation | 24.43 | 42.01 | 87.24 | 87.24 | 89.80 | 89.80 | 85.52 | 85.52 | |
| Agriculture | 94.83 | 95.74 | n/a | n/a | n/a | n/a | n/a | n/a | |
| Water | 56.56 | 57.85 | n/a | n/a | n/a | n/a | n/a | n/a | |
| Under Development | 9.33 | 28.78 | 82.93 | 82.13 | 87.66 | 82.56 | 82.54 | 80.57 | |
| Overall | 47.05 | 50.68 | 80.97 | 80.24 | 85.17 | 82.39 | 80.91 | 79.79 | |
| Method | LR | GAM | SA | ||||
|---|---|---|---|---|---|---|---|
| Land-Use Change | FB | RB | FB | RB | FB | RB | |
| Low-Density Residential | 67.05 | 67.05 | 70.11 | 70.11 | 70.50 | 70.50 | |
| Medium-Density Residential | 89.83 | 87.63 | 93.78 | 89.30 | 90.01 | 89.90 | |
| High-Density Residential | 69.22 | 67.33 | 78.24 | 76.67 | 69.35 | 68.67 | |
| Commercial | 78.82 | 83.67 | 92.15 | 90.17 | 80.12 | 81.67 | |
| Industrial | 91.19 | 91.19 | 91.82 | 91.82 | 91.19 | 91.19 | |
| Institution | n/a | n/a | n/a | n/a | n/a | n/a | |
| Transportation | 79.05 | 79.67 | 83.98 | 80.00 | 78.70 | 76.59 | |
| Protected Area and Recreation | 90.32 | 90.32 | 88.39 | 88.39 | 88.24 | 88.24 | |
| Agriculture | n/a | n/a | n/a | n/a | n/a | n/a | |
| Water | n/a | n/a | n/a | n/a | n/a | n/a | |
| Under Development | 83.86 | 82.33 | 85.87 | 82.00 | 82.05 | 76.67 | |
| Overall | 81.17 | 81.15 | 85.54 | 83.56 | 81.27 | 80.43 | |
| Method | MC | LR | GAM | SA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Land-Use Change | FB | RB | FB | RB | FB | RB | FB | RB | |
| Low-Density Residential | 35.37 | 50.76 | 67.43 | 67.43 | 66.06 | 66.06 | 69.15 | 69.15 | |
| Medium-Density Residential | 68.35 | 28.20 | 89.38 | 89.67 | 92.87 | 86.78 | 89.25 | 90.35 | |
| High-Density Residential | 41.09 | 40.80 | 66.72 | 69.50 | 73.92 | 78.19 | 68.86 | 72.03 | |
| Commercial | 25.41 | 28.36 | 79.82 | 78.92 | 88.29 | 78.59 | 78.99 | 77.70 | |
| Industrial | 45.56 | 45.57 | 89.37 | 89.37 | 90.52 | 90.52 | 90.03 | 90.03 | |
| Institution | 80.00 | 80.00 | n/a | n/a | n/a | n/a | n/a | n/a | |
| Transportation | 57.82 | 60.32 | 76.77 | 76.91 | 82.52 | 78.80 | 79.40 | 76.54 | |
| Protected Area and Recreation | 27.78 | 45.57 | 85.68 | 85.68 | 84.51 | 84.51 | 84.32 | 84.32 | |
| Agriculture | 90.71 | 97.36 | n/a | n/a | n/a | n/a | n/a | n/a | |
| Water | 63.78 | 41.65 | n/a | n/a | n/a | n/a | n/a | n/a | |
| Under Development | 9.90 | 27.29 | 77.09 | 78.98 | 78.58 | 78.92 | 74.98 | 76.34 | |
| Overall | 49.62 | 49.63 | 79.03 | 79.56 | 82.16 | 80.30 | 79.37 | 79.56 | |
| Method | LR | GAM | SA | ||||
|---|---|---|---|---|---|---|---|
| Land-Use Change | FB | RB | FB | RB | FB | RB | |
| Low-Density Residential | 70.88 | 70.88 | 69.35 | 69.35 | 67.82 | 67.82 | |
| Medium-Density Residential | 88.20 | 89.67 | 93.71 | 92.98 | 89.89 | 90.00 | |
| High-Density Residential | 69.61 | 67.33 | 77.65 | 79.33 | 70.00 | 67.33 | |
| Commercial | 81.33 | 80.27 | 91.37 | 82.94 | 80.62 | 79.67 | |
| Industrial | 97.48 | 97.48 | 94.34 | 94.34 | 91.19 | 91.19 | |
| Institution | n/a | n/a | n/a | n/a | n/a | n/a | |
| Transportation | 79.58 | 77.00 | 83.98 | 83.33 | 78.70 | 77.00 | |
| Protected Area and Recreation | 89.30 | 89.30 | 87.74 | 87.74 | 87.74 | 87.74 | |
| Agriculture | n/a | n/a | n/a | n/a | n/a | n/a | |
| Water | n/a | n/a | n/a | n/a | n/a | n/a | |
| Under Development | 82.96 | 82.33 | 84.75 | 81.67 | 81.61 | 82.33 | |
| Overall | 82.42 | 81.78 | 85.36 | 83.96 | 80.95 | 80.39 | |
| Land-Use Change | FB | RB | ||
|---|---|---|---|---|
| Method | Accuracy | Method | Accuracy | |
| Low-Density Residential | LR-SCV | 70.88 | LR-SCV | 70.88 |
| Medium-Density Residential | GAM-SCV | 93.71 | GAM-SCV | 92.98 |
| High-Density Residential | GAM-SCV | 77.65 | GAM-SCV | 79.33 |
| Commercial | GAM-SCV | 91.37 | GAM-SCV | 82.94 |
| Industrial | LR-SCV | 97.48 | LR-SCV | 97.48 |
| Institution | MC-SCV | 25 | MC-SCV | 40 |
| Transportation | GAM-SCV | 83.98 | GAM-SCV | 83.33 |
| Protected Area and Recreation | LR-SCV | 89.30 | GAM-SCV | 89.30 |
| Agriculture | MC-SCV | 96.58 | MC-SCV | 96.03 |
| Water | MC-CCV | 55 | MC-SCV | 53.85 |
| Under Development | GAM-SCV | 84.75 | LR-SCV/SA-SCV | 82.33 |
| Overall 1 | 78.70 | 78.95 | ||
| Overall 2 | 86.14 | 84.82 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Robinson, D.T. Comparison of Statistical Approaches for Modelling Land-Use Change. Land 2018, 7, 144. https://doi.org/10.3390/land7040144
Sun B, Robinson DT. Comparison of Statistical Approaches for Modelling Land-Use Change. Land. 2018; 7(4):144. https://doi.org/10.3390/land7040144
Chicago/Turabian StyleSun, Bo, and Derek T. Robinson. 2018. "Comparison of Statistical Approaches for Modelling Land-Use Change" Land 7, no. 4: 144. https://doi.org/10.3390/land7040144
APA StyleSun, B., & Robinson, D. T. (2018). Comparison of Statistical Approaches for Modelling Land-Use Change. Land, 7(4), 144. https://doi.org/10.3390/land7040144






