Towards a Simpler Characterization of Urban Sprawl across Urban Areas in Europe

1. Introduction

Urban sprawl is a concept commonly used to describe the physical expansion of urban areas at the expense of rural and natural areas. It is traditionally associated with negative impacts, such as poorer connectivity, reduced levels of public services, increased energy consumption for heating and transport, traffic congestion, air pollution, as well as a source of irreversible damage to local ecosystems [1,2,3,4,5]. Recognized as a key issue in spatial planning in the United States for some time [1,6], urban sprawl was only recently officially recognized as an issue in Europe [7,8]. It is now also appearing as a major issue in rapidly developing India and China, where it has been the object of numerous studies [9,10,11,12,13,14,15]. There is no universally agreed upon definition of what constitutes sprawl, nor is there an agreed upon methodology on how to measure and define it in a quantitative manner [16]. Numerous attempts at characterizing urban sprawl have been made in the past. In their review, [17] reported at least eleven separate definitions for urban sprawl. Ewing, R, 1997 [4], 1994 [18] suggested five major characteristics of sprawl: (1) a scattered and discontinuous development pattern; (2) the development of residential areas with low densities; (3) commercial strip development alongside the main transportation axes; (4) the segregation of land uses; and (5) low accessibility and a high dependency on private vehicles. Jaeger et al. [19] added an element of visual perception to the definition of urban sprawl and emphasized the fundamental role played by both urban size and urban morphology in characterizing urban sprawl.

Quantitative methods that systematically classify and analyze the multidimensional phenomenon of urban sprawl have been proposed by numerous authors [20,21,22,23]. Most have focused on the production of a plethora of indicators that can be classified into five major groups: indicators of growth rates; density; accessibility; aesthetic; and spatial geometry. The production of these indicators is usually very data hungry, requiring time and a series of satellite or aerial images [24], land-use and population maps [25], or a transport network. They also often require the calculation of complex metrics, such as density, continuity, concentration, clustering, centrality, nuclearity, mixed uses, and proximity [17,21,26], which makes them computationally expensive.

However, such detailed data is rarely available at a broader scale, which makes it very challenging to provide a sprawl analysis beyond the regional or national level. Schwarz, N [27] produced one of the most comprehensive statistical analyses of urban form in Europe, by producing seven landscape metrics and population-related indicators for 231 European cities ((1) area of discontinuous urban fabric; (2) edge density; (3) mean patch size; (4) number of patches; (5) compactness index of the largest patch; (6) population number; and (7) population density).

A major drawback associated with the production of such a diversity of indicators of urban sprawl is that they are very complex and difficult to communicate to policy makers and the public. This emphasizes the need for a single “unified” sprawl indicator that could be easily calculated for a wide range of locations and that could be explained easily to decision makers.

Jaeger, J.A.G. and Schwick, C. [28] recently proposed the Weighted Urban Proliferation (WUP) as a new indicator to quantify urban sprawl. It is based on the following definition of urban sprawl: “Urban sprawl is a phenomenon that can be visually perceived in the landscape. A landscape suffers from urban sprawl if it is permeated by urban development or solitary buildings and when land uptake per inhabitant or job is high. The more area built over and the more dispersed the build-up area, and the higher the land uptake per inhabitant or job (lower utilization intensity in the built-up area), the higher the degree of urban sprawl” [28]. One of the major advantages of the WUP is that it is a relatively simple indicator to calculate and explain, based on a combination of (1) the degree of urban penetration (distance between built-up cells), (2) the density of the built-up area, and (3) the population present in this built-up area. The data needs of the WUP are also relatively modest, as it only requires a “snapshot” of the spatial distribution of population and jobs.

This paper describes an attempt at characterizing urban sprawl in urban areas at a pan European scale, by presenting a new indicator, the Averaged Concentric Weighted Urban Proliferation (ACWUP) index. This index is calculated by aggregating the “sprawl profile” of urban areas, derived from an adapted version of Jaeger’s WPU index [28]. Our analysis made use of EU28-wide, 100 m resolution gridded population and land-use data, produced by the European Commission LUISA Territorial Modelling Platform1 under the 2013 reference scenario, for the year 2010 (see https://ec.europa.eu/jrc/en/luisa).

2. Materials and Methods

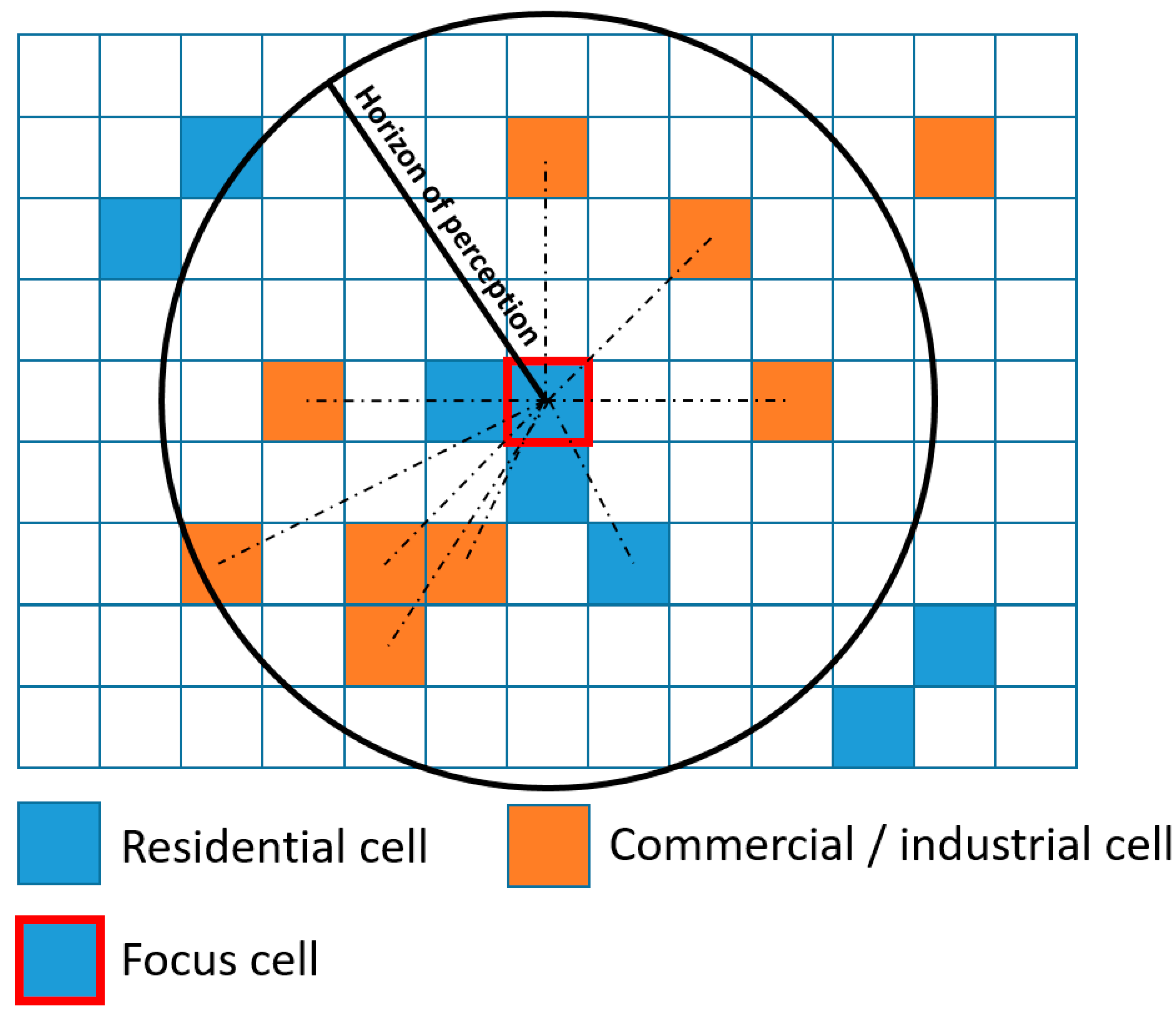
2.1. Adaptation of the Weighted Urban Proliferation Index

The approach described by [7,28] to calculate WUP made use of a combination of the number of inhabitants and jobs to estimate an “utilization density” of land-uses. Due to the lack of spatially explicit EU wide employment data, our approach substituted population with “inhabitants + jobs” in the calculation of the utilization density. The implications of this substitution are that our approach only produces WUP values for “residential” land-use cells.

We adapted the method, published by [28], by using pixels of 1 ha (rather than 9 ha as used in Jaeger’s example applications) as minimal settlement units. The calculations of the WUP were performed for each urban pixel (i) of EU-wide maps, by making use of Equation (1) below, where $U{P}_i$ corresponds to Urban Permeation (see Equation (2)), ${W1}_i$ is a weighting associated with dispersion (see Equation (5)) and $W{2}_i$ is a weighting associated with utilization density (see Equation (6)).

$${WUP}_i={UP}_i\times {W1}_i\times {W2}_i$$

(1)

The calculation of the degree of urban permeation (UP) was based on Equation (2), where PBA_i is the percentage of built-up area in each pixel i and $DI{S}_i$ (see Equation (3)) is the degree of dispersion calculated for each built-in cell i within the specified horizon of perception.

$$U{P}_i=DI{S}_i\times PB{A}_i$$

(2)

The calculation of the degree of urban dispersion for each built-up cell i ($DI{S}_i$) was based on Equation (3)2, where $n_i$ is the number of built-in cells located within the horizon of perception surrounding i; $D_{ij}$ is the Euclidian distance between i and built-in cell j, and WCC is the within-cell contribution using a cell size $C_s$ of 100 m (see Equation (4)3).

$$DI{S}_i=\frac{WCC+{{\displaystyle \sum }}_{j=0}^{n_i}\left(\sqrt{2.0\times D_{ij}+1.0}-1.0\right)}{n_i}$$

(3)

$$WCC=\sqrt{0.97428\times C_s+1.046}-0.996249$$

(4)

The weighting functions for dispersion W1_i (Equation (5)) and utilization density $W{2}_i$ (Equation (6)) were calculated using Jaeger’s original formulas.

$$W{1}_i=0.5+\frac{e^{(0.294431\times DI{S}_i-12.955)}}{1+e^{(0.294432\times DI{S}_i-12.955)}}.$$

(5)

$$W{2}_i=\frac{e^{(4.159-0.000613125\times U{D}_i)}}{1+e^{(4.159-0.000613125\times U{D}_i)}}.$$

(6)

PBAi, the percentage of built-up area per cell, was calculated by Jaeger using remote sensing images [28]. To minimize the data requirements and speed up computations, we derived this information directly from the LUISA land use map, based on the following hypothesis:

-

Raster cells classified as residential land-use were attributed a PBA value of 100.

-

For raster cell hosting populations not classified as residential land-use by LUISA, PBA was approximated using a population dependent step function assuming 200 m² of built-up area per group of 1–4 people and reaching a maximum of 100% of the cell.

The utilization density of each pixel i ($U{D}_i$) was calculated as described in Equation 7 by dividing the percentage of built-up area per cell (PBA_i ) by the population present at that cell ($Po{p}_i$).

$$U{D}_i=\frac{PBA{i}_i}{Po{p}_i}$$

(7)

Jaeger, J.A.G. and Schwick, C. [28] suggested the value of 2 km as the most suitable horizon of perception to investigate urban sprawl for Switzerland. Our study area covers the whole EU28 and we chose to explore the implications of using various horizons of perception, ranging from 1 km to 30 km.

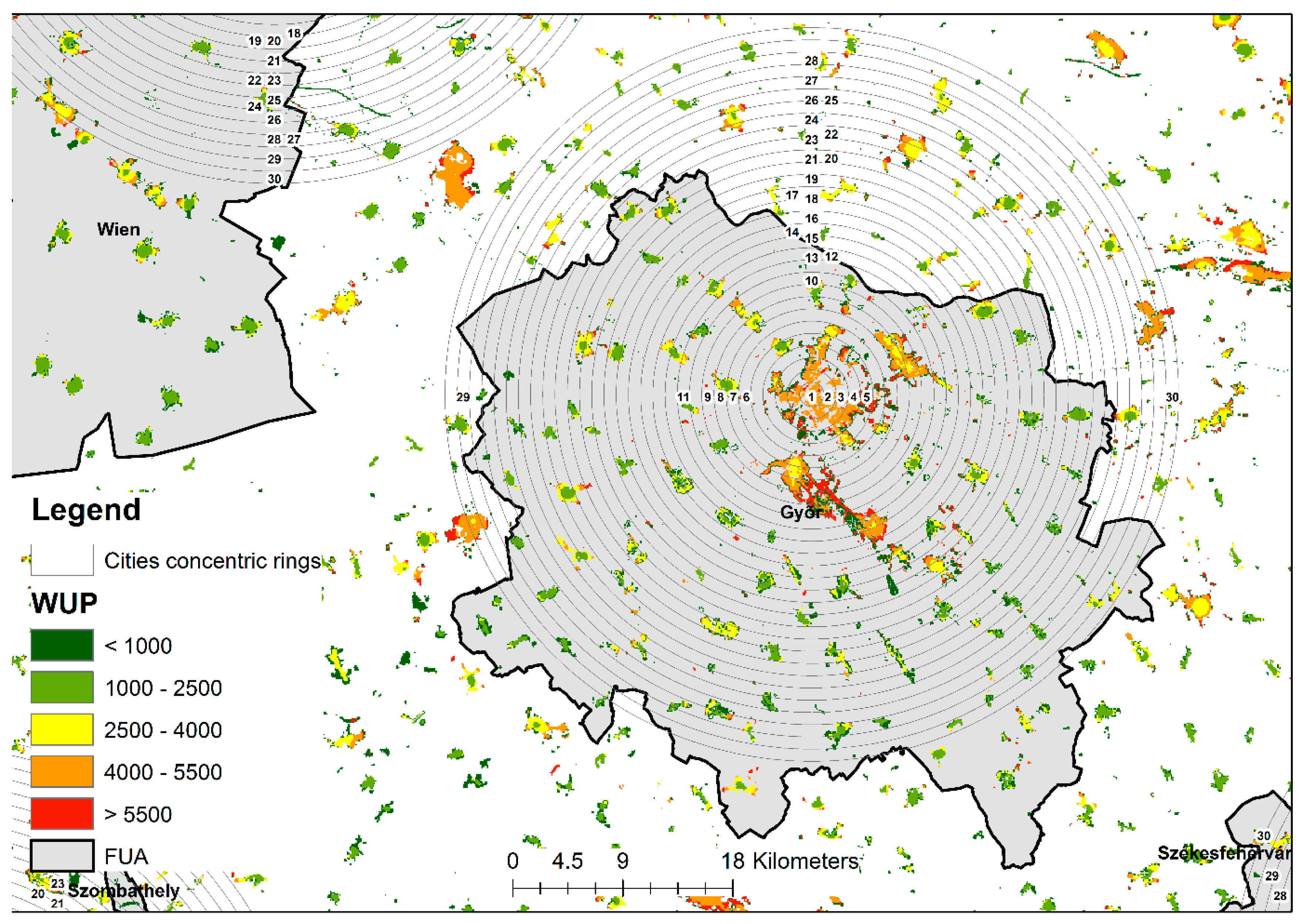
2.2. Input Data

We used a combination of population and land-use maps produced by the European Commission LUISA Territorial Modelling Platform [29,30] as inputs to our calculations. This platform provides a consistent EU28-wide population dataset downscaled at a 1 ha resolution [28]. It also provides population projections (up to 2050), fully in line with EU policies that could be used to estimate “future sprawl” across European cities.

Cells corresponding to industrial and commercial areas (with no population) were added to the population map and attributed a value of 0. All cells of the population map containing data (including 0) were assumed to contain a percentage of built-up area. The inclusion of commercial and industrial land-uses directly in the land-use map avoided the use of two separate maps for population (from which weighting factors were calculated) and built-up area (from which the degree of urban dispersion (DIS) was calculated). During the processing phase, WUP values for industrial cells were populated with dummy values, which were then removed in the post-processing phase.

2.3. Computations of the WUP

To deal with the very large number of computations associated with the calculation of the WUP at the EU28 scale (containing over 25 million 100 × 100 m populated built-in cells), a set of computer scripts was developed using the Python programming language (http://www.python.org) to (1) “smart tile” (including a buffer distance corresponding to the horizon of perception) the dataset into smaller samples that were easier to handle, and (2) processed each tile in parallel independently of the others. This set of scripts allowed us to make use of a multi-core computing infrastructure to greatly improve calculation speed and produce EU28-wide calculations of WUP in a matter of a few hours.

Following the WUP calculations, only values of WUP for inhabited cells were kept and “dummy” WUP values for commercial and industrial land-uses were clipped out. This step was added to the processing routine to account for the idea that residents perceive sprawl from commercial and industrial areas but commercial and industrial areas, being empty of residents, have no perception of sprawl by themselves.

3. Results

We performed WUP calculations based on the LUISA 2010 reference scenario population data for 14 horizons of perceptions: from 1 to 10 km using a 1 km increment and from 15 to 30 km using a 5 km increment. Our WUP calculations were performed for one ha pixel settlement units, using a different method of approximation of the percentage of built-up area (PBA) than the one used by Jaeger. As a consequence, the range of WUP values we obtained for the whole EU28 (ranging from 0 to 8000 for a 2 km horizon of perception) differed from the values obtained by [28] for their case study area in Switzerland (ranging from 0 to 68). These discrepancies can be explained by the fact that (1) the whole EU28 territory contains proportionally more areas devoid of population than that of Jaeger and Schwick’s case study, and (2) we used population only as an input data instead of a combination of jobs, population, and aerial imagery.

A preliminary “visual analysis” of the results at the pixel level (illustrated in Figure 1) suggests that the calculated WUP values follow a spatial pattern consistent with the theory of [31]. Densely populated areas display low WUP values (green) while less dense, more sparsely populated areas display higher values (orange and red).

Our exploration of the effect of using various horizons of perception (illustrated in Figure 2) indicated that higher horizons of perception led to higher WUP values. The maximum EU WUP values increased from 8580 for a 2 km horizon of perception to 33,000 for a 30 km horizon. However, the increase in WUP value was spatially uneven, with very dense urban areas seeing almost no changes while small, isolated clusters of built-in cells saw a much higher increase in WUP with increasing horizons of perceptions.

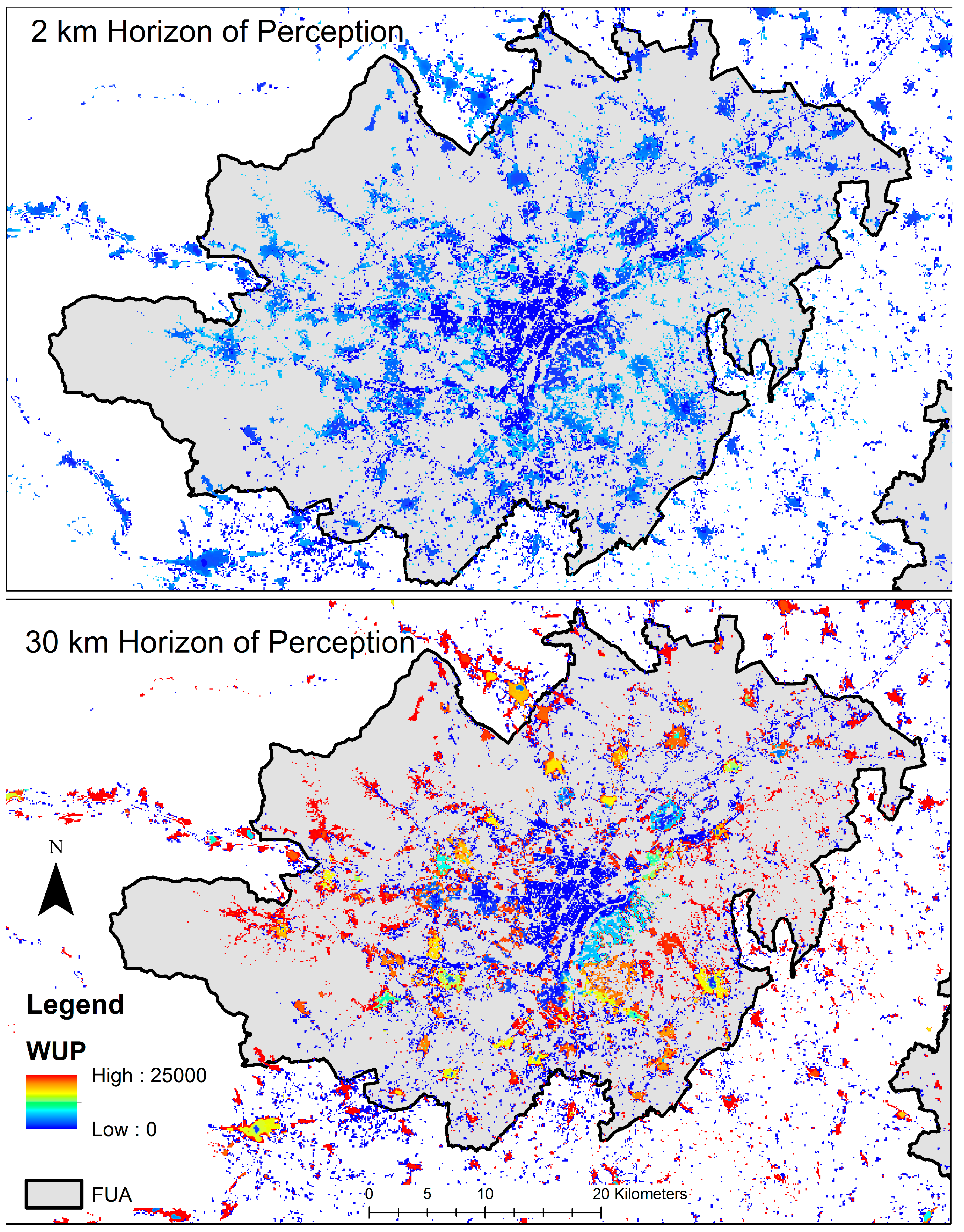
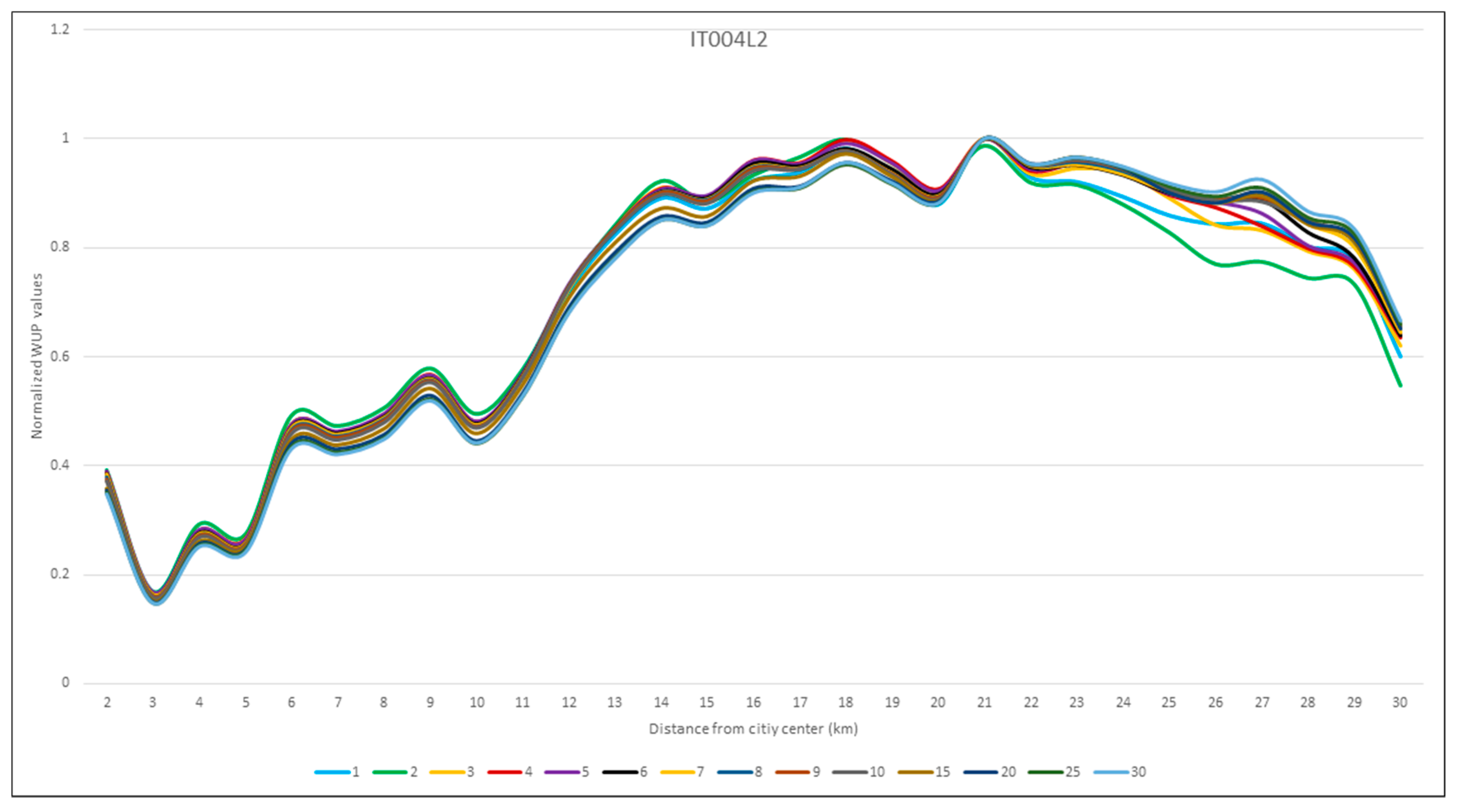
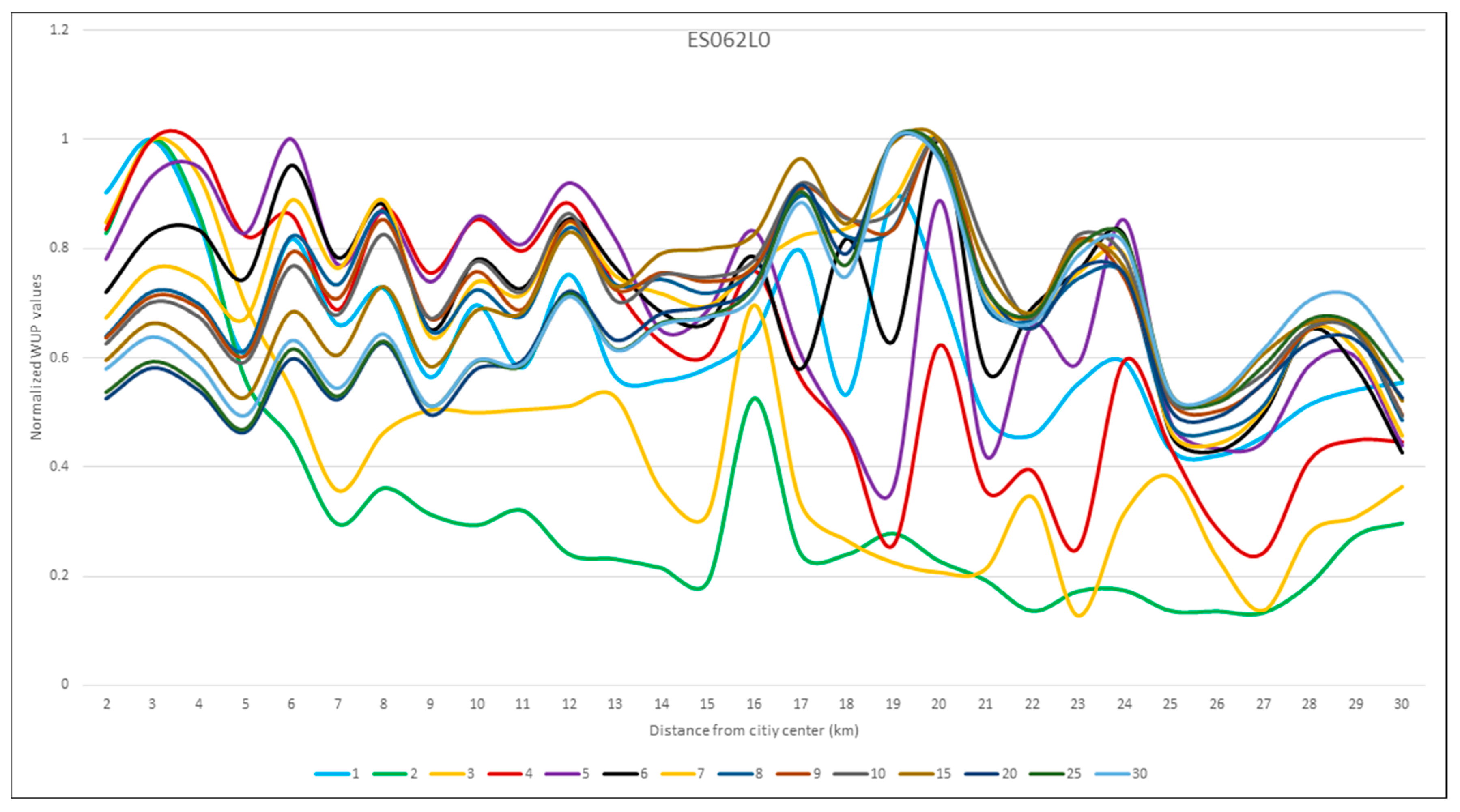
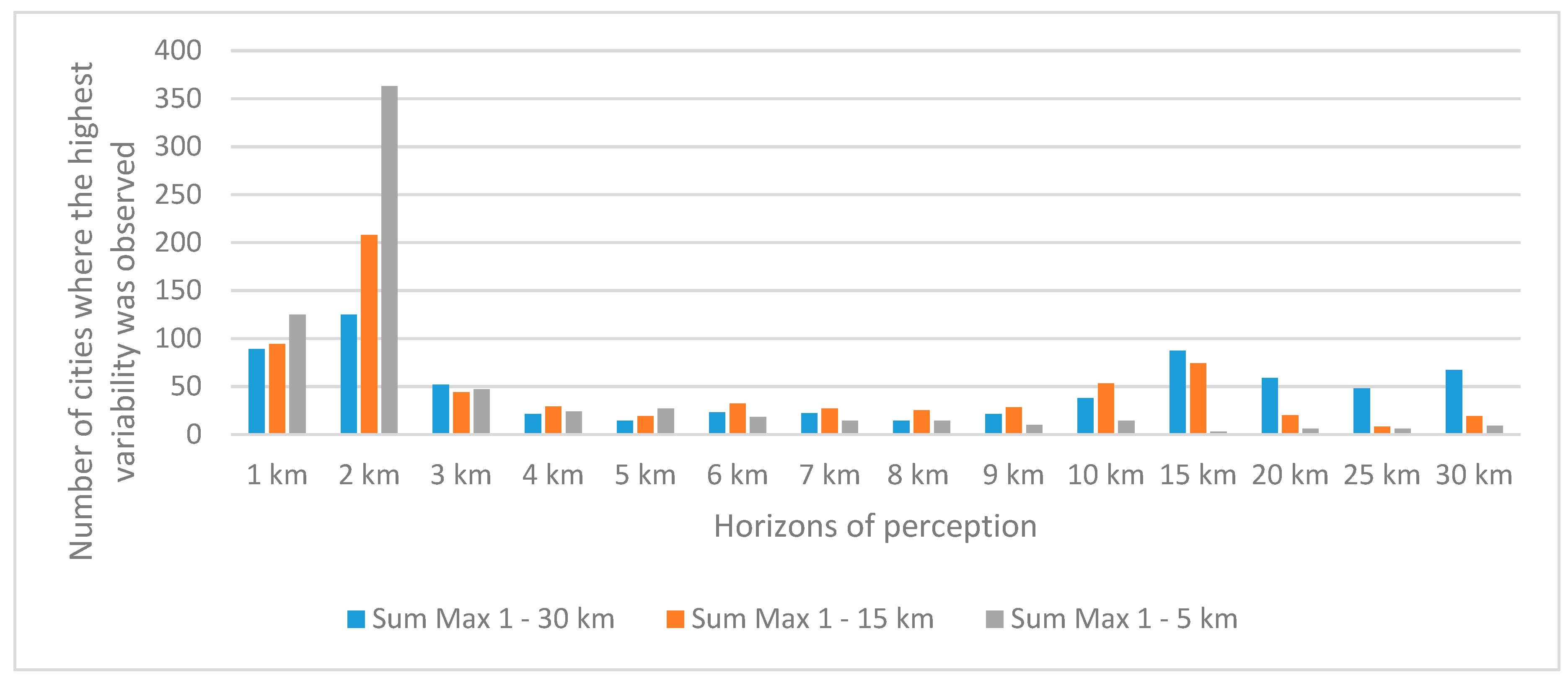
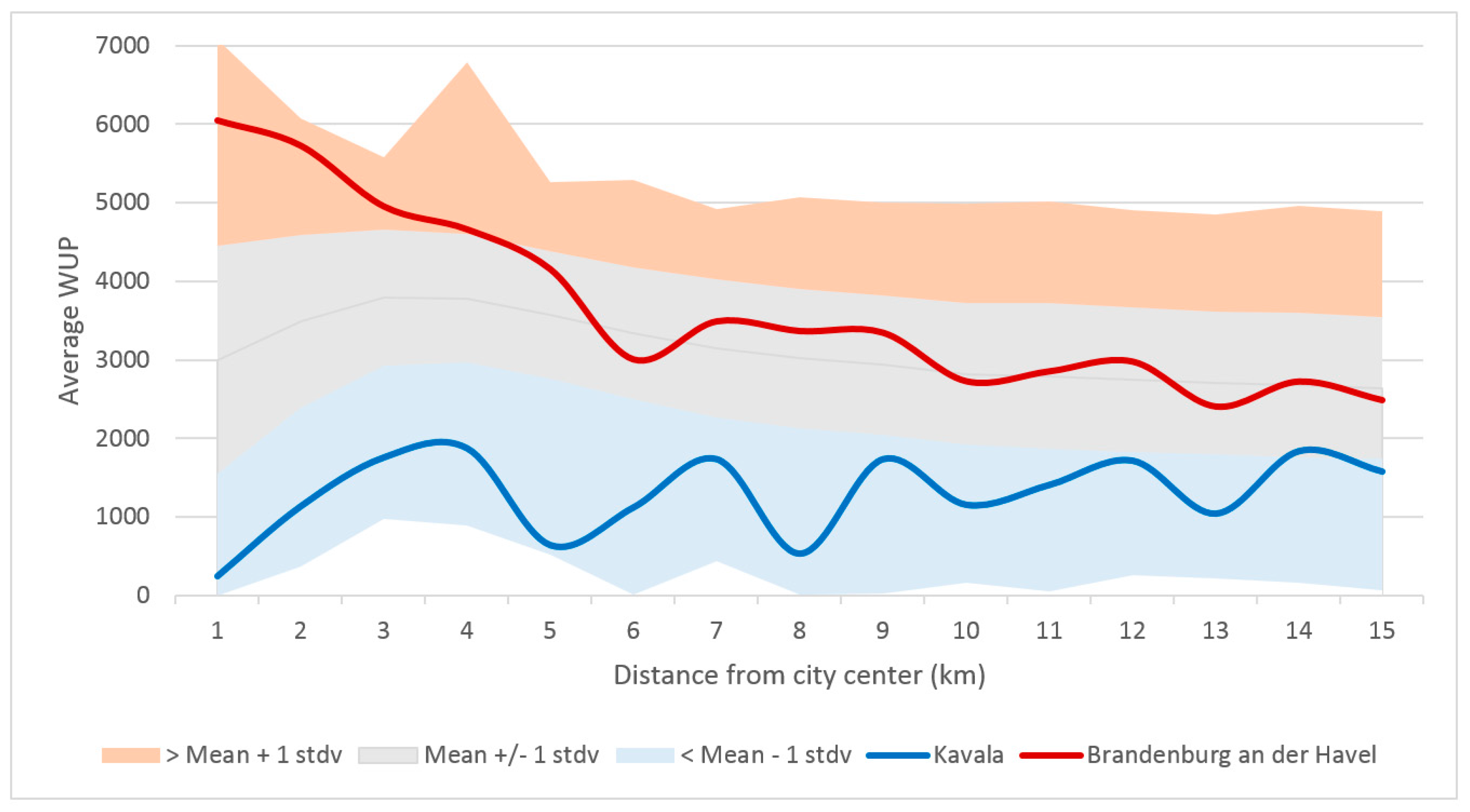
3.1. Identification of the Optimal Horizon of Perception

The horizon of perception is a critical element of the WUP. It corresponds to the maximum distance at which a focus cell (residential cell in our adapted method) is influenced (perceived sprawl) by the presence of other built-up cells (both residential and commercial/industrial). Figure 3 illustrates this concept.

To identify which horizons of perception would be most suitable to characterize sprawl in cities across Europe, we conducted an analysis of the variation in WUP values averaged across 1 km-wide concentric rings (from 1 to 30 km) centered on city-centers. The use of concentric rings rather than city boundaries (which can vary greatly) allowed us to provide a common metric that could be uniformly applied across European urban areas.

To compensate for the fact that a higher horizon of perception leads to higher WUP values and allows averaged WUP values to be compared across horizons of perception within cities, we plotted for each of the 672 European cities’ variations in WUP and normalized them as a function of the maximum value recorded within the concentric rings for each specific horizon of perception. This analysis identified two main city profiles:

(1)

Cities where the normalized WUP value profile remained almost identical across horizons of perception (see Figure 4).

(2)

Cities where the normalized WUP value profile varied strongly across horizons of perception (see Figure 5).

The high variations in WUP across concentric rings were likely caused by the spatial heterogeneity in population and the distribution of population within areas surrounding the cities (for example a small city surrounded by multiple smaller, dense villages (Figure 6)) as well as by the presence of certain landscape features (such as coastline, or mountains).

To identify the “optimal horizon of perception” most suitable to highlight variations in population distribution across rings for the EU28, we looked, for each city, at the sum of absolute differences of normalized average WUP values across the concentric rings for each horizon of perception. We computed for each horizon of perception the absolute difference in normalized WUP value between ring 1 and ring 2, and then added it to the absolute difference between ring 2 and ring 3, etc.

From this analysis, we summed the number of cities, which displayed the highest variability (sum of absolute differences) for each investigated horizon of perception. For most cities, a horizon of perception of 2 km provided the highest sum of absolute difference in average WUP when accumulated across concentric rings from 1 to 30 km distance from the city centers (see Figure 7). We observed that this value of horizon of perception also provided the highest sum of absolute difference when considering concentric rings from 1 to 5 km, and from 1 to 15 km.

As a result, we concluded that a horizon of perception of 2 km was the best choice to highlight the most variability within European cities.

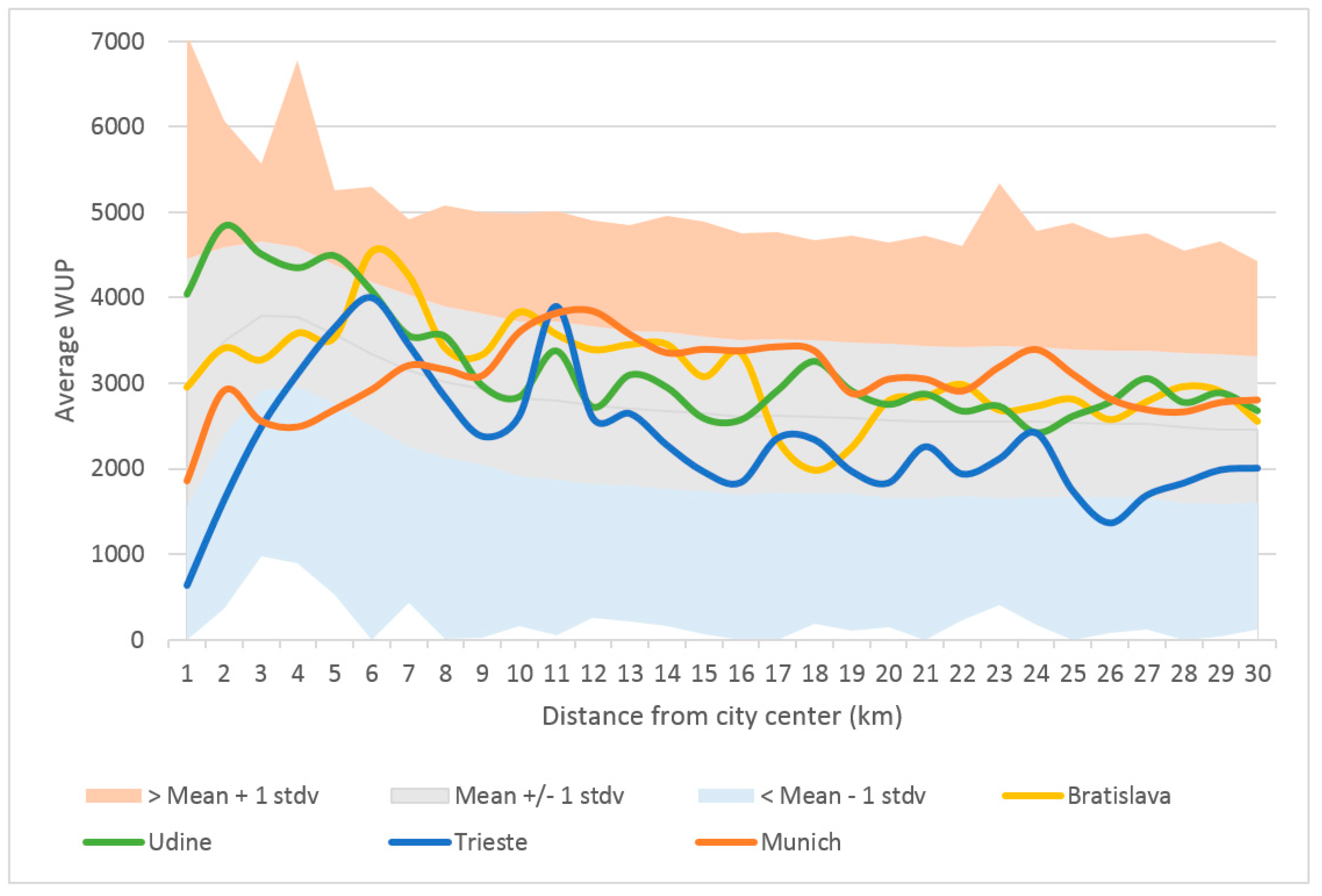
3.2. Towards a New Indicator of Sprawl

Using a 2 km horizon of perception, we could create a WUP profile for all European cities by averaging the WUP values across 1 km concentric rings. An example of such a profile is presented in Figure 8. The average concentric WUP profile for European cities shows a relatively compact city center rapidly becoming more sprawled and peaking at 4 to 5 km distance before slowly decreasing and plateauing past 15 km. The relatively high WUP values of this plateau is likely attributable to the fact that most small and medium cities do not extend very far and that past 15 km, a large proportion of habitations are relatively spread out, isolated, and therefore characterized by high WUP values. The profile for the agglomeration of Munich, Germany indicates a compact city center with very low WUP values, gradually becoming less compact and reaching a plateau from a 10 km distance from the center. The profile for the city of Udine, Italy shows an opposite trend, with a sprawled center (high WUP values), becoming less sprawled past 6 km from the center (where more compact small towns and villages are present), and plateauing past 10 km.

We believe this type of city profiling can provide a valuable tool to compare sprawl in cities and their surrounding areas and understand how their profiles differ spatially from each other. However, such profiles are too complex to compare across a large number of cities and a more concise indicator is needed. To identify a simple, more concise indicator relative to sprawl, we investigated three possible candidates derived from the averaged concentric ring WUP profile: (1) the sum of concentric WUP; (2) the average of concentric WUP; and (3) the average WUP aggregated at the level of the Functional Urban Area (FUA) [8]. These candidate indicators were selected because they are simple to calculate and explain to non-technical audiences.

Each of the three candidate indicators were calculated for all 672 cities in the EU28. The obtained values were then compared with the work published on urban sprawl by the European Environment Agency and European Commission’s Joint Research Centre [8], who ranked 22 European cities based on their level of sprawl (see

Table 1. Correspondence between the European Environment Agency and European Commission’s Joint Research Centre’s sprawl classification and the ACWUP classification, aggregated using natural breaks (cities are listed in the order by which they were ranked in the European Environment Agency and European Commission Joint Research Centre’s classification: e.g., Udine is more sprawled than Pordenone). Cities with * in the ACWUP ranking column correspond to matches with the EEA classification while cities in bold correspond to miss-matches.

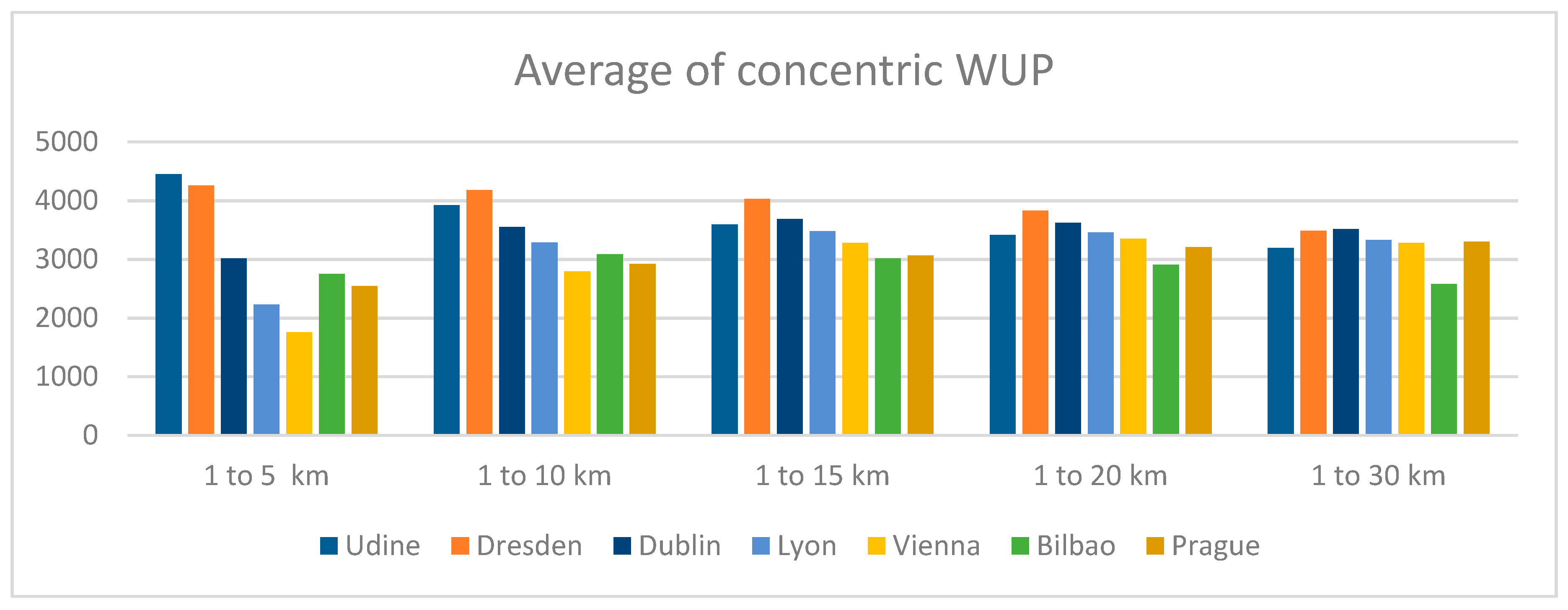
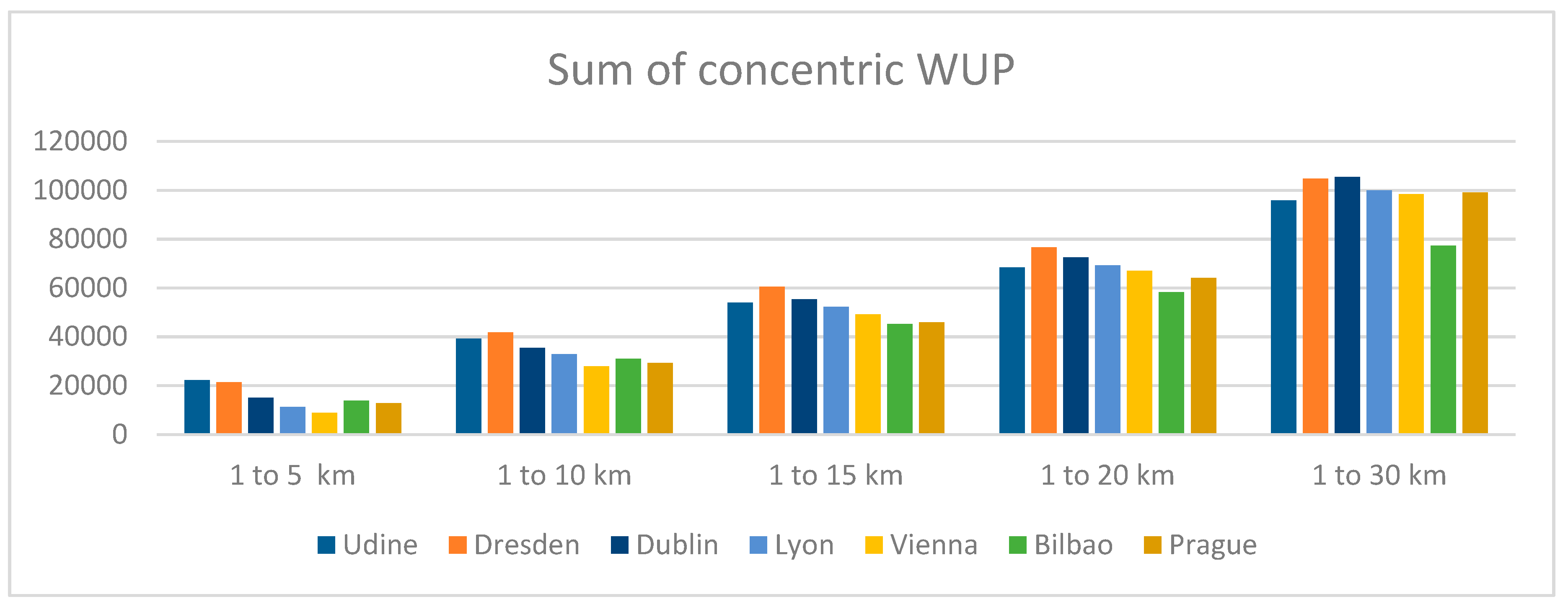
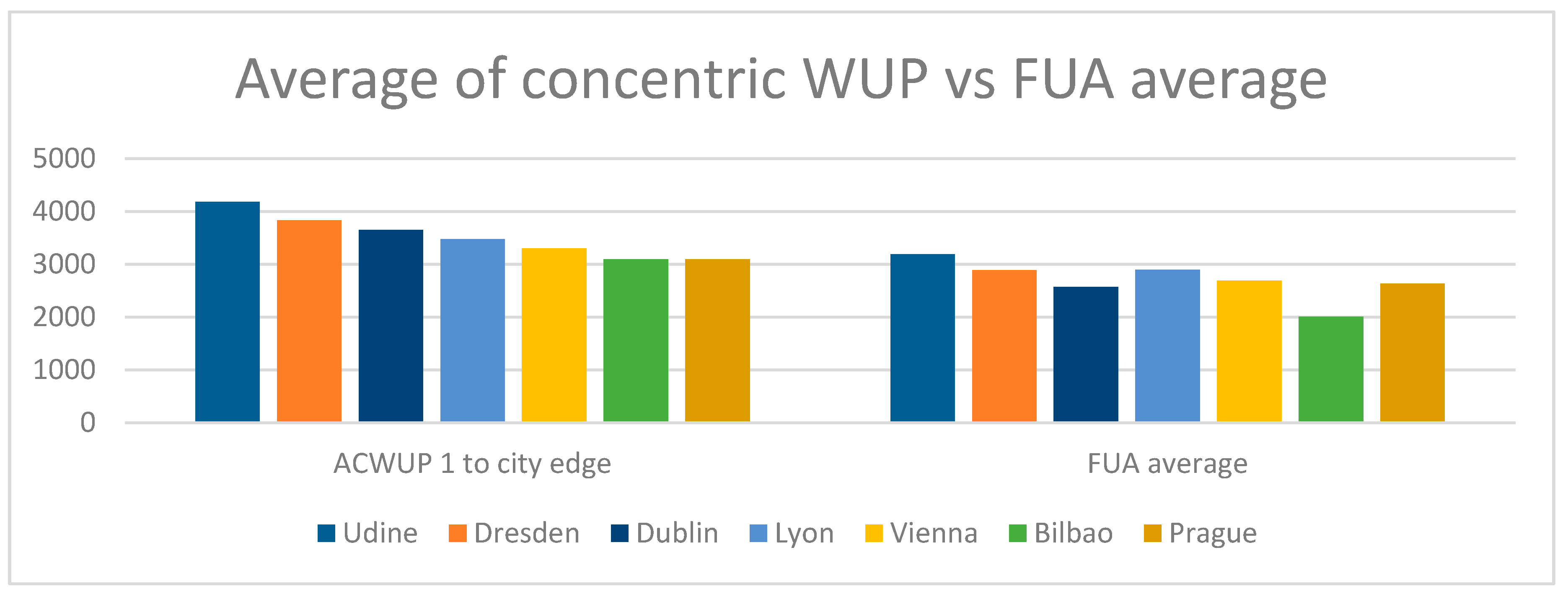
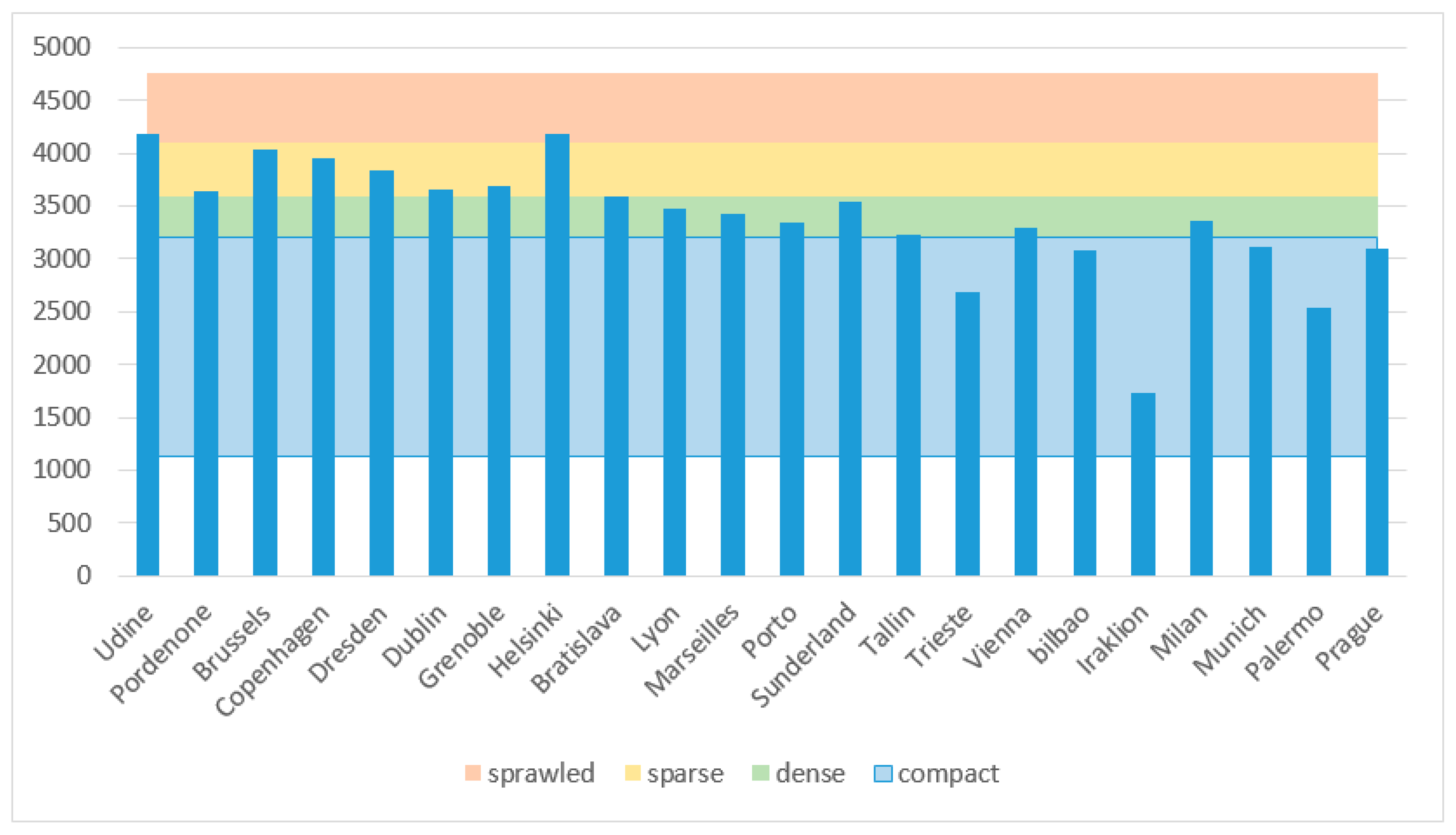
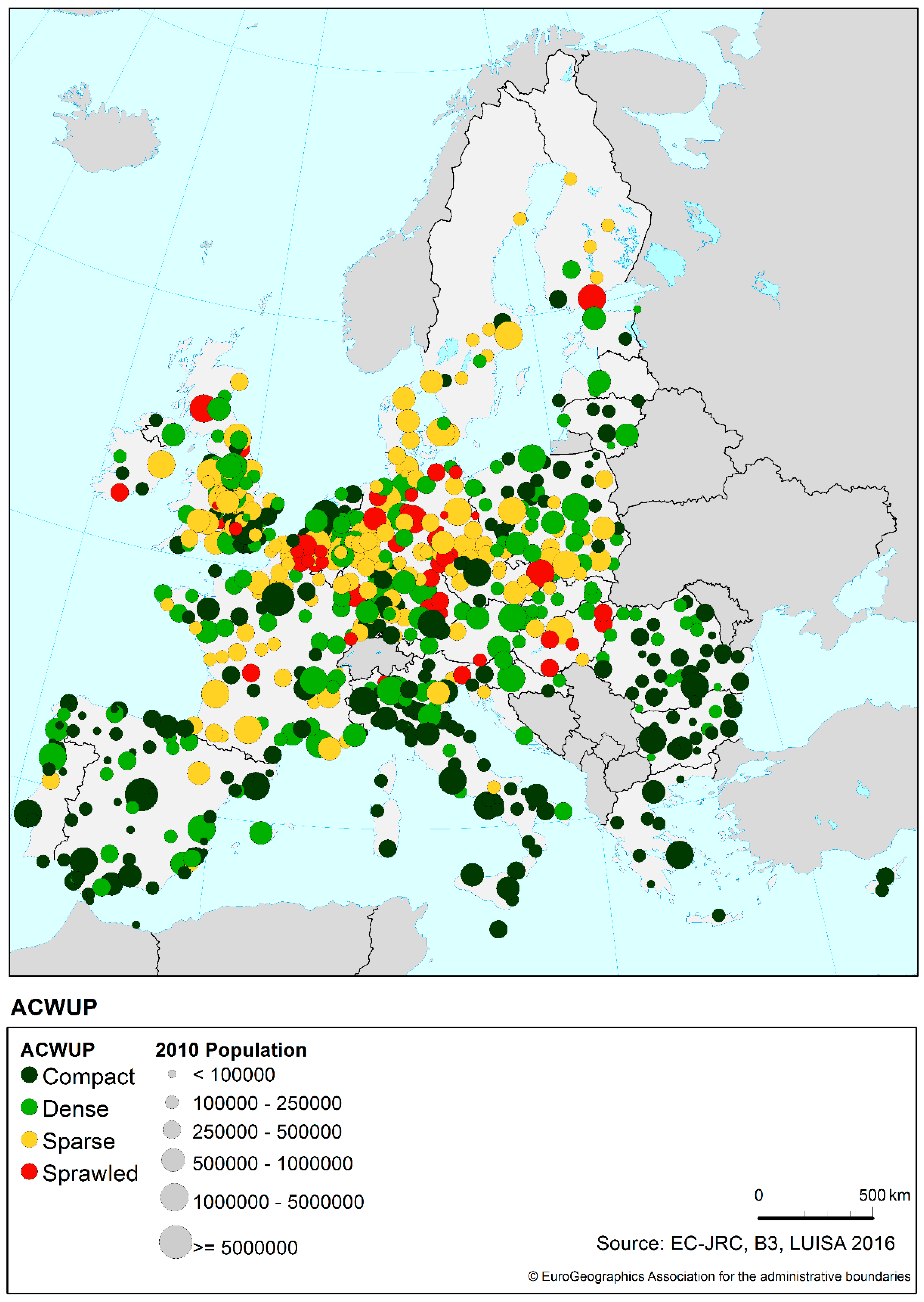
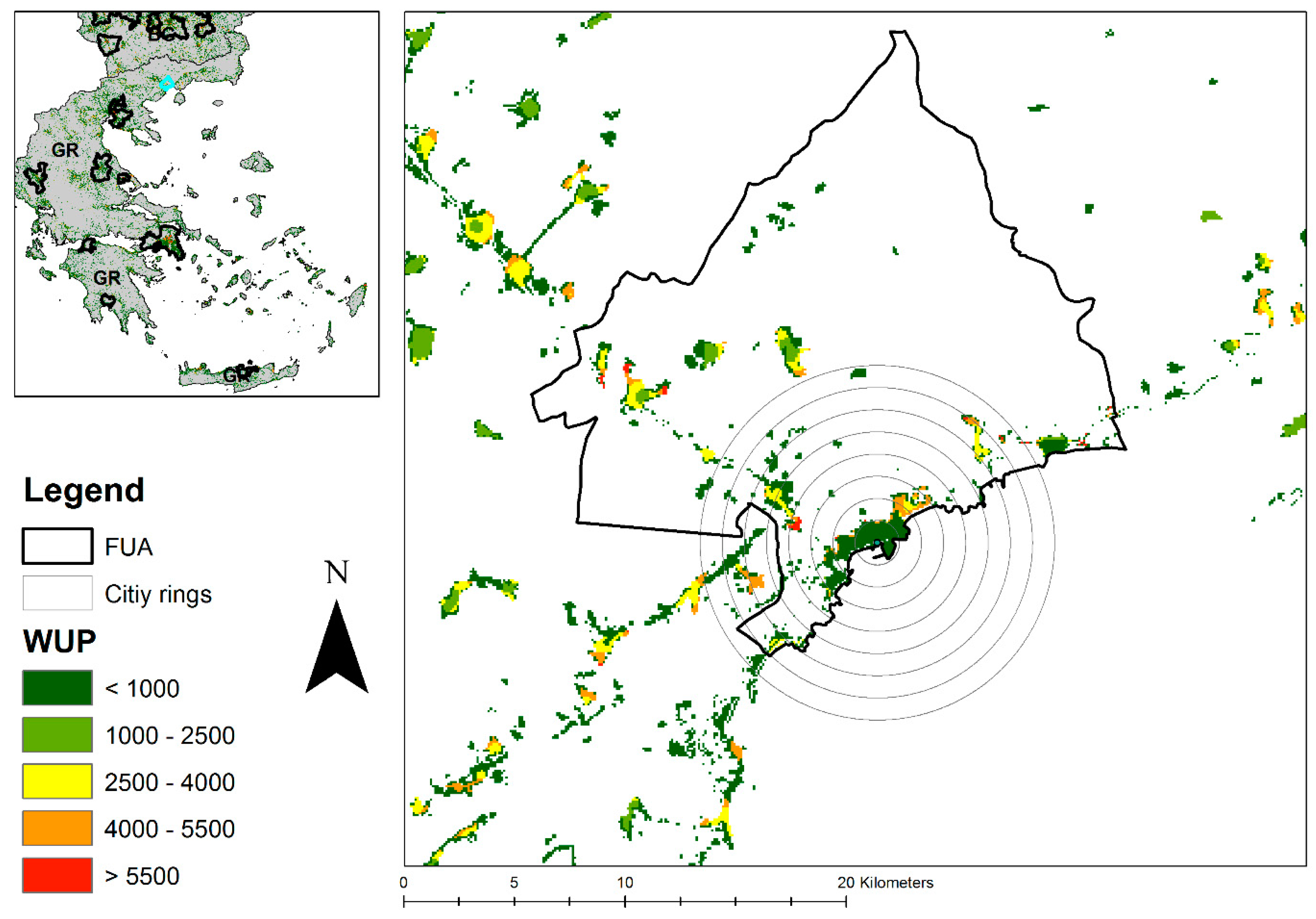
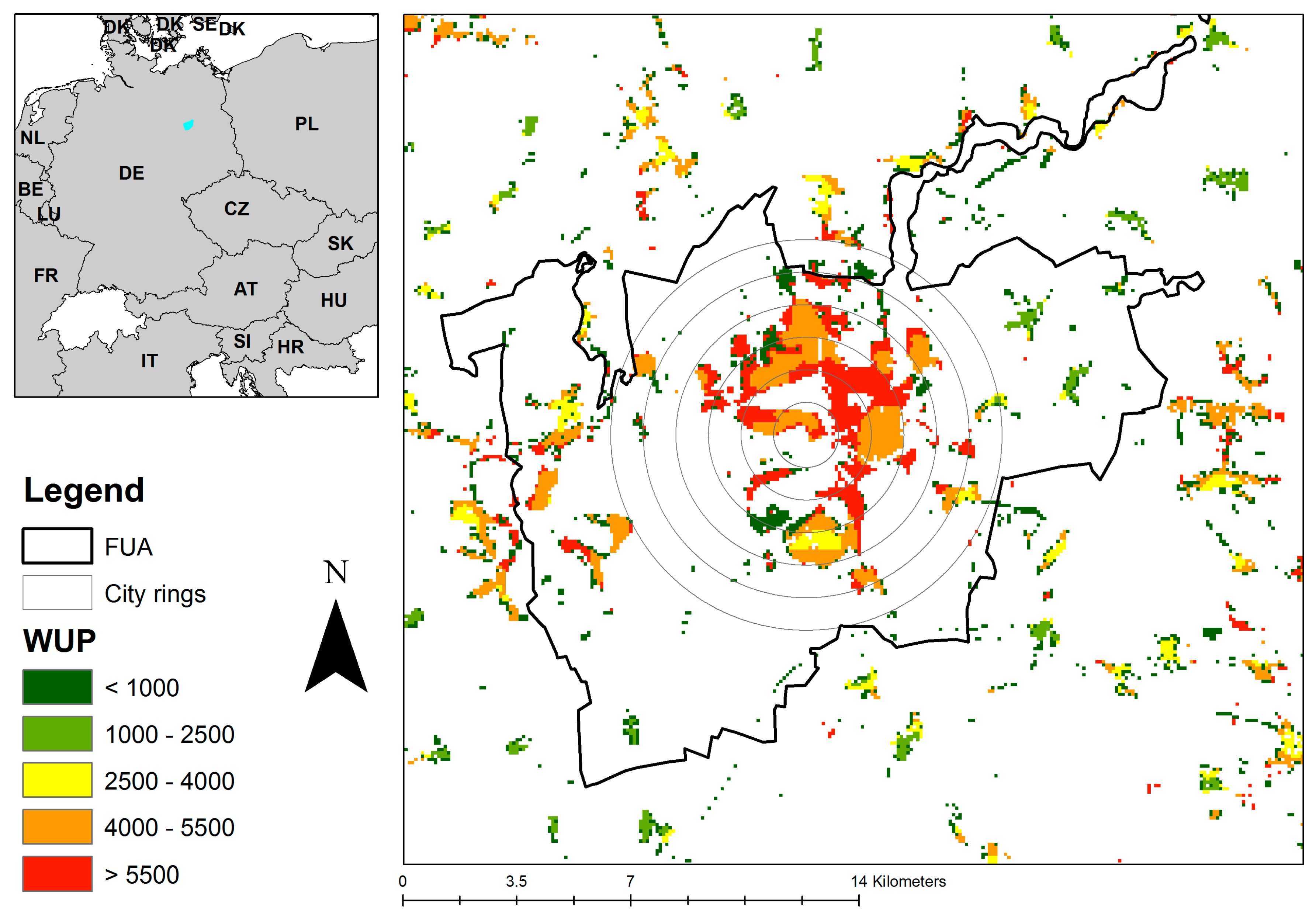
Sprawl Level	ACWUP Classification	European Environment Agency and European Commission’s Joint Research Centre Classification	ACWUP ranking
Sprawled	≥4100	Udine Pordenone	Helsinki Udine *
Sparse	3600–4100	Brussels Copenhagen Dresden Dublin Grenoble Helsinki	Brussels * Copenhagen * Dresden * Dublin * Grenoble * Pordenone
Dense	3200–3600	Bratislava Lyon Marseille Porto Sunderland Tallin Trieste Vienna	Bratislava * Sunderland * Lyon * Marseilles * Porto * Milan Vienna * Tallin *
Compact	≤3200	Bilbao Iraklion Milan Munich Palermo Prague	Munich * Prague * Bilbao * Palermo * Trieste Iraklion *

). This report provided a ranking, split into a 4-category classification, of the most sprawled and compact cities in Europe, by combining six indicators taking into consideration elements such as the growth of built-up areas, the share of residential areas, population density, and growth rates. It identified Udine, Italy as the most sprawled city and Bilbao, Spain as the most compact. Although the European Environment Agency published an updated report on urban sprawl in Europe in 2016, this updated report did not provide any ranking of cities based on their level of urban sprawl, and could not be used as an updated reference in our analysis.

We performed a comparison between the city ranking proposed by [8] and the ranking provided by each of the three proposed indicators. The ranking provided by the average of concentric WUP (Figure 9) and by the sum of concentric WUP (Figure 10) followed a similar pattern. However, the ACWUP presented an advantage over the sum of concentric WUP in that ACWUP values could be compared across different aggregation levels.

To account for the fact that most cities have a radius inferior to 30 km, we identified for each city an edge within which concentric WUP values could be averaged. The edges of these cities were identified by converting population raster to vectors, selecting population polygons within 5 km distance from the city center, and then selecting the intersection of polygons with city rings. For cases where the rings of nearby cities overlapped, checking and individual adjustment were applied. To compensate for potential uncertainty, the edge distance was rounded up to the closest even number of rings. For example, 5 km would become 6, 1 become 2, etc.

The incorporation of a city’s edge to identify the level of aggregation at which to average concentric WUP values (Figure 11) improved the matching of the sprawling status of cities with the European Environment Agency and European Commission’s Joint Research Centre’s classification compared to averaging done from 1 to 5 km, 1 to 15 km, and 1 to 30 km (see Figure 9). This ACWUP ranking, using city’s edge, also provided a better match to that obtained using the FUA WUP average (Figure 10) and was therefore selected as the preferred sprawl indicator.

As [8] does not provide quantitative values characterizing sprawl in cities, but rather a classification, we could not provide a rigorous comparison of the performance of our indicator with their estimation. However, by averaging concentric WUP values from 1 km to the city’s edge (see Table 1 and Figure 12: Classification of European cities based on their ACWUP score. Cities are placed in order of their level of sprawl based on the European Environment Agency and European Commission’s Joint Research Centre’s classification.) split into 4 classes (compact below 3200, dense below 3600, sparse below 4100 and sprawled above 4100), we could fit our distribution to match 18 cities out of 22 (81% match) with the EEA sprawl ranking [8]. The main discrepancies found were for Helsinki, Finland, classified as very highly sprawled while listed as high by the European Environment Agency and European Commission’s Joint Research Centre report, Pordenone, Italy, classified as high but listed as very high, Milan, Italy, classified as medium but listed as sprawled, and Trieste, Italy, classified as sprawled but listed as medium.

Assuming that the correspondence ratio between our classification and the work [28] extends to the rest of cities in the EU28, the averaged concentric WUP could provide a cheap, first-pass indicator to classify cities as a function of their sprawl.

We propose the Averaged Concentric Weighted Urban Proliferation (ACWUP) index as a new metric to quantify sprawl for European urban areas. Its application to classify cities, using the above-defined classification, in the EU28 for the year 2010 is presented in Figure 13. These results indicate that overall, Greece appears to have the most cities with a low ACWUP and therefore potentially the least sprawl while Belgium appears to have the most sparse and sprawled cities.

Table 2. Most and least sprawled cities with a population above 500 thousand inhabitants, classified based on their ACWUP values.

Most Sprawled Cities	ACWUP Values	Least Sprawled Cities	ACWUP Values
Osnabrück	4317	Thessaloniki	1772
Saarbrücken	4286	Athina	2215
Braunschweig-Salzgitter-Wolfsburg	4237	Madrid	2297
Ostrava	4237	Plovdiv	2320
Gent	4192	Granada	2506
Glasgow	4190	Palermo	2533
Helsinki	4181	Freiburg im Breisgau	2654
Antwerpen	4050	Genova	2686
Rzeszów	4033	Bari	2736
Brussels	4030	Barcelona	2751
Ruhrgebiet	4025	Rotterdam	2815
West Midlands urban area	3999	Frankfurt am Main	2832
Rouen	3986	Rennes	2834
Liège	3986	Amsterdam	2881

provides a list of 15 highly populated cities (population higher than 500,000) with the highest (most sprawled) and lowest (most compact) ACWUP values. It confirms the trend visible in Figure 13, where the most sprawled cities seem to be found in the northern half of Europe, while the most compact cities tend to be in the southern half, with the exception of Freiburg, and Frankfurt, Germany, Amsterdam, and Rotterdam, the Netherlands, and Rennes, France.

Looking at European extremes, we identified the region centered on the town of Kavala, Greece as having the lowest ACWUP value (Figure 14), and the area surrounding Brandenburg an der Havel, Germany as having the highest value (Figure 15).

We propose the ACWUP be used as a first-pass investigation of sprawl and be complemented by an analysis of the average WUP profile to identify local spatial variability. For example, a closer observation of the average WUP variations between Kavala (Figure 14) and Brandenburg an der Havel (Figure 15) provides a clearer picture of their structure.

The WUP profile for the city of Kavala (blue line in Figure 16) shows very low WUP values in the city center, then slowly increasing up to a distance of 4 km and following a wave pattern while remaining in the lower European WUP distribution. This wave pattern indicates the presence of sparse, dense aggregations of population (villages) around the city center.

The WUP profile for the city of Brandenburg an der Havel (red line in Figure 16), shows very high WUP values in the city center indicating a relatively open and spatially spread center, decreasing steadily and stabilizing past 6 km distance from the center.

4. Discussion and Conclusions

We developed a method to calculate an “adapted” version of Jaeger’s Weighted Urban Proliferation (WUP) index at a very large scale [28] at 100 m resolution. Exploring a range of horizons of perception, we confirmed the value of 2 km, selected for practical reasons by [8], was optimal to highlight the highest level of variability across cities in Europe. The WUP map we produced provides a consistent, high resolution quantification of urban sprawl across the entire EU28. This represents a hundred fold improvement in spatial resolution compared to previously published work on EU-wide WUP [28], and a threefold improvement over work published by [8] in their local application in Switzerland.

To allow for the comparison of sprawl across urban zones, we proposed two indicators, the ACWUP, which provides a single value comparison across a large number of locations, and the average WUP profile, which provides a more detailed way to look at sprawl and compare a smaller number of cities.

The ACWUP-based classification of cities we proposed provided a good level of correlation with the European Environment Agency and European Commission’s Joint Research Centre’s previously published characterizations of sprawl across EU cities [8]. However, our approach is considerably simpler than that of [8], who based their assessment on a combination of six separate indicators, three of them time-series. The low data requirements of our adapted approach combined with the high speed with which it can produce computations (on a modern computing infrastructure) makes the ACWUP a cheap “first path” alternative indicator to broadly categorize sprawl across cities. We propose the ACWUP be combined, in a second step, with the WUP profile to explore variations in WUP within urban areas to identify features of interests for which more data hungry analyses may be worth performing.

The reason why the ACWUP provides a grouping of cities similar to the sprawl-based grouping of [29] is unclear and will be the object of future work.

The results presented in this paper were based on 2010 land-use and population maps provided by the LUISA Territorial Modelling Platform [32]. As the LUISA platform also produces policy specific scenario projections of both datasets up to the year 2050, our WUP computations for 2010 could be used as a reference (t0) from which to assess possible future changes in urban sprawl across all European urban areas. Such outputs also have the potential be used to evaluate the impact of different policies on the structure of cities, define urban sprawl thresholds, special intervention, or restricted building areas.