How to Improve Collaboration in Sustainable Urban Community Renewal? An Evolutionary Game Model

Abstract

Urban community renewal is an important direction for sustainable urban development in the era of building stock. Unlike traditional construction projects, the deeper involvement of residents in community renewal leads to more complex stakeholder relationships and new conflict-of-interest issues, requiring collaboration for the development of sustainable human settlements. Grounded in collaborative governance theory, this study constructed a tripartite evolutionary game model and employed simulations to analyze the evolutionary paths and key influencing factors to improve collaboration. The findings suggest that there are three main scenarios of urban community renewal: government-led, market-led, and multi-participation, and that the realization of sustainable collaboration is determined by the creation of collaborative advantages, the magnitude of speculative benefits for companies, and the regulatory costs incurred by the government. In conclusion, this study reveals the strategic choices and necessary conditions for each subject under different scenarios. It is necessary to improve the top-level design of the collaborative governance of urban community renewal, strengthen the construction of information sharing and feedback channels of urban community renewal, and establish the whole process supervision system of urban community renewal.

1. Introduction

As China’s urbanization enters the mid-to-late stage, urban renewal has shifted from large-scale incremental construction to a sustainable model emphasizing the quality-driven restructuring of existing stock, guided by the national strategy of “organic renewal” [1,2], guided by top-level policies such as the 2025 “Opinions on Continuously Promoting Urban Renewal Actions”. This policy emphasizes the development of complete community construction and the promotion of the renovation and transformation of old neighborhoods, old factory areas, urban villages, and other areas. [3]. From 2019 to 2024, a total of 280,000 old urban residential communities were renovated across China, benefiting 48 million households and over 120 million residents. In 2025, a new batch of urban renewal and renovation projects will be planned and implemented to fully complete the renovation of all old urban residential communities built before the end of 2000. These communities exhibit three systemic deficiencies: infrastructural decay, spatial inefficiency, and service gaps [4,5]. According to data from the Ministry of Housing and Urban-Rural Development, in 2024, renovation work began on 56,000 urban old residential communities, with over 25,000 elevators installed. Positive results were achieved in the pilot development of 106 complete communities across the country. These initiatives aim to improve residents' living conditions and quality of life and to achieve sustainable urban community development through the enhancement of overall community quality and the living environment [6].

However, implementation faces structural challenges rooted in multi-stakeholder conflicts [7,8]. These include coordination failures among stakeholders due to divergent interests, such as the roughly decade-long “Enning Road Incident” in Guangzhou, where residents resisted top-down redevelopment plans [9], as well as recent deadlocks in elevator installations. The policy document issued by the Ministry of Natural Resources explicitly advocates for the promotion of “collaborative governance and shared benefits” [10]. Approaches relying on a single actor—whether government-led planning, market-driven development, or resident-led initiatives—have proven insufficient to achieve desired outcomes [11]. The government, acting as the custodian of public interest, orchestrates urban renewal initiatives. It is responsible for formulating policies, leading planning and design efforts, and selecting developers and contractors for implementation [12]. Companies, guided by market mechanisms, contribute their expertise and capital, aiming to maximize economic returns through project development and execution [13]. Residents, as the most directly impacted stakeholders, are both beneficiaries and potential losers of these projects [14]. Their participation, driven by a desire to protect interests and enhance living conditions, often manifests through public discussions and deliberations [15]. If the three parties fail to achieve goal and behavioral coordination, it will result in high transaction costs and obstacles to progression, which will ultimately harm the overall social interests. Due to differences in rights, obligations, resources, and knowledge, as well as conflicts of interest, behavior games often arise during interactions among the three groups in urban renewal.

Participatory approach and collaboration play a central role in making urban renewal decisions based on a multi-party needs framework [16], and have been actively practiced in several first-tier cities in China, such as Shanghai’s Meiyuan Park, Beijing’s Jinsong Neighborhood, and Guangzhou’s Yongqingfang, among other projects. Collaborative governance refers to the governance process and structure of solving public problems through cooperation among equals, whereby a collaborative community is formed based on an urban renewal project, which carries out dialog and cooperation under the guidance of common goals, eliminates differences, and builds consensus [17,18]. Under collaborative governance, relative subjects both compete and cooperate, forming a synergistic mechanism for the integration of resources, interests, and values, effectively avoiding the conflicts formed by the inconsistent interests of the subjects, and jointly controlling and preventing the problems and challenges caused by the external macro-environment [19]. Conducting in-depth research on the collaborative governance of multiple stakeholders in urban community renewal and exploring a system based on collaboration, participation and common interests is of great practical significance for reducing transaction costs, improving the overall efficiency of community renewal projects, achieving excess returns, and maximizing social benefits [20,21].

Scholars have extensively explored the dynamics of stakeholder collaborative governance in urban renewal projects from various angles. These include public participation [22], conflict coordination [23], and decision-making mechanisms [12]. However, much of the existing literature remains anchored in the context of the “big demolition and construction” phase of urban renewal, which predominantly discusses demolition, compensation, and resettlement issues among the government, residents, and developers, focusing on temporary and one-time actions, with limited attention to residents’ roles in project decision making [19]. As China starts the renovation of old urban residential communities, the decision making and governance issues in urban community renewal have become more persistent and intricately linked to residents, making it necessary for specificity in research and modeling. Additionally, the costs associated with communication, supervision, and trust during the collaborative process are increasingly critical to effective governance [7]. Given the long-term nature of these projects, evolutionary game theory emerges as a valuable tool for studying cooperation and conflict in ongoing governance, capturing the decision-making evolution among different stakeholders [24]. This study aims to construct a tripartite evolutionary game model to visualize and analyze the collaborative governance process in urban community renewal, seeking to thoroughly investigate the research questions as follows. First, what are the respective interests and action mechanisms of the government, companies, and residents in the multi-participation model of urban community renewal? Secondly, what are the key influencing factors that affect the decision making of the three main participants, and how can these contribute to a win–win situation for all parties?

In response to the research questions, this study is structured as follows: First, the study delves into a review of related literature and the research methodology. Second, it introduces a novel three-party evolutionary game model comprising government, companies, and residents to elucidate the behavioral evolution of these key stakeholders. Third, the study employs numerical simulations to dissect the impact of critical elements on the decision-making processes of the involved parties and proposes specific recommendations. This study extends collaborative governance and game theory from the “mass demolition and construction” scenario to the stock renewal stage, filling the gap in existing research regarding the dynamic interaction analysis of the sustainable governance process. It reveals the theoretical logic of collaborative advantage creation as the core driving force of multi-party cooperation. Through numerical simulation, it verifies the impact mechanism of key variables such as collaborative advantage on strategy evolution, deepening the application of collaborative governance theory in the field of sustainable urban renewal. At the same time, it provides countermeasure references for constructing multi-party participation implementation paths in urban community renewal in practice, and provides a basis for urban community renewal policy formulation.

2. Research Background

2.1. Game Theory in Urban Community Renewal

Urban community renewal encompasses the modernization and upgrading of old urban communities, including hutongs and lanes, to meet evolving urban development needs and enhance residents’ quality of life. Community renewal with the core concepts of enhancing community resilience, building an age-friendly environment, and promoting intelligent upgrading has become an important strategic path for urban sustainable development. For example, in the context of China’s deep demographic transformation, the systematic renewal of community aging adaptability, as a key infrastructure reconstruction to cope with the aging society, is accelerating its evolution from the policy advocacy level to the practical necessity level [25]. Due to the multiple interests and numerous subjects involved in urban community renewal, many scholars have adopted different game models to carry out related research. Based on bargaining theory, Liu [12] established an incomplete information strategy game model between developers and residents in the negotiation process of demolition and relocation compensation to visualize efficiency and fairness; Mayer [26] used the joint application of decision support tools and simulation games, to support decision making on sustainable urban development and to improve the efficiency of the agenda. While these studies have used game theory to portray stakeholder relationships, evolutionary games are better at portraying dynamic stakeholder interactions in problems involving decision making [27,28]. Evolutionary game models are often used in win–win analyses of multi-party cooperation and have previously been applied in scenarios such as age-friendly renewal [15], urban industrial land redevelopment [29], mega projects [30], and PPP projects [31]. However, the discussion on the collaborative governance of multiple subjects in urban community renewal under the framework of evolutionary game is yet to be in-depth, and most of the studies only consider the relationship of interests between the subjects, the choice of modes, or are only limited to the two parties of the developer and the residents. Therefore, this study adopts a tripartite evolutionary game model to portray the collaborative process of governance in urban community renewal, to visualize the influence of different factors on the evolutionary path, and to explore the path to achieve a win–win situation for all parties.

2.2. Diverse Stakeholder Interest Claims in Urban Community Renewal

The government is crucial at all stages in urban community renewal, from pre-planning policy and standards setting to mid- and post-project coordination, supervision, and management [13,32]. It ensures common governance by linking grassroots organizations and standardizing public demand expression, interest coordination, and rights protection. The government also enforces legal compliance and protects public and resident interests. However, Kinossian [33] observes that administrative over-centralization can lead to governmental inaction, seeking to boost efficiency and control costs, which hampers the involvement of other governance participants.

Companies leverage their technical prowess, resource availability, and talent to design programs, operate capital, and manage development and construction, thereby generating economic profits [12]. Trillo [34] notes that, when companies consider the public good, they can effectively blend market-oriented and reciprocal values, aiding the successful execution of urban renewal initiatives by public agencies, entrepreneurs, and communities. However, companies primarily act as agents with a core objective of maximizing their economic interests [35], which often leads to profit-oriented policies that prioritize the privatization of public-owned assets and the pursuit of financial gains. Such an approach tends to neglect the conceptualization of urban community renewal as proper commons, where shared resources are managed for collective benefit rather than private profit [36,37]. This goal can sometimes conflict with the public interest goals of urban renewal. Jones and Ward [38] observe that this divergence of interests may lead to speculative behaviors, where companies prioritize profit at the expense of the broader public interest.

Residents are the primary stakeholders in urban community renewal projects, directly experiencing both the benefits of transformations and the adverse impacts of these initiatives. Collaborative governance success hinges on effective community participation, capitalizing on residents’ local knowledge to make decisions tailored to local nuances and diverse community needs. However, residents often find themselves in a disadvantaged position compared to the politically powerful government and economically resourceful companies, necessitating empowerment to balance this dynamic [15]. The active cooperation of residents creates the conditions for two-way communication in urban renewal, allowing governments, businesses, and the public to freely express and exchange opinions, thus enhancing accountability in the decision-making process, the long-term viability of the project, and the positive impacts on the community [6]. However, in the case where residents are aiming to safeguard their personal interests, when they hold objections to the renewal project and have negative risk perceptions, in order to safeguard their rights and interests, they may express their objections to the government and companies that hold resources and power through protests, petitions, or even social conflicts.

3. Methodology

Evolutionary game theory, initially developed to understand the evolution of biological populations, systematically examines the search for stable strategies within populations in dynamic evolutionary environments [39]. It is broadly applied in non-biological fields like economics, management, and sociology to study equilibrium outcomes in interacting populations where strategies evolve adaptively [27]. In the context of sustainable urban community renewal, this theory finds relevance in analyzing the public program governance process, involving the government, companies, and residents. Through ongoing communication and coordination, these parties strive for a balance of interests, leading to widely accepted governance outcomes. This aligns with the core principles of evolutionary game theory.

Three key aspects make evolutionary game theory particularly applicable to urban community renewal. First, participants exhibit bounded rationality due to information asymmetries, power imbalances, inconsistent interests, and a dynamically changing operational environment, making complete rationality elusive in collaborative governance [40,41]. Second, a replication dynamic exists in the strategy selection of participants [42]. Governments, companies, and residents iteratively refine their strategies through practice and simulation, seeking an evolutionarily stable equilibrium. Lastly, the strategies of participants are asymmetric. The government, companies, and residents have distinct interests and resources, each employing unique mechanisms and strategies in the collaborative process. Therefore, evolutionary game theory is adept at exploring the dynamic interactions among diverse stakeholders in urban renewal projects, revealing the decision-making mechanisms of stakeholders with limited rationality in collaborative governance.

According to the previous analysis of the interest claims and the action mechanism of the government, companies, and residents considering the evolutionary game mechanism, the theoretical framework illustrating the game relationship is depicted in Figure 1 below.

4. Tripartite Evolutionary Game Model for Collaborative Governance

4.1. Model Assumptions and Establishment

Assumption 1.

In the evolutionary game of collaborative governance during the implementation phase of urban community renewal projects, the key players are the government (G), companies (C), and residents (R). Each of these players is characterized by bounded rationality. Over time, their strategy selections are anticipated to evolve and ultimately stabilize at an optimal strategy.

Assumption 2.

The strategy set for each player in the collaborative governance evolutionary game is defined, as shown in Table 1. For local government, the strategy space comprises {positive action, negative action}, with $x$ and $\left(1-x\right)$ representing the probabilities of positive and negative actions, respectively. For companies, the strategy space is {valuing demands, ignoring demands}, with $y$ and $\left(1-y\right)$ denoting the probabilities of valuing and ignoring demands, respectively. Finally, for residents, the strategy space includes {supporting, dissenting}, with $z$ and $\left(1-z\right)$ indicating the probabilities of supporting and dissenting, respectively.

Assumption 3.

Each player will get direct or indirect benefits after urban community renewal. The provision and development of efficient public goods or services will enhance the attractiveness of the city, which will promote economic development and land appreciation, and this development dividend will be the initial benefits $R_g$ for the government. Companies will build more houses than the original number of units under the supervision of the government, and they can provide houses to the original owners while selling the excess quantity to earn profits; in addition, companies can also earn considerable profits through commercial operation and land appreciation; these economic gains are the initial benefits $R_c$ of companies. The initial benefits $R_r$ for the residents include the elimination of all types of problems arising from the deterioration of the living environment and the dilapidated infrastructure, thus contributing to the physical, health, and functional improvement of their living conditions. According to the theory of collaborative advantage [43,44], collaborative work may yield potential collaborative benefits beyond the scope of individuals’ capabilities; therefore, it is assumed that the successful implementation of the renewal project will induce a gain in revenue coefficient $\alpha , \alpha >1$, if the three parties reach a collaborative governance.

Table 1. Strategy sets and behavioral patterns.

Player	Strategy	Behavioral Logic	Interest Motivation
G	Positive action	Proactive establishment of communication channels, coordination through institutionalized negotiation platforms, and strict supervision [45].	Maximizing policy performance while avoiding social conflicts.
	Negative action	Reducing fiscal oversight, and tolerating corporate opportunism to accelerate project completion.	Minimizing administrative costs and political risks when resident-corporate conflicts.
C	Valuing demands	Integrating resident preferences into design, sharing incremental benefits.	Pursuing long-term ROI through social license to operate.
	Ignoring demands	Concealing construction risks, exploiting regulatory loopholes for excess profits, and bypassing resident consultations [46].	Short-term profit maximization under information asymmetry, amplified when government supervision weakens.
R	Supporting	Collective action through formal channels, accepting temporary inconvenience for long-term gains.	Securing property rights protection and welfare improvements.
	Dissenting	Exercising veto power, initiating rights movements, or refusing cost-sharing.	Loss aversion when perceived risks exceed benefits.

Table 1. Strategy sets and behavioral patterns.

Player	Strategy	Behavioral Logic	Interest Motivation
G	Positive action	Proactive establishment of communication channels, coordination through institutionalized negotiation platforms, and strict supervision [45].	Maximizing policy performance while avoiding social conflicts.
	Negative action	Reducing fiscal oversight, and tolerating corporate opportunism to accelerate project completion.	Minimizing administrative costs and political risks when resident-corporate conflicts.
C	Valuing demands	Integrating resident preferences into design, sharing incremental benefits.	Pursuing long-term ROI through social license to operate.
	Ignoring demands	Concealing construction risks, exploiting regulatory loopholes for excess profits, and bypassing resident consultations [46].	Short-term profit maximization under information asymmetry, amplified when government supervision weakens.
R	Supporting	Collective action through formal channels, accepting temporary inconvenience for long-term gains.	Securing property rights protection and welfare improvements.
	Dissenting	Exercising veto power, initiating rights movements, or refusing cost-sharing.	Loss aversion when perceived risks exceed benefits.

Assumption 4.

Each player chooses different strategies which will correspond to different costs. The government and companies need to open up the channels for residents to express their demands and strengthen the grassroots community services to promote public participation [47], and they pay the basic coordination costs $C_r$ when residents support, and $C_r^{\prime }$ when residents dissent with the government sharing the proportion $\theta$. When companies ignore the residents’ demands, the government needs additional coordination costs to appease the residents and promote the project, when there is a cost increase ratio $\beta$. When the government’s prudent intervention and lack of communication channels for the renewal project makes the residents only put their demands on the other side of the companies, the companies need to pay extra ratio $\gamma$ communication costs with the residents. In addition, when the government takes positive action, it strengthens the supervision and promotion work in the process of development and implementation of renewal projects, and pays the supervision cost $C_g$. Companies will pay the investing cost $C_c$of bidding, development, implementation, and communication in the renewal project.

Assumption 5.

Losses are negative impacts of poor project coordination. When the residents’ opposition causes social risks, the government will suffer reputational losses (reduced government credibility, negative news spread on social media, etc.) and bear the cost of maintaining stability $L_g$. Companies will increase the cost of investment because of the delay and bear other losses caused by the damage to the image of the companies or even compensation for residents$L_c$. Residents’ normal life is affected and they cannot benefit from the renewal and bear the losses $L_r$. At the same time, the residents, by opposing the renewal can obtain compensation from the government and businesses in the proportions of $\tau$ and $\nu$, respectively.

Assumption 6.

Speculation and regulation. When companies ignore residents’ demands, they will sacrifice the interests of a part of the population in order to obtain excessive profits $R_e$; at this time, if the government carefully supervise [12], the government will have a certain probability $\phi$ of discovering the speculative behaviour of the companies and imposing fines $F$.

Assumption 7.

When the residents dissent regarding the renewal project, there is a probability $\rho$ generating social risk. When the government acts negatively, the lack of openness and insufficiency of public participation channels creates information asymmetry between the residents and other players, with $\lambda$ probability of exacerbating the risk of public trustworthiness. When companies ignore the demands of residents, they will neglect part of the public interest because of the profit-seeking nature, resulting in the residents’ economic, living, and environmental interests being affected, such as the “gentrification” effect or quality and safety issues, which generate a $\mu$ probability of triggering social risks. The model involves parameter symbols and implications as shown in

Table 2. Model parameters in the tripartite evolutionary game.

Notation	Meaning	Note
$x$	Probability that the government chooses a “positive action” strategy	$x\in \left(0,1\right)$
$y$	Probability that a company will choose the strategy of “valuing demands”	$y\in \left(0,1\right)$
$z$	Probability that a resident chooses the “supporting” strategy	$z\in \left(0,1\right)$
$R_g$	Initial benefits for government in urban community renewal projects
$R_c$	Initial benefits for companies in urban community renewal projects
$R_r$	Initial benefits for residents in urban community renewal projects
$R_e$	Speculative benefits for companies when disregarding residents’ demands and engaging in speculative behavior
$F$	Fines for speculative behavior of companies found under government regulation
$C_r$	Costs of coordination when residents support urban community renewal	$C_r^{\prime }>C_r$
$C_r^{\prime }$	Costs of coordination when residents dissent urban community renewal
$C_g$	Government’s basic cost, including regulation, when actively intervening
$C_c$	Companies’ basic cost for bidding, developing, and implementing projects
$L_g$	Losses suffered by the government in the event of social instability
$L_c$	Losses suffered by companies in the event of social instability
$L_r$	Losses suffered by residents in the event of social instability
$\alpha$	Benefit increase coefficient when achieving collaborative governance	$\alpha >1$
$\beta$	Cost increase ratio for the government when solely bearing coordination costs	$\beta >1$
$\gamma$	Cost increase ratio for companies when solely bearing coordination costs	$\gamma >1$
$\rho$	Probability of social risk when residents are dissenting	$\rho \in \left(0,1\right)$
$\lambda$	Probability of social risk when the government acts negatively	$\lambda \in \left(0,1\right)$
$\mu$	Probability of social risk when companies belittle demands	$\mu \in \left(0,1\right)$
$\phi$	Probability of detecting corporate speculation when the government acts positively	$\phi \in \left(0,1\right)$
$\theta$	Government’s proportion of shared costs with companies for resident engagement	$\theta \in \left(0,1\right)$
$\tau$	Proportion of benefits obtained by residents from the government when dissenting	$\tau \in \left(0,1\right)$
$\upsilon$	Proportion of benefits obtained by residents from the companies when dissenting	$\upsilon \in \left(0,1\right)$

.

Building on the foundational assumptions and parameter symbols of the model, this study identifies eight distinct scenarios in the collaborative governance of urban community renewal projects. The evolutionary game payoffs for these three players, under each scenario, are detailed in

Table 3. Game payoff matrix.

Residents	Government	Companies
		Valuing Demands  $\mathit{y}$	Ignoring Demands  $\left(1-\mathit{y}\right)$
Supporting $z$	Positive action $x$	$\alpha R_g-\theta C_r-C_g;$ $\alpha R_c-\left(1-\theta \right)C_r-C_c;$ $\alpha R_r$	$R_g-\beta C_r-C_g+\phi F;$ $R_c-C_c+\left(1-\phi \right)R_e-\phi F;$ $R_r-\left(1-\phi \right)R_e$
	Negative action $\left(1-x\right)$	$R_g;$ $R_c-\gamma C_r-C_c;$ $R_r$	$R_g;$ $R_c-C_c+R_e;$ $R_r-R_e$
Dissenting $\left(1-z\right)$	Positive action $x$	$R_g-\theta C_r^{\prime }-C_g-p_1{L}_g;$ $R_c-\left(1-\theta \right)C_r^{\prime }-C_c-p_1{L}_c;$ $R_r-p_1\left(L_r-\tau L_g-\upsilon L_c\right)$	$R_g-\beta C_r^{\prime }-C_g+\phi F-p_3{L}_g;$ $R_c-C_c+\left(1-\phi \right)R_e-\phi F-p_3{L}_c;$ $R_r-\left(1-\phi \right)R_e-p_3\left(L_r-\tau L_g-\upsilon L_c\right)$
	Negative action $\left(1-x\right)$	$R_g-p_2{L}_g;$ $R_c-\gamma C_r^{\prime }-C_c-p_2{L}_c;$ $R_r-p_2\left(L_r-\tau L_g-\upsilon L_c\right)$	$R_g-p_4{L}_g;$ $R_c-C_c-p_4{L}_c+R_e;$ $R_r-p_4\left(L_r-\tau L_g-\upsilon L_c\right)-R_e$

Note: $p_1=p;p_2=p+\lambda -p\lambda ;p_3=p+\mu -p\mu$; $p_4=p+\lambda +\mu -p\lambda -\lambda \mu -p\mu -p\lambda \mu$.

.

4.2. Replicating Dynamic Equations

Utilizing the evolutionary game matrix, this study calculates the expected and average returns for the three key players—the government, companies, and residents. Subsequently, it constructs the replicator dynamic equations for each of these entities.

The government’s expected payoff from choosing the “positive action” strategy is $E_{x1}$:

$$\begin{array}{c}{E}_{x1}=y\left[z\left(\alpha R_g-\theta C_r-C_g\right)+\left(1-z\right)\left(R_g-\theta C_r^{\prime }-C_g-p_1{L}_g\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} + \left(1-y\right)\left[z\left(R_g-\beta C_r-C_g+\phi F\right)+\left(1-z\right)\left(R_g-\beta C_r^{\prime }-C_g+\phi F-p_3{L}_g\right)\right]\hfill \end{array}$$

(1)

The government’s expected payoff from choosing the “negative action” strategy is $E_{x2}$:

$$E_{x2}=y\left[z{R}_g+\left(1-z\right)\left(R_g-p_2{L}_g\right)\right]+\left(1-y\right)\left[z{R}_g+\left(1-z\right)\left(R_g-p_4{L}_g\right)\right]$$

(2)

The average expected payoff of the government is $E_x$:

$$E_x = x{E}_{x1}+\left(1-x\right)E_{x2}$$

(3)

According to the evolutionary game theory, the replication dynamics equation for the government choosing the “positive action” strategy $F_g\left(x\right)$ is

$$\begin{array}{c}{F}_g\left(x\right) = {\displaystyle \frac{dx}{dt}}=x\left(1-x\right)\{yz\left[\left(\alpha -1\right)R_g-\left(1-\rho \right)\mu \lambda L_g-\left(\beta -\theta \right)\left(C_r^{\prime }-C_r\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +y\left[\left(\beta -\theta \right)C_r^{\prime }+\left(1-\rho \right)\mu \lambda L_g-\phi F\right]+z\left[-\lambda \left(1-\rho \right)\left(1-\mu \right)L_g+\beta \left(C_r^{\prime }-C_r\right)\right]+\phi F\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\lambda \left(1-\rho \right)\left(1-\mu \right)L_g-\beta C_r^{\prime }-C_g\}\hfill \end{array}$$

(4)

Similarly, the expected payoff of a company choosing the “valuing demands” strategy is $E_{y1}$, the expected payoff of a company choosing the “ignoring demands” strategy is $E_{y2}$, and the replication dynamics equation for companies choosing the “valuing demands” strategy $F_c\left(y\right)$ is

$$\begin{array}{c}{E}_{y1}=x\left\{z\left[\alpha R_c-\left(1-\theta \right)C_r-C_c\right]+\left(1-z\right)\left[R_c-\left(1-\theta \right)C_r^{\prime }-C_c-p_1{L}_c\right]\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(1-x\right)\left[z\left(R_c-\gamma C_r-C_c\right)+\left(1-z\right)\left(R_c-\gamma C_r^{\prime }-C_c-p_2{L}_c\right)\right]\end{array}$$

(5)

$$\begin{array}{c}{E}_{y2}=x\left\{z\left[R_c+\left(1-\phi \right)R_e-C_c-\phi F\left]+\left(1-z\right)\right[R_c+\left(1-\phi \right)R_e-C_c-\phi F-p_3{L}_c\right]\right\}+(1\\ -x)[z\left(R_c+R_e-C_c\right)+\left(1-z\right)\left(R_c+R_e-C_c-p_4{L}_c)\right]\end{array}$$

(6)

$$\begin{array}{c}{F}_c\left(y\right)={\displaystyle \frac{dy}{dt}}=y\left(1-y\right)\{xz\left[\left(\alpha -1\right)R_c-\left(1-\rho \right)\mu \lambda L_c\right]+x\left[\phi \left(F+R_e\right)+\left(1-\rho \right)\mu \lambda L_c+\left(\gamma +\theta -1\right)C_r^{\prime }\right]+\\ z\left[\gamma \left(C_r^{\prime }-C_r\right)+\mu \left(1-\lambda \right)\left(1-\rho \right)L_c\right]-\mu \left(1-\lambda \right)\left(1-\rho \right)L_c-\gamma C_r^{\prime }-R_e\}\end{array}$$

(7)

The expected payoff for a resident choosing the “supporting” strategy is $E_{z1}$, the expected payoff for the “dissenting” strategy is $E_{z2}$, and the replication dynamics equation for residents $F_r\left(z\right)$ choosing the “supporting” strategy is given in the equation:

$$E_{z1}=x\left\{y\alpha R_r+\left(1-y\right)\left[R_r-\left(1-\phi \right)R_e\right]\right\}+\left(1-x\right)\left[y{R}_r+\left(1-y\right)\left(R_r-R_e\right)\right]$$

(8)

$$\begin{array}{c}{E}_{z2}=x\left\{y\left[R_r-p_1\left(L_r-\tau L_g-\upsilon L_c\right)\right]+\left(1-y\right)\left[R_r-\left(1-\phi \right)R_e-p_3\left(L_r-\tau L_g-\upsilon L_c\right)\right]\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\left(1-x\right)\left\{y\left[R_r-p_2\left(L_r-\tau L_g-\upsilon L_c\right)\right]+\left(1-y\right)\left[R_r-p_4\left(L_r-\tau L_g-\upsilon L_c\right)-R_e\right]\right\}\end{array}$$

(9)

$$\begin{array}{c}{F}_r\left(z\right)={\displaystyle \frac{dz}{dt}}=z\left(1-z\right)\{xy\left[\left(\alpha -1\right)R_r+\left(1-\rho \right)\mu \lambda \left(\tau L_g+\nu L_c-L_r\right)\right]+x\left(1-\rho \right)\left(1-\mu \right)\lambda (\tau L_g+\nu L_c-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} L_r)+y\left(1-\rho \right)\left(1-\lambda \right)\mu \left(\tau L_g+\nu L_c-L_r\right)-\left[1-\left(1-\rho \right)\left(1-\mu \right)\left(1-\lambda \right)\right]\left(\tau L_g+\nu L_c-L_r\right)\}\end{array}$$

(10)

4.3. Equilibrium Analysis of Evolutionary Game

Based on the above analysis, the three-dimensional dynamical system of the evolutionary game can be obtained by $F_g\left(x\right)$, $F_c\left(y\right)$ and $F_r\left(z\right)$. As a multi-group game should reach a strict Nash equilibrium [48], let $F_g\left(x\right)=0$, $F_c\left(y\right)=0$ and $F_r\left(z\right)=0$, and then eight equilibrium points can be obtained. Friedman’s method [39] enables the analytical determination of the stability of a differential system’s equilibrium point by examining the eigenvalues of the system’s Jacobian matrix. The Jacobian matrix of this system is presented as follows:

$$J=\left[\begin{array}{ccc}{\displaystyle \frac{\partial F_g\left(x,y,z\right)}{\partial x}}& {\displaystyle \frac{\partial F_g\left(x,y,z\right)}{\partial y}}& {\displaystyle \frac{\partial F_g\left(x,y,z\right)}{\partial z}}\\ {\displaystyle \frac{\partial F_c\left(x,y,z\right)}{\partial x}}& {\displaystyle \frac{\partial F_c\left(x,y,z\right)}{\partial y}}& {\displaystyle \frac{\partial F_c\left(x,y,z\right)}{\partial z}}\\ {\displaystyle \frac{\partial F_r\left(x,y,z\right)}{\partial x}}& {\displaystyle \frac{\partial F_r\left(x,y,z\right)}{\partial y}}& {\displaystyle \frac{\partial F_r\left(x,y,z\right)}{\partial z}}\end{array}\right]=\left[\begin{array}{ccc}{\lambda }_{11}& {\lambda }_{12}& {\lambda }_{13}\\ {\lambda }_{21}& {\lambda }_{22}& {\lambda }_{23}\\ {\lambda }_{31}& {\lambda }_{32}& {\lambda }_{33}\end{array}\right]$$

(11)

When the eight pure strategy equilibrium points of the evolutionary system are substituted into the Jacobian matrix, the eigenvalues ${\lambda }_{11}$, ${\lambda }_{22}$, ${\lambda }_{33}$ are obtained. Post-substitution, the remaining matrix elements are zeros, except for ${\lambda }_{11}, {\lambda }_{22}, {\lambda }_{33}$ which are the eigenvalues. Stability analysis is then conducted on these equilibrium points. An equilibrium point is considered an evolutionarily stable strategy (ESS) if all its eigenvalues are less than zero. Conversely, if at least one eigenvalue is greater than zero, the point is unstable. The stability analysis for each equilibrium point is detailed in

Table 4. Stability analysis of the equilibrium point.

Equilibrium Point	Jacobian Matrix Eigenvalues	Stable Condition
	${\mathit{\lambda }}_{11}, {\mathit{\lambda }}_{22},{\mathit{\lambda }}_{33}$
$E_1\left(0,0,0\right)$	$\phi F+\left(p_4-p_3\right)L_g-\beta C_r^{\prime }-C_g,$ $\left(p_4-p_2\right)L_c-\gamma C_r^{\prime }-R_e,$ $-p_4\left(\tau L_g+\nu L_c-L_r\right)$	$\phi F+\left(p_4-p_3\right)L_g<\beta C_r^{\prime }+C_g,$ $\left(p_4-p_2\right)L_c<\gamma C_r^{\prime }+R_e,$ $\tau L_g+\nu L_c-L_r>0$
$E_2\left(1,0,0\right)$	$\beta C_r^{\prime }+C_g-\phi F-\left(p_4-p_3\right)L_g,$ $\phi F+\left(p_3-p_1\right)L_c-\left(1-\theta \right)C_r^{\prime }-\left(1-\phi \right)R_e,$ $-p_3\left(\tau L_g+\nu L_c-L_r\right)$	$\beta C_r^{\prime }+C_g<\phi F+\left(p_4-p_3\right)L_g,$ $\phi F+\left(p_3-p_1\right)L_c<\left(1-\theta \right)C_r^{\prime }+\left(1-\phi \right)R_e,$ $\tau L_g+\nu L_c-L_r>0$
$E_3\left(0,1,0\right)$	$\left(p_2-p_1\right)L_g-\theta C_r^{\prime }-C_g,$ $\gamma C_r^{\prime }+R_e-\left(p_4-p_2\right)L_c,$ $-p_2\left(\tau L_g+\nu L_c-L_r\right)$	$\left(p_2-p_1\right)L_g<\theta C_r^{\prime }+C_g,$ $\gamma C_r^{\prime }+R_e<\left(p_4-p_2\right)L_c,$ $\tau L_g+\nu L_c-L_r>0$
$E_4\left(0,0,1\right)$	$\phi F-\beta C_r-C_g,-\gamma C_c-R_e,$ $p_4\left(\tau L_g+\nu L_c-L_r\right)$	$\phi F<\beta C_r+C_g,$ $\tau L_g+\nu L_c-L_r<0$
$E_5\left(1,1,0\right)$	$\theta C_r^{\prime }+C_g-\left(p_2-p_1\right)L_g,$ $\left(1-\theta \right)C_r^{\prime }+\left(1-\phi \right)R_e-\phi F-\left(p_3-p_1\right)L_c,$ $\left(\alpha -1\right)R_r-p_1\left(\tau L_g+\nu L_c-L_r\right)$	$\theta C_r^{\prime }+C_g<\left(p_2-p_1\right)L_g,$ $\left(1-\theta \right)C_r^{\prime }+\left(1-\phi \right)R_e<\phi F+\left(p_3-p_1\right)L_c,$ $\left(\alpha -1\right)R_r<p_1\left(\tau L_g+\nu L_c-L_r\right)$
$E_6\left(0,1,1\right)$	$\left(\alpha -1\right)R_g-C_g-\theta C_r,\gamma C_r+R_e,$ $p_2\left(\tau L_g+\nu L_c-L_r\right)$	Unstable point
$E_7\left(1,0,1\right)$	$\beta C_r+C_g-\phi F,$ $\phi F+\left(\alpha -1\right)R_c-\left(1-\theta \right)C_r-\left(1-\phi \right)R_e,$ $p_3\left(\tau L_g+\nu L_c-L_r\right)$	$\beta C_r+C_g<\phi F,$ $\phi F+\left(\alpha -1\right)R_c<\left(1-\theta \right)C_r+\left(1-\phi \right)R_e,$ $\tau L_g+\nu L_c-L_r<0$
$E_8\left(1,1,1\right)$	$C_g+\theta C_r-\left(\alpha -1\right)R_g,$ $\left(1-\phi \right)R_e+\left(1-\theta \right)C_r-\phi F-\left(\alpha -1\right)R_c,$ $p_1\left(\tau L_g+\nu L_c-L_r\right)-\left(\alpha -1\right)R_r$	$C_g+\theta C_r<\left(\alpha -1\right)R_g,$ $\left(1-\phi \right)R_e+\left(1-\theta \right)C_r<\phi F+\left(\alpha -1\right)R_c,$ $p_1\left(\tau L_g+\nu L_c-L_r\right)<\left(\alpha -1\right)R_r$

.

When considering the long-term collaborative governance of urban community renewal construction and operation stages in this study, the core contradiction lies in the lack of engineering quality issues and regulatory mechanisms after the completion of community renewal projects. Residents’ supervision behavior tends to protect their own rights and interests through rectification demands, while the government and companies will not be “kidnapped” in decision-making, which may result in residents obtaining excessive compensation. In other words, this goes against the original intention of collaborative governance. Therefore, it is necessary to exclude or avoid atypical (undesirable) situations such as $\tau L_g+\nu L_c-L_r>0$.

The stability analysis of the eight equilibrium points, as detailed in Table 4, reveals that three points $E_4\left(0,0,1\right)$, $E_7\left(1,0,1\right),$ and $E_8\left(1,1,1\right)$ can become ESS under certain conditions. These points are influenced by factors such as collaborative advantage, speculative benefits, and coordination costs, which affect the strategic decisions of the participants. Reflecting on the developmental history of urban renewal in China and Western countries, three distinct governance scenarios can be identified: government-led scenario, market-led scenario, and multi-participated scenario. This section delves into analyzing the stabilization strategies of the evolutionary game within three varied scenarios:

(1)

Government-led scenario. Early urban renewal was governed by a government-led model, prioritizing basic livelihoods and social welfare with strong governmental leadership and investment, yet lacking in management and disregarding social and market forces. The government, as the main implementer and funder, favored “positive action” for smooth project execution, while companies engaging in direct government contracts, driven by economic interests, favored an “ignoring demands” strategy. Residents, facing information asymmetry and limited government empowerment, have minimal influence on government decisions regarding urban community renewal. As beneficiaries of government welfare policies, they tend to adopt a strategy of “supporting”. This scenario corresponds to the equilibrium point $E_7\left(1,0,1\right)$. In this context, the equilibrium point $E_7\left(1,0,1\right)$ from Table 4 becomes stable under two conditions: ① When government fines on companies exceed its regulatory and coordination costs ($\beta C_r+C_g<\phi F$), indicating strict penalties on non-compliance and low resident coordination costs. ② When the companies’ net profit from profit-centric strategies outstrips the benefits of collaborative governance ($\left(\alpha -1\right)R_c-\left(1-\theta \right)C_r<\left(1-\phi \right)R_e-\phi F$), reflecting the early phase of urban renewal dominated by government, with high profits from speculation and less visible benefits of cooperation.

(2)

Market-led scenario. The reform of land and housing systems has led to increased private investment and market dominance, focusing more on economic than public interests. The government now mainly offers preferential policies and limited initial funding to companies, reducing financial burdens in urban renewal projects and adopting a “negative action” approach. Companies, driven by profit, dominate projects with commercial developments, often overlooking social responsibilities and favoring an “ignoring demands” strategy. This has marginalized residents, evidenced by gentrification and displacement, compelling them to adopt a “supporting” strategy. This situation aligns with equilibrium point $E_4\left(0,0,1\right)$, as per Table 4. For $E_4\left(0,0,1\right)$ to be stable, the government’s regulatory fines must be less than its regulatory costs plus coordination costs ($\phi F<\beta C_r+C_g$), reflecting minimal government intervention, over-reliance on companies for project construction, and resident marginalization.

(3)

Multi-participatory scenario (ideal stabilization point): For high-quality, human-centered urban development, community residents have emerged as the third balancing force in urban community renewal, alongside the government and companies, with their interests and needs increasingly considered within the governance system. The government focuses on coordination and promotion, aiming for “positive action” to advance public interests and improve living standards, thus enhancing its reputation. Companies, as major investors, participate in collaborative governance, gaining collaborative benefits and boosting their social responsibility, tending to “value demands”. Residents exercise participatory rights through local committees and organizations, aiming for conflict mediation and joint governance, opting for “supporting”. This model corresponds to equilibrium point $E_8\left(1,1,1\right)$ in Table 4. To be stable, two conditions must be met: ① the government’s costs in active participation must be offset by the benefits of collaborative governance ($C_g+\theta C_r<\left(\alpha -1\right)R_g$), indicating active involvement and significant synergistic advantages. ② the net profit companies’ gain from profit-centric strategies must be lower than the benefits of collaborative governance ($\left(1-\phi \right)R_e-\phi F<\left(\alpha -1\right)R_c-\left(1-\theta \right)C_r$), reflecting reduced profit margins and increased synergies due to active government and resident involvement.

5. Numerical Simulation and Analysis

5.1. Data and Parameters

In the study of evolutionary games, numerical simulation can describe the evolution process of strategy selection among game subjects more graphically. An urban renewal project in Tianjin, which includes community renewal, is selected as the case background for calculating the initial values of the above variables. The project covers 825,400 square meters of floor space in old districts, with a construction investment of CNY 149.73 million and an average of CNY 250 per square meter, focusing on issues such as unblocking and widening traffic arteries, replenishing car-link charging facilities, and repairing old and dilapidated floor surfaces. Based on this context, the model parameters are calibrated as follows. Basic benefits and costs are scaled proportionally according to the actual financial dimensions of the Tianjin case and typical distribution patterns observed in Chinese urban renewal practice [28,49,50]. For instance, corporate speculative benefits $R_e$ is estimated considering potential extra profit margins from reduced compliance, often ranging between 15–50% of base profit. Parameters implying qualitative mechanisms—including the collaborative advantage coefficient α, participation effect coefficient β, complaint effect γ, and resident tolerance threshold θ—are informed through field survey data and stakeholder interviews conducted within Tianjin communities, based on relevant theoretical research [51,52]. These reflect empirical realities; for example, α = 1.5 captures efficiency improvements from multi-party coordination, consistent with findings in collaborative governance literature, while θ = 0.5 aligns with the current situation in existing urban community renewal practices where the government contributes 40–60% of the shared costs (coordination costs). On this basis, initial values are established, as detailed in

Table 5. Initial parameter values for numerical simulation.

Parameter	Initial Value	Parameter	Initial Value	Parameter	Initial Value
$x$	0.4	$C_r$	1.0	$\rho$	0.5
$y$	0.4	$C_r^{\prime }$	2.0	$\lambda$	0.4
$z$	0.4	$F$	2.5	$\mu$	0.4
$R_g$	10	$L_g$	10	$\phi$	0.8
$R_c$	10	$L_c$	8	$\theta$	0.5
$R_r$	5	$L_r$	5	$\tau$	0.2
$R_e$	5	$\alpha$	1.5	$\upsilon$	0.3
$C_g$	1.0	$\beta$	1.2
$C_c$	2.0	$\gamma$	1.5

.

Utilizing Python 3.10, the study simulates the dynamic evolution of strategic decisions under various initial states for the government, companies, and residents. The evolution path of the game system, as derived from the simulation, is illustrated in Figure 2 below, corroborating the stability analysis results of the equilibrium points in Table 4.

The analysis in Figure 2 shows that, in a three-dimensional system, paths from different starting points converge at two stable equilibrium points, $E_4\left(0,0,1\right)$ and $E_8\left(1,1,1\right)$. This suggests that the different initial probabilities of the strategies of the three parties in the game have different evolutionary directions in the evolutionary game system. If the government initially leans towards negative action, the strategy evolves to {negative action, ignoring demands, supporting}. In contrast, a positive action bias leads to the ideal equilibrium of {positive action, valuing demands, supporting}.

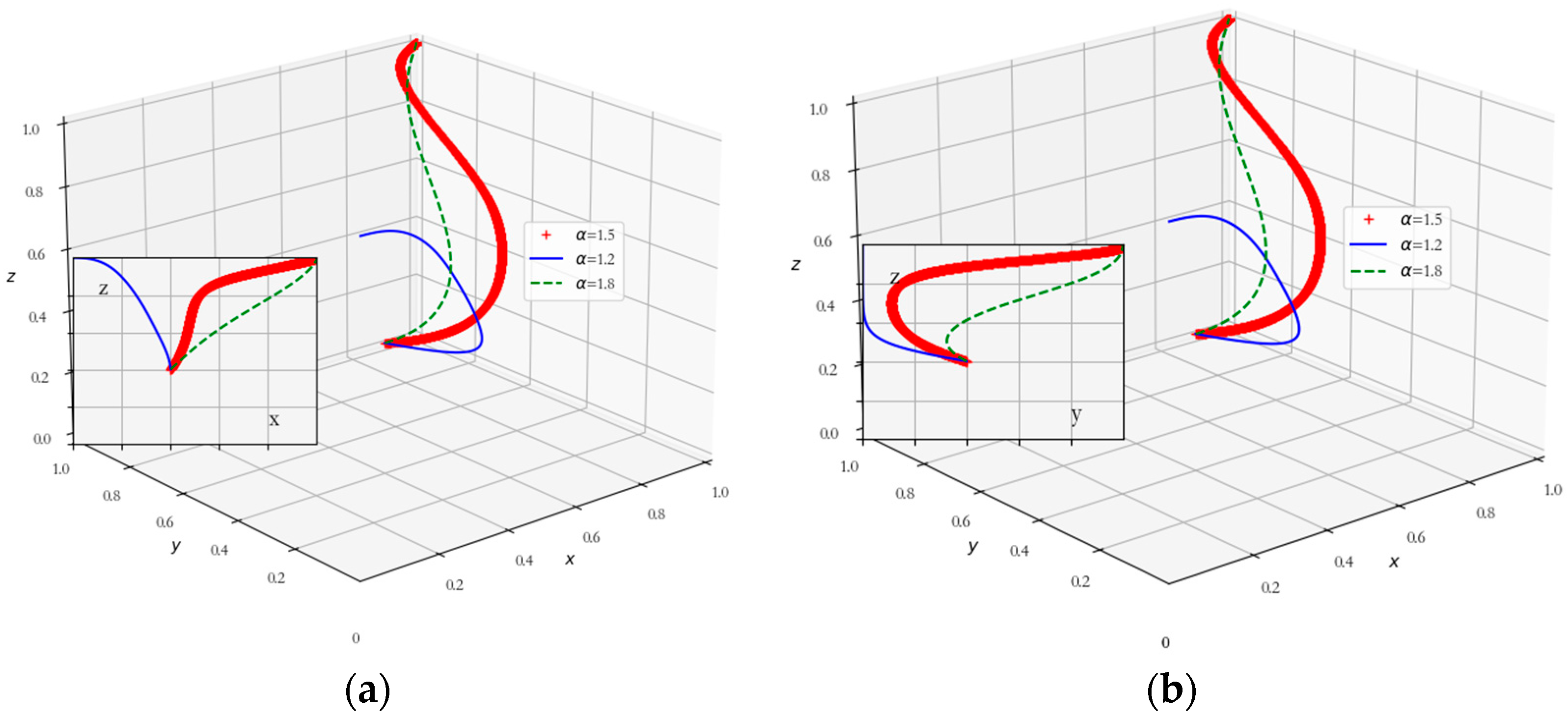
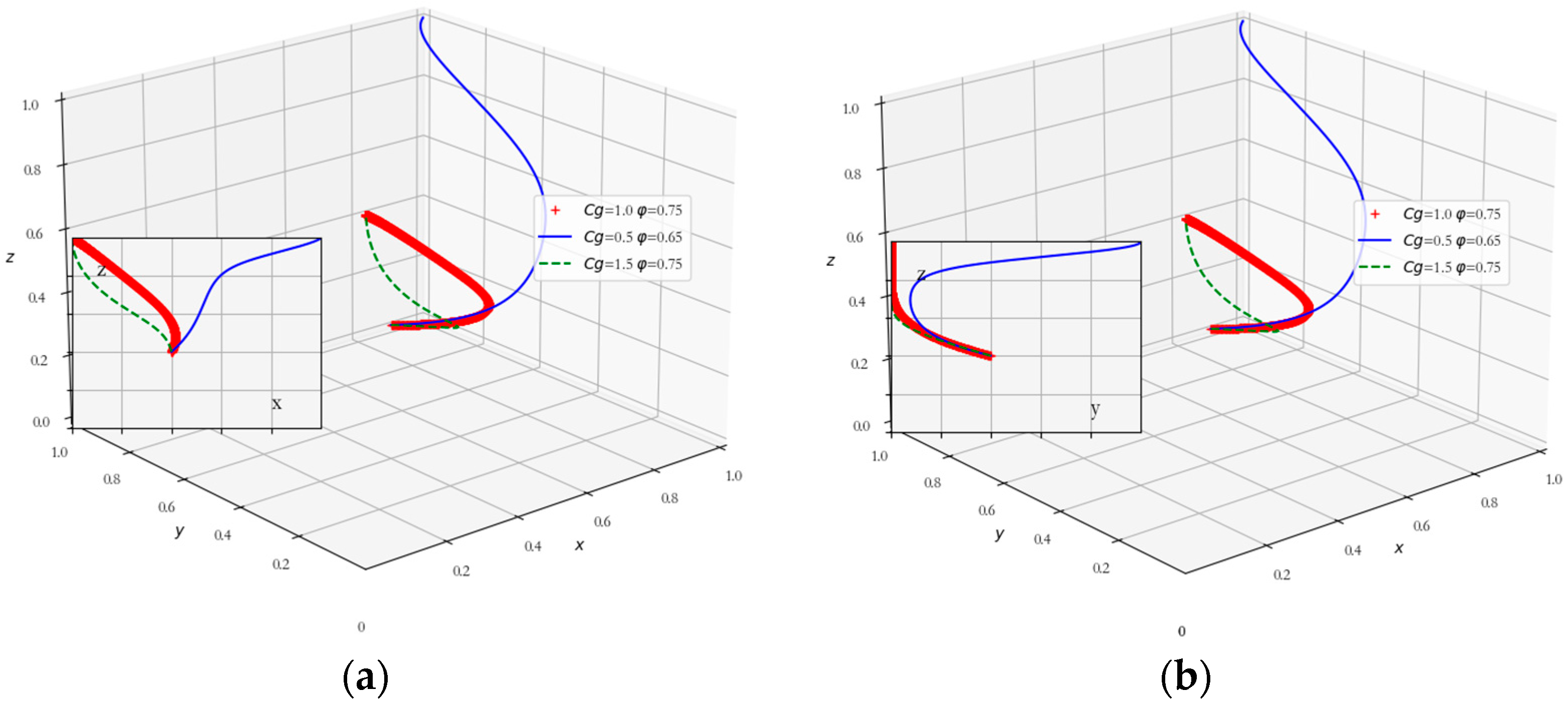
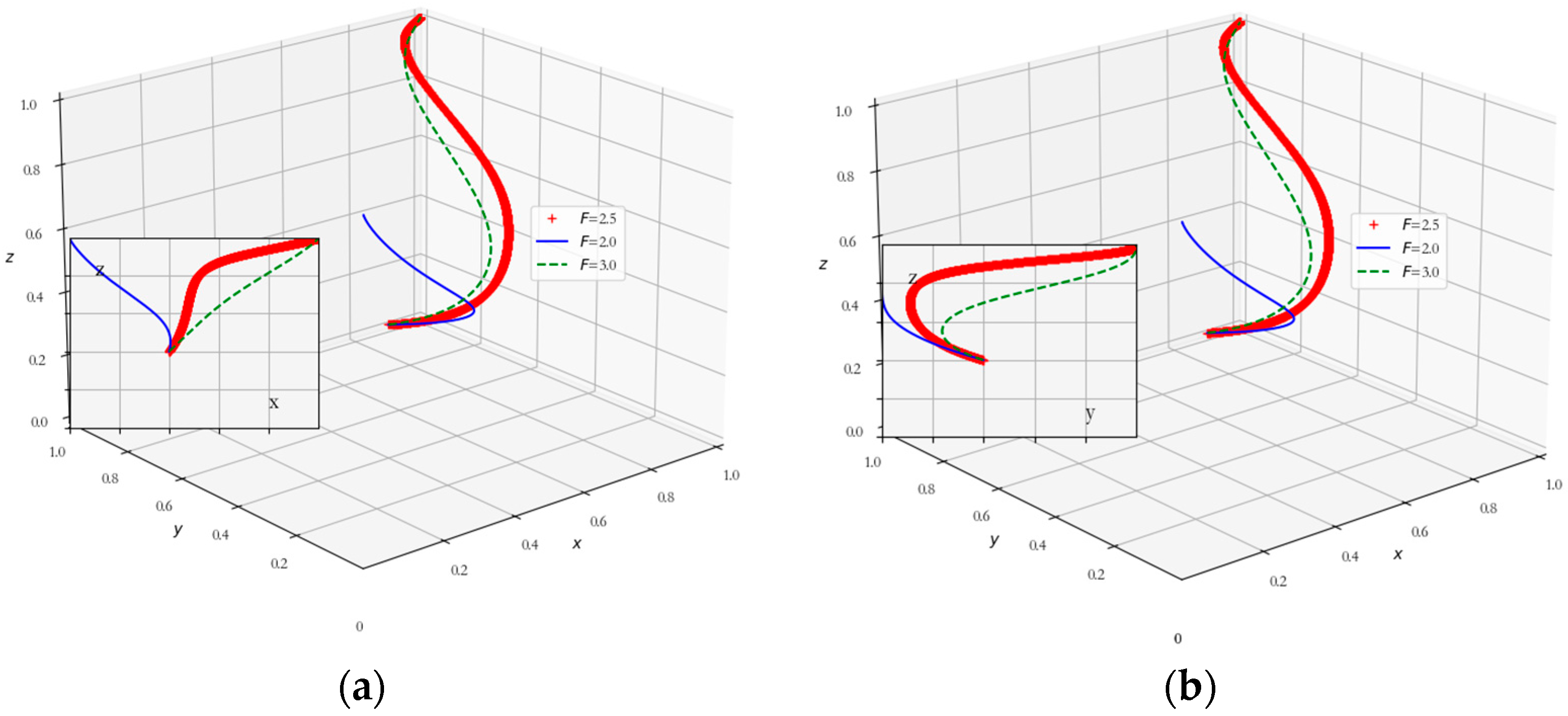
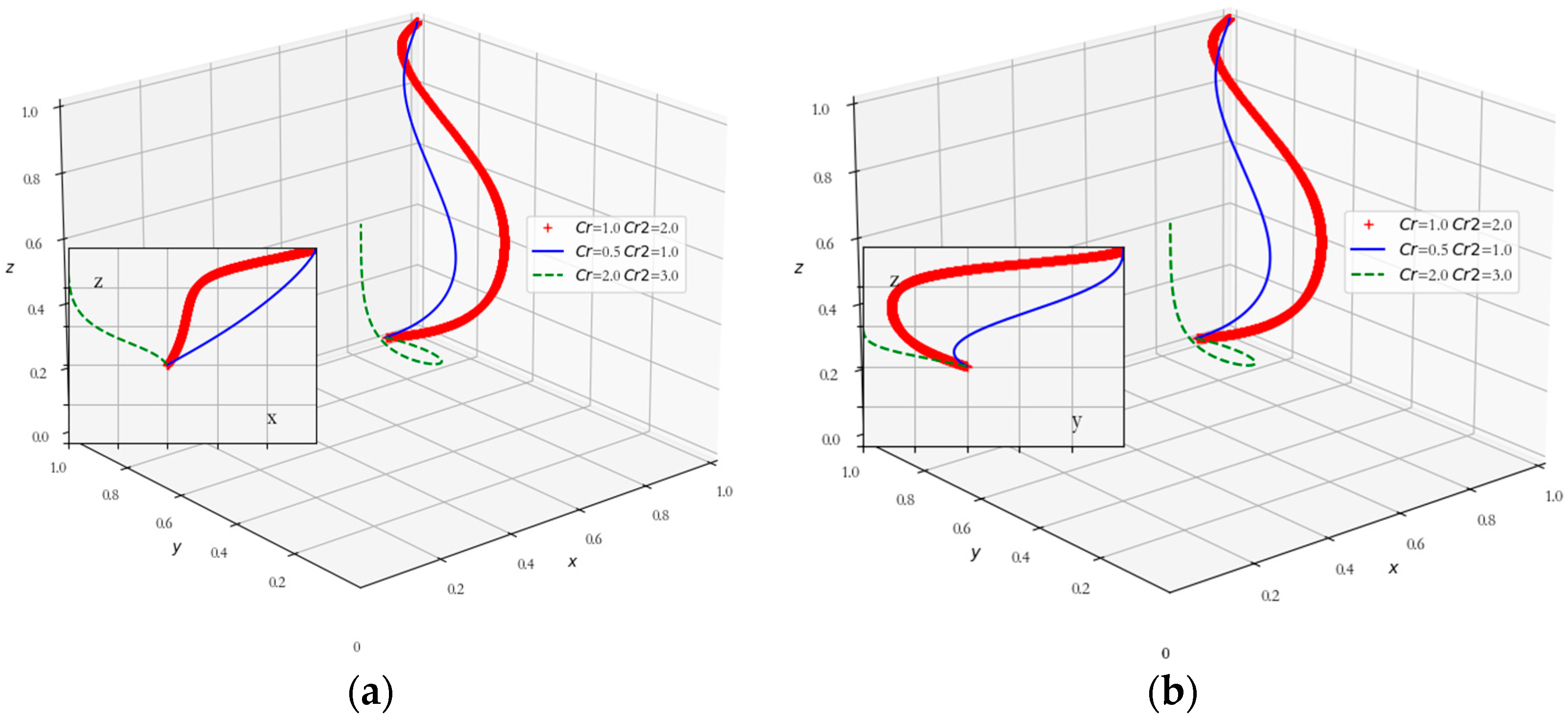
5.2. Collaborative Advantage Effects on Evolutionary Game Models

This study explores the impact of collaborative advantage on the evolutionary game process and outcomes of urban community renewal. To do so, the gain coefficients of collaborative governance, denoted by $\alpha$, are assigned values of 1.5, 1.2, and 1.8, respectively. These values are then incorporated into the replicator dynamic equation set and evolved over a period of 100 iterations. The outcomes of this numerical simulation are depicted in Figure 3.

Figure 3 illustrates that, during the game model’s evolution towards stabilization, an enhanced collaborative advantage effect significantly influences the strategic decisions of the government and companies, encouraging a shift towards collaborative governance. Specifically, when $\alpha \ge 1.5$, the probability of government active engagement rises on average compared to $\alpha =1.2$ scenarios, while companies’ willingness to prioritize public welfare increases—reflecting the “cost–benefit amplification” mechanism observed in urban renewal cases such as Tianjin’s subsidized coordination model. The floor plan indicates that, as the collaborative governance gain coefficient $\alpha$ increases, there is a corresponding rise in the probability of the government engaging actively and the companies considering public welfare, eventually stabilizing at the equilibrium solution $E_8\left(1,1,1\right)$. This convergence pattern aligns with evolutionary game theory on public goods provision, where $\alpha$ above critical thresholds (e.g., α > 1.2) accelerates collective action by aligning marginal benefits with collaborative costs [53]. Conversely, if the collaborative advantage in urban community renewal is insufficient, $\alpha$ is below a certain threshold, and the system evolves towards $E_4\left(0,0,1\right)$. This divergence occurs because low $\alpha$ values fail to offset the opportunity costs of collaboration, as demonstrated in industrial cluster transitions and lead to fragmented governance [17]. The threshold α = 1.2 thus serves as a critical tipping point, below which individual rationality dominates collective optimization.

Therefore, it is crucial to leverage the unique strengths of each stakeholder, aligning them towards a common goal to maximize the collaborative advantage and enhance overall governance capacity. Policy interventions that elevate $\alpha$—such as government subsidies covering ≥40% of coordination costs or institutionalizing multi-party negotiation platforms—can push $\alpha$ beyond the 1.5 threshold, enabling sustained convergence to $E_8\left(1,1,1\right)$. Specifically, the government should focus on organizing, coordinating, and managing urban community renewal governance, intensifying supervision throughout the project. Companies should actively consider public interests, uphold social responsibility, and respect residents’ demands. Residents, meanwhile, can capitalize on their “local knowledge” in shaping their communities.

5.3. Impact of Speculative Benefits on Evolutionary Game Models

Speculative benefits, in the context of urban community renewal projects, is defined as revenue acquired irregularly, often by companies through reduced management or material expenses at the expense of certain residents’ interests due to profit-centric motives. To examine the impact of such extra income derived from companies’ “ignoring demands” on the urban community renewal’s tripartite evolutionary game, this study assigns values of 5, 4, and 6 to the speculative benefits parameter $R_e$. The outcomes of this numerical simulation are depicted in Figure 4.

Analysis of Figure 4 in the evolutionary game model shows that reducing companies’ extra income from profit-seeking accelerates the shift towards collaborative governance $E_8\left(1,1,1\right)$. Specifically, when $R_e$ ≤ 4 (≤40% of $R_c$), companies’ willingness to prioritize public welfare increases compared to $R_e$ = 6 scenarios, as lower opportunistic returns diminish the appeal of short-term rent-seeking. Conversely, as $R_e$ rises to 6 (60% of $R_c$), companies’ inclination to ignore demands intensifies despite potential penalties, mirroring the “dominant strategy equilibrium” identified in construction supervision studies where speculative behavior becomes the dominant strategy for participants [54]. This aligns with principal-agent theory in public projects, where information asymmetry enables companies to exploit regulatory gaps when $R_e$ exceeds the opportunity costs of penalties.

Therefore, the government should implement strict quality and spatial standards from the bidding phase of urban renewal projects, clearly defining company roles and responsibilities within the governance framework, and capping profit margins to discourage ignoring demands. Meanwhile, residents should vigilantly oversee companies, reporting actions against public interest to prevent hidden profiteering. For example, resident-led oversight committees raise the reputational cost of opportunism by 40% in a Chengdu’s community renewal project.

5.4. Impact of Government Regulation on Evolutionary Game Models

Government regulation plays a crucial role in urban renewal projects, especially during their implementation and operation phases. An active government stance involves investing in regulatory costs, and, with a certain probability, detecting and penalizing companies for speculative behaviors. Such fines increase the government’s benefits while decreasing those of the companies. The three critical variables in this context are the cost of regulation $C_g$, the probability of punishment $\phi$, and the fines imposed by the government on companies$F$. Given that the likelihood of detecting and punishing companies’ speculative actions is directly linked to the government’s regulatory expenditure $C_g$, this study investigates the impact of government regulatory investment on the urban community renewal’s tripartite evolutionary game. At the same time, the regulatory expenditure $C_g$ is assigned values of 1.0, 0.5, and 1.5. The probability of punishment $\phi$ is set in two groups, with values, respectively, assigned as 0.8, 0.75, 0.85, and 0.75, 0.65, 0.75. The results of this numerical simulation are presented in Figure 5 and Figure 6.

Figure 5 and Figure 6 demonstrate that, in the evolution from equilibrium $E_8\left(1,1,1\right)$ to $E_4\left(0,0,1\right)$ in the game model, an increase in regulatory cost $C_g$ and punishment probability $\phi$ directly leads to the government adopting a more passive strategy to reduce costs. This shift indirectly influences companies to choose a profit-seeking strategy, resulting in a transition between equilibrium solutions. The comparison of Figure 5 and Figure 6 shows that, at a fixed government regulatory cost of 1.0, a higher average punishment probability $\phi$ more effectively leads to the collaborative governance equilibrium $E_8\left(1,1,1\right)$. This suggests that the efficiency of regulatory cost utilization, $\phi /C_g$, significantly influences the evolution of stable strategies among stakeholders.

Consequently, the government should refine its regulatory framework and enhance administrative efficiency by lowering regulatory costs while maintaining high penalties for speculative actions, thereby improving regulatory cost efficacy. Companies are encouraged to actively adopt social responsibilities, beyond merely responding to incentives and penalties. Active community involvement in monitoring and reporting can also aid in reducing government supervision costs.

Beyond regulatory costs, the fines imposed on companies for speculative behaviors serve as an indicator of regulatory intensity. To assess the impact of government-imposed fines on the tripartite evolutionary game dynamics in urban community renewal, the fines $F$ are set at values of 2.5, 2.0, and 3.0. The outcomes of this numerical simulation are presented in Figure 7.

Figure 7 demonstrates that the evolution towards a collaborative governance scenario accelerates with an increase in these policy-mandated fines. The analysis of the plane diagrams reveals that the impact of fine fluctuations on company strategic decision is more pronounced than on governmental strategies. As the fine increases from its initial value, the risk cost associated with companies’ lopsided profit-seeking rises, prompting them to consider resident interests and public welfare to avoid penalties. However, beyond a certain threshold, the marginal effect of increasing fines diminishes.

This suggests that fines are a critical factor in achieving collaborative governance, necessitating a certain threshold to deter companies’ non-compliant profit-driven behaviors. Conversely, after reaching this threshold, the marginal impact of the fine wanes. Therefore, the government should not solely rely on increasing fines to achieve collaborative governance. It is also essential to enhance the efficiency of regulatory cost utilization, fostering a cooperative environment where multiple stakeholders work together and leverage each other’s strengths.

5.5. Impact of Coordination Costs on Evolutionary Game Models

The foundation of collaborative governance in urban community renewal lies in establishing mechanisms and platforms for symmetric information sharing and joint participation among stakeholders like the government, companies, residents, design units, and street authorities. The establishment and maintenance of these communication channels incur certain costs, which are borne by the government and companies. To explore the impact of coordination costs between the government, companies, and residents on the urban community renewal process, this study assigns values of 1.0, 0.5, and 2.0 to the coordination cost for residents supporting urban community renewal $C_r$, and values of 2.0, 1.0, and 3.0 to the coordination cost for residents opposing urban community renewal $C_r^{\prime }$. These values are then integrated into the replicator dynamic equation system, with the results of this numerical simulation presented in Figure 8.

Figure 8 demonstrates that lower coordination costs lead to stabilization at the ideal point of collaborative governance $E_8\left(1,1,1\right)$. Conversely, higher coordination costs tend to compel the government and companies to minimize resident participation in urban community renewal projects for cost-saving and process simplification, culminating in stabilization at a different equilibrium solution $E_4\left(0,0,1\right)$.

Therefore, the government needs to clearly define roles and responsibilities of all stakeholders through institutional design, ensuring effective conflict resolution and facilitating multi-party discussions. Companies should apply their construction and operational expertise, while understanding local culture and resident needs. Residents are encouraged to actively participate in community affairs, fostering collaboration, improving communication, and reducing coordination costs. Showcasing successful urban renewal pilot projects by the government and companies can serve as practical examples, building trust among residents and further enhancing communication efficiency.

5.6. Discussion and Practical Suggestions

Numerical simulations reveal key factors that promote active participation in collaborative urban governance: leveraging the respective strengths of all parties to create synergistic effects and anticipated benefits for companies during urban renewal processes. These findings highlight the importance of multi-stakeholder collaboration and the need to guide proactive public engagement, among other patterns. Based on these insights, this study proposes several practical recommendations for the process of community renewal.

Firstly, establish a comprehensive process supervision system. The “full cycle supervision + digital supervision” model can be adopted. For example, in practice, a “code supervision” platform is established to bind compliance requirements, resident feedback, and construction progress to the QR code system, achieving real-time warning and accountability for violations. However, this method faces the challenge of departmental fragmentation: the overlapping functions of planning, housing and urban management departments may lead to regulatory duplication or vacuum, requiring the government to coordinate various departments, clarify the leading units at each stage, introduce public participation mechanisms, ensure that public opinions at each stage can be accurately fed back to each department, and each department can make timely responses. At the same time, various methods such as third-party evaluation can be used to assess the update status of the community.

Secondly, it is essential to strengthen the information-sharing mechanism and enhance communication efficiency among the government, companies and residents. It is recommended to introduce a community planner system, where these planners serve as a bridge for policy interpretation and public communication. Community planners can help translate official policy language into expressions that are easily understandable to residents, promptly address public inquiries, and facilitate the accurate delivery and effective implementation of policy intentions. Meanwhile, a regular information feedback and coordination mechanism should be established. By leveraging community planners to collect and consolidate public opinions, and systematically relay them to the relevant departments, a virtuous cycle of “policy-feedback-optimization” can be promoted. This will further enhance the public’s sense of involvement and policy implementation capability, helping to foster a new model of governance characterized by multi-party collaboration, openness, and transparency.

In practice, a synergistic implementation of approaches—such as leveraging technology to reduce compliance costs and establishing more robust incentive and accountability mechanisms—can transform game-theoretic equilibria into sustainable means of governance.

6. Conclusions and Limitations

How to stimulate the active participation of stakeholders in urban community renewal and develop effective ways to improve collaboration for more efficient and equal decision making is an important issue in building sustainable cities and human settlements. This study delves into the roles and interests of key participants in urban community renewal. It determines the game strategies of each stakeholder within the collaborative process and constructs a tripartite evolutionary game model for the collaborative governance of urban community renewal. Taking into account practical scenarios, $E_8\left(1,1,1\right)$ is identified as the ideal ESS for collaborative governance. The study further employs Python 3.10 simulations to analyze the impacts of collaborative advantage, speculative benefits, government regulation, and coordination cost on the system’s evolution. The principal research findings include:

The strategic decisions of the game participants interact with each other, with different initial probabilities of strategies evolving into different ESS.

As speculative benefits increase, a shift from prioritizing public welfare to pursuing unilateral profit is observed, which necessitates vigilant monitoring and stringent regulation by all involved parties.

Higher government regulatory costs may lead to a preference for passive governmental actions. Concurrently, relaxation in government oversight and inadequate communication with residents can prompt companies to solely focus on profit maximization. Additionally, fines from regulatory penalties have been found to expedite progression towards collaborative governance.

The establishment of an effective multi-party participation system can mitigate coordination costs and prevent the government and companies from sidelining resident involvement in urban community renewal projects as a means of reducing coordination expenses and streamlining processes.

This study extends collaborative governance and game theory from the scenario of “large-scale demolition and construction” to the stage of stock renewal. Through quantitative analysis, it reveals the dynamic laws of the tripartite interest game between the government, companies, and residents in urban community renewal projects, providing theoretical support for balancing conflicting interests and constructing a collaborative governance framework. Incorporating the creation of collaborative advantages into the game theory system of urban renewal provides a new theoretical tool for explaining the transformation of multi-party cooperation from short-term compromise to long-term symbiosis. The research results provide actionable path guidance for solving the governance dilemma of “government hot, company cold, and resident resistance” in urban renewal. It helps to build a sustainable governance model of “benefit sharing--risk sharing” and promotes the paradigm shift from physical space transformation to social relationship reconstruction.

This study constructs a tripartite game model applicable to various community renewal projects. By adjusting the parameters, the model can be adapted to simulate the strategic interactions and behavioral evolution processes among the government, companies, and residents in community renewal initiatives under different modes or characteristics. Although this research strives to comprehensively depict the interaction mechanisms among the three major stakeholders in community renewal, it still has certain limitations that warrant further in-depth exploration in the future.

First, while the study proposes a generalized urban community renewal process requiring the participation of these three parties, offering a degree of universality, it does not detail the specific impacts of different renewal models such as government-led, market-led, or resident-initiated approaches. Future research could further analyze how these different renewal models influence governance mechanisms. Second, due to the one-off nature of projects and data ambiguities, the evaluation of benefits, costs, and losses in the tripartite evolutionary game model remains relatively simplified.

Moving forward, research could advance in several directions: firstly, conducting separate modeling and case analyses tailored to the specific characteristics of different types of community renewal projects; secondly, introducing a phased dynamic game framework to examine the strategic choices and evolutionary paths of each participant at different stages of community renewal projects; and thirdly, further refining the interaction mechanisms between any two of the three stakeholders—government, companies, and residents—to deepen the understanding of bilateral relationships and their impact on the overall game dynamics.