Spatial Heterogeneity of Traditional Villages in Southern Sichuan, China: Insights from GWR and K-Means Clustering
Abstract
1. Introduction
2. Materials and Methods
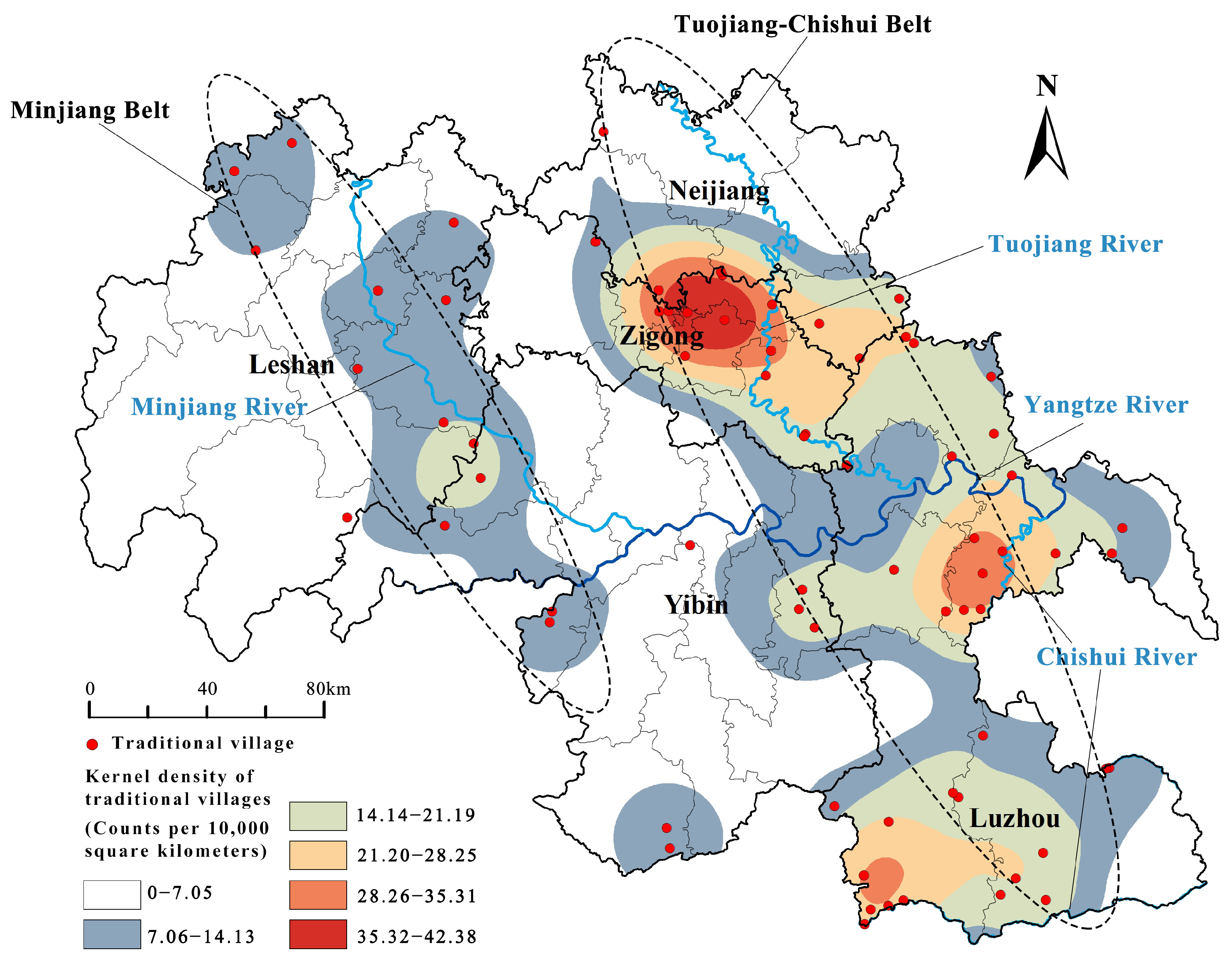
2.1. Study Area
2.2. Data Sources and Processing
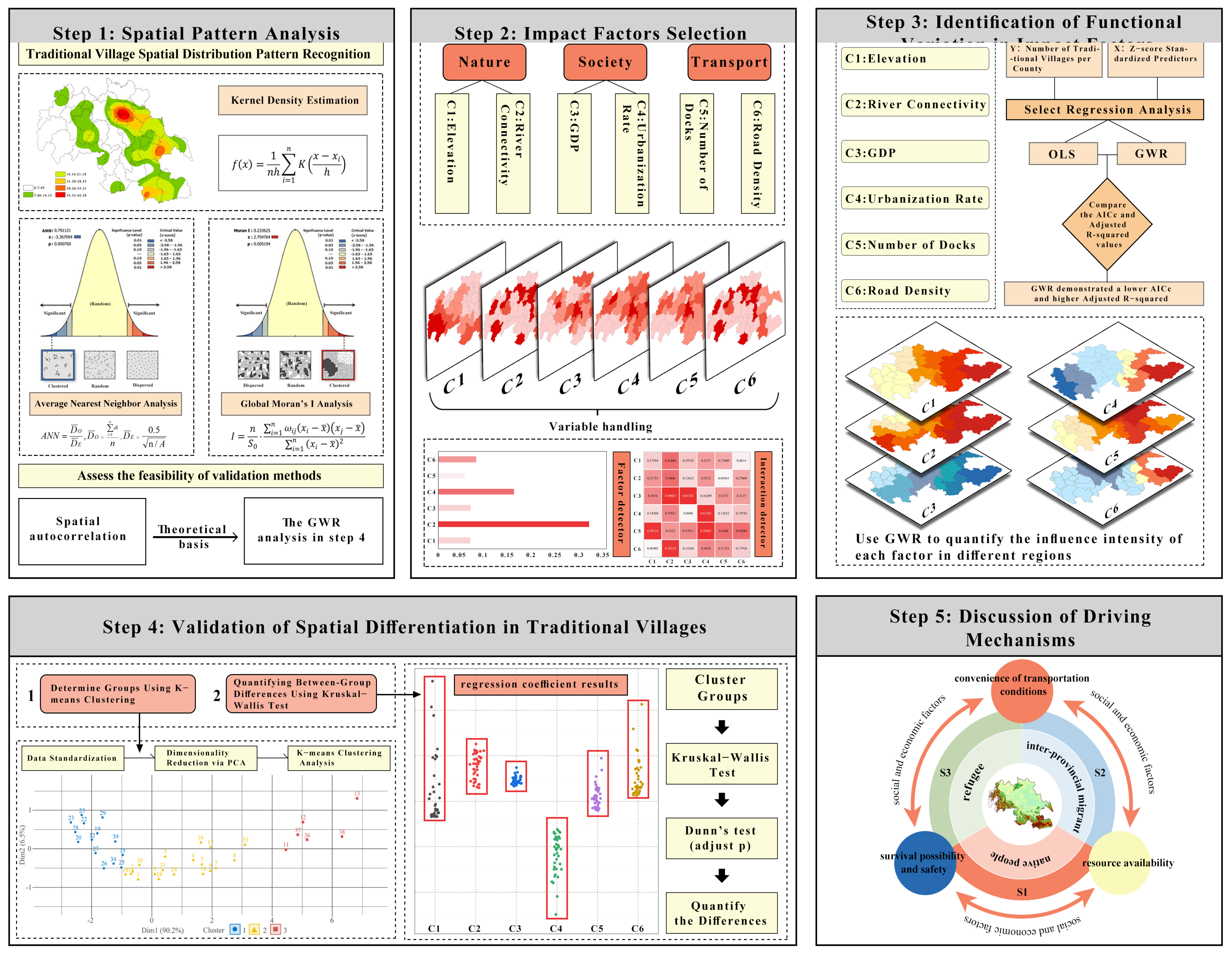
2.3. Methodological Framework
2.3.1. Average Nearest Neighbor Index
2.3.2. Kernel Density Estimation (KDE)
2.3.3. Global Moran’s I
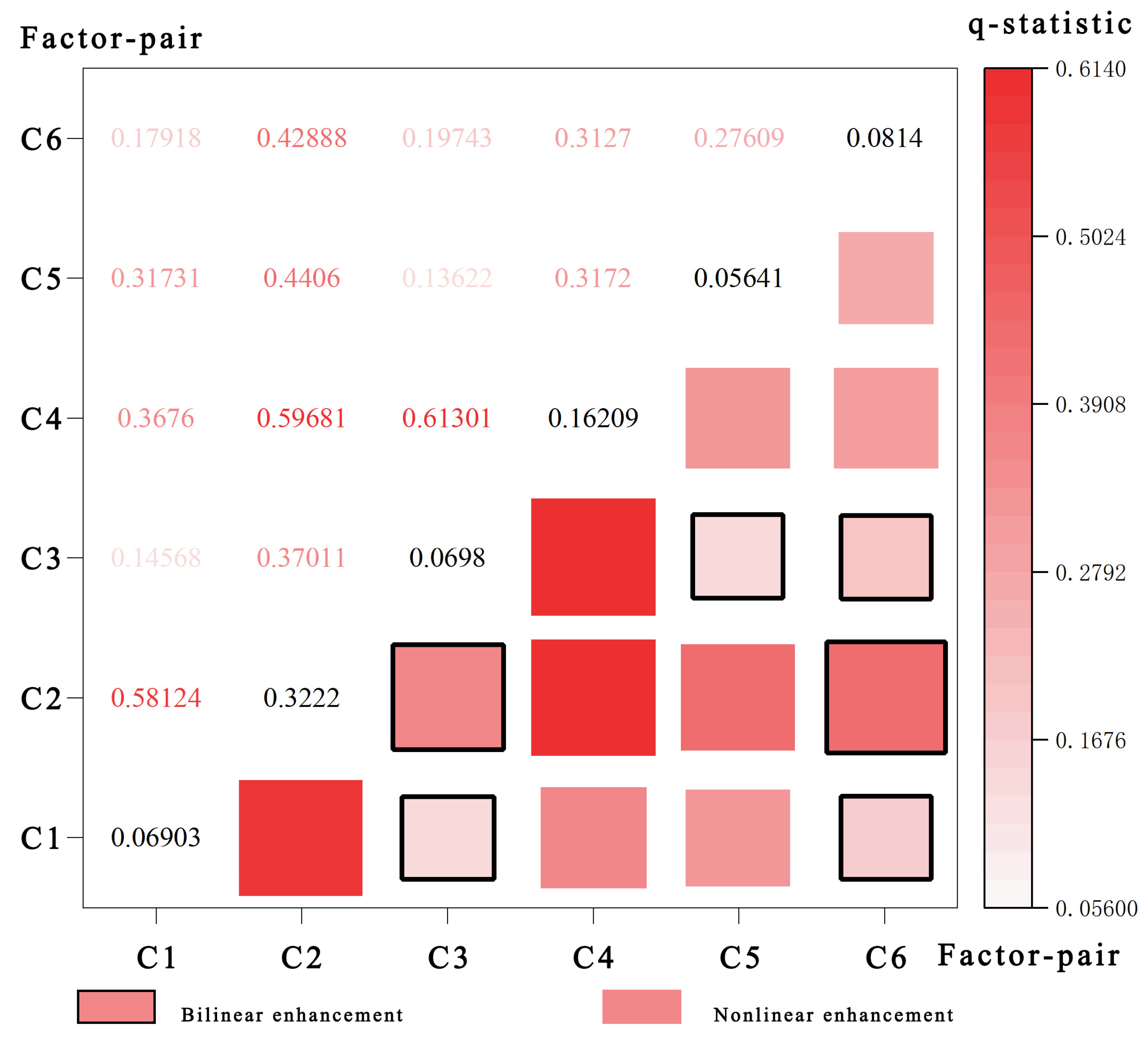
2.3.4. Geodetector
2.3.5. Geographically Weighted Regression (GWR)
2.3.6. K-Means Clustering Analysis
2.3.7. Differentiation Analysis (Kruskal–Wallis Test)
2.4. Indicator System
3. Results
3.1. Spatial Distribution Characteristics
3.1.1. Overall Spatial Distribution Characteristics
3.1.2. Distribution Density
3.2. Detection of Driving Factors Behind Spatial Heterogeneity
3.3. Results of Geographically Weighted Regression Analysis
3.3.1. Comparison of Preliminary Methods
3.3.2. Regression Results
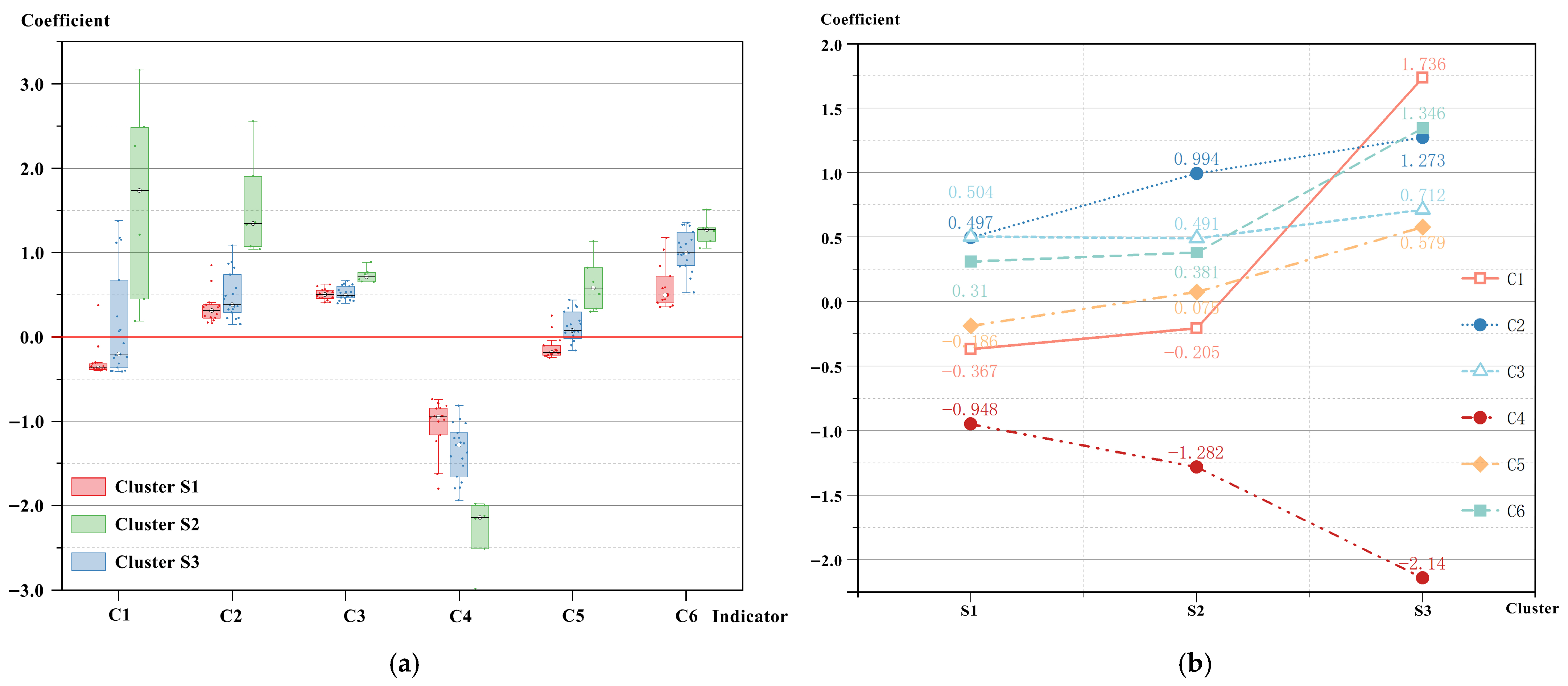
3.4. Clustering Analysis Results
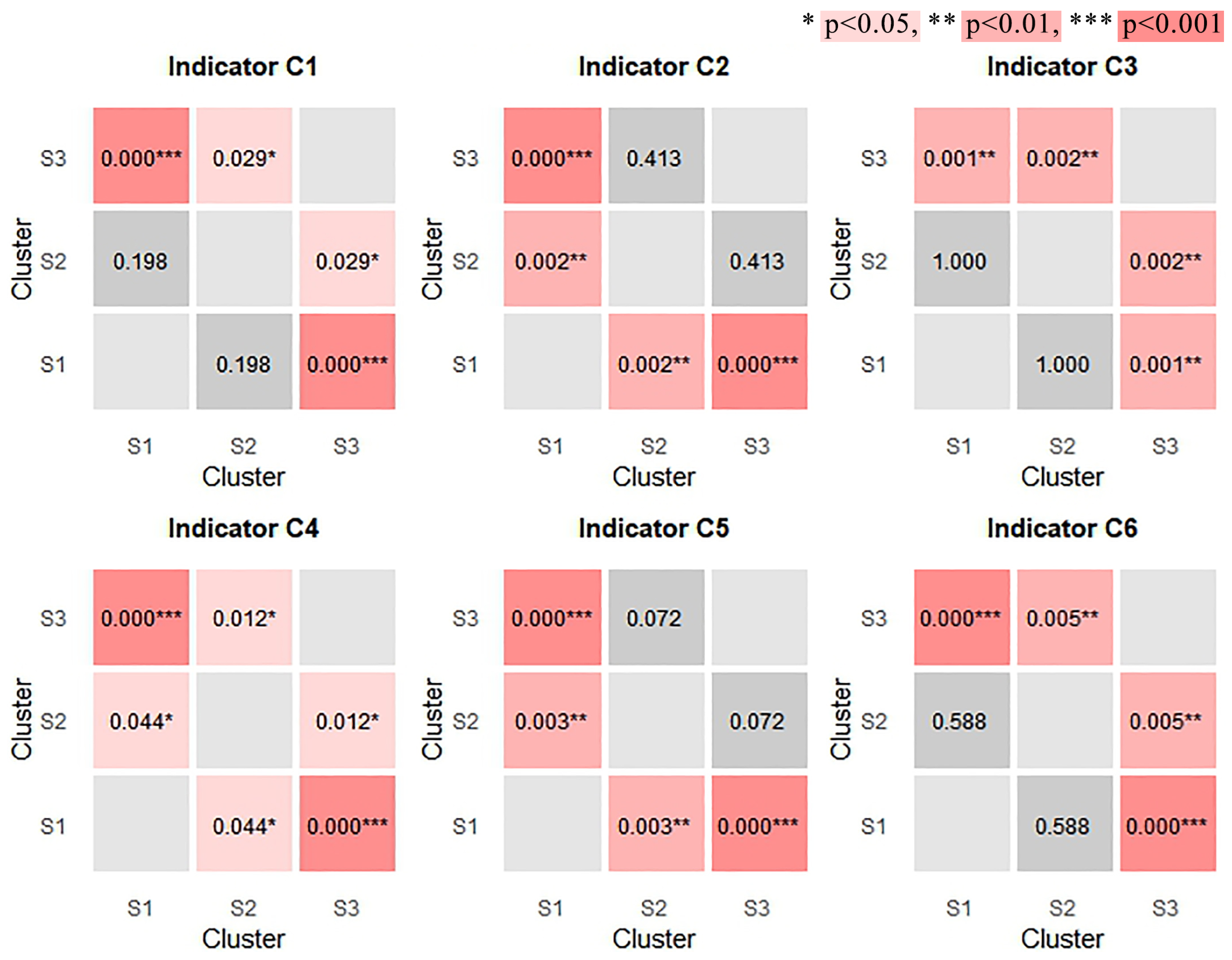
3.5. Difference Analysis
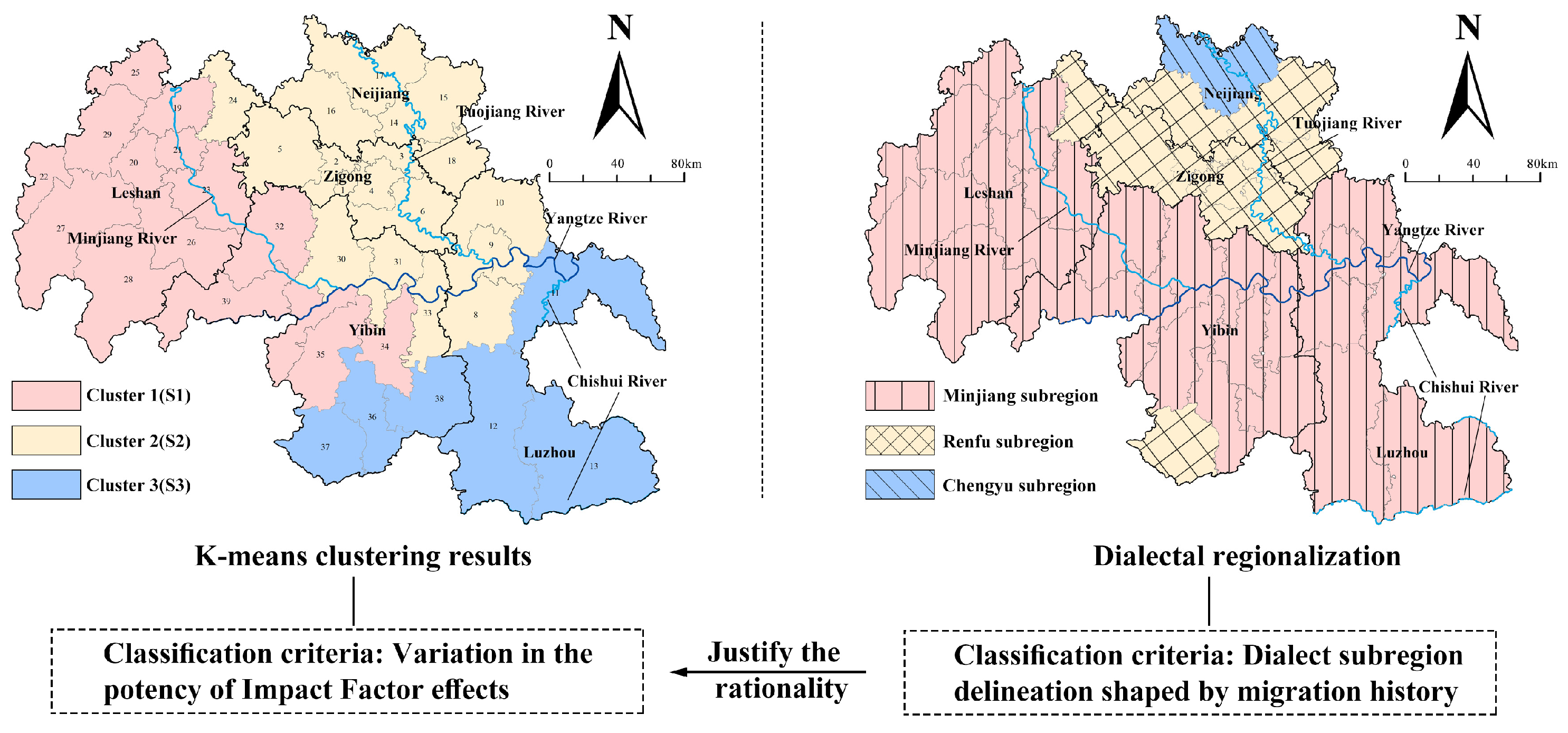
3.6. Verification of the Spatial Heterogeneity
4. Discussion
4.1. Mechanism of the Spatial Heterogeneity
4.1.1. Elevation
4.1.2. River Connectivity
4.1.3. GDP and Urbanization Rate
4.1.4. Number of Historical Docks
4.1.5. Road Density
4.2. Revisiting Spatial Patterns of Traditional Villages in Southern Sichuan
4.3. Protection and Utilization Strategies Based on Different Clusters
5. Conclusions
- (1)
- Methodological innovation: By integrating GWR, K-means clustering, and the Kruskal–Wallis test, this integrated approach uncovers the heterogeneous mechanisms underlying spatial patterns, enabling the development of a nuanced typology and tailored strategies.
- (2)
- Cluster typology: We proposed a meaningful classification, which translated the complex underlying mechanisms into a clear typology. The classification is constructed not only on spatial characteristics but also on historical and cultural contexts, offering deeper insights into the mechanisms of spatial heterogeneity.
- (3)
- Planning guidance: Beyond generic recommendations, this study proposed targeted conservation strategies—preserving the historical fabric of indigenous villages (S1), highlighting multicultural heritage in immigrant villages (S2), and improving transportation accessibility of refuge-type villages (S3)—thus enabling more efficient resource allocation by policymakers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
| Cluster | Included Districts and Counties |
|---|---|
| S1 | Leshan: Shizhong District, Shawan District, Wutongqiao District, Jinkouhe District, Jiajiang County, Qianwei County, Muchuan County, Ebian Yi Autonomous County, Mabian Yi Autonomous County, Emeishan City; Yibin: Xuzhou District, Pingshan County, Gao County, Changning County. |
| S2 | Leshan: Jingyan County; Luzhou: Jiangyang District, Naxi District, Longmatan District, Luxian County; Yibin: Cuiping District, Nanxi District, Jiang’an County; and the entire jurisdictions of Zigong and Neijiang; |
| S3 | Luzhou: Hejiang County, Xuyong County, Gulin County; Yibin: Gong County, Junlian County, Xingwen County. |
References
- Feng, J. The dilemmas and prospects of traditional villages: On traditional villages as another type of cultural heritage. Folk Cult. Forum 2013, 1, 7–12. [Google Scholar] [CrossRef]
- Guiding Opinions on Strengthening the Protection and Development of Traditional Villages. Available online: https://www.mohurd.gov.cn/gongkai/zc/wjk/art/2012/art_17339_212337.html (accessed on 23 August 2025).
- Ancient Villages in Southern Anhui–Xidi and Hongcun. Available online: https://whc.unesco.org/en/list/1002 (accessed on 23 August 2025).
- Niu, Y.; Wang, Y. Spatial differentiation pattern and influencing mechanisms of traditional villages in the Taihang Mountains based on the MGWR model. J. Arid Land Resour. Environ. 2024, 38, 87–96. [Google Scholar]
- Wang, X.; Fang, J. Analysis and countermeasures of homogenization in rural tourism products. Jiangsu Agric. Agric. Sci. 2020, 48, 14–19. [Google Scholar] [CrossRef]
- Bian, J.; Chen, W.; Zeng, J. Spatial distribution characteristics and influencing factors of traditional villages in China. Int. J. Environ. Res. Public Health 2022, 19, 4627. [Google Scholar] [CrossRef]
- Su, X.; Zhou, H.; Guo, Y.; Zhu, Y. Multi-dimensional influencing factors of spatial evolution of traditional villages in Guizhou Province of China and their conservation significance. Buildings 2024, 14, 3088. [Google Scholar] [CrossRef]
- Ding, K.; Ding, S. Spatial distribution and influencing factors of traditional villages in Shangrao City. South-Cent. Agric. Sci. Technol. 2025, 46, 194–197. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, S. Spatial distribution characteristics and formation mechanisms of traditional villages in the southern Taihang subregion. Agric. Technol. 2025, 45, 95–100. [Google Scholar] [CrossRef]
- Huang, X.; Si, Z.; Chen, X.; Li, J. Distribution characteristics and mechanisms of traditional villages influenced by the Qiantang River system. J. Southwest For. Univ. (Soc. Sci.) 2024, 8, 43–50. [Google Scholar]
- Chen, Y.; Li, R. Spatial distribution and type division of traditional villages in Zhejiang Province. Sustainability 2024, 16, 5262. [Google Scholar] [CrossRef]
- Guo, Y.; Zhai, S.; Huang, J.; Guo, H. Characteristics of the spatial structure of traditional villages in the Xinjiang Uygur Autonomous Region in China and their influence mechanisms. Buildings 2024, 14, 3420. [Google Scholar] [CrossRef]
- Li, D.; Gao, X.; Lv, S.; Zhao, W.; Yuan, M.; Li, P. Spatial distribution and influencing factors of traditional villages in Inner Mongolia Autonomous Region. Buildings 2023, 13, 2807. [Google Scholar] [CrossRef]
- Chen, Z.; Meng, Y.; Yang, D.; Xiao, Y.; Yuan, Y. Spatial distribution characteristics and driving mechanisms of traditional villages on Hainan Island. Areal Res. Dev. 2025, 44, 114–121. [Google Scholar] [CrossRef]
- Fang, Q.; Li, Z.; Huang, L. Spatial distribution and influencing factors of traditional villages in the Huizhou cultural ecological protection subregion. Ind. Archit. 2024, 54, 105–113. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, Z. Spatial patterns and accessibility of traditional villages in the middle reaches of the Yangtze River urban agglomeration based on a GWR model. Hum. Geogr. 2017, 32, 78–85. [Google Scholar] [CrossRef]
- Sauer, C.O. The Morphology of Landscape; University of California Publications in Geography; University of California Press: Berkeley, CA, USA, 1925; Volume 2, pp. 19–53. [Google Scholar]
- Zheng, Z.; Jiao, S.; Xiong, Y. Characteristics of regional historical and cultural resources and research on cluster-based protection. Archit. J. 2020, S1, 98–102. [Google Scholar]
- Huang, Q.; Yang, G. Sichuan migrant place names and the ‘Hu-Guang Migration to Sichuan’: Spatial distribution and provincial origin ratio. J. Southwest China Norm. Univ. (Humanit. Soc. Sci.) 2005, 3, 111–118. [Google Scholar] [CrossRef]
- Chen, J. A Geographical Study of Sichuan River Ports from the Late Qing Dynasty to 1949. Doctoral Dissertation, Southwest University, Chongqing, China, 2023. [Google Scholar]
- Su, H.; Wang, Y.; Zhang, Z.; Dong, W. Characteristics and influencing factors of traditional village distribution in China. Land 2022, 11, 1631. [Google Scholar] [CrossRef]
- Kang, J.; Zhang, J.; Hu, H.; Zhou, J.; Xiong, J. Spatial distribution characteristics of traditional villages in China. Prog. Geogr. 2016, 35, 839–850. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Liu, F.; Xu, W.; Niu, Q. Spatial Pattern of Traditional Villages in Remote Mountainous Areas and Their Development Potential Assessment: The Case of Enshi, China. Sustainability 2025, 17, 1138. [Google Scholar] [CrossRef]
- Zhong, Q.; Xie, L.; Wu, J. Reimagining heritage villages’ sustainability: Machine learning–driven human settlement suitability in Hunan. Humanit. Soc. Sci. Commun. 2025, 12, 661. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, C. A review of research on the K-means clustering algorithm. Comput. Eng. Appl. 2019, 55, 7–14. [Google Scholar] [CrossRef]
- Zhang, L. Principles and empirical analysis of the Kruskal–Wallis test for multiple independent samples. J. Suzhou Univ. Sci. Technol. (Nat. Sci. Ed.) 2014, 31, 14–16. [Google Scholar] [CrossRef]
- Li, L. The subregional division of Southwestern Mandarin (draft). Dialect 2009, 31, 72–87. [Google Scholar]
- Zhou, J.; Zhou, M. Phonetic features and subregional dialect divisions in the Minjiang–Jialing River basins. Stud. Hist. Linguist. 2023, 1, 1–48+251–252. [Google Scholar]
- Sun, Y. A Phonetic Study of Southwestern Mandarin in Sichuan; Publishing House of Electronics Industry: Beijing, China, 2016. [Google Scholar]
- Hu, Z. A Critical Study on Zhang Xianzhong’s Massacre in Sichuan; Sichuan People’s Publishing House: Chengdu, China, 1980; Volume 44. [Google Scholar]
- Chen, Q.; Luo, Y.; Zhang, H.; Tan, X.; Teng, L.; Yang, H. Spatial distribution characteristics and influencing factors of traditional villages in Sichuan Province. Geomat. Spat. Inf. Technol. 2018, 41, 49–52. [Google Scholar] [CrossRef]
- Zheng, Z.; Yuan, X.; Mo, Q. Spatial distribution characteristics and causation analysis of traditional villages in Sichuan Province. In People’s Cities, Planning Empowerment, Proceedings of the 2022 China Urban Planning Annual Conference (Vol. 09: Urban Cultural Heritage Protection), Suzhou, China, 12–13 November 2022; Architecture & Building Press: Beijing, China, 2023; pp. 1394–1399. [Google Scholar]



| Dataset | Resolution | Date | Pre-Processing Steps |
|---|---|---|---|
| Traditional village locations | Point coordinates | 2012–2020 | Transforming from BD-09 to WGS84 geographic coordinate system. |
| DEM | 30 m | 2022 | Clipping to the study area boundary. Projected to a projected coordinate system (EPSG:3395). |
| GDP | County-level | 2022 | Digitizing and joining to the county boundary attribute table. |
| Urbanization rate | County-level | 2022 | Digitizing and joining to the county boundary attribute table. |
| Administrative boundaries | County-level | 2020 | Joining with the socioeconomic data. |
| Dialect boundaries | County-level | 1987 | Vectorize in ArcGIS. Translate into discrete units that align with modern administrative divisions. |
| River network | 1:250,000 | 2015 | Clipping to the study area boundary. |
| Road network | 1:250,000 | 2015 | Clipping to the study area boundary. |
| dock data | County-level | historical | Digitizing and joining to the county boundary attribute table. |
| Code | Indicator | Definition and Calculation Method | Strata | VIF |
|---|---|---|---|---|
| Y | number of traditional villages | The number of traditional village points located within a county areal unit in ArcGIS. (count) | / | / |
| C1 | elevation | Average elevation of each county in southern Sichuan. , where is the elevation of grid , is its area, is the total number of grids. (meter). | Natural breaks (Jenks), 4 strata | 1.591643 |
| C2 | river connectivity | Density of traditional villages within 5000 m of rivers. , where refers to the number of traditional villages within the 5000 m river buffer in the i-th county, and refers to the total number of traditional villages in that county. | 1.091692 | |
| C3 | GDP | GDP of Southern Sichuan Counties in 2022. (10,000 CNY) | 2.497414 | |
| C4 | urbanization rate | Urbanization rates of counties in southern Sichuan in 2022. | 2.994305 | |
| C5 | number of historical docks | Number of docks in southern Sichuan counties. (count) | 1.710928 | |
| C6 | road density | Ratio of total road length to county area in southern Sichuan (km/km2) | 2.338274 |
| Observed Mean Distance (m) | Expected Mean Distance (m) | ANN | Z | p-Value | Distribution Pattern |
|---|---|---|---|---|---|
| 12,415.53 | 14,873.8 | 0.834724 | −2.664201 | 0.007717 ** | significant clustered |
| Moran’s I | Z | p-Value |
|---|---|---|
| 0.233625 | 2.794764 | 0.005194 ** |
| Indicator | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| q-value | 0.069028 | 0.322196 | 0.069801 | 0.162088 | 0.056415 | 0.081395 |
| Factor Interaction | Interaction Value Comparison | Interaction Results |
|---|---|---|
| C3∩C4 | 0.6130 > q (C3 + C4 = 0.2319) | Nonlinear enhancement |
| C2∩C4 | 0.5961 > q (C2 + C3 = 0.3920) | Nonlinear enhancement |
| C1∩C2 | 0.5812 > q (C1 + C2 = 0.3912) | Nonlinear enhancement |
| Method | Global R2 | Adjusted R2 | AICc | ΔAICc (OLS-GWR) |
|---|---|---|---|---|
| OLS | 0.3923 | 0.2791 | 177.2496 | 24.3524 |
| GWR | / | 0.7019 | 152.8972 |
| Cluster | Number of Counties | Number of Traditional Villages |
|---|---|---|
| S1 | 14 | 14 |
| S2 | 19 | 30 |
| S3 | 6 | 27 |
| Indicator | Cluster Median M (P25, P75) | H | p | Effect Size (η2) | ||
|---|---|---|---|---|---|---|
| S1 (n = 14) | S2 (n = 19) | S3 (n = 6) | ||||
| C1 | −0.367 (−0.4, −0.3) | −0.205 (−0.4, 0.7) | 1.736 (0.4, 2.7) | 14.586 | 0.001 ** | 0.349611 |
| C2 | 0.497 (0.4, 0.8) | 0.994 (0.8, 1.2) | 1.273 (1.1, 1.3) | 19.247 | 0.000 *** | 0.479083 |
| C3 | 0.504 (0.5, 0.6) | 0.491 (0.5, 0.6) | 0.712 (0.7, 0.8) | 14.368 | 0.001 ** | 0.343556 |
| C4 | −0.948 (−1.2, −0.8) | −1.282 (−1.7, −1.1) | −2.140 (−2.6, −2.0) | 20.806 | 0.000 *** | 0.522389 |
| C5 | −0.186 (−0.2, −0.1) | 0.075 (−0.0, 0.3) | 0.579 (0.3, 0.9) | 23.366 | 0.000 *** | 0.5935 |
| C6 | 0.310 (0.2, 0.4) | 0.381 (0.3, 0.7) | 1.346 (1.1, 2.1) | 15.927 | 0.000 *** | 0.386861 |
| Indicator | (Cluster1) Code | (Cluster2) Code | (Cluster1) Median | (Cluster2) Median | (Cluster1–2) Median Difference | p-Value |
|---|---|---|---|---|---|---|
| C1 | S1 | S2 | −0.367 | −0.205 | −0.162 | 0.198 |
| S1 | S3 | −0.367 | 1.736 | −2.102 | 0.000 *** | |
| S2 | S3 | −0.205 | 1.736 | −1.94 | 0.029 * | |
| C2 | S1 | S2 | 0.497 | 0.994 | −0.497 | 0.002 ** |
| S1 | S3 | 0.497 | 1.273 | −0.776 | 0.000 *** | |
| S2 | S3 | 0.994 | 1.273 | −0.279 | 0.413 | |
| C3 | S1 | S2 | 0.504 | 0.491 | 0.013 | 1 |
| S1 | S3 | 0.504 | 0.712 | −0.208 | 0.001 ** | |
| S2 | S3 | 0.491 | 0.712 | −0.221 | 0.002 ** | |
| C4 | S1 | S2 | −0.948 | −1.282 | 0.334 | 0.044 * |
| S1 | S3 | −0.948 | −2.14 | 1.191 | 0.000 *** | |
| S2 | S3 | −1.282 | −2.14 | 0.858 | 0.012 * | |
| C5 | S1 | S2 | −0.186 | 0.075 | −0.26 | 0.003 ** |
| S1 | S3 | −0.186 | 0.579 | −0.765 | 0.000 *** | |
| S2 | S3 | 0.075 | 0.579 | −0.504 | 0.072 | |
| C6 | S1 | S2 | 0.31 | 0.381 | −0.071 | 0.588 |
| S1 | S3 | 0.31 | 1.346 | −1.036 | 0.000 *** | |
| S2 | S3 | 0.381 | 1.346 | −0.965 | 0.005 ** |
| Cluster | Chengyu Subregion | Minjiang Subregion | Renfu Subregion |
|---|---|---|---|
| S1 | 0.000 | 1.000 | 0.000 |
| S2 | 0.053 | 0.368 | 0.579 |
| S3 | 0.000 | 0.833 | 0.167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Tang, Y.; Guo, J. Spatial Heterogeneity of Traditional Villages in Southern Sichuan, China: Insights from GWR and K-Means Clustering. Land 2025, 14, 1817. https://doi.org/10.3390/land14091817
Guo H, Tang Y, Guo J. Spatial Heterogeneity of Traditional Villages in Southern Sichuan, China: Insights from GWR and K-Means Clustering. Land. 2025; 14(9):1817. https://doi.org/10.3390/land14091817
Chicago/Turabian StyleGuo, Huakang, Youhai Tang, and Jingwen Guo. 2025. "Spatial Heterogeneity of Traditional Villages in Southern Sichuan, China: Insights from GWR and K-Means Clustering" Land 14, no. 9: 1817. https://doi.org/10.3390/land14091817
APA StyleGuo, H., Tang, Y., & Guo, J. (2025). Spatial Heterogeneity of Traditional Villages in Southern Sichuan, China: Insights from GWR and K-Means Clustering. Land, 14(9), 1817. https://doi.org/10.3390/land14091817





