The Spatiotemporal Impact of Socio-Economic Factors on Carbon Sink Value: A Geographically and Temporally Weighted Regression Analysis at the County Level from 2000 to 2020 in China’s Fujian Province

Abstract

Evaluating the economic value of carbon sinks is fundamental to advancing carbon market mechanisms and supporting sustainable regional development. This study focuses on Fujian Province in China, aiming to assess the spatiotemporal evolution of carbon sink value and analyze the influence of socio-economic drivers. Carbon sink values from 2000 to 2020 were estimated using Net Ecosystem Productivity (NEP) simulation combined with the carbon market valuation method. Eleven socio-economic variables were selected through correlation and multicollinearity testing, and their impacts were examined using Geographically and Temporally Weighted Regression (GTWR) at the county level. The results indicate that the total carbon sink value in Fujian declined from CNY 3.212 billion in 2000 to CNY 2.837 billion in 2020, showing a spatial pattern of higher values in the southern region and lower values in the north. GTWR analysis reveals spatiotemporal heterogeneity in the effects of socio-economic factors. For example, the influence of urbanization and retail sales of consumer goods shifts direction over time, while the effects of industrial structure, population, road, and fixed asset investment vary across space. This study emphasizes the necessity of incorporating spatial and temporal dynamics into carbon sink valuation. The findings suggest that northern areas of Fujian should prioritize ecological restoration, rapidly urbanizing regions should adopt green development strategies, and counties guided by investment and consumption should focus on sustainable development pathways to maintain and enhance carbon sink capacity.

1. Introduction

In the current era, given the increasingly severe climate change and environmental challenges, human society urgently needs to seek sustainable solutions to mitigate and adapt to the escalating environmental issues. Achieving carbon neutrality has emerged as a critical and urgent goal. Carbon neutrality refers to the balance between the amount of greenhouse gases emitted into the atmosphere and the amount removed. This can be achieved by reducing emissions through sustainable practices and technologies, as well as implementing measures to offset an equivalent amount of carbon from the atmosphere. In 2015, 195 countries signed the Paris Agreement, with the core objective of limiting the global temperature increase to below 2 °C and striving to keep it within 1.5 °C. To achieve this goal, global greenhouse gas emissions need to be reduced by half by the year 2030, reaching carbon neutrality around 2050. Currently, many countries have adopted measures to control carbon emissions [1]. Considering the responsibility for emission reduction amidst the backdrop of global warming, the Chinese government continues to strengthen environmental legislation and climate policy efforts. In 2020, China committed to striving for a peak in carbon dioxide emissions before 2030 and making efforts to achieve carbon neutrality by 2060 [2]. Assigning a clear economic value to carbon sinks is a critical step toward achieving carbon neutrality because it translates abstract ecosystem services into concrete monetary terms that policymakers, investors, and local stakeholders can readily understand and act upon. By quantifying the value of carbon sequestration in market or compensation schemes, we create financial incentives for conservation and restoration, effectively mobilizing private capital and guiding land use decisions toward low-carbon pathways. Moreover, an explicit valuation enables rigorous cost–benefit analyses of mitigation measures, helps integrate carbon sinks into national accounting and trading mechanisms, and ensures that carbon sink enhancement is recognized as an investible ‘asset’—all of which are essential for designing efficient, scalable policies to meet carbon neutrality targets.

There are mainly two approaches to address carbon neutrality. The first involves reducing carbon dioxide emissions, while the second entails absorbing more carbon dioxide from the atmosphere, also known as “carbon sink”. Carbon sink refers to the process, activities, or mechanisms such as afforestation and vegetation restoration that absorb carbon dioxide from the atmosphere, thereby reducing the concentration of greenhouse gases [3]. In addition to atmospheric carbon dioxide reduction, carbon sink also holds significant development potential. It is considered one of the core assets in the carbon trading market, where enterprises and countries can purchase carbon sinks to offset emissions exceeding specified standards [4]. This trading mechanism imparts economic value to carbon sinks. From this perspective, the value of carbon sinks can be defined as their economic potential and commercial value in the carbon market [5]. Therefore, the carbon sink value has gradually gained attention from the Chinese government. In 2022, the Central Committee’s Number One Document from the State Council of China emphasized the need to research and apply agriculture technologies that reduce emissions and increase carbon sequestration, exploring mechanisms to realize the value of carbon sink products [6]. It can be said that the assessment and realization of the carbon sink value are innovative strategic measures and tasks proposed by the Chinese government. This constitutes a systematic project involving economic, social, political, and other related fields, representing an essential aspect of future research on resources and the environment.

Estimating the physical quantity of carbon sinks is the first step in evaluating the carbon sink value of an area. The assessment methods for carbon sink mainly include sample plot measurement, the assimilation method, micrometeorological method, and model simulation method. The sample plot measurement involves measuring the vegetation and soil carbon concentration in selected plots, combined with continuous observations of the changes in carbon stock over a certain period [7]. This method typically calculates carbon stocks by multiplying the biomass by a carbon content coefficient after estimating it. The assimilation method involves determining plant leaf photosynthetic physiological indicators, such as net photosynthetic rate, transpiration rate, intercellular CO₂ concentration, and stomatal conductance, to calculate the total net assimilation and net carbon fixation of vegetation. This, combined with structural parameters like leaf area and green biomass, provides the amount of carbon fixed by plants [8], commonly used to assess the carbon-fixation capacity of different plants at a small scale. The micrometeorological method, based on monitoring climate characteristics, enables continuous and dynamic observation of CO₂ flux between green spaces and the atmosphere. It is widely used in studying carbon flux changes and their environmental response mechanisms [9]. The model simulation method involves using climate conditions such as temperature, humidity, light, precipitation, and vegetation type as input variables. It simulates the processes of photosynthesis, respiration, and microbial decomposition in forest ecosystems to calculate carbon dioxide flux [10].

The evaluation of carbon sink value involves determining the value using different methods based on the calculation of the physical quantity of carbon sink. It can be assessed through both the cost–benefit method and the market value method. The cost–benefit method typically measures the value of carbon sink using afforestation costs [11] or carbon taxes [12]. For example, Ge et al. (2017) compared carbon sink costs in different regions, identifying suitable areas in southwest China for developing a carbon sink economy [13]. On the other hand, the market value method determines the price of carbon sink by averaging historical transaction data and subsequently calculates its value [14]. For instance, Bherwani et al. (2022) quantified the carbon sink value of urban green spaces in India using market prices [15].

The factors influencing carbon sink value constitute a complex and multi-layered research domain, involving various ecological, economic, and social aspects. Firstly, land use types play a crucial role. Different land types, such as cropland, forestland, and grassland, exhibit significant variations in the vegetation and soil’s capacity for carbon absorption [16]. Secondly, the impact of climate conditions on carbon sink cannot be overlooked. Climate factors like temperature, precipitation, and sunlight directly affect vegetation growth and soil carbon cycling in ecosystems, influencing carbon absorption and storage processes [17]. Climate change may alter the carbon sink capacity of certain ecosystems, thereby exerting a significant impact on carbon sink value. Lastly, beyond the factors that impact carbon sink value on the physical layer, there are also some factors that influence it on the economic layer. Factors such as the scale of carbon markets, price fluctuations, and the stability of policy frameworks can profoundly affect the economic benefits of carbon sink projects [18,19]. Additionally, community acceptance and public participation also play a role in shaping the long-term benefits of carbon sink projects [20,21].

While previous research has yielded fruitful results regarding the study of carbon sink value and its influencing factors, there are still evident gaps in terms of research scale, factor selection, and methodological approach, which limit our understanding of localized carbon sink dynamics and their policy implications. Firstly, regarding spatial scale, existing studies have predominantly focused on the national [22] and provincial levels [23], with limited attention paid to the county scale where land use decisions, ecological investments, and policy implementation actually occur. This mismatch reduces the practical relevance of many findings. Secondly, in terms of influencing factors, previous studies have predominantly focused on biophysical elements such as vegetation coverage and climate variables, while economic and social drivers—such as income levels, urbanization, and industrial structure—have been discussed more frequently in the context of micro-level project evaluations. However, at the county scale, where both ecological processes and socio-economic decisions interact, these human-driven factors play an equally critical role in shaping carbon sink value. Thirdly, methodologically, multivariate linear regression remains the dominant tool for identifying influencing factors [24], yet it typically assumes spatial and temporal stationarity, failing to capture the complex, location-specific and evolving relationships between carbon sink value and its drivers. The resulting question is, given the differences in social and economic development conditions among county-level units, how can we analyze the influencing factors of carbon sink value over space and time?

The main purpose of this study is to characterize the spatiotemporal trends of carbon sink value and analyze the spatiotemporal effects of influencing factors at the county level. Fujian Province in China was selected as the study area due to its favorable natural environment and distinctive policy advantages. With a forest coverage rate of 65.12 percent, which has ranked first nationally for 45 consecutive years, Fujian demonstrates strong ecological quality and considerable potential for carbon sink development. As an economically advanced region and one of China’s eight pilot areas for carbon emissions trading, it also provides a practical pathway for monetizing ecosystem-based carbon sinks. The combination of strong carbon sequestration capacity and rapid urbanization makes Fujian a compelling case for examining the factors that influence carbon sink valuation. We first assessed the carbon sink value for each five-year period from 2000 to 2020 using the Net Ecosystem Production (NEP) modeling method and, subsequently, the market value method. In a further step, we considered a set of influencing factors (with their different time and spatial heterogeneity) and employed geographically and temporally weighted regression to analyze the spatiotemporal heterogeneity of these factors. The innovation of this study lies in breaking through the limitations of previous research, which often had short time scales, overly macroscopic spatial scales, and primarily focused on natural factors. While depicting the spatiotemporal characteristics of carbon sink values, this study takes into account the spatiotemporal heterogeneity of carbon sink values and various influencing factors, thereby elucidating the driving degrees of each influencing factor. The remaining sections of this paper are organized as follows: Section 2 describes the research materials and methods; Section 3 presents the assessment results of carbon sink value and spatiotemporal differences in the effects of influencing factors; Section 4 further discusses the research findings; and Section 5 concludes with future research prospects.

2. Material and Methods

2.1. Study Area

The Fujian Province is located along the southeastern coast of China (23°33′–28°20′ N, 115°50′–120°40′ E) and administratively governs 84 county-level administrative units (Figure 1). The topography is primarily characterized by mountainous terrain and hills, with a dense network of water systems and several rivers. The predominant soil types in the Fujian Province are red and yellow soil. The province falls under a subtropical maritime monsoon climate, ranking as one of the provinces with the highest rainfall in China and providing favorable conditions for the growth of flora and fauna. With a forest coverage rate of 66.8%, Fujian Province leads the nation and is recognized as one of the six major forestry regions in China. The region has high-quality and well-preserved habitats. Due to its rich natural ecological resources, especially ecosystems such as forests and grasslands, Fujian Province exhibits significant carbon sink potential. In 2022, three prefecture-level cities in Fujian Province were selected as national forestry carbon sink pilot areas by the National Forestry and Grassland Administration. Therefore, choosing Fujian Province as the research area for carbon sink value evaluation and analysis is both paradigmatic and informative.

2.2. Data Sources

The data used in this study include land use cover data, soil organic carbon data, net primary productivity (NPP) data, precipitation data, temperature data, carbon trading data, as well as social and economic statistics (

Table 1. Data sources.

Data	Source	Resolution
Land use cover	RESDC, 2021 [25]	30 m × 30 m
Soil organic carbon	Xu et al., 2018 [26]	-
Net primary productivity	MODIS, 2021 [27]	1 km × 1 km
Precipitation	Muñoz, 2019 [29]	0.1° × 0.1°
Temperature	NCEI, 2021 [30]	-
Carbon trading	Wind Information Co., Ltd., 2021 [31]	-
Social and economic statistics	Fujian Provincial Bureau of Statistics, 2021 [32]	-

). Land use cover data are provided by the Data Center for Resources and Environmental Sciences, Chinese Academy of Sciences [25]. This dataset covers the years 2000, 2005, 2010, 2015, and 2020, utilizing Landsat remote sensing imagery as the primary information source. Through manual visual interpretation, the data was obtained with a precision of 30 m. The land cover is classified into six types as follows: cropland, forestland, grassland, construction land, water areas, and unused land. Soil organic carbon data are sourced from Xu et al. (2018) [26]. This soil carbon stock database contains 186 soil sampling points in Fujian Province, offering a more current representation compared to the more widely used 1980s SOC data. Spatial interpolation analysis tools were employed to derive the distribution range of soil organic carbon density in Fujian Province. Net Primary Productivity (NPP) data come from MODIS (2021), validated through on-site observations with high accuracy on a global scale [27]. The data of MODIS are widely used in carbon sink research due to its moderate spatial resolution, global continuous coverage, and free accessibility. Moreover, MODIS data have been extensively validated and generally show good agreement with ground-based observations or high-precision model outputs. For example, previous studies have demonstrated a strong consistency between MODIS products and site-level measurements [28]. The dataset is in TIF format with a resolution of approximately 1 km. Precipitation data is sourced from the ERA5-Land dataset, released by the European Union and the European Centre for Medium-Range Weather Forecasts [29]. ERA5-Land is based on the ECMWF ERA5 climate reanalysis, combining model data with global observations. Temperature data are obtained from the National Centers for Environmental Information [30] under the National Oceanic and Atmospheric Administration. For instance, for 2022, there are 12,319 meteorological observation stations worldwide. We downloaded data from the NCEI website for meteorological observation stations in Fujian Province and obtained annual average temperatures through steps involving inverse distance weighting interpolation and raster calculations. Carbon trading data are sourced from the carbon emission database published by Wind Information Co., Ltd., Shanghai, China. (2021) [31]. Wind Information has formulated China’s leading carbon market database by referencing international benchmarks and incorporating Chinese market and industry characteristics. This database compiles transaction data from various carbon trading platforms in China, including details such as the time, location, quantity, and price of each transaction. Social and economic statistics data are sourced from the Fujian Provincial Statistical Yearbook published annually by the Fujian Provincial Bureau of Statistics (2021) [32]. The yearbook systematically includes statistical data on various aspects of economic and social development in different regions and sectors of Fujian Province, covering national economic accounts, population, employment, wages, energy, industry, public administration, and other social activities.

2.3. Research Methods

The technical roadmap of this study is illustrated in Figure 2. The first step is to compute the carbon sink value (frame 1 in Figure 2). For this, we first employ Net Ecosystem Productivity (NEP) simulation to calculate the carbon sink; second, based on this, we use the market value method to compute the carbon sink value. The second step (frame 2 in Figure 2) involves constructing an indicator system for potential influencing factors and identifying key explanatory variables through correlation analysis and collinearity diagnostics. This process helps ensure that only relevant variables are included in the model, with carbon sink value as the dependent variable. In the third step (frame 3 in Figure 2), we analyze the impact mechanisms of influencing factors using a geographically and temporally weighted regression model. We acknowledge the merits of panel data models and spatial econometric models in analyzing spatial and temporal data. However, these approaches generally assume fixed or random effects over space or time, which may not fully capture the localized and continuously varying relationships between carbon sink values and their drivers. In contrast, GTWR allows model coefficients to vary simultaneously across both space and time, making it particularly suitable for identifying spatiotemporal non-stationarity. Given our research objective to explore how the effects of factors evolve across counties and years, GTWR provides a more flexible and detailed analytical framework.

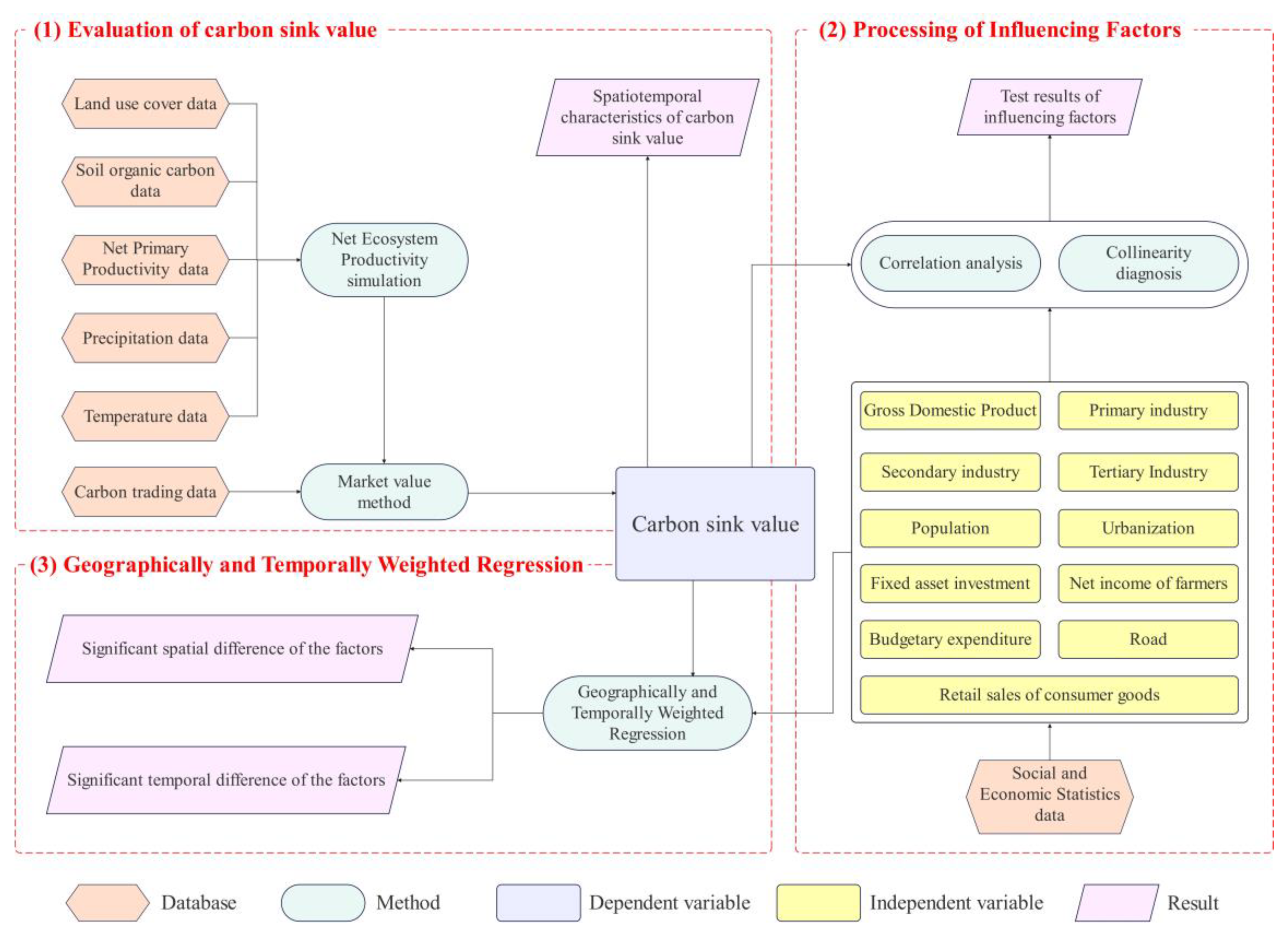
2.3.1. Evaluation of Carbon Sink Value

Net Ecosystem Productivity Simulation

There are various methods for calculating the physical quantity of carbon sink, each with different applicability and precision. The advantage of the sample plot measurement method is its ability to directly measure the carbon storage of vegetation and soil at the plot scale [9]. However, its limitation lies in the strong spatial heterogeneity of terrestrial ecosystems, leading to significant uncertainty in the conversion of carbon reserves from plot to regional scales. The assimilation method has the advantage of accurately calculating the carbon sequestration amount of plant leaves [33]. However, due to differences in photosynthetic rates at different growth stages of tree species, extrapolating leaf-scale carbon fixation to the whole plant or even landscape scale can introduce uncertainty, thereby affecting the results of carbon sink monitoring. The micrometeorological method has the main advantage of enabling long-term continuous and fine-scale (e.g., every half hour) monitoring of carbon flux. However, flux data obtained through this method are typically local and may not be applicable to other locations [34]. Therefore, these methods are challenging to apply to regional-scale carbon sink calculations. In contrast, NEP simulation can be applied at the regional scale [35] for assessing carbon sinks in large areas. Additionally, NEP simulation is typically based on time series data, allowing for the modeling of long-term trends. This aids in observing the dynamic changes in ecosystem carbon sinks, identifying seasonal and interannual variations, and gaining a better understanding of how ecosystems respond to climate and environmental changes. In ecological research, NEP is commonly used to assess whether an ecosystem functions as a carbon sink [36]. If $NEP\ge 0$, it indicates a carbon sink; if $NEP<0$, it indicates a carbon source. To facilitate computation and reduce data redundancy, we chose a grid with a side length of 5 km. The study area was divided into 5373 grids, and the NEP for each grid was calculated. The NEP simulation model is as follows:

$$NEP=NPP-Rh$$

(1)

where $NPP$ represents Net Primary Productivity (g C/m²/yr), and $Rh$ represents the annual heterotrophic respiration of the soil (g C/m²/yr). The calculation method for $Rh$ is based on the study by Ye and Chuai (2022) [37]. They collected 233 observational results from existing research and used the least squares method to find an equation for estimating soil heterotrophic respiration. These observations are distributed across various terrestrial ecosystems such as forests, croplands, and grasslands, covering the majority of regions in China. The fitted equation for Rh is as follows:

$$Rh=1.598\times {Rs}^{0.862}+23.92 { R}^2=0.85$$

(2)

where $Rs$ represents the annual soil respiration (g C/m²/yr). The model developed by Yu et al. (2010) can be employed to simulate $Rs$ [38]. This model, based on data from 390 sample points, is more suitable for soil respiration studies in China compared to other models. The equation is as follows:

$${Rs}_{month}=\left(0.588+0.118\times SOC\right)\times e^{ln\left(1.83\times e^{-0.006\times T}\right)\times T÷10}\times \left(P+2.972\right)÷\left(P+5.657\right)\times 30$$

(3)

$${Rs}_{annual}={\sum }_{i=1}^{12}{Rs}_{month}$$

(4)

where ${Rs}_{month}$ and ${Rs}_{annual}$ represent the monthly and annual soil respiration, respectively. $T$ and $P$ represent the monthly average temperature (°C) and monthly precipitation (cm). SOC is the organic carbon storage density (kg C/m²) in the surface soil layer (0–20 cm).

Market Value Method

There are various accounting methods for assessing carbon sink value, and the results often differ significantly. The cost–benefit method commonly uses the costs of afforestation projects to measure carbon sink value [13]. However, due to differences in tree species and regional economic development levels, costs can vary. Moreover, this method often focuses on the initial planting and management costs of the project, without fully considering the entire project’s lifecycle costs, including maintenance, monitoring, reporting, verification, etc. This may lead to an underestimation of the carbon sink value. In contrast, the market value method, based on the average carbon prices in transactions, provides an economically viable way to assess the value of carbon sinks. It connects the economic benefits of carbon sink with the actual market conditions. Additionally, one of China’s eight carbon trading exchanges, the Straits Equity Exchange Center, is located in Fujian Province, where carbon sink projects are widely promoted. Utilizing the trading data from the Straits Equity Exchange Center can reflect the actual market potential of carbon sinks in the province. Therefore, adopting the market value method in this study is feasible. The calculation formula of the market value method [14] is as follows:

$$V=NEP\times P$$

(5)

where $V$ is the carbon sink value (CNY); $NEP$ is the physical quantity of carbon sink (t C); and $P$ is the price of carbon (CNY/ t C). The carbon price is referenced from the 2020 average transaction price of carbon trading in Fujian Province, which was CNY 17.34 per ton of carbon dioxide [31]. Converting carbon dioxide to carbon by molecular weight, this is equivalent to CNY 63.64 per ton of carbon.

2.3.2. Processing of Influencing Factors

Definition of Variables

Economic and social development can influence carbon sink value through two primary channels as follows: by affecting both carbon sink prices and the physical quantity of carbon sinks. However, as the Fujian Carbon Exchange was only established in 2016 and does not fully cover the study period, and given that carbon prices fluctuate dynamically with market conditions, this study focuses on how economic and social development affects the physical quantity of carbon sinks. Based on a review of the existing literature, economic and social development can theoretically impact carbon sink value through four key pathways:

Firstly, economic and social development influence land use types. The scale of the economy and the structure of industries reflect regional development modes and land use preferences, which directly shape land use composition and thus determine the amount of land available to function as carbon sink carriers. For example, the expansion of the secondary industry is often accompanied by industrial park development and increased demand for construction land, which results in the occupation or replacement of ecological lands such as forests and grasslands [39,40]. In contrast, the development of the primary industry—especially ecological agriculture and forestry—is closely linked to land conservation and the enhancement of ecosystem carbon sink functions [41]. The impact of the tertiary industry on carbon sinks is more complex. Its low-carbon service industry may bring environmentally friendly benefits, but sectors such as tourism that rely heavily on land resources may also have negative effects [42].

Secondly, economic and social development affect the intensity of land use. Population growth and urbanization lead to significantly increased exploitation of land, water, and biological resources. Excessive human disturbance can cause ecosystems to remain in a quasi-stable state, thus reducing the long-term stability of carbon sink supply [43]. This is particularly true in rapidly urbanizing areas, where large areas of forest are converted to residential and commercial land, leading to disrupted vegetation growth and unstable carbon sequestration processes. In addition, the net income of farmers is a key indicator of rural development. Higher income levels can promote sustainable land use practices such as afforestation, soil conservation, and reduced overgrazing, thereby enhancing the stability of carbon sinks [44].

Thirdly, economic and social developments reshape land landscape patterns. Infrastructure construction and capital investment are indispensable components of economic development. Large-scale infrastructure activities often alter the landscape configuration, fragmenting natural ecological units into isolated patches, which obstructs species migration and disrupts ecological processes, thereby undermining ecosystem service provision. For instance, increased road density not only reduces native vegetation cover but also accelerates landscape fragmentation. Studies have shown that the viability of certain plant populations depends not only on road density but also on the size and shape of habitat patches [45]. In particular, plant mortality rates rise sharply at road edges, which can negatively impact regional carbon sink supply [46].

Fourthly, economic and social development influence the carbon sequestration potential of ecosystems. In this process, budgetary expenditure is an integral part of socio-economic development and reflects the resource allocation preferences of local governments. It also plays a key role in determining the level of investment in ecological protection and restoration. Budgetary expenditure can support projects such as forest management, wetland restoration, and reforestation, thereby strengthening the carbon sequestration capacity of the land. Moreover, it can facilitate the construction of green infrastructure, which helps maintain baseline ecological services amid urban development and fosters synergy between ecological protection and economic growth [47]. Thus, budgetary expenditure is not only an external factor regulating changes in carbon sink value but also potentially a key positive driver.

In summary, based on data availability and the need to cover all years and county-level units in the study area, we selected 11 influencing factors as listed in

Table 2. Independent variables and descriptive statistics.

Variables	Description	Mean	Std. Dev	Min	Max
Gross Domestic Product	GDP per capita (CNY 10,000)	4.78	4.12	0.16	30.76
Primary Industry	Gross value of primary industry per capita (CNY 10,000)	0.53	0.50	0.00	3.39
Secondary Industry	Gross value of secondary industry per capita (CNY 10,000)	2.30	2.24	0.09	16.54
Tertiary Industry	Gross value of tertiary industry per capita (CNY 10,000)	1.95	2.31	0.00	26.24
Population	Population density (person/square kilometer)	1447.49	3714.07	57.21	27,065.65
Urbanization	Urbanization rate	0.58	0.24	0.06	1.00
Fixed Asset Investment	Fixed asset investment per capita (CNY 10,000 /person)	2.59	2.76	0.01	12.97
Net Income of Farmers	Per capita net income of farmers (CNY 10,000)	1.03	0.69	0.21	3.28
Budgetary Expenditure	Per capita budgetary expenditure (CNY 10,000/person)	0.45	0.43	0.03	2.46
Road	Highways density (km/square kilometer)	0.86	0.63	0.00	4.64
Retail Sales of Consumer Goods	Per capita retail sales of consumer goods (CNY 10,000/person)	1.74	2.02	0.11	19.48

. As statistical data for Jinmen County are lacking, our county-level observation sample consists of 83 counties. Descriptive statistical results of independent variables are normal.

Correlation Analysis and Collinearity Diagnosis

In statistical modeling, correlation analysis and collinearity diagnosis are crucial steps used to eliminate redundant information and ensure the robustness of a model. Correlation analysis is a useful preliminary tool for identifying whether variables are linearly related [48]. When correlation coefficients are near zero and statistically insignificant, they suggest no evident linear association. This helps screen out irrelevant variables, reducing redundancy and improving model explanatory power. The most commonly used correlation coefficient is the Pearson correlation coefficient, and its calculation formula is as follows:

$$R={\sum }_{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)/\left(\sqrt{{\sum }_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(X_i-\overline{X}\right)}^2}\right)$$

(6)

where $R$ represents the correlation coefficient between variables $X$ and $Y$, while $\overline{X}$ and $\overline{Y}$ represents the mean values of variables $X$ and $Y$, respectively.

Although correlation analysis can reveal bivariate linear relationships between variables and provide a preliminary means of identifying irrelevant variables, its results have certain limitations, especially in the context of multivariable modeling. Therefore, it is necessary to conduct further collinearity diagnostics. Collinearity diagnostics aim to detect multicollinearity among independent variables, which can distort regression estimates and reduce model reliability. Even variables with good correlation may cause such issues. Tools like the Variance Inflation Factor (VIF) help identify and eliminate redundant variables, with a VIF above 10 typically signaling problematic collinearity. The calculation formula [49] is as follows:

$$VIF=1/\left(1-R_i^2\right)$$

(7)

where $R_i$ represents the coefficient of determination of the independent variable $X_i$ with the remaining independent variables in the regression analysis.

2.3.3. Geographically and Temporally Weighted Regression

Location and time are two crucial factors that influence the distribution and evolution of geographic phenomena. In identifying the mechanisms influencing carbon sink value, traditional global regression models typically assume that the relationships between variables remain consistent across space and time, implying a stable overall effect. However, in reality, the factors influencing carbon sink value often exhibit significant spatial variation and temporal dynamics. For example, the strength of the impacts of policies, land use changes, and economic development stages may differ across regions or periods. The Geographically and Temporally Weighted Regression (GTWR) model, which extends the traditional Geographically Weighted Regression (GWR) model by introducing a temporal dimension, assigns spatial and temporal weights to each observation point [50]. This approach enables local modeling of variable relationships across both space and time. It can capture the spatiotemporal non-stationarity of the effects of influencing factors on carbon sink value, revealing the heterogeneity of variable effects in different regions and stages. This helps to more accurately design differentiated and dynamic policy responses and regulatory strategies. The computational formula [51] is as follows:

$$V_i={\beta }_0\left(u_i,v_i,t_i\right)+{\sum }_{k=1}^p{\beta }_k\left(u_i,v_i,t_i\right)X_{ik}+{\epsilon }_i$$

(8)

where $V_i$ represents the carbon sink value for the county $i$; $u_i$ and $v_i$ denote the longitude and latitude for the county $i$, respectively; $t_i$ represents the time coordinate for the county $i$; ${\beta }_0\left(u_i,v_i,t_i\right)$ is the spatiotemporal intercept term which refers to the location- and time-specific baseline value of the dependent variable when all explanatory variables are zero; $X_{ik}$ represents the observed value of the independent variable $k$ in the county $i$; ${\beta }_k\left(u_i,v_i,t_i\right)$ represents the regression coefficient for the independent variable $k$ in the county $i$; and ${\epsilon }_i$ is the random error term.

3. Results

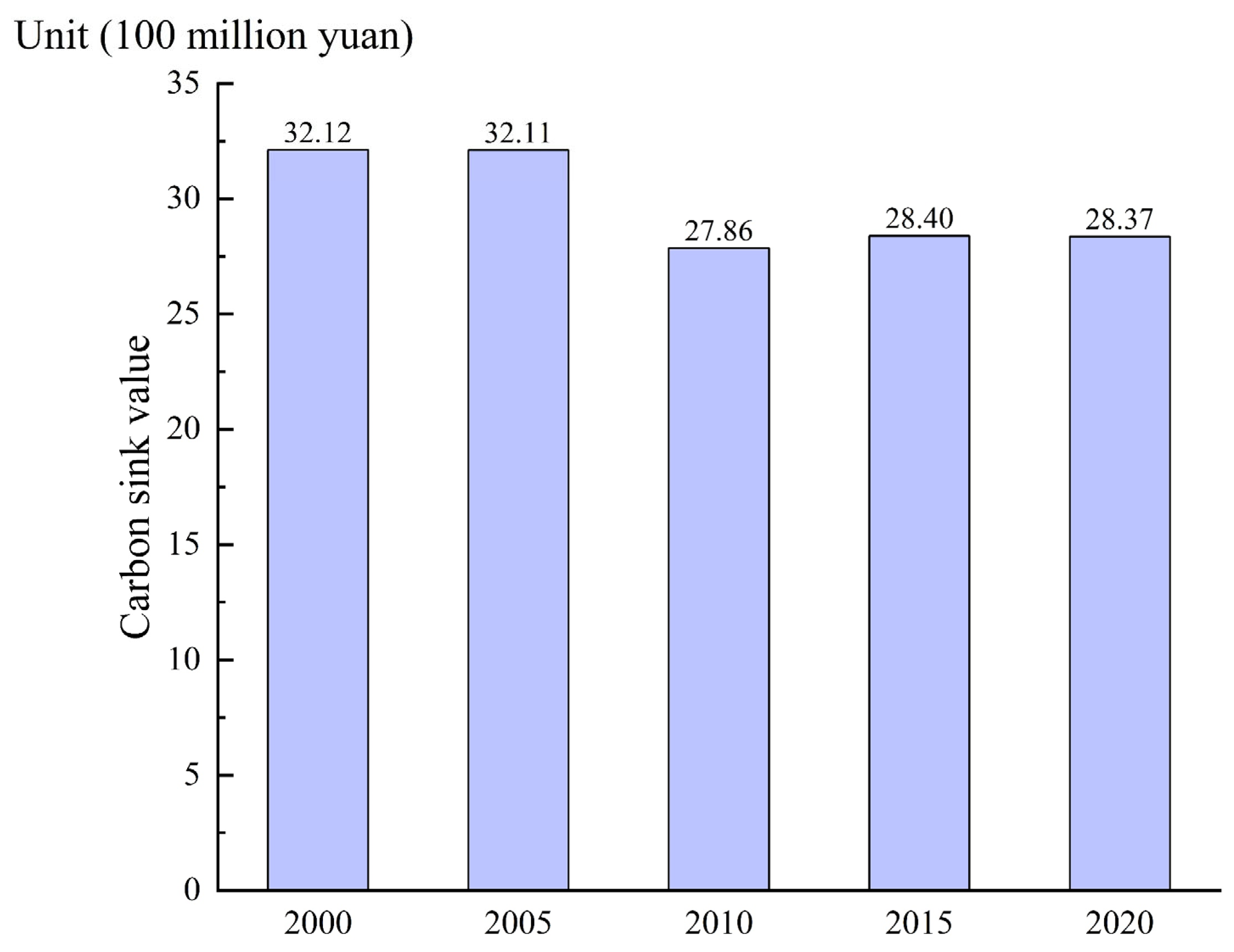
3.1. Spatiotemporal Characteristics of Carbon Sink Value

The aggregated results (sum over the whole study area) of the carbon sink value using the market value method are depicted in Figure 3. In 2000 and 2005, the carbon sink value in Fujian Province remained relatively stable at CNY 3.212 billion and CNY 3.211 billion, respectively. However, a significant change is observed in 2010, decreasing to CNY 2.786 billion. Subsequently, there was a slight rebound to CNY 2.840 billion in 2015, remaining at CNY 2.837 billion in 2020.

Figure 4 displays the spatiotemporal distribution of carbon sink value assessments using 25 km² grid cells as the smallest evaluation unit. The carbon sink values were classified into the following six levels: None, Low, Relatively Low, Moderate, Relatively High, and High. These categories were defined using the equal interval method, with each level representing a CNY 400,000 increment in carbon sink value. Grids with no carbon sink value are typically found in urban construction areas, especially concentrated in the southeastern coastal zones where vegetation coverage is minimal due to high-intensity land use.

Grids with low carbon sink values showed a slight decline from 2000 to 2005, followed by a continuous increase through 2020. These low-value grids are primarily located in the northwestern part of Fujian Province, which may be characterized by fragmented landscapes or limited forest coverage. Grids categorized as relatively low are the most numerous across all five time points, indicating that a large portion of the province exhibits moderate vegetation productivity and carbon sequestration capacity. These are mainly distributed across the central and eastern regions, where human activity and ecological conditions are moderately balanced.

Grids with moderate and relatively high carbon sink values are spatially scattered and tend to cluster in the eastern and southern parts of Fujian. However, their number has gradually declined and stabilized over time, possibly due to increasing development pressure in these areas. Notably, grids with high carbon sink values only appeared sporadically in 2000 and 2005 and disappeared entirely after 2010. This suggests that areas with exceptionally strong carbon sequestration potential have been either reduced in extent or their function has diminished, possibly due to urbanization or land use changes.

Overall, the share of grids categorized as low and relatively low increased from 70% in 2000 to 79% in 2020, reflecting a provincial-scale shift toward lower carbon sink performance. In terms of spatial trends, the carbon sink value distribution generally decreases from southeast to northwest. This spatial gradient likely reflects the combined influence of climatic factors, such as temperature and precipitation gradients, as well as regional differences in forest cover, land use intensity, and ecological restoration efforts. These patterns indicate that while the overall carbon sink capacity remains relatively stable at the landscape level, regional disparities persist and have intensified over time.

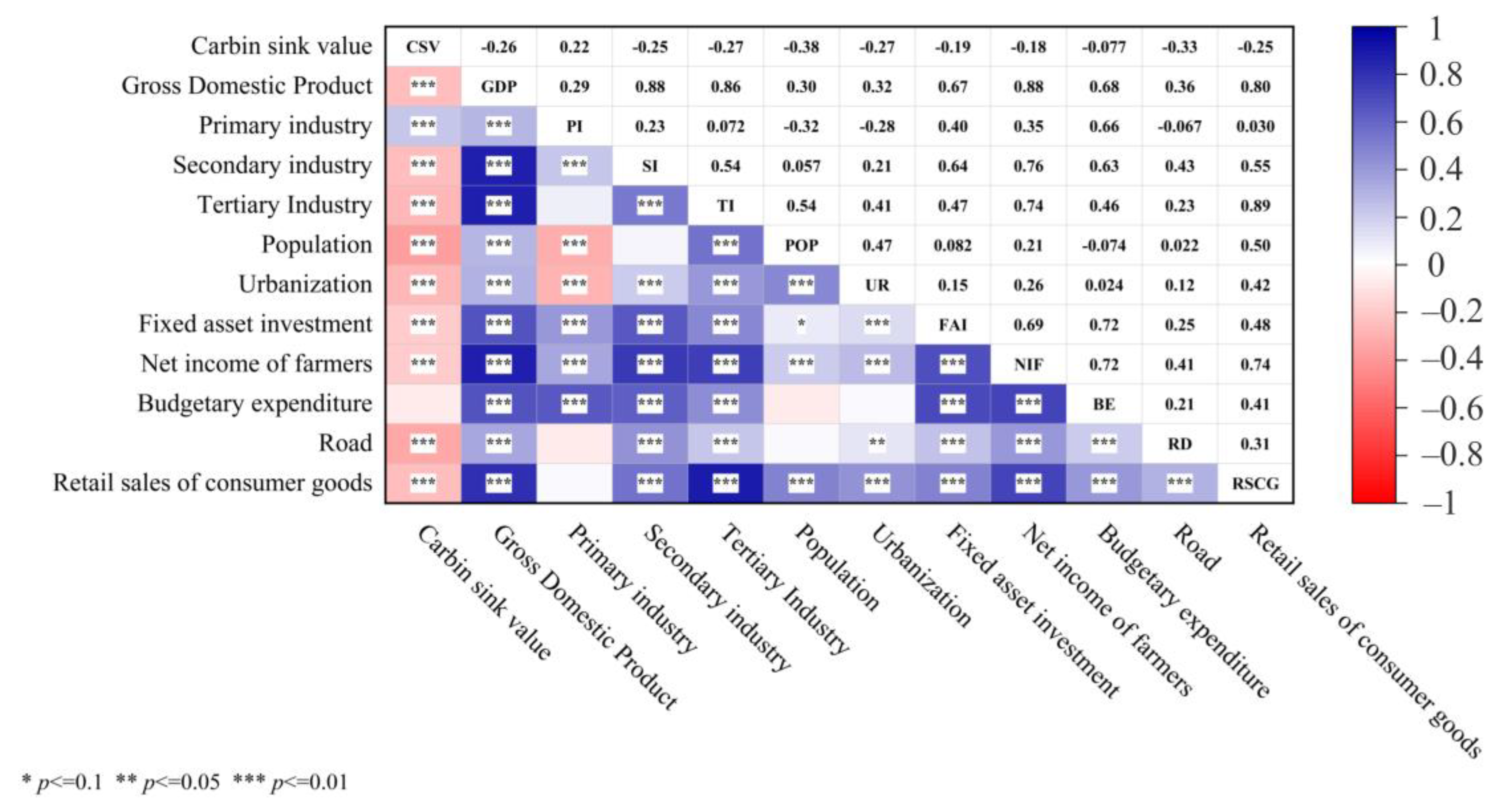
3.2. Test Results of Influencing Factors

Figure 5 illustrates the results of the correlation analysis in a matrix form, with the numbers and color-scale representing the Pearson correlation coefficients. Only the primary industry shows a significant positive correlation with carbon sink value. Except for budgetary expenditure, all other influencing factors exhibit varying degrees of negative correlation with carbon sink value. Since budgetary expenditure does not demonstrate correlation with carbon sink value, we need to remove this factor.

The results of collinearity diagnosis are presented in

Table 3. Results of collinearity diagnosis.

Independent Variable	Collinearity Diagnosis (1)			Collinearity Diagnosis (2)
	Standard Error	Tolerance	VIF	Standard Error	Tolerance	VIF
Constant term	4.499	-	-	4.489	-	-
Gross domestic product	12.604	0.001	1668.399	-	-	-
Primary industry	12.515	0.041	24.208	7.240	0.552	1.818
Secondary industry	12.625	0.002	493.524	−2.834	0.356	2.808
Tertiary industry	12.621	0.002	524.499	−1.886	0.155	6.458
Population	0.000	0.505	1.980	−0.003	0.505	1.980
Urbanization	6.447	0.677	1.476	−5.262	0.678	1.475
Fixed asset investment	0.698	0.436	2.292	−1.880	0.447	2.238
Net income of farmers	4.342	0.181	5.540	10.367	0.182	5.481
Road	2.406	0.707	1.415	−14.365	0.707	1.415
Retail sales of consumer goods	1.501	0.175	5.715	2.647	0.175	5.715

Note: Dependent variable: carbon sink value.

. In the column labeled “Collinearity diagnosis (1)”, the collinearity diagnosis results after excluding budgetary expenditure are shown. Since the VIF for gross domestic product, primary industry, secondary industry, and tertiary industry are all greater than 10, indicating the presence of collinearity in the model. Therefore, further adjustments to the indicator system are necessary. After removing gross domestic product, which has the highest VIF, the results in the column labeled “Collinearity diagnosis (2)” indicate that the VIF for all influencing factors is now below 10. This suggests that the collinearity issue has been resolved.

After conducting correlation analysis and collinearity diagnosis, we proceeded with the subsequent analysis using these nine factors: primary industry, secondary industry, tertiary industry, population, urbanization, fixed asset investment, net income of farmers, road, and retail sales of consumer goods.

3.3. Estimation Results of GTWR Model

After processing the influencing factors through correlation analysis and collinearity diagnosis, we used GTWR to analyze the impact of the remaining nine factors on carbon sequestration value. Based on the optimal bandwidth and corrected Akaike information criterion (AICc), the regression results of GTWR are presented in

Table 4. Regression coefficient of the GTWR results of various variables.

Independent Variable	Minimum	1/4 Quantile	Median	3/4 Quantile	Maximum	Mean
Primary industry	−49.5488	−1.4441	7.3157	17.9365	69.9834	6.0898
Secondary industry	−49.1867	−5.2318	−3.1118	−1.4656	7.9933	−4.1046
Tertiary industry	−65.2613	−6.8220	−1.5396	−0.4838	28.8074	−4.4327
Population	−0.1289	−0.0047	−0.0021	−0.0013	0.5397	0.0126
Urbanization	−70.3012	−22.9614	−3.0294	11.7660	27.8079	−6.9772
Fixed asset investment	−4.2803	−1.7524	−0.8884	0.0848	6.5773	−0.7108
Net income of farmers	−60.0863	6.5300	11.4480	22.3873	211.8266	19.2612
Road	−109.4564	−38.5274	−19.5869	−7.7354	151.2679	−19.6275
Retail sales of consumer goods	−16.9561	0.0122	1.1097	5.2346	23.7884	2.8191
R2	0.8446
Adjust R2	0.8412
Bandwidth	0.1147
AICc	3568.0500

. It shows that the bandwidth and AICc values are 0.1147 and 3568.0500, respectively. The R² and Adjusted R² are 0.8446 and 0.8412, indicating a good fit of the model. The wide range of minimum, median, and maximum values of the regression coefficients for each factor indicates non-stationarity in both time and space for the intensity of these influencing factors. In the following sections, we will separately describe the temporal and spatial differences between these influencing factors and carbon sink value.

3.3.1. Temporal Difference of the Factors

Further calculations of the annual average coefficients were conducted, and a scatter plot was generated (Figure 6). The results reveal that the regression coefficients for the primary industry, population, and net income of farmers are positive, indicating that these three factors have a positive impact on the variation of carbon sequestration value. The coefficients for the secondary industry, tertiary industry, fixed asset investment, and road are all less than 0, suggesting a negative impact on the carbon sequestration value. The impact of urbanization on carbon sink value gradually transitions from positive to negative, while the impact of retail sales of consumer goods on carbon sink value shifts from negative to positive. It is evident that these socio-economic factors exhibit inconsistent effects on the carbon sequestration value and demonstrate strong temporal non-stationarity characteristics.

3.3.2. Spatial Difference of the Factors

Based on the calculation results of GTWR, spatial distribution maps of the coefficients were generated using ArcGIS 10.2 software (Figure 7). The regression coefficients for each county can be found in

Table A1. Spatial regression coefficient of socio-economic factors on carbon sink value in counties of Fujian Province from 2000 to 2020.

County	PI	SI	TI	P	U	FAI	NIF	R	RSCG
Anxi	15.9835	−5.7673	−1.2651	−0.0051	−21.2941	−2.1037	10.9893	−14.0270	5.2536
Cangshan	8.8788	−1.9835	−1.1384	−0.0017	−29.0175	−0.0188	10.3049	−28.8745	0.6232
Chengxiang	20.0342	−2.1125	−0.0390	−0.0023	18.4363	−2.2427	7.9319	−10.4282	−0.4235
Datian	−3.8477	−8.8413	1.2828	−0.0110	−28.6159	−1.8464	10.3711	−2.4936	8.4232
Dehua	13.4107	−4.5800	−0.1686	−0.0048	4.8074	−3.1556	8.4121	−13.0038	2.1451
Dongshan	5.0761	−5.8513	7.4950	−0.0084	−23.9610	3.5304	11.4672	−64.9250	2.1555
Fengze	11.2150	−2.5918	−1.3550	−0.0030	9.5419	−1.5021	10.5588	−6.0279	0.5888
Fuan	3.6149	−0.1216	−4.4796	−0.0019	10.1476	−1.7602	19.6113	−27.3902	0.4491
Fuding	−6.5422	0.1979	−9.2500	0.0344	8.0865	−0.8461	36.9477	−26.5257	−3.4205
Fuqing	13.3989	−0.7732	−1.0263	−0.0014	−5.3436	−0.8225	7.3752	−14.9573	0.7975
Gutian	10.8123	−1.7650	−3.1211	−0.0028	−15.8005	−1.3829	19.5899	−52.5323	1.3747
Guangze	0.8108	−9.4161	−6.7397	0.2061	9.2886	0.2996	26.4849	−25.3611	3.2549
Haicang	27.2940	−3.9389	−1.3549	−0.0020	−15.1728	−0.5708	9.7382	−11.2566	1.7532
Hanjiang	21.5382	−1.6765	−0.4132	−0.0018	4.4943	−1.5197	5.0720	−12.3989	0.5073
Huli	28.6625	−3.4724	−1.2039	−0.0018	−10.0029	−0.6424	8.9791	−7.9062	1.2785
Huaan	13.6809	−6.3855	−2.1600	−0.0060	−25.9712	−0.1420	13.0881	−36.1001	7.2464
Huian	0.6042	−1.9923	−1.3053	−0.0030	13.5705	−1.3786	10.2117	−6.0096	0.0800
Jimei	26.8871	−4.0031	−1.4885	−0.0022	−15.0372	−0.8623	10.0563	−9.4766	2.0621
Jianning	2.8362	−3.1674	−14.6309	0.2031	−0.1744	−1.1020	22.0334	−1.6436	11.8220
Jianou	−18.0136	−6.4318	−27.5936	0.0008	12.3906	−2.6985	94.1063	−42.8972	−0.2384
Jianyang	−7.6294	−20.6415	−36.9458	0.1613	17.7213	−0.0977	116.6125	−44.4926	2.4651
Jiangle	0.1786	−4.0249	−11.3893	0.0483	10.7043	−0.6618	21.2068	−15.8052	9.7711
Jiaocheng	6.5005	−1.4329	−1.8377	−0.0022	−6.7726	−1.3153	16.5175	−33.2570	0.0346
Jinan	6.5984	−2.1421	−1.3715	−0.0019	−33.4590	−0.1567	12.8428	−34.9172	0.6224
Jinjiang	19.9467	−2.7332	−1.1227	−0.0022	3.6877	−0.8670	8.9202	−5.3283	0.6921
Licheng	15.8145	−2.8844	−1.3542	−0.0029	7.3582	−1.5053	10.5764	−6.2045	0.8368
Licheng	15.8191	−1.1498	−0.0577	−0.0019	15.2564	−1.5740	5.1410	−9.8433	−0.0260
Liancheng	−31.8773	−4.3220	7.8831	−0.0700	3.0263	−1.8521	−15.5766	99.8694	3.7051
Lianjiang	5.9563	−2.0791	−1.1380	−0.0020	−25.9351	−0.1622	12.7255	−33.8748	0.2822
Longhai	24.4829	−4.5431	−1.3205	−0.0025	−17.6674	0.4032	10.0577	−22.4954	2.4910
Longwen	24.1939	−4.9482	−1.5757	−0.0029	−20.0591	0.1473	10.7507	−23.0865	3.2122
Luoyuan	6.2674	−1.9399	−1.4290	−0.0021	−21.2059	−0.6389	14.8537	−35.9559	0.2597
Luojiang	14.3876	−2.8777	−1.5686	−0.0036	17.5183	−2.5359	13.3443	−7.6264	0.1165
Mawei	6.9668	−1.9977	−1.0756	−0.0018	−28.1739	0.1083	10.9850	−30.4082	0.4459
Minhou	9.3518	−2.3502	−1.4217	−0.0020	−35.2623	−0.2477	12.2613	−34.6093	0.7886
Minqing	15.0397	−3.7658	−0.6501	−0.0022	−29.3771	0.0064	8.1183	−30.4012	0.3178
Mingxi	−23.0039	−0.8529	−14.5784	−0.0580	−5.2053	−1.0323	16.7737	27.0507	16.5909
Nanan	21.7802	−3.7071	−1.4066	−0.0035	4.0494	−2.0122	11.4684	−7.5072	1.6034
Nanjing	15.2288	−6.4448	0.7825	−0.0078	−23.5032	2.2457	6.2642	−56.6368	7.0914
Ninghua	−10.5000	−3.3309	−14.4794	0.1669	6.0106	−1.4643	1.3143	54.1184	20.1179
Pinghe	18.5964	−6.2333	6.9075	−0.0092	−21.8422	3.7642	−2.6871	−63.6388	4.0584
Pingtan	10.4525	−0.9499	−1.5337	−0.0013	−5.0219	−0.5565	12.1137	−17.4390	0.8790
Pingnan	8.4313	−1.0697	−5.5519	−0.0027	2.5837	−2.2154	26.4037	−50.4884	1.9172
Pucheng	−24.3845	−17.6214	−42.7575	−0.0206	5.7070	0.2531	131.6210	−55.9426	2.3173
Qingliu	−26.5408	−1.3609	−15.8289	−0.0274	−1.8379	−1.6829	4.5883	73.8125	20.3702
Quangang	8.6700	−2.0773	−0.9396	−0.0028	18.5730	−1.8944	10.3016	−7.9788	−0.3249
Sanyuan	−25.5173	−2.7965	−10.6180	−0.0855	−9.8307	−1.1238	25.6155	18.3518	11.0254
Shaxian	−8.7242	−4.3818	−13.6242	0.0246	−10.8210	−1.1600	40.9681	−1.5539	4.2562
Shanghang	−26.5362	0.3799	17.3336	−0.0582	−34.5489	−0.2164	0.1090	−8.5871	−11.4173
Shaowu	1.5683	−8.5746	−9.7489	0.1148	15.5562	0.0900	26.5249	−30.4564	7.5602
Shishi	10.7804	−2.2088	−1.0441	−0.0023	6.6847	−0.8411	8.4767	−4.9772	0.3999
Shouning	1.7816	1.1590	−13.6201	−0.0002	14.8781	−2.0040	34.8969	−31.9156	1.9322
Shunchang	−3.9663	−7.5184	−28.2301	0.1487	13.6330	−0.8177	76.3143	−36.2856	5.3270
Siming	28.6986	−3.3946	−1.1185	−0.0017	−9.7850	−0.5334	8.7474	−8.3471	1.1029
Songxi	−24.4696	−5.3516	−41.1911	0.0102	16.3446	−1.8369	119.7730	−51.1740	1.5911
Taijiang	8.5239	−2.0626	−1.1965	−0.0018	−31.0669	−0.0425	10.8259	−30.4142	0.6441
Taining	2.9268	−3.9289	−12.4313	0.0996	7.8697	−0.6529	20.3418	−16.4452	10.5275
Tongan	25.3661	−4.1573	−1.5752	−0.0026	−13.2786	−1.1877	10.4935	−8.1721	2.4291
Wuping	−22.0098	5.7757	11.7330	−0.0231	−54.0756	0.3769	7.4760	−69.2838	−9.9003
Wuyishan	−3.1201	−30.1463	−32.1573	0.0663	11.8937	0.8983	108.2856	−52.9214	7.8438
Xiapu	2.6438	−0.7260	−3.5878	−0.0020	10.0864	−1.4939	20.6550	−27.6305	−0.3679
Xianyou	23.5510	−3.4250	−0.4356	−0.0028	21.2699	−3.3208	13.8602	−11.5404	−0.9080
Xiangcheng	21.9094	−5.5884	−1.7257	−0.0038	−21.6420	0.5666	11.1377	−31.3730	4.6838
Xiangan	27.2147	−3.5030	−1.3106	−0.0021	−6.1582	−0.8514	9.3777	−6.4137	1.4563
Xinluo	−10.8335	−3.7299	3.0146	−0.0199	−21.2234	−0.3040	14.9816	−33.7534	0.2996
Xiuyu	8.7767	−0.8465	0.0214	−0.0019	16.3443	−1.1580	5.0299	−8.6935	−0.2183
Yanping	7.2043	−6.6162	−8.9568	−0.0011	−11.1001	−2.3276	32.9429	−23.6696	2.3887
Yongan	−25.9435	−5.5793	−10.4141	−0.0747	−10.9063	−1.5680	21.1559	32.7433	16.4764
Yongchun	14.5084	−5.3248	−0.2097	−0.0063	−4.0425	−2.8872	8.7405	−12.2749	4.3721
Yongtai	22.0466	−3.8467	−0.1849	−0.0021	−8.5873	−1.1718	5.5810	−15.2251	0.2854
Youxi	11.1033	−6.7803	−0.6224	−0.0017	−30.2510	−2.1009	9.0971	−0.3129	0.2499
Yunxiao	15.1080	−5.6282	5.7846	−0.0078	−19.6982	3.9461	3.0070	−66.5510	4.7222
Zhangping	−1.7381	−6.8265	1.1870	−0.0112	−20.9779	−0.8888	12.2294	−28.6895	5.9364
Zhangpu	19.3500	−4.8568	−1.1677	−0.0032	−17.1030	1.7983	9.9953	−37.2112	3.8912
Changle	8.5916	−1.7102	−1.0305	−0.0016	−20.7526	0.0836	10.1019	−25.7139	0.4738
Changtai	22.9546	−5.0117	−1.8746	−0.0031	−22.4598	−0.8272	11.5862	−16.5333	3.6464
Changting	29.6196	−10.9522	9.3002	0.4234	−15.4957	0.1178	−51.7748	65.1048	9.1367
Zhaoan	8.7088	−6.5803	18.5141	−0.0149	−28.6439	3.5316	−0.2910	−66.7754	−2.6343
Zherong	0.3971	0.8197	−9.7115	−0.0007	14.8247	−1.5743	29.7526	−30.1623	0.4705
Zhenghe	−1.2476	−0.4244	−21.2517	−0.0001	19.6837	−2.8706	61.2792	−49.4016	2.8838
Zhouning	5.5590	−0.1925	−5.5249	−0.0021	8.2904	−2.0338	22.2778	−34.1989	1.4103
Gulou	8.1579	−2.1120	−1.2493	−0.0018	−32.2988	−0.0584	11.3085	−31.6739	0.6570
Yongding	−4.5524	−1.8789	16.7254	−0.0272	−38.9686	1.7607	−13.0309	−49.6323	−5.0154

Abbreviation: PI—Primary Industry; SI—Secondary Industry; TI—Tertiary Industry; P—Population; U—Urbanization; FAI—Fixed Asset Investment; NIF—Net Income of Farmers; R—Road; RSCG—Retail Sales of Consumer Goods.

of Appendix A. In Figure 7, blue and red correspond to positive and negative regression coefficients, respectively. The intensity of color represents the magnitude of the coefficient, indicating the strength of the impact on the carbon sink value. It can be observed that there are differences in the impact of various factors on the carbon sink value across counties from 2000 to 2020.

The primary industry has a positive impact on the carbon sink value for approximately 75% of counties, mainly concentrated in coastal areas. In contrast, the counties in which primary industry has a negative impact are primarily distributed inland. The primary industry involves diverse agricultural activities such as cultivation, livestock farming, fishing, and forestry. There are significant differences in the agricultural development foundation across counties, leading to a range of different agricultural production methods and levels of agricultural development, thereby generating distinct environmental benefits. This may lead to spatial heterogeneity in the impact of the primary industry on carbon sink value. For example, in coastal counties like Zhangpu and Yunxiao, tea plantations and ecological orchards are common, which enhance long-term vegetation cover and carbon sink. In contrast, some inland counties such as Ninghua or Liancheng rely more on traditional dryland farming or hillside cultivation, which may lead to soil erosion and reduced carbon sink.

The secondary industry has a negative impact on the carbon sink value for nearly 94% of counties, with only five counties showing a positive impact. The secondary industry primarily includes economic sectors such as industry and manufacturing, which often involve extensive industrial production and energy consumption. The development of these sectors may lead to excessive resource exploitation and ecosystem degradation, thereby suppressing the growth of the carbon sink value.

The tertiary industry primarily has a positive impact on the carbon sink value for counties in the southeast region of Fujian Province, while it has a negative impact on most counties in the study area. Despite some progress in sustainability within certain tertiary industries, such as promoting green finance and providing environmental consulting services, the research results indicate that the negative impact of the tertiary industry on the carbon sink cannot be ignored. There is an urgent need to encourage the tertiary industry to actively adopt environmental protection measures to promote the conservation and increase of carbon sink value.

The population has both positive and negative impacts on carbon sink value. Counties with a positive impact are mainly located in the northwest part of Fujian Province, but they represent only 17% of the total. Counties where the population has a strongly negative impact on carbon sink value are distributed in the central and western parts of Fujian Province. Population growth is often associated with changes in land use, such as urban expansion and the conversion of agricultural land into non-agricultural uses. These changes may lead to deforestation, loss of wetlands, and a reduction in vegetation cover, thereby decreasing carbon sink value.

Urbanization has a positive impact on carbon sink values in 41% of counties and a negative impact in 59% of counties. Counties with a positive impact are mainly located in the northern and eastern coastal areas of Fujian Province. Different stages of urbanization may have varying effects on carbon sink value, leading to spatial non-stationarity.

Fixed asset investment has a negative impact on 77% of counties. The impact of fixed asset investment on carbon sink value depends on the direction of investment and the sustainability of projects. On the one hand, fixed asset investment can be used for the construction of sustainable infrastructure and ecological restoration projects, enhancing the carbon sink capacity of areas. On the other hand, it may lead to overdevelopment and changes in land use, disrupting ecosystems and reducing the carbon sink potential of the land.

The net income of farmers has a negative impact on carbon sink values in 6% of counties, but it exerts a positive impact on carbon sink values in nearly 94% of counties. The increase in net income of farmers may imply more investment and resources being used in agricultural production. If these investments are directed towards sustainable agricultural practices, such as organic farming, agricultural diversification, and the maintenance of ecosystem health, it can contribute to improving soil quality and increasing vegetation cover, thereby enhancing the carbon storage capacity of farmland.

The impact of roads on the carbon sink value is predominantly negative. Only in eight counties clustered in the western part of Fujian Province, roads have a positive impact on the carbon sink value. The increase in road density is usually associated with changes in land cover, especially in areas with dense urbanization and infrastructure development. This can lead to habitat fragmentation, where originally continuous natural ecosystems are fragmented into smaller, isolated fragments. Habitat fragmentation can have adverse effects on vegetation, animal habitats, and the overall integrity of ecosystems, reducing the stability and value of carbon sinks.

The spatial heterogeneity of the impact of retail sales of consumer goods on the carbon sink value is primarily positive, as its growth has a promoting effect on the carbon sink value in 86% of the counties. This may be attributed to the increasing environmental awareness in society, leading some consumers and businesses to pay more attention to sustainable consumption and production methods. In response to market demands, businesses may adopt more environmentally friendly measures, channeling more funds into environmental protection and carbon sink projects, thereby promoting ecosystem conservation.

4. Discussion

4.1. Comparison with International Findings on Carbon Sink Value

The results of this study share several commonalities with findings from international research. Some studies have estimated global forest carbon sinks over the long term, from 1990 to 2019, and highlighted the critical role of large-scale afforestation in sustaining carbon sequestration [52]. In light of China’s ongoing efforts to expand carbon sink projects across broader terrestrial ecosystems, our assessment includes not only forests but also croplands and grasslands in the calculation of carbon sink value.

Regarding the analysis of influencing factors, our findings both align with and diverge from existing research. In many countries, factors such as urbanization, industrial development, and land use change are consistently identified as key drivers shaping carbon sink values. For instance, studies conducted in Europe and North America have shown that increasing urbanization and the expansion of transportation infrastructure often result in a decline in carbon sink capacity, thereby directly reducing carbon sink value [43,53]. Similarly, research in tropical regions such as North Africa and South America has underscored the negative effects of urban expansion and population growth on carbon sink performance [54,55]. However, differences also exist due to national contexts and development stages. In some developed countries, carbon sink value changes are mainly driven by forest management and conservation policies [56,57]. In contrast, in rapidly developing regions like China, socioeconomic factors such as infrastructure investment, urban growth, and shifting consumption patterns also play a prominent role [58,59]. Moreover, compared to studies that focus primarily on deforestation or reforestation trends, this study identifies additional economic and demographic factors (e.g., fixed asset investment, retail sales, and net income of farmers) that are more specific to the Chinese context.

The use of GTWR in this study is not merely a methodological choice, but a necessity to capture the spatial and temporal non-stationarity in how socio-economic factors influence carbon sink value. Spatiotemporal heterogeneity refers to the variation in the strength and direction of relationships between variables across different locations and time periods. Traditional regression models assume spatial homogeneity and constant relationships across regions and time, which can mask localized dynamics and lead to misleading or overly generalized conclusions. By contrast, GTWR allows us to observe how the strength and direction of relationships vary across space and time, providing a more realistic understanding of human–environment interactions. The discovery of heterogeneity effects highlights that socio-economic drivers do not uniformly impact carbon sink value. For example, while population growth may stimulate ecological investment in one region, it could lead to land degradation and carbon loss in another. These differences arise from variations in local land use practices, policy implementation, ecological conditions, industrial structure, and governance capacity. Similarly, a single factor such as investment in fixed assets may enhance green infrastructure in urbanized counties but accelerate deforestation or land conversion in ecologically fragile areas. Recognizing this heterogeneity is crucial for designing place-based and time-sensitive environmental policies. It reinforces the need to avoid one-size-fits-all approaches and instead develop differentiated carbon sink management strategies that account for local development stages and ecological constraints.

4.2. Spatio-Temporal Distribution Characteristics of Carbon Sink Value

The research results based on the market value method reveal the spatiotemporal distribution characteristics of carbon sink value. In the temporal variation of carbon sink value in Fujian Province, a significant decrease is observed from 2005 to 2010, followed by slight fluctuations from 2010 to 2020. This trend aligns with the observed changes in carbon sink quantities in Fujian Province reported by Wu et al. (2023) [60]. During the period from 2005 to 2010, rapid expansion of construction land in Fujian Province led to the conversion of large areas of forests and grasslands into construction land, resulting in a reduction in carbon sink values. After 2010, the urban-rural construction land gradually approached a balanced state, leading to more stable fluctuations in carbon sink values. Furthermore, the uneven spatial distribution of carbon sink values reflects the impact of natural conditions (such as precipitation, temperature, and soil) on vegetation growth and carbon sequestration [61]. In terms of spatial distribution patterns, regions with high carbon sink values are concentrated in the southwest and eastern areas of Fujian Province. Firstly, counties such as Shanghang, Wuping, Xinluo, Zhangping, and Yongding belong to the Longyan prefecture-level city. Longyan City is one of the three national forestry carbon sink pilot cities in Fujian Province, endowing these counties with high carbon sink values due to abundant forest resources. Secondly, counties like Hua’an, Nanjing, Pinghe, Yunxiao, Zhangpu, Changtai, and Zhao’an are well-known for fruit and flower production, serving as agricultural development zones and ecological functional areas with a favorable ecological background, conducive to the development of carbon sinks. Finally, counties including Yongtai, Hanjiang, Xianyou, Dehua, and Yongchun become high carbon sink areas because they are located along the ecological functional protection zone centered around Daiyun Mountain, which is the largest mountain range along the southeast coast of China.

4.3. Implications for Differentiated Policies

To examine the factors driving changes in carbon sink value, we used the GTWR model. This method is well-suited for capturing complex variations across both space and time. Previous studies have demonstrated the unidirectional impact of factors such as population [62], roads [60], GDP [63], and urbanization [35] on carbon sinks and their values. However, our research reveals that these influencing factors exhibit spatiotemporal non-stationarity. The impact of urbanization on carbon sink value exhibits typical temporal non-stationarity, as its influence shifts from a positive effect to a negative impact. This may be related to the urbanization process in China. Around the year 2000, urbanization in China was in different stages of development. After 2000, China’s urbanization entered a new phase. It shifted from steady development focused on small town construction to rapid growth characterized by the coordinated expansion of large, medium, and small cities [64]. The excessive expansion of cities led to a reduction and fragmentation of ecological lands [65], resulting in an increasingly negative impact on carbon sink values. Moreover, the spatial heterogeneity of these factors is particularly complex. This is largely due to differences in development levels and natural resource endowments across counties. The non-stationary characteristics necessitate the implementation of targeted and differentiated strategies by Fujian Province, tailored to the specific conditions of each county.

Firstly, for counties such as Songxi, Jianyang, Qingliu, Mingxi, and Sanyuan, where all three industrial sectors (primary, secondary, and tertiary) show negative impacts on carbon sink value, industrial transformation is urgently needed. These counties are located in Sanming and Nanping, two national pilot cities for forestry carbon sinks. They have abundant forest resources but face difficulties in coordinating industrial development with ecological preservation. Therefore, we recommend building a vertically integrated carbon sink industry chain tailored to local resource advantages. Specifically, in the primary industry, sustainable forestry practices (e.g., afforestation, rotation logging systems, and ecological thinning) should be prioritized to enhance forest carbon sink capacity. In the secondary industry, which is likely dominated by resource-intensive industries, carbon market entry thresholds can be used to guide high-emission enterprises toward carbon neutrality. The tertiary industry, particularly local financial and tech service providers, should develop localized support services for carbon credit transactions, monitoring, and project financing to strengthen the ecosystem for green industries. These integrated strategies can address the systemic nature of carbon sink degradation in these regions.

Secondly, in counties including Pingtan, Jimei, Anxi, Yongchun, and Zhangpu, urbanization, population, and road have collectively exerted pressure on regional carbon sink values. These counties, located primarily in coastal or peri-urban zones, are experiencing rapid urban expansion, leading to green space fragmentation and ecological stress. In these areas, we recommend implementing spatially responsive urban greening strategies, such as the following: (1) incorporating multi-scale ecological corridors into land use planning to maintain landscape connectivity and biodiversity [66]; (2) applying green infrastructure principles to road networks to minimize ecological disruption; and (3) promoting vertical greening and rooftop forestry in densely built areas where land resources are limited. Additionally, urban carbon accounting systems should be piloted in these counties to integrate carbon sink planning into municipal performance assessments, thereby enhancing policy accountability.

Thirdly, in counties such as Fuding, Quangang, Xianyou, and Shanghang, where fixed asset investment and retail sales of consumer goods negatively affect carbon sink values, a key issue is the misalignment between capital flows and ecological sustainability. These areas are often characterized by investment-driven growth and rising consumerism, which may lead to land use change, energy consumption, and emissions. To address this, we propose the following: (1) strengthening green investment screening mechanisms to guide fixed asset investments toward low-carbon infrastructure, renewable energy, and ecological restoration projects; (2) establishing incentive schemes for ecological return on investment to attract private capital to forestry carbon sink projects; and (3) promoting carbon-labeled consumer goods [67], especially for agricultural and forestry products, to nudge consumer behavior toward low-emission options. These counties should also explore county-level green bond mechanisms to channel sustainable finance toward long-term ecological goals.

While these differentiated policy recommendations offer targeted pathways to enhance carbon sink value, their implementation may face several practical challenges. These include limited local governance capacity and technical expertise in carbon accounting, the lack of established mechanisms for cross-sectoral policy coordination, and potential resistance from stakeholders with short-term economic interests. Additionally, data availability and monitoring infrastructure at the county level may constrain effective policy execution, while aligning fiscal incentives and regulatory frameworks with ecological goals remains a long-term institutional task.

4.4. Uncertainty

Several uncertainties and limitations may affect the interpretation and generalizability of our results. First, the assumption that soil organic carbon levels remain constant from 2000 to 2020 simplifies data processing but may overlook gradual changes driven by land use shifts. Moreover, carbon sinks, particularly those based on vegetation and soil systems, are part of the short-term carbon cycle. Their sequestration is reversible and susceptible to both natural disturbances and anthropogenic activities, which may reduce the long-term reliability of carbon storage estimates. Second, this study does not include marine carbon sinks, which may result in an underestimation of the total carbon sink value in coastal areas. Given that Fujian is a coastal province with abundant marine resources, this limitation may lead to incomplete assessments of spatial carbon sink capacity. Third, we employed a fixed carbon price based on the 2020 national average trading price to ensure comparability across years. However, this simplification overlooks the dynamic fluctuations of carbon prices in the carbon trading market and the evolving estimation of social cost of carbon. These factors may influence the time-sensitive accuracy of our valuation, particularly for earlier years. Fourth, although the use of 25 km² grid cells is sufficient to capture broad spatial distribution patterns, finer-resolution grids could reveal more local-level variation in areas with highly fragmented land use. Similarly, our county-level spatial regression analysis may not fully capture localized ecological processes, which limits the applicability of our findings to finer policy scales. Fifth, this study does not incorporate climate extremes or ecological disturbances such as typhoons, pest outbreaks, or large-scale wildfires. These factors can significantly impact vegetation growth and carbon fluxes, especially in subtropical regions like Fujian, and may lead to estimation bias when omitted. Lastly, while Geographically and Temporally Weighted Regression enhances spatial interpretability, it cannot fully explain the underlying causal mechanisms. Socioeconomic factors interact with ecological processes in complex and nonlinear ways. Thus, field investigations and interdisciplinary research are still needed to validate and interpret spatial patterns and statistical associations.

5. Conclusions

In this study, we conducted a systematic assessment of carbon sink value in Fujian Province from 2000 to 2020, based on NEP simulations and the market value approach. The results indicate a declining trend in total carbon sink value, decreasing from CNY 3.212 billion to CNY 2.837 billion over the study period, along with a distinct spatial pattern characterized by higher values in the south and lower values in the north. Using Geographically and Temporally Weighted Regression, we further identified spatiotemporal non-stationary effects of influencing factors. Specifically, the temporal effects of urbanization and retail sales of consumer goods shifted between positive and negative impacts. The spatial effects of factors such as the structure of the three industries, population, fixed asset investment, and road varied in direction across different regions. Based on these findings, the study offers several key insights, as follows: (1) There are substantial regional disparities in carbon sink value. The southern part of Fujian shows relatively higher carbon sink value, indicating stronger ecosystem functions and vegetation recovery capacity, while the northern regions should focus on ecological restoration and forest development. (2) As socioeconomic conditions evolve, the direction and intensity of the impact of various factors on carbon sink value change over time, suggesting that policy design should take into account stage-specific effects. (3) Primary industry and net income of farmers show a positive contribution to carbon sink value, whereas industrialization and infrastructure construction may exert a suppressive effect. Therefore, it is necessary to balance economic development with ecological protection based on local conditions. We propose the following policy recommendations. Counties where all industrial sectors negatively affect carbon sink value should prioritize coordinated industrial upgrading and the integration of carbon sink strategies. In urbanized areas under pressure from population growth and infrastructure expansion, green planning should be adopted to enhance urban carbon sinks. In counties where investment and consumption appear to hinder carbon sink performance, policy should guide capital flows toward low-carbon industries and promote sustainable consumption patterns.

Carbon sink value and its related issues are currently hot topics in environmental research, and there are several areas that require further investigation. Future research can be improved in the following aspects: (1) The integration of higher-resolution satellite imagery, long-term ground observations, and ecological modeling could improve the accuracy of carbon sink estimation and the monitoring of spatiotemporal dynamics. (2) Studies could evaluate carbon sink value at the township level and incorporate variables related to climate conditions and biodiversity to better understand the interaction mechanisms between carbon sink value and ecosystem functions. (3) Exploring how carbon sink trading rules and market participant behavior influence carbon sink valuation could help establish scientifically grounded mechanisms for realizing carbon sink value, thereby offering practical guidance for policy formulation.