Evaluation of Noah-MP Land Surface Model-Simulated Water and Carbon Fluxes Using the FLUXNET Dataset
Abstract
1. Introduction
2. Methodology
2.1. Noah-MP Model
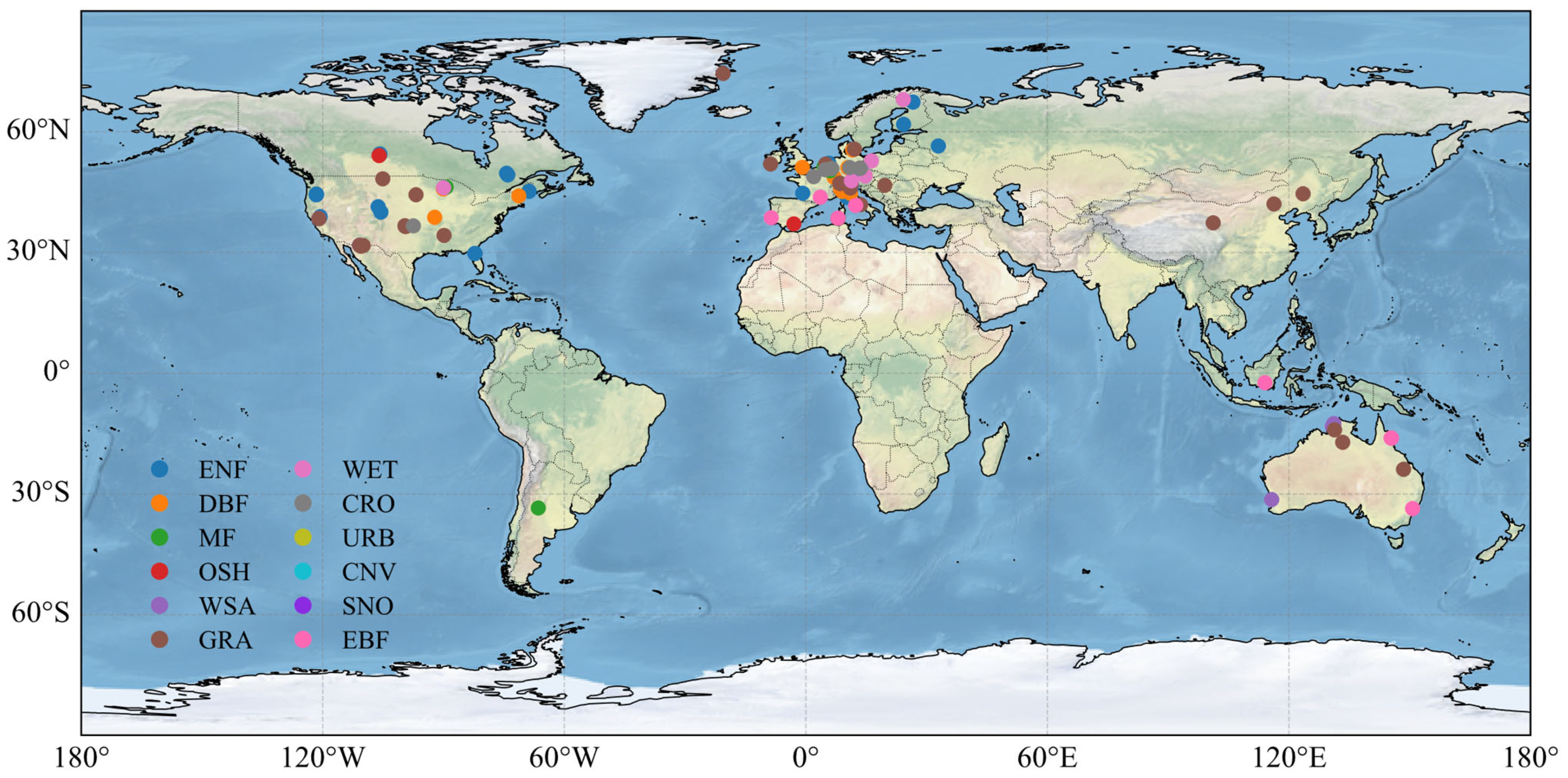
2.2. FLUXNET2015 Dataset
2.3. Experimental Design
2.4. Analysis Methods
3. Results and Discussion
3.1. Annual Scale
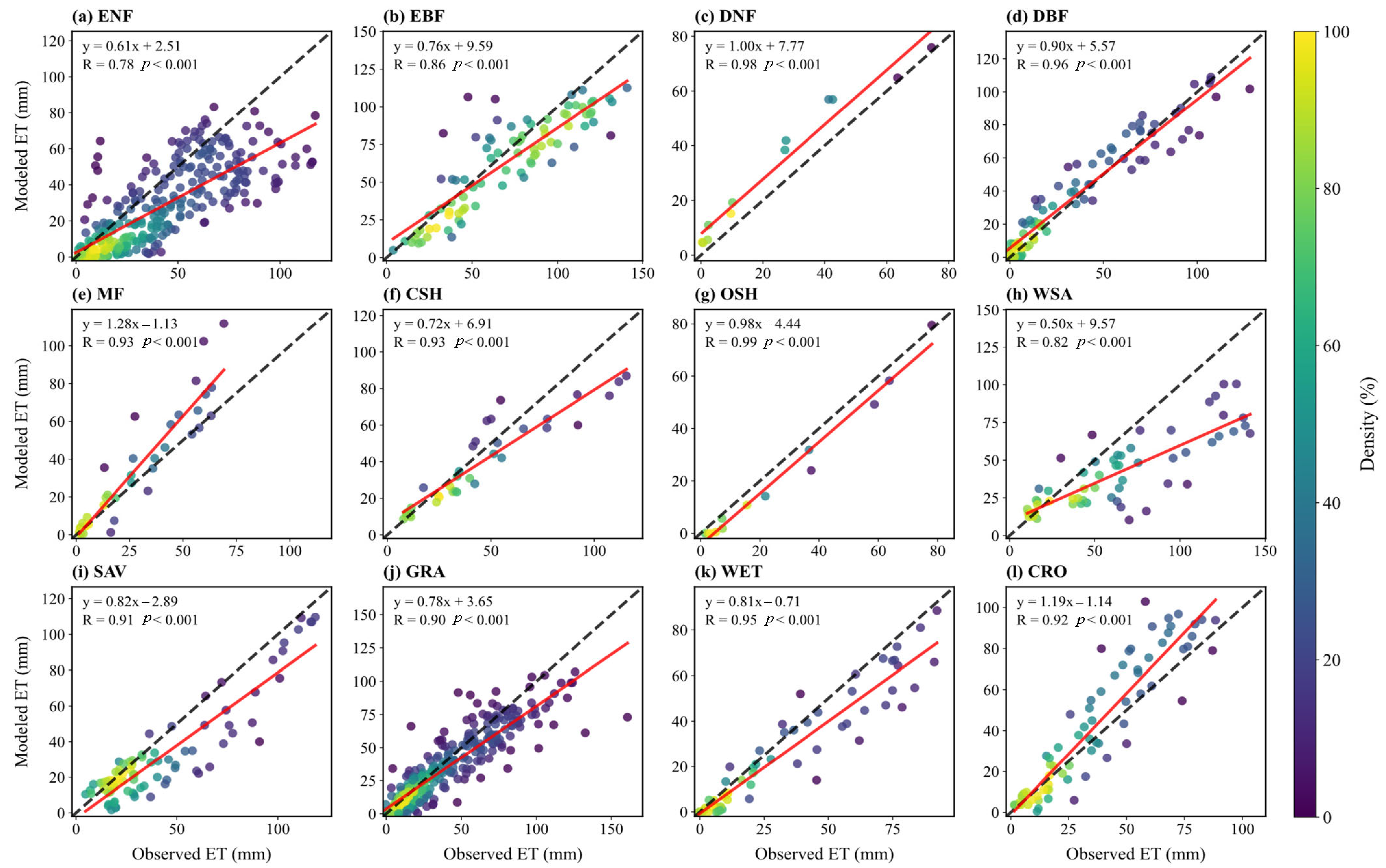
3.1.1. Evapotranspiration (ET)
3.1.2. Gross Primary Productivity (GPP)
3.2. Monthly Scale
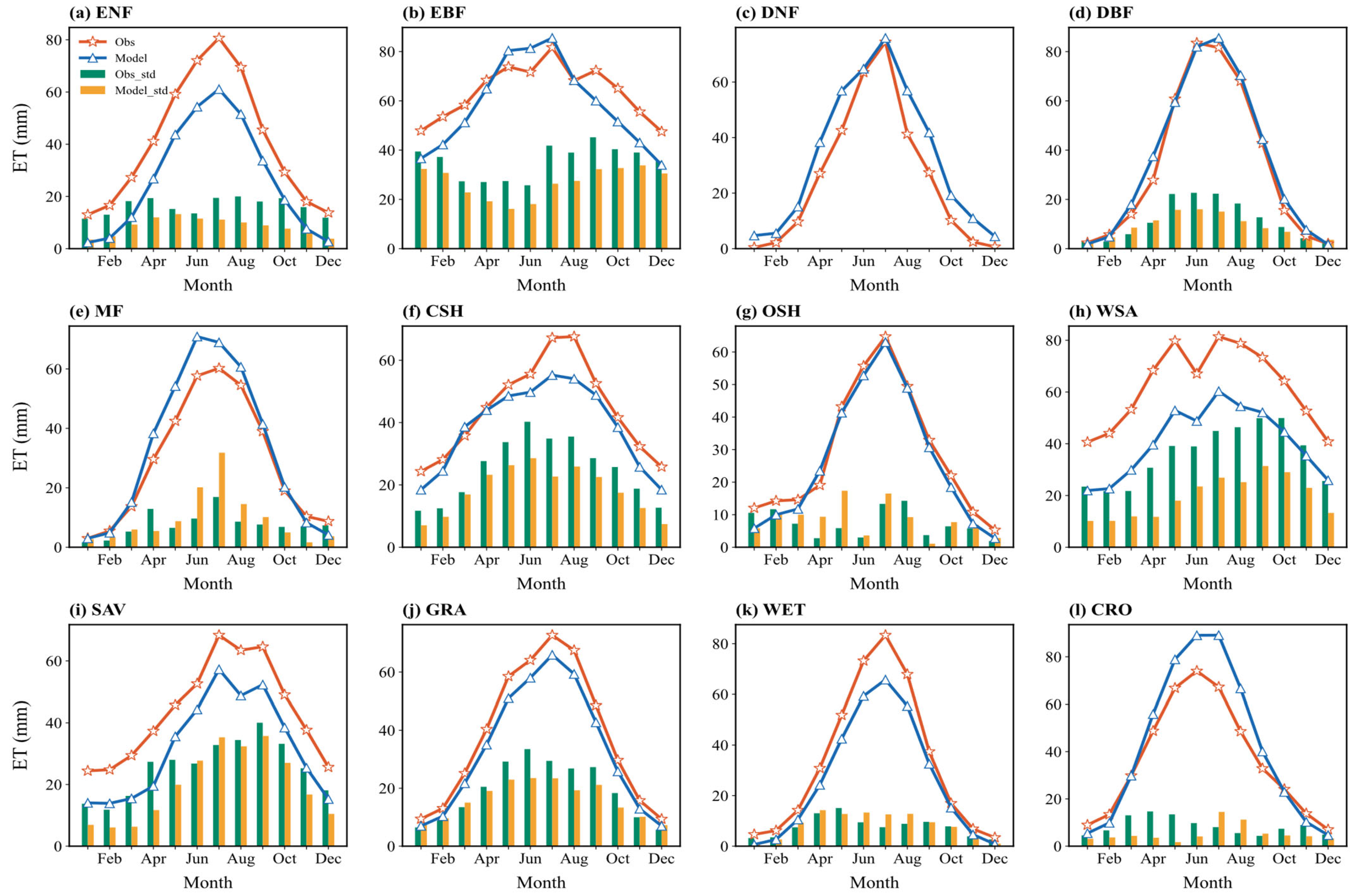
3.2.1. Evapotranspiration (ET)
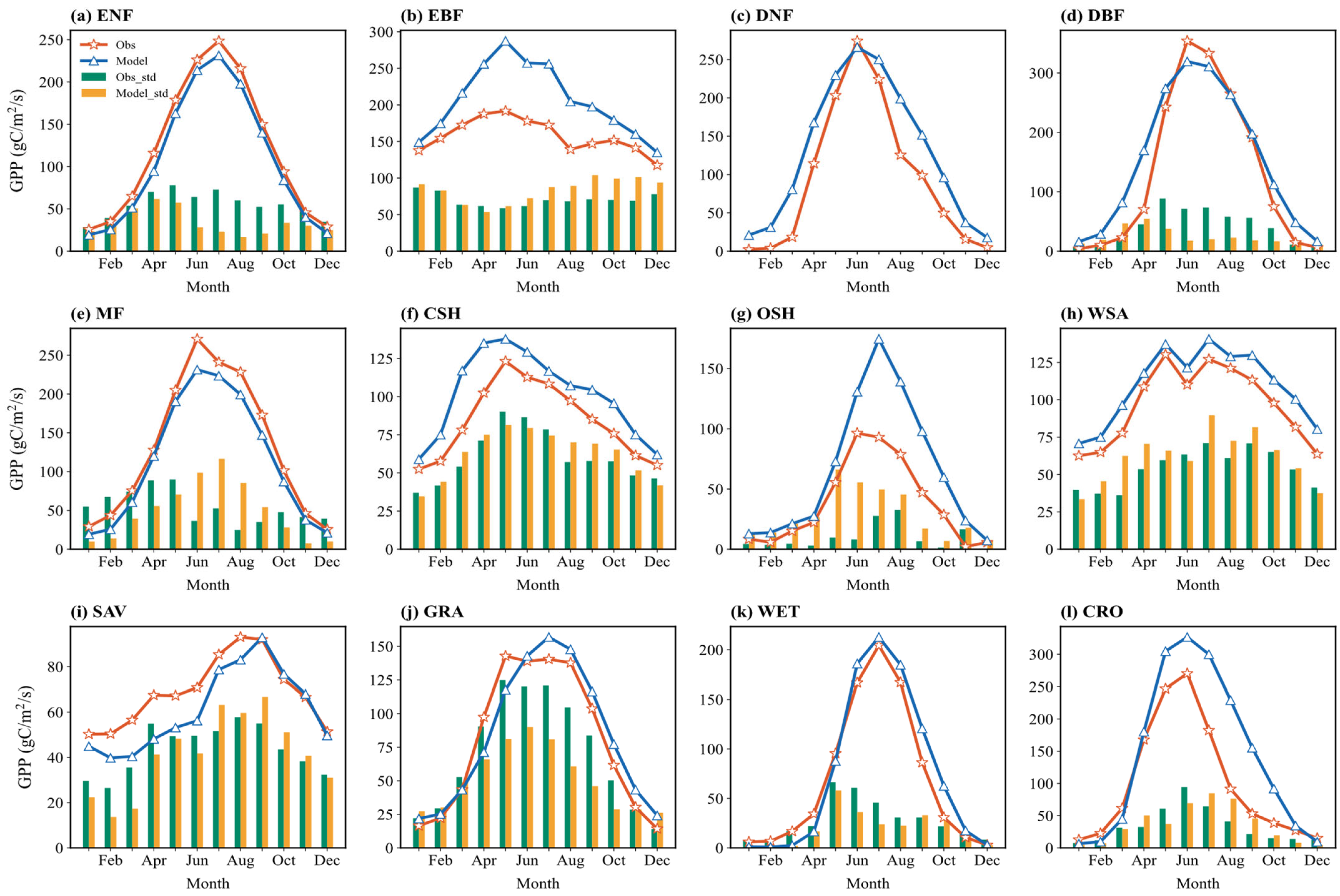
3.2.2. Gross Primary Productivity (GPP)
3.3. Diurnal Variation
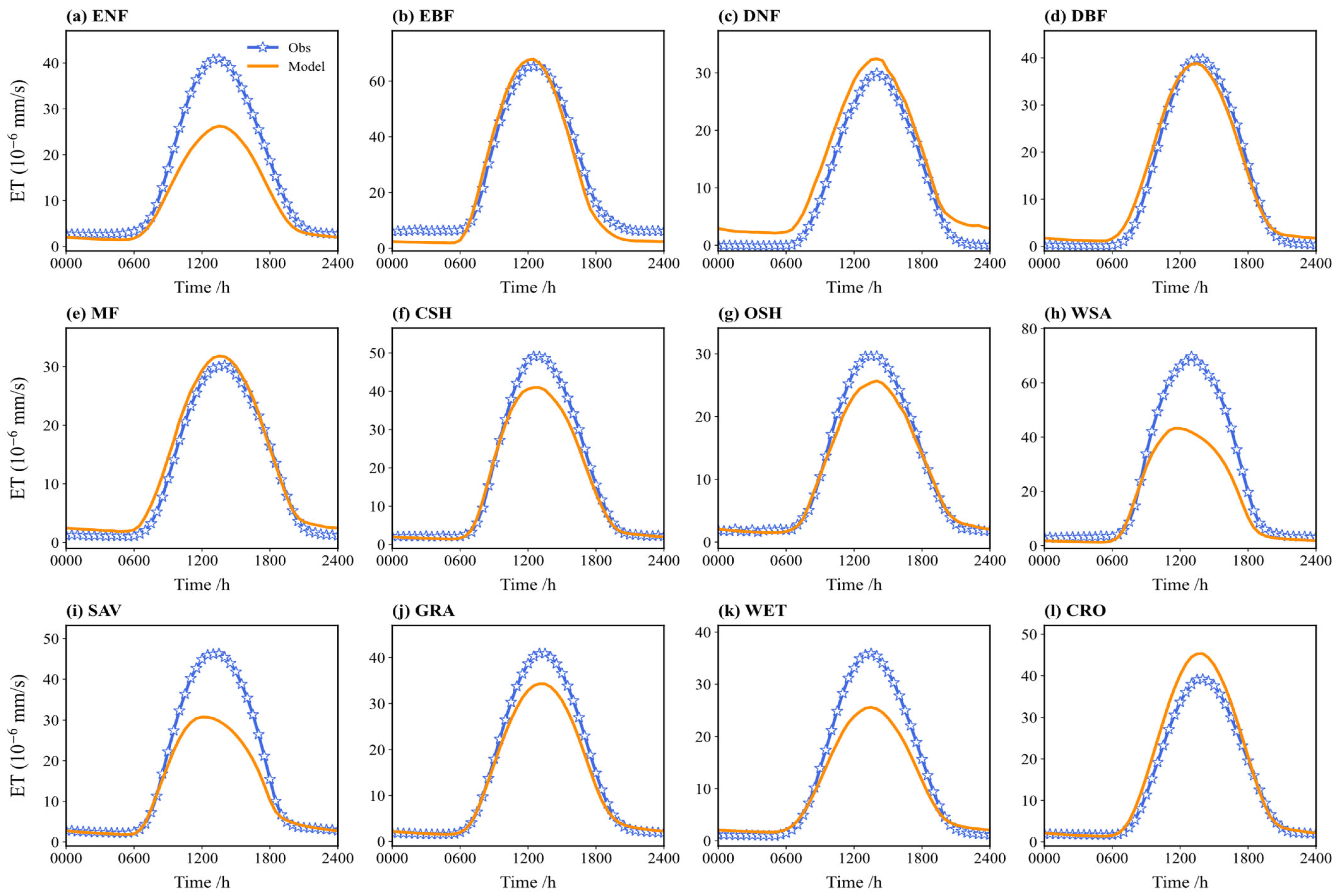
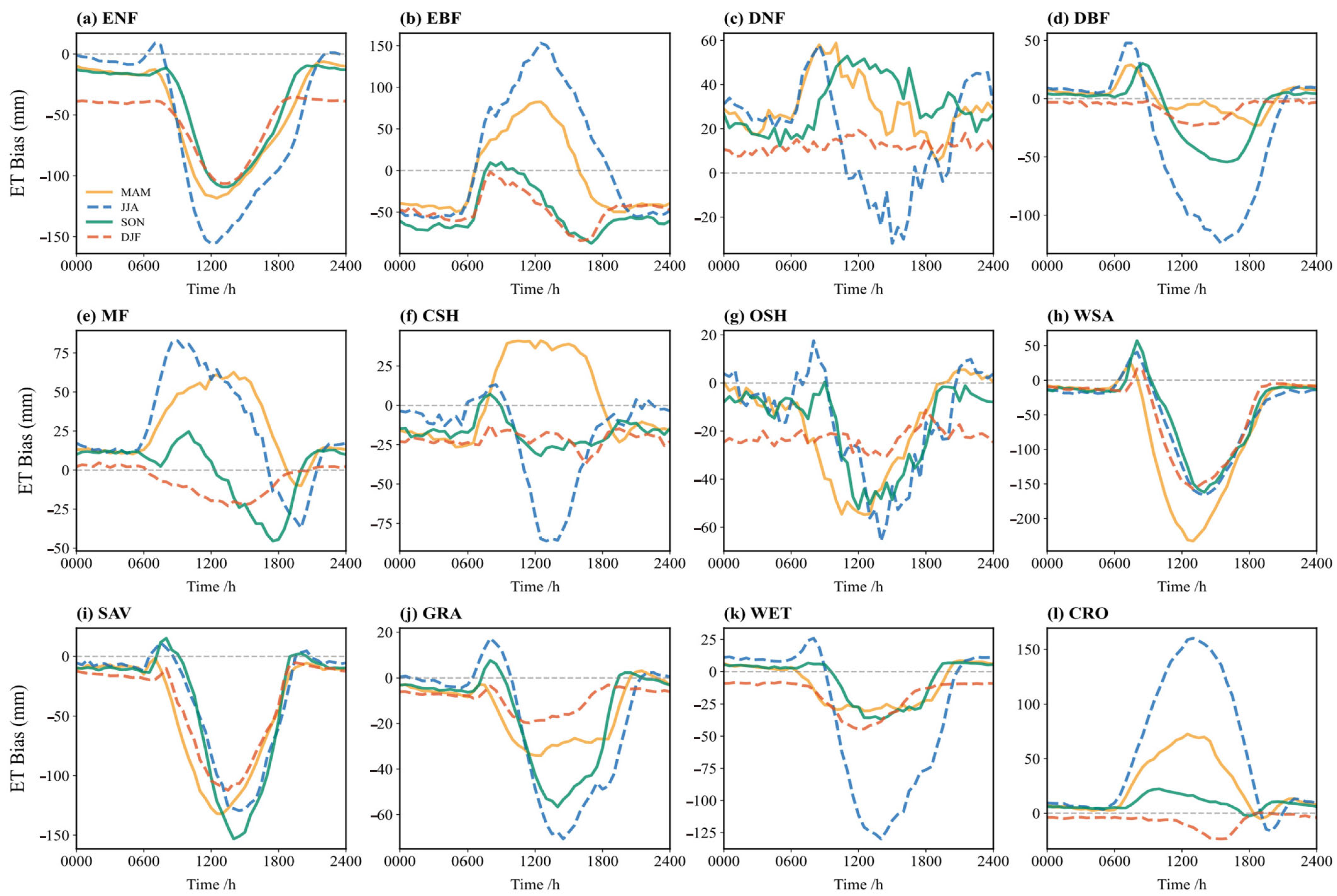
3.3.1. Evapotranspiration (ET)
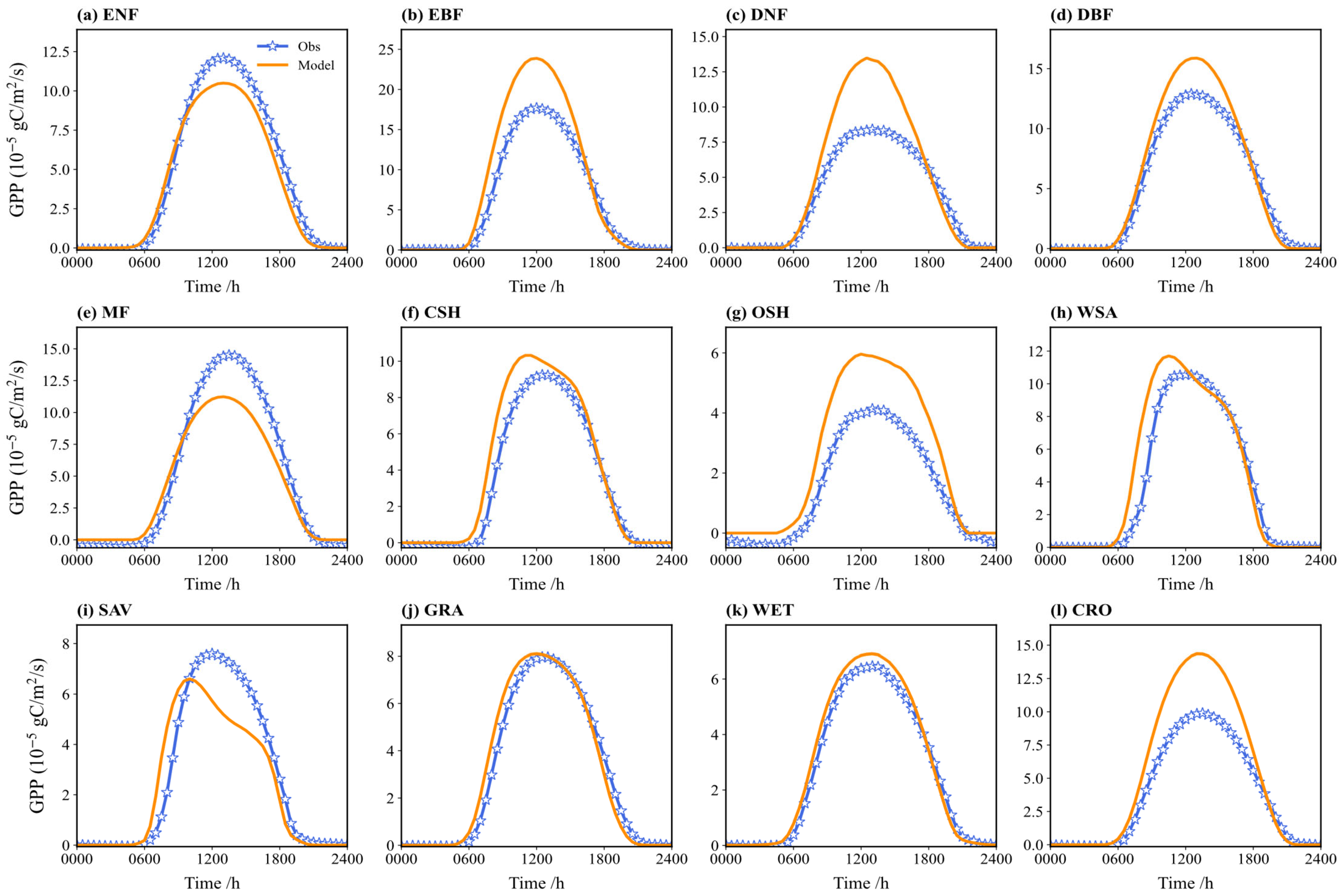
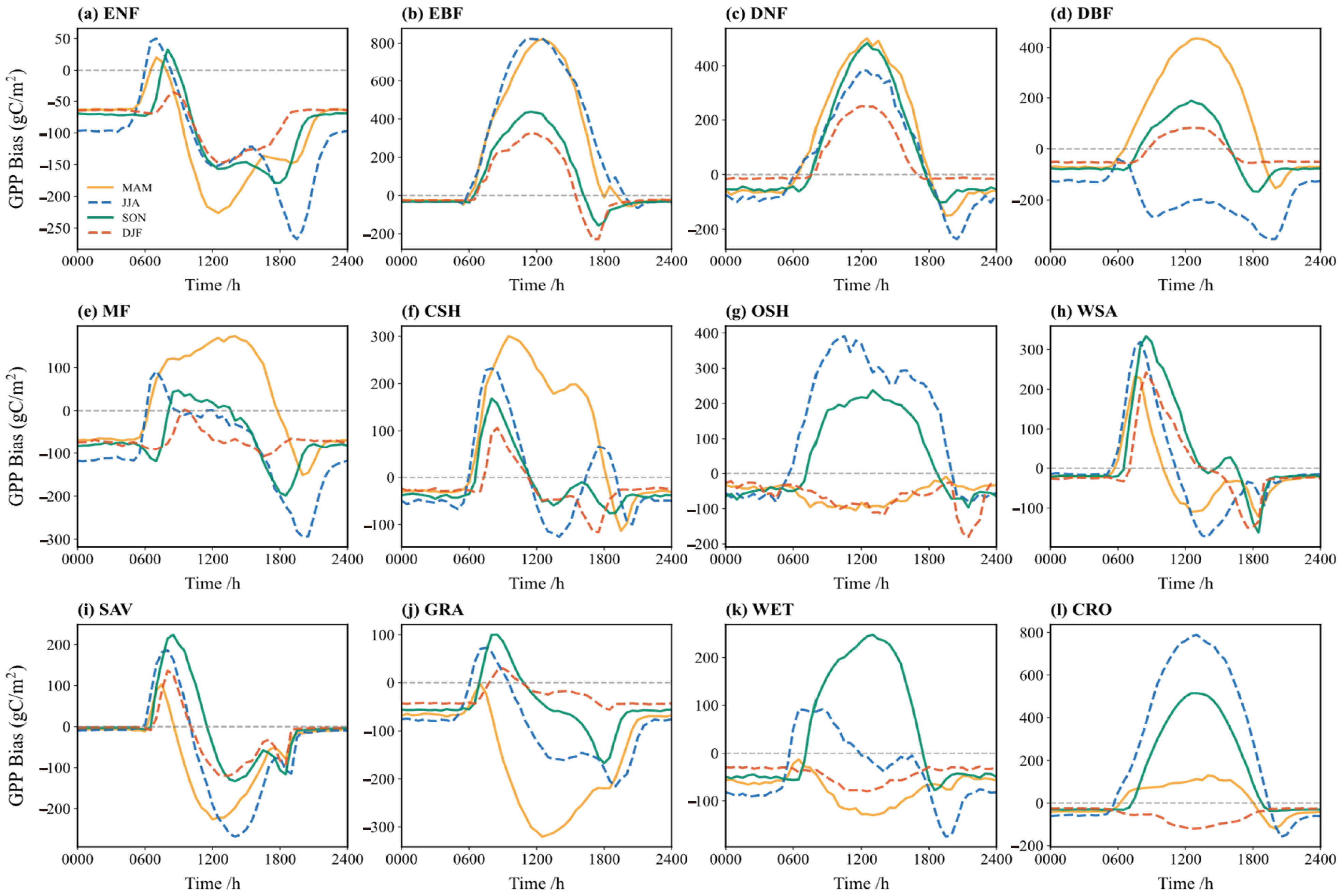
3.3.2. Gross Primary Productivity (GPP)
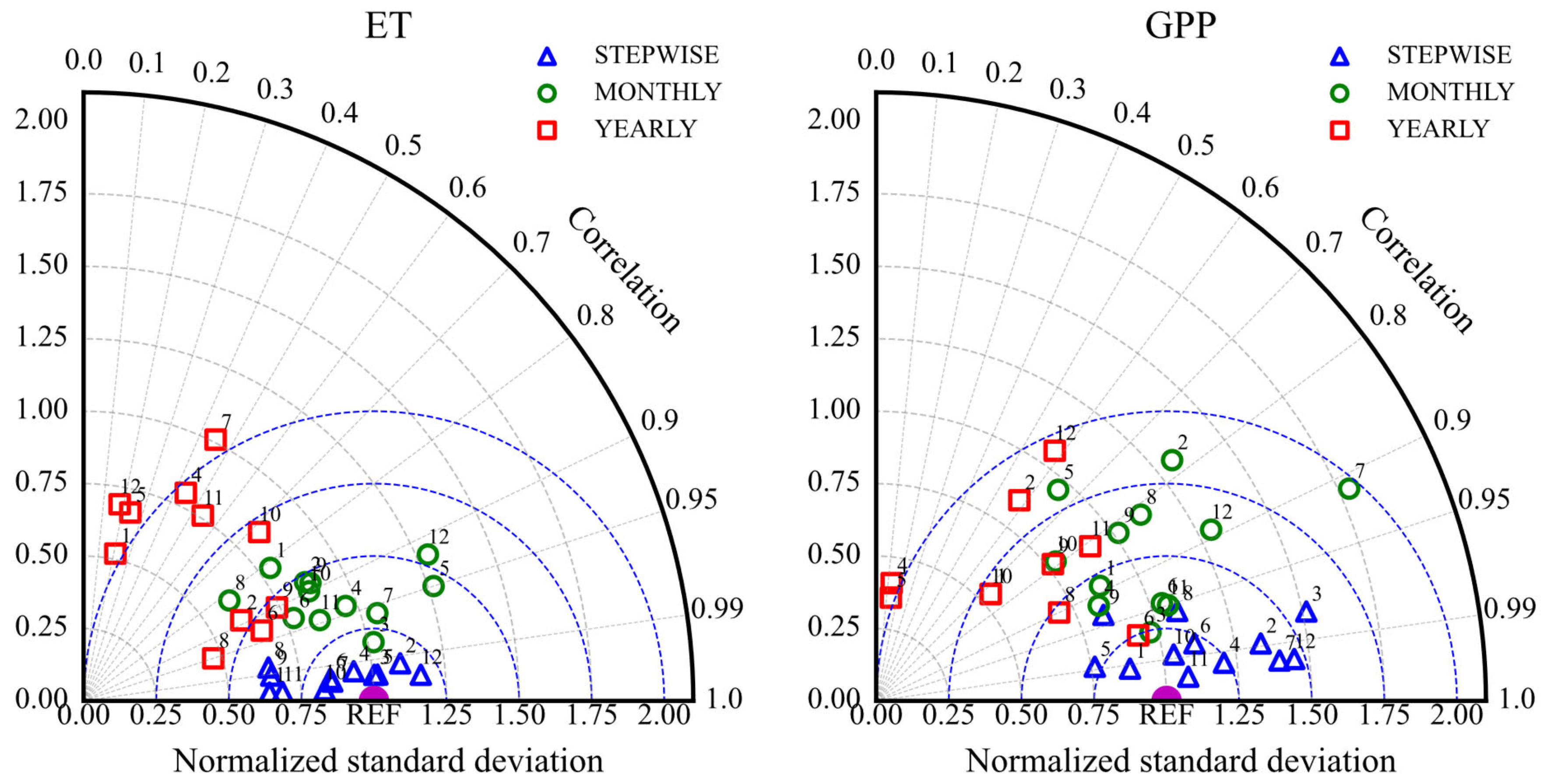
3.4. Comparison of Simulation Performance Across Different Temporal Scales
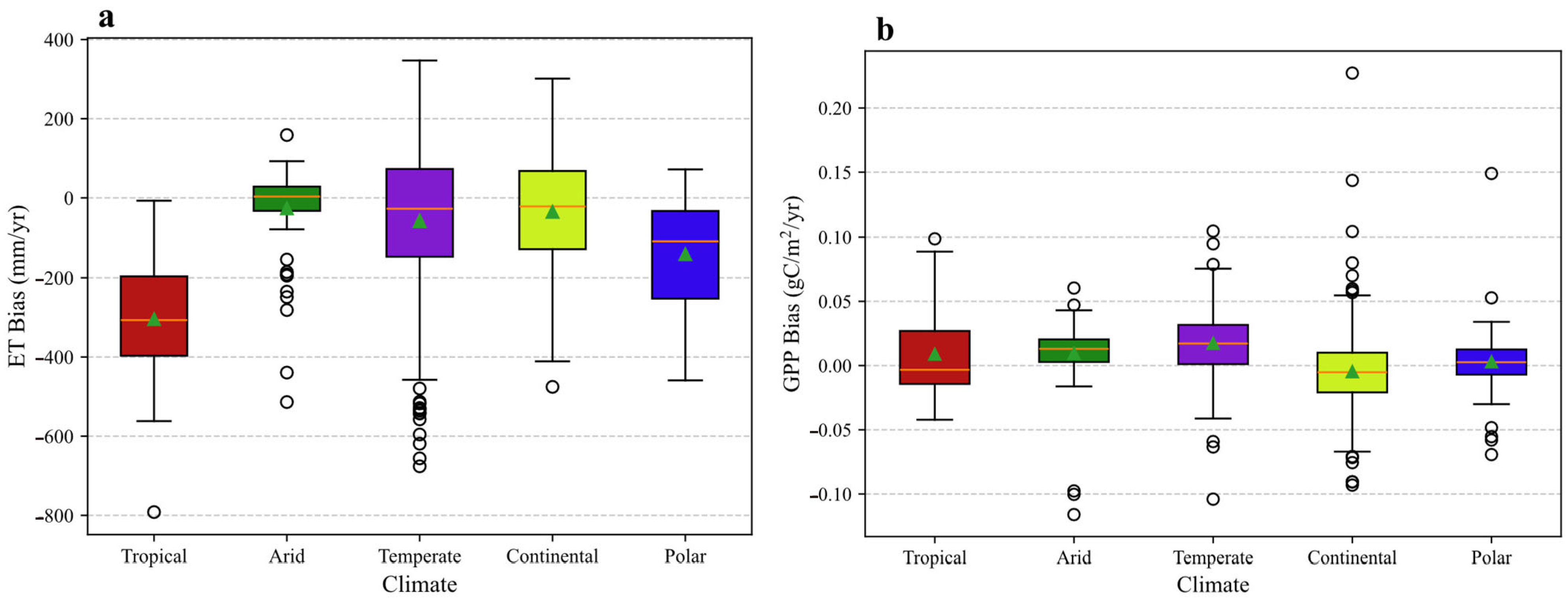
3.5. Comparison of Simulation Performance Across Climate Zones
3.5.1. Evapotranspiration (ET)
3.5.2. Gross Primary Productivity (GPP)
4. Discussion
4.1. Discrepancies in Model Capability Across Temporal Scales
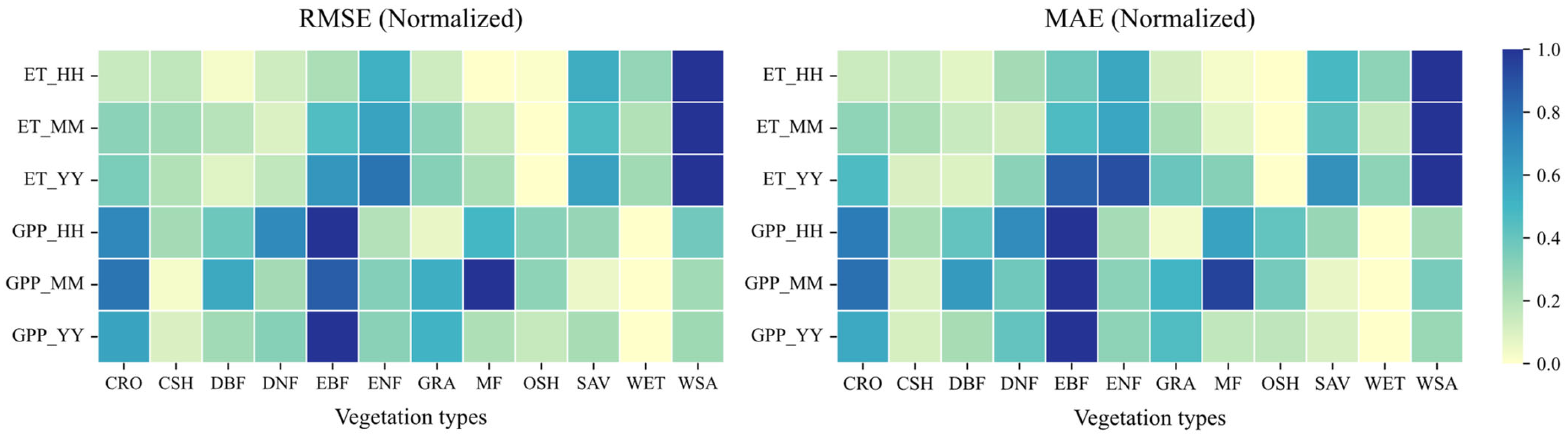
4.2. Challenges in Simulating Complex and Heterogeneous Canopies
4.3. The “Midday Depression” Simulation Gap
4.4. Limitations
5. Conclusions
- (1)
- Noah-MP generally performed well in simulating ET and GPP fluxes, capturing their variability characteristics with relatively small biases compared to the observations. The ET simulations showed slightly better agreement with the observations than the GPP simulations.
- (2)
- Simulation performance varied significantly with temporal scales, systematically decreasing as the time scale lengthened. At the half-hourly scale, simulated ET and GPP showed high consistency with observations, indicating strong capability in capturing responses to short-term drivers. At the annual scale, cumulative errors increased substantially.
- (3)
- Noah-MP generally captured the characteristic diurnal, seasonal, and interannual variations of ET and GPP. Diurnal simulation biases were often largest around noon. Seasonally, simulation biases for both fluxes were smallest in winter. Inter-site simulation performance showed greater variability during the summer compared to the winter. The standard deviation across sites was smaller for ET than for GPP, suggesting less spread in the ET simulation performance.
- (4)
- Based on the evaluation metrics, the ET simulations performed relatively well for OSH, DBF, and MF, with the largest bias observed for WSA. The GPP simulations performed relatively well for WET, CSH, and SAV, with the largest bias occurring for EBF.
- (5)
- Noah-MP exhibits a strong dependence on the climatic region. For ET, the model fails to capture the inter-annual variability in temperate and continental climates, indicating a fundamental weakness in simulating mid-latitude hydrology. For GPP, the model exhibits severe magnitude biases, particularly as overestimation in arid and temperate zones, while also failing to capture the temporal dynamics in arid and continental climates.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Reichstein, M.; Bahn, M.; Ciais, P.; Frank, D.; Mahecha, M.D.; Seneviratne, S.I.; Zscheischler, J.; Beer, C.; Buchmann, N.; Frank, D.C.; et al. Climate Extremes and the Carbon Cycle. Nature 2013, 500, 287–295. [Google Scholar] [CrossRef]
- Gong, K.; Huang, Z.; Qu, M.; He, Z.; Chen, J.; Wang, Z.; Yu, Q.; Feng, H.; He, J. Influences of Climate Change on Carbon and Water Fluxes of the Ecosystem in the Qinling Mountains of China. Ecol. Indic. 2024, 166, 112504. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The Future of Evapotranspiration: Global Requirements for Ecosystem Functioning, Carbon and Climate Feedbacks, Agricultural Management, and Water Resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Xue, B.; A, Y.; Wang, G.; Helman, D.; Sun, G.; Tao, S.; Liu, T.; Yan, D.; Zhao, T.; Zhang, H.; et al. Divergent Hydrological Responses to Forest Expansion in Dry and Wet Basins of China: Implications for Future Afforestation Planning. Water Resour. Res. 2022, 58, e2021WR031856. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. Bioscience 2004, 54, 547. [Google Scholar] [CrossRef]
- Pitman, A.J. The Evolution of, and Revolution in, Land Surface Schemes Designed for Climate Models. Int. J. Climatol. 2003, 23, 479–510. [Google Scholar] [CrossRef]
- Wang, Y.-P.; Zhang, L.; Liang, X.; Yuan, W. Coupled Models of Water and Carbon Cycles from Leaf to Global: A Retrospective and a Prospective. Agric. For. Meteorol. 2024, 358, 110229. [Google Scholar] [CrossRef]
- Oleson, K.; Lawrence, D.; Bonan, G.; Flanner, M.; Kluzek, E.; Lawrence, P.; Levis, S.; Swenson, S.; Thornton, P.; Dai, A.; et al. Technical Description of Version 4.0 of the Community Land Model (CLM); UCAR/NCAR: Boulder, CO, USA, 2010; pp. 2612 KB. [Google Scholar]
- Lawrence, D.M.; Fisher, R.A.; Koven, C.D.; Oleson, K.W.; Swenson, S.C.; Bonan, G.; Collier, N.; Ghimire, B.; van Kampenhout, L.; Kennedy, D.; et al. The Community Land Model Version 5: Description of New Features, Benchmarking, and Impact of Forcing Uncertainty. J. Adv. Model. Earth Syst. 2019, 11, 4245–4287. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 1. Model Description and Evaluation with Local-Scale Measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Wiltshire, A.J.; Duran Rojas, M.C.; Edwards, J.M.; Gedney, N.; Harper, A.B.; Hartley, A.J.; Hendry, M.A.; Robertson, E.; Smout-Day, K. JULES-GL7: The Global Land Configuration of the Joint UK Land Environment Simulator Version 7.0 and 7.2. Geosci. Model Dev. 2020, 13, 483–505. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting Carbon Dioxide and Energy Fluxes across Global FLUXNET Sites Withregression Algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Anderson, R.; Arain, M.A.; Baker, I.; Barr, A.; Black, T.A.; Chen, G.; Chen, J.M.; et al. A Model-Data Intercomparison of CO2 Exchange across North America: Results from the North American Carbon Program Site Synthesis. J. Geophys. Res. Biogeosciences 2010, 115, G00H05. [Google Scholar] [CrossRef]
- Reddy, K.N.; Baidya Roy, S.; Rabin, S.S.; Lombardozzi, D.L.; Varma, G.V.; Biswas, R.; Naik, D.C. Improving the Representation of Major Indian Crops in the Community Land Model Version 5.0 (CLM5) Using Site-Scale Crop Data. Geosci. Model Dev. 2025, 18, 763–785. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.; David, C.H.; Niu, G.; Rodell, M. Hydrological Evaluation of the noah-MP Land Surface Model for the Mississippi River Basin. J. Geophys. Res. Atmos. 2014, 119, 23–38. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, H.; Harrison, S.P.; Prentice, I.C.; Mengoli, G.; Zhao, L.; Reich, P.B.; Yang, K. Incorporating the Acclimation of Photosynthesis and Leaf Respiration in the Noah-MP Land Surface Model: Model Development and Evaluation. J. Adv. Model. Earth Syst. 2025, 17, e2024MS004599. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, T.; Du, M.; Gao, H.; Zhang, Q.; Sun, R. A Better Carbon-Water Flux Simulation in Multiple Vegetation Types by Data Assimilation. For. Ecosyst. 2022, 9, 100013. [Google Scholar] [CrossRef]
- He, C.; Lin, T.-S.; Mocko, D.M.; Abolafia-Rosenzweig, R.; Wegiel, J.W.; Kumar, S.V. Benchmarking and Evaluating the NASA Land Information System (Version 7.5.2) Coupled with the Refactored Noah-MP Land Surface Model (Version 5.0). EGUsphere 2025, 1–34, preprint. [Google Scholar]
- Song, Z.; Zeng, Y.; Wang, Y.; Tang, E.; Yu, D.; Alidoost, F.; Ma, M.; Han, X.; Tang, X.; Zhu, Z.; et al. Investigating Plant Responses to Water Stress via Plant Hydraulics Pathway. EGUsphere 2024, preprint. [Google Scholar]
- Alton, P.B. How Useful Are Plant Functional Types in Global Simulations of the Carbon, Water, and Energy Cycles? J. Geophys. Res. 2011, 116, G01030. [Google Scholar] [CrossRef]
- Heskel, M.A.; O’Sullivan, O.S.; Reich, P.B.; Tjoelker, M.G.; Weerasinghe, L.K.; Penillard, A.; Egerton, J.J.G.; Creek, D.; Bloomfield, K.J.; Xiang, J.; et al. Convergence in the Temperature Response of Leaf Respiration across Biomes and Plant Functional Types. Proc. Natl. Acad. Sci. USA 2016, 113, 3832–3837. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.; Wang, H.; Prentice, I.C.; Yang, K.; Nóbrega, R.L.B.; Liu, X.; Wang, Y.; Yang, Y. Towards a Universal Evapotranspiration Model Based on Optimality Principles. Agric. For. Meteorol. 2023, 336, 109478. [Google Scholar] [CrossRef]
- Ma, N.; Niu, G.; Xia, Y.; Cai, X.; Zhang, Y.; Ma, Y.; Fang, Y. A Systematic Evaluation of noah-MP in Simulating Land-atmosphere Energy, Water, and Carbon Exchanges over the Continental United States. J. Geophys. Res. Atmos. 2017, 122, 12245–12268. [Google Scholar] [CrossRef]
- Liang, J.; Yang, Z.; Lin, P. Systematic Hydrological Evaluation of the Noah-MP Land Surface Model over China. Adv. Atmos. Sci. 2019, 36, 1171–1187. [Google Scholar] [CrossRef]
- Yang, Z.-L.; Niu, G.-Y.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 2. Evaluation over Global River Basins. J. Geophys. Res. 2011, 116, D12110. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 Dataset and the ONEFlux Processing Pipeline for Eddy Covariance Data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- IGBP. Global Soil Data Task (IGBP-DIS, ISO-Image of CD); PANGAEA: Bremen, Germany, 2000. [Google Scholar] [CrossRef]
- Gui, H.; Xin, Q.; Zhou, X.; Xiong, Z.; Xiao, K. Embedding a Novel Phenology Model into the Common Land Model for Improving the Modeling of Land-Atmosphere Fluxes. Ecol. Model. 2024, 494, 110782. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “Goodness-of-fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Huntingford, C.; Li, Y.; Zeng, Z.; Wang, X.; Ciais, P.; McVicar, T.R.; Peng, S.; Ottlé, C.; et al. Partitioning Global Land Evapotranspiration Using CMIP5 Models Constrained by Observations. Nat. Clim. Chang. 2018, 8, 640–646. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, X.; Zhuang, Q. An Optimal Ensemble of the CoLM for Simulating the Carbon and Water Fluxes over Typical Forests in China. J. Environ. Manag. 2024, 356, 120740. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Park, H.; Kimball, J.S.; Colliander, A.; McCabe, M.F. Global Estimates of Daily Evapotranspiration Using SMAP Surface and Root-Zone Soil Moisture. Remote Sens. Environ. 2023, 298, 113803. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Von Caemmerer, S.; Berry, J.A. A Biochemical Model of Photosynthetic CO2 Assimilation in Leaves of C3 Species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Rogers, A.; Medlyn, B.E.; Dukes, J.S.; Bonan, G.; von Caemmerer, S.; Dietze, M.C.; Kattge, J.; Leakey, A.D.B.; Mercado, L.M.; Niinemets, Ü.; et al. A Roadmap for Improving the Representation of Photosynthesis in Earth System Models. New Phytol. 2017, 213, 22–42. [Google Scholar] [CrossRef]
- E Silva, I.A.; Rodriguez, D.A.; Espíndola, R.P. Improving Physiological Simulations in Seasonally Dry Tropical Forests with Limited Measurements. Theor. Appl. Climatol. 2024, 155, 7133–7146. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Balsamo, G.; Agusti-Panareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Blyth, E.; Bousserez, N.; Boussetta, S.; Brown, A.; et al. Satellite and In Situ Observations for Advancing Global Earth Surface Modelling: A Review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
- Moradi, M.; Cho, E.; Jacobs, J.M.; Vuyovich, C.M. Seasonal Soil Freeze/Thaw Variability across North America via Ensemble Land Surface Modeling. Cold Reg. Sci. Technol. 2023, 209, 103806. [Google Scholar] [CrossRef]
- Sun, S.; Du, W.; Song, Z.; Zhang, D.; Wu, X.; Chen, B.; Wu, Y. Response of Gross Primary Productivity to Drought Time-scales across China. J. Geophys. Res. Biogeosciences 2021, 126, e2020JG005953. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, D.; Fan, J.; Guo, Q.; Chen, S.; Wang, R.; Li, Y. Contrasting the Performance of Eight Satellite-Based GPP Models in Water-Limited and Temperature-Limited Grassland Ecosystems. Remote Sens. 2019, 11, 1333. [Google Scholar] [CrossRef]
- Mengoli, G.; Harrison, S.P.; Prentice, I.C. The Response of Carbon Uptake to Soil Moisture Stress: Adaptation to Climatic Aridity. Glob. Change Biol. 2025, 31, e70098. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Chen, S.; Zhang, Y.; Song, C.; Ju, W.; Wang, L.; Jiang, J. Improved Estimation of the Gross Primary Production of Europe by Considering the Spatial and Temporal Changes in Photosynthetic Capacity from 2001 to 2016. Remote Sens. 2023, 15, 1172. [Google Scholar] [CrossRef]
- Trnka, M.; Možný, M.; Jurečka, F.; Balek, J.; Semerádová, D.; Hlavinka, P.; Štěpánek, P.; Farda, A.; Skalák, P.; Cienciala, E.; et al. Observed and Estimated Consequences of Climate Change for the Fire Weather Regime in the Moist-Temperate Climate of the Czech Republic. Agric. For. Meteorol. 2021, 310, 108583. [Google Scholar] [CrossRef]
- Tang, X.; Ma, M.; Ding, Z.; Xu, X.; Yao, L.; Huang, X.; Gu, Q.; Song, L. Remotely Monitoring Ecosystem Water Use Efficiency of Grassland and Cropland in China’s Arid and Semi-Arid Regions with MODIS Data. Remote Sens. 2017, 9, 616. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, G.; Seth, A. Climatic Drivers for the Variation of Gross Primary Productivity across Terrestrial Ecosystems in the United States. J. Geophys. Res. Biogeosciences 2024, 129. [Google Scholar] [CrossRef]
- Liu, X.; Chen, F.; Barlage, M.; Niyogi, D. Implementing Dynamic Rooting Depth for Improved Simulation of Soil Moisture and Land Surface Feedbacks in Noah-MP-Crop. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001786. [Google Scholar] [CrossRef]
- Niu, G.; Fang, Y.; Chang, L.; Jin, J.; Yuan, H.; Zeng, X. Enhancing the noah-MP Ecosystem Response to Droughts with an Explicit Representation of Plant Water Storage Supplied by Dynamic Root Water Uptake. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002062. [Google Scholar] [CrossRef]
- Hassani, F.; Zhang, Y.; Kumar, S.V. Improved Representation of Vegetation Soil Moisture Coupling Enhances Soil Moisture Data Assimilation in Water-limited Regimes: A Case Study over Texas. Water Resour. Res. 2024, 60, e2023WR035558. [Google Scholar] [CrossRef]
- Yuan, K.; Zhu, Q.; Riley, W.J.; Li, F.; Wu, H. Understanding and Reducing the Uncertainties of Land Surface Energy Flux Partitioning within CMIP6 Land Models. Agric. For. Meteorol. 2022, 319, 108920. [Google Scholar] [CrossRef]
- Hosseini, A.; Mocko, D.M.; Brunsell, N.A.; Kumar, S.V.; Mahanama, S.; Arsenault, K.; Roundy, J.K. Understanding the Impact of Vegetation Dynamics on the Water Cycle in the Noah-MP Model. Front. Water 2022, 4, 925852. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Yang, W.; Tu, Z.; Han, J.; Li, S.; Yang, H. CAMELE: Collocation-Analyzed Multi-Source Ensembled Land Evapotranspiration Data. Earth Syst. Sci. Data 2024, 16, 1811–1846. [Google Scholar] [CrossRef]
- Ukkola, A.M.; Abramowitz, G.; De Kauwe, M.G. A Flux Tower Dataset Tailored for Land Model Evaluation. Earth Syst. Sci. Data 2022, 14, 449–461. [Google Scholar] [CrossRef]
- Ferreira, R.R.; Mendes, K.R.; Oliveira, P.E.S.; Mutti, P.R.; Moreira, D.S.; Antonino, A.C.D.; Menezes, R.S.C.; Lima, J.R.S.; Araújo, J.M.; Amorim, V.L.; et al. Simulating Energy Balance Dynamics to Support Sustainability in a Seasonally Dry Tropical Forest in Semi-Arid Northeast Brazil. Sustainability 2025, 17, 5350. [Google Scholar] [CrossRef]
- Mendes, K.R.; Marques, A.M.S.; Mutti, P.R.; Oliveira, P.E.S.; Rodrigues, D.T.; Costa, G.B.; Ferreira, R.R.; da Silva, A.C.N.; Morais, L.F.; Lima, J.R.S.; et al. Interannual Variability of Energy and CO2 Exchanges in a Remnant Area of the Caatinga Biome under Extreme Rainfall Conditions. Sustainability 2023, 15, 10085. [Google Scholar] [CrossRef]
- Alves, M.P.; da Silva, R.B.C.; e Silva, C.M.S.; Bezerra, B.G.; Rêgo Mendes, K.; Marinho, L.A.; Barbosa, M.L.; Nunes, H.G.G.C.; Dos Santos, J.G.M.; de Araújo Tiburtino Neves, T.T.; et al. Carbon and Energy Balance in a Primary Amazonian Forest and Its Relationship with Remote Sensing Estimates. Remote Sens. 2024, 16, 3606. [Google Scholar] [CrossRef]
- Mendes, K.R.; Oliveira, P.E.S.; Lima, J.R.S.; Moura, M.S.B.; Souza, E.S.; Perez-Marin, A.M.; Cunha, J.E.B.L.; Mutti, P.R.; Costa, G.B.; De Sá, T.N.M.; et al. The Caatinga Dry Tropical Forest: A Highly Efficient Carbon Sink in South America. Agric. For. Meteorol. 2025, 369, 110573. [Google Scholar] [CrossRef]
- Zhang, Z.; Chatterjee, A.; Ott, L.; Reichle, R.; Feldman, A.F.; Poulter, B. Effect of Assimilating SMAP Soil Moisture on CO2 and CH4 Fluxes through Direct Insertion in a Land Surface Model. Remote Sens. 2022, 14, 2405. [Google Scholar] [CrossRef]


| Physical Process | Code | Parameterization Option |
|---|---|---|
| Dynamic Vegetation Model (DVEG) | 2 | Dynamic Vegetation Process Model |
| Canopy Stomatal Resistance (CRS) | 1 | Ball–Berry |
| Surface Layer Drag Coefficient (SFC) | 1 | M-O |
| Canopy Radiation Transfer (RAD) | 1 | Three-Dimensional Canopy Morphology |
| Soil Water Potential Factor (BTR) | 1 | Noah |
| Frozen Soil Permeability (INF) | 1 | NY06 |
| Soil Bottom Temperature (TBOT) | 2 | Noah |
| Runoff and Groundwater (RUN) | 1 | SIMGM |
| Supercooled Water Process (FRZ) | 1 | NY06 |
| Snow Albedo (ALB) | 2 | CLASS |
| Rain and Snow Separation (SNF) | 1 | Jordan91 |
| Snow/Soil Temperature Integration (STC) | 1 | Semi-Implicit |
| IGBP Types | Site-Year * | Observed ET /mm·yr−1 | Modelled ET /mm·yr−1 | Absolute Error/ mm·yr−1 | Relative Error/% | Correlation Coefficient | RMSE/ mm·yr−1 | p-Value |
|---|---|---|---|---|---|---|---|---|
| ENF | 225 | 483.50 | 322.71 | 160.79 | 33.26 | 0.21 | 237.78 | 0.0019 |
| EBF | 45 | 716.77 | 699.05 | 17.72 | 2.47 | 0.89 | 207.27 | <0.001 |
| DNF | 3 | 302.13 | 396.04 | 93.91 | 31.08 | −0.37 | 100.61 | 0.7555 |
| DBF | 55 | 406.94 | 408.41 | 1.47 | 0.36 | 0.44 | 82.74 | <0.001 |
| MF | 35 | 340.62 | 405.27 | 64.65 | 18.98 | 0.24 | 113.26 | 0.1676 |
| CSH | 22 | 463.09 | 435.19 | 27.90 | 6.02 | 0.93 | 109.39 | <0.001 |
| OSH | 4 | 340.13 | 294.32 | 45.81 | 13.47 | 0.45 | 64.42 | 0.545 |
| WSA | 45 | 664.80 | 500.85 | 163.95 | 24.66 | 0.95 | 284.89 | <0.001 |
| SAV | 34 | 536.71 | 401.12 | 135.59 | 25.26 | 0.90 | 196.18 | <0.001 |
| GRA | 149 | 425.90 | 384.26 | 41.64 | 9.78 | 0.72 | 134.56 | <0.001 |
| WET | 24 | 394.16 | 344.54 | 49.62 | 12.59 | 0.54 | 119.49 | 0.0068 |
| CRO | 56 | 417.06 | 503.64 | 86.58 | 20.76 | 0.18 | 140.32 | 0.1862 |
| All | 697 | 476.67 | 405.39 | 71.28 | 14.95 | 0.66 | 188.99 | <0.001 |
| IGBP Types | Site-Year * | Observed GPP/ gC·m−2·yr−1 | Modelled GPP/ gC·m−2·yr−1 | Absolute Error/ gC·m−2·yr−1 | Relative Error% | Correlation Coefficient | RMSE/ gC·m−2·yr−1 | p-Value |
|---|---|---|---|---|---|---|---|---|
| ENF | 229 | 1412.73 | 1256.74 | 155.99 | 11.04 | 0.73 | 410.1 | <0.001 |
| EBF | 45 | 1798.20 | 2558.12 | 759.92 | 42.26 | 0.58 | 969.62 | <0.001 |
| DNF | 3 | 1136.76 | 1553.96 | 417.2 | 36.70 | −0.09 | 418.91 | 0.9428 |
| DBF | 58 | 1675.78 | 1764.98 | 89.20 | 5.32 | 0.13 | 363.54 | 0.3342 |
| MF | 35 | 1586.20 | 1681.39 | 95.19 | 6.00 | 0.14 | 334.56 | 0.4111 |
| CSH | 22 | 922.32 | 1107.31 | 184.99 | 20.06 | 0.97 | 240.9 | <0.001 |
| OSH | 4 | 472.18 | 727.10 | 254.92 | 53.99 | −0.72 | 284.51 | 0.2793 |
| WSA | 45 | 1128.52 | 1299.12 | 170.60 | 15.12 | 0.9 | 366.37 | <0.001 |
| SAV | 34 | 831.80 | 748.25 | 83.55 | 10.04 | 0.79 | 349.79 | <0.001 |
| GRA | 143 | 1090.49 | 1008.17 | 82.32 | 7.55 | 0.73 | 573.77 | <0.001 |
| WET | 24 | 893.20 | 947.08 | 53.88 | 6.03 | 0.81 | 159.54 | <0.001 |
| CRO | 56 | 1161.88 | 1665.09 | 503.21 | 43.31 | 0.58 | 634.11 | <0.001 |
| All | 698 | 1295.48 | 1346.85 | 51.37 | 3.97 | 0.67 | 500.62 | <0.001 |
| Climate | Site-Year * | Observed ET /mm·yr−1 | Modelled ET /mm·yr−1 | Absolute Error/ mm·yr−1 | Relative Error/% | Correlation Coefficient | RMSE/mm·yr−1 | MAE/mm·yr−1 | p-Value |
|---|---|---|---|---|---|---|---|---|---|
| Tropical | 42 | 1127.30 | 822.82 | 304.48 | 27.01 | 0.62 | 343.51 | 304.48 | p < 0.001 |
| Arid | 77 | 343.73 | 317.30 | 26.42 | 7.69 | 0.64 | 108.11 | 60.52 | p < 0.001 |
| Temperate | 142 | 525.08 | 468.05 | 57.03 | 10.86 | 0.15 | 222.48 | 160.44 | 0.07 |
| Continental | 328 | 433.80 | 399.56 | 35.34 | 8.14 | 0.01 | 156.46 | 121.82 | 0.84 |
| Polar | 108 | 388.01 | 245.20 | 140.44 | 36.52 | 0.64 | 191.98 | 149.04 | p < 0.001 |
| Climate | Site-Year * | Observed GPP/ gC·m−2·yr−1 | Modelled GPP/ gC·m−2·yr−1 | Absolute Error/ gC·m−2·yr−1 | Relative Error/% | Correlation Coefficient | RMSE/ gC·m−2·yr−1 | MAE/gC·m−2·yr−1 | p-Value |
|---|---|---|---|---|---|---|---|---|---|
| Tropical | 42 | 1978.61 | 2094.31 | 115.71 | 5.85 | 0.74 | 619.52 | 436.28 | p < 0.001 |
| Arid | 73 | 383.50 | 587.15 | 203.66 | 53.11 | 0.31 | 371.36 | 295.30 | 0.008 |
| Temperate | 142 | 1274.84 | 1616.54 | 341.70 | 26.80 | 0.59 | 601.14 | 475.46 | p < 0.001 |
| Continental | 335 | 1565.99 | 1456.60 | 109.40 | −6.99 | 0.24 | 516.24 | 406.98 | p < 0.001 |
| Polar | 106 | 825.58 | 865.74 | 40.16 | 4.86 | 0.74 | 277.40 | 218.17 | p < 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, B.; Wu, X.; Cai, X. Evaluation of Noah-MP Land Surface Model-Simulated Water and Carbon Fluxes Using the FLUXNET Dataset. Land 2025, 14, 1400. https://doi.org/10.3390/land14071400
Pan B, Wu X, Cai X. Evaluation of Noah-MP Land Surface Model-Simulated Water and Carbon Fluxes Using the FLUXNET Dataset. Land. 2025; 14(7):1400. https://doi.org/10.3390/land14071400
Chicago/Turabian StylePan, Bofeng, Xiaolu Wu, and Xitian Cai. 2025. "Evaluation of Noah-MP Land Surface Model-Simulated Water and Carbon Fluxes Using the FLUXNET Dataset" Land 14, no. 7: 1400. https://doi.org/10.3390/land14071400
APA StylePan, B., Wu, X., & Cai, X. (2025). Evaluation of Noah-MP Land Surface Model-Simulated Water and Carbon Fluxes Using the FLUXNET Dataset. Land, 14(7), 1400. https://doi.org/10.3390/land14071400




