Abstract
In this study, we explore the impact of land investment introduction on efficiency loss at both the enterprise and urban levels and discuss the role of factor-biased technological progress in minimizing these losses. Using a nested constant elasticity of substitution (CES) production function, we theoretically validate the premise that land investment introduction disrupts the optimal allocation of productive factors and reduces the “threshold selection” effect of land cost, leading to efficiency losses. Empirically, the systematic generalized method of moments (GMM) is applied to analyze panel data from 284 prefecture-level cities in China between 2007 and 2019. The findings reveal that land investment introduction brings about efficiency losses and prolonged land investment strategies that deepen enterprise efficiency loss, while urban efficiency loss may be temporarily alleviated but tends to deepen over the long term. Enterprise efficiency loss can be reduced by selecting land-biased, labor-biased, and capital-biased technological progress; however, its impact on urban efficiency loss remains uncertain. These findings provide insights into the optimal selection of factor-biased technological progress for industrial enterprises and provide policy-oriented recommendations for enhancing production and improving efficiency.
1. Introduction
Technological progress is widely recognized as a key driver of sustainable economic development [1] and serves a moderating role in the government policies influencing enterprise output [2,3]. Given their pivotal role in enhancing profitability and improving production efficiency, industrial enterprises1 have increasingly prioritized technological innovation. This is reflected in the establishment of dedicated Research and Utilization (R&U) departments, the recruitment of professional personnel, and the expansion of investment in R&U to institutionalize technological progress. As technological progress has become an integral part of daily industrial operations, the theory of induced technological progress has gradually become a research hotspot. This perspective suggests that technological advancements are driven not only by shifts in market demand but also by relative changes in factor prices resulting from variations in resource endowments. Building upon the theory of induced technological progress, Acemoglu [4] found that the marginal output intensity of different selections of factor-biased technological progress is widely divergent, with the dual nature of technological progress and resource allocation. Industrial enterprises can increase their productive output by promoting technological progress and improving allocative efficiency through different selections of factor-biased technological progress.
In the report of the 19th CPC National Congress, it was stated that the Chinese economy had been transformed from high-speed growth to high-quality development. Efficiency reform is essential to further guide Chinese economic development. However, the broad definition of efficiency, including single-factor efficiency and total factor productivity (TFP), requires that more attention be paid to improving TFP to ensure the continuous development of the national economy. The World Economic Forum stated that an economy’s competitiveness is related to TFP growth [5]; however, according to the Penn World Table (PWT) 10.0, the average annual TFP growth rate in China decreased from 0.4216 during the 2011–2015 period to 0.4164 during the 2016–2019 period. Many research works have shown that an unreasonable allocation of factors is primarily responsible for this [6,7,8,9,10,11,12]. At present, as an important resource element, local governments depend on land control to maintain a monopoly over non-market environments oriented towards the first-level market for transferring industrial land. Therefore, in recent years, an unreasonable allocation of industrial land has often been cited as the main reason for the decrease in China’s TFP [13].
Although some countries, such as Germany and the Netherlands, have adjusted their industrial land allocation policies to seek economic effectiveness [14], others continuously expand industrial land for economic growth; for instance, South Korea has experienced a disorderly spread and misallocation of industrial land by building many industrial estates [15]. China has mainly adopted a competitive strategy of land investment introduction; that is, following a value-orientated motivation, local governments will reduce the unit price for transferring industrial land to attract more enterprise projects through surrendering a part of the profits, which not only wins the horizontal competition with GDP as the main performance goal but also helps to obtain more power over fiscal and taxation systems through “soft constraints for reverse budget” from vertical competition against the central government. Hence, for policy dividends, local governments generally carry out land investment introductions. This also has many adverse effects; for example, local governments compete to adopt the strategy of land investment introduction as a competitive tool [16]. The result is a “race to the bottom” of the transfer price of industrial land [17,18]. This “low-price competition” behavior of excessive intervention in the transfer of industrial land may lead to resource misallocation and efficiency loss [19]. So far, research on the efficiency loss caused by land investment introduction has been limited to studying its single impact on urban efficiency or enterprise efficiency using the empirical analysis method. Considering that urban efficiency is not simply the sum of enterprise efficiency, in this paper, we subdivide the enterprise level and urban level within the same benchmark model and systematically discuss the impact of land investment introduction on enterprise TFP and city TFP. Thus, land investment introduction is shown to lead to efficiency loss, which is an important premise for exploring the selection of industrial enterprises regarding factor-biased technological progress.
Land investment introduction not only leads to efficiency loss but also catalyzes technological progress. According to the theory of induced technological progress, the relative change in price for productive factors influences input structure in the short run and drives technological advancements in the long run [20]. Given that land investment introduction alters the relative price of factors, it will induce technological progress. At the same time, due to the factor-biased nature of induced technological progress, industrial enterprises can mitigate the efficiency losses associated with land investment introduction by strategically promoting technological advancements and optimizing resource allocation based on different choices of factor-biased technological progress [21]. In this study, we aim to explore how industrial enterprises determine factor-biased induced technological progress to minimize both enterprise and urban efficiency losses in the context of land investment introduction. To achieve this, a nested constant elasticity of substitution (CES) production function is used as the benchmark model to theoretically assess whether land investment leads to efficiency losses at both levels. Additionally, the question of how industrial enterprises make strategic decisions regarding factor-biased technological progress to mitigate these losses is investigated. The key contributions of this paper are twofold: theoretically, it integrates land investment introduction, efficiency loss, and factor-biased technological progress within a unified economic framework, while also distinguishing enterprise-level and urban-level efficiency with the same economic model. Practically, it provides insights into the optimal selection of factor-biased technological progress for industrial enterprises and offers valuable guidance on increasing production and efficiency in the context of strategic land investment policies.
2. Materials and Methods
2.1. Research Review
Many efforts have been made to show that resource allocation, industrial structure, technological innovation, and industrial distribution are closely related to efficiency loss [22,23,24,25] and that resource allocation is key to efficiency improvement [26]. As both a spatial carrier and an essential production factor, land entails high reallocation costs due to its immobility. Therefore, land resource misallocation is an important factor affecting TFP [27]. Land investment introduction results in land resource misallocation and exerts an unknown impact on TFP. Therefore, the impact of land investment introduction on TFP can be estimated through the impact of land resource misallocation on TFP. Rafaela and Nicolas [28] discovered that resource misallocation can lower aggregate TFP, and Kumari et al. [29] concluded that rising misallocation could explain 55% of the manufacturing TFP growth slowdown in Sri Lanka. However, Xu et al. [30] found that there is one single-threshold effect between land transfer marketization (LTM), resource allocation, and TFP: when the degree of resource mismatch is below the threshold, LTM significantly increases TFP.
A review of the existing studies shows that research on this influence path is mainly divided into two categories. The first category concerns direct impact; due to land resource misallocation, the allocation ratio of enterprise factors is suboptimal, which affects the efficiency of a single enterprise [26,27,31]. Kumari et al. [32] compared industrial TFP loss due to misallocation in industrial land with that of capital, concluding that TFP gain from removing land distortion is five times that of capital. The second category is related to indirect impact; that is, reducing industrial land cost is not conducive to the “threshold selection” effect, thus affecting enterprise efficiency in the whole region [33,34]. The price of industrial land is considered an important driving force for urban economy growth [35], which can improve industrial structures and enhance the effect of industrial agglomeration [36]. However, Meina C [37] found that local politicians allocate more land to the industrial sector, and inefficient enterprises are more protected [38], which reduces the filtering role of land price as a market signal. In addition, some studies adopt counterfactual methods to find that in response to the decline in TFP resulting from market misallocation, the main driving force of TFP improvement in Asian countries is technological change, while that in European countries is efficiency change [39]. Moreover, factor market distortion can stimulate the technological progress of industrial enterprises [40,41]. In a study involving industrial land by Zhao et al. [20], the hypothesis of induced technological progress is used to establish an analysis framework showing that marketization for the transfer of industrial land brings about structural adjustments in productive factors in the short term and induces technological progress in the long term. With further development in the theory of induced technological progress, scholars have found that the relative change in factor price directly leads to technological progress [42,43], and different choices of factor-biased technological progress may promote marginal efficiency in vastly different ways [44].
Although the viewpoint that resource misallocation has a negative impact on efficiency has become a consensus, validated mainly by phenomenon analysis and empirical demonstration, no attempts have been made to either perform mathematical deduction based on economic models or to elaborate on how to reduce efficiency losses caused by resource misallocation through biased technological progress. To this end, in this study, we aim to integrate land investment introduction, efficiency loss, and factor-biased technological progress into an analytical economic model, thereby scientifically demonstrating that land investment introduction leads to efficiency losses while also exploring how industrial enterprises mitigate efficiency losses through factor-biased technological progress.
2.2. Analysis of Frame Construction
The literature reveals that land investment introduction brings about enterprise efficiency loss by deviating from the optimal ratio of productive factors, as well as resulting in urban efficiency loss by lowering the “entry threshold” effect and weakening the competitive atmosphere, which reduces critical productivity, as enterprises merely maintain their operations and their profit is 0. Moreover, since land investment introduction not only causes efficiency loss but also induces technological progress [20], enterprises with different selections of factor-biased technological progress may have different output intensities, which results in different influences on enterprise efficiency. Thus, to a certain extent, it is implied that factor-biased technological progress has the dual nature of technological progress and resource allocation. This paper will discuss the effect of the factor-biased induced technological progress determined by industrial enterprises on reducing both enterprise and urban efficiency loss. The constructed analysis framework is depicted in Figure 1.
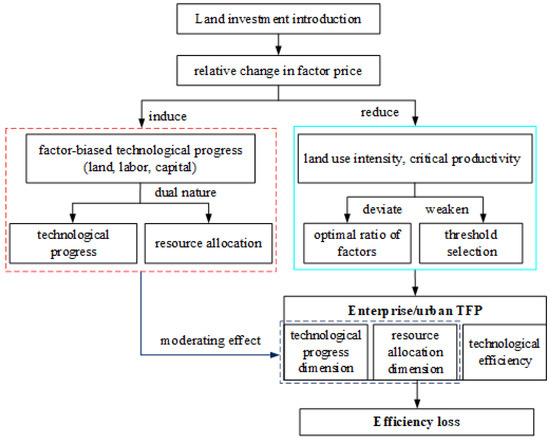
Figure 1.
Analytical framework of how land investment introduction leads to efficiency loss and induces technological progress, as well as of how to reduce efficiency loss.
2.3. Mathematical Derivation Based on CES Production Function
Efficiency is the core of economic research. The production function describes the relationship between factor input and output as a mathematical model, which includes essential components of the micro-production process and macroeconomic development, such as factor quantity, price, substitutability, production scale, and technological level. It is an important tool for efficiency assessment. Through mathematical derivation, the simplified relationship among factors, as well as technological capability and efficiency status, can be reflected, meeting the research needs. Therefore, this paper uses an economic model to more scientifically analyze the impacts of land investment introduction and the factor-biased selection of industrial enterprises on efficiency. The most fundamental production function is the Cobb–Douglas (C-D) production function.
2.3.1. Reference Production Function
To describe the substitution degree and the input share change in productive factors exactly, the restrictive assumption conditions of the C-D function, such as “unit elasticity of substitution is 1”, “Hicks Neutral technological progress”, and “constant factor input share”, are unconstrained, and the nested CES production function is adopted to reflect the variables of factor price [45]. The baseline model is as follows:
where and represent the price and quantity of the final industrial product, respectively; is the parameter of technological progress; , , and are the input quantity of capital, labor, and industrial land, respectively; , , and represent the input price of capital, labor, and industrial land, respectively; is the scale effect; and both represent the output elasticity of factors; and represents the substitution elasticity of factors, with > 1 indicating that the productive factors of industrial enterprises generally manifest a substitution effect.
2.3.2. Enterprise Efficiency Loss
In order to explain how land investment introduction may lead to enterprise efficiency loss through deviating from the optimal allocation of productive factors, the nested CES production function is used to reveal the inter-relationship between land investment introduction and enterprise TFP. The enterprise efficiency difference is studied by comparing the local government’s strategies of land investment introduction. To accurately extract enterprise TFP, as described in Winford et al. [46], a logarithm is taken on both sides in Equation (1) and Taylor’s second-order expansion is performed at σ = 1.
where the coefficient . According to the Solow calculation formula, the output efficiency of an enterprise mainly includes two parts: single-factor productivity and total factor productivity (TFP), that is, , where and are the price and the quantity of industrial intermediate product, respectively; refers to single-factor productivity; and tfpr refers to TFP. Therefore, the efficiency function of enterprise output can be calculated by using the following equations:
Ignoring the single-factor productivity in Equation (3), the relationship between enterprise TFP (tfpr) and industrial land price can be obtained:
The requirement for factor market equilibrium is that the price be equal to the marginal value of the product; therefore, when industrial land is optimally allocated, , where MRPT is the marginal value of product on industrial land. When a misallocation of industrial land occurs, land investment introduction can be expressed as , in which is the distortion degree of industrial land price, assuming that the strategy of land investment introduction is carried out universally.
Thus, when land investment introduction is not adopted, enterprise TFP () can be given by
Enterprise TFP () with land investment introduction can be represented by
According to the theory of Hicks Neutral technological progress, the efficiency difference between the two situations is
Because Equation (7) is greater than 0, we have , which means that enterprise TFP without adopting land investment introduction is higher than that achieved by adopting the strategy, indicating that land investment introduction will reduce enterprise TFP. Furthermore, when , implying the degree of deviation from the optimal allocation of industrial land, becomes larger, the differential value between and increases, which widens the efficiency gap.
Therefore, the first hypothesis (H1) of this paper is put forward: Compared with the non-deviated allocation of industrial land price, land investment introduction will reduce enterprise TFP due to deviating from the optimal allocation ratio of factors, resulting in enterprise efficiency loss.
2.3.3. Urban Efficiency Loss
This section aims to evaluate the critical TFP of a city at which enterprises, under the condition of land investment introduction, maintain operation while generating zero profit. Additionally, it explores how land investment introduction affects the “threshold selection” effect by comparing the allocation of industrial land prices under both deviated and non-deviated conditions. In general, the fundamental condition for an enterprise to remain operational is that its profit (π) must be non-negative. The critical TFP (*) is defined as the level of productivity required for an enterprise to sustain operations when its profit equals zero. If the enterprise’s productivity falls below the critical TFP, the enterprise has to withdraw or transfer. Therefore, the profit of critical TFP can be expressed mathematically as follows:
According to the different definitions on TFP (practical and receipt form) in Hang Jing et al. [47], assuming that enterprise TFP without distorting the factor price is , substituting it into Equation (8), it yields
The first partial derivative of can be given by
With , , , , , , , we can derive the following result from Cauchy–Schwarz2 inequality:
Due to , there is a negative relationship between critical TFP and land investment introduction; with the increment in the distortion degree of industrial land price (), the critical value of urban TFP () will decrease, which can weaken the “threshold selection” effect of industrial land cost.
A more detailed explanation is that markets are in a dynamic environment where enterprises can enter and exit at any time; moreover, timely exit and entry may be conducive to optimizing city TFP. However, on the one hand, land investment introduction means that existing inefficient enterprises cannot be removed in time. When they are “unable to get out”, this will reduce the critical TFP of urban () by weakening the competitive atmosphere. On the other hand, potentially efficient enterprises are also affected and may be “unable to get in”, which obstructs the resource flow of industrial land from inefficient to efficient enterprises and reduces the critical TFP of urban efficiency.
Therefore, the second hypothesis (H2) of this paper is proposed: Compared with the non-deviated allocation of industrial land price, land investment introduction will reduce enterprise TFP based on lowering the “threshold selection” effect of industrial land cost, resulting in urban efficiency loss.
2.3.4. Selection of Factor-Biased Technological Progress of Industrial Enterprises
In this selection, the factor-biased technological progress of industrial enterprises is determined and explored based on the nested CES production function to reduce enterprise efficiency loss and urban efficiency loss under land investment introduction. In the previous section, the baseline model is assumed to be Hicks Neutral to simplify the deduction; however, technological progress is non-Hicks Neutral. Thus, Equation (1) can be rewritten as follows:
where AK, AL, and AT represent the enhancement coefficients of technological progress on capital, labor, and land, respectively, so as to reflect the output intensity of technological progress on the three factors.
According to existing research on the different definitions of TFP, two forms—a practical form and a receipt form—can be distinguished, , where , , and are the output elasticity of capital, labor, and land, respectively. The relationship between enterprise TFP and the marginal value of product for a factor can be established as , where , .
When MRPK = MRPL = MRPT, enterprise TFP reaches the maximum3. The enhancement coefficients of technological progress can be derived by
It can be seen from Equations (13) and (14) that land investment introduction is negatively correlated with the enhancement coefficient of capital-biased and labor-biased technological progress. That is, land investment introduction will reduce the output intensity of factor-biased technological progress on capital and labor; meanwhile, compared with capital and labor, the essential attribute of industrial land is non-renewable and needs to be utilized intensively through technical means. Therefore, industrial enterprises tend to give priority to land-biased technological progress when all three productive factors are involved, expecting to minimize enterprise efficiency loss under land investment introduction. After giving priority to land-biased technological progress, it is necessary to further analyze the relative trend of the enhancement coefficient of technological progress between capital and labor to determine the factor-biased technological progress of industrial enterprises. Based on the condition of maximum enterprise TFP, the enhancement coefficients of technological progress can be given by
It can be seen from Equation (15) that the enhancement coefficients of factor-biased technological progress are determined by both factor price and factor quantity. On the one hand, factor price is inversely related to enhancement coefficients; these decrease with the increment in factor price, which is selected as a chief input direction of technological progress. The theory of the marginal value of product on factor gives VMRP = P × MRP, so, when the marginal value of product on factor is constant, the increment in factor price will reduce its marginal output, and the output intensity resulting from technological progress will also decrease. Therefore, factors with relatively low prices are inclined to choose the input of technological progress. On the other hand, there is a reverse relationship between factor quantity and the enhancement coefficient of technological progress; the latter will increase when a factor with low quantity is selected as a chief input direction of technological progress. Because the ratio of profuse factors may already be in a saturated state, the output contribution to industrial enterprise reaches the “ceiling” level, and the technological progress is too low to improve its output intensity. So, the factor-biased technological progress of relatively scarce factors will be conducive to optimizing the inter-factor allocation, reducing enterprise efficiency loss under land investment introduction to some extent.
Based on the analysis, the third hypothesis (H3) of this study is formulated: To minimize enterprise efficiency loss under the introduction of land investment, industrial enterprises should prioritize land-biased technological progress when all three factors are involved. In cases where two productive factors, namely capital and labor, are considered, enterprises should focus on technological progress that favors the factor with a relatively lower price and smaller quantity, as shown in Table 1. This approach aims to optimize resource allocation and reduce efficiency losses in the context of land investment.

Table 1.
Choice of factor-biased technological progress to minimize enterprise efficiency loss under land investment introduction.
In Equation (9), the parameter representing technological progress (A) is not included, which may limit its ability to reduce urban efficiency loss under land investment introduction. This exclusion prevents the modification of the enhancement coefficients associated with induced technological progress in industrial enterprises (AK, AL, and AT), thereby restricting their potential to influence urban efficiency improvements. Enterprise TFP refers to the extra productivity of industrial enterprises, except for the productivity of a single factor, such as capital, labor, and land, which has a dual meaning of both technological progress and a factor proportioning efficiency. So, enterprise efficiency loss under land investment introduction can be decreased by selecting industrial enterprises using factor-biased technological progress with the nature of resource allocation. However, city TFP refers to the extra efficiency of the macroeconomy, except for the input efficiency of a single factor. The macroeconomy, which covers a broader scope, includes not only industrial enterprises but also other sectors. The effect of technological progress induced by industrial enterprises in the micro-field on reducing urban efficiency loss under land investment introduction is negligible.
Therefore, the fourth hypothesis (H4) of this study is put forward: Factor-biased technological progress of industrial enterprises cannot reduce urban efficiency loss under land investment introduction.
2.4. Metrological Model Settings
Efficiency loss is difficult to measure directly, so enterprise and urban efficiency loss can be evaluated via the effect of land investment introduction on enterprise TFP and city TFP. Considering that the current TFP is affected by that of the past, this generates the endogeneity problem of path dependence of the explained variable. GMM is the fundamental model for solving this problem. Its basic idea is to incorporate the lag period of the explained variable as an explanatory variable into the formula, and it has three methods of estimation: differential GMM, horizontal GMM, and systematic GMM. Systematic GMM synthetically takes into account the difference change and the horizontal change in the observed variables. Systematic GMM is adopted to investigate the effect of land investment introduction on enterprise TFP and city TFP. Given that the effect of land investment introduction on TFP is non-concurrent and non-real-time, the second-phase lag term of land investment introduction is introduced. Then, the systematic GMM model can be briefly explained using Equation (16).
where is the explained variable that represents enterprise TFP () and city TFP (), respectively; i refers to the city, and t refers to the year; is the core explanatory variable representing land investment introduction, and is its second-phase lag term; is the constant term; , , and θ3 are the correlation coefficients; controls are the control variables; represents the regional fixed effect; and is the error term.
In order to investigate whether the factor-biased technological progress of industrial enterprises can reduce enterprise efficiency loss and urban efficiency loss under land investment introduction, we need to analyze the direction of influence and the degree of land investment introduction on the TFP dimensions of technological progress and allocation efficiency, with and without the effect of factor-biased technological progress. This conforms to the paradigm of studying whether the influence of one thing on another is affected by moderating variables in moderation models. So, the effect can be estimated by the moderating effect model (Equations (17) and (18)) of explicit variables proposed by Wen et al. [48]:
where is the explained variable, including the technological progress dimension (techchit) and allocative efficiency dimension (sechit) of enterprise TFP, as well as the technological progress dimension (techchJt) and allocative efficiency dimension (sechit) of city TFP. The core explanatory variable is the second-phase lag term of land investment introduction (considering the lag of time). M is modulation. According to Equations (13) and (14), the enhancement coefficients of technological progress on land (AT) are negatively correlated with the quantity of industrial land (T), and according to Equation (15), the enhancement coefficients of technological progress on capital (AK) and labor (AL) are also negatively correlated with their price and quantity. Therefore, the area of the enterprise’s land, its net fixed assets, and the number of its employees represent the quantities of industrial land, capital, and labor, respectively; the quoted interest rate of the loan market (five-year period of LPR) and the average wage of an enterprise employee represent the price of capital and labor. is the interaction term reflecting a moderating effect. , , , , and are correlation coefficients. A significant coefficient of intersection term () means the existence of a moderating effect, which, whether it is positive or negative, can be determined by comparing the value of and .
Notably, in 2006, the central government stated that the transfer of industrial land must be carried out by bidding, auction, and hanging signs; moreover, the spread of COVID-19 caused economic fluctuations at the end of 2019. Therefore, to reduce external influences on the model results, the enterprise TFP of 284 prefecture-level cities from 2007 to 2019 was considered. The DEA method was used to measure enterprise TFP through the Deap2.1 program [49]. In general, the DEA method needs an output index and input index. In this paper, the output index of enterprise TFP is the total output value of state-owned enterprises and non-state-owned enterprises above a designated size. The input indexes include the net fixed assets of state-owned and non-state-owned enterprises above a designated size, the employment figures of secondary industry (because the proportion of enterprises below a designated size in prefecture-level cities is small, limited by the availability of data, the measurement error can be negligible), and the industrial land area (limited by data availability as well). The original data are all from the Statistical Yearbook of Urban Construction in China. Furthermore, to overcome the effect of inflation, the gross output value of state-owned enterprises and non-state-owned enterprises above a designated size and the net fixed assets of enterprises are modified by the factory-producer price index for industrial production and the investment price index of fixed assets (the base period is 2007).
Similarly to enterprise TFP, the Deap2.1 program was used to measure city TFP in 284 prefecture-level cities from 2007 to 2019. The output index of city TFP is gross domestic product (GDP); the input indexes of city TFP are the stock of material capital, the employment figure, and the construction land area nationwide. The original data are also from the Statistical Yearbook of Urban Construction in China. The stock of material capital can be measured by Kit = Ki(t − 1) × (1 − δit) + Iit [50,51]. (Kit and Ki(t − 1), respectively, refer to the stock of constant price on material capital in region i in years adjacent to year t and year t − 1; δit represents the depreciation rate, and it is usually measured by 1%.) The nominal value of GDP is obtained from the index of the gross domestic product (the base period is 2007). The original data of the output and input index are given by enterprise TFP and city TFP, and technological progress and allocative efficiency are measured through the Malmquist Index method using the Deap2.1 program.
The core explanatory variable is land investment introduction (pd), which is defined based on the deviation in land transfer prices, that is, the transfer of agreement and the transfer of bidding, auctions, and hanging signs. Land transfer agreement refers to the government and land users negotiating and signing a transfer contract to determine the land price, and the transfers of bidding, auctions, and hanging signs mean that the land price is determined based on the marketization approach through public bidding. According to Liu and Yan [52], if local governments want to attract investment by lowering the price of industrial land, they need to adopt the non-marketization approach. Although the central government has stipulated that industrial land must be transferred through bidding, auctions, and hanging signs since 2006, there is still some operating space for local governments to adopt the non-marketization approach. Compared to transfer prices based on bidding, auctions, and hanging signs, agreement-based land grants include a large bargaining space in terms of negotiating land prices with land users, which is considered the main non-marketization approach. Therefore, the larger the price difference between the agreement and bidding, auctions, and hanging signs, the more severe the land price deviation under government intervention, and the greater the efforts to attract land investment. As described by Liu and Yan [52], land investment introduction can be represented by pd = ln[(Pzpg − Pxy)/Pxy], where Pzpg is the average price of land transfer on bidding, auctions, and hanging signs, and Pxy is the average price of land transfer on agreement. The original data are all from the Network of Land Market in China (python 2.7).
Except for the core explanatory variable, there are five explanatory variables, including the area of enterprise land (indu), the number of employees (labor), the average employee salary (pay), the logarithmic form of net fixed assets (fix), and the five-year LPR (loan: the quoted interest rate of the loan market). The original data on loans comes from the Statistical Yearbook in China, and all other data is taken from the Statistical Yearbook of Urban Construction in China. Because loans are only available at the national level, according to Gao et al. [53], the financial geographic structure has an important impact on financial geographic aggregation, with an increment in the geographical slope and a decrease in the enterprise loan interest rate. Thus, the panel data of a city is constructed by assuming that the quoted interest rate of the loan market is inversely proportional to the geographical slope, that is, loan = the annual average of national LPR (five-year period)/geographical slope of urban.
Five variables are selected as control variables, including economic development (pgdp), the industrial structure (stru), the expenditure level of sci-technology (tech), the level of opening up (fore), and transport infrastructure (infr). The level of economic development will decrease the efficiency loss caused by land investment introduction, so pgdp can be estimated by per capita GDP from previous studies. A high percentage of tertiary industry means that the industrial structure has been optimized, which will reduce efficiency loss under land investment introduction, so stru can be measured by the proportion of output value of the tertiary industry to GDP. Sci-technology expenditure is beneficial for reducing efficiency loss under land investment introduction, so tech can be evaluated by the proportion of sci-technology expenditure in the total expenditure of local general finance. The introduction of foreign direct investment can reduce the efficiency loss caused by land investment introduction, so fore can be measured by the proportion of foreign direct investment in GDP. Finally, improving urban accessibility will reduce efficiency loss under land investment introduction, so infr can be assessed by the per capita area of city roads. The interpolation method is used to complete the missing data in the statistical yearbook. The descriptive statistics of relevant variables are shown in Table 2.

Table 2.
Descriptive statistics of variables.
3. Results and Discussion
3.1. Reference Regression
A collinearity test was performed before model estimation. Since the maximum value of the variance inflation factor (VIF) of every variable is 4.357, it could be considered that there is no serious collinearity problem. Secondly, the Hausman test is needed to determine whether the panel data model is a random-effects or fixed-effects model; because the p-value is less than 0.05, the original hypothesis of establishing a random-effects model is rejected. According to the condition of model selection, it can be concluded that a fixed-effects model will reduce the endogeneity issues brought about by missing variables. Thus, a fixed-effects model is more suitable for this study.
Based on the results calculated by the three models in Table 3, the values of Sargan P and AR (2) show that there are no over-recognition and second-order sequence autocorrelation problems, and the model is relatively reliable. The regression coefficients of enterprise TFP and city TFP with a first-phase lag term are both significantly positive for the three models, indicating that the current enterprise TFP and city TFP are affected by previous values. According to the results of model (1), the influence of land investment introduction on both enterprise TFP and city TFP is negative, with coefficients of −0.154 and −0.029, respectively, indicating that land investment introduction leads to the loss of enterprise and urban efficiency. When the second-phase lag term of land investment introduction is considered in model (2), the negative effect of land investment introduction on the current enterprise TFP increases from −0.154 to −0.217, indicating that land investment introduction has a sustained effect on enterprise efficiency loss. Meanwhile, land investment introduction has a positive effect on city TFP in the current period, with the coefficient of influence rising from −0.029 to 0.084, and the second-phase lag term still has a negative impact on city TFP due to the scale economy formed by the rapid agglomeration of enterprises under land investment introduction. Note that the advantage of the scale economy will be weakened sometime later, which brings about urban efficiency loss.

Table 3.
Regression results of efficiency loss caused by land investment introduction.
Finally, in model (3), with the addition of control variables, the current period and the second-phase lag term of land investment introduction both have a negative impact on enterprise TFP and city TFP. In general, the regression results from the three models show that land investment introduction has a negative influence on enterprise TFP and city TFP, indicating that it leads to efficiency loss, which verifies hypothesis (H1) and hypothesis (H2).
The coefficients of influence on the level of sci-technology expenditure, level of opening up, and transport infrastructure are all positive, which is in line with our expectations. However, the coefficient of industrial structure for the impact of land investment introduction on enterprise TFP is negative, which is not consistent with our expectations because of the high proportion of tertiary industry crowding out secondary industry. The influence of coefficients on economic development in land investment introduction affecting enterprise TFP and city TFP is also negative, indicating that the efficiency loss caused by land investment introduction in developed areas is significantly higher than that in less-developed areas, resulting in an inconsistent prediction.
3.2. Robustness Test
An improved TFP is the result of developing the urban economy and increasing enterprise profits to some degree, which attracts more enterprises and projects. A strong demand for industrial land also decreases the degree of land investment introduction; that is, an endogenous problem of reverse causality occurs between land investment introduction and TFP. GMM can solve the path dependence problem of the explained variable, but for reverse causality, a robustness test needs to be conducted to validate the accuracy of the regression results. The instrumental variable method is the most frequently used for this purpose; the key to this method is selecting external instrumental variables.
To verify the regression result, enterprise TFP and city TFP, measured by the statistical method of least productivity (LP), are used as external instrumental variables to replace the explained variables. Moreover, the core explanatory variable is the panel data calculated by multiplying the geographical slope by the national urban consumer price index (CPI) with one-phase lag. It should be noted that the instrumental variables need to simultaneously meet the requirements of being related to the explanatory variable and not being related to the explained variable; some works have studied this and concluded that although terrain conditions will affect the land transfer strategy of local governments [54], they will not affect TFP directly as a natural variable. Thus, terrain conditions can be regarded as an instrumental variable. Based on the method proposed by Li et al. [8], the geographical slope at the prefecture level is set to be an instrumental variable, representing the degree of land investment introduction. Thus, the panel data can be formed using the method presented by Xi et al. [33]. Table 4 lists the results of a robustness test that replaces two instrumental variables. As can be seen, the results of the regression test and robustness test are generally consistent. The results of model (5) show that the geographical slope multiplied by the national urban CPI in model (5) has a positive but non-significant effect on enterprise TFP, which strengthens the reliability of the hypothesis that land investment introduction will lead to enterprise efficiency loss and urban efficiency loss.

Table 4.
Robustness test.
3.3. Selection of Factor-Biased Technological Progress of Industrial Enterprise
3.3.1. Reducing Enterprise Efficiency Loss
The maximum value of the variant inflation factor (VIF) of every variable is 2.974, indicating that there is no serious collinearity problem. The regression result is listed in Table 5. The moderating effect of enterprise land (indu), the number of employees (labor), the average employee salary (pay), the net fixed assets of the enterprise (fix), and the five-year period of LPR (loan) on the technological progress and allocation efficiency dimensions of enterprise TFP affected by land investment introduction are included in models (6) to (15). The significant coefficients of the intersection terms indicate that there is a moderating effect of factor-biased technological progress. The aim of the following analysis is to determine whether this moderating effect is positive or negative.

Table 5.
Regression results of effect of induced technological progress on reducing enterprise efficiency loss.
It can be seen from model (6) and model (7) that the negative influences of land investment introduction on the technological progress and allocative efficiency dimensions of enterprise TFP both increase when the intersection term of enterprise land (indu) and land investment introduction is considered in the model. Moreover, compared with other intersection terms in models (8) to (15), the negative value of the intersection term between indu and land investment introduction in model (6) is the smallest, which indicates that the moderating effect of enterprise land on the technological progress and allocation efficiency dimensions is the most significant under land investment introduction. Industrial enterprises should give priority to land-biased technological progress and make intensive use of industrial land through technological means, which is conducive to improving enterprise TFP to the greatest extent. Thus, hypothesis (H3) is verified.
According to model (8) and model (9), when the moderating effect is not included in the model, the influence of land investment introduction on the technological progress dimension is positive, and that on the allocative efficiency dimension is negative. Meanwhile, when the moderating effect is considered, the effect on both the technological progress and allocative efficiency dimensions is negative. Therefore, when the labor quantity is already large, if an industrial enterprise still focuses on labor-biased technological progress, neither dimension of enterprise TFP can be improved. Instead, capital-biased technological progress should be facilitated to reduce enterprise efficiency loss. Based on model (10) and model (11), the effects of land investment introduction on the technological progress dimension and the allocative efficiency dimension are positive and negative, respectively, when the moderating effect between the net fixed assets of an enterprise and land investment introduction is not considered. After introducing the intersection term of the moderating effect into the model, the positive impact of land investment introduction on the former dimension decreases, and the negative impact on the latter dimension increases. The net fixed assets of enterprises are the input of capital factor; thus, capital quantity under land investment has a negative moderating effect on the technological progress dimension and the allocative efficiency dimension. Therefore, when the capital quantity is already large, industrial enterprises should focus on labor-biased technological progress to reduce enterprise efficiency loss.
According to model (12) and model (13), the impact of land investment introduction on the technological progress dimension changes from positive to negative when the intersection term of the moderating effect between average employee salary and land investment introduction is added to the model, whereas the negative impact of land investment introduction on the technological progress dimension increases. By setting the average employee salary as the price of labor factor, this price has a negative moderating effect on the technological progress dimension and allocation efficiency dimension of enterprise TFP under land investment introduction. Therefore, when the labor price is relatively high, industrial enterprises should facilitate capital-biased technological progress to reduce enterprise efficiency loss. Comparing model (14) and model (15), the negative effect of land investment introduction on both the technological progress and allocative efficiency dimensions increases by introducing the intersection term of the moderating effect between the five-year period of LPR and land investment introduction. The five-year period of LPR is the price of capital factor, which has a negative moderating effect on the technological progress and allocation efficiency dimension of enterprise TFP under land investment introduction. Therefore, when capital price is relatively high, industrial enterprises should focus on labor-biased technological progress in order to reduce enterprise efficiency loss.
In general, the price and quantity factors of labor and capital as moderating variables will increase the negative impact of land investment introduction on the technological progress and allocation efficiency dimensions of enterprise TFP, resulting in enterprise efficiency loss. Therefore, industrial enterprises should give preference to productive factors with relatively low prices and small quantities to improve biased technological progress and minimize efficiency loss.
3.3.2. Urban Efficiency Loss Reduction
The maximum value of the variance inflation factor (VIF) of every variable is 4.796, so there is no serious collinearity problem in the models. Table 6 lists the specific regression results, showing that the intersection term coefficients, such as laborit × pdit and lnfixit × pdit, are not all significant. The following section analyzes whether the moderating effect of factor-biased technological progress is positive or negative.

Table 6.
Regression results of effect of induced technological progress on reducing urban efficiency loss.
Comparing the models with and without intersection terms in models (16) and (17), it can be found that the effect on the technological progress dimension changes from positive to negative, and the effect on the allocative efficiency dimension decreases from 0.337 to 0.001, indicating that enterprise land, as the quantity of land factor, has a negative moderating effect on both dimensions of city TFP under land investment introduction. It can be seen from model (18) and model (19) that the intersection term coefficient of laborit × pdit is not significant; even when the allocative efficiency dimension of city TFP decreases from 0.568 to 0.184, it is still impossible to determine the moderating effect of labor quantity under land investment introduction. The intersection term coefficient of lnfixit × pdit is not significant in model (20) and model (21); when the coefficient of pdit affecting the technological progress dimension increases from 0.293 to 0.391, it is impossible to judge the moderating effect of capital quantity under land investment introduction.
By introducing the moderating effect of average employee salary in model (22) and model (23), the value of decreases from 0.934 to 0.139 in the technological progress dimension and increases from 0.157 to 0.382 in the allocative efficiency dimension. Notably, the effect of land investment introduction on the technological progress dimension is greater than that on the allocation efficiency dimension. The average salary of an enterprise’s employees, as the price of labor factor under land investment introduction, has a negative moderating effect on city TFP. Therefore, when the price of labor factor is relatively high, the industrial enterprise should facilitate capital-biased technological progress to reduce urban efficiency loss. In model (24) and model (25), the positive effect of land investment introduction on both the technological progress dimension and allocation efficiency dimension of city TFP decreases when the moderating effect of the five-year period of LPR is taken into account. Specifically, as the price of capital factor increases under land investment introduction, the five-year period of LPR exerts a negative moderating effect on city TFP. Consequently, when the price of capital factor is relatively high, industrial enterprises should prioritize labor-biased technological progress to mitigate urban efficiency loss.
In general, the intersection term coefficient of laborit × pdit and lnfixit × pdit is not significant; it is therefore unable to determine the moderating effect of factor-biased technological progress under land investment introduction. Additionally, it should be noted that the value of the intersection term between the five-year period of LPR and land investment introduction is excessively large, which undermines the validation of land-biased technological progress as a priority, contradicting hypothesis (H4).
3.4. Discussion
As land investment introduction is a special product of a system specific to China, this section mainly focuses on Chinese research. Although the empirical testing methods, variable measurement, and research scope and time in previous studies in the literature differ from those in our study, the views on the negative impact of land investment introduction on output and efficiency are all supported. Li et al. [8] first systematically studied the relationship between land investment introduction and TFP, showing that the agreement-oriented transfer of industrial land hindered productivity improvement based on allocation efficiency. Zhang et al. [27] measured land investment introduction by constructing a dummy variable of whether enterprises purchased industrial land and concluded that land investment introduction reduced the overall productivity level on the basis of affecting the exit of inefficient enterprises. By analyzing the intensity of land subsidy and land and enterprise micro-transaction data from 2004 to 2013, Tian et al. [10] found that the enterprise TFP attracted by land investment introduction was relatively low. Cao [55] studied the evolution process from land investment introduction to land financialization through micro tax data from 2007 to 2015, concluding that land financialization significantly inhibits enterprise TFP. Other scholars have also conducted research on TFP from the perspective of resource misallocation, such as land supply misallocation, and all have affirmed the result is efficiency loss [56,57,58].
However, there is a lack of research on the impact of biased technological progress on land resource misallocation and productivity. It is difficult to verify H3 and H4 by comparing our results to those of relevant studies, and it is expected that similar studies will attract more academic attention in the future.
4. Conclusions
In this study, mathematical deduction and a metrology model were employed to verify the efficiency loss caused by land investment introduction at both an enterprise and city level. Strategies that industrial enterprises can use to minimize these losses through factor-biased technological progress were also explored. Land investment introduction leads to a deviation from the optimal allocation of productive factors and reduces the “threshold selection” effect of land cost, resulting in a sustained negative impact on both enterprise TFP and city TFP in the short and long term. Moreover, industrial enterprises can reduce enterprise efficiency loss under land investment introduction through induced technological progress. Different choices of factor-biased technological progress have varying effects on reducing efficiency loss. However, their impact on alleviating urban efficiency loss remains uncertain. Regarding the reduction in enterprise efficiency loss, we found that land investment introduction diminishes the output intensity of capital- and labor-biased technological progress. As a result, land-biased technological progress is often prioritized. The relative trends in the enhancement coefficients for capital- and labor-biased technological progress reveal that these coefficients are influenced by price and quantity factors, both of which exhibit a negative relationship.
To reduce the efficiency loss resulting from land investment introduction, both the government and industrial enterprises must implement some actions and measures. The central government should establish a supervision and accountability mechanism for the market-oriented transformation of industrial land through competitive transfer and allocation modes. It should align with policies aimed at creating an optimal market-oriented allocation mechanism for productive factors, as outlined in the opinion on building such a mechanism (30 March 2020). Local governments can adopt short-term strategies to attract enterprises, and once the local economy has sufficiently progressed, they should transition to market-based solutions as the economy matures to avoid the negative consequences of indiscriminate and disorderly land investment strategies. These practices will facilitate the orderly flow of productive factors, promote competitive marketization in industrial land allocation, and help select enterprises based on land cost considerations, ultimately leading to a transformation that enhances both enterprise efficiency on the micro-scale and nation development quality on the macro-scale.
For industrial enterprises, prioritizing technological progress based on price factors is crucial. Industrial enterprises should prioritize land-biased technological progress, such as improving production lines or manufacturing techniques based on existing factory premises. When capital price and quantity are relatively high, enterprises should focus on labor-biased technological progress, such as increasing the proportion of highly skilled and educated human capital. Conversely, when labor price and labor quantity are high, enterprises should prioritize capital-biased technological progress, such as strengthening the intensity of capital investment in independent research or technology acquisition.
Although this paper has made a preliminary exploration of the relationship among land investment introduction, TFP, and factor-biased technological progress, there are still some limitations. Firstly, land investment introduction is a unique product of the combination of China’s fiscal and taxation decentralization, GDP competition, and dual-structure land system. While other developed countries have a good substitutability between land and capital due to their mature land markets, land is often considered within the scope of capital, without its independent function. In fact, there are also spatial mismatches caused by urban sprawl in other countries, which may impose constraints on economic growth and efficiency improvement. Secondly, China has a vast territory, and differences in industrial foundation and resource endowment lead to different strategies of local governments regarding land-driven development, resulting in spatial differences in land investment introduction; at the same time, variations in governance capacity across cities can also influence the efficiency of land investment strategies, both of which may bias the research results. Finally, there are differences in scale, ownership, and sector among industrial enterprises, so the question of whether the factor-biased technological progress of different types of enterprises plays a role in alleviating the efficiency loss caused by land investment introduction in combination with enterprise heterogeneity remains to be analyzed. Therefore, to further explore the impact of China’s land resource allocation on improving TFP, further research should aim to include data and analytical templates from other countries, as well as the different results from regions of China with different levels of economic development, different governance capabilities, and different types of enterprise.
Author Contributions
N.Z. and L.Z.: conceptualization, data curation, writing—review and editing. L.Z.: investigation, supervision, editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | Generally speaking, industrial enterprises include industrial enterprises and productive services. Note that productive services are usually not involved in industrial land issues due to their flexible operation mode. For this reason, only industrial enterprises are addressed in this study. |
| 2. | Based on the fundamental theorem of inequality and the two-dimensional deformation of Cauchy–Schwarz inequality, it can be concluded that a2 + b2 + c2 ≥ 3abc ≥ 1/3 (a + b + c)2, and then, we have . Meanwhile, because of a + b + c = 1/2 [(a + b) + (b + c) + (a + c)], inequality can be derived as follows: abc ≥ 1/36 [(a + b) + (b + c) + (a + c)]2. The split deformation can be obtained as follows: ≥ 1/36 [(a + b) + (b + c) + (a + c)]. According to the objective of this study, we can assume that PKK = a > 1, PLL = b > 1 and 0 < (1 − distT)MRPTT2 = c < 1, so ; following this, abc > 1/36 [(a + b) + (b + c) + (a + c)] can be drawn. Therefore, we can conclude that . |
| 3. | According to the multiplier maximum principle, when a = b = c, the value of a*b*c is the largest. |
References
- Liu, W.; Zhang, H. Structural change and technical advance of Chinese economic growth. Econ. Res. J. 2008, 43, 4–15. [Google Scholar]
- Zhu, P.; Yu, F. The impact of economic policy uncertainty on industrial output: The regulatory role of technological progress. Sustainability 2022, 14, 10428. [Google Scholar] [CrossRef]
- Han, C. Structural reform, technological progress and total factor productivity in manufacturing. Sustainability 2023, 15, 432. [Google Scholar] [CrossRef]
- Acemoglu, D. Equilibrum bias of technology. Econometric 2007, 75, 1371–1410. [Google Scholar] [CrossRef]
- Kluge, J.; Lappöhn, S.; Plank, K. Predictors of TFP growth in European countries. Empirica 2023, 50, 109–140. [Google Scholar] [CrossRef]
- Wen, L.; Shen, T.; Huang, Y. A multi-regional CGE model for the optimization of land resource allocation: A simulation of the impact of high-quality development policies in China. Land 2025, 14, 450. [Google Scholar] [CrossRef]
- Zhao, D.; Ma, L.; Qu, T. Marketization level of industrial land in China and its impacting factors from the perspective of resource value manifesting. Resour. Sci. 2016, 38, 217–227. [Google Scholar]
- Li, X.; Huang, Y.; Ma, R. Land resource mismatch and productivity difference of Chinese industrial enterprise. J. Manag. World 2016, 8, 86–96. [Google Scholar]
- Zhang, H.; Yu, Z.; Du, S. The constraint of local economic growth target and manufacturing export technological sophistication. J. World Econ. 2019, 42, 120–142. [Google Scholar]
- Tian, J.; Zhang, H.; Gong, T. Does land investment introduction promote local industrial development? Based on land, enterprises on matching data. China Econ. Q. 2020, 19, 33–60. [Google Scholar]
- Xue, B. Fiscal decentralization, inter-governmental competition and structural deviation of land price. Financ. Econ. 2011, 3, 49–57. [Google Scholar]
- Li, S.; Xia, T. Is it feasible for China’s resource-based cities to achieve sustainable development? An actual resource dependence perspective. Land 2025, 14, 710. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J.; Feng, Y.; Wu, Q. The impact of the regional differentiation of land supply on total factor productivity in China: From the perspective of total factor productivity decomposition. Land 2022, 11, 1859. [Google Scholar] [CrossRef]
- Vandermeer, M.C.; Halleux, J. Evaluation of the spatial and economic effectiveness of industrial land policies in northwest Europe. Eur. Plan. Stud. 2017, 25, 1454–1475. [Google Scholar] [CrossRef]
- Park, J.; Kim, J. Does industrial land sprawl matter in land productivity? A case study of industrial parks of South Korea. J. Clean. Prod. 2022, 334, 130209. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Ou, H. Financial competition, investment-attraction competition and implementation deviation of land binding index control policy. China Popul. Resour. Environ. 2018, 28, 123–131. [Google Scholar]
- Tao, R.; Wang, H. Chinese unfinished transformation of land reform: Challenge and solution. Int. Econ. Rev. 2010, 2, 93–123. [Google Scholar]
- Jin, W.; Zhou, C. Effect of land marketization level and land prices on foreign direct investment in China. Land 2022, 11, 1433. [Google Scholar] [CrossRef]
- Li, T.; Ma, J.; Mo, B. Does the land market have an impact on green total factor productivity? A case study on China. Land 2021, 10, 595. [Google Scholar] [CrossRef]
- Zhao, D.; Lan, J.; Ma, L. The impact of land price marketization on inputted factor and technology choice about Chinese industrial sector. J. Financ. Econ. 2016, 42, 85–96. [Google Scholar]
- Qian, J.; Ji, B. Impact of energy-biased technological progress on inclusive green growth. Sustainability 2022, 14, 16151. [Google Scholar] [CrossRef]
- Ye, J.Q.; Guo, G.X.; Yu, K.H.; Lu, Y.J. Allocation efficiency of public sports resources based on the DEA model in the top 100 economic counties of China in Zhejiang. Sustainability 2023, 15, 9585. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, X.; Meng, W.; He, Y.; Zhang, C. Industrial structure optimization of Wuhan urban agglomeration based on TFP and industrial spatial linkages. Land 2022, 11, 1703. [Google Scholar] [CrossRef]
- Xiao, Z.M.; Peng, H.F.; Pan, Z.Y. Innovation, external technological environment and the total factor productivity of enterprises. Account. Financ. 2021, 62, 3–29. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, J.; Liu, X. Heterogeneous industrial agglomeration, its coordinated development and total factor energy efficiency. Environ. Dev. Sustain. 2023, 25, 5511–5537. [Google Scholar] [CrossRef]
- Li, C.; Luo, M.; Jin, R. Resource misallocation and distribution characteristic of Chinese enterprise scale. Soc. Sci. China 2017, 2, 25–43. [Google Scholar]
- Zhang, L.; Huang, X.; Liu, J. Land investment introduction and enterprise’s behavior: Micro evidence from industrial enterprise with purchased land. Econ. Perspect. 2019, 9, 82–96. [Google Scholar]
- Rafaela, B.; Nicolás, A. Misallocation and manufacturing TFP in Ecuador: Formal, semi-formal and informal firms. J. Econ. Struct. 2019, 8, 16. [Google Scholar]
- Kumari, R.D.T.S.; Tang, S.H.K.; Chen, S.X.; Li, B. Misallocation and productivity slowdown over two decades: Evidence from Sri Lanka. Appl. Econ. 2021, 53, 4417–4435. [Google Scholar] [CrossRef]
- Jiang, X.; Lu, X.H.; Gong, M.Q. Assessing the effects of land transfer marketization on green total factor productivity from the perspective of resource allocation: Evidence from China. Front. Environ. Sci. 2022, 10, 975282. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, G.; Li, G. Market environment, key industrial policy and enterprise’s productivity differential. J. Manag. World 2019, 35, 114–126. [Google Scholar]
- Ranpati, K.; Shawn, C.; Bei, L.; Sam, T. Can land misallocation be a greater barrier to development than capital? Evidence from manufacturing firms in Sri Lanka. Econ. Model. 2023, 126, 106368. [Google Scholar]
- Xi, M.; Mei, L. Industrial land price, selection effect and industrial efficiency. Econ. Res. J. 2019, 54, 102–118. [Google Scholar]
- Peng, S.; Wang, J.; Sun, H.; Guo, N. How does the spatial misallocation of land resources affect urban industrial transformation and upgrading? evidence from China. Land 2022, 11, 1630. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X.; Skitmore, M. Industrial land price and its impact on urban growth: A Chinese case study. Land Use Policy 2014, 36, 199–209. [Google Scholar] [CrossRef]
- Wang, J.; Han, P. The impact of industrial agglomeration on urban green land use efficiency in the Yangtze River. Econ. Belt 2023, 13, 974. [Google Scholar] [CrossRef]
- Meina, C. Revenue, time horizon, and land allocation in China. Land Use Policy 2017, 62, 101–112. [Google Scholar]
- Kilumelume, M.; Morando, B.; Newman, C.; Rand, J. Tariffs, productivity and resource misallocation. World Bank Econ. Rev. 2025, lhaf010. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, F.; Li, K. Impact of market misallocations on green TFP: Evidence from countries along the belt and road. Environ. Sci. Pollut. Res. 2019, 26, 35034–35048. [Google Scholar] [CrossRef]
- Wei, X.; Wang, H.; Wang, H. The relationship among factor substitution, technological progress and intensive construction of land-using. Resour. Sci. 2014, 36, 1356–1364. [Google Scholar]
- Xu, Y.; Li, P. Factor price-distortion and direction of Chinese technological progress. Forum Sci. Technol. China 2017, 8, 12–19. [Google Scholar]
- Acemoglu, D.; Gancia, G.; Zilibotti, F. Off shorting and directed technical change. Am. Econ. J. 2015, 7, 84–122. [Google Scholar]
- Lei, L.; Xu, C. Biased technological progress, biased factor allocation and TFP growth in China. Stat. Res. 2015, 32, 10–16. [Google Scholar]
- Wang, Z.; Zhao, X.G.; Zhou, Y. Biased technological progress and total factor productivity growth: From the perspective of China’s renewable energy industry. Renew. Sustain. Energy Rev. 2021, 146, 11136. [Google Scholar]
- Lagomarsino, E. Which nesting structure for the CES? A new selection approach based on input separability. Econ. Model. 2021, 102, 105562. [Google Scholar] [CrossRef]
- Winford, H.; Masanjala, C.P. The Solow model with CES technology: Nonlinearities and parameter heterogeneity. J. Appl. Econom. 2004, 19, 171–201. [Google Scholar]
- Hang, J.; Guo, M.; Niu, Q. Resource misallocation, capacity utilization and productivity. China Econ. Q. 2021, 21, 93–112. [Google Scholar]
- Wen, L.; Hou, T.; Zhang, L. A comparison and application of moderator and mediator. Acta Psychol. Sinca 2005, 2, 268–274. [Google Scholar]
- Wang, Q.; Dong, Y.; Song, F. Study on TFP of Chinese economy and its influencing factors. Stat. Decis. 2022, 3, 97–101. [Google Scholar]
- Zhang, J.; Wu, Y.; Zhang, P. The estimation of Chinese provincial capital stock: 1952–2000. Econ. Res. J. 2004, 10, 35–44. [Google Scholar]
- Shan, J. Reestimating the capital stock of China: 1952–2006. J. Quant. Tech. Econ. 2008, 25, 17–31. [Google Scholar]
- Liu, W.; Yan, X. The crowding in/out effects of FDI against the background of local governments’ land investment introduction. J. Financ. Econ. 2016, 42, 17–29. [Google Scholar]
- Gao, Y.; Wang, Q.; Yu, S. Financial geography structure and short-term loan and long-term investment of enterprise. J. Shanxi Univ. Financ. Econ. 2022, 44, 43–57. [Google Scholar]
- Chen, T.; Kung, K. Does land revenue windfall create a political resource curse? Evidence from China. J. Dev. Econ. 2016, 123, 86–106. [Google Scholar] [CrossRef]
- Cao, J. Land financialization, resource misallocation and total factor productivity of enterprises. Chin. Rev. Financ. Stud. 2024, 16, 71–85+155. [Google Scholar]
- Zhang, S.; Yu, Y. Land transfer, resource misallocation and total factor productivity. J. Financ. Econ. 2019, 45, 73–85. [Google Scholar]
- Peng, S.; Li, M.; Wang, J. The total factor productivity loss effect and formation mechanism of land resource misallocation. China Land Sci. 2022, 36, 55–65. [Google Scholar]
- Cheng, K.; Yu, J. Mismatch of urban land supply in China: Characteristic facts and its impact on total factor productivity. China Land Sci. 2022, 36, 43–54. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).