Applying Machine Learning Algorithms for Spatial Modeling of Flood Susceptibility Prediction over São Paulo Sub-Region
Abstract
1. Introduction
2. Materials and Methods
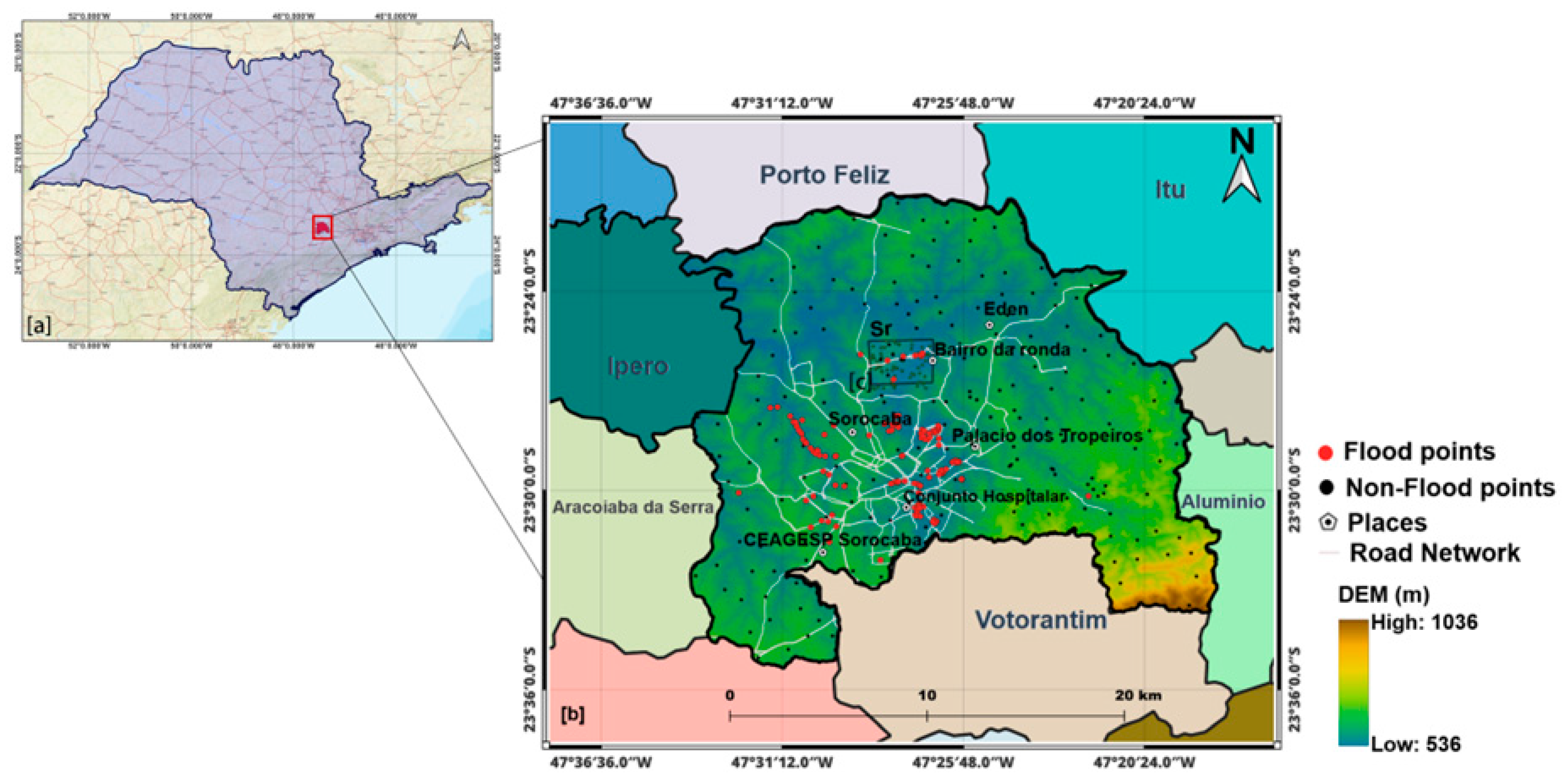
2.1. Study Area
2.2. Geospatial Data
2.2.1. Flood Inventory
2.2.2. Flood Driving Factors
3. Model Feature Importance (MFI) and ML Models
3.1. Recursive Feature Elimination (RFE)
| Algorithm 1. RFE Algorithm in Pseudocode with Bars for Routines and Tabulation. |
| Input: X—Feature matrix (n_samples x n_features) Y—Target vector model: Machine learning Model with feature importance k: Desired number of features to select Initialize: X_remaining ← X // Start with the full dataset feature_set ← All feature indices while len (X_remaining) > k: // Continue until k features remain Train Phase: Model.fit (X_remaining, y) Ranking Phase: importance_scores ← model.feature_importances_ ranked_features ← argsort (importance_scores) Elimination Phase: least_important ← ranked_features [0] feature_set ← feature_set \ {least_important} X_remaining ← X [:, feature_set] Output: X_remaining—Feature matrix with top k features |
3.2. Methodology Flowchart and Models
3.2.1. Random Forest (RF) Model
3.2.2. Support Vector Machine (SVM) Model
3.2.3. Differential Evolution (DE) Model
3.2.4. Naïve Bayes (NB) Model
3.3. Model Explainability and Feature Importance
Model Performance Metrics
4. Results and Discussion
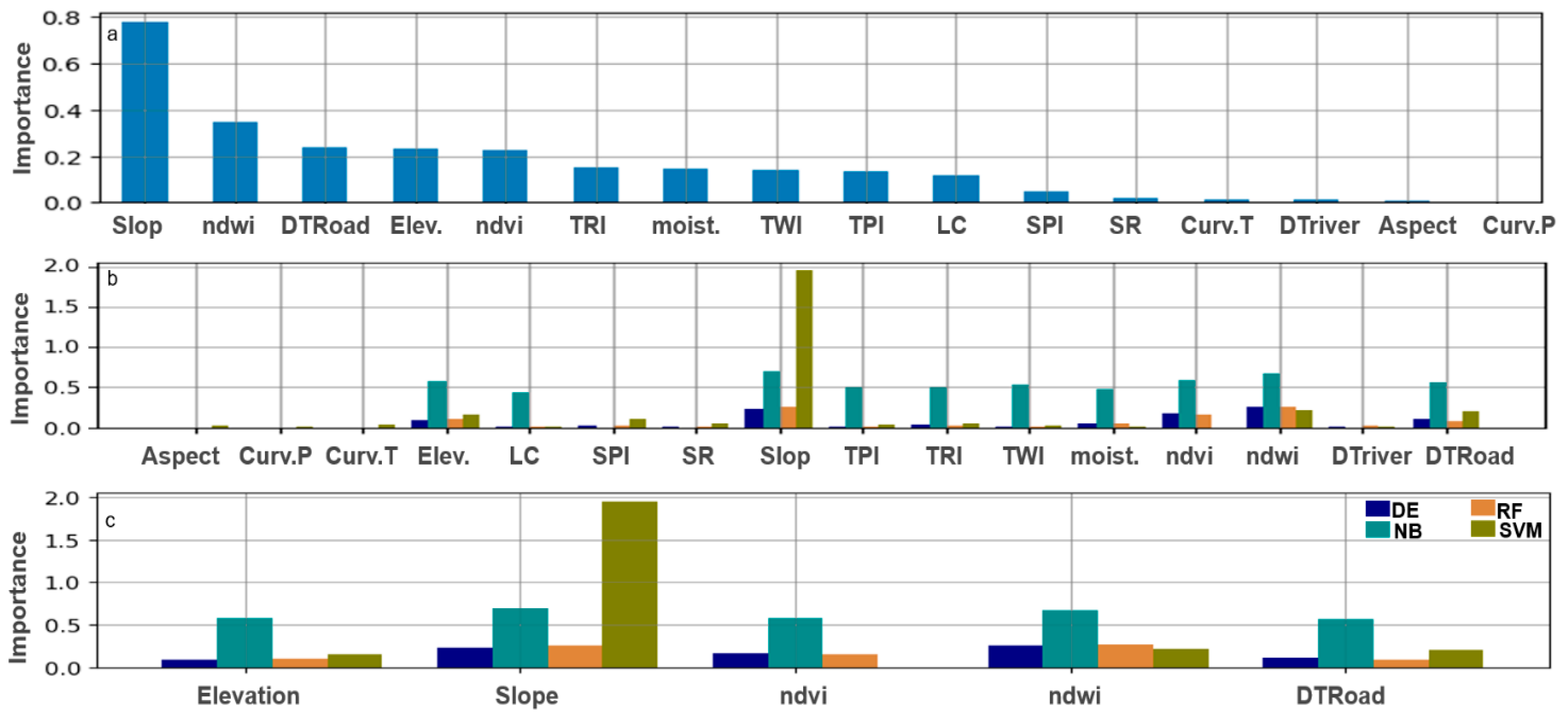
4.1. RFE as an Anti-Multicollinearity
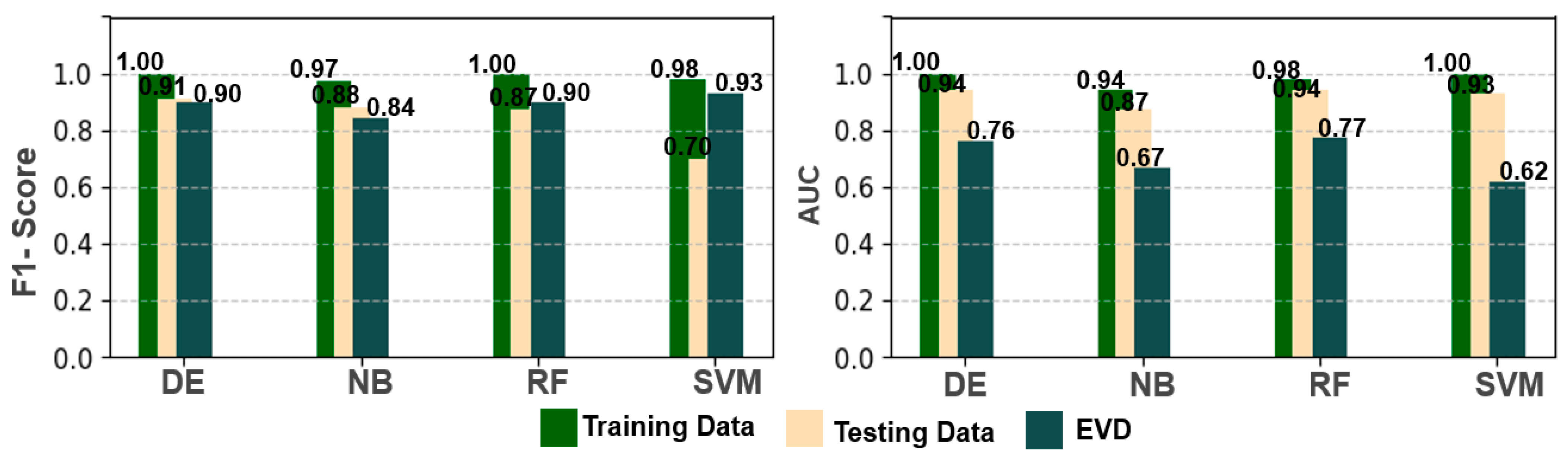
4.2. Model Performance Comparison and Validation
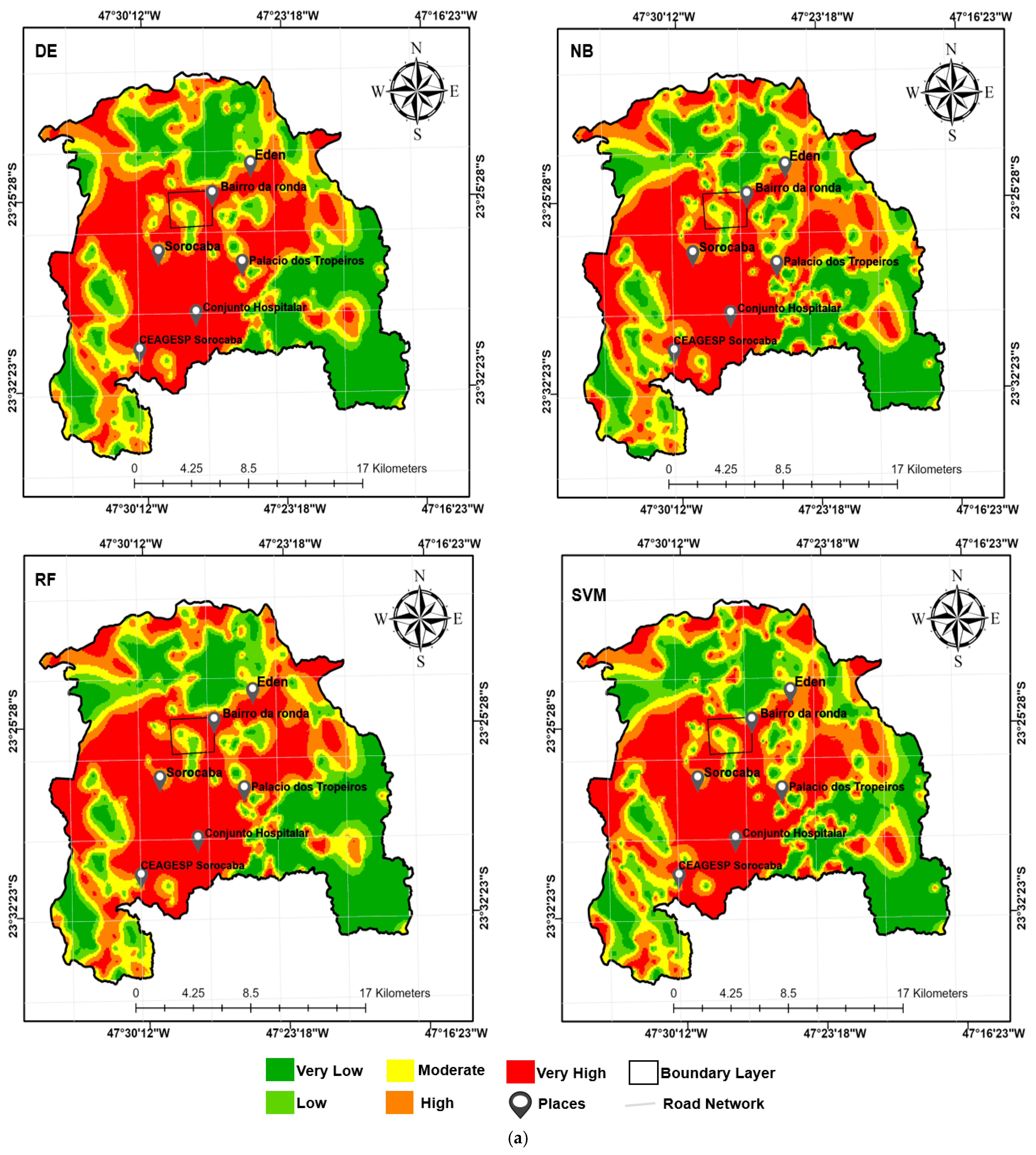
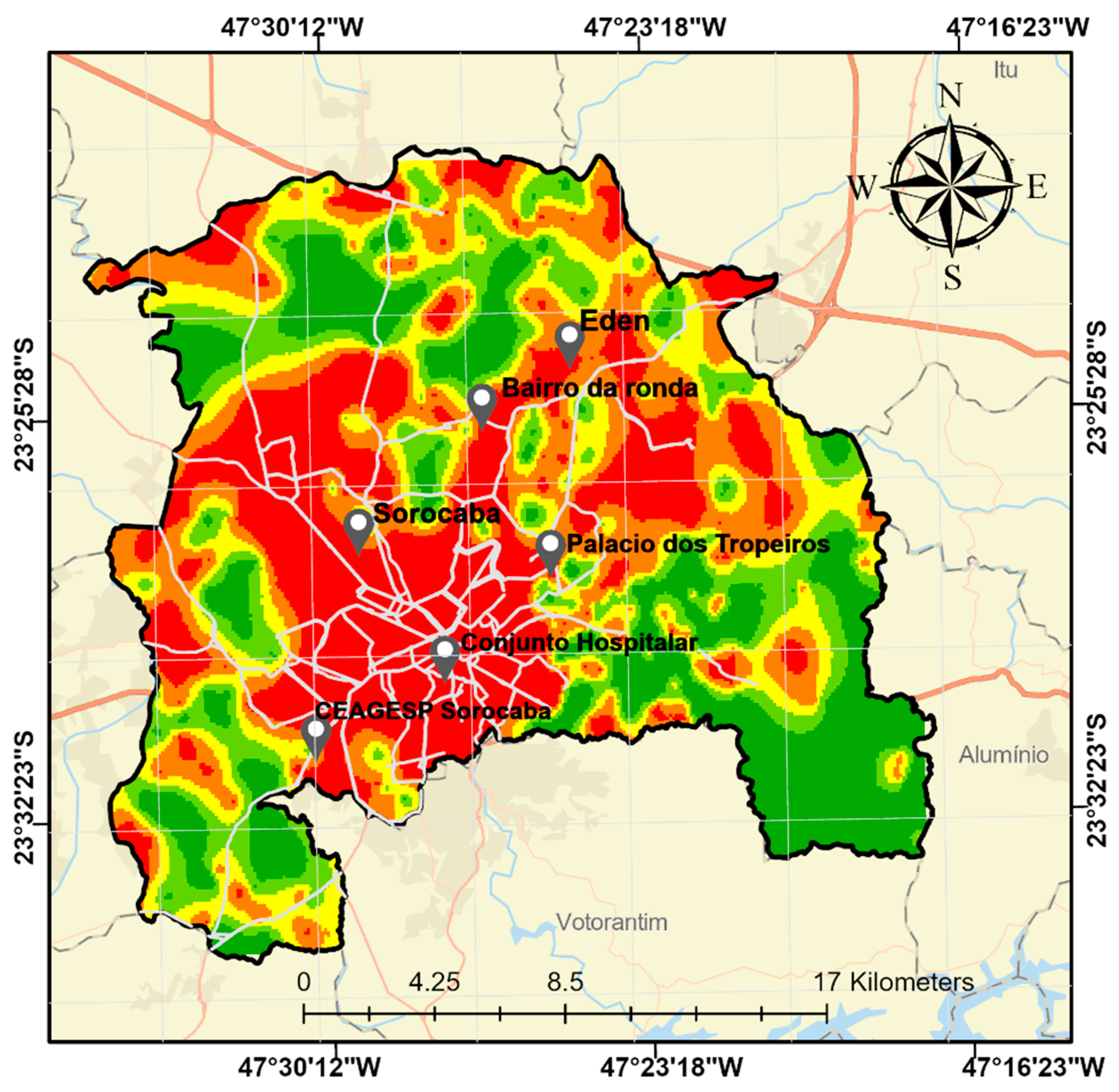
4.3. Flood Model Susceptibility in São Paulo Sub-Region
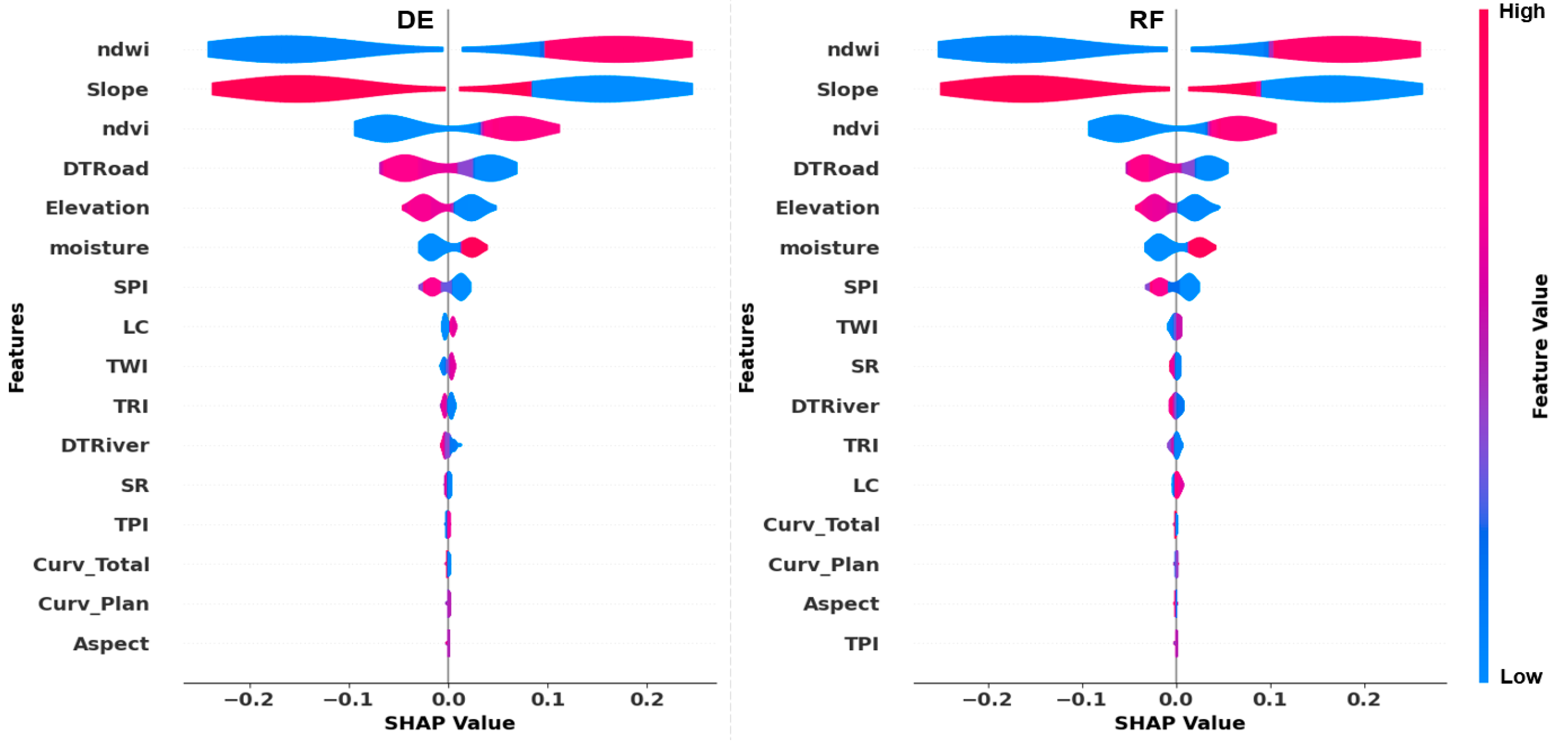
4.4. Model Feature Importance Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNDRR. The Human Cost of Disasters: An Overview of the Last 20 Years (2000–2019); United Nations Office for Disaster Risk Reduction: Geneva, Switzerland, 2020; pp. 13–17. Available online: https://www.undrr.org/publication/human-cost-disasters-overview-last-20-years-2000-2019 (accessed on 1 November 2024).
- Doocy, S.; Daniels, A.; Packer, C.; Dick, A.; Kirsch, T.D. The Human Impact of Earthquakes: A Historical Review of Events 1980–2009 and Systematic Literature Review. PLoS Curr. 2013, 5, e50bb9494b3c1. [Google Scholar] [CrossRef] [PubMed]
- Opolot, E. Application of Remote Sensing and Geographical Information Systems in Flood Management: A Review. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 1884–1894. [Google Scholar] [CrossRef]
- CRED; UNDRR. Economic Losses, Poverty, and Disasters (1998–2017); Centre for Research on the Epidemiology of Disasters and United Nations Office for Disaster Risk Reduction: Brussels, Belgium, 2018; pp. 8–13. Available online: https://www.undrr.org/publication/economic-losses-poverty-disasters-1998-2017 (accessed on 1 November 2024).
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood Risk and Climate Change: Global and Regional Perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2021; Available online: https://inthistogetheramerica.org/2021/08/11/the-ipcc-report-and-what-it-means (accessed on 1 January 2023).
- Bradshaw, C.J.A.; Sodhi, N.S.; Peh, K.S.H.; Brook, B.W. Global evidence that deforestation amplifies flood risk and severity in the developing world. Glob. Change Biol. 2007, 13, 2379–2395. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L. A Comparative Assessment of Flood Susceptibility Modeling Using Multi-Criteria Decision-Making Analysis and Machine Learning Methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; Wiley-Blackwell: Hoboken, NJ, USA, 2012; pp. 1–456. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Siraj, S.; Hodgett, R.E. An Overview of Multi-Criteria Decision Analysis (MCDA) Application in Managing Water-Related Disaster Events: Analyzing 20 Years of Literature for Flood and Drought Events. Water 2021, 13, 1358. [Google Scholar] [CrossRef]
- Mendoza, G.A.; Martins, H. Multi-criteria decision analysis in natural resource management: A critical review of methods and new modelling paradigms. For. Ecol. Manag. 2006, 230, 1–22. [Google Scholar] [CrossRef]
- Seleem, O.; Heistermann, M.; Bronstert, A. Efficient Hazard Assessment for Pluvial Floods in Urban Environments: A Benchmarking Case Study for the City of Berlin, Germany. Water 2021, 13, 2476. [Google Scholar] [CrossRef]
- Petroselli, A. Lidar Data and Hydrological Applications at the Basin Scale. GISci. Remote Sens. 2012, 49, 139–162. [Google Scholar] [CrossRef]
- Wu, W.; Emerton, R.; Duan, Q.; Wood, A.W.; Wetterhall, F.; Robertson, D.E. Ensemble Flood Forecasting: Current Status and Future Opportunities. WIREs Water 2020, 7, e1432. [Google Scholar] [CrossRef]
- Rahmati, O.; Zeinivand, H.; Besharat, M. Flood hazard zoning in Yasooj region, Iran, using GIS and multi-criteria decision analysis (MCDA). Geomat. Nat. Hazards Risk 2015, 7, 1000–1017. [Google Scholar] [CrossRef]
- Meyer Oliveira, A.; Fleischmann, A.S.; Paiva, R.C.D. On the Contribution of Remote Sensing-Based Calibration to Model Hydrological and Hydraulic Processes in Tropical Regions. J. Hydrol. 2021, 597, 126184. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.; Wilby, R.L. Modelling the Impact of Land Subsidence on Urban Pluvial Flooding: A Case Study of Downtown Shanghai, China. Sci. Total Environ. 2016, 544, 744–753. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Shao, J. Advances in Hydrological Modeling with GIS and RS Integration for Flood Assessment and Management. J. Hydrol. 2021, 598, 126456. [Google Scholar] [CrossRef]
- Khan, M.; Khan, A.U.; Ullah, B. Developing a machine learning-based flood risk prediction model for the Indus Basin in Pakistan. Water Pract. Technol. 2024, 19, 2213–2225. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-Based Groundwater Potential Mapping Using Boosted Regression Tree, Classification and Regression Tree, and Random Forest Machine Learning Models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood Susceptibility Analysis and Its Verification Using a Novel Ensemble Support Vector Machine and Frequency Ratio Method. Stoch. Environ. Res. Risk Assess. 2015, 29, 1149–1165. [Google Scholar] [CrossRef]
- Al-Juaidi, A.E.M.; Nassar, A.M.; Al-Juaidi, O.E.M. Flood Risk Assessment for Urban Areas in Gaza Strip, Palestine. Arab. J. Geosci. 2018, 11, 765. [Google Scholar] [CrossRef]
- Rhyme, R.R.; Showmitra, K.S. Artificial neural network (ANN) for flood susceptibility mapping in Bangladesh. Heliyon 2023, 9, e16459. [Google Scholar] [CrossRef]
- Madhuri, R.; Sistla, S.; Srinivasa Raju, K. Application of Machine Learning Algorithms for Flood Susceptibility Assessment and Risk Management. J. Water Clim. Change 2021, 12, 2608–2623. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W. Flood Susceptibility Mapping Using Frequency Ratio, Statistical Index and Weights-of-Evidence Models in GIS. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Lee, S.; Lee, M.J.; Jung, H.S. Spatial Prediction of Flood Susceptibility Using Random-Forest and Boosted-Tree Models in Seoul Metropolitan City, Korea. Geocarto Int. 2017, 32, 500–519. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Peng, D.; Xu, L. Assessment of Urban Flood Susceptibility Using Semi-Supervised Machine Learning Model. Sci. Total Environ. 2019, 659, 940–949. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.; Turek, G.; Schumann, A. Flood Susceptibility Mapping Using Random Forest and Boosted Regression Tree Models in the Mulde River Basin, Germany. J. Flood Risk Manag. 2020, 13, e12621. [Google Scholar] [CrossRef]
- McGrath, H.; Gohl, P.N. Accessing the Impact of Meteorological Variables on Machine Learning Flood Susceptibility Mapping. Remote Sens. 2022, 14, 1656. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, T.; Wu, H. Convolutional Neural Networks for Flood Susceptibility Mapping Using Remote Sensing Data. Remote Sens. Environ. 2020, 242, 111739. [Google Scholar] [CrossRef]
- Shi, X.; Cui, Y.; Yang, Z.; Wang, L. Flood Risk Assessment Using Deep Learning and Satellite Data: A Case Study of the Yangtze River Basin. J. Hydrol. 2021, 596, 125707. [Google Scholar] [CrossRef]
- Liu, J.; Liu, K.; Wang, M. A Residual Neural Network (ResNET) Integrated with a Hydrological Model for Global Flood Susceptibility Mapping Based on Remote Sensing Datasets. Remote Sens. 2023, 15, 2447. [Google Scholar] [CrossRef]
- Magalhães, I.A.L.; de Carvalho Junior, O.A.; Sano, E.E. Delimitation of Flooded Areas Based on Sentinel-1 SAR Data Processed through Machine Learning: A Study Case from Central Amazon, Brazil. Finisterra 2023, 58, 87–109. [Google Scholar] [CrossRef]
- Seleem, O.; Ayzel, G.; de Souza, A.C.T.; Bronstert, A.; Heistermann, M. Towards Urban Flood Susceptibility Mapping Using Data-Driven Models in Berlin, Germany. Geomat. Nat. Hazards Risk 2022, 13, 1640–1662. [Google Scholar] [CrossRef]
- Khosravi, K.; Nohani, E.; Alami, M.T.; Pourghasemi, H.R. A comparative assessment of decision trees algorithms for flood susceptibility mapping in a semi-arid region of Iran. Sci. Total Environ. 2018, 615, 438–449. [Google Scholar] [CrossRef]
- IBGE. Instituto Brasileiro de Geografia e Estatística (IBGE). Available online: https://www.ibge.gov.br/ (accessed on 1 November 2024).
- Alves, G.; Cláudia, B. Metropolitan Governance in São Paulo State: The Case of Sorocaba. Sci. Finisterra 2025, 59, 45–60. Available online: https://revistas.rcaap.pt/finisterra/article/view/36381/28301 (accessed on 6 January 2025).
- Martines, M.R.; Cavagis, A.D.M.; Kawakubo, F.S.; Morato, R.G.; Ferreira, R.V.; Toppa, R.H. Spatial Segregation in Floodplain: An Approach to Correlate Physical and Human Dimensions for Urban Planning. Cities 2020, 97, 102551. [Google Scholar] [CrossRef]
- G1.globo. Sorocaba Records the Highest Volume of Rain. Available online: https://g1.globo.com/sp/sorocaba-jundiai/noticia/2023/02/13/sorocaba-registra-maior-volume-de-chuvas-para-o-mes-de-fevereiro-nos-ultimos-10-anos-diz-prefeitura.ghtml (accessed on 1 November 2024).
- UOL. Sorocaba (SP): Rain Causes Damage and River Overflows in the City of Sorocaba. Available online: https://noticias.uol.com.br/cotidiano/ultimas-noticias/2022/03/12/chuvas-sorocaba-sp-estragos.html (accessed on 1 November 2024).
- CEPAGRI. Centro de Pesquisas Meteorológicas e Climáticas Aplicadas à Agricultura—CEPAGRI/UNICAMP. 2020. Available online: https://www.cpa.unicamp.br/ (accessed on 1 November 2024).
- Marengo, J.A.; Seluchi, M.E.; Cunha, A.P.; Cuartas, L.A.; Goncalves, D.; Sperling, V.B.; Ramos, A.M.; Dolif, G.; Saito, S.; Bender, F.; et al. Heavy Rainfall Associated with Floods in Southeastern Brazil in November–December 2021. Nat. Hazards 2023, 116, 3617–3644. [Google Scholar] [CrossRef]
- Marengo, J.A.; Cunha, A.P.; Seluchi, M.E.; Camarinha, P.I.; Dolif, G.; Sperling, V.B.; Alcântara, E.H.; Ramos, A.M.; Andrade, M.M.; Stabile, R.A.; et al. Heavy Rains and Hydrogeological Disasters on February 18th–19th, 2023, in the City of São Sebastião, São Paulo, Brazil. Meteorological Causes to Early Warnings. Nat. Hazards 2024, 120, 7997–8024. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Phong, T.V.; Yen, H.P.H.; Tuyen, T.T.; Luong, V.V.; Nguyen, H.D.; Le, L.H.V.; Foong, K. Improved Flood Susceptibility Mapping Using a Best First Decision Tree Integrated with Ensemble Learning Techniques. Geosci. Front. 2021, 12, 101105. [Google Scholar] [CrossRef]
- Meliho, M.; Khattabi, A.; Asinyo, J. Spatial Modeling of Flood Susceptibility Using Machine Learning Algorithms. Arab. J. Geosci. 2021, 14, 2243. [Google Scholar] [CrossRef]
- Kurugama, K.M.; Kazama, S.; Hiraga, Y.; Samarasuriya, C. A Comparative Spatial Analysis of Flood Susceptibility Mapping Using Boosting Machine Learning Algorithms in Rathnapura, Sri Lanka. J. Flood Risk Manag. 2024, 17, e12980. [Google Scholar] [CrossRef]
- Lehner, B.; Grill, G. Global River Hydrography and Network Routing: Baseline Data and New Approaches to Study the World’s Large River Systems. Hydrol. Process. 2013, 27, 2171–2186. [Google Scholar] [CrossRef]
- Dottori, F.; Salamon, P.; Bianchi, A.; Alfieri, L.; Hirpa, F.A.; Feyen, L. Development and Evaluation of a Framework for Global Flood Hazard Mapping. Adv. Water Resour. 2016, 94, 87–102. [Google Scholar] [CrossRef]
- Haklay, M.; Weber, P. OpenStreetMap: User-Generated Street Maps. IEEE Pervasive Comput. 2008, 7, 12–18. [Google Scholar] [CrossRef]
- Aristizabal, F.; Chegini, T.; Petrochenkov, G.; Salas, F.; Judge, J. Effects of High-Quality Elevation Data and Explanatory Variables on the Accuracy of Flood Inundation Mapping via Height Above Nearest Drainage. Hydrol. Earth Syst. Sci. 2024, 28, 1287–1315. [Google Scholar] [CrossRef]
- Al-Juaidi, A.E.M. The Interaction of Topographic Slope with Various Geo-Environmental Flood-Causing Factors on Flood Prediction and Susceptibility Mapping. Environ. Sci. Pollut. Res. 2023, 30, 59327–59348. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.D. Spatial Modeling of Flood Hazard Using Machine Learning and GIS in Ha Tinh Province, Vietnam. J. Water Clim. Change 2023, 14, 200–222. [Google Scholar] [CrossRef]
- Edamo, M.L.; Ayele, E.G.; Ukumo, T.Y.; Kassaye, A.A.; Haile, A.P. Capability of Logistic Regression in Identifying Flood-Susceptible Areas in a Small Watershed. H2Open J. 2024, 7, 351–374. [Google Scholar] [CrossRef]
- Moazzam, M.F.U.; Vansarochana, A.; Rahman, A.U. Analysis of Flood Susceptibility and Zonation for Risk Management Using Frequency Ratio Model in District Charsadda, Pakistan. Int. J. Environ. Geoinform. 2018, 5, 140–153. [Google Scholar] [CrossRef]
- Altunel, A.O. The Effect of DEM Resolution on Topographic Wetness Index Calculation and Visualization: An Insight to the Hidden Danger Unraveled in Bozkurt in August, 2021. Int. J. Eng. Geosci. 2022, 7, 153–164. [Google Scholar] [CrossRef]
- Yochum, S.E.; Sholtes, J.S.; Scott, J.A.; Bledsoe, B.P. Stream Power Framework for Predicting Geomorphic Change: The 2013 Colorado Front Range Flood. Geomorphology 2017, 292, 178–192. [Google Scholar] [CrossRef]
- Merwade, V.; Liu, Z. Investigating the Role of Model Structure and Surface Roughness in Generating Flood Inundation Extents Using One-and Two-Dimensional Hydraulic Models. J. Flood Risk Manag. 2019, 12, e12347. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nazari, R.; Nikoo, M.R.; Karimi, M. Enhancing Flood Risk Assessment in Urban Areas by Integrating Hydrodynamic Models and Machine Learning Techniques. Sci. Total Environ. 2024, 938, 175859. [Google Scholar] [CrossRef]
- Bashir, B. Morphometric Parameters and Geospatial Analysis for Flash Flood Susceptibility Assessment: A Case Study of Jeddah City along the Red Sea Coast, Saudi Arabia. Water 2023, 15, 870. [Google Scholar] [CrossRef]
- Ndiaye, A.; Arnault, J.; Mbaye, M.L.; Sy, S.; Camara, M.; Lawin, A.E.; Kunstmann, H. Potential Contribution of Land Cover Change on Flood Events in the Senegal River Basin. Front. Water 2024, 6, 1447577. [Google Scholar] [CrossRef]
- Shafapour Tehrany, M.; Shabani, F.; Neamah Jebur, M.; Hong, H.; Chen, W.; Xie, X. GIS-Based Spatial Prediction of Flood Prone Areas Using Standalone Frequency Ratio, Logistic Regression, Weight of Evidence and Their Ensemble Techniques. Geomat. Nat. Hazards Risk 2017, 8, 1538–1561. [Google Scholar] [CrossRef]
- Alves, P.B.R.; Amanguah, E.; McNally, D.; Espinoza, M.; Ghaedi, H.; Reilly, A.C.; Hendricks, M.D. Navigating the Definition of Urban Flooding: A Conceptual and Systematic Review of the Literature. Water Sci. Technol. 2024, 90, 2796–2812. [Google Scholar] [CrossRef]
- Chang, K.T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating Scale Effects of Topographic Variables in Landslide Susceptibility Models Using GIS-Based Machine Learning Techniques. Sci. Rep. 2019, 9, 12296. [Google Scholar] [CrossRef]
- Mahdizadeh Gharakhanlou, N.; Perez, L. Spatial Prediction of Current and Future Flood Susceptibility: Examining the Implications of Changing Climates on Flood Susceptibility Using Machine Learning Models. Entropy 2022, 24, 1630. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Li, Y.; Guo, F. Mapping Landslide Susceptibility with the Consideration of Spatial Heterogeneity and Factor Optimization. Nat. Hazards 2024, 121, 4067–4093. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Peng, D.; Zuo, D. Urban Flood Susceptibility Assessment Based on Convolutional Neural Networks. J. Hydrol. 2020, 590, 125235. [Google Scholar] [CrossRef]
- Pal, S.C.; Deswal, S. Flash Flood Susceptibility Modeling Using New Approaches of Hybrid and Ensemble Tree-Based Machine Learning Algorithms. Remote Sens. 2020, 12, 3568. [Google Scholar] [CrossRef]
- Ahmed, M.R.; Kabir, I.; Hassan, Q.K. A Novel Framework for Addressing Uncertainties in Machine Learning-Based Geospatial Approaches for Flood Prediction. J. Environ. Manag. 2022, 326, 116813. [Google Scholar] [CrossRef]
- Chang, F.J.; Hsu, K.; Chang, L.C. Flood Forecasting Using Machine Learning Methods. Water 2019, 11, 9. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yilmaz, M.; Tosunoglu, F.; Demirel, M.C. Comparison of Conventional and Differential Evolution-Based Parameter Estimation Methods on the Flood Frequency Analysis. Acta Geophys. 2021, 69, 1887–1900. [Google Scholar] [CrossRef]
- Hong, H.; Panahi, M.; Shirzadi, A.; Liu, J.; Zhu, A.X.; Chen, W.; Kougias, I.; Kazakis, N. Flood susceptibility assessment in Hengfeng area coupling adaptive neuro-fuzzy inference system with genetic algorithm and differential evolution. Sci. Total Environ. 2018, 621, 1124–1141. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Wu, Z.; Zhou, Y. Using Multi-Factor Analysis to Predict Urban Flood Depth Based on Naive Bayes. Water 2021, 13, 432. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Zhou, Y.; Wang, H. Prediction of urban water accumulation points and water accumulation process based on machine learning. Environ. Earth Sci. 2021, 14, 2317–2328. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Pradhan, B.; Lee, S.; Dikshit, A.; Kim, H. Spatial Flood Susceptibility Mapping Using an Explainable Artificial Intelligence (XAI) Model. Geosci. Front. 2023, 14, 101625. [Google Scholar] [CrossRef]
- Sim, J.; Wright, C.C. The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requirements. Phys. Ther. 2005, 85, 257–268. [Google Scholar] [CrossRef]
- Duwal, S.; Liu, D.; Pradhan, P.M. Flood Susceptibility Modeling of the Karnali River Basin of Nepal Using Different Machine Learning Approaches. Geomat. Nat. Hazards Risk 2023, 14. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Cui, L.; Wang, J.; Zuo, D.; Peng, D. Improving Urban Flood Susceptibility Mapping Using Transfer Learning. J. Hydrol. 2021, 602, 126777. [Google Scholar] [CrossRef]
- Chen, C.-J.; Chi, M.-H.; Ye, J.-R. Assessing hydroclimate response to land use/cover change using coupled atmospheric-hydrological models. Geosci. Lett. 2023, 10, 54. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oluwadare, T.S.; Ribeiro, M.P.; Chen, D.; Babadi Ataabadi, M.; Tabesh, S.H.; Daomi, A.E. Applying Machine Learning Algorithms for Spatial Modeling of Flood Susceptibility Prediction over São Paulo Sub-Region. Land 2025, 14, 985. https://doi.org/10.3390/land14050985
Oluwadare TS, Ribeiro MP, Chen D, Babadi Ataabadi M, Tabesh SH, Daomi AE. Applying Machine Learning Algorithms for Spatial Modeling of Flood Susceptibility Prediction over São Paulo Sub-Region. Land. 2025; 14(5):985. https://doi.org/10.3390/land14050985
Chicago/Turabian StyleOluwadare, Temitope Seun, Marina Pannunzio Ribeiro, Dongmei Chen, Masoud Babadi Ataabadi, Saba Hosseini Tabesh, and Abiodun Esau Daomi. 2025. "Applying Machine Learning Algorithms for Spatial Modeling of Flood Susceptibility Prediction over São Paulo Sub-Region" Land 14, no. 5: 985. https://doi.org/10.3390/land14050985
APA StyleOluwadare, T. S., Ribeiro, M. P., Chen, D., Babadi Ataabadi, M., Tabesh, S. H., & Daomi, A. E. (2025). Applying Machine Learning Algorithms for Spatial Modeling of Flood Susceptibility Prediction over São Paulo Sub-Region. Land, 14(5), 985. https://doi.org/10.3390/land14050985






