Evaluating Territorial Space Use Efficiency: A Geographic Data Envelopment Model Considering Geospatial Effects
Abstract
1. Introduction
2. Literature Review
2.1. Evolution of the Efficiency Evaluation Models
2.2. Principles and Development of the DEA Model
2.3. Limitations of the DEA Model Applied to the Evaluation of Territorial Space Use Efficiency
3. GeoDEA Model Construction
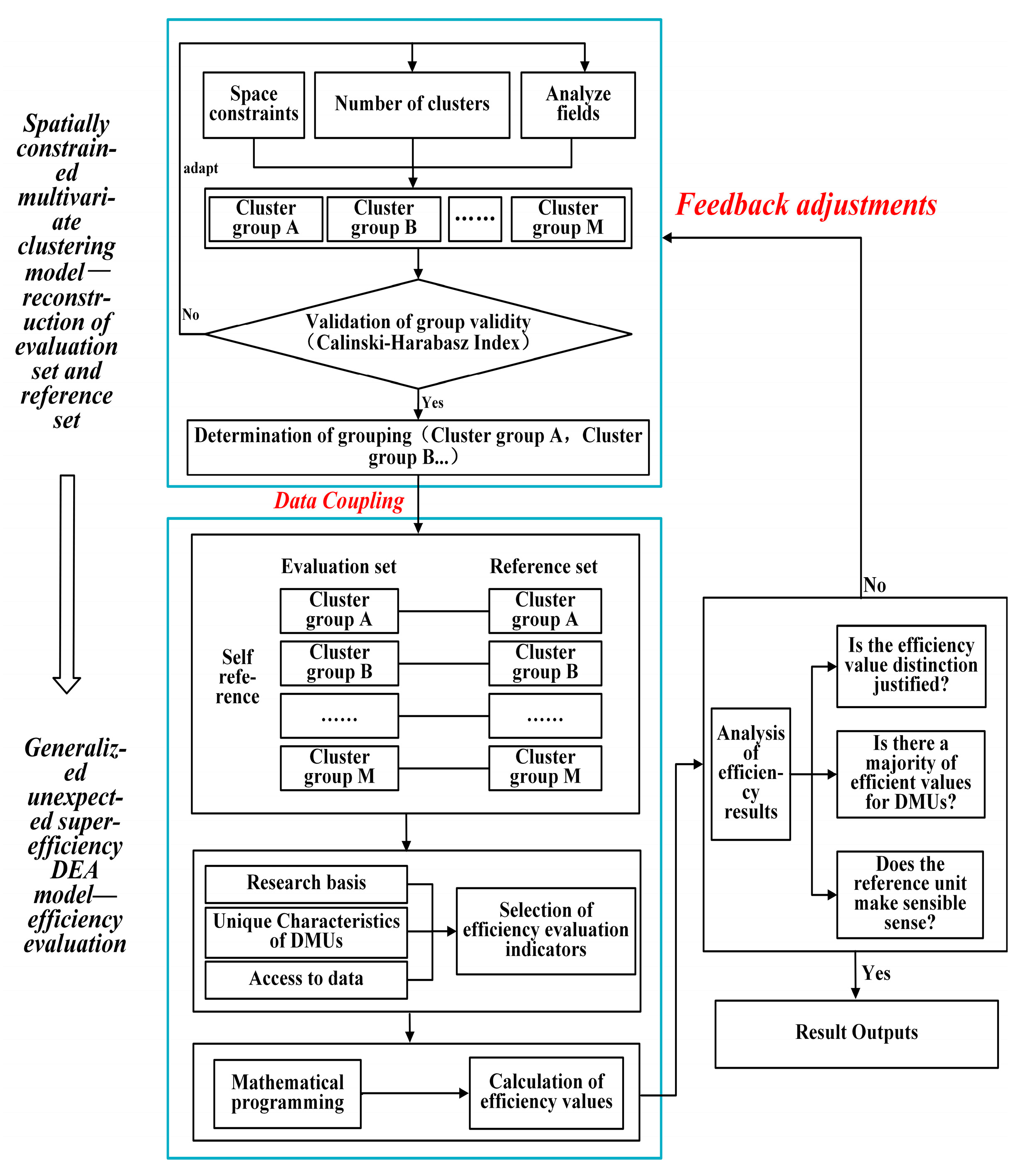
3.1. Coupling and Operational Mechanisms of the GeoDEA Model
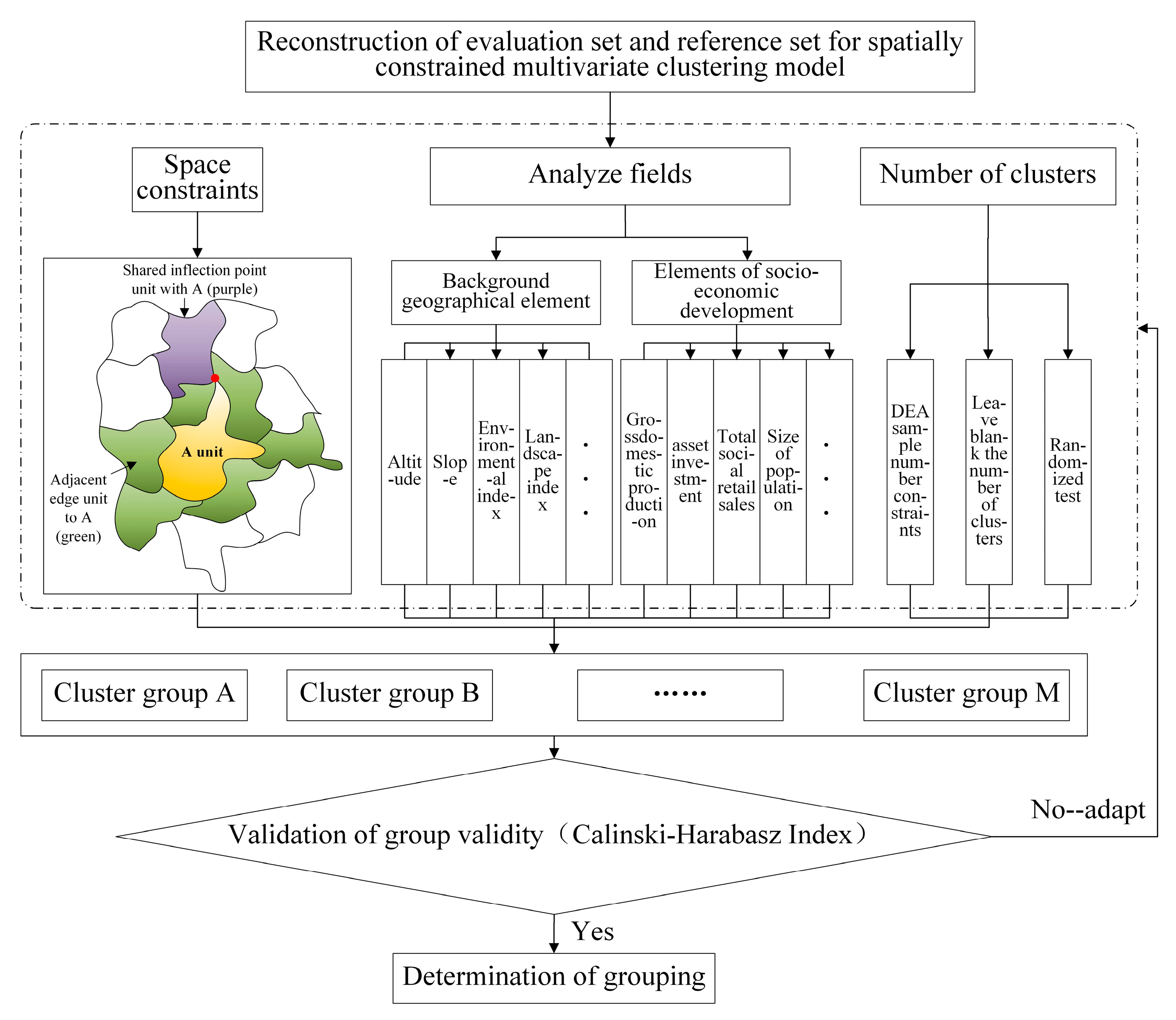
3.2. GeoDEA Model Parameterization
3.2.1. Spatially Constrained Multivariate Clustering Model Parameterization
3.2.2. Generalized DEA Model Parameterization
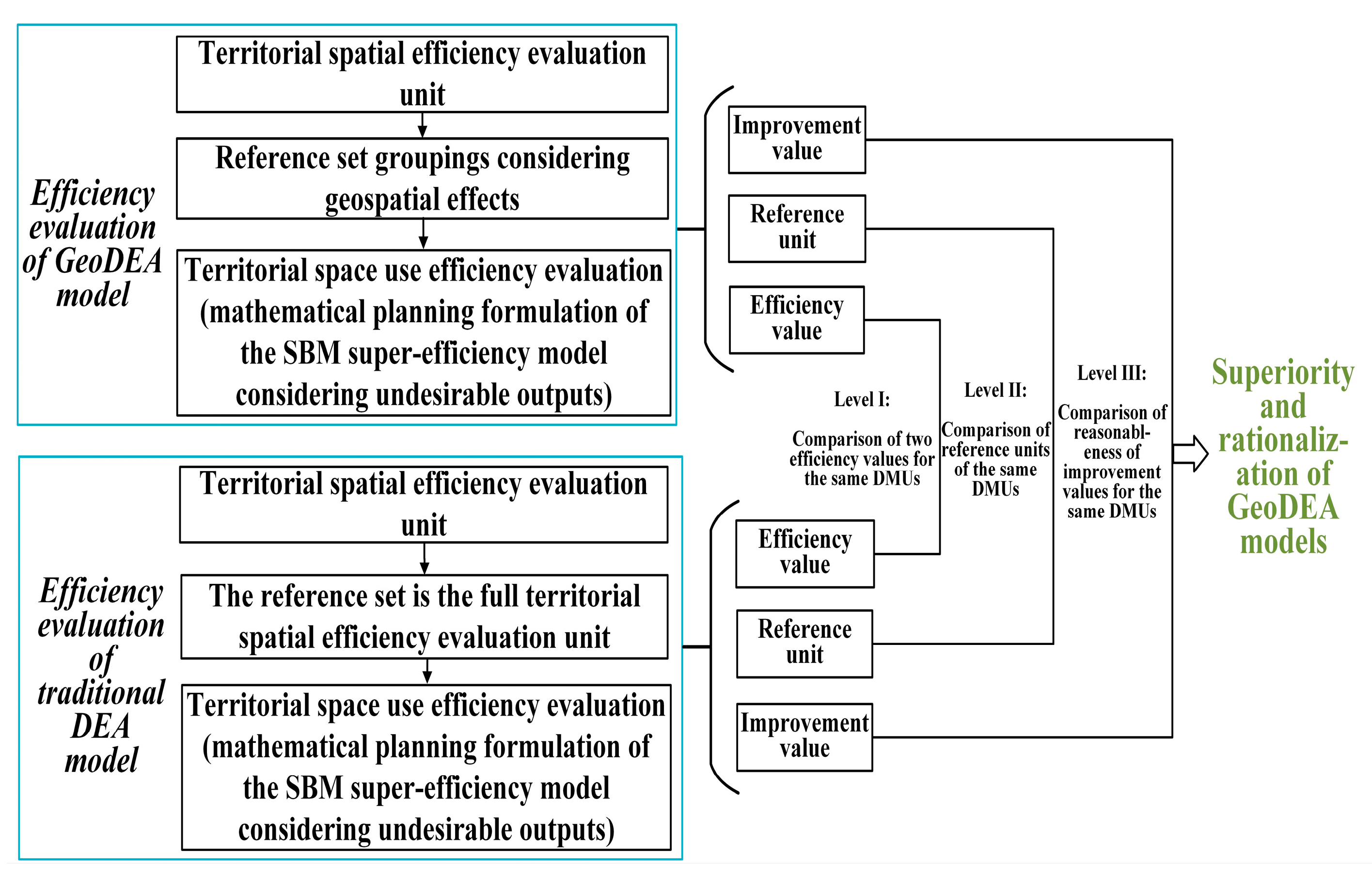
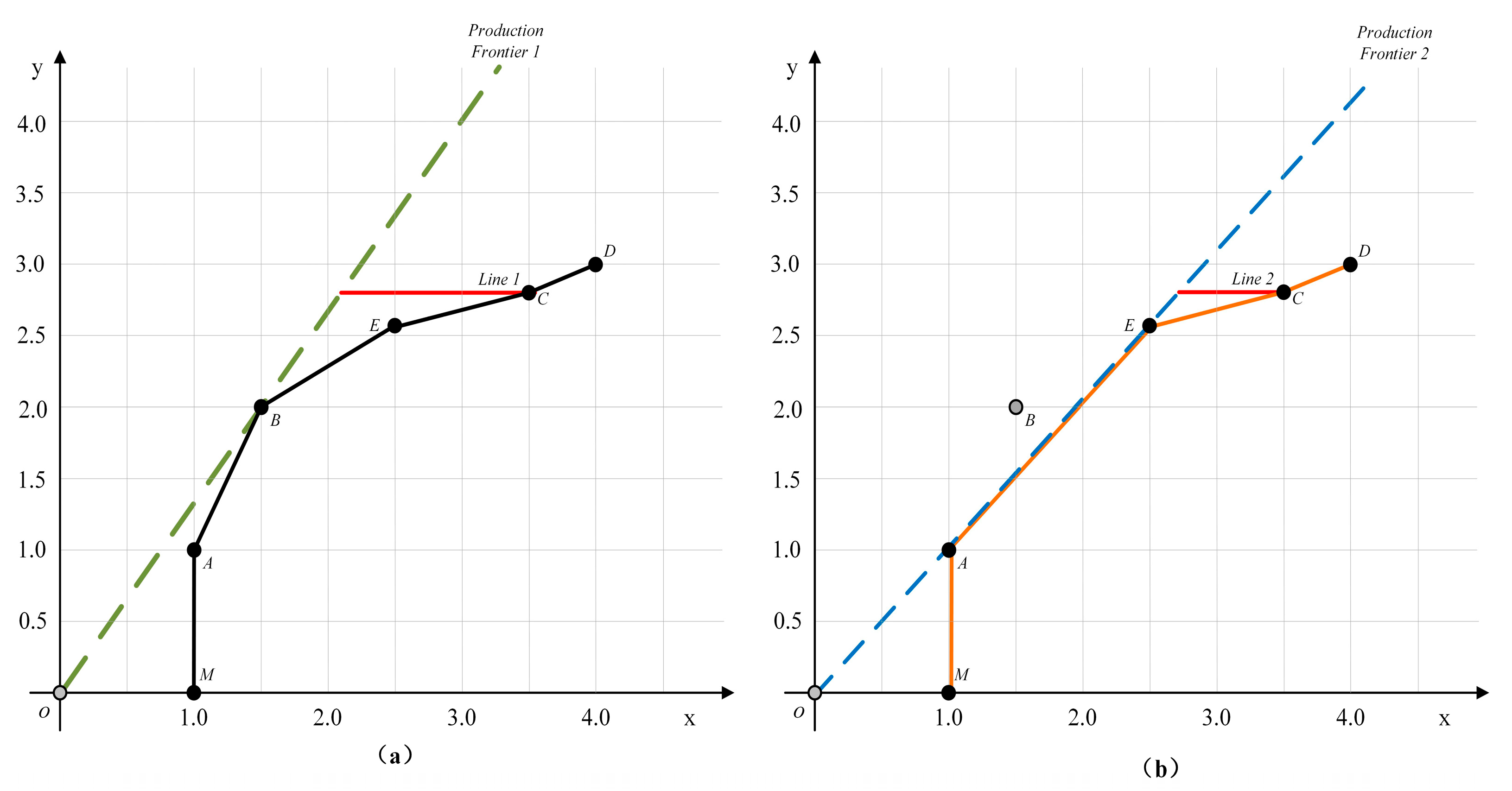
3.3. GeoDEA Model Validation
4. Model Validation Results
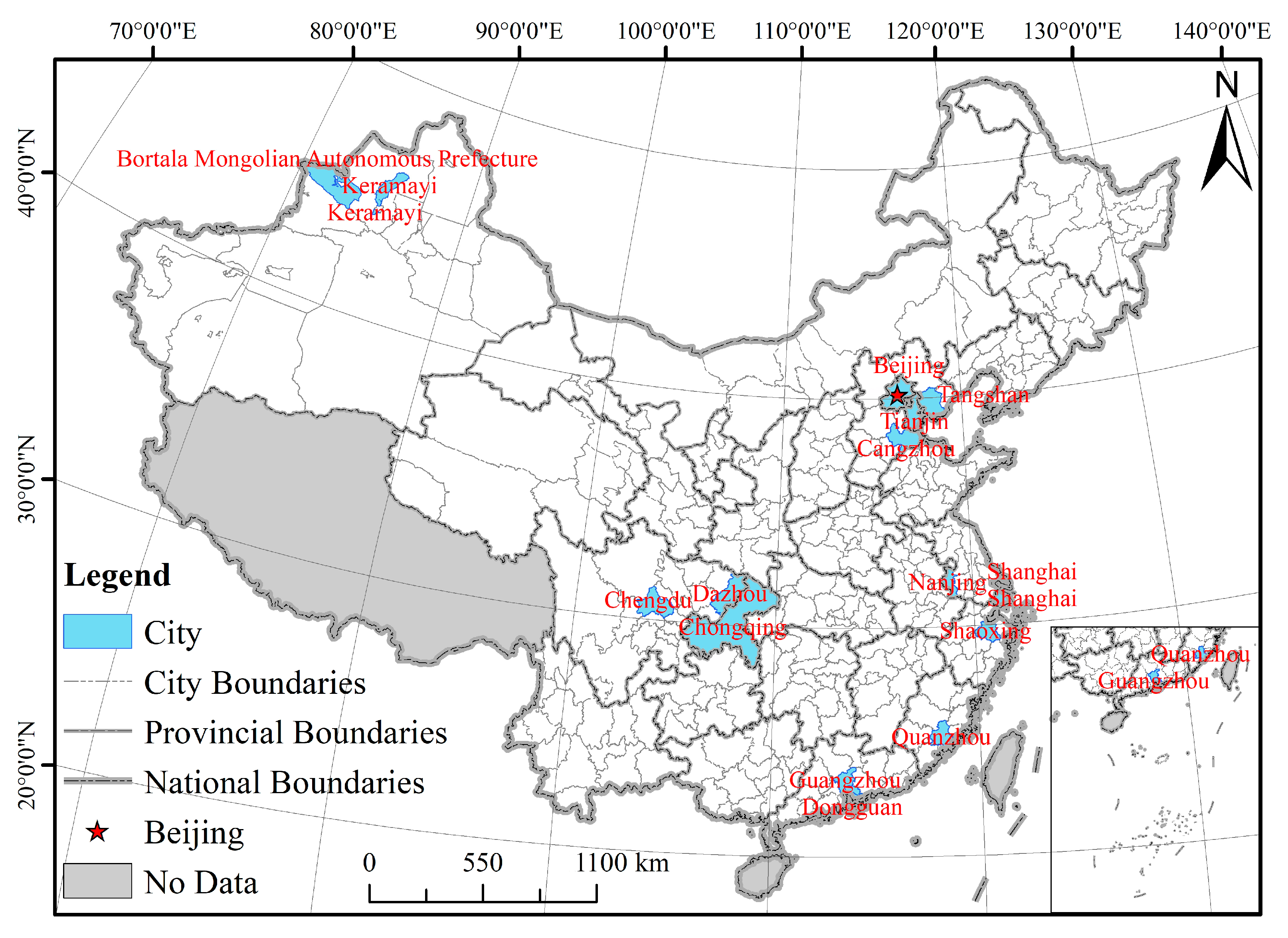
4.1. Study Area and Data
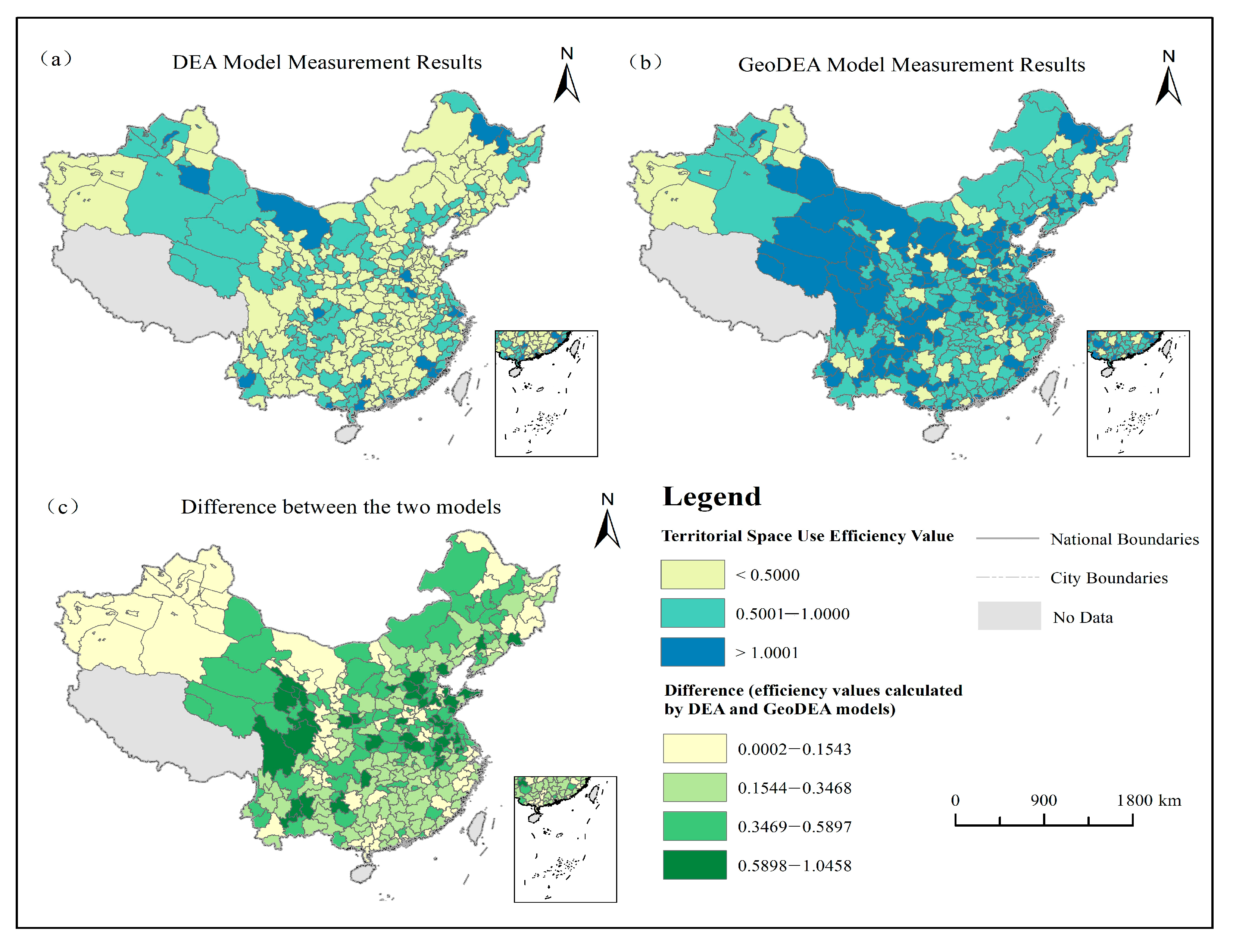
4.2. Differences in the Evaluation Results of the Two Models
4.3. Match Between the Results of Efficiency Evaluations and the Actual State of Development
4.4. Rationalization of Reference Frontiers
5. Discussion
5.1. Importance of Choosing the Appropriate Reference Set
5.2. Rationalization of the GeoDEA Model
5.3. Limitations and Future Development of the Model
5.4. Suggestions for Improving Territorial Space Use Efficiency Based on Geospatial Effects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Type of Space | Input/Output Indicators | Specific Indicators |
|---|---|---|
| Production Space | Input indicators | Cultivated land area, built-up area, average number of urban non-private workers on the job, investment in fixed assets, total gas supply (gas, natural gas), and landscape pattern index |
| Output indicators | Gross regional product (GDP), GDP growth rate, share of secondary sector in GDP, patch multiplicity density, Shannon diversity, and industrial particulate emissions | |
| Living Space | Input indicators | Core area of green infrastructure, number of practicing physicians, number of general secondary schools, number of full-time teachers in general higher education, number of cultural venues, expenditure on science and technology funds, total household liquid petroleum gas supply |
| Output indicators | Gross regional product per capita, total retail sales of consumer goods, natural growth rate, Shannon diversity index, domestic wastewater output, and core area of green infrastructure per capita | |
| Ecological Space | Input indicators | Green coverage of built-up areas, branching area and perforation area, total population, and total energy consumption |
| Output indicators | Green space per capita, ecological service value, Shannon’s uniformity index, dryness index, heat index, and separation index |
| City | Efficiency Type | Evaluation Results of Traditional DEA Model | Evaluation Results of GeoDEA Model | Difference |
|---|---|---|---|---|
| Shanghai | Productive space use efficiency | 1.0281 | 1.1357 | 0.1076 |
| Living space use efficiency | 1.0310 | 1.2336 | 0.2026 | |
| Ecological space use efficiency | 1.0213 | 1.0736 | 0.0523 | |
| Territorial space use total efficiency | 1.0284 | 1.1694 | 0.1410 | |
| Beijing | Productive space use efficiency | 1.0304 | 1.1396 | 0.1092 |
| Living space use efficiency | 1.0872 | 1.3528 | 0.2656 | |
| Ecological space use efficiency | 0.2007 | 0.3228 | 0.1221 | |
| Territorial space use total efficiency | 0.9471 | 1.1247 | 0.1776 | |
| Shenzhen | Productive space use efficiency | 1.2576 | 1.2620 | 0.0044 |
| Living space use efficiency | 1.3850 | 1.6945 | 0.3095 | |
| Ecological space use efficiency | 1.1893 | 1.3375 | 0.1482 | |
| Territorial space use total efficiency | 1.3032 | 1.4566 | 0.1534 | |
| Chongqing | Productive space use efficiency | 0.1388 | 1.0457 | 0.9069 |
| Living space use efficiency | 1.0544 | 1.1359 | 0.0815 | |
| Ecological space use efficiency | 0.8067 | 1.1026 | 0.2959 | |
| Territorial space use total efficiency | 0.6165 | 1.0916 | 0.4751 | |
| Guangzhou | Productive space use efficiency | 1.0031 | 1.0080 | 0.0049 |
| Living space use efficiency | 0.0029 | 1.0027 | 0.9998 | |
| Ecological space use efficiency | 0.7397 | 0.7695 | 0.0298 | |
| Territorial space use total efficiency | 0.5417 | 0.9748 | 0.4331 | |
| Chengdu | Productive space use efficiency | 1.1642 | 1.1645 | 0.0003 |
| Living space use efficiency | 0.0010 | 1.0264 | 1.0254 | |
| Ecological space use efficiency | 0.6910 | 0.7726 | 0.0816 | |
| Territorial space use total efficiency | 0.6059 | 1.0547 | 0.4488 | |
| Tianjin | Productive space use efficiency | 1.0012 | 1.1198 | 0.1186 |
| Living space use efficiency | 0.0002 | 0.5892 | 0.5890 | |
| Ecological space use efficiency | 1.0254 | 1.2048 | 0.1794 | |
| Territorial space use total efficiency | 0.5767 | 0.9041 | 0.3274 |
| City | Efficiency Type | Evaluation Results of Traditional DEA Model | Evaluation Results of GeoDEA Model | Difference |
|---|---|---|---|---|
| Wuhan | Productive space use efficiency | 0.3902 | 1.0272 | 0.6370 |
| Living space use efficiency | 0.0006 | 0.1055 | 0.1049 | |
| Ecological space use efficiency | 0.6938 | 0.7950 | 0.1012 | |
| Territorial space use total efficiency | 0.2631 | 0.6033 | 0.3402 | |
| Xi’an | Productive space use efficiency | 0.3961 | 1.1193 | 0.7232 |
| Living space use efficiency | 1.0019 | 1.2013 | 0.1994 | |
| Ecological space use efficiency | 1.0377 | 1.4224 | 0.3847 | |
| Territorial space use total efficiency | 0.7381 | 1.1936 | 0.4555 | |
| Hangzhou | Productive space use efficiency | 1.0843 | 1.0843 | 0.0000 |
| Living space use efficiency | 0.0019 | 0.6293 | 0.6274 | |
| Ecological space use efficiency | 0.8553 | 0.9071 | 0.0518 | |
| Territorial space use total efficiency | 0.5922 | 0.8669 | 0.2747 | |
| Foshan | Productive space use efficiency | 1.0060 | 1.0395 | 0.0335 |
| Living space use efficiency | 0.0003 | 0.0759 | 0.0756 | |
| Ecological space use efficiency | 1.0024 | 1.0024 | 0.0000 | |
| Territorial space use total efficiency | 0.5759 | 0.6230 | 0.0471 | |
| Nanjing | Productive space use efficiency | 0.5648 | 1.0061 | 0.4413 |
| Living space use efficiency | 1.0436 | 1.1344 | 0.0908 | |
| Ecological space use efficiency | 1.0021 | 1.0066 | 0.0045 | |
| Territorial space use total efficiency | 0.8261 | 1.0610 | 0.2349 | |
| Shenyang | Productive space use efficiency | 0.4395 | 1.0305 | 0.5910 |
| Living space use efficiency | 0.0019 | 1.0993 | 1.0974 | |
| Ecological space use efficiency | 0.4831 | 0.6861 | 0.2030 | |
| Territorial space use total efficiency | 0.2582 | 1.0152 | 0.7570 | |
| Qingdao | Productive space use efficiency | 1.0153 | 1.0651 | 0.0498 |
| Living space use efficiency | 1.0476 | 1.2392 | 0.1916 | |
| Ecological space use efficiency | 0.1541 | 1.0793 | 0.9252 | |
| Territorial space use total efficiency | 0.9174 | 1.1413 | 0.2239 | |
| Jinan | Productive space use efficiency | 0.4207 | 1.0476 | 0.6269 |
| Living space use efficiency | 0.0035 | 1.1213 | 1.1178 | |
| Ecological space use efficiency | 0.6785 | 0.8821 | 0.2036 | |
| Territorial space use total efficiency | 0.2759 | 1.0576 | 0.7817 | |
| Changsha | Productive space use efficiency | 1.0285 | 1.0491 | 0.0206 |
| Living space use efficiency | 0.0087 | 1.0143 | 1.0056 | |
| Ecological space use efficiency | 0.6294 | 0.6533 | 0.0239 | |
| Territorial space use total efficiency | 0.5411 | 0.9829 | 0.4418 | |
| Harbin | Productive space use efficiency | 0.1165 | 0.2557 | 0.1392 |
| Living space use efficiency | 0.0155 | 0.2344 | 0.2189 | |
| Ecological space use efficiency | 0.9405 | 0.9499 | 0.0094 | |
| Territorial space use total efficiency | 0.1802 | 0.3366 | 0.1564 | |
| Zhengzhou | Productive space use efficiency | 0.4494 | 1.0727 | 0.6233 |
| Living space use efficiency | 0.0003 | 1.1093 | 1.1090 | |
| Ecological space use efficiency | 0.7456 | 1.0475 | 0.3019 | |
| Territorial space use total efficiency | 0.2960 | 1.0851 | 0.7891 | |
| Kunming | Productive space use efficiency | 0.2498 | 1.0679 | 0.8181 |
| Living space use efficiency | 0.0092 | 1.0205 | 1.0113 | |
| Ecological space use efficiency | 0.5006 | 1.0085 | 0.5079 | |
| Territorial space use total efficiency | 0.1795 | 1.0400 | 0.8605 | |
| Dalian | Productive space use efficiency | 1.0266 | 1.0768 | 0.0502 |
| Living space use efficiency | 0.0012 | 0.1317 | 0.1305 | |
| Ecological space use efficiency | 0.1465 | 1.0008 | 0.8543 | |
| Territorial space use total efficiency | 0.4744 | 0.6632 | 0.1888 | |
| Dongguan | Productive space use efficiency | 1.0927 | 1.1142 | 0.0215 |
| Living space use efficiency | 1.1277 | 1.1505 | 0.0228 | |
| Ecological space use efficiency | 1.0486 | 1.1136 | 0.0650 | |
| Territorial space use total efficiency | 1.1019 | 1.1297 | 0.0278 |
Appendix B
References
- Hu, Q.; Shen, W.; Zhang, Z. How does urbanisation affect the evolution of territorial space composite function? Appl. Geogr. 2023, 155, 102976. [Google Scholar] [CrossRef]
- Peng, J.; Xu, D.; Xu, Z.; Tang, H.; Jiang, H.; Dong, J.; Liu, Y. Ten key issues for ecological restoration of territorial space. Natl. Sci. Rev. 2024, 11, nwae176. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Bu, Z.; Jiang, D.; Lin, G.; Li, X. Sustainable land use diagnosis based on the perspective of production–living–ecological spaces in China. Land Use Policy 2022, 122, 106386. [Google Scholar] [CrossRef]
- O’Driscoll, C.; Crowley, F.; Doran, J.; McCarthy, N. Land-use mixing in Irish cities: Implications for sustainable development. Land Use Policy 2023, 128, 106615. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Y.; Zhang, M.; Duan, Y. Land use efficiency and energy transition in Chinese cities: A cluster-frontier super-efficiency SBM-based analytical approach. Energy 2024, 304, 132049. [Google Scholar] [CrossRef]
- Ferreira, M.D.P.; Féres, J.G. Farm size and Land use efficiency in the Brazilian Amazon. Land Use Policy 2020, 99, 104901. [Google Scholar] [CrossRef]
- Koroso, N.H.; Lengoiboni, M.; Zevenbergen, J.A. Urbanization and urban land use efficiency: Evidence from regional and Addis Ababa satellite cities, Ethiopia. Habitat Int. 2021, 117, 102437. [Google Scholar] [CrossRef]
- Koroso, N.H.; Zevenbergen, J.A.; Lengoiboni, M. Urban land use efficiency in Ethiopia: An assessment of urban land use sustainability in Addis Ababa. Land Use Policy 2020, 99, 105081. [Google Scholar] [CrossRef]
- Ma, Y.; Zheng, M.; Zheng, X.; Huang, Y.; Xu, F.; Wang, X.; Liu, J.; Lv, Y.; Liu, W. Land Use Efficiency Assessment under Sustainable Development Goals: A Systematic Review. Land 2023, 12, 894. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, K.; Yang, S. Land use efficiency and influencing factors of urban agglomerations in China. Land Use Policy 2019, 88, 104143. [Google Scholar] [CrossRef]
- Seipord, L.M. Data Envelopment Analysis The Evolution of the State of the Art (1978–1995). J. Product. Anal. 1996, 7, 99–137. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.Y.; Lu, W.-M.; Lin, B.J.Y. Data envelopment analysis 1978–2010: A citation-based literature survey. Omega 2013, 41, 3–15. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Xing, X.; Guo, H.; Zhang, W.; Luo, Q. On spatial effects in geographical analysis. Acta Geogr. Sin. 2023, 78, 517–531. [Google Scholar]
- Yu, H.C.; Fotheringham, A.S.; Li, Z.Q.; Oshan, T.; Kang, W.; Wolf, L.J. Inference in Multiscale Geographically Weighted Regression. Geogr. Anal. 2020, 52, 87–106. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Zhang, J. Geo-Spatial Cognition:An Overview. Geogr. Geo-Inf. Sci. 2005, 21, 1–10. [Google Scholar]
- Fotheringham, A.S.; Yang, W.B.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, F.-R.; An, P.-L.; Dong, M.-L.; Wang, Z.-Y.; Zhao, T. Industrial land-use efficiency and planning in Shunyi, Beijing. Landsc. Urban Plan. 2008, 85, 40–48. [Google Scholar] [CrossRef]
- Chen, W.; Shen, Y.; Wang, Y.; Wu, Q. The effect of industrial relocation on industrial land use efficiency in China: A spatial econometrics approach. J. Clean. Prod. 2018, 205, 525–535. [Google Scholar] [CrossRef]
- Melchiorri, M.; Pesaresi, M.; Florczyk, A.J.; Corbane, C.; Kemper, T. Principles and Applications of the Global Human Settlement Layer as Baseline for the Land Use Efficiency Indicator—SDG 11.3.1. ISPRS Int. J. Geo-Inf. 2019, 8, 96. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Feng, Y.; Gu, J. Evaluation of the Coordinated Relationship between Land Consumption Rate and Population Growth Rate in the Pearl River Delta based on the 2030 Sustainable Development Goals. Remote Sens. Technol. Appl. 2021, 36, 1168–1177. [Google Scholar]
- Holobâcă, I.-H.; Benedek, J.; Ursu, C.-D.; Alexe, M.; Temerdek-Ivan, K. Ratio of Land Consumption Rate to Population Growth Rate in the Major Metropolitan Areas of Romania. Remote Sens. 2022, 14, 6016. [Google Scholar] [CrossRef]
- Masini, E.; Tomao, A.; Barbati, A.; Corona, P.; Serra, P.; Salvati, L. Urban Growth, Land-use Efficiency and Local Socioeconomic Context: A Comparative Analysis of 417 Metropolitan Regions in Europe. Environ. Manag. 2018, 63, 322–337. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Jin, X.; Xu, W.; Gu, Z.; Yang, X.; Ren, J.; Fan, Y.; Zhou, Y. A new framework of land use efficiency for the coordination among food, economy and ecology in regional development. Sci. Total Environ. 2020, 710, 135670. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, Y.; Chen, W.; Li, M.; Fang, X. Does improvement of industrial land use efficiency reduce PM2.5 pollution? Evidence from a spatiotemporal analysis of China. Ecol. Indic. 2021, 132, 108333. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Y.; Liu, J.; Zhang, C.; Sang, X.; Zhong, Q. Parcel-level evaluation of urban land use efficiency based on multisource spatiotemporal data: A case study of Ningbo City, China. Trans. GIS 2021, 25, 2766–2790. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Zhou, G.; Ma, Z.; Sun, H.; Fu, H. Coordinated Relationship between Compactness and Land-Use Efficiency in Shrinking Cities: A Case Study of Northeast China. Land 2022, 11, 366. [Google Scholar] [CrossRef]
- Lu, S.; Wang, H. Market-oriented reform and land use efficiency: Evidence from a regression discontinuity design. Land Use Policy 2022, 115, 106006. [Google Scholar] [CrossRef]
- Zhang, X.; Jie, X.; Ning, S.; Wang, K.; Li, X. Coupling and coordinated development of urban land use economic efficiency and green manufacturing systems in the Chengdu-Chongqing Economic Circle. Sustain. Cities Soc. 2022, 85, 104012. [Google Scholar] [CrossRef]
- Song, Y.; Yeung, G.; Zhu, D.; Xu, Y.; Zhang, L. Efficiency of urban land use in China’s resource-based cities, 2000–2018. Land Use Policy 2022, 115, 106009. [Google Scholar] [CrossRef]
- Wang, K.; Li, G.; Liu, H. Does natural resources supervision improve construction land use efficiency: Evidence from China. J. Environ. Manag. 2021, 297, 113317. [Google Scholar] [CrossRef]
- Liu, S.-C.; Lin, Y.-B.; Ye, Y.-M.; Xiao, W. Spatial-temporal characteristics of industrial land use efficiency in provincial China based on a stochastic frontier production function approach. J. Clean. Prod. 2021, 295, 126432. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G.L. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Camanho, A.S.; Silva, M.C.; Piran, F.S.; Lacerda, D.P. A literature review of economic efficiency assessments using Data Envelopment Analysis. Eur. J. Oper. Res. 2023, 315, 1–18. [Google Scholar] [CrossRef]
- Kao, C. Network data envelopment analysis: A review. Eur. J. Oper. Res. 2014, 239, 1–16. [Google Scholar] [CrossRef]
- Wu, J.L.; Xie, W.X.; Sheng, Y.H. A Generalized Dea Model with Imprecise Data. J. Ind. Manag. Optim. 2024, 20, 2617–2639. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, L.; Lui, S.; Ma, C. A generalized fuzzy DEA/AR performance assessment model. Math. Comput. Model. 2012, 55, 2117–2128. [Google Scholar] [CrossRef]
- Ma, S.Y.; Ma, Z.X.; Ji, R.M.T. Research on the Energy Consumption Efficiency Based on Generalized DEA Method with Cluster Analysis. In Proceedings of the 2nd International Conference on Energy and Environmental Protection (ICEEP 2013), Guilin, China, 19–21 April 2013; pp. 921–924. [Google Scholar]
- Azadi, M.; Jafarian, M.; Saen, R.F.; Mirhedayatian, S.M. A new fuzzy DEA model for evaluation of efficiency and effectiveness of suppliers in sustainable supply chain management context. Comput. Oper. Res. 2015, 54, 274–285. [Google Scholar] [CrossRef]
- Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Ning, L.X. The existence of equilibrium solution of the nonlinear dynamic input-output stochastic model. In Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, China, 10–14 June 2002; pp. 2236–2239. [Google Scholar]
- Su, B.; Ang, B.W. Multiplicative decomposition of aggregate carbon intensity change using input-output analysis. Appl. Energ. 2015, 154, 13–20. [Google Scholar] [CrossRef]
- Hubacek, K.; van den Bergh, J.C.J.M. Changing concepts of ‘land’ in economic theory: From single to multi-disciplinary approaches. Energ. Econ. 2006, 56, 5–27. [Google Scholar] [CrossRef]
- Xie, Y.; Eftelioglu, E.; Ali, R.; Tang, X.; Li, Y.; Doshi, R.; Shekhar, S. Transdisciplinary Foundations of Geospatial Data Science. ISPRS Int. J. Geo-Inf. 2017, 6, 395. [Google Scholar] [CrossRef]
- Dong, Y.; Jin, G.; Deng, X. Optimization of territorial space layout in China. J. Geogr. Sci. 2024, 34, 1719–1738. [Google Scholar] [CrossRef]
- Lee, S.K.; Mogi, G.; Hui, K.S. A fuzzy analytic hierarchy process (AHP)/data envelopment analysis (DEA) hybrid model for efficiently allocating energy R&D resources: In the case of energy technologies against high oil prices. Renew. Sust. Energ. Rev. 2013, 21, 347–355. [Google Scholar]
- Lessani, M.N.; Li, Z. SGWR: Similarity and geographically weighted regression. Int. J. Geogr. Inf. Sci. 2024, 38, 1232–1255. [Google Scholar] [CrossRef]
- Liu, J.; Wei, D.; Tian, Y.; Li, Q. Evolution and policy effect assessment for the spatial heterogeneity pattern of regional energy efficiency in China. Energ. Effic. 2021, 14, 83. [Google Scholar] [CrossRef]
- Ma, J.; Li, W.; Wang, Z.; He, L.; Han, L. Measuring Multi-Faceted Land Use Efficiency of Large-Scale Urban Agglomerations under Multi-Scale Drivers: Evidence from China. Land 2022, 11, 91. [Google Scholar] [CrossRef]
- Huang, Y.G.; Cao, L.B.; Zhang, J.; Pan, L.; Liu, Y.Y. Exploring Feature Coupling and Model Coupling for Image Source Identification. IEEE Trans. Inf. Forensics Secur. 2018, 13, 3108–3121. [Google Scholar] [CrossRef]
- Chin, Y.P.; Song, W.Y.; Islam, M.M.; Bates, D.W.; Zhou, L.; Li, Y.C. Sequential coupling of dry and wet COVID-19 screening to reduce the number of quarantined individuals. Comput. Meth. Prog. Bio 2022, 218, 106715. [Google Scholar]
- Karandikar, J.; Saleeby, K.; Feldhausen, T.; Kurfess, T.; Schmitz, T.; Smith, S. Evaluation of automated stability testing in machining through closed-loop control and Bayesian machine learning. Mech. Syst. Signal Process. 2022, 181, 109531. [Google Scholar] [CrossRef]
- Kannan, N.; Yeh, C.Y.C.; Chou, C.Y.; Chan, T.W. A Machine Learning Approach to Estimating Student Mastery by Predicting Feedback Request and Solving Time in Online Learning System. In Proceedings of the 29th International Conference on Computers in Education (ICCE), Electr Network, Virtual, 22–26 November 2021; pp. 241–250. [Google Scholar]
- Liao, M.Y.; Zhu, K.G.; Wang, G.S. Can human-machine feedback in a smart learning environment enhance learners’ learning performance? A meta-analysis. Front. Psychol. 2024, 14, 1288503. [Google Scholar] [CrossRef]
- Tandra, A.; Sakti, S.; Nakamura, S. Machine Speech Chain. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 976–989. [Google Scholar] [CrossRef]
- Zha, Q.B.; Dong, Y.C.; Zhang, H.J.; Chiclana, F.; Herrera-Viedma, E. A Personalized Feedback Mechanism Based on Bounded Confidence Learning to Support Consensus Reaching in Group Decision Making. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3900–3910. [Google Scholar] [CrossRef]
- Wu, J.; Dai, L.F.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E. A minimum adjustment cost feedback mechanism based consensus model for group decision making under social network with distributed linguistic trust. Inform. Fusion 2018, 41, 232–242. [Google Scholar] [CrossRef]
- Sisman, S.; Aydinoglu, A.C. Improving performance of mass real estate valuation through application of the dataset optimization and Spatially Constrained Multivariate Clustering Analysis. Land Use Policy 2022, 119, 106167. [Google Scholar] [CrossRef]
- Chen, L.R.; Guan, Q.F.; Xiong, Y.H.; Liang, J.Y.; Wang, Y.; Xu, Y.Q. A Spatially Constrained Multi-Autoencoder approach for multivariate geochemical anomaly recognition. Comput. Geosci. 2019, 125, 43–54. [Google Scholar] [CrossRef]
- Lee, H.S. An integrated model for SBM and Super-SBM DEA models. J. Oper. Res. Soc. 2021, 72, 1174–1182. [Google Scholar] [CrossRef]
- Li, H.; Shi, J.F. Energy efficiency analysis on Chinese industrial sectors: An improved Super-SBM model with undesirable outputs. J. Clean. Prod. 2014, 65, 97–107. [Google Scholar] [CrossRef]
- Zhao, D.; Li, C.; Wang, Q.; Yuan, J. Comprehensive evaluation of national electric power development based on cloud model and entropy method and TOPSIS: A case study in 11 countries. J. Clean. Prod. 2020, 277, 123190. [Google Scholar] [CrossRef]
- Kohl, S.; Schoenfelder, J.; Fügener, A.; Brunner, J.O. The use of Data Envelopment Analysis (DEA) in healthcare with a focus on hospitals. Health Care Manag. Sci. 2019, 22, 245–286. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energ. Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Xu, P.P.; Huang, H.L. Modeling crash spatial heterogeneity: Random parameter versus geographically weighting. Accident. Anal. Prev. 2015, 75, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.D.; Li, H.L.; Zhang, J.Y.; Niu, S.Y.; Miao, M.M. Urban economic resilience within the Yangtze River Delta urban agglomeration: Exploring spatially correlated network and spatial heterogeneity. Sustain. Cities Soc. 2024, 103, 105270. [Google Scholar] [CrossRef]
- Ma, Y.; Zheng, X.Q.; Liu, M.L.; Liu, D.Y.; Ai, G.; Chen, X.Y. Spatio-temporal evolution characteristics analysis and optimization prediction of urban green infrastructure: A case study of Beijing, China. Sci. Rep. 2022, 12, 10702. [Google Scholar] [CrossRef] [PubMed]


| Decision Unit | DEA Model | Living Space Use Efficiency | Output Non-Radial Null | Reference Frontier |
|---|---|---|---|---|
| Guangzhou | Traditional DEA model | 0.0029 | 339.0343 | Bortala Mongolian Autonomous Prefecture (0.0594); Quanzhou (0.4126); Shanghai (0.1557); Shaoxing (0.0010); Shenzhen (0.4344); Chongqing (0.0689) |
| GeoDEA model | 1.0027 | −0.0027 | Dongguan (0.3918); Quanzhou (0.4517); Shenzhen (0.6019) | |
| Chengdu | Traditional DEA model | 0.0010 | 1028.4464 | Bortala Mongol Autonomous Prefecture (0.3731); Nanjing (0.2110); Shanghai (0.1108); Chongqing (0.4084) |
| GeoDEA model | 1.0264 | −0.0258 | Dazhou (0.4715); Keramayi (0.1497); Chongqing (0.5200) | |
| Tianjin | Traditional DEA model | 0.0002 | 4495.3649 | Bortala Mongol Autonomous Prefecture (0.8501); Shanghai (0.1832); Shaoxing (0.0329); Shenzhen (0.0626) |
| GeoDEA model | 0.5892 | 0.6972 | Beijing (0.1947); Cangzhou (0.8369); Tangshan (0.2896) |
| Decision Unit | Type of Space | DEA Model | Efficiency Value | Output Non-Radial Null | Reference Frontier |
|---|---|---|---|---|---|
| Wuhan | Production space use efficiency | Traditional DEA model | 0.3902 | 1.5626 | Chengdu (0.3200); Luohe (0.6121); Qingdao (0.1127); Shenzhen (0.2511); Zhoushan (0.4215) |
| GeoDEA model | 1.0272 | −0.0265 | Hefei (0.2457); Shanghai (0.1542); Wuxi (0.0678); Xuzhou (0.0539); Zhenjiang (0.8211) | ||
| Jinan | Living space use efficiency | Traditional DEA model | 0.0035 | 280.8307 | Beijing (0.0016); Bortala Mongol Autonomous Prefecture (0.0881); Qingdao (0.6862); Quanzhou (0.1270); Shaoxing (0.0412); Urumqi (0.1072) |
| GeoDEA model | 1.1213 | −0.1082 | Beijing (0.06889); Langfang (0.7631); Tangshan (0.3460) | ||
| Shenyang | Ecological space use efficiency | Traditional DEA model | 0.4831 | 1.0698 | Baise (0.0843); Bortala Mongol Autonomous Prefecture (0.0001); Hegang (0.2089); Huaian (0.1640); Huaibei (0.3931); Yangzhou (0.0876) |
| GeoDEA model | 0.6861 | 0.4574 | Hegang (0.2800); Jinzhou (0.0161); Panjin (0.1434); Tianjin (0.3480) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Ma, Y.; Zheng, X.; Wang, X.; Li, L.; Xu, F.; Zhang, X.; Gan, F.; Wang, J.; Zhu, Z. Evaluating Territorial Space Use Efficiency: A Geographic Data Envelopment Model Considering Geospatial Effects. Land 2025, 14, 635. https://doi.org/10.3390/land14030635
Zheng M, Ma Y, Zheng X, Wang X, Li L, Xu F, Zhang X, Gan F, Wang J, Zhu Z. Evaluating Territorial Space Use Efficiency: A Geographic Data Envelopment Model Considering Geospatial Effects. Land. 2025; 14(3):635. https://doi.org/10.3390/land14030635
Chicago/Turabian StyleZheng, Minrui, Yin Ma, Xinqi Zheng, Xvlu Wang, Li Li, Feng Xu, Xiaoyuan Zhang, Fuping Gan, Jianchao Wang, and Zhengkun Zhu. 2025. "Evaluating Territorial Space Use Efficiency: A Geographic Data Envelopment Model Considering Geospatial Effects" Land 14, no. 3: 635. https://doi.org/10.3390/land14030635
APA StyleZheng, M., Ma, Y., Zheng, X., Wang, X., Li, L., Xu, F., Zhang, X., Gan, F., Wang, J., & Zhu, Z. (2025). Evaluating Territorial Space Use Efficiency: A Geographic Data Envelopment Model Considering Geospatial Effects. Land, 14(3), 635. https://doi.org/10.3390/land14030635







