Study on the Probability of Meteorological-to-Hydrological Drought Propagation Based on a Bayesian Network
Abstract
1. Introduction
2. Study Area Profile and Data Sources
3. Research Method
3.1. Construction of Drought Index
3.2. Meteorological and Hydrological Drought Identification
3.3. Meteorological Drought and Hydrological Drought Matching
3.4. Propagation Probability of Meteorological to Hydrological Drought Based on Bayesian Networks
3.5. Heuristic Segmentation
4. Results
4.1. Propagation Probability of Meteorological to Hydrological Drought Based on the Drought Index
4.1.1. Calculation and Monthly Variation of the Drought Index
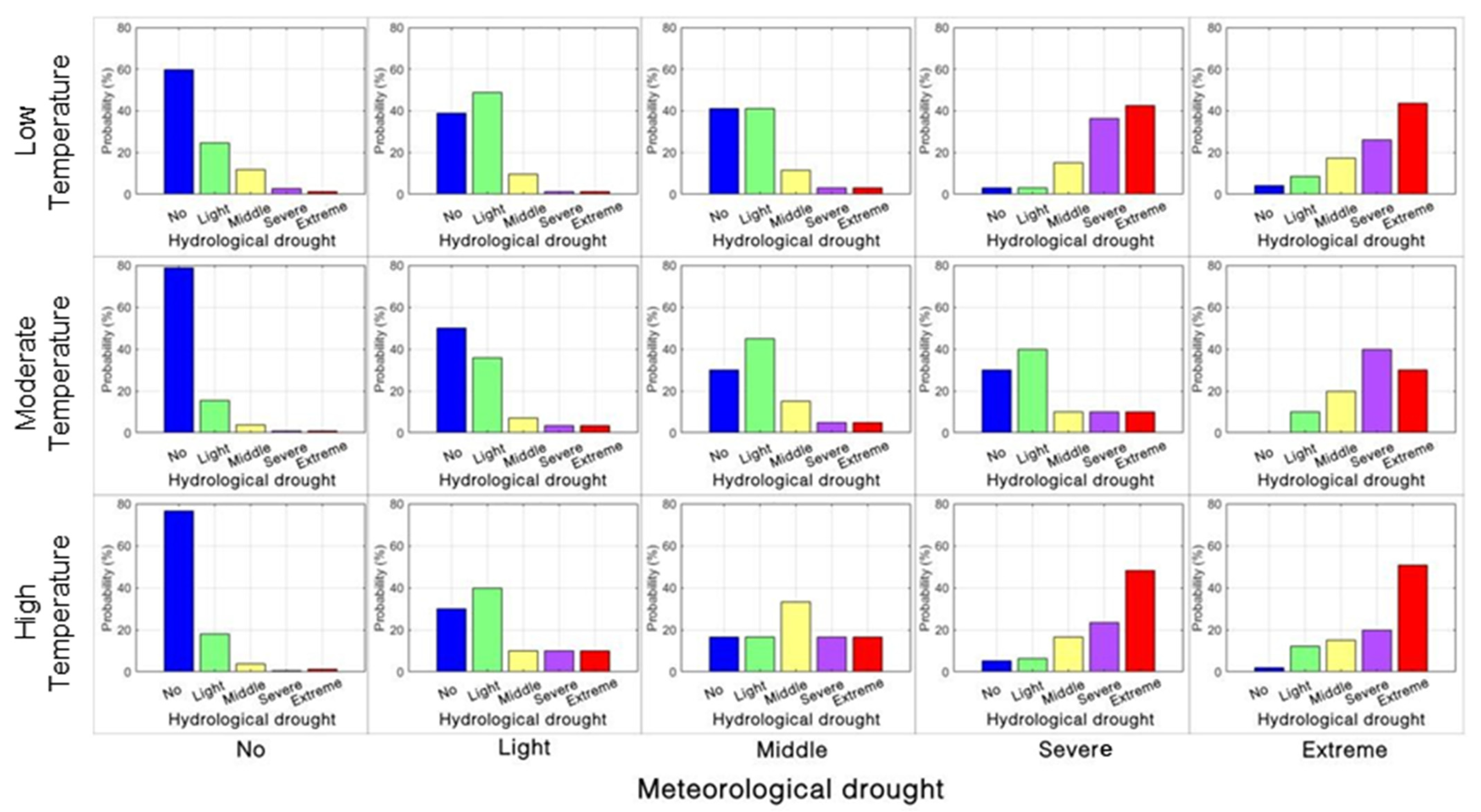
4.1.2. Probability of Hydrological Drought Under a Single Factor
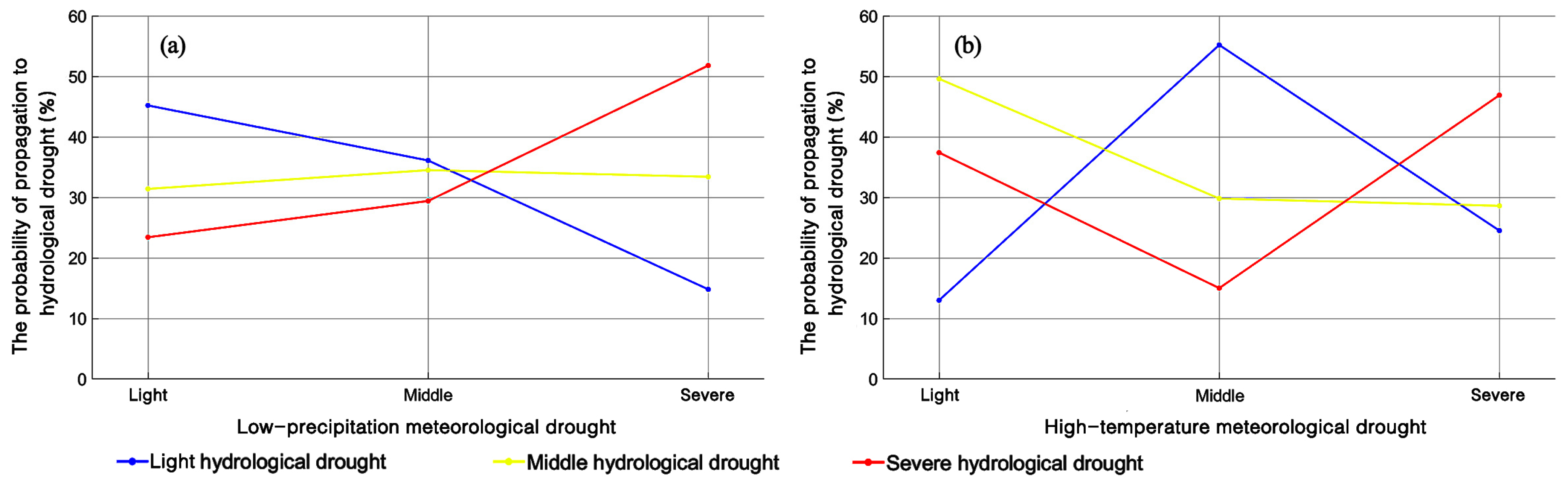
4.1.3. Probability of Hydrological Drought Under the Influence of Two Factors
4.2. Propagation Probability of Meteorological to Hydrological Drought Based on Characteristics of Drought Events
4.2.1. Identification of Drought Events and Their Characteristics
4.2.2. Probability of Monotype Meteorological Drought Scenario Propagation to Hydrological Drought Events
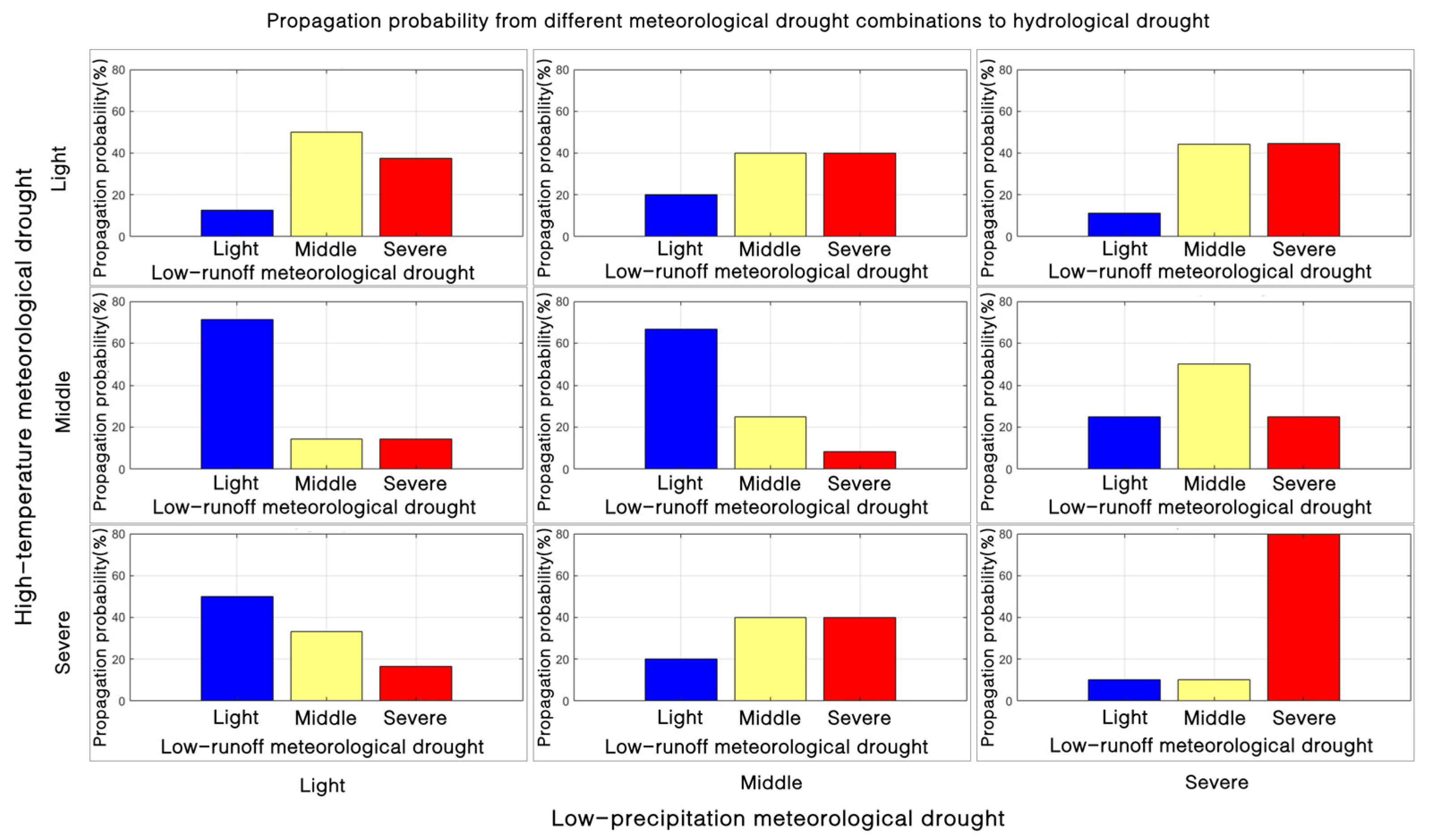
4.2.3. Probability of Dual-Type Meteorological Drought Scenario Propagation to Hydrological Drought Events
4.3. Hydrologic Drought Under Non-Stationary Meteorological Conditions
4.3.1. Meteorological Factors Abrupt Changes Test
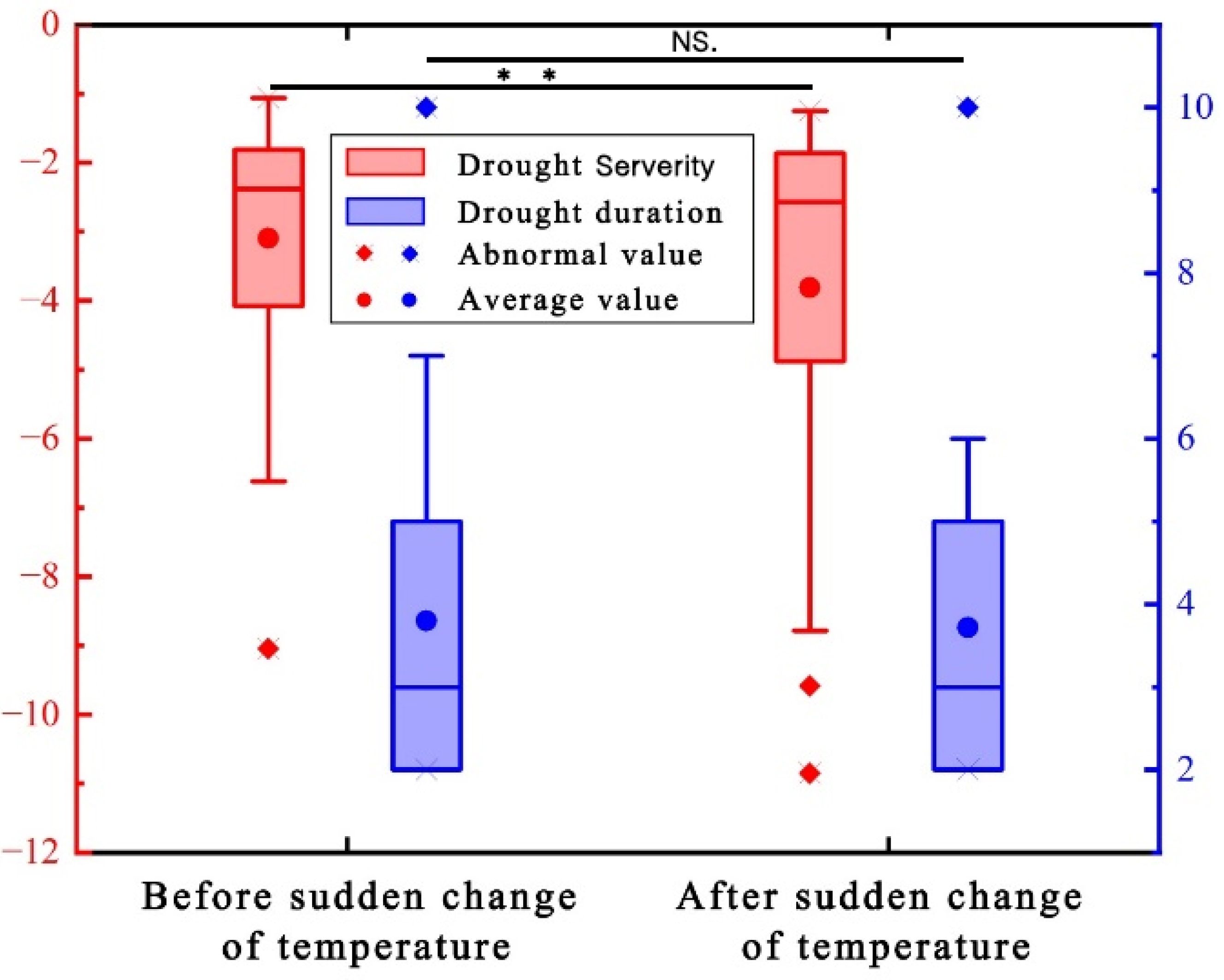
4.3.2. Hydrological Drought Characteristics Before and After Abrupt Changes in Meteorological Conditions
5. Discussion
5.1. Rationality and Applicability of the STI
5.2. Importance of Temperature Factors
5.3. Research Limitations and Prospects
6. Conclusions
- (1)
- The probability of hydrological drought gradually increased as precipitation deficiency intensified, and the probability of light hydrological droughts diminished, whereas that of severe and extreme hydrological droughts increased by almost 10%. Rising temperature increased the probability of meteorological-to-severe/extreme-hydrological drought propagation by about 5%. Under the combined influence of extreme precipitation deficiency and high temperatures, the probability of meteorological droughts propagating into extreme hydrological droughts reached 46%.
- (2)
- The probability of a meteorological drought event propagating into a severe hydrological drought event increased with increasing of the level of the L-PMD scenario, hitting 52% under severe L-PMD scenarios. The drought propagation probability was lowest in middle H-TMD scenarios but rose when H-TMD scenarios were light or severe. Severe hydrological droughts were more common in severe H-TMD scenarios, making up about 47% of all droughts. Under the combined impact of severe L-PMD and H-TMD scenarios, the propagation probability to severe hydrological droughts surged to 80%.
- (3)
- Around 1998, the mean annual temperature abruptly rose by about 0.6 °C. After this abrupt change, hydrological droughts due to low precipitation and high temperatures became more frequent, with the average intensity increased by around 0.78.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peterson, T.J.; Saft, M.; Peel, M.C.; John, A. Watersheds may not recover from drought. Science 2021, 372, 745–749. [Google Scholar] [CrossRef]
- Ault, T.R. On the essentials of drought in a changing climate. Science 2020, 368, 256–260. [Google Scholar] [CrossRef] [PubMed]
- Phillips, O.L.; Aragão, L.E.O.C.; Lewis, S.L.; Fisher, J.B.; Lloyd, J.; López-González, G.; Malhi, Y.; Monteagudo, A.; Peacock, J.; Quesada, C.A.; et al. Drought Sensitivity of the Amazon Rainforest. Science 2009, 323, 1344–1347. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Linderholm, H.W.; Song, Y.; Wang, F.; Liu, Y.; Tian, J.; Xu, J.; Song, Y.; Ren, G. Impacts of Drought on Maize and Soybean Production in Northeast China During the Past Five Decades. Int. J. Environ. Res. Public Health 2020, 17, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wu, Z.; Wang, H.; He, C.; Zhang, F.; Zhou, Y. Urban meteorological drought comprehensive index based on a composite fuzzy matter element-moment estimation weighting model. iScience 2024, 27, 110798. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Ye, A.; Zhang, Y.; Zhou, J. The Peer-To-Peer Type Propagation From Meteorological Drought to Soil Moisture Drought Occurs in Areas With Strong Land-Atmosphere Interaction. Water Resour. Res. 2022, 58, 14. [Google Scholar] [CrossRef]
- Tian, F.; Yang, J.; Liu, L.; Wu, J. Progress of research on the conception, characteristic, and influencing factors of drought propagation from the perspective of geographic sciences. Prog. Geogr. 2022, 41, 173–184. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, H.; Fu, Q.; Ding, Y.; Li, T.; Liu, S. Investigating the Propagation From Meteorological to Hydrological Drought by Introducing the Nonlinear Dependence With Directed Information Transfer Index. Water Resour. Res. 2021, 57, 21. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Hao, F.H.; Hao, Z.C. Characteristics and risk analysis of drought propagation from meteorological drought to hydrological drought in Luanhe River Basin. J. Hydraul. Eng. 2022, 53, 165–175. [Google Scholar]
- Wu, G.; Chen, J.; Shi, X.; Kim, J.; Xia, J.; Zhang, L. Impacts of Global Climate Warming on Meteorological and Hydrological Droughts and Their Propagations. Earths Future 2022, 10, 24. [Google Scholar] [CrossRef]
- Wossenyeleh, B.K.; Kasa, A.S.; Verbeiren, B.; Huysmans, M. Drought propagation in the hydrological cycle in a semiarid region: A case study in the Bilate catchment, Ethiopia. Hydrogeol. J. 2022, 30, 751–766. [Google Scholar] [CrossRef]
- Bevacqua, A.G.; Chaffe, P.L.; Chagas, V.B.; AghaKouchak, A. Spatial and temporal patterns of propagation from meteorological to hydrological droughts in Brazil. J. Hydrol. 2021, 603, 9. [Google Scholar] [CrossRef]
- Zheng, L.; Liu, Y.; Ren, L.; Zhu, Y.; Yin, H.; Yuan, F.; Zhang, L. Spatio-temporal characteristics and propagation relationship of meteorological drought and hydrological drought in the Yellow River Basin. Water Resour. Prot. 2022, 38, 87. [Google Scholar]
- Gu, L.; Chen, J.; Yin, J.; Xu, C.-Y.; Chen, H. Drought hazard transferability from meteorological to hydrological propagation. J. Hydrol. 2020, 585, 18. [Google Scholar] [CrossRef]
- Shi, H.; Zhou, Z.; Liu, L.; Liu, S. A global perspective on propagation from meteorological drought to hydrological drought during 1902–2014. Atmos. Res. 2022, 280, 10. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim. Dyn. 2008, 31, 79–105. [Google Scholar] [CrossRef]
- Murray, V.; Ebi, K.L. IPCC Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (SREX). J. Epidemiol. Community Health 2012, 66, 759–760. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Z.; Singh, V.P.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought propagation under global warming: Characteristics, approaches, processes, and controlling factors. Sci. Total Environ. 2022, 838, 19. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, P.; Han, Y.; Chang, X.; Dai, S. Quantitative analysis of self-purification capacity of non-point source pollutants in watersheds based on SWAT model. Ecol. Indic. 2022, 143, 12. [Google Scholar] [CrossRef]
- He, R.M.; Wang, G.Q.; Zhang, J.Y. Impacts of Environmental Change on Runoff in the Yiluohe River Basin of the Middle Yellow River. Res. Soil Water Conserv. 2007, 14, 297. [Google Scholar]
- Liu, X.; Dai, X.; Zhong, Y.; Li, J.; Wang, P. Analysis of changes in the relationship between precipitation and streamflow in the Yiluo River, China. Theor. Appl. Climatol. 2013, 114, 183–191. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Y.; Qin, T.; Zhang, X. Study on the propagation probability characteristics and prediction model of meteorological drought to hydrological drought in basin based on copula function. Front. Earth Sci. 2022, 10, 961871. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z.; Cui, B.; Sun, T. Temporal trends of hydro-climatic variables and runoff response to climatic variability and vegetation changes in the Yiluo River basin, China. Hydrol. Process. 2009, 23, 3030–3039. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K.; Li, K.; Jiang, Z. GPRChinaTemp1km: A high-resolution monthly air temperature dataset for China (1951–2020) based on machine learning. Earth Syst. Sci. Data Discuss 2021, 2021, 1–29. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Sorí, R.; Gimeno-Sotelo, L.; Nieto, R.; Liberato, M.L.; Stojanovic, M.; Pérez-Alarcón, A.; Fernández-Alvarez, J.C.; Gimeno, L. Oceanic and terrestrial origin of precipitation over 50 major world river basins: Implications for the occurrence of drought. Sci. Total Environ. 2023, 859, 160288. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Shen, Z.; Xie, H. Drought impacts on hydrology and water quality under climate change. Sci. Total Environ. 2023, 858, 159854. [Google Scholar] [CrossRef] [PubMed]
- Dabanlı, İ.; Mishra, A.K.; Şen, Z. Long-term spatio-temporal drought variability in Turkey. J. Hydrol. 2017, 552, 779–792. [Google Scholar] [CrossRef]
- Boulle, M. Optimal bin number for equal frequency discretizations in supervized learning. Intell. Data Anal. 2005, 9, 175–188. [Google Scholar] [CrossRef]
- Cao, F.; Ge, Y.; Wang, J. Spatial data discretization methods for geocomputation. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 432–440. [Google Scholar] [CrossRef]
- Zhou, Z.; Tu, X.; Wang, T.; Singh, V.P.; Chen, X.; Lin, K. Bivariate socioeconomic drought assessment based on a hybrid framework and impact of human activities. J. Clean. Prod. 2023, 409, 137150. [Google Scholar] [CrossRef]
- Niu, J.; Chen, J.; Sun, L. Exploration of drought evolution using numerical simulations over the Xijiang (West River) basin in South China. J. Hydrol. 2015, 526, 68–77. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, 7. [Google Scholar] [CrossRef]
- Rosenthal, R. An Application of the Kolmogorov-Smirnov Test for Normality with Estimated Mean and Variance. Psychol. Rep. 1968, 22, 570. [Google Scholar] [CrossRef]
- Wang, L.; Yu, H.; Yang, M.; Yang, R.; Gao, R.; Wang, Y. A drought index: The standardized precipitation evapotranspiration runoff index. J. Hydrol. 2019, 571, 651–668. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference:Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Yevjevich, V.M. An objective approach to definitions and investigations of continental hydrologic droughts. J. Hydrol. 1969, 7, 353. [Google Scholar] [CrossRef]
- Yang, M.; He, Z.; Zhang, L.; Pi, G.; You, M. Propagation Process of Meteorological Drought to Hydrological Drought in Different Time Scales. J. Soil Water Conserv. 2021, 35, 350–360. [Google Scholar]
- Wu, J.; Chen, X.; Yao, H.; Zhang, D. Multi-timescale assessment of propagation thresholds from meteorological to hydrological drought. Sci. Total Env. 2021, 765, 144232. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Yao, H.; Chen, X.; Wang, G.; Bai, X.; Zhang, D. A framework for assessing compound drought events from a drought propagation perspective. J. Hydrol. 2022, 604, 12. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation thresholds of meteorological drought for triggering hydrological drought at various levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Huang, S.; Guo, Y.; Liu, Y.; Li, Z.; Huang, Q. Propagation threshold of meteorological drought to different levels of hydrological drought.A case study of Qinhe River basin. J. Hydroelectr. Eng. 2022, 41, 9–19. [Google Scholar]
- Wang, Z.; Huang, S.; Huang, Q.; Duan, W.; Leng, G.; Guo, Y.; Zheng, X.; Nie, M.; Han, Z.; Dong, H.; et al. Seasonal Propagation Characteristics from Meteorological to Hydrological Drought and Their Dynamics in the Headstreams of the Tarim River Basin. J. Hydrometeorol. 2022, 23, 1487–1506. [Google Scholar] [CrossRef]
- Sattar, M.N.; Lee, J.-Y.; Shin, J.-Y.; Kim, T.-W. Probabilistic Characteristics of Drought Propagation from Meteorological to Hydrological Drought in South Korea. Water Resour. Manag. 2019, 33, 2439–2452. [Google Scholar] [CrossRef]
- Liu, X.; Jia, C.; Chai, Y. A catastrophe identification method for rainfall time series coupled sequential Mann-Kendall algorithm and Bernaola Galvan algorithm: A case study of the Qinglong River watershed, China. Water Supply 2023, 23, 3205–3220. [Google Scholar] [CrossRef]
- Zhang, J.; Lan, Y.; Chen, X.; Tan, Y.; Wu, T.; Lyu, S.; Zhou, Y.; Zhang, Y.; Cheng, L.; Chen, Y.; et al. Baseflow characteristics and drivers in headwater catchment of the Yellow River, Tibetan Plateau. J. Hydrol. Reg. Stud. 2024, 56, 101991. [Google Scholar] [CrossRef]
- Teuling, A.J. A hot future for European droughts. Nat. Clim. Change 2018, 8, 364–365. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Climate change—Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Ukkola, A.M.; De Kauwe, M.G.; Roderick, M.L.; Abramowitz, G.; Pitman, A.J. Robust Future Changes in Meteorological Drought in CMIP6 Projections Despite Uncertainty in Precipitation. Geophys. Res. Lett. 2020, 47, 9. [Google Scholar] [CrossRef]
- Depsky, N.; Pons, D. Meteorological droughts are projected to worsen in Central America’s dry corridor throughout the 21st century. Environ. Res. Lett. 2021, 16, 14. [Google Scholar] [CrossRef]
- Bernaola-Galván, P.; Ivanov, P.C.; Amaral, L.A.N.; Stanley, H.E. Scale invariance in the nonstationarity of human heart rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Sato, M.; Ruedy, R.; Lo, K.; Lea, D.W.; Medina-Elizade, M. Global temperature change. Proc. Natl. Acad. Sci. USA 2006, 103, 14288–14293. [Google Scholar] [CrossRef] [PubMed]
- da Silva, D.R.; Crespi, M.S.; Capela, J.M.V.; Khan, M.A.; Khan, S.; Khan, M.M.; Ye, J.-S.; Gong, Y.-H.; Zhang, F.; Ren, J.; et al. GISS analysis of surface temperature change. J. Geophys. Res. Atmos. 1999, 104, 30997–31022. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, R.; Jia, X.; Zhang, Y. Contribution of precipitation and temperature to multiscale drought variations over Asia: Dependence on the time scale. Int. J. Climatol. 2022, 42, 8804–8821. [Google Scholar] [CrossRef]
- Bateni, M.M.; Behmanesh, J.; De Michele, C.; Bazrafshan, J.; Rezaie, H. Composite Agrometeorological Drought Index Accounting for Seasonality and Autocorrelation. J. Hydrol. Eng. 2018, 23, 6. [Google Scholar] [CrossRef]
- Bhardwaj, K.; Shah, D.; Aadhar, S.; Mishra, V. Propagation of Meteorological to Hydrological Droughts in India. J. Geophys. Res.-Atmos. 2020, 125, 22. [Google Scholar] [CrossRef]
- Shukla, S.; Safeeq, M.; AghaKouchak, A.; Guan, K.; Funk, C. Temperature impacts on the water year 2014 drought in California. Geophys. Res. Lett. 2015, 42, 4384–4393. [Google Scholar] [CrossRef]
- Woodhouse, C.A.; Meko, D.M.; MacDonald, G.M.; Stahle, D.W.; Cook, E.R. A 1,200-year perspective of 21st century drought in southwestern North America. Proc. Natl. Acad. Sci. USA 2010, 107, 21283–21288. [Google Scholar] [CrossRef]
- Rahmani, F.; Fattahi, M.H. A multifractal cross-correlation investigation into sensitivity and dependence of meteorological and hydrological droughts on precipitation and temperature. Nat. Hazards 2021, 109, 2197–2219. [Google Scholar] [CrossRef]
- Easterling, D.R.; Wallis, T.W.R.; Lawrimore, J.H.; Heim, R.R. Effects of temperature and precipitation trends on US drought. Geophys. Res. Lett. 2007, 34, 4. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, S.; Fang, W.; Ma, L.; Zheng, X.; Huang, Q. Propagation and dynamic change of meteorological drought to hydrological drought in different seasons. J. Hydraul. Eng. 2021, 52, 93–102. [Google Scholar]
- Wang, L.; Yuan, X. Two Types of Flash Drought and Their Connections with Seasonal Drought. Adv. Atmos. Sci. 2018, 35, 1478–1490. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Bai, Q.; Zhao, J.; Ma, L.; Wang, L.; Du, M. Propagation dynamics from meteorological to groundwater drought and their possible influence factors. J. Hydrol. 2019, 578, 124102. [Google Scholar] [CrossRef]
- Yang, F.; Duan, X.; Guo, Q.; Lu, S.; Hsu, K. The spatiotemporal variations and propagation of droughts in Plateau Mountains of China. Sci. Total Environ. 2022, 805, 13. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhu, Z.; Liu, X.; Yu, M. Thresholds of key disaster-inducing factors and drought simulation in the Xilinguole Grassland. Ecol. Inform. 2021, 64, 101380. [Google Scholar] [CrossRef]
- Schumacher, D.L.; Keune, J.; Dirmeyer, P.; Miralles, D.G. Drought self-propagation in drylands due to land-atmosphere feedbacks. Nat. Geosci. 2022, 15, 262–268. [Google Scholar] [CrossRef]


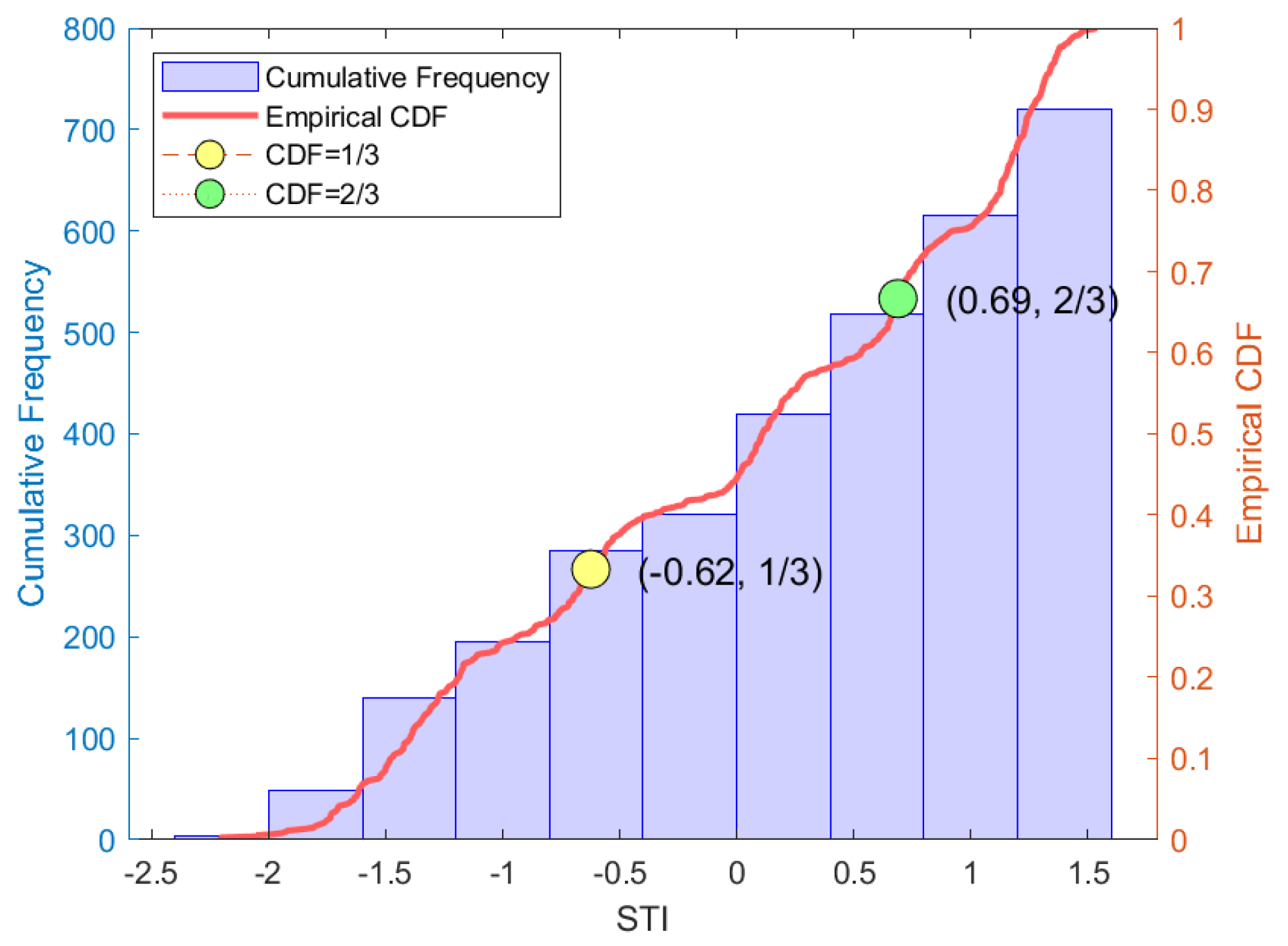
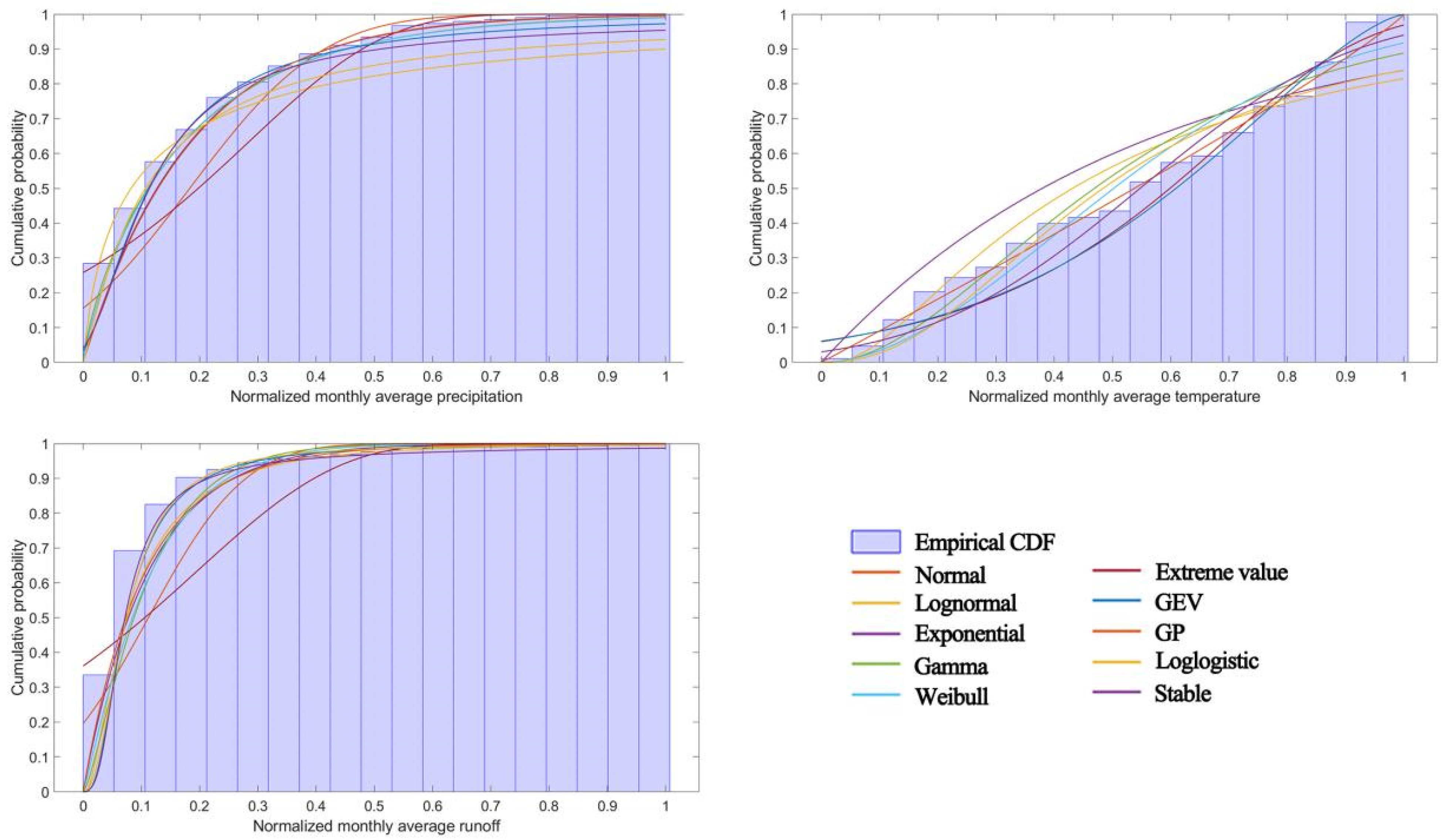
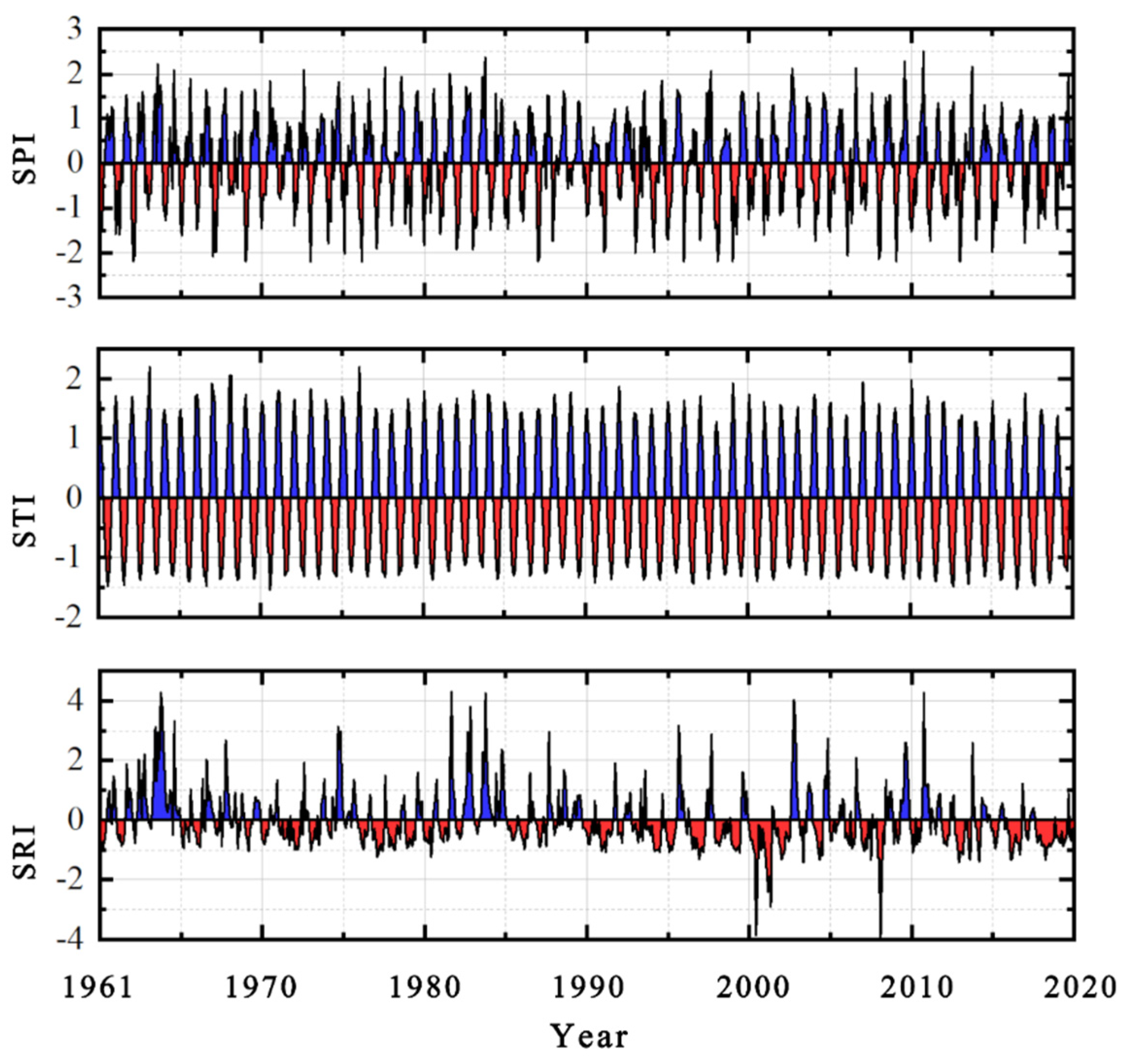

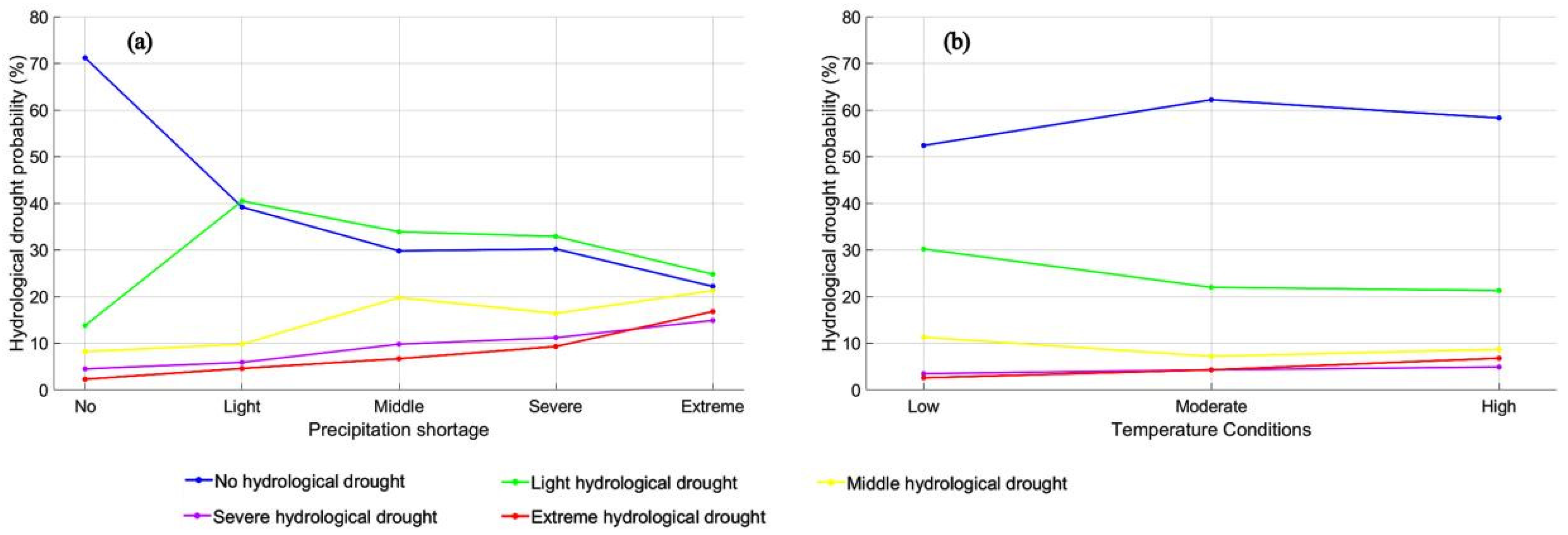

| SPI or SRI Value | Drought Grade |
|---|---|
| SPI or SRI > −0.5 | No drought |
| −1.0 < SPI or SRI ≤ −0.5 | Light drought |
| −1.5 < SPI or SRI ≤ −1.0 | Middle drought |
| −2.0 < SPI or SRI ≤ −1.5 | Severe drought |
| SPI or SRI ≤ −2.0 | Extreme drought |
| Precipitation | Temperature | Runoff | ||||
|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | |
| Normal | −418.21 | −409.05 | 268.74 | 277.90 | −883.17 | −874.01 |
| Lognormal | −588.04 | −578.88 | 742.47 | 751.62 | −1730.18 | −1721.02 |
| Exponential | −1003.87 | −999.29 | 574.09 | 578.67 | −1709.82 | −1705.24 |
| Gamma | −1045.34 | −1036.18 | 356.49 | 365.65 | −1759.14 | −1749.98 |
| Weibull | −1026.64 | −1017.48 | 273.06 | 282.22 | −1723.17 | −1714.01 |
| Extreme value | −27.14 | −17.99 | 265.39 | 274.54 | −106.92 | −97.76 |
| GEV | −834.39 | −820.65 | 169.14 | 182.88 | −1976.98 | −1963.24 |
| GP | −1000.08 | −986.34 | −9.46 | 4.28 | −1715.21 | −1701.47 |
| Loglogistic | −837.86 | −828.70 | 497.25 | 506.41 | −1932.86 | −1923.70 |
| Stable | −771.21 | −752.90 | 272.76 | 291.08 | −1981.20 | −1962.89 |
| Drought Severity_SPI | Drought Severity_SRI | Drought Severity_STI | Drought Events Grade |
|---|---|---|---|
| 0~−2.59 | 0~−1.98 | 0~−1.51 | Light Drought Event |
| −2.59~−4.25 | −1.98~−3.72 | −1.51~−4.75 | Middle Drought Event |
| −4.25~−∞ | −3.72~−∞ | −4.75~−∞ | Severe Drought Event |
| Starting Month | Number of Droughts | Average Drought Duration (Month) | Average Drought Severity | Average Drought Intensity |
|---|---|---|---|---|
| 1 | 5 | 2.40 | −2.97 | −1.23 |
| 2 | 2 | 2.00 | −1.71 | −0.85 |
| 3 | 1 | 2.00 | −1.60 | −0.80 |
| 10 | 3 | 4.33 | −4.99 | −1.15 |
| 11 | 19 | 3.42 | −3.90 | −1.15 |
| 12 | 30 | 3.10 | −3.95 | −1.31 |
| Starting Month | Number of Droughts | Average Drought Duration (Month) | Average Drought Severity | Average Drought Intensity |
|---|---|---|---|---|
| 5 | 56 | 4.95 | −5.07 | −1.03 |
| 6 | 4 | 4.00 | −4.33 | −1.08 |
| Starting Month | Number of Droughts | Average Drought Duration (Month) | Average Drought Severity | Average Drought Intensity |
|---|---|---|---|---|
| 1 | 13 | 3.15 | −3.07 | −0.90 |
| 2 | 3 | 3.00 | −2.41 | −0.72 |
| 4 | 5 | 3.00 | −2.17 | −0.72 |
| 5 | 4 | 2.00 | −1.35 | −0.67 |
| 6 | 3 | 5.67 | −5.17 | −0.93 |
| 9 | 2 | 2.00 | −1.28 | −0.64 |
| 10 | 4 | 5.00 | −4.93 | −0.99 |
| 11 | 8 | 5.25 | −5.68 | −1.09 |
| 12 | 13 | 3.92 | −3.18 | −0.79 |
| p-Value | February | April | May | June | September | October | November | December |
|---|---|---|---|---|---|---|---|---|
| January | 0.666 | 0.203 | 0.024 | 0.395 | 0.018 | 0.023 | 0.045 | 0.899 |
| February | 0.866 | 0.481 | 0.307 | 0.457 | 0.171 | 0.095 | 0.611 | |
| April | 0.007 | 0.262 | 0.003 | 0.001 | 0.009 | 0.113 | ||
| May | 0.187 | 0.714 | 0.000 | 0.003 | 0.009 | |||
| June | 0.183 | 0.913 | 0.829 | 0.416 | ||||
| September | 0.002 | 0.003 | 0.007 | |||||
| October | 0.485 | 0.020 | ||||||
| November | 0.048 |
| Causes | Number | Frequency | ||
|---|---|---|---|---|
| Before | After | Before | After | |
| Lack of precipitation | 20 | 9 | 0.69 | 0.36 |
| High temperature | 5 | 6 | 0.17 | 0.24 |
| High temperature and lack of precipitation | 4 | 9 | 0.14 | 0.36 |
| Other reasons | 0 | 1 | 0.00 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, H.; Yu, Z.; Yan, D.; Liu, R.; Liu, S.; Zhu, Y.; Chen, Y.; Wu, Z. Study on the Probability of Meteorological-to-Hydrological Drought Propagation Based on a Bayesian Network. Land 2025, 14, 445. https://doi.org/10.3390/land14030445
Zhang X, Wang H, Yu Z, Yan D, Liu R, Liu S, Zhu Y, Chen Y, Wu Z. Study on the Probability of Meteorological-to-Hydrological Drought Propagation Based on a Bayesian Network. Land. 2025; 14(3):445. https://doi.org/10.3390/land14030445
Chicago/Turabian StyleZhang, Xiangyang, Huiliang Wang, Zhilei Yu, Dengming Yan, Ruxue Liu, Simin Liu, Yujia Zhu, Yifan Chen, and Zening Wu. 2025. "Study on the Probability of Meteorological-to-Hydrological Drought Propagation Based on a Bayesian Network" Land 14, no. 3: 445. https://doi.org/10.3390/land14030445
APA StyleZhang, X., Wang, H., Yu, Z., Yan, D., Liu, R., Liu, S., Zhu, Y., Chen, Y., & Wu, Z. (2025). Study on the Probability of Meteorological-to-Hydrological Drought Propagation Based on a Bayesian Network. Land, 14(3), 445. https://doi.org/10.3390/land14030445








