Dynamic Simulation and Reduction Path of Carbon Emission in “Three-Zone Space”: A Case Study of a Rapidly Urbanizing City
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
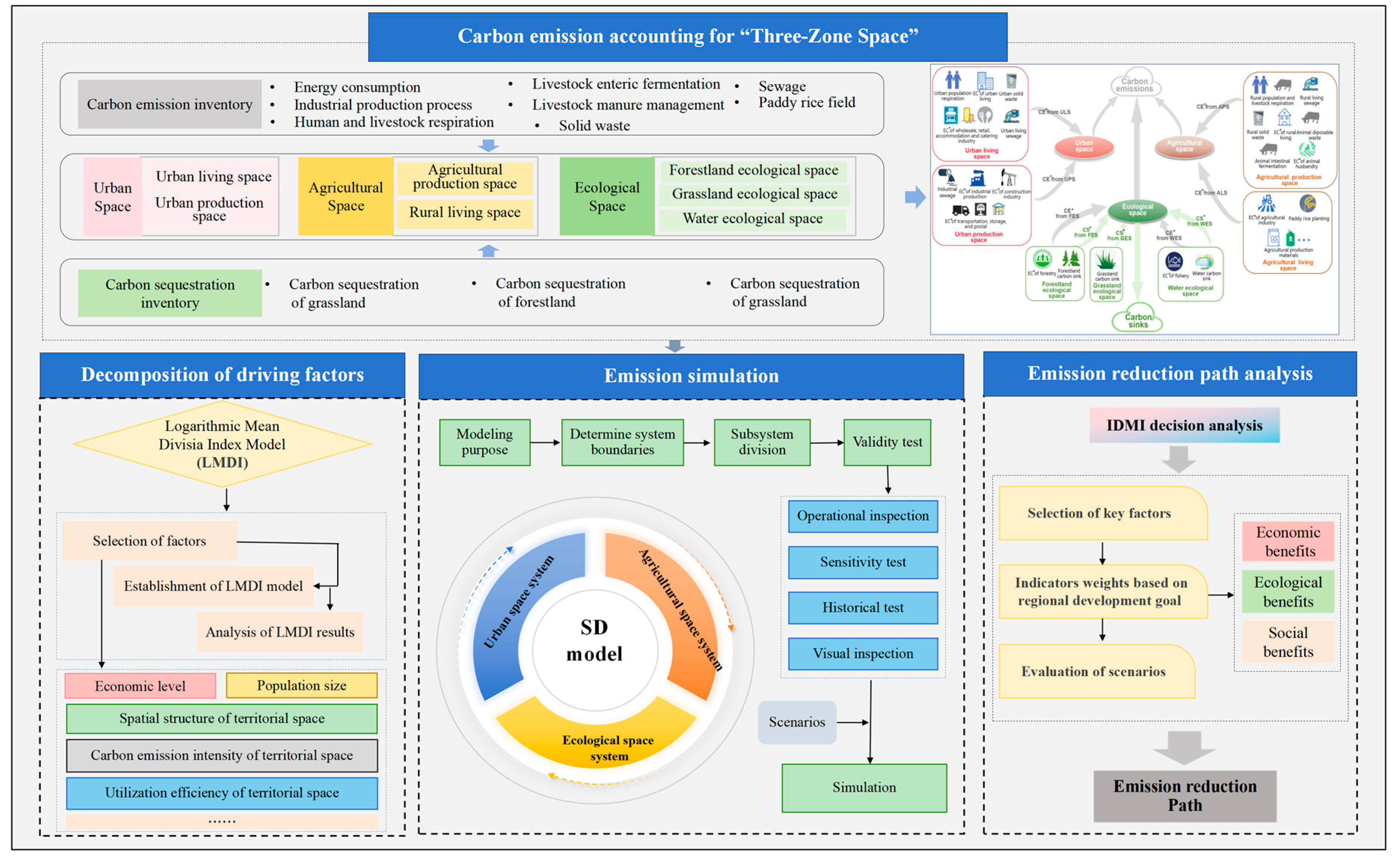
3.1. Research Framework
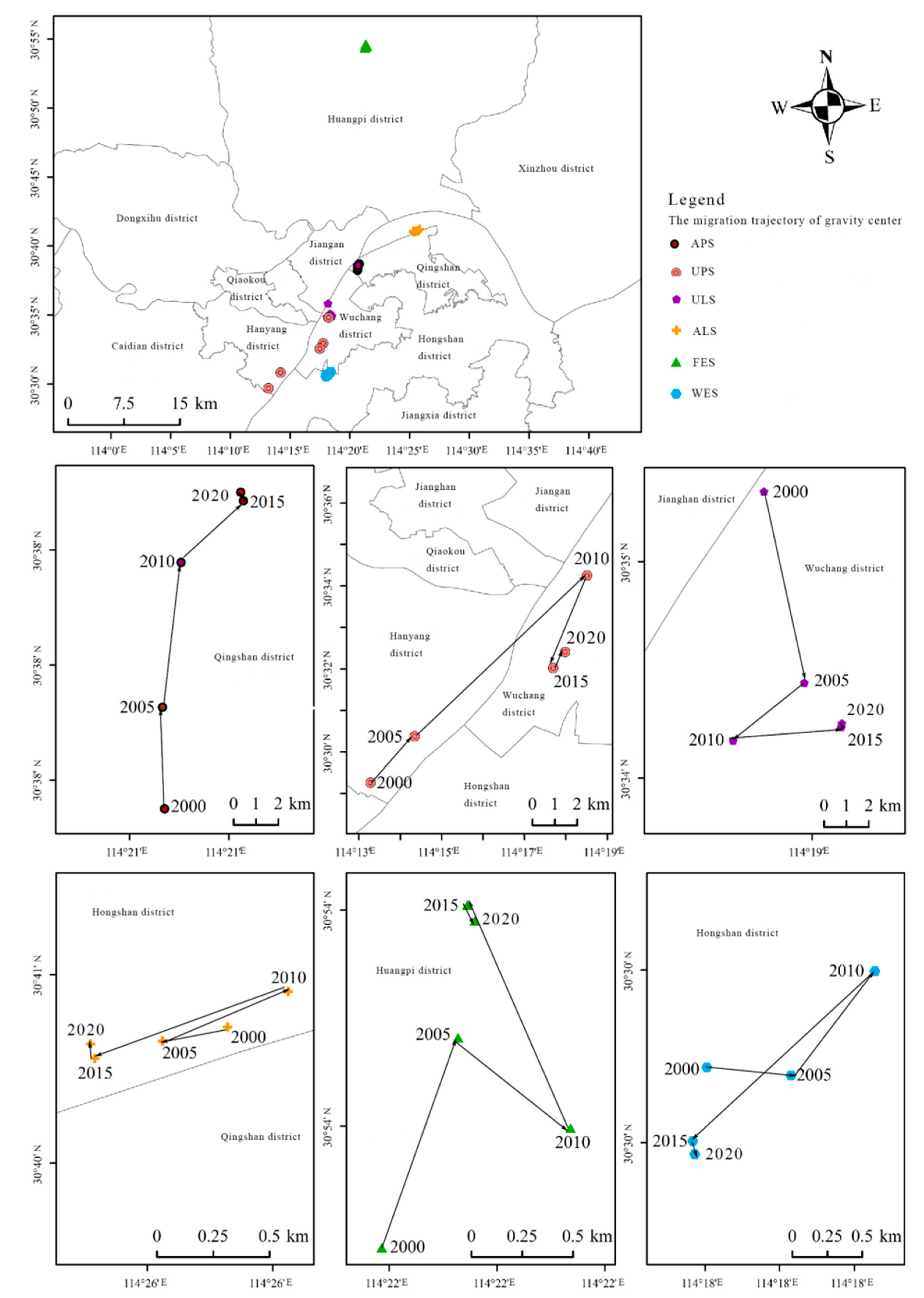
3.2. Study Area
3.3. Datasets
3.4. Estimation of Carbon Emissions and Sequestration in “Three-Zone Space”
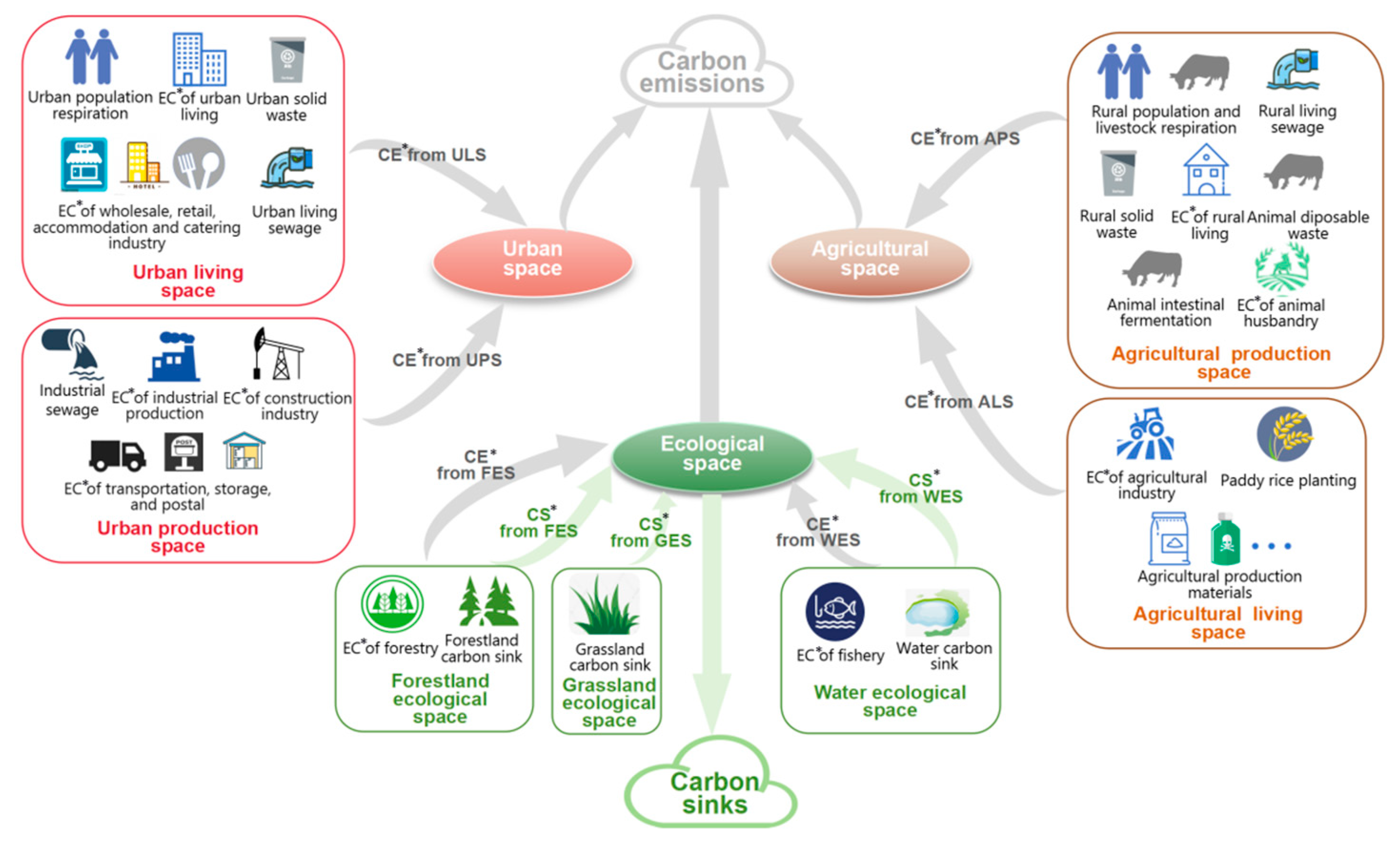
3.4.1. Carbon Emission and Sequestration Accounting
- (1)
- Carbon emissions from energy consumption
- (2)
- Carbon emissions from the industrial production process
- (3)
- Carbon emissions from solid waste
- (4)
- Carbon emissions from waste water
- (5)
- Carbon emissions from human and livestock respiration
- (6)
- Carbon emissions from the agricultural production process
- (7)
- Carbon emissions from the paddy rice field
- (8)
- Animal enteric fermentation carbon emissions with manure management
- (9)
- Terrestrial ecosystem carbon sequestration
3.4.2. The Relationship Between the “Three-Zone Space” Classification and Carbon Emission/Sequestration Inventories
3.5. Decomposition of Net Carbon Emissions in “Three-Zone Space”
3.5.1. The Extended Kaya Identity
3.5.2. Logarithmic Mean Divisia Index (LMDI) Decomposition Method
3.6. Simulation of Future Carbon Emissions and Sequestration in “Three-Zone Space”
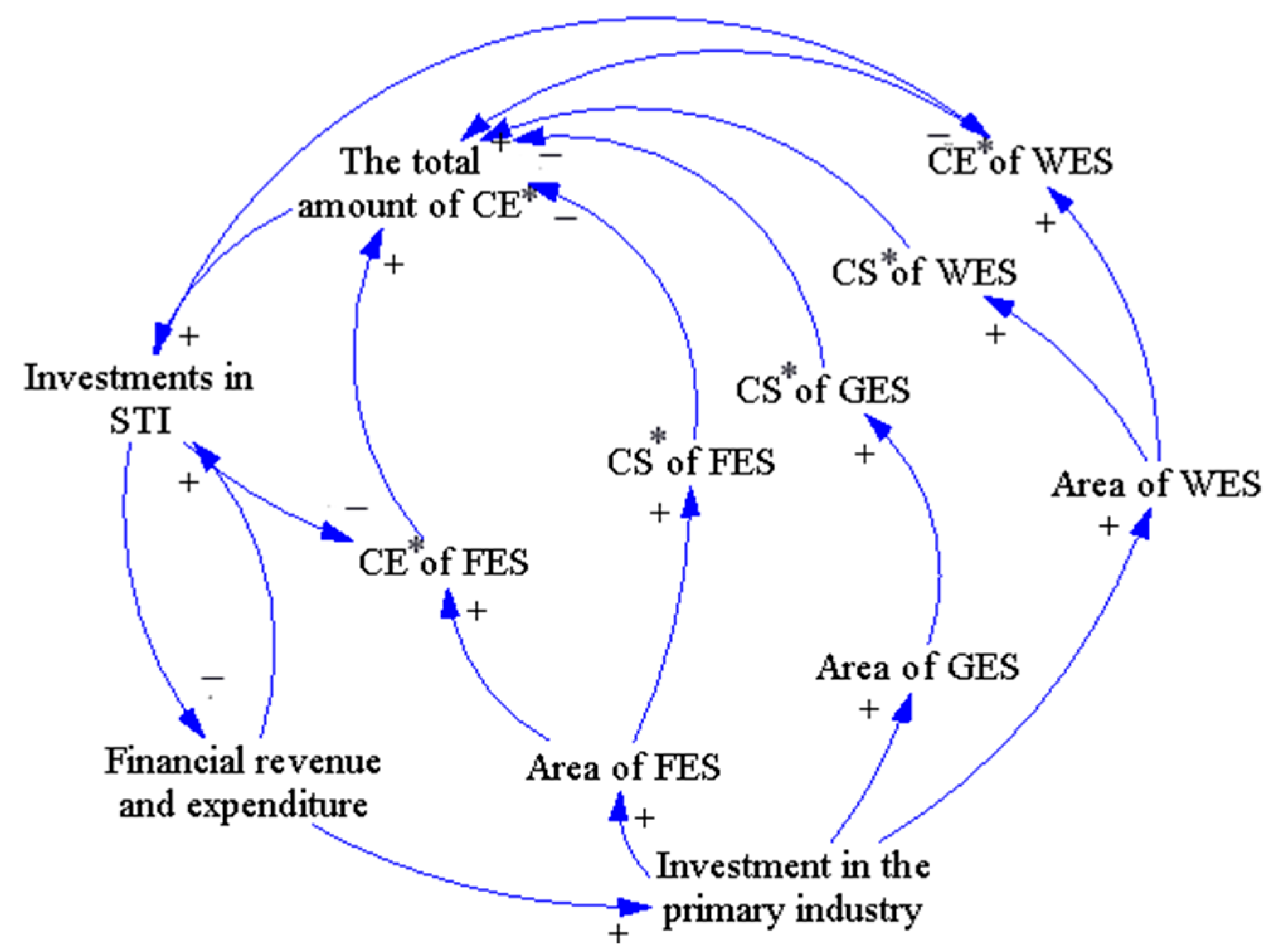
3.6.1. System Dynamic Model
- (1)
- The urban space subsystem
- (2)
- The agricultural space subsystem
- (3)
- The ecological space subsystem
3.6.2. Scenario Design
3.6.3. Historical Simulation and Model Verification
3.7. Intelligent Decision-Making Index (IDMI) Decision Analysis
4. Results
4.1. Spatial-Temporal Changes in Net Carbon Emissions in “Three-Zone Space” from 2000 to 2020
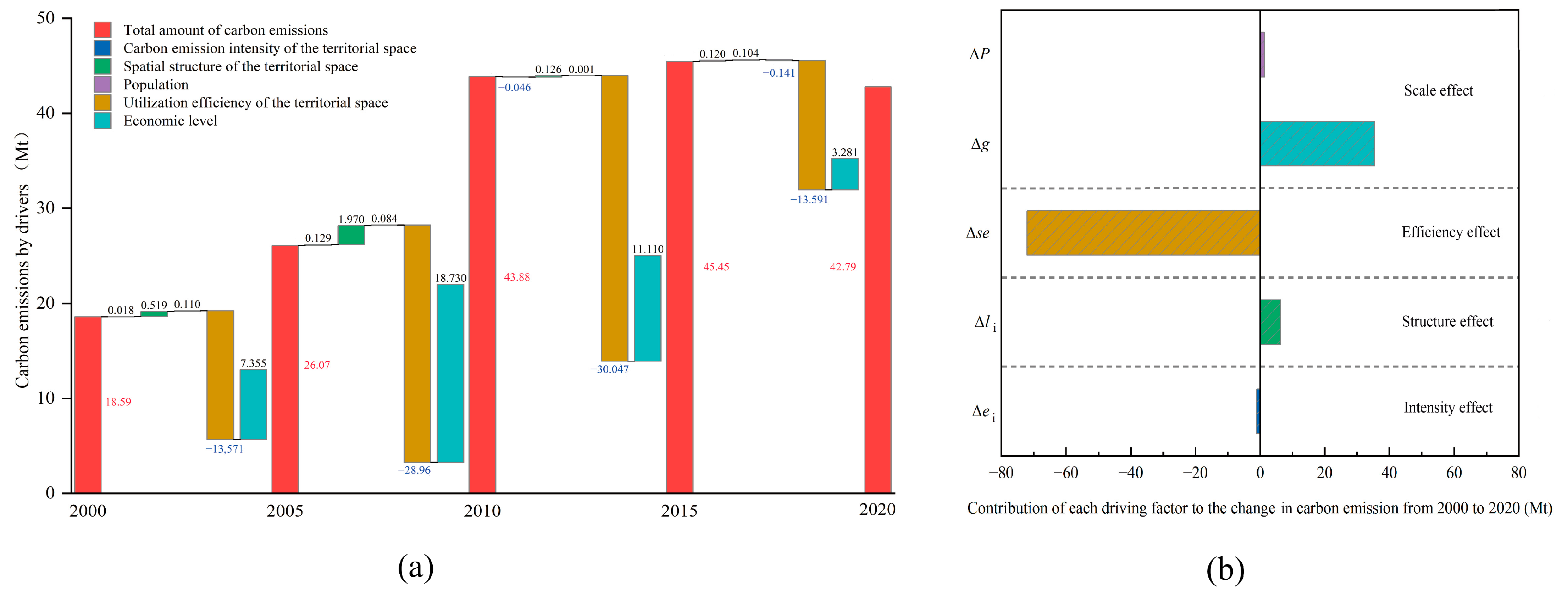
4.2. Logarithmic Mean Divisia Index (LMDI) Decomposition Results
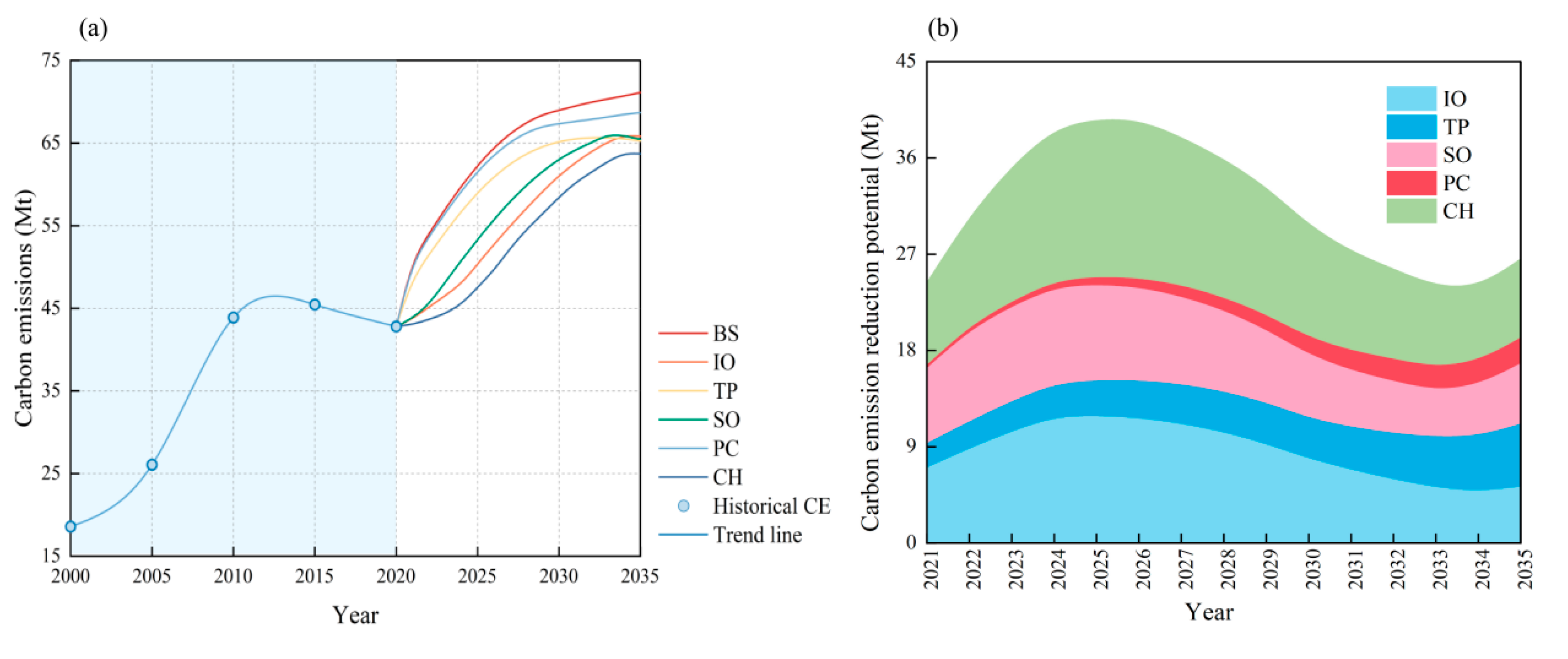
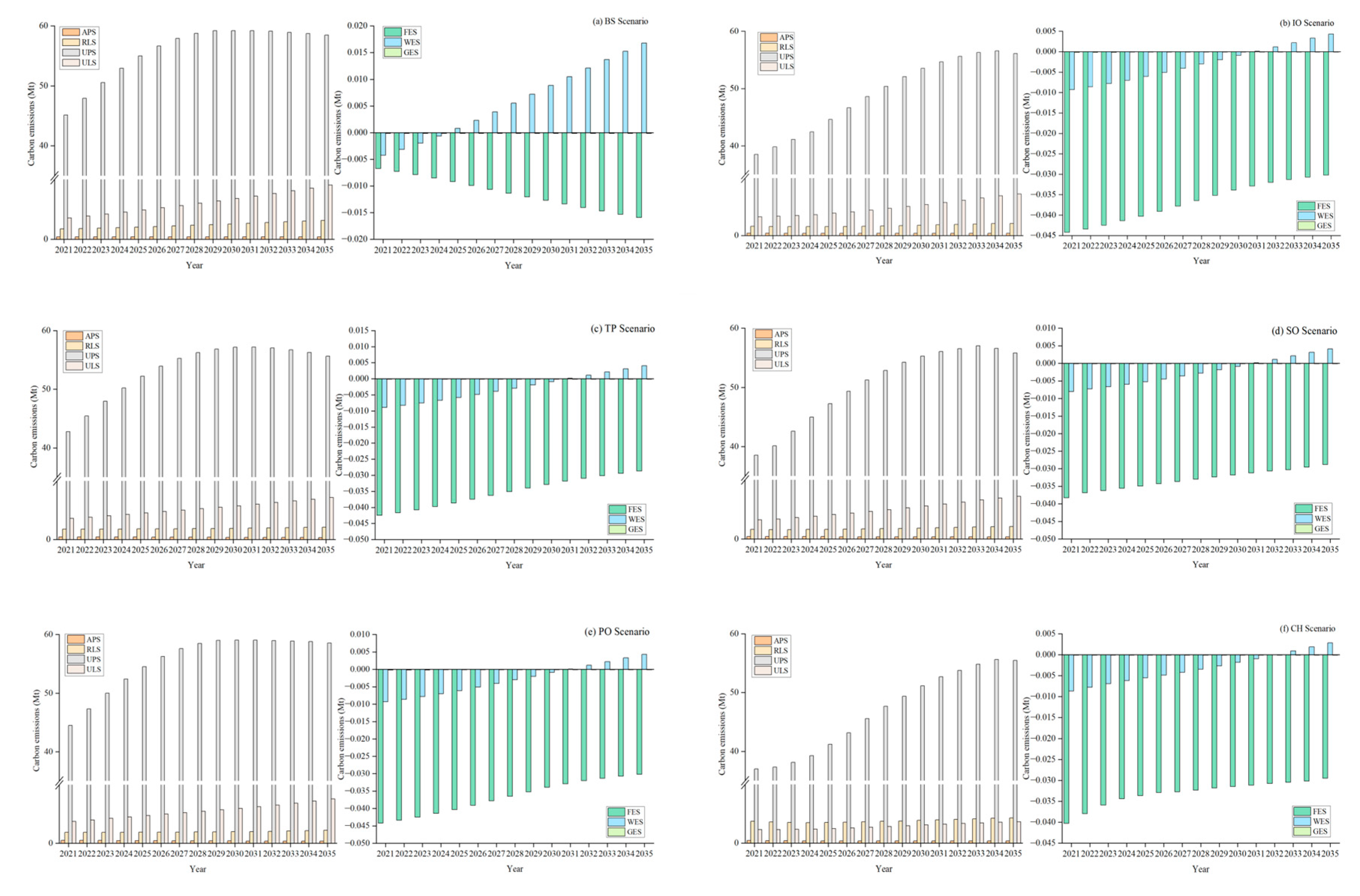
4.3. Scenario Analysis of Net Carbon Emissions in “Three-Zone Space” from 2021 to 2035
4.4. Decision Analysis of Emission Reduction Paths
5. Discussion
6. Conclusions and Policy Implications
6.1. Conclusions
6.2. Policy Implications
6.3. Limitations
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, G.; Guo, B.; Deng, X. Is there a decoupling relationship between CO2 emission reduction and poverty alleviation in China? Technol. Forecast. Soc. Change 2020, 151, 119856. [Google Scholar] [CrossRef]
- Adger, W.N.; Barnett, J.; Heath, S.; Jarillo, S. Climate change affects multiple dimensions of well-being through impacts, information, and policy responses. Nat. Hum. Behav. 2022, 6, 1465–1473. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, B.C. Envisioning a future with climate change. Nat. Clim. Change 2023, 13, 874–876. [Google Scholar] [CrossRef]
- UNFCCC. Adoption of the Paris Agreement. 2015. Available online: http://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf (accessed on 15 June 2023).
- UNFCCC. FCCC/CP/2021/L.13/CP.26—Glasgow Climate Pact. 2021. Available online: https://unfccc.int/sites/default/files/resource/cp2021_L13adv.pdf (accessed on 15 June 2023).
- van de Ven, D.-J.; Mittal, S.; Gambhir, A.; Lamboll, R.D.; Doukas, H.; Giarola, S.; Hawkes, A.; Koasidis, K.; Köberle, A.C.; McJeon, H.; et al. A multimodel analysis of post-Glasgow climate targets and feasibility challenges. Nat. Clim. Change 2023, 13, 570–578. [Google Scholar] [CrossRef]
- Pianta, S.; Brutschin, E. Increased ambition is needed after Glasgow. Nat. Clim. Change 2023, 13, 505–506. [Google Scholar] [CrossRef]
- Wang, S.; Fang, C.; Guan, X.; Pang, B.; Ma, H. Urbanisation, energy consumption, and carbon dioxide emissions in China: A panel data analysis of China’s provinces. Appl. Energy 2014, 136, 738–749. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Fang, C.; Feng, K. Inequalities in carbon intensity in China: A multi-scalar and multi-mechanism analysis. Appl. Energy 2019, 254, 113720. [Google Scholar] [CrossRef]
- Wang, W.; Wang, W.; Xie, P.; Zhao, D. Spatial and temporal disparities of carbon emissions and interregional carbon compensation in major function-oriented zones: A case study of Guangdong province. J. Clean. Prod. 2020, 245, 118873. [Google Scholar] [CrossRef]
- Xinhua Agency. Opinions of the CPC Central Committee and the State Council on the Establishment and Supervision of Territorial Space Planning System. 2019. Available online: https://www.gov.cn/zhengce/2019-05/23/content_5394187.htm (accessed on 20 June 2024).
- Liu, Y.; Zhou, Y. Territory spatial planning and national governance system in China. Land Use Policy 2021, 102, 105288. [Google Scholar] [CrossRef]
- Fang, K.; Tang, Y.; Zhang, Q.; Song, J.; Wen, Q.; Sun, H.; Ji, C.; Xu, A. Will China peak its energy-related carbon emissions by 2030? Lessons from 30 Chinese provinces. Appl. Energy 2019, 255, 113852. [Google Scholar] [CrossRef]
- Luo, X.; Liu, C.; Zhao, H. Driving factors and emission reduction scenarios analysis of CO2 emissions in Guangdong-Hong Kong-Macao Greater Bay Area and surrounding cities based on LMDI and system dynamics. Sci. Total Environ. 2023, 870, 161966. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Akashi, Y.; Takaguchi, H.; Sumiyoshi, D.; Lim, J.; Ueno, T.; Maruyama, K.; Baba, Y. Forecasting model of activities of the city-level for management of CO2 emissions applicable to various cities. J. Environ. Manag. 2021, 286, 112210. [Google Scholar] [CrossRef] [PubMed]
- Zhan, J.; Wang, C.; Wang, H.; Zhang, F.; Li, Z. Pathways to achieve carbon emission peak and carbon neutrality by 2060: A case study in the Beijing-Tianjin-Hebei region, China. Renew. Sustain. Energy Rev. 2024, 189, 113955. [Google Scholar] [CrossRef]
- Barrett, J.; Peters, G.; Wiedmann, T.; Scott, K.; Lenzen, M.; Roelich, K.; Le Quéré, C. Consumption-based GHG emission accounting: A UK case study. Clim. Policy 2013, 13, 451–470. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Zhang, C.; Liu, C. Is ecological protection and restoration of full-array ecosystems conducive to the carbon balance? A case study of Hubei Province, China. Technol. Forecast. Soc. Change 2021, 166, 120578. [Google Scholar] [CrossRef]
- Chen, W.; Lei, Y.; Feng, K.; Wu, S.; Li, L. Provincial emission accounting for CO2 mitigation in China: Insights from production, consumption and income perspectives. Appl. Energy 2019, 255, 113754. [Google Scholar] [CrossRef]
- Wu, S.; Hu, S.; Frazier, A.E. Spatiotemporal variation and driving factors of carbon emissions in three industrial land spaces in China from 1997 to 2016. Technol. Forecast. Soc. Change 2021, 169, 120837. [Google Scholar] [CrossRef]
- Le Quéré, C.; Korsbakken, J.I.; Wilson, C.; Tosun, J.; Andrew, R.; Andres, R.J.; Canadell, J.G.; Jordan, A.; Peters, G.P.; van Vuuren, D.P. Drivers of declining CO2 emissions in 18 developed economies. Nat. Clim. Change 2019, 9, 213–217. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.; Liu, G.; Zhang, M.; Bai, Y.; Zhang, F. Carbon emission accounting and spatial distribution of industrial entities in Beijing—Combining nighttime light data and urban functional areas. Ecol. Inform. 2022, 70, 101759. [Google Scholar] [CrossRef]
- Azar, C.; Johansson, D.J.A. DICE and the Carbon Budget for Ambitious Climate Targets. Earths Future 2021, 9, e2021EF002041. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Ma, L.; Li, Z. Using system dynamics to analyse key factors influencing China’s energy-related CO2 emissions and emission reduction scenarios. J. Clean. Prod. 2021, 320, 128811. [Google Scholar] [CrossRef]
- Hao, J.; Gao, F.; Fang, X.; Nong, X.; Zhang, Y.; Hong, F. Multi-factor decomposition and multi-scenario prediction decoupling analysis of China’s carbon emission under dual carbon goal. Sci. Total Environ. 2022, 841, 156788. [Google Scholar] [CrossRef] [PubMed]
- Maheen, R.; Cai, L.; Zhang, Y.; Zhao, M. Quantitative analysis of carbon dioxide emission reduction pathways: Towards carbon neutrality in China’s power sector. Carbon Capture Sci. Technol. 2023, 7, 100112. [Google Scholar] [CrossRef]
- Li, G.; Chen, X.; You, X.-Y. System dynamics prediction and development path optimization of regional carbon emissions: A case study of Tianjin. Renew. Sustain. Energy Rev. 2023, 184, 113579. [Google Scholar] [CrossRef]
- Zhang, F.; Deng, X.; Phillips, F.; Fang, C.; Wang, C. Impacts of industrial structure and technical progress on carbon emission intensity: Evidence from 281 cities in China. Technol. Forecast. Soc. Change 2020, 154, 119949. [Google Scholar] [CrossRef]
- Hu, E.; Abley, W.; Zou, L. Environmental related decision making using the Interlink Decision Making Index (IDMI). Int. J. Environ. Waste Manag. 2008, 2, 257–266. [Google Scholar] [CrossRef]
- Chuai, X.; Huang, X.; Wang, W.; Zhao, R.; Zhang, M.; Wu, C. Land use, total carbon emissions change and low carbon land management in Coastal Jiangsu, China. J. Clean. Prod. 2015, 103, 77–86. [Google Scholar] [CrossRef]
- Wen, J.; Chuai, X.; Zuo, T.; Huifen Cai, H.; Cai, L.; Zhao, R.; Chen, Y. Land use change on the surface area and the influence on carbon. Ecol. Indic. 2023, 153, 110400. [Google Scholar] [CrossRef]
- NDRC (National Development and Reform Commission). The Guidelines for the Preparation of Provincial GHG Inventories (Trial). 2011. Available online: https://scholar.google.com/scholar_lookup?title=Guidelines%20for%20the%20Preparation%20of%20Provincial%20Greenhouse%20Gas%20Inventories%20(Trial)&author=National%20Development%20and%20Reform%20Commission&publication_year=2011 (accessed on 20 June 2024).
- Wu, H.; Huang, H.; Chen, W.; Meng, Y. Estimation and spatiotemporal analysis of the carbon-emission efficiency of crop production in China. J. Clean. Prod. 2022, 371, 133516. [Google Scholar] [CrossRef]
- Tian, Y.; Yin, M. Reestimation of agricultural carbon emissions in China: Basic status, dynamic evolution and spatial spillover effect. China Rural. Econ. 2022, 104–127. [Google Scholar]
- Fang, J.; Guo, Z.; Piao, S.; Chen, A. Estimation of China’s terrestrial vegetation carbon sink from 1981 to 2000. Sci. China (Ser. D Earth Sci.) 2007, 50, 804–812. [Google Scholar]
- Zhang, J.; Zhang, A.; Dong, J. Carbon emission effect analysis and factor decomposition of land use in Wuhan urban circle. Resour. Environ. Yangtze River Basin 2014, 23, 595–602. [Google Scholar]
- Duan, X.; Wang, X.; Lu, F.; Ou, Z. Current status and potential of carbon sequestration in wetland ecosystems in China. Chin. J. Ecol. 2008, 463–469. [Google Scholar]
- Chen, X.; Di, Q.; Jia, W.; Hou, Z. Spatial correlation network of pollution and carbon emission reductions coupled with high-quality economic development in three Chinese urban agglomerations. Sustain. Cities Soc. 2023, 94, 104552. [Google Scholar] [CrossRef]
- Tong, D.; Chu, J.; MacLachlan, I.; Qiu, J.; Shi, T. Modelling the Impacts of land finance on urban expansion: Evidence from Chinese cities. Appl. Geogr. 2023, 153, 102896. [Google Scholar] [CrossRef]
- Li, R.; Li, L.; Wang, Q. The impact of energy efficiency on carbon emissions: Evidence from the transportation sector in Chinese 30 provinces. Sustain. Cities Soc. 2022, 82, 103880. [Google Scholar] [CrossRef]
- Adebayo, T.S.; Ullah, S.; Kartal, M.T.; Ali, K.; Pata, U.K.; Ağa, M. Endorsing sustainable development in BRICS: The role of technological innovation, renewable energy consumption, and natural resources in limiting carbon emission. Sci. Total Environ. 2023, 859, 160181. [Google Scholar] [CrossRef]
- Ge, Q.; Liu, X.; Zhang, Y.; Liu, S. Has China’s Free Trade Zone policy promoted the upgrading of service industry structure?: Based on the empirical test of 185 prefecture-level cities in China. Econ. Anal. Policy 2023, 210, 100008. [Google Scholar]
- Du, K.; Cheng, Y.; Yao, X. Environmental regulation, green technology innovation, and industrial structure upgrading: The road to the green transformation of Chinese cities. Energy Econ. 2021, 98, 105247. [Google Scholar] [CrossRef]
- Gu, S.; Fu, B.; Thriveni, T.; Fujita, T.; Ahn, J.W. Coupled LMDI and system dynamics model for estimating urban CO2 emission mitigation potential in Shanghai, China. J. Clean. Prod. 2019, 240, 118034. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Mangla, S.K.; Song, M.; Wen, J. Effects of technological changes on China’s carbon emissions. Technol. Forecast. Soc. Change 2020, 153, 119938. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, X.; Ni, X. Scenario setting and simulation of land use carbon emission in Hunan Province based on SD method. J. Hunan Univ. Technol. 2019, 33, 67–74. [Google Scholar]
- Ye, X.; Chuai, X. Carbon sinks/sources’ spatiotemporal evolution in China and its response to built-up land expansion. J. Environ. Manag. 2022, 321, 115863. [Google Scholar] [CrossRef] [PubMed]
- Long, H.; Qu, Y. Land use transitions and land management: A mutual feedback perspective. Land Use Policy 2018, 74, 111–120. [Google Scholar] [CrossRef]
- Bai, Y.; Deng, X.; Gibson, J.; Zhao, Z.; Xu, H. How does urbanization affect residential CO2 emissions? An analysis on urban agglomerations of China. J. Clean. Prod. 2019, 209, 876–885. [Google Scholar] [CrossRef]
- Yang, H.; Wu, Q. Dynamic simulation of land use carbon emissions in Nanjing under different policy schemes. Areal Res. Dev. 2021, 40, 121–126. (In Chinese) [Google Scholar]
- Hong, S.; Hui, E.C.M.; Lin, Y. Relationships between carbon emissions and urban population size and density, based on geo-urban scaling analysis: A multi-carbon source empirical study. Urban Clim. 2022, 46, 101337. [Google Scholar] [CrossRef]
- Tang, L.; Yang, J.; Zheng, J.; Sun, X.; Cheng, L.; He, K.; Li, L.; Li, J.; Cai, W.; Wang, S.; et al. Assessing the impacts of fertility and retirement policies on China’s carbon emissions. Nat. Clim. Chang. 2024, 14, 1261–1267. [Google Scholar] [CrossRef]
- CSC (China’s State Council). Enhanced actions on climate change: China’s intended nationally determined contributions. 2015. Available online: http://www.gov.cn/xinwen/2015-06/30/content_2887330.htm (accessed on 26 June 2022).
- Deng, X.; Wang, Y.; Song, M. Development Geography for exploring solutions to promote regional development. Geogr. Sustain. 2023, 4, 49–57. [Google Scholar] [CrossRef]
- Yu, L. Carbon emission scenario analysis of Wuhan City based on STIRPAT model. J. Hubei Inst. Technol. 2022, 38, 1–6+16. (In Chinese) [Google Scholar]
- Ding, S.; Xu, N.; Ye, J.; Zhou, W.; Zhang, X. Estimating Chinese energy-related CO2 emissions by employing a novel discrete grey prediction model. J. Clean. Prod. 2020, 259, 120793. [Google Scholar] [CrossRef]
- Maraseni, T.; An-Vo, D.-A.; Mushtaq, S.; Reardon-Smith, K. Carbon smart agriculture: An integrated regional approach offers significant potential to increase profit and resource use efficiency, and reduce emissions. J. Clean. Prod. 2021, 282, 124555. [Google Scholar] [CrossRef]
- An, R.; Yu, B.; Li, R.; Wei, Y.M. Potential of energy savings and CO2 emission reduction in China’s iron and steel industry. Appl. Energy 2018, 226, 862–880. [Google Scholar] [CrossRef]





| First-Level Classification | Second-Level Classification | Third-Level Classification |
|---|---|---|
| Urban space | UPS | Urban land |
| ULS | Other construction land | |
| Agricultural space | APS | Paddy field, dryland |
| RLS | Rural settlements | |
| Ecological space | FES | Forested land, scrubland, open woodland, other forest land |
| GES | High-coverage grassland, moderate-coverage grassland, low-coverage grassland | |
| WES | River and canals, lakes, reservoir, bench land |
| Scenarios | Parameter Settings |
|---|---|
| BS | The original data of the model; each variable develops according to the natural trend. |
| IO | The industrial structure is adjusted and the investment in the primary industry is unchanged, making the investment in fixed assets in the secondary industry decrease by 3% and the investment in fixed assets in the tertiary industry increase by 3%. |
| TP | Investment in scientific and technological innovation is adjusted and investment in scientific and technological innovation by 3% is increased. |
| SO | The area of construction land is reduced by 10%, the area of arable land is increased by 5%, and the area of forestland is increased by 5%. |
| PC | The total population of Wuhan is controlled to 16.6 million in 2035 according to the requirements of the “The Territory Space Plan of Wuhan City (2021–2035)”. |
| CH | The parameter settings in IO, TP, SO, and PC are integrated. |
| “Three-Zone Space” | 2000 | 2005 | 2010 | 2015 | 2020 |
|---|---|---|---|---|---|
| ULS | 0.88948 | 1.29975 | 3.73169 | 3.21434 | 3.08103 |
| UPS | 15.67990 | 22.16868 | 37.48381 | 39.35701 | 37.4863 |
| APS | 0.49853 | 0.55665 | 0.52671 | 0.51770 | 0.47783 |
| RLS | 1.58904 | 2.10596 | 2.19021 | 2.39737 | 1.78774 |
| FES | −0.05040 | −0.04929 | −0.04878 | −0.04517 | −0.0418 |
| GES | −0.00017 | −0.00016 | −0.00018 | −0.00016 | −0.00016 |
| WES | −0.01762 | −0.01002 | −0.00211 | 0.01111 | 0.00355 |
| Key Variable | IO | TP | SO | PC | CH | |
|---|---|---|---|---|---|---|
| No key variable (focusing on the balance of economic, social, and ecological benefits) | IDMI value | 2.954 | 2.980 | 2.914 | 2.649 | 2.637 |
| Ranking | 4 | 5 | 3 | 2 | 1 | |
| Per capita GDP (focusing on economic benefits) | IDMI value | 2.954 | 3.138 | 2.927 | 1.926 | 2.178 |
| Ranking | 4 | 5 | 3 | 1 | 2 | |
| Farmland area (focusing on social benefits) | IDMI value | 2.774 | 3.059 | 2.962 | 2.733 | 2.590 |
| Ranking | 3 | 5 | 4 | 2 | 1 | |
| Carbon emission intensity of the territorial space (focusing on ecological benefits) | IDMI value | 2.954 | 2.761 | 2.682 | 2.441 | 2.304 |
| Ranking | 5 | 4 | 3 | 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Fan, Y.; Li, H.; Shang, Z. Dynamic Simulation and Reduction Path of Carbon Emission in “Three-Zone Space”: A Case Study of a Rapidly Urbanizing City. Land 2025, 14, 245. https://doi.org/10.3390/land14020245
Wang Y, Fan Y, Li H, Shang Z. Dynamic Simulation and Reduction Path of Carbon Emission in “Three-Zone Space”: A Case Study of a Rapidly Urbanizing City. Land. 2025; 14(2):245. https://doi.org/10.3390/land14020245
Chicago/Turabian StyleWang, Ying, Yiqi Fan, Haiyang Li, and Zhiyu Shang. 2025. "Dynamic Simulation and Reduction Path of Carbon Emission in “Three-Zone Space”: A Case Study of a Rapidly Urbanizing City" Land 14, no. 2: 245. https://doi.org/10.3390/land14020245
APA StyleWang, Y., Fan, Y., Li, H., & Shang, Z. (2025). Dynamic Simulation and Reduction Path of Carbon Emission in “Three-Zone Space”: A Case Study of a Rapidly Urbanizing City. Land, 14(2), 245. https://doi.org/10.3390/land14020245




