Symbiotic Evolution of Rural Settlements and Traditional Agricultural Water Conservancy Facilities Based on the Lotka-Volterra Model
Abstract
1. Introduction
2. Materials and Methods
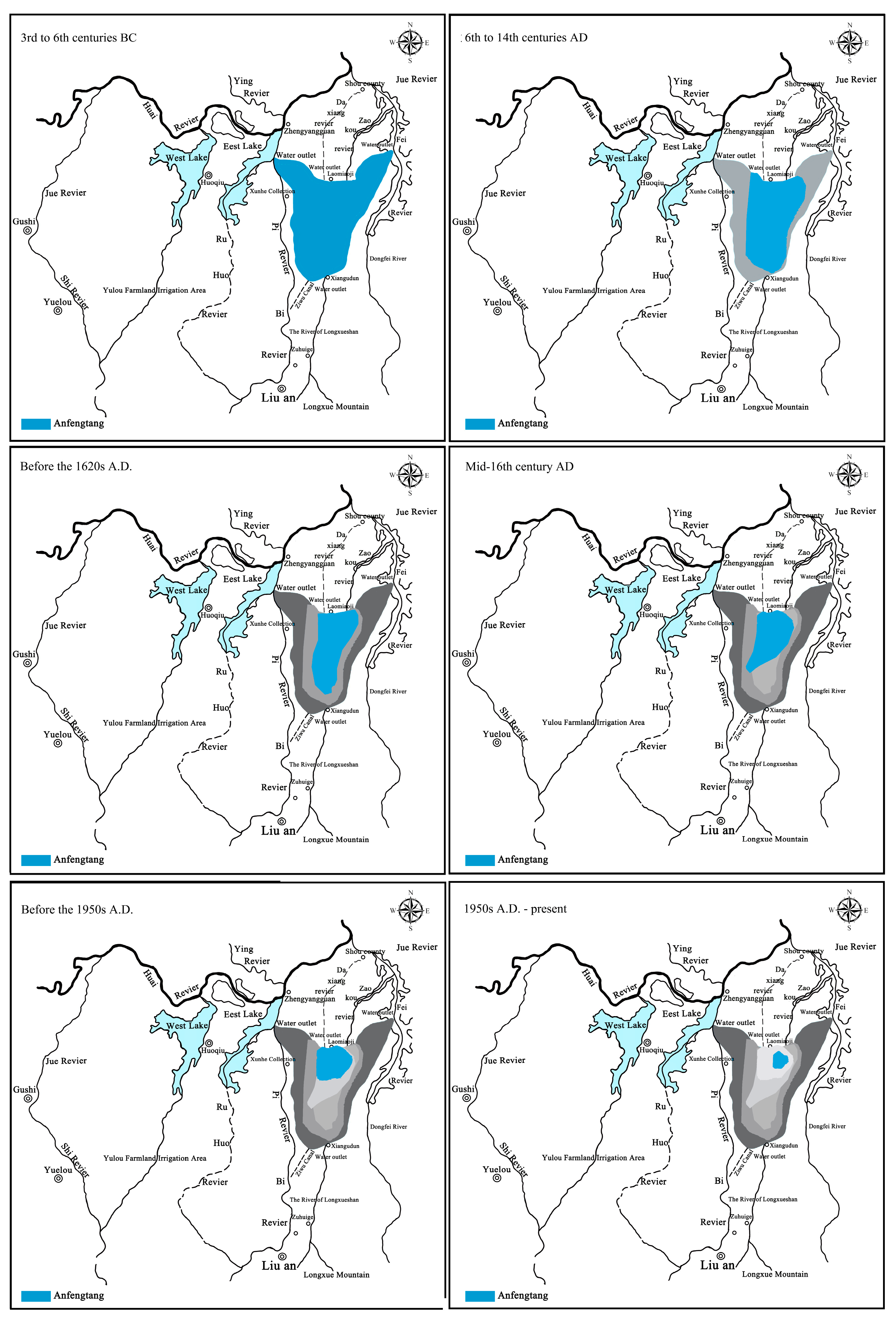
2.1. Study Area
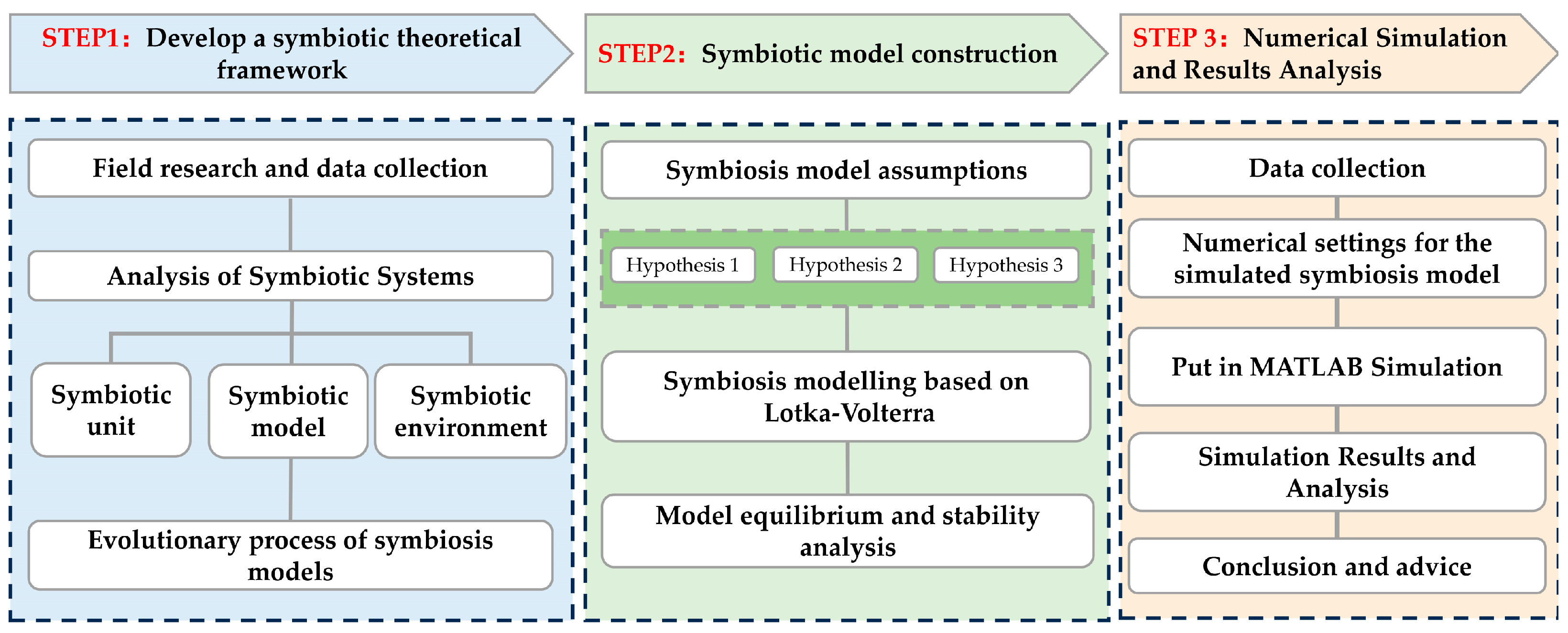
2.2. Study Framework
2.3. Symbiotic Theory Framework Construction
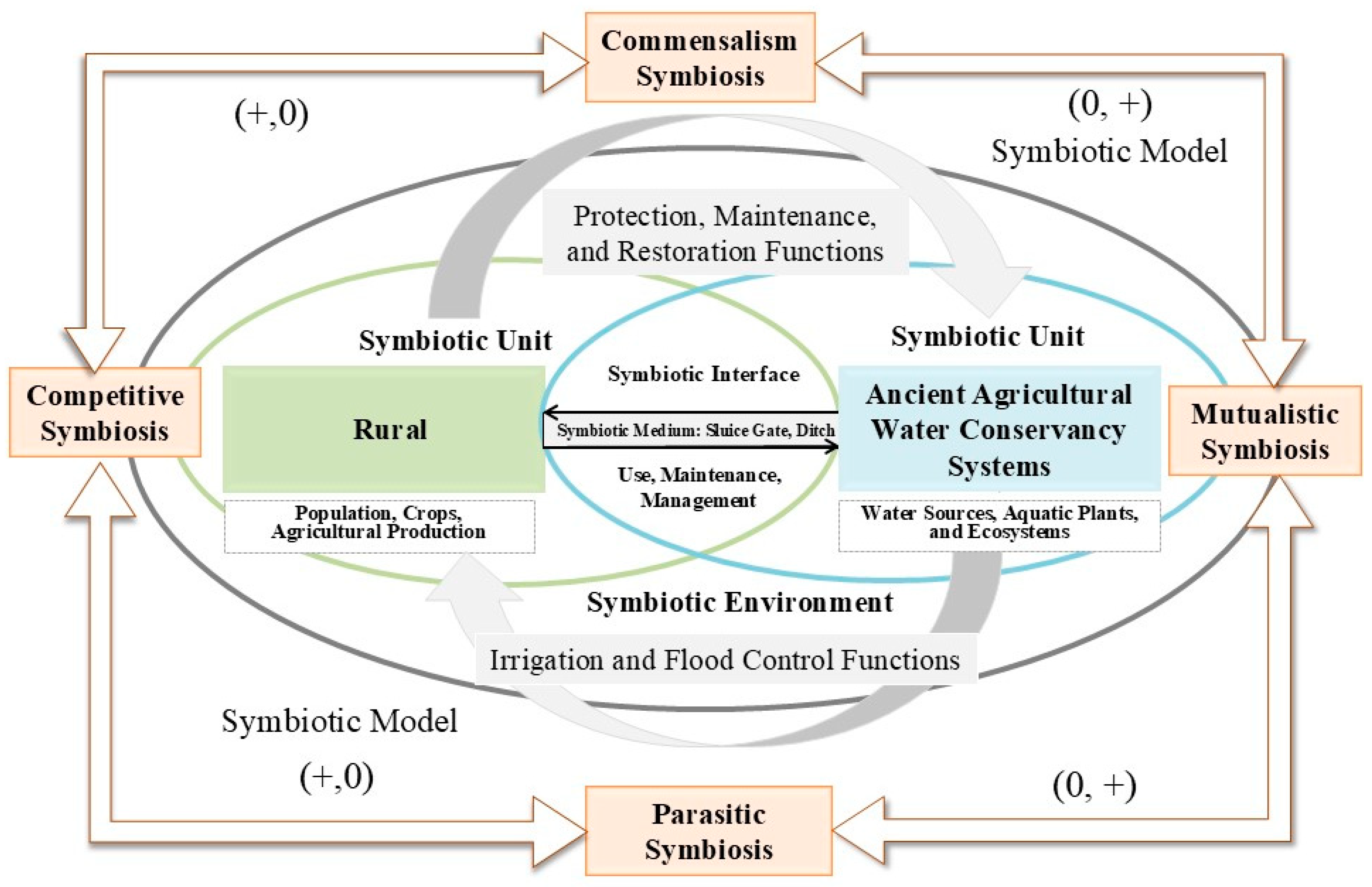
2.3.1. Symbiotic Unit
2.3.2. Symbiotic Model
2.3.3. Symbiotic Environment
2.3.4. Evolutionary Process of Symbiosis Models
2.4. Symbiotic Model Construction
2.4.1. Symbiosis Model Assumptions
2.4.2. Symbiosis Modelling Based on Lotka-Volterra
2.4.3. Model Equilibrium and Stability Analysis
3. Results
3.1. Numerical Settings for the Simulated Symbiosis Modell
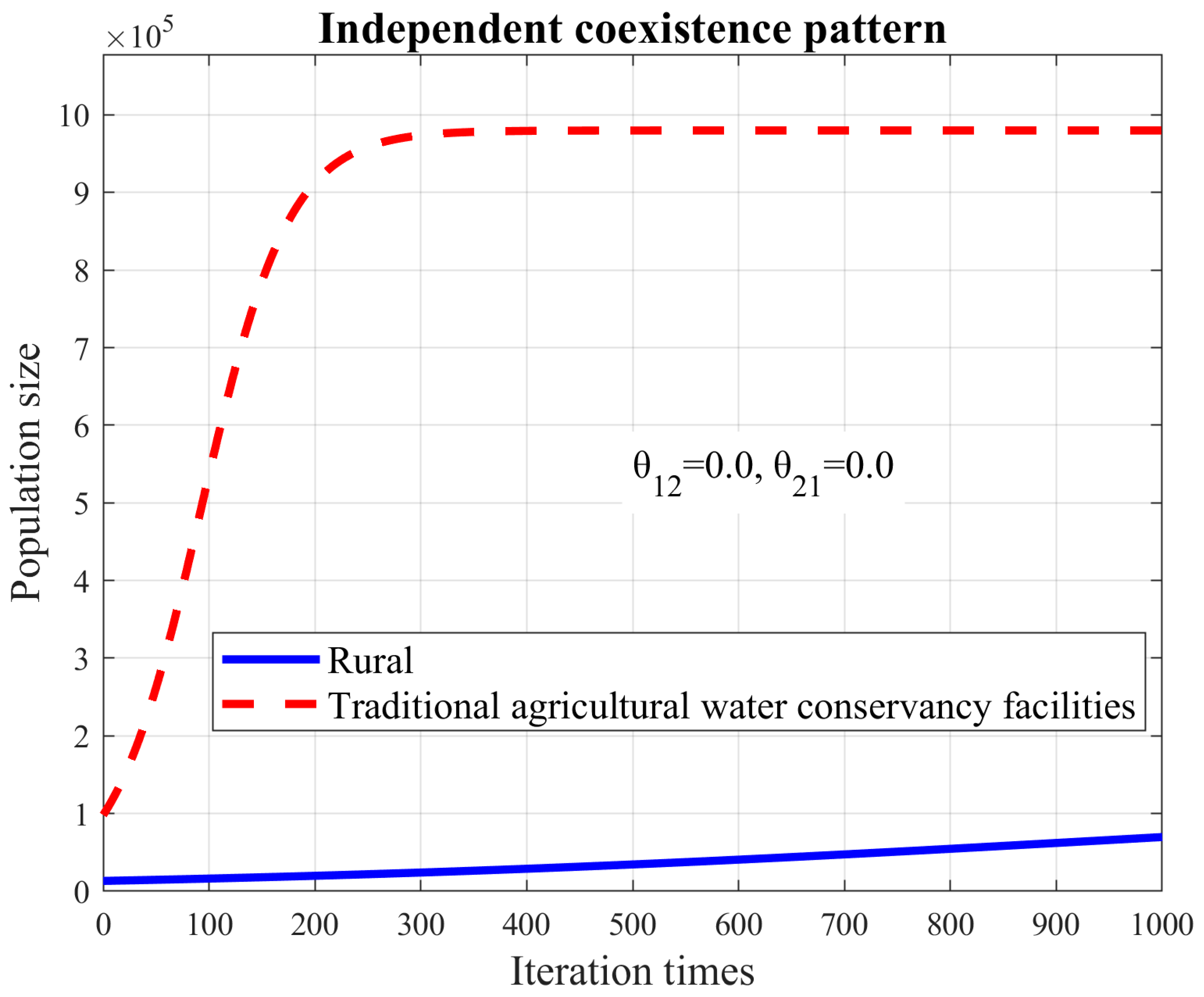
3.2. Analysis of the Independent Coexistence Pattern
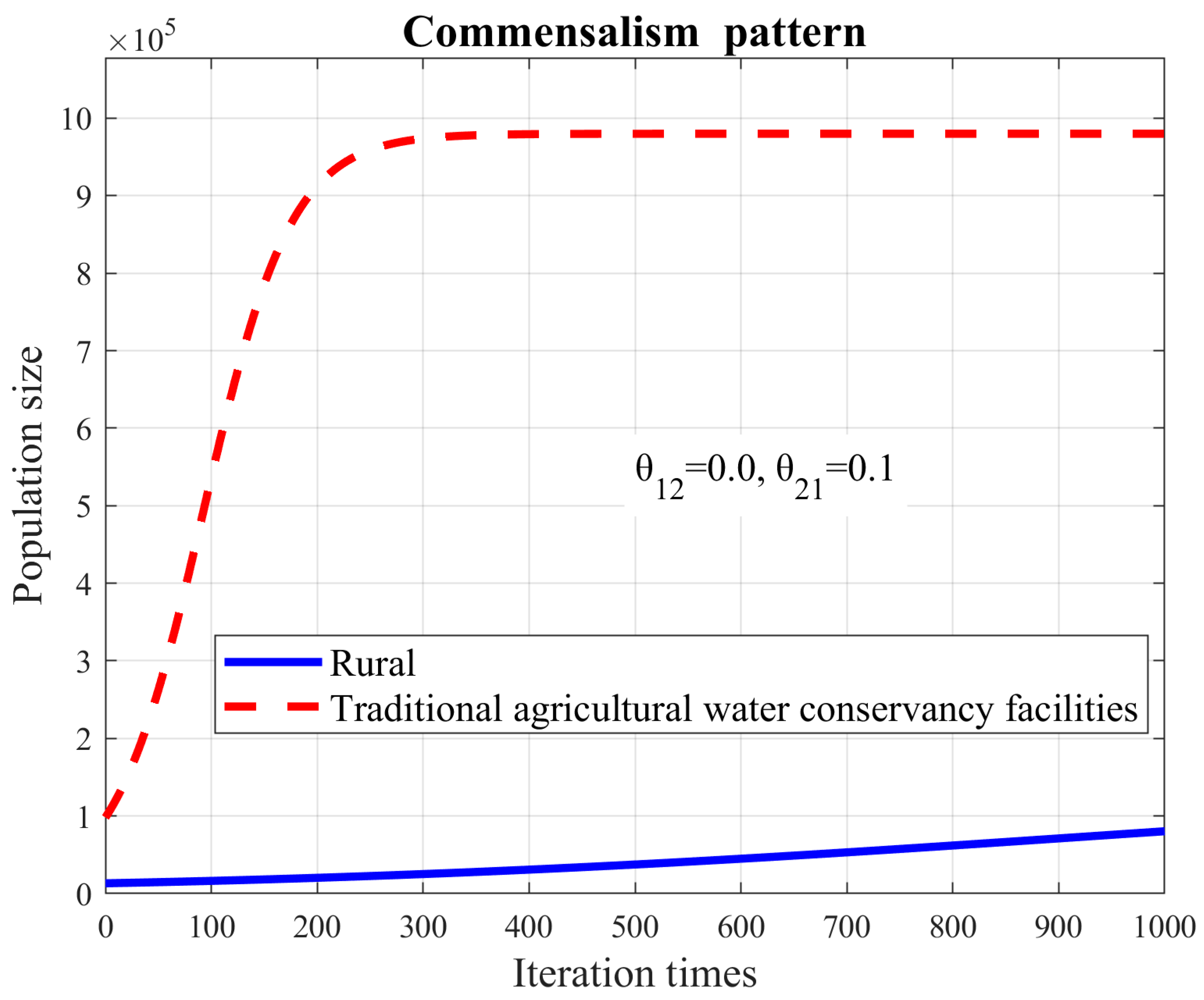
3.3. Analysis of the Commensalism Pattern
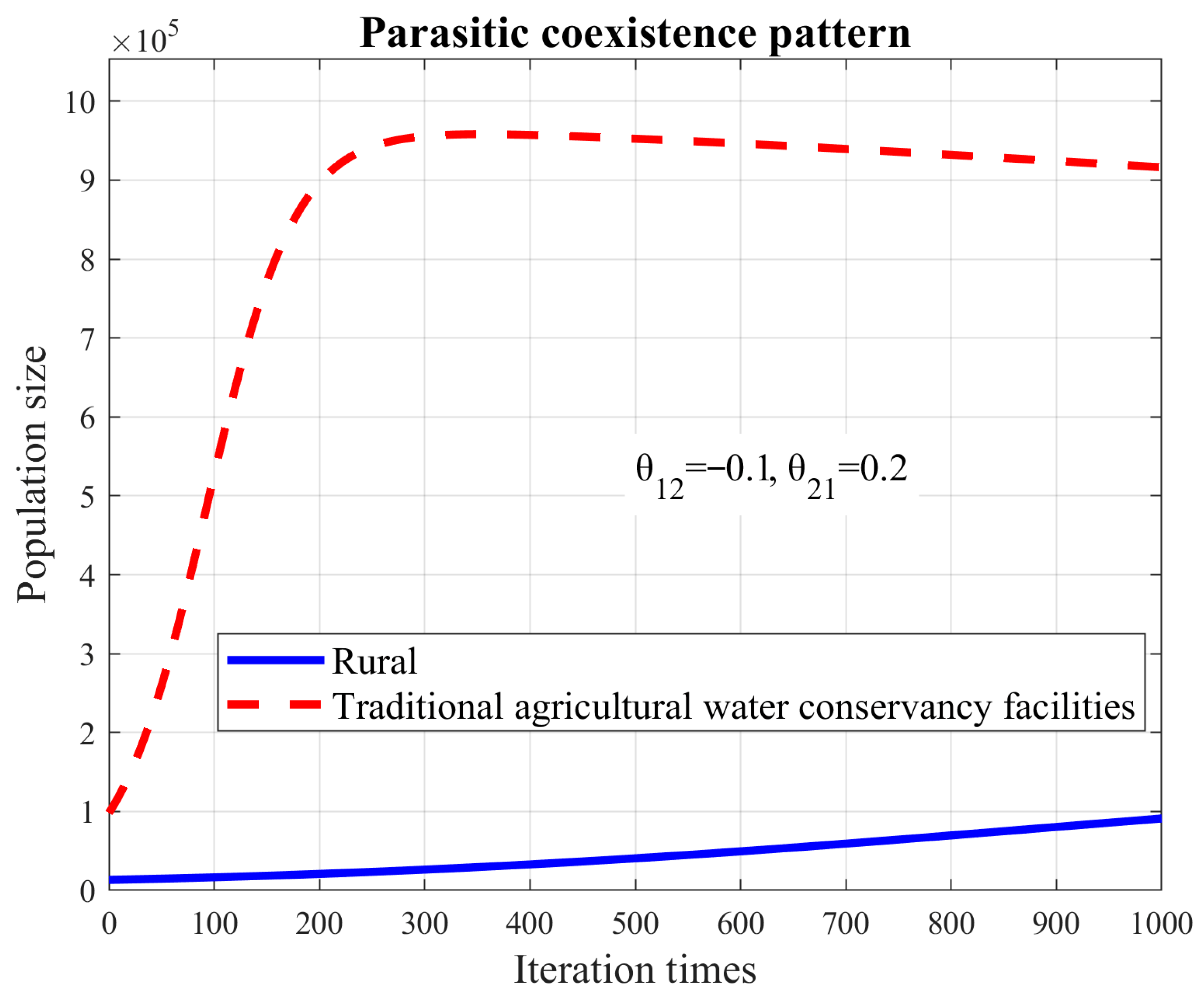
3.4. Analysis of the Parasitic Coexistence Pattern
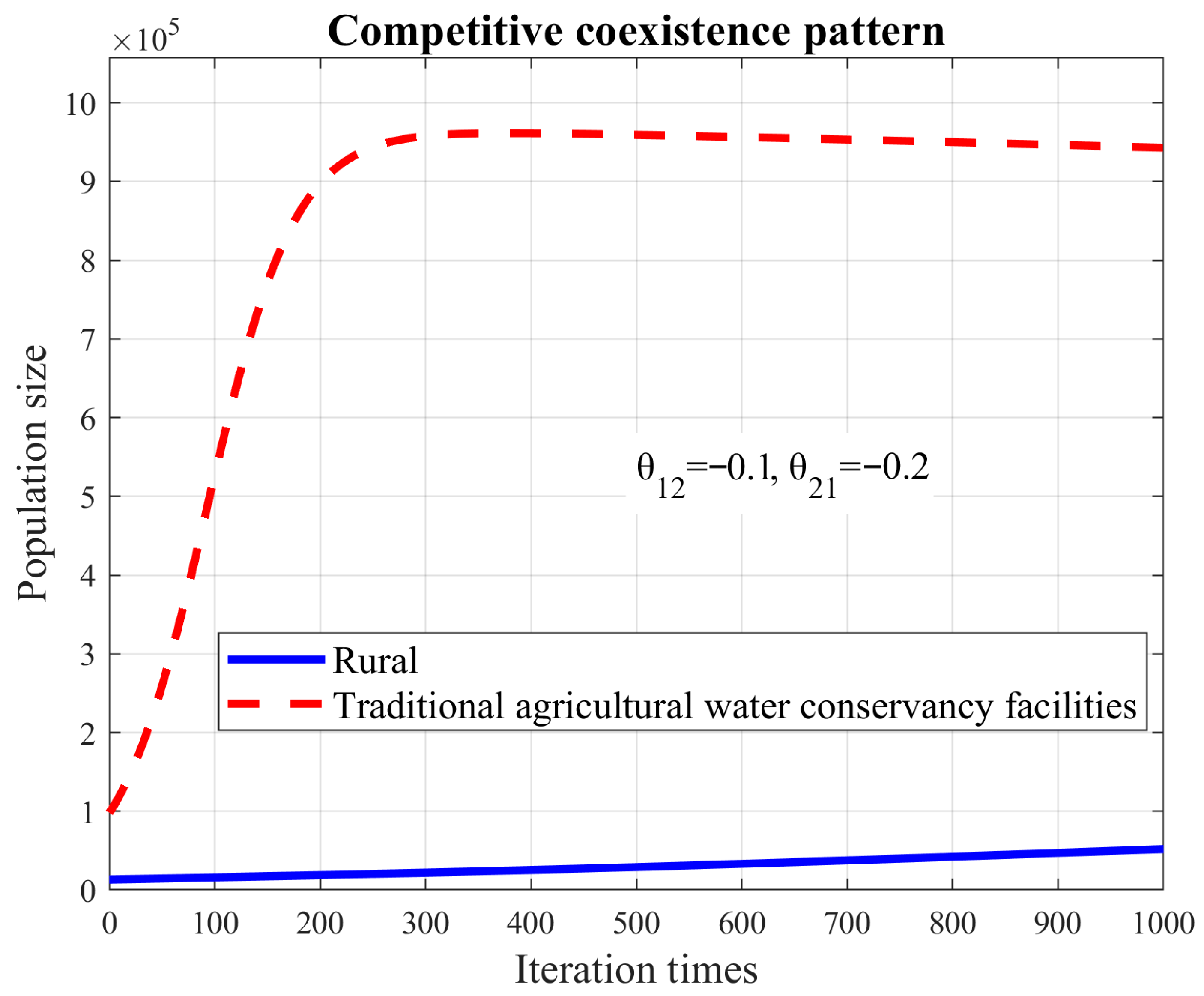
3.5. Analysis of the Competitive Coexistence Pattern
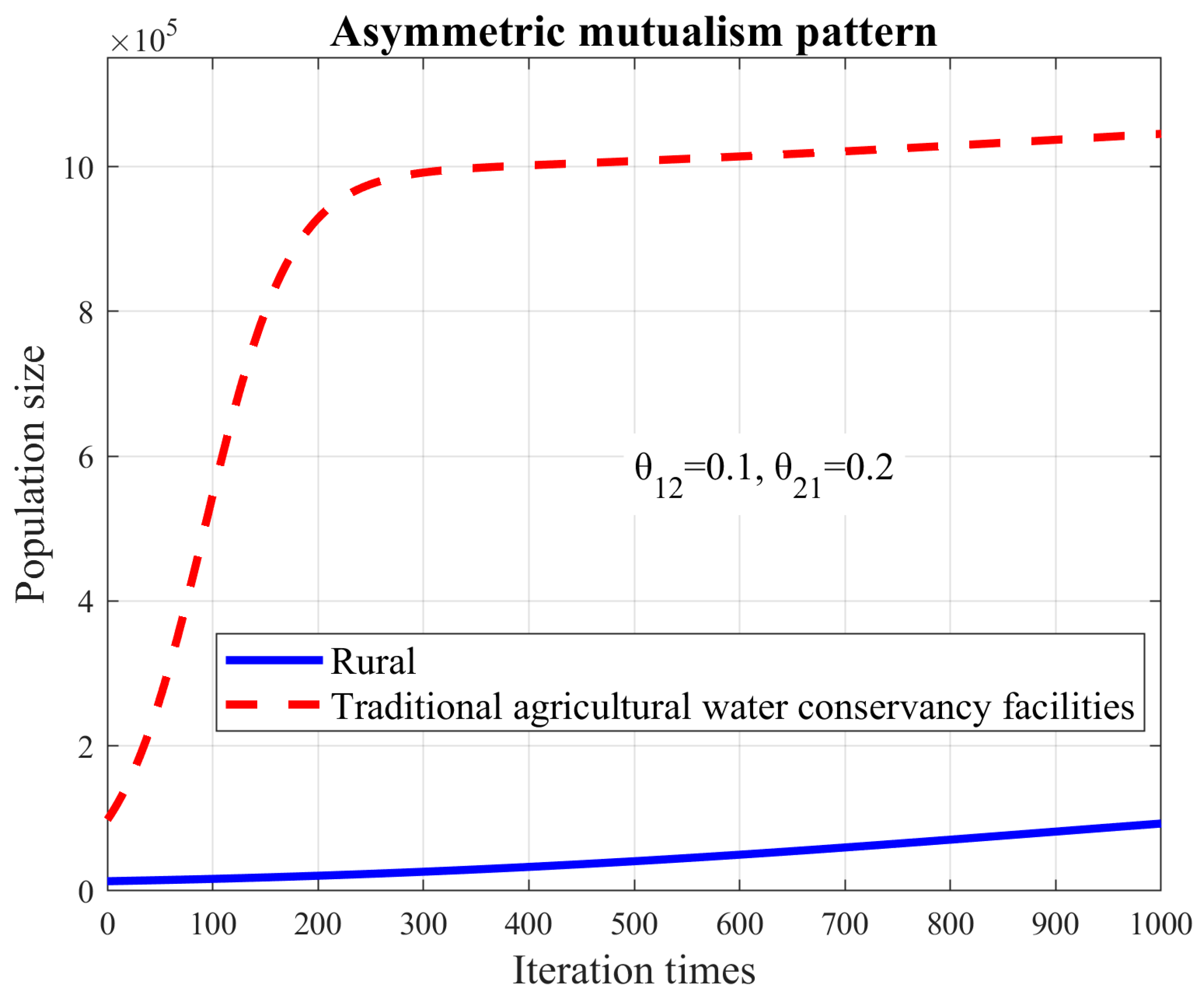
3.6. Analysis of the Asymmetric Mutualism Pattern
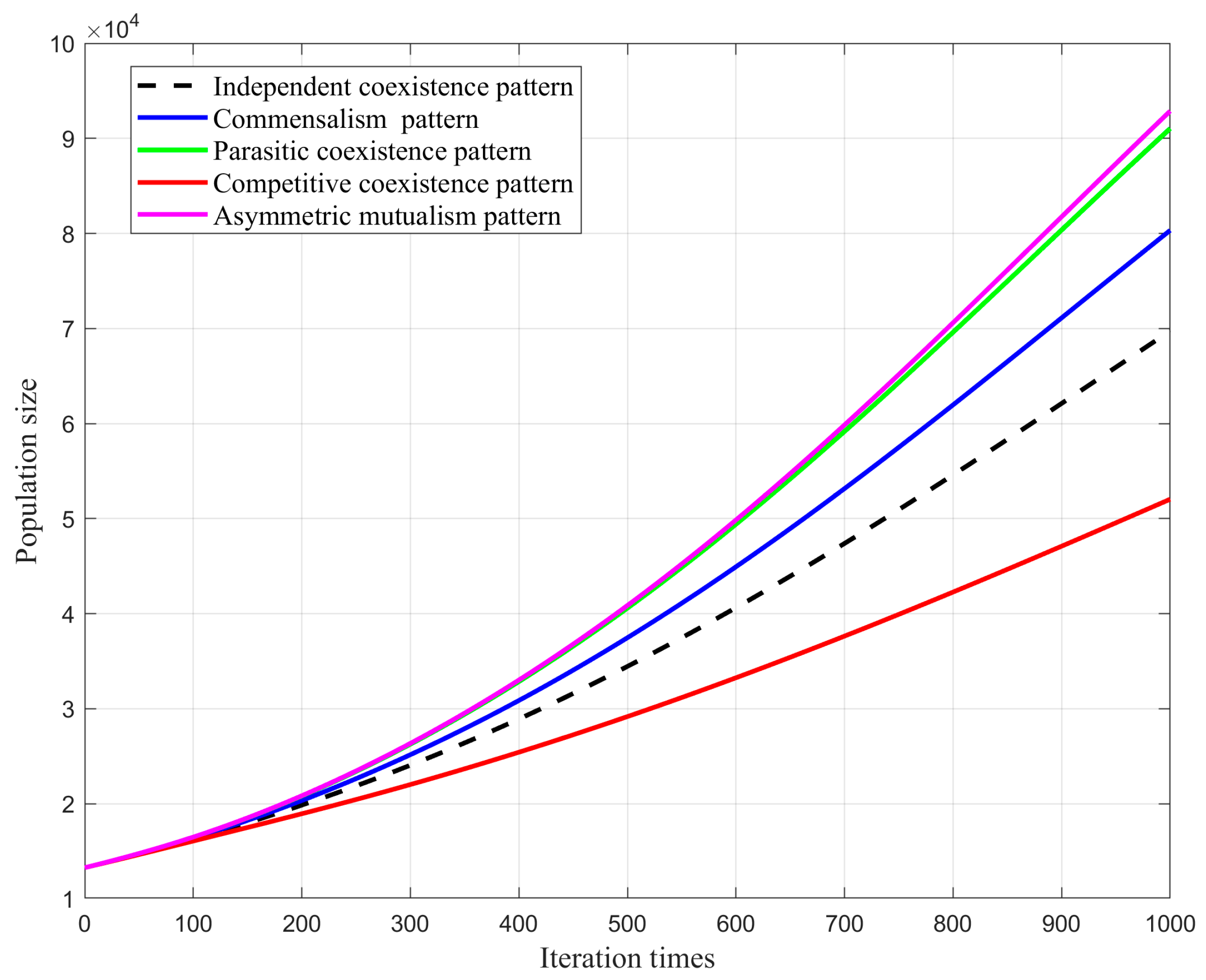
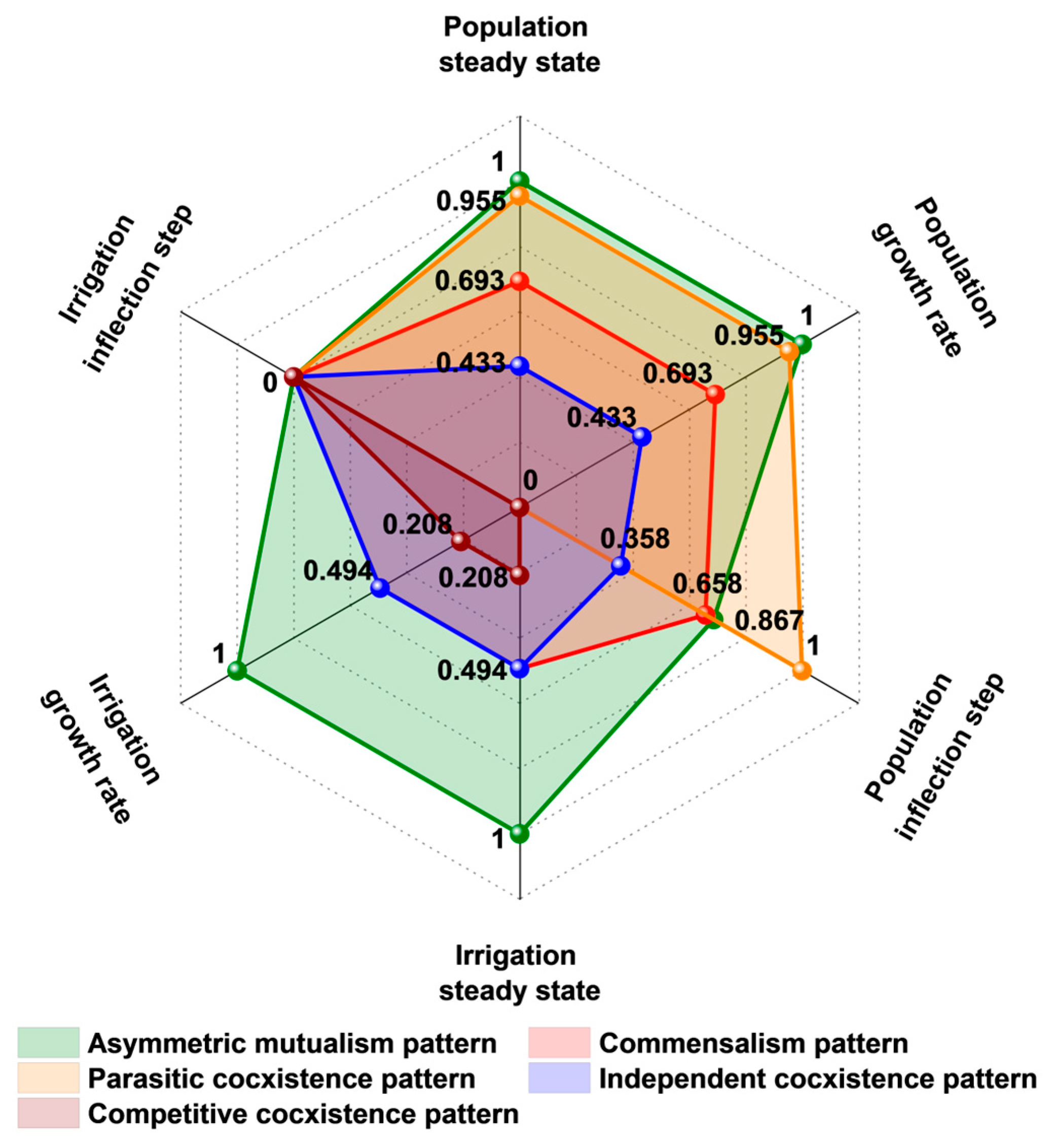
3.7. Results Comparison of Five Symbiotic Patterns
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skaf, L.; Buonocore, E.; Dumontet, S.; Capone, R.; Franzese, P.P. Food security and sustainable agriculture in Lebanon: An environmental accounting framework. J. Clean. Prod. 2019, 209, 1025–1032. [Google Scholar] [CrossRef]
- Wijerathna-Yapa, A.; Pathirana, R. Sustainable Agro-Food Systems for Addressing Climate Change and Food Security. Agriculture 2022, 12, 1554. [Google Scholar] [CrossRef]
- Yang, S.; Wang, L.; Bi, Y. A Study on the Price Spatial Differentiation and Influencing Factors of Rural Homestay in Suzhou Based on the Hedonic Price Model. Buildings 2025, 15, 1610. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate Extremes and Compound Hazards in a Warming World. Annu. Rev. Earth Planet. Sci. 2020, 48, 519–548. [Google Scholar] [CrossRef]
- Wakil, W.; Kavallieratos, N.G.; Eleftheriadou, N.; Ghazanfar, M.U.; El-Shafie, H.A.F.; Blankson, A.; Gurr, G.M.; Dáttilo, W.; González-Tokman, D.; Hernández, A.; et al. Climate change consequences for insect pest management, sustainable agriculture and food security. Entomol. Gen. 2025, 45, 37–51. [Google Scholar] [CrossRef]
- Wang, L.; Bi, Y.; Hu, Y.; Yang, S. Interpretation of Sustainable Spatial Patterns in Chinese Villages Based on AHP-GIS-FCE: A Case Study of Chawan Village, East Mountain Island, Taihu Lake, Suzhou. Buildings 2025, 15, 3198. [Google Scholar] [CrossRef]
- Adeniran, A.; Daniell, K.A.; Pittock, J. Water Infrastructure Development in Nigeria: Trend, Size, and Purpose. Water 2021, 13, 2416. [Google Scholar] [CrossRef]
- Barghouth, J.M.; Al-Sa, R.M.Y. Sustainability of Ancient Water Supply Facilities in Jerusalem. Sustainability 2009, 1, 1106–1119. [Google Scholar] [CrossRef]
- Rajabi, M. Towards a Regenerative Role of Cultural Heritage in Climate Resilience; the Case of the Indian Water Infrastructure Heritage. Land 2023, 12, 1539. [Google Scholar] [CrossRef]
- Portmann, F.T.; Siebert, S.; Döll, P. MIRCA2000—Global monthly irrigated and rainfed crop areas around the year 2000: A new high-resolution data set for agricultural and hydrological modeling. Glob. Biogeochem. Cycles 2010, 24, GB1011. [Google Scholar] [CrossRef]
- Zhu, X.; Li, Y.; Li, M.; Pan, Y.; Shi, P. Agricultural irrigation in China. J. Soil Water Conserv. 2013, 68, 147A–154A. [Google Scholar] [CrossRef]
- Baki, C.B.; Wellens, J.; Traoré, F.; Palé, S.; Djaby, B.; Bambara, A.; Thao, N.T.T.; Hié, M.; Tychon, B. Assessment of Hydro-Agricultural Infrastructures in Burkina Faso by Using Multiple Correspondence Analysis Approach. Sustainability 2022, 14, 13303. [Google Scholar] [CrossRef]
- Goff, L.J. Symbiosis and parasitism: Another viewpoint. BioScience 1982, 32, 255–256. [Google Scholar] [CrossRef]
- Xue, Q.; Liu, C.; Zhao, M.; Wu, J.; Su, Y. Evolutionary Analysis of Innovation Development in a Metropolitan Area from a Symbiosis Perspective: Empirical Research on the Shanghai Metropolitan Area. Discret. Dyn. Nat. Soc. 2022, 2022, 1631931. [Google Scholar] [CrossRef]
- Podobnik, B.; Romano, A. A Study of Tourism Dynamics in Three Italian Regions Using a Nonautonomous Integrable Lotka–Volterra Model. PLoS ONE 2016, 11, e0162559. [Google Scholar] [CrossRef]
- Xia, M.; He, X.; Zhou, Y.; Jiang, J. Symbiosis Evolution of Science Communication Ecosystem Based on Social Media: A Lotka–Volterra Model-Based Simulation. Complexity 2021, 2021, 6655469. [Google Scholar] [CrossRef]
- Rogy, N.; Roux, P.; Salou, T.; Pradinaud, C.; Sferratore, A.; Géhéniau, N.; Hélias, A.; Loiseau, E. Water supply scenarios of agricultural areas: Environmental performance through Territorial Life Cycle Assessment. J. Clean. Prod. 2022, 366, 132862. [Google Scholar] [CrossRef]
- Carrillo, M.J. Migrant Flows: Hydraulic Infrastructure, Agricultural Industrialization, and Environmental Change in Western Mexico, 1940–64. Environ. Hist. 2021, 26, 231–254. [Google Scholar] [CrossRef]
- Morote, Á.-F.; Olcina, J.; Rico, A.-M. Challenges and Proposals for Socio-Ecological Sustainability of the Tagus–Segura Aqueduct (Spain) under Climate Change. Sustainability 2017, 9, 2058. [Google Scholar] [CrossRef]
- Stensrud, A.B. The social embeddedness of hydraulic engineers in the regulation of water and infrastructure in Peru. Environ. Plan. C Politics Space 2019, 37, 1235–1251. [Google Scholar] [CrossRef]
- Li, S. Quebei Shihua; Anhui Education Publishing House: Hefei, China, 2019. [Google Scholar]
- Zhang, C.; Min, Q.; Lü, J.; Shao, J. (Eds.) Quebei (Anfengtang) and the Agricultural System of Its Irrigation Area in Shou County; Agriculture Press: Beijing, China, 2017. [Google Scholar]
- Lan, Q.; Liu, C.; Ling, S. Research on Measurement of Symbiosis Degree Between National Fitness and the Sports Industry from the Perspective of Collaborative Development. Int. J. Environ. Res. Public Health 2019, 16, 2191. [Google Scholar] [CrossRef]
- Yuan, C. Symbiosis Theory: A Discussion of Small Economies; Economic Science Press: Beijing, China, 1998. [Google Scholar]
- Wu, H.; Gu, C. The cooperation-competition of regional tourism based on the symbiosis theory: A case study on Huaihai economic region. Econ. Geography. 2004, 24, 104–109. [Google Scholar]
- Wu, B.; Negassi, S. Symbiotic Evolution Mechanism of the Digital Innovation Ecosystem for the Smart Car Industry. Sustainability 2023, 15, 14939. [Google Scholar] [CrossRef]
- Liu, A.; Hu, Y. Huainanzi; 21st Century Publishing House: Nanchang, China, 2018. [Google Scholar]
- Li, D.; Yang, S.; Xiong, H. ShuijingzhuShu; Ancient Books Publishing House: Nanjing, China, 1989; Volume 1, p. 1096. [Google Scholar]
- Ban, G.; Ma, Y.; Hu, X. Han Shu; Shanxi Ancient Books Publishing House: Taiyuan, China, 2004; p. 334. [Google Scholar]
- Qian, D. 22 Shi Kao Yi; Phoenix Publishing House: Nanjing, China, 2023; Volume 1, p. 634. [Google Scholar]
- Xu, Z. The Historical Evolution of the Quebei Project and Its Relationship with Social and Economic Development. Agric. Hist. China 1984, 4, 43–63. [Google Scholar]
- Gao, Y. The Origins and Evolution of the Quebei Reservoir. Water Culture 2023, 12, 47–51. [Google Scholar]
- Hu, C. An Investigation of the Northern Song Dynastys Repairs and Maintenance of Quebei. J. Xuzhou Inst. Technol. Soc. Sci. Ed. 2014, 29, 74–77+92. [Google Scholar]
- Li, S.; Tao, L. The Collected Annotations and Historical Materials of the Records of the Quebei; University of Science and Technology of China Press: Hefei, China, 2016; p. 576. [Google Scholar]
- Anhui Provincial Water Resources Commission. Annals of Anfengtang; Huangshan Publishing House: Hefei, China, 1995. [Google Scholar]
- Chinese Water Resources History Editorial Board. Chronicle of Chinese Water Resources: Huaihe Volume 1; China Water & Power Press: Beijing, China, 2015; p. 928. [Google Scholar]
- Zhu, L.; Wang, H.; Zheng, D. Strategic Thoughts on the Protection and Development of the Quebei Water Conservancy Project. J. Econ. Water Resour. 2019, 37, 73–78+82. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, M.-X.; Lai, P.-Y. General two-species interacting Lotka-Volterra system: Population dynamics and wave propagation. Phys. Rev. E 2018, 97, 052413. [Google Scholar] [CrossRef] [PubMed]
- Voroshilova, A.; Wafubwa, J. Discrete Competitive Lotka–Volterra Model with Controllable Phase Volume. Systems 2020, 8, 17. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, W.; Zhang, C.; Li, H.; Wu, Y. Stakeholder Symbiosis in the Context of Corporate Social Responsibility. Symmetry 2020, 12, 1897. [Google Scholar] [CrossRef]
- Ren, X.; Wang, J. Symbiotic evolution mechanism of urban air mobility industrial innovation ecosystem: Evidence from low altitude air mobility in Shenzhen. J. Air Transp. Manag. 2025, 124, 102750. [Google Scholar] [CrossRef]


| Period | Phenomenon | Symbiotic Model | References |
|---|---|---|---|
| Spring and Autumn—Western Han | The creation of Anfengtang facilitated the irrigation of tens of thousands of hectares of fertile land, significantly promoting the development of rural agriculture. | Commensalism pattern | The Book of Han: biographies of model officials records [29] |
| Northern Wei—Yuan dynasty | Water source blockage, drying of the reservoir surface, and farmers occupying the embankments for farmland, intensifying land resource conflicts. | Parasitic coexistence pattern | Jin Xie, Inscription of the reconstruction of quebei by wei gong in the ming dynasty |
| Mid-Ming Dynasty | The government set boundaries and constructed ditches to prevent farmers from occupying the embankments, with weak irrigation benefits from Anfengtang. | ||
| Republic of China period | Anfengtang lost its irrigation function, leading to disasters in rural areas and damage to both parties. | Competitive coexistence pattern | The chronicle of Chinese water resources [36] |
| 1953 | The government undertook channel restoration and repairs, gradually restoring the irrigation and ecological functions. | Asymmetric mutualism pattern | Shou County Water Resources Bureau |
| 1976 | Anfengtang underwent slope protection works; although the surface area was 34 square kilometers, the irrigated area increased to 630,000 mu. | ||
| 2022 | The irrigation area of Anfengtang was approximately 980,000 mu |
| Equilibrium | Tr (J) | Det (J) | Stability Condition |
|---|---|---|---|
| F1 (0, 0) | r1 + r2 | r1r2 | unstable |
| F2 (0, V2) | stable | ||
| F3 (0, V1) | stable | ||
| Symbiotic Pattern | Rural Population Steady State (Persons) | Rural Population Growth (%) | Rural Population Inflection Step | Irrigation Area Steady State (mu) | Irrigation Area Growth (%) | Irrigation Area Inflection Step |
|---|---|---|---|---|---|---|
| independent | 69,741 | 425.4 | 957 | 980,000 | 900.0 | 93 |
| commensalism | 80,329 | 505.1 | 921 | 980,000 | 900.0 | 93 |
| parasitic | 91,034 | 585.8 | 880 | 916,278 | 835.0 | 93 |
| competitive | 52,041 | 292.0 | 1000 | 943,157 | 862.4 | 93 |
| mutualism | 92,874 | 599.6 | 896 | 1,045,359 | 966.7 | 93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Bi, Y.; Yang, S. Symbiotic Evolution of Rural Settlements and Traditional Agricultural Water Conservancy Facilities Based on the Lotka-Volterra Model. Land 2025, 14, 2242. https://doi.org/10.3390/land14112242
Wang L, Bi Y, Yang S. Symbiotic Evolution of Rural Settlements and Traditional Agricultural Water Conservancy Facilities Based on the Lotka-Volterra Model. Land. 2025; 14(11):2242. https://doi.org/10.3390/land14112242
Chicago/Turabian StyleWang, Lei, Yu Bi, and Sheng Yang. 2025. "Symbiotic Evolution of Rural Settlements and Traditional Agricultural Water Conservancy Facilities Based on the Lotka-Volterra Model" Land 14, no. 11: 2242. https://doi.org/10.3390/land14112242
APA StyleWang, L., Bi, Y., & Yang, S. (2025). Symbiotic Evolution of Rural Settlements and Traditional Agricultural Water Conservancy Facilities Based on the Lotka-Volterra Model. Land, 14(11), 2242. https://doi.org/10.3390/land14112242






