Nonlinear Effects of Land Resource Misallocation and Carbon Emission Efficiency Across Various Industrial Structure Regimes: Evidence from PSTR Model

Abstract

Carbon emission efficiency plays a vital role in the realization of the “dual carbon” goals. Taking land resource allocation as the entry point, this paper explores how land resource misallocation (LRM) affects carbon emission efficiency (CEE) to support the enhancement of CEE and the optimal allocation of land resources. Using 108 cities in the Yangtze River Economic Belt from 2003 to 2021 as an example, this paper constructs a panel smooth transition model (PSTR), with industrial structure as the transition variable, to examine the nonlinear impact effects of LRM on CEF and its regional heterogeneity. The research results show that the LRM index as a whole presents a fluctuating downward trend, while CEF shows a fluctuating but slow upward trend, and the regional differences in both LRM and CEF continue to expand. There exists a significant nonlinear relationship between LRM and CEF. When the advancement of industrial structure index shifts from the low regime to the high regime, the impact of LRM on CEF presents an inverted “U”-shaped curve characteristic. The nonlinear impact of LRM on CEF exhibits regional heterogeneity, and the threshold effect of industrial structure is the main reason for the regional differences in the nonlinear impact. Therefore, it is necessary to accelerate the market-oriented reform of land factor allocation, and to formulate phased and differentiated land resource allocation policies adapted to the stages of industrial structure development, so as to effectively serve the goals of green, low-carbon, and high-quality development.

1. Introduction

To actively respond to the challenge of global climate change, the Chinese government has made a political commitment to the international community that “China will strive to peak carbon dioxide emissions before 2030 and achieve carbon neutrality by 2060” (the “dual carbon” goals), elevating the low-carbon development objective to an unprecedented strategic height. At present, in international studies on low-carbon development, carbon-related issues involving land use change are a key focus in addressing climate change [1]. It is estimated that emissions related to land use change account for about one-fifth of total global anthropogenic greenhouse gas emissions [2,3]. As a fundamental factor of production underpinning the development of the national economy, the allocation of land resources profoundly influences the process of low-carbon economic and social transformation. China has long relied on a “land-based development” growth model, in which the government monopolized the supply of land factors and promoted extensive development to drive industrialization and urbanization. Although this institutional arrangement released growth momentum at specific historical stages [4], it also resulted in a severe misallocation of regional land resources, leading to persistent high energy consumption intensity and excessive spatial occupation of carbon emissions [5,6,7]. Carbon emission efficiency (CEF), a core indicator for assessing the development of a green economy, accurately reflects the relationship between regional economic growth and CO₂ emissions. Enhancing CEF plays a vital role in advancing the realization of the “dual carbon” goals. Against this background, revealing the impact of LRM on CEF holds significant practical implications for optimizing land resource distribution and improving CEF.

At present, a large number of studies in the academic community have been carried out around LRM, mainly focusing on analyzing the degree, causes, and economic and social impacts of LRM. Scholars attribute LRM to fiscal decentralization and government intervention [8], which is mainly manifested in the behavior of local governments relying on their monopoly power over the land market: supplying industrial land extensively at low prices to attract investment, while restricting the supply of commercial and residential land to maintain high prices and increase fiscal revenue. The economic impacts of LRM are mainly reflected in the following paths: inducing diminishing marginal returns of labor and capital factors, undermining the fair institutional environment of cities, strengthening credit financing constraints on enterprises, and locking in low- and middle-end industrial structures, which in turn hinder high-quality economic development [9], delay industrial transformation and upgrading [10,11], and crowd out innovation space [12]. The social impacts of LRM are mainly reflected in the following aspects: the unfair distribution of differential land benefit between urban and rural areas exacerbates income inequality [13], and the insufficient supply of land for affordable housing raises housing costs [14]. As China enters the stage of green transformation and development, scholars have gradually paid attention to the relationship between LRM and the ecological environment. This is mainly reflected in the fact that LRM on the one hand, promotes local governments to attract energy-intensive and highly polluting enterprises, and on the other hand, may lead to insufficient supply of public green space, which in turn affects regional green development and its efficiency [15,16], reduces green total factor productivity [17], aggravates environmental pollution [18,19], and increases regional carbon emissions [20]. However, at the present stage, studies involving LRM and CEF mostly start indirectly from perspectives such as land transfer modes, land supply scale, and land prices, to reveal the impact of land resource allocation on CEF [21,22]. Although the existing traditional linear analysis methods can, to some extent, reveal the overall direction of the impact of LRM on CEF, they often fail to capture its dynamic process and potential stage characteristics. Moreover, the impact of LRM on CEF is closely related to industrial structure [23], while previous studies have almost ignored the influence of industrial structure on the relationship between LRM and CEF. In general, existing studies provide numerous experiences and insights for this paper, but there is still room for further research. First, the nonlinear characteristics of the impact of LRM on CEF have received little attention. However, LRM at different stages may have different effects on CEF, and empirical tests in this regard are relatively limited. In particular, industrial structure, as a mechanism variable through which LRM affects CEF, lacks in-depth discussion regarding this impact path and its internal mechanism. Second, in terms of research methods, existing studies mostly adopt linear regression models or panel fixed effect models to examine the single positive or negative linear relationship between LRM and CEF. Using industrial structure as the transition variable to deeply analyze the dynamic impact path of LRM on CEF is a research direction that this paper seeks to supplement and deepen.

As the vanguard in leading China’s high-quality economic development and the innovation-driven belt guiding transformational development, the Yangtze River Economic Belt gathers more than 40% of the nation’s chemical industry and over 70% of the textile dyeing industry. The traditional development of “three-high” industries has kept carbon emissions in this region at a high level, and the corresponding CEF is far from optimistic. However, current research on land resource allocation and carbon emissions mostly concentrates on inter-provincial or urban agglomeration levels, with relatively little consideration given to regional analysis on a macro scale. Therefore, it is highly necessary to carry out research on the nonlinear effects of LRM on CEF in the Yangtze River Economic Belt, using industrial structure as the transition variable.

In view of this, taking 108 cities in the Yangtze River Economic Belt during 2003–2021 as the research sample, this paper, on the basis of analyzing the spatio-temporal evolution of LRM and CEF, constructs a panel smooth transition model (PSTR) to explore the deeper linkage among LRM, industrial structure, and CEF. The main contributions are as follows: First, in terms of research perspective, this paper provides a nonlinear analytical framework for understanding the carbon emission effects of LRM. Existing studies on LRM and CEF are mostly based on linear assumptions, whereas this paper attempts to construct a theoretical framework with industrial structure as the transition mechanism from a nonlinear perspective, offering new empirical evidence and analytical insight into the more complex dynamic relationship between the two. Second, in terms of research methodology, this paper constructs a Panel Smooth Transition Regression (PSTR) model to test the nonlinear relationship between LRM and CEF. This model allows parameters to undergo smooth nonlinear transitions with the transition variable, thus overcoming the limitation of traditional linear models in accurately capturing cross-sectional heterogeneity. Third, in terms of research scope, this study focuses on the Yangtze River Economic Belt as a typical region and further deepens the analysis of its internal heterogeneity. The research conclusions are therefore more comprehensive, robust, and reliable, providing theoretical and policy support for promoting the region’s green, low-carbon, and coordinated development.

2. Theoretical Analysis and Research Hypotheses

The issue of land resource allocation can be analyzed and discussed from several aspects, including the allocation between agricultural land and construction land, the allocation of construction land quotas among different cities, and the allocation of construction land across different industries and uses within cities [24]. Considering data availability, as well as the fact that many local governments adopt a land supply strategy of low-priced transfers for industrial land and high-priced transfers for commercial and residential land, which has led to the sprawl and expansion of industrial land, the abandonment and inefficient utilization of industrial parks [8], and the structural distortion between industrial and commercial–residential land use, these circumstances profoundly impact urban economic development patterns and the quality of resources and the environment. Therefore, this paper focuses on the LRM across different industries and uses within construction land, mainly examining the distortions in the supply of urban industrial land and commercial–residential land, and analyzing the nonlinear impact mechanism of LRM on CEF.

Under the current performance evaluation system, local governments’ preference for industrial land leads to LRM, which affects CEF. However, the relationship between the two is not simply linear, but rather characterized by complexity and dynamics. Specifically, in the early or accelerated stages of industrialization and urbanization, the goal of economic development is to achieve rapid capital accumulation and industrial expansion. At this stage, LRM characterized by the “low-priced transfers for industrial land” often manifests as a tilt of land factors toward industrial sectors or key development zones. This is not a pure efficiency loss—low-cost land factors strongly attract external capital and industrial enterprises to settle in. Although this process is accompanied by an increase in total energy consumption and carbon emissions, it effectively clears inefficient and idle land and promotes the rapid agglomeration of industries and populations. Such agglomeration effects can generate significant technological spillovers and shared infrastructure, thereby improving the overall regional energy utilization efficiency and CEF in the short term. Therefore, during this stage, LRM objectively brings about a phased improvement in CEF, forming a passive emission reduction mechanism under the specific constraints of the development stage. However, as the degree of LRM continues to intensify, its negative effects gradually accumulate and become dominant, mainly reflected in the long-term institutionalized LRM (such as excessive inclination toward energy-intensive and high-emission heavy industries), which locks in the regional economic and energy structure [15]. It not only crowds out valuable factor resources that should have flowed to green technologies and innovative enterprises but also gives rise to an irreversible path dependence of high-carbon industrial clusters, which undoubtedly reduces CEF.

The impact of LRM on CEF is closely related to industrial structure [15]. As one of the key pathways through which LRM affects CEF, the effectiveness of industrial structure in this regard has a dual nature. Specifically, in the initial and accelerating stages of advancement of industrial structure, LRM by local governments through the low-priced transfer of industrial land, to a certain extent, reallocates land factors from idle or low carbon productivity agricultural sectors to higher carbon productivity industrial sectors. Even though the industrial sector itself has significant carbon-intensive characteristics, as long as its marginal carbon productivity exceeds the original use, this factor reallocation process will lead to a short-term improvement in CEF, which in essence can be regarded as a Kaldor–Hicks improvement based on factor allocation optimization. With the advancement of industrial structure toward the middle and advanced stages, the demand structure for land factors undergoes a fundamental transformation. However, the government-led pattern of LRM formed in the early stages not only fails to adapt to the new factor demand structure but also locks the region into the existing high-carbon development model through path dependence. This structural contradiction is reflected in two aspects: on the one hand, the low-cost industrial land policy prolongs the survival of low- and medium-end manufacturing industries that should have been eliminated [25], forming a rigid low-end path dependence in the industrial structure and hindering its natural evolution; on the other hand, the distortion of land resource allocation crowds out residential and commercial land, while innovative enterprises and modern service industries face constraints such as “high land costs and difficult access” [26], which suppresses green technological innovation and diffusion, thereby impeding the reduction in regional carbon emission intensity and the improvement of CEF. Based on this, this paper proposes the following hypothesis:

Hypothesis 1: 

There exists a nonlinear relationship between LRM and CEF.

Hypothesis 2: 

Advancement of industrial structure will dynamically affect the effectiveness of LRM on CEF.

3. Materials and Methods

3.1. Study Area

The Yangtze River Economic Belt (21°8′–35°20′ N, 92°21′–123°10′ E) spans China’s eastern, central, and western regions, encompassing 11 provincial-level regions such as Shanghai, Zhejiang, Jiangsu, Jiangxi, Hubei, Hunan, Anhui, Chongqing, Sichuan, Gui-zhou, and Yunnan. It covers an area of approximately 2.0523 million km², representing 21.4% of China’s total land area. Geographically, the middle and lower reaches of the Yangtze River, including Hunan, Jiangxi, Anhui, Jiangsu, and Zhejiang, experience a typical subtropical monsoon climate. In the upper reaches, southern Yunnan and a few high-altitude cities in western Sichuan experience a transition zone between a tropical monsoon climate and a plateau climate. This diverse climate fosters a rich variety of biomes and ecosystems, including evergreen broad-leaved forests, mixed coniferous and broad-leaved forests, bamboo forests, wetlands, lakes, and alpine ecosystems. Dongting Lake, Poyang Lake, Taihu Lake and the Three Gorges Reservoir in the region are important barriers to the ecological security of the Yangtze River Basin. They are home to rare aquatic species such as the Baiji dolphin, the Yangtze River porpoise, and the Chinese sturgeon, and have global biodiversity conservation value.

The Yangtze River Economic Belt, a key region of strategic importance in China, accounts for more than 40% of both the national population and GDP. In 2023, the average urbanization rate was 66%, and the average per capita disposable income of all residents was 42,467 yuan, both significantly higher than the national average. Educational resources are concentrated in the region, with a high density of higher education and scientific research institutions. Represented by cities such as Shanghai, Nanjing, Wuhan, Chengdu, and Hangzhou, it has formed a highland for scientific and techno-logical innovation and talent gathering. Social structure exhibits multi-layered characteristics with distinct regional variations: the Yangtze River Delta urban agglomeration in the eastern coastal region boasts a high proportion of middle- and high-income groups, and its industrial structure is dominated by knowledge- and capital-intensive industries. Regions in the midstream region, such as the Wuhan Metropolitan Area and the Changsha-Zhuzhou-Xiangtan Urban Agglomeration, have a strong manufacturing base. In recent years, driven by policy guidance and industrial transfer, regions such as Chongqing, Guizhou, and Yunnan in the west have experienced rapid eco-nomic growth, and the urban-rural income gap has gradually narrowed. Overall, the Yangtze River Economic Belt exhibits a gradient of development, with higher incomes in the east and lower incomes in the west, while regional synergy is gradually increasing.

To ensure the scientific rigor and data consistency of this study, cities with substantial data gaps during the study period were removed, and a total of 108 cities within the Yangtze River Economic Belt were retained for analysis. The spatial distribution of the study area is presented in Figure 1.

3.2. Methods

3.2.1. Panel Smooth Threshold Regression (PSTR) Model Construction

The PSTR model replaces the discrete transition function in the Panel Threshold Regression (PTR) model with a continuous transition function, so that the model coefficients can change continuously with the transition variable, more realistically and dynamically reflecting the relationship between LRM and CEF under industrial structure transformation. In addition, the PSTR model, while accurately capturing the nonlinear dynamic relationship among variables, can also maintain the robustness and interpretability of the model. According to existing research [27,28,29], the PSTR model of the impact of land resource misallocation on carbon emission efficiency under industrial structure transformation is set as follows:

$${CEF}_{it}={\beta }_1{LRM}_{it}+{\beta }_2{LRM}_{it}h({AIS}_{it};\gamma ,c)+\delta {controls}_{it}+{\mu }_i+{\epsilon }_{it}$$

(1)

where ${CEF}_{it}$ is the CEF of city i in year t; ${LRM}_{it}$ is the LRM index of city i in year t; ${controls}_{it}$ are a series of control variables of city i in year t; ${\epsilon }_{it}$ is the random error term; ${\mu }_i$ is the cross-sectional unit fixed effect value; ${\beta }_1$ and ${\beta }_2$ are the regression coefficients of the linear and nonlinear parts of the transition variable, respectively; $\delta$ is the regression coefficient of the control variables; the transition function $h({AIS}_{it};\gamma ,c)$ is a continuous function of the transition variable ${AIS}_{it}$ (industrial structure upgrading), $\gamma$ is the slope of the transition function, reflecting the transition speed of the function, and $c$ is the location parameter, representing the position where the transition function occurs. The general expression form of the transition function in the PSTR model is as follows:

$$\begin{array}{c}h({AIS}_{it};\gamma ,c)={[1+\mathit{exp}(-\gamma \prod _{j=1}^m{AIS}_{it}-c_j)]}^{-1}\\ (\gamma >0,c_1⩽\cdots ⩽c_m)\end{array}$$

(2)

where m is the total number of location parameters. When ${AIS}_{it}\to -\infty$, the transition function h = 0, and the model is in the low regime; when ${AIS}_{it}\to +\infty$, the transition function h = 1, and the model is in the high regime; when 0 < h < 1, the PSTR model smoothly transitions between the above two regimes. When $\gamma$ = 0, h = 0.5, and the PSTR model degenerates into an ordinary panel model.

The coefficient of the impact of LRM on CEF estimated by the PSTR model can be expressed as follows:

$$h_{it}^{LRM}={\displaystyle \frac{\partial {CEF}_{it}}{\partial {LRM}_{it}}}={\beta }_1+{\beta }_{2}h({AIS}_{it};\gamma ,c)$$

(3)

where the impact coefficient of LRM on CEF is jointly composed of the linear part ${\beta }_1$ and the nonlinear part ${\beta }_2$, and this value changes with different time points and cross-sectional units.

3.2.2. PSTR Model Estimation and Tests

Before conducting parameter estimation using the PSTR model, it is necessary to test whether there exists a nonlinear effect between LRM and CEF, that is, to verify the applicability of the PSTR model in this study. To test whether the null hypothesis holds, LM, LM_F, and LRT statistics are constructed to test the PSTR model:

$$LM=TN({SSR}_0-{SSR}_1)/{SSR}_0\sim {\chi }_{mk}^2$$

(4)

$${LM}_F={\displaystyle \frac{({SSR}_0-{SSR}_1)/mk}{{SSR}_0/(TN-N-mk)}}\sim F(mk,TN-N-mk)$$

(5)

$$LRT=-2\left[log\left({SSR}_1\right)-log\left({SSR}_0\right)\right]\sim {\chi }_{mk}^2$$

(6)

where k and m are the numbers of explanatory variables and location parameters, respectively, and SSR₀ and SSR₁ represent the sums of squared residuals under the null and alternative hypotheses. Under the null hypothesis, the LM statistic and the LRT statistic both follow a χ² distribution with mk degrees of freedom, while the LMF statistic follows an $F(mk,TN-N-mk)$ distribution. The threshold value m of the transition function is determined by comparing the sizes of AIC and BIC. T is the time period, and N is the number of cross-sectional units.

3.3. Variable Definition and Data Processing

3.3.1. Core Explanatory Variable

Land Resource Misallocation (LRM): Based on the preceding theoretical analysis and existing research results, this paper defines LRM as the distorted supply behavior between urban industrial land and commercial–service land. Drawing on mainstream methods in the existing literature, LRM is measured by the ratio of land transferred by agreement to the total transferred land area. Considering that after 2006 the proportion of land transferred by agreement showed a cliff-like decline due to policy changes, to ensure the reliability and robustness of the research findings, LRM was operationalized as the share of agreement-based land transfers within the total transferred area during the period 2003–2006, and the share of land designated for industrial, mining, and storage purposes in the aggregate area of state-owned construction land transfers for the period 2007–2021. In addition, from the viewpoint of the total supply scale of industrial, mining, and storage land, this paper also selects the logarithm of the supply area of industrial, mining, and storage land as a proxy variable for LRM to conduct robustness testing.

3.3.2. Explained Variable

Carbon Emission Efficiency (CEF): Referring to existing studies, and in order to better simulate the production process in socio-economic activities, this paper adopts the super-efficiency SBM model with undesirable outputs proposed by Tone. The fixed asset investment of each city is adopted as a proxy for capital input, the year-end employee count of each city is adopted as a proxy for labor input, the total energy consumption of each city is adopted as a proxy for energy input, the expected output is the city’s gross domestic product, and the undesirable output is the city’s CO₂ emissions, thus constructing the input-output system of CEF for cities in the Yangtze River Economic Belt. Since this model is already relatively mature, this paper will not provide specific mathematical formulas here, and details can be found in the relevant literature [30].

3.3.3. Transition Variable

Advancement of Industrial Structure (AIS): Considering that the AIS mainly reflects the transformation of the industrial system from a lower-level form to a higher-level form, this paper adopts the AIS index as the core transition variable. It is measured by the ratio of the added value of the tertiary industry to that of the secondary industry. Specifically, when this ratio is relatively low, it indicates that the regional economy is still in a development stage driven by the secondary industry (manufacturing and industry). As the ratio increases, it signifies that the regional economic structure is gradually shifting toward the tertiary industry (services), which is oriented by technology, knowledge, and consumption. This transition not only represents the core feature of industrial upgrading but is also inevitably accompanied by profound changes in energy consumption, technological levels, and environmental governance. Therefore, selecting this indicator as the transition variable can effectively test whether the impact of LRM on CEF changes nonlinearly along with this fundamental structural transformation.

3.3.4. Control Variables

Population Size (pop), measured by year-end regional population; Economic Density (ed), operationalized as GDP per land area; Foreign Direct Investment (fdi), proxied by the ratio of foreign direct investment to GDP; Openness (ow), represented by total imports and exports relative to GDP; Urbanization (ur), quantified by the ratio of urban to permanent population.

3.4. Data Source and Processing

The research dataset consists of 108 prefecture-level and above cities in the Yangtze River Economic Belt over 2003–2021. LRM information was sourced from the China Land and Resources Statistical Yearbook and the China Land Market Network, carbon emissions data were obtained from the Emissions Database for Global Atmospheric Research (EDGAR), while data for other variables were obtained from the China City Statistical Yearbook, the China Statistical Yearbook, as well as statistical yearbooks of some provinces. Missing observations were supplemented via linear interpolation.

4. Results

4.1. Temporal and Spatial Characteristics of LRM and CEF

4.1.1. Temporal Characteristics of LRM and CEF

As shown in the boxplot of LRM in Figure 2, the LRM index of 108 cities in the Yangtze River Economic Belt from 2003 to 2021 presents an overall fluctuating downward trend. The average misallocation index declined from 0.633 in 2003 to 0.232 in 2021, with a total decrease of 63.314%, indicating that with the standardization of policies and institutions, the land transfer behavior of local governments has become increasingly lawful and compliant. Furthermore, the kernel density curve of LRM exhibited a gradual leftward shift, with its peak transitioning from concentration at higher values to concentration at lower values. The height of the main peak increased, but the curve still exhibits a significant right-tail phenomenon, indicating that there remain considerable differences in the degree of LRM among cities within the study area.

As shown in the boxplot of CEF in Figure 2, the CEF of 108 cities in the Yangtze River Economic Belt from 2003 to 2021 shows a fluctuating and slowly rising trajectory. However, the overall average efficiency is 0.504, which remains at a relatively low level, indicating considerable room for improvement. Specifically, the mean CEF of cities gradually shifted from being concentrated at lower values to being concentrated around the median and dispersed toward both ends, while the CEF of a small number of cities remained at a low level throughout the study period, suggesting large disparities among cities in the study area. Combined with the kernel density curve of CEF, the curve shows a “rising-falling” trend, characterized by a decrease in the main peak’s height and a widening of its width. This indicates that the degree of dispersion in CEF has expanded, and the gaps in CEF among cities within the region have continued to widen.

4.1.2. Spatial Characteristics of LRM and CEF

As shown in Figure 3, during the study period, the LRM index of cities in the Yangtze River Economic Belt initially presented a gradient distribution pattern of being high in the eastern and central regions and relatively high in the western region, while the number of cities with high values significantly decreased over time. From a stage-by-stage perspective, in the early stage of the study period, the high-value areas of misallocation were mainly concentrated in the eastern region, while the low-value areas were mainly distributed in the inland regions. However, the degree of misallocation in cities across the economic belt was generally high, possibly because under the dual drive of political promotion and economic growth, local governments were more inclined toward the short-term benefits of “financing through land.” In the mid-to-late stages of the study period, with the maturity of a series of land market-oriented allocation reforms such as the Bidding, Auction and Quotation system, the LRM index of cities in the research area decreased significantly. Nevertheless, medium- and high-value areas were still scattered in the central region in a “dotted” spatial distribution. This may be because the eastern region had gradually entered the post-industrialization stage, where the supply of industrial land was relatively strict and government intervention and regulation were stronger, while the central and western regions undertook a large number of industrial enterprise transfers from the eastern region, resulting in greater demand for industrial land.

As shown in Figure 4, during the study period, the high-value areas of CEF in cities of the Yangtze River Economic Belt were mainly concentrated in the eastern and southeastern coastal cities. Over time, the number of high-value cities gradually increased from the coastal areas toward the inland. Meanwhile, the eastern and central regions transitioned from a “scattered” to a “clustered” spatial distribution, showing significant agglomeration characteristics. Specifically, in the eastern region, a high-efficiency agglomeration area of CEF has basically formed within the Yangtze River Delta urban agglomeration, spreading outward layer by layer with Shanghai as the core, and a significant diffusion effect exists in the region. In the central region, diffusion circles have also gradually formed with provincial capital cities as the core. However, compared with the eastern region, the central Yangtze River urban agglomeration is currently developing from a policy-oriented area into an economic zone, and the diffusion and driving effects of core cities such as Wuhan, Changsha, and Nanchang are relatively weak. This also indirectly reflects that the CEF of cities in the economic belt has a circular and cumulative path dependence effect. Therefore, it may be possible to promote the overall improvement of CEF in the cities of the economic belt by creating multi-core development zones.

4.2. Analysis Estimation Results of PSTR Model

4.2.1. Results of Linearity Tests and Remaining Nonlinearity Tests

Before applying the PSTR model, it is necessary to test the nonlinear characteristics of the model. The results (

Table 1. Linearity and remaining nonlinearity tests results.

Hypothesis	m = 1			m = 2
	LM Statistics	LMF Statistics	LRT Statistics	LM Statistics	LMF Statistics	LRT Statistics
H0: r = 0 vs. H1: r = 1	86.175 *** (0.000)	14.159 *** (0.000)	88.037 *** (0.000)	163.230 *** (0.000)	13.914 *** (0.000)	170.089 *** (0.000)
H0: r = 1 vs. H1: r = 2	27.910 *** (0.000)	4.426 *** (0.000)	4.426 *** (0.000)	43.161 *** (0.000)	3.438 *** (0.000)	43.622 *** (0.000)
AIC	−3.737			−3.735
BIC	−3.698			−3.694

Note: r denotes the number of transition functions. ***, ** and * indicate significance of the coefficients at 1%, 5%, and 10% levels, respectively.

) show that whether m = 1 or m = 2, the LM, LM_F, and LRT tests all reject the null hypothesis that the regression model is linear at the 1% significance level, indicating that the panel data used in this paper exhibit obvious heterogeneity, that is, the impact of LRM on CEF has nonlinear characteristics. The remaining nonlinearity test can further determine the number of transition functions. Under the cases of m = 1 and m = 2, when r = 2, the location parameter is not within the selection range, thus r = 1 is chosen and the number of transition functions is set to 1. According to the AIC and BIC criteria, the model minimizing these values is considered optimal for selecting the number of location parameters. Since both AIC and BIC reach their minimum at m = 1, this value is selected. Therefore, the optimal combination of the transition function and location parameter in the PSTR model is r = 1, m = 1.

4.2.2. Estimation Results of PSTR Model

On the basis of determining the optimal combination of the transition function and location parameter in the PSTR model, we estimated the impact of LRM on CEF. The results are shown in

Table 2. Estimation of PSTR model.

Variables	Linear Component (${\mathit{\beta }}_1$)		Nonlinear Component (${\mathit{\beta }}_2$)
	Coefficients	t-Statistics	Coefficients	t-Statistics
LRM	0.207 ***	3.974	−0.244 ***	−3.376
pop	0.001 ***	3.887	−0.001 ***	−3.585
ed	0.857 ***	8.400	−0.634 ***	−6.088
fdi	−3.195 ***	−5.650	3.061 ***	4.064
ow	0.095 ***	2.570	−0.214 ***	−3.988
ur	−0.248 ***	−3.920	0.290 ***	3.922
Slope parameter (γ)	5.798
Location parameter (c)	0.700

Note: ***, ** and * indicate significance of the coefficients at 1%, 5%, and 10% levels, respectively.

. When AIS is used as the transition variable, LRM has a significant nonlinear impact effect on CEF, hypotheses 1 and 2 are both supported. When the level of AIS is below 0.700, the transition function h = 0, and the impact coefficient of LRM on CEF is 0.207; at this time, the model is in the low regime. When the level of AIS completely exceeds the threshold of 0.700, the transition function h = 1, and the model is in the high regime; at this time, the impact coefficient of LRM on CEF is −0.037 (that is, 0.207 + (−0.244)). It can be seen that the AIS threshold of 0.700 is an important turning point in the impact of LRM on CEF, with a continuity point between the low and high regimes ensuring a relatively smooth transition (Figure 5).

First, we focus on the core explanatory variable, LRM. The impact of LRM on CEF shows significant differences under different regimes. When AIS remains below the threshold of 0.700, LRM exerts a significantly positive influence on CEF (coefficient = 0.207). Conversely, once AIS exceeds 0.700, the effect of LRM on CEF turns significantly negative, with a combined coefficient of −0.037 (0.207 + (−0.244)). The above results indicate that under the influence of AIS, the effect of LRM on CEF follows an inverted “U”-shaped curve. Exploring its underlying mechanism, when the degree of AIS is relatively low, most regions are in the early stage of development, with heavy industry and energy-intensive industries gradually becoming dominant. At this time, local governments take advantage of the time window formed by LRM—such as clearing inefficient and idle land—to generate short-term gains in CEF. However, this belongs to a passive emission reduction mechanism under the constraints of a specific development stage. When moving beyond the early development stage, with the improvement of AIS, the industrial structure system gradually shifts toward technology-intensive services and advanced manufacturing industries. At this time, LRM restricts the establishment and clustering development of high-tech and low-emission industries, hinders the deep decarbonization of the industrial structure, and leads to a decline in CEF.

Other explanatory variables also show some meaningful results. The five control variables—pop, ed, fdi, ow, ur—all pass the significance test in terms of their nonlinear impacts on CEF, indicating that each control variable has an important effect on CEF. Specifically, regardless of whether in the low regime or the high regime, the coefficient of ed is significantly positive, suggesting that the higher the level of regional economic density, the more attention is paid to the protection of resources and the environment, and the higher the CEF. The coefficient of fdi is significantly negative, which may be because local governments, in order to attract high-end foreign investment, provide low-cost energy and land, thereby indirectly lowering the carbon cost for foreign investment. At the same time, foreign-investment-led industrial chains suppress emerging domestic low-carbon industries, weakening the driving force for improving CEF. The impact coefficient of ow on CEF changes from 0.095 to −0.119 (0.095 + (−0.214)), which verifies the “pollution haven” hypothesis. This shows that while regions introduce advanced foreign management models, a large number of high-energy-consuming projects also enter the domestic market, which lowers regional CEF. The impact of ur on CEF changes from −0.248 to 0.042 (−0.248 + 0.290). In the early stage of urbanization, population agglomeration may lead to rising congestion costs and excessive production scales, creating negative externalities, with excessive energy consumption reducing utilization efficiency, which is unfavorable for the improvement of CEF. When entering the mid-stage of urbanization, the promoted population agglomeration, as a compact spatial economic form, can generate positive externalities such as knowledge spillovers and economies of scale, thereby improving regional CEF.

4.3. Endogeneity Test

To mitigate potential endogeneity concerns in the PSTR model, we followed established research practices by using the lag period of the LRM as an instrumental variable for testing [29]. The results presented in

Table 3. Endogeneity test.

Variables	Linear Component	Nonlinear Component
LRM	0.325 *** (3.709)	−0.346 *** (−3.169)
Control variable	yes
Slope parameter (γ)	4.788
Location parameter (c)	0.530

Note: ***, ** and * indicate significance of the coefficients at 1%, 5%, and 10% levels, respectively.

show that, with AIS as the transition variable, LRM continues to exert a significant nonlinear impact on CEF, suggesting that the findings of this study are highly robust.

4.4. Robustness Test

To examine the robustness of our findings, we conducted two tests based on existing research [31]: replacing the measurement of the core explanatory variable and changing the sample size. The results presented in

Table 4. Robustness test.

Variables	Change the Measure of Dependent Variable		Change the Sample Size
	Linear Component	Nonlinear Component	Linear Component	Nonlinear Component
LRM	0.064 *** (5.168)	−0.062 *** (−4.084)	0.101 *** (3.257)	−0.190 *** (−3.490)
Control variable	yes		yes
Slope parameter (γ)	5.112		6.711
Location parameter (c)	0.608		0.901

Note: ***, ** and * indicate significance of the coefficients at 1%, 5%, and 10% levels, respectively.

show that, first, the logarithmic value of the supply area of industrial, mining, and storage land is used as a proxy variable for LRM, and the PSTR model regression is carried out to verify the robustness of the model. Second, based on the annual average value of CEF, the 108 cities in the Yangtze River Economic Belt are ranked, and the top and bottom 2.5% of cities are removed, after which regression is re-conducted with the reduced sample size. When the measurement method of the core explanatory variable is replaced and the sample size is changed, the robustness test results are basically consistent with those of the original model, which verifies the robustness of the previous research conclusions.

4.5. Heterogeneity Analysis

Since the Yangtze River Economic Belt as a whole exhibits considerable differences in terms of economic level, development characteristics, and other aspects, this paper further explores the nonlinear impact differences in LRM on CEF among cities within different regions from the perspectives of regional type and government intervention heterogeneity. The results are shown in

Table 5. Heterogeneity analysis.

		LRM	Control Variable	Slope Parameter (γ)	Location Parameter (c)
East (1)	Linear Component	0.074 ** (−2.020)	yes	7.696	0.948
	Nonlinear Component	−0.124 * (−1.750)
Mid/West (2)	Linear Component	0.185 (1.410)	yes	9.110	0.501
	Nonlinear Component	−0.156 (−1.055)
High (3)	Linear Component	0.150 ** (2.074)	yes	7.693	0.847
	Nonlinear Component	−0.416 *** (−3.761)
Mid/Low (4)	Linear Component	0.059 (0.433)	yes	17.913	0.468
	Nonlinear Component	0.021 (0.150)

Note: ***, ** and * indicate significance of the coefficients at 1%, 5%, and 10% levels, respectively.

.

(1)

Analysis of Cities in Different Regions: To examine whether the nonlinear impact of LRM on CEF exhibits regional heterogeneity, we divided the 108 sample cities into two groups based on their geographical location and alignment with the national strategic plan for functional zones of the Yangtze River Economic Belt: the eastern region (Shanghai, Jiangsu, and Zhejiang) and the central-western region (Hubei, Hunan, Jiangxi, Anhui, Chongqing, Sichuan, Yunnan, and Guizhou). The estimation results for these two subsamples are presented in Models East (1) and Mid/West (2). The results show that the impact of LRM on CEF demonstrates significant regional heterogeneity. In the eastern cities of the economic belt, when the level of AIS is below the threshold of 0.948, the coefficient of LRM on CEF is 0.074, significant at the 5% level; when the level of AIS upgrading exceeds the threshold of 0.948, the coefficient becomes −0.050 (0.074 + (−0.124)), significant at the 10% level. This is similar to the overall development pattern of the Yangtze River Economic Belt, but with a relatively higher threshold of AIS. The possible reason is that at the current stage, eastern cities still host many important industrial and economic bases, and land supply there is relatively scarce and more strictly controlled, making the marginal crowding-out effect of LRM on industrial transformation and technological innovation more pronounced. In contrast, in the central–western cities of the economic belt, the coefficients of LRM on CEF are not significant, which may be due to lagging development stages, weak institutional environments, and barriers to factor mobility. This also confirms the decisive role of the “factor–structure–institution” three-dimensional adaptation in regional green and low-carbon development.

(2)

Analysis of Different Fiscal Decentralization Levels: The LRM is closely linked to the fiscal incentives of local governments. Under a decentralized fiscal system, governments facing fiscal pressures often resort to “excessively low-priced industrial land transfers” to attract investment, while implementing “high-priced, restricted commercial and residential land transfers” to maximize land conveyance revenues. These practices are a key institutional cause of LRM. To examine whether the impact of LRM on CEF varies with regional fiscal autonomy, we use the degree of fiscal decentralization (local government budgetary revenue/local government budgetary expenditure) as a proxy for the intensity of government intervention. Based on this measure, we classify the 108 sample cities into a high-intensity group (those in the top quartile of fiscal decentralization) and a medium-low intensity group (the remainder). The estimation results for these two subsamples are presented in Models High (3) and Mid/Low (4). The results show that in cities with different degrees of local government fiscal decentralization, the impact of LRM on CEF is significantly different. In high-intensity cities, when the level of AIS is below the threshold of 0.847, the coefficient of LRM on CEF is 0.150, significant at the 5% level; when the level of AIS is above the threshold of 0.847, the coefficient is −0.266 (0.150 + (−0.416)), significant at the 1% level. This is similar to the overall economic belt and the eastern cities, but compared with the eastern cities of the economic belt, the threshold level of AIS is lower. This indicates that fiscal autonomy will intensify contradictions earlier: local governments that have not yet fully reached industrial advancement but have strong fiscal independence will fall into the transitional pains of land allocation earlier. In medium–low intensity cities, the coefficients of LRM on CEF are not significant. This may be because medium–low fiscal decentralization cities rely on central transfer payments, which weakens the policy execution power of LRM, thus leading to the impact of LRM on CEF not being statistically significant.

5. Discussion

Land is one of the fundamental factors of urban development, and the allocation of land resources profoundly affects the process of low-carbon transformation of the economy and society. As a key indicator of the green economy, CEF plays a crucial role in promoting the achievement of the “dual carbon” goals. Different from previous studies that explored whether urban land marketization, land transfer methods, land supply scale, and land prices affect carbon emissions/carbon emission efficiency [18,22,32,33], this paper, for the first time, incorporates LRM, industrial structure, and CEF into a unified analytical framework. By taking AIS as a transition variable, we construct a Panel Smooth Transition Regression (PSTR) model to analyze in depth the dynamic impact path of LRM on CEF. Our empirical analysis shows that, under the influence of AIS, the impact of LRM on CEF presents a significant inverted “U-shaped” characteristic, which resonates with and extends the inherent logic of the Environmental Kuznets Curve (EKC) theory. Specifically, during the initial and accelerating stages of AIS, LRM dominated by the government’s low-cost and abundant transfer of industrial land may, under specific historical development conditions, provide momentum for agglomeration economies, transferring land factors from idle or low carbon productivity agricultural sectors to industrial sectors with higher carbon productivity. This may unexpectedly lead to a short-term improvement in CEF, which is consistent with many scholars’ conclusions regarding the positive role of AIS in carbon emission reduction [34]. However, when AIS enters a more advanced stage, the drawbacks of the early land development model begin to emerge [35]. Mobility barriers of land factors result in their being locked into low-quality, inefficient, and high-emission enterprises, forming a rigid low-end path dependence of the industrial structure, which directly hinders the development of modern service industries and knowledge-intensive industries [36]. This is similar to the conclusion of Meng et al. [22] that LRM inhibits CEF.

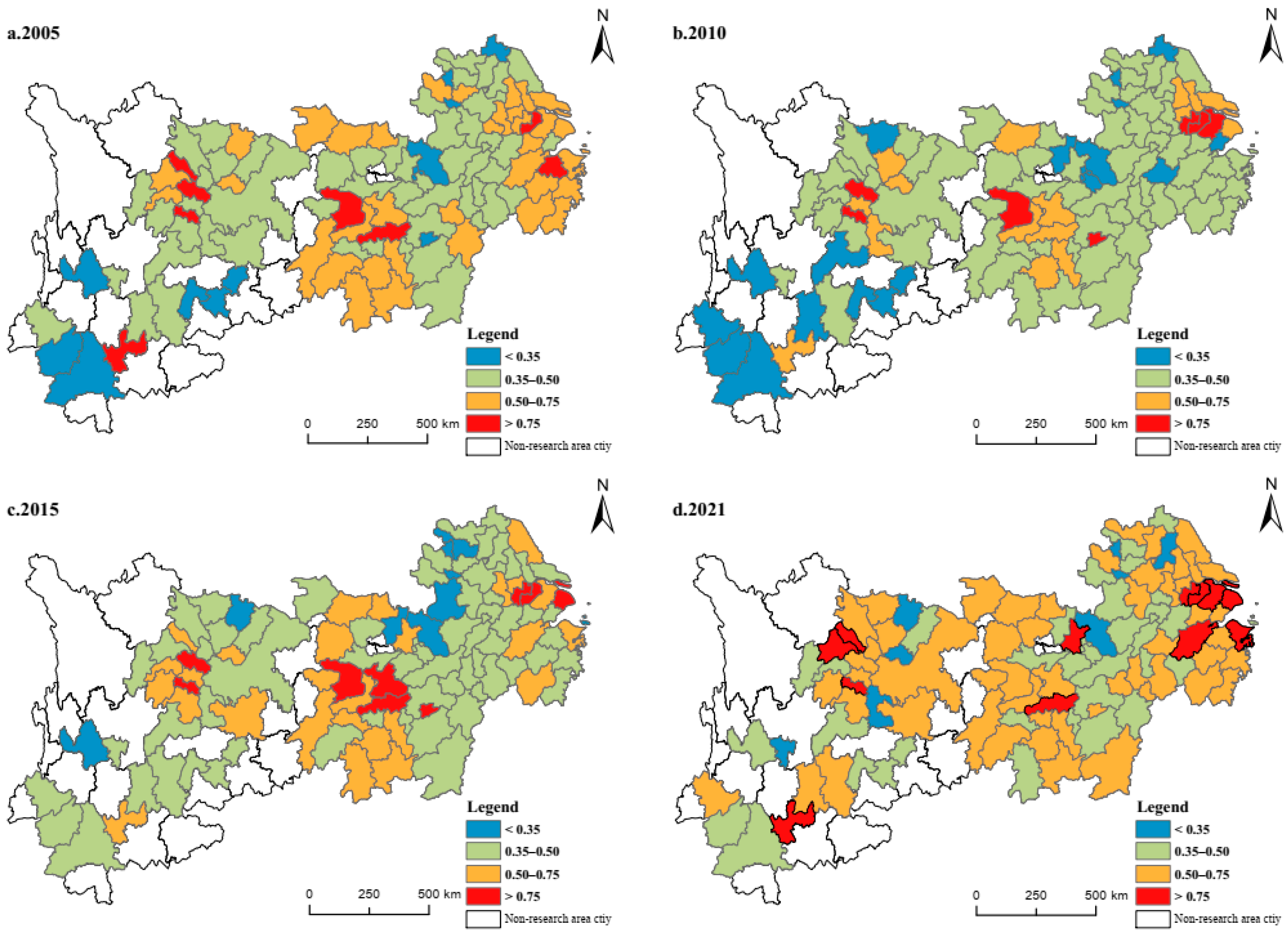
In addition, given the vast geographic span of the Yangtze River Economic Belt, there exist significant differences across regions in terms of resource endowment and economic development level, so we cannot ignore the regional heterogeneity in the impact of LRM on CEF. Our empirical analysis of regional sub-samples reveals that the impact of LRM on CEF exhibits distinct phase-specific characteristics. The eastern region, with its higher level of industrial development, has largely moved beyond the critical threshold of this nonlinear relationship, thus making the negative lock-in effect of LRM fully apparent. In contrast, industrial development in central and western regions may still be in a “catch-up phase” that relies heavily on land-based factor inputs, such that the nonlinear relationship between LRM and CEF is not yet statistically significant. Furthermore, the sub-sample results based on different levels of fiscal decentralization indicate that in regions with high fiscal decentralization, local governments possess stronger fiscal autonomy and resource allocation capacity. This enables them to promote industrial structure development more effectively through land supply policies, but at the same time, it also makes them more prone to path dependence on traditional growth models. By contrast, in regions with low fiscal decentralization, land resource allocation is more constrained by regulations from higher-level governments, and its impact on CEF fails to show significant nonlinear characteristics. These findings also highlight the crucial role and influence of regional development stages and institutional environments in shaping the land–ecological environment relationship. In the future, attention should be paid to the threshold effects of industrial structure in the impact of LRM on CEF. Policymakers should formulate phased and differentiated development policies to align land resource allocation with industrial structure, thereby efficiently advancing regional low-carbon and green development.

6. Conclusions and Policy Implications

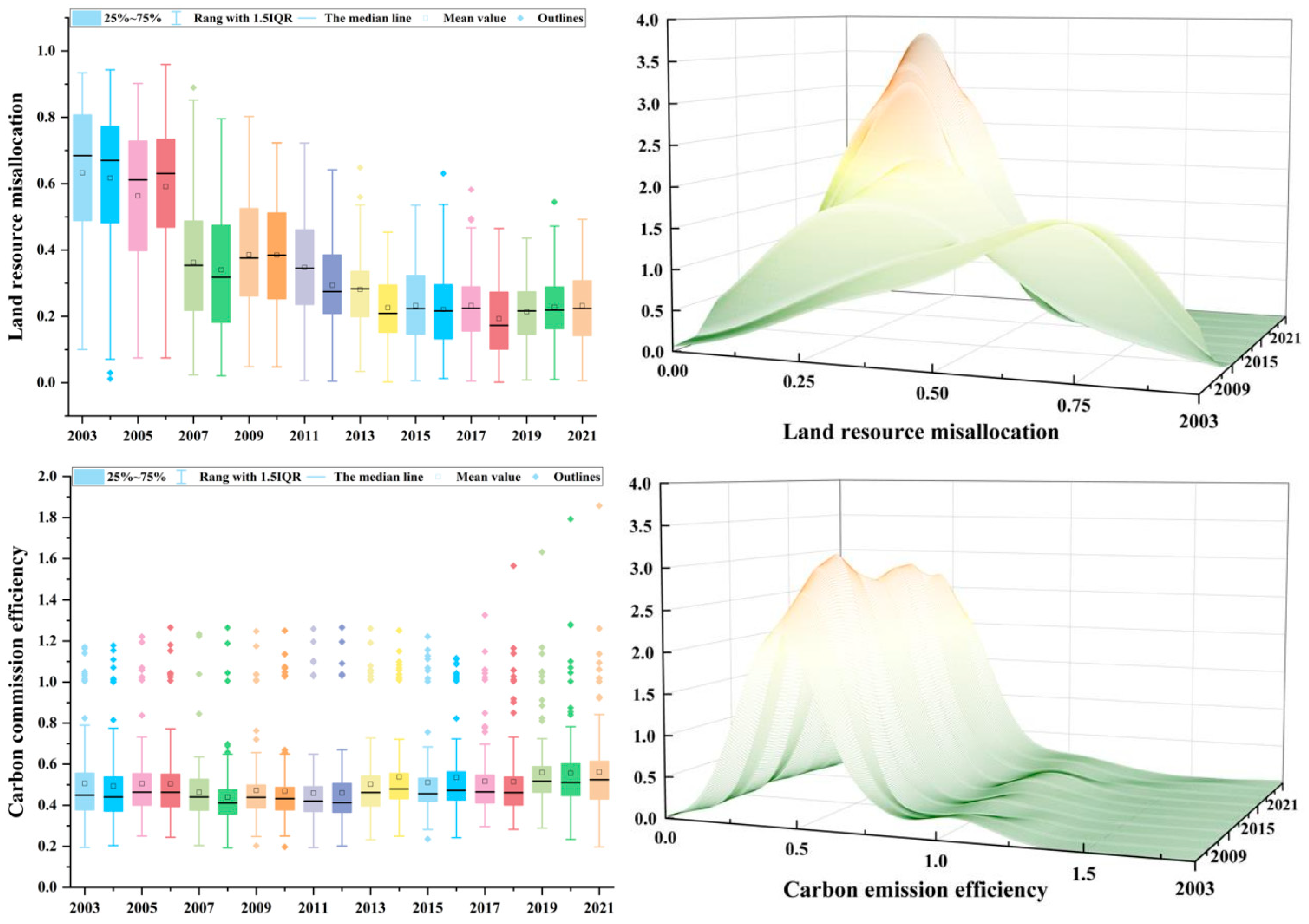
This paper systematically analyzes the spatiotemporal evolution characteristics of LRM and CEF in 108 cities of the Yangtze River Economic Belt from 2003 to 2021. On this basis, it constructs a panel smooth transition model (PSTR) to reveal the nonlinear impact of LRM on CEF and its regional heterogeneity. The main conclusions are as follows: First, during the study period, the LRM index of the 108 cities in the Yangtze River Economic Belt showed a fluctuating downward trend, with an overall decline of 63.314%. In contrast, CEF displayed a slowly rising trajectory with fluctuations, but overall remained at a relatively low level, leaving substantial room for improvement. Notably, the regional gaps in both LRM and CEF have been continuously widening. Second, the empirical results indicate that there exists a significant nonlinear relationship between LRM and CEF. Robustness tests confirm that the research conclusions are both stable and reliable. As the AIS index shifts from a low state to a high state, the impact of LRM on CEF exhibits an inverted “U-shaped” curve. Third, the nonlinear effect of LRM on CEF demonstrates significant regional heterogeneity. Specifically, in eastern cities of the economic belt and in cities with high fiscal decentralization, the impact of LRM on CEF is similar to the overall sample. However, in the central and western cities and in cities with medium-to-low fiscal decentralization, the effect is statistically insignificant. The threshold effect of industrial structure is the main reason for the regional differences in the nonlinear impact effect.

The above research conclusions provide important policy implications for improving the current situation of LRM and promoting low-carbon development: First, deepen the market-oriented reform of land factors and break rigid resource lock-in. The inverted “U”-shaped curve identified in this study indicates that once industrial structure advancement surpasses a specific threshold, the negative impact of LRM on CEF is fully revealed. Therefore, we should establish a linkage mechanism between existing land resources, industries, and carbon emission efficiency, improve the mechanism for reclaiming low-quality, inefficient, and high-emission industrial land, and free up space for high-end industries. Simultaneously, we should establish innovative land resource trading mechanisms to shift the land market from government-led allocation to market-driven competition. Additionally, we should explore the creation of regional “land banks” or quota trading platforms to ensure the efficient cross-regional and cross-sectoral circulation of land resources. This institutional strategy will dismantle the foundation that enables high-emission enterprises to lock up land resources. Second, dynamically adapt land resource allocation policies to the development stages of industrial structure. Local governments may establish “industrial structure thresholds” based on the development stage of regional industries. When the regional industrial structure approaches this threshold, targeted land resource allocation policies are triggered. For instance, they can establish an industrial land supply and evaluation system centered on carbon efficiency, which helps control new construction land, optimize existing land use, and redirect resources toward strategic emerging industries, high-end green manufacturing, and modern services. This approach decouples economic growth from carbon emissions at the source. Third, fully leverage regional resource endowments and locational advantages to implement differentiated land policies and industrial guidance. Specifically, in eastern regions and areas with high fiscal autonomy, policies should mandate stringent environmental standards and the revitalization of existing land reserves to compel industrial upgrading; simultaneously, their substantial fiscal autonomy should be channeled into supporting low-carbon technologies and future industries. Conversely, for central and western regions and those with low fiscal decentralization, the priority lies in leveraging scientific territorial spatial planning to preemptively lock in ecological redlines and industrial park boundaries, thereby incentivizing the development of distinctive low-carbon industries. This dual-track strategy fosters a complementary industrial ladder between the east and the rest of the country, promoting a competitive economic landscape characterized by distinctive specializations and strong interregional linkages.