Improving Landslide Susceptibility Assessment Through Non-Landslide Sampling Strategies
Abstract
1. Introduction
2. Material and Methods
2.1. Study Area
2.2. Data
2.2.1. Data Collection
2.2.2. Data Processing
2.3. Method
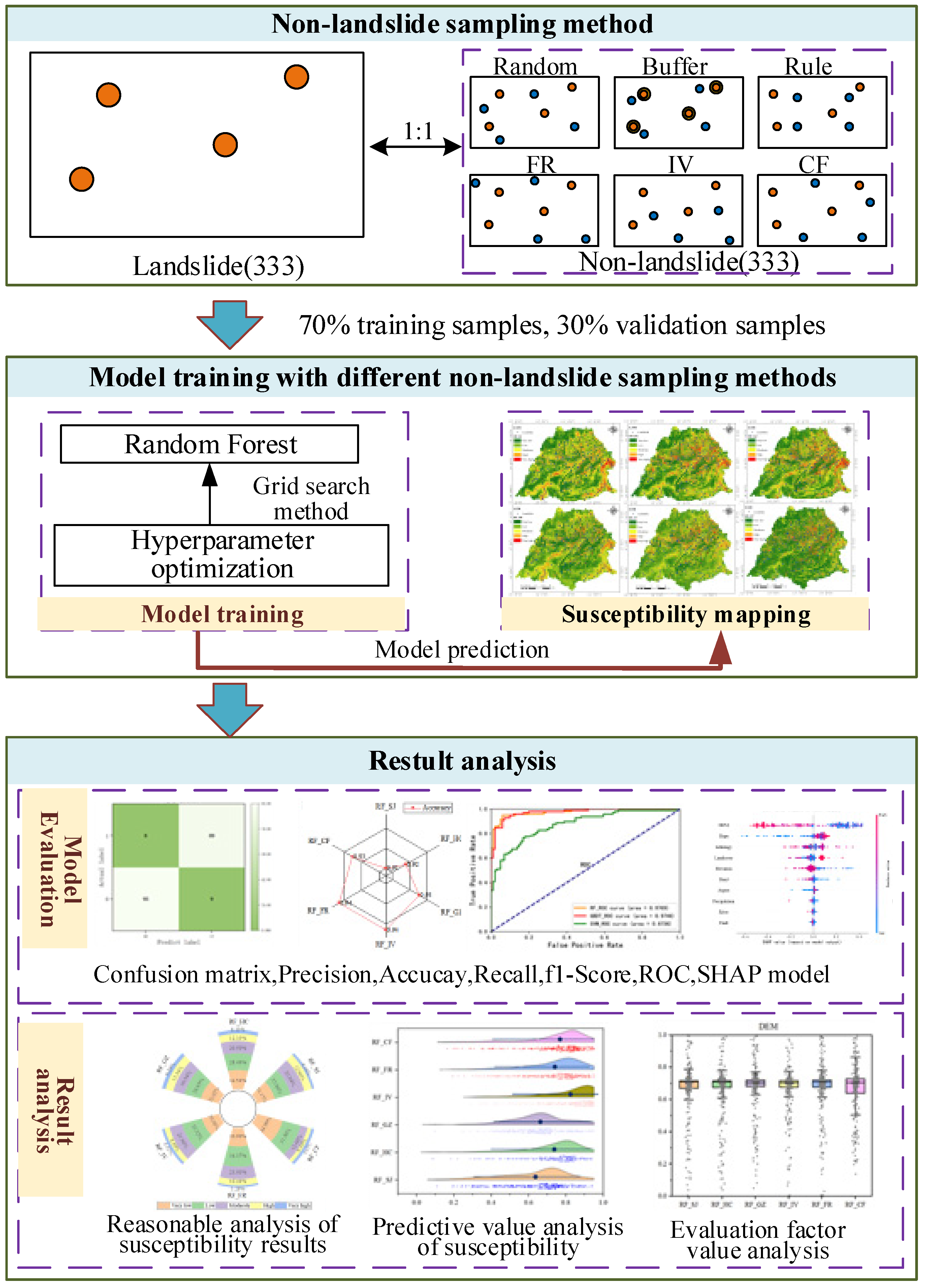
2.3.1. Sampling Method of Non-Landslide Samples
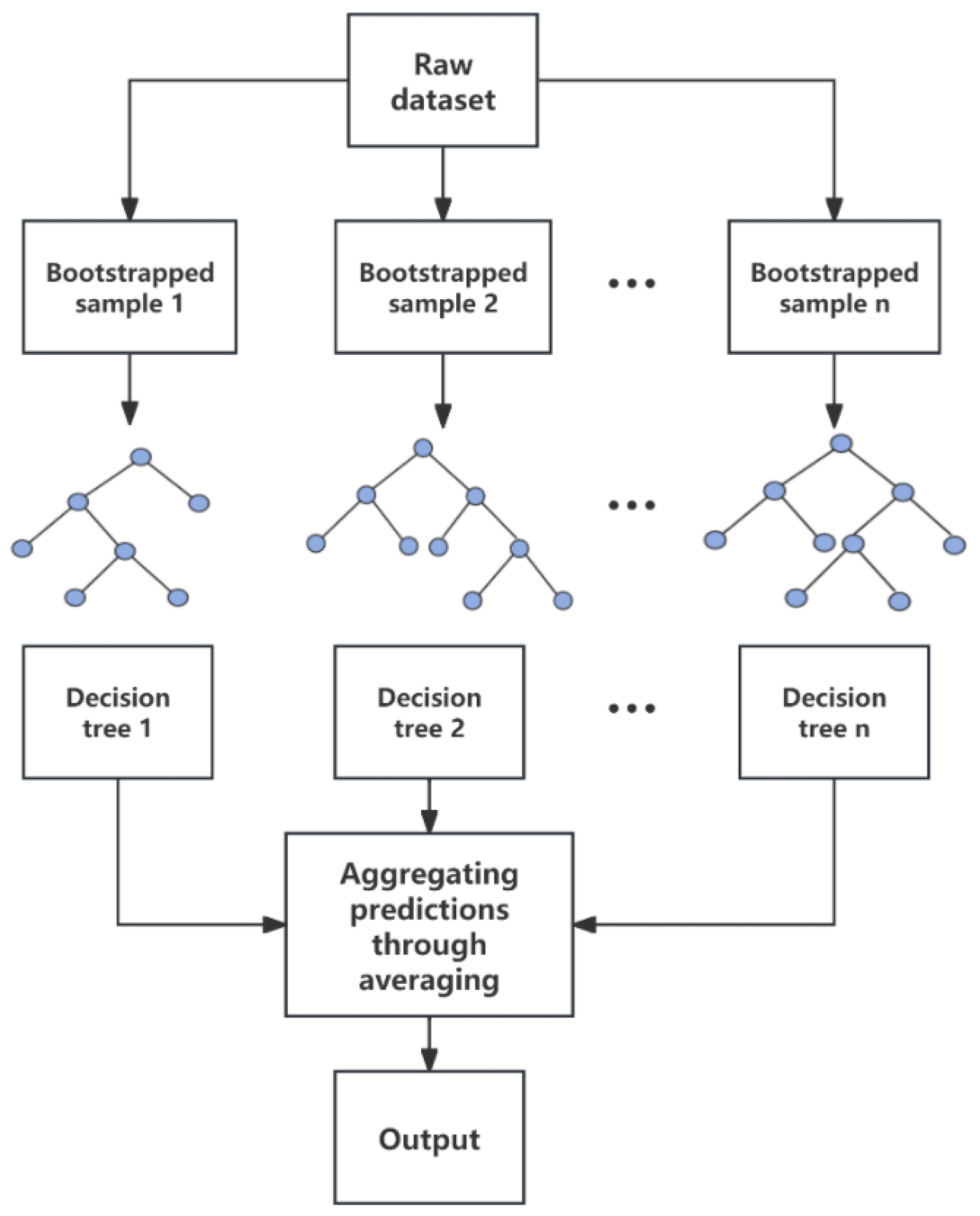
2.3.2. Random Forest
2.3.3. Evaluation Index of Accuracy
- (1)
- Confusion Matrix
- (2)
- ROC Curve
- (3)
- SHAP Model Calculation Principle
3. Results
3.1. Distribution of Non-Landslide Point Samples
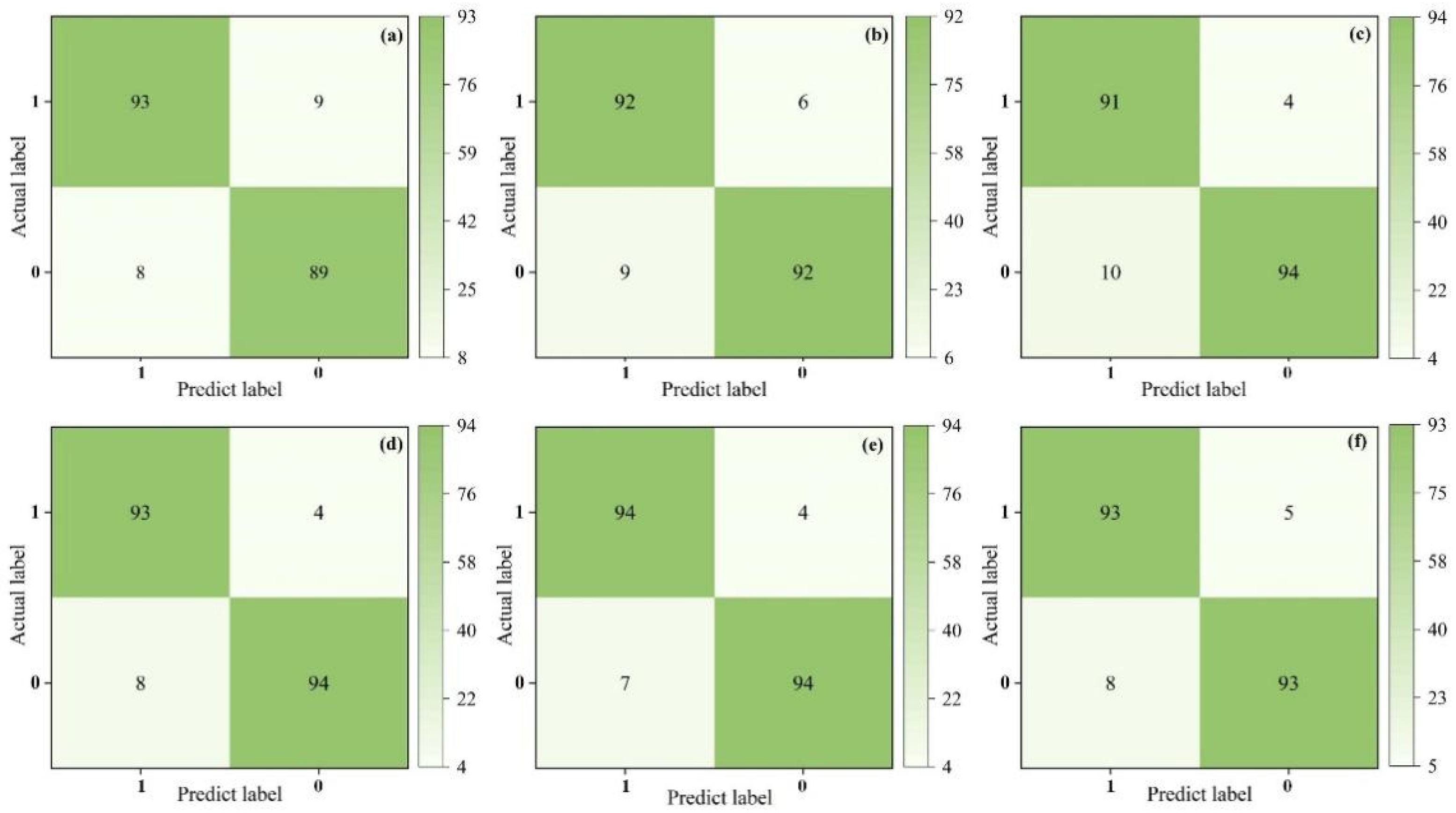
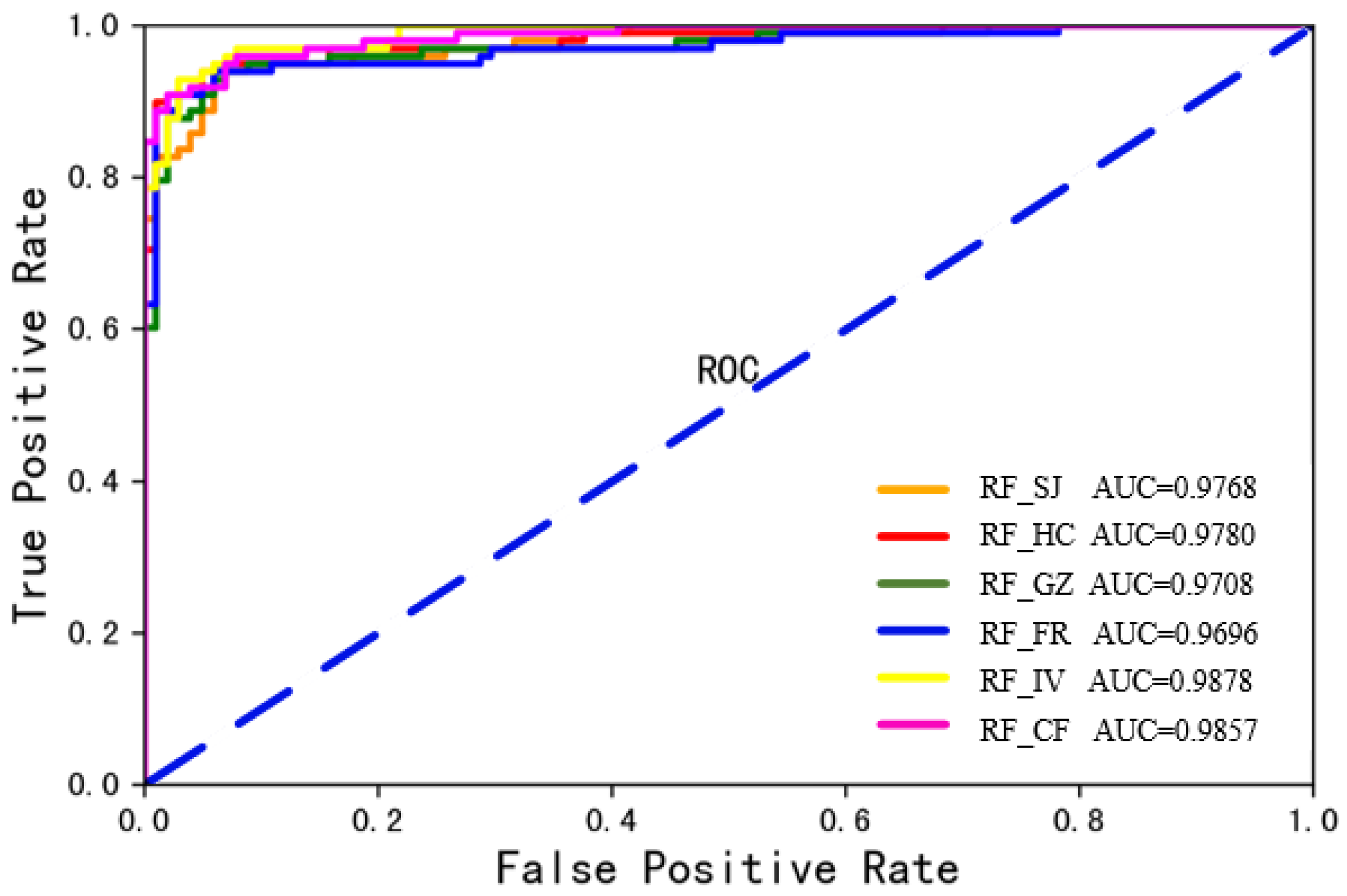
3.2. Evaluation Results of Model Accuracy
3.3. Contribution Analysis Results of Evaluation Factors Using the SHAP Model
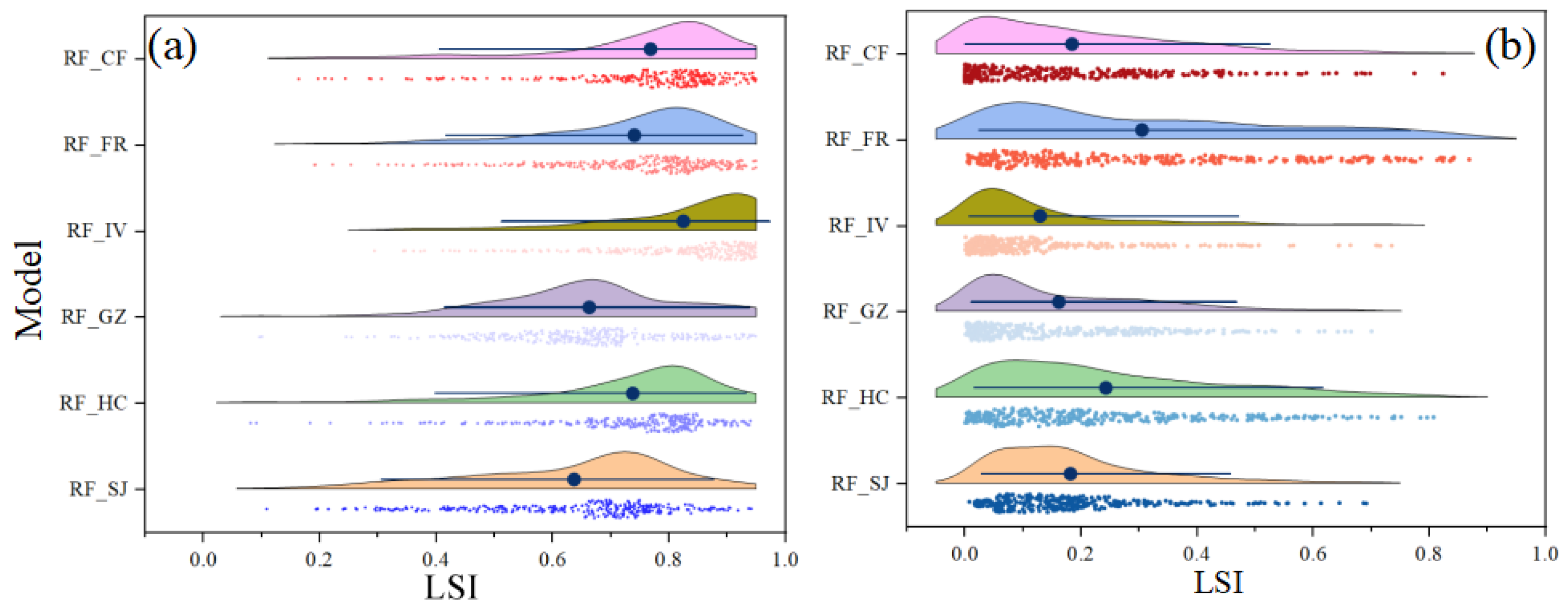
3.4. Mapping of Susceptibility Assessment Results Based on Different Non-Landslide Samples
3.4.1. Mapping of Susceptibility Assessment
3.4.2. Analysis of Susceptibility Evaluation Results
4. Discussion
4.1. Comparison of Different Sampling Methods for Non-Landslide Samples
4.2. Compared with Models from Other Studies
5. Conclusions
- (1)
- Among the six different non-landslide sample selection methods, the RF_IV model achieved the highest accuracy, precision, recall, and F1 score, with values of 0.94, 0.96, 0.93, and 0.94, respectively, outperforming other models. It also had the highest AUC value, 0.9878, indicating that the IV method provided the best quality non-landslide samples.
- (2)
- The SHAP model analysis revealed that different models have distinct decision-making mechanisms. NDVI, slope, lithology, land cover, and DEM were identified as the primary contributing factors for susceptibility evaluation, while fault distance, river distance, and slope aspect had relatively small SHAP values, indicating a minimal influence on the model.
- (3)
- According to the susceptibility evaluation statistics, the RF_IV model predicted that 97.60% of landslides corresponded to areas with high or very high susceptibility, covering 12.99% of the area. This indicates that most landslide sample points are located within a small area, aligning with the susceptibility results, and significantly outperforming other models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSP | Landslide susceptibility prediction. |
| LSI | Landslide susceptibility indexes. |
| RF | Random forest. |
| FR | Frequency Ratio. |
| IV | Information Value. |
| CF | Certainty Facto. |
| SJ | It indicates that the non-landslide samples are randomly selected. |
| GZ | It indicates that non-landslide samples are selected according to the rules. |
| HC | Non-landslide samples are selected according to the buffer zone. |
| RF_SJ, RF_GZ, RF_HC, RF_FR, RF_IV, RF_CF | It represents a coupled model in which the random forest model is successively combined with non-landslide sample sampling using methods such as randomness, regularity, buffer zone, frequency ratio, information quantity, and deterministic coefficient. |
| F1-score | It is a balanced measure of a model’s accuracy. |
| ROC | Receiver Operating Characteristic curve. |
| AUC | Area Under ROC. |
| LSM | Landslide Susceptibility Mapping. |
| NDVI | Normalized Difference Vegetation Index. |
| DEM | Digital Elevation Model. |
References
- Alcántara-Ayala, I.; Sassa, K. Landslide risk management: From hazard to disaster risk reduction. Landslides 2023, 20, 2031–2037. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- He, F.; Gu, L.; Wang, T.; Zhang, Z. The synthetic geo-ecological environmental evaluation of a coastal coal-mining city using spatiotemporal big data: A case study in Longkou, China. J. Clean. Prod. 2017, 142, 854–866. [Google Scholar] [CrossRef]
- Vakhshoori, V.; Pourghasemi, H.R.; Zare, M.; Blaschke, T. Landslide Susceptibility Mapping Using GIS-Based Data Mining Algorithms. Water 2019, 11, 2292. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Aryal, J.; Pradhan, B. A Novel Rule-Based Approach in Mapping Landslide Susceptibility. Sensors 2019, 19, 2274. [Google Scholar] [CrossRef]
- Ganesh, B.; Vincent, S.; Pathan, S. Machine learning based landslide susceptibility mapping models and GB-SAR based landslide deformation monitoring systems: Growth and evolution. Remote Sens. Appl. Soc. Environ. 2023, 29, 100905. [Google Scholar]
- Liu, G.; Dai, E.; Xu, X. Quantitative Assessment of Regional Debris-Flow Risk: A Case Study in Southwest China. Sustainability 2018, 10, 2223. [Google Scholar] [CrossRef]
- Franny, G.M.; Mauro, R.; Francesca, A. Hazard and population vulnerability analysis: A step towards landslide risk assessment. J. Mt. Sci. 2017, 14, 1241–1261. [Google Scholar] [CrossRef]
- Kim, S.; Lee, H. Assessment of Risk Due to Debris Flow and Its Application to a Marine Environment. Mar. Georesour. Geotechnol. 2015, 33, 7–23. [Google Scholar]
- Abhijit, S.P.; Sachin, S.P. Remote sensing and GIS-based landslide susceptibility mapping using LNRF method in part of Western Ghats of India. Quat. Sci. Adv. 2023, 11, 100095. [Google Scholar] [CrossRef]
- Lai, F.; Shao, Q.; Lin, Y. A method for the hazard assessment of regional geological disasters: A case study of the Panxi area, China. J. Spat. Sci. 2021, 66, 143–162. [Google Scholar] [CrossRef]
- Cao, J.S.; Qin, S.W.; Yao, J.Y. Debris flow susceptibility assessment based on information value and machine learning coupling method: From the perspective of sustainable development. Environ. Sci. Pollut. Res. 2023, 30, 87500–87516. [Google Scholar] [CrossRef] [PubMed]
- Tang, R.X.; Yan, E.C.; Wen, T. Comparison of Logistic Regression, Information Value, and Comprehensive Evaluating Model for Landslide Susceptibility Mapping. Sustainability. 2021, 13, 3803. [Google Scholar] [CrossRef]
- Ke, K.; Zhang, Y.C.; Zhang, J.Q. Risk Assessment of Earthquake-Landslide Hazard Chain Based on CF-SVM and Newmark Model-Using Changbai Mountain as an Example. Land 2023, 12, 696. [Google Scholar] [CrossRef]
- Huangfu, W.; Qiu, H.; Wu, W. Enhancing the Performance of Landslide Susceptibility Mapping with Frequency Ratio and Gaussian Mixture Model. Land 2024, 13, 1039. [Google Scholar] [CrossRef]
- Ke, C.Y.; He, S.; Qin, Y.G. Comparison of natural breaks method and frequency ratio dividing attribute intervals for landslide susceptibility mapping. Bull. Eng. Geol. Environ. 2023, 82, 384–402. [Google Scholar] [CrossRef]
- Topaçli, Z.K.; Ozcan, A.K.; Gokceoglu, C. Performance Comparison of Landslide Susceptibility Maps Derived from Logistic Regression and Random Forest Models in the Bolaman Basin, Türkiye. Nat. Hazards Rev. 2024, 25, 481–494. [Google Scholar] [CrossRef]
- Shang, H.; Su, L.X.; Chen, W. Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China. Remote Sens. 2023, 15, 4952. [Google Scholar] [CrossRef]
- Huang, W.; Ding, M.; Li, Z. Landslide susceptibility mapping and dynamic response along the Sichuan-Tibet transportation corridor using deep learning algorithms. Catena 2023, 222, 106866. [Google Scholar] [CrossRef]
- Nam, B.H.; Park, K.; Kim, Y.J. Prediction of karst sinkhole collapse using a decision-tree (DT) classifier. Geomech. Eng. 2024, 36, 441–453. [Google Scholar]
- Chen, Z.; Tang, J.F.; Song, D.Q. Modeling landslide susceptibility using alternating decision tree and support vector. Terr. Atmos. Ocean. Sci. 2024, 35, 44195. [Google Scholar]
- Guo, Z.; Shi, Y.; Huang, F. Landslide susceptibility zonation method based on C5.0 decision tree and K-means cluster algorithms to improve the efficiency of risk management. Geosci. Front. 2021, 12, 101249. [Google Scholar] [CrossRef]
- Zhang, A.; Zhao, X.; Zhao, X. Comparative study of different machine learning models in landslide susceptibility assessment: A case study of Conghua District, Guangzhou, China. China Geol. 2024, 7, 104–115. [Google Scholar]
- Ye, C.M.; Tang, R.; Wei, R.L. Generating accurate negative samples for landslide susceptibility mapping: A combined self-organizing-map and one-class SVM method. Front. Earth Sci. 2023, 10, 4027. [Google Scholar] [CrossRef]
- Amatya, P.; Emberson, R.; Kirschbaum, D. Multitemporal landslide inventory and susceptibility map for the Arun River Basin, Nepal. Geosci. Data J. 2024, 11, 669–679. [Google Scholar] [CrossRef]
- Fan, H.D.; Lu, Y.F.; Shao, S.W. Evaluation and analysis of statistical and coupling models for highway landslide susceptibility. Geomat. Nat. Hazards Risk 2023, 14, 7612. [Google Scholar] [CrossRef]
- Li, X.; Cheng, J.L.; Yu, D.H. Research on landslide hazard assessment in data-deficient areas: A case study of Tumen City, China. Acta Geophys. 2023, 71, 1763–1774. [Google Scholar] [CrossRef]
- Wei, R.; Ye, C.; Sui, T. Combining spatial response features and machine learning classifiers for landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102681. [Google Scholar] [CrossRef]
- Yang, K.; Niu, R.Q.; Song, Y.X. Dynamic Hazard Assessment of Rainfall-Induced Landslides Using Gradient Boosting Decision Tree with Google Earth Engine in Three Gorges Reservoir Area, China. Water 2024, 16, 1638. [Google Scholar] [CrossRef]
- Saad, M.; Kamel, M.; Moftah, H. Landslide susceptibility mapping for the Red Sea Mountains: A multi-criteria decision analysis approach. J. Afr. Earth Sci. 2024, 209, 105–125. [Google Scholar]
- Ma, J.W.; Lei, D.Z.; Ren, Z.Y. Automated Machine Learning-Based Landslide Susceptibility Mapping for the Three Gorges Reservoir Area, China. Math. Geosci. 2024, 56, 975–1010. [Google Scholar]
- Shahabi, H.; Ahmadi, R.; Alizadeh, M. Landslide Susceptibility Mapping in a Mountainous Area Using Machine Learning Algorithms. Remote Sens. 2023, 15, 3112. [Google Scholar] [CrossRef]
- Pereira, P.; Fernandes, L.; Do Valle, R.J. Geomorphologic risk zoning to anticipate tailings dams’ hazards: A study in the Brumadinho’s mining area, Minas Gerais, Brazil. Sci. Total Environ. 2024, 912, 169136. [Google Scholar] [CrossRef]
- Pana, T.; Taipodia, J.; Philley, P.D. Landslide hazard vulnerability assessment using surface wave method coupled with slope stability analysis: A case study. Sādhanā Acad. Proc. Eng. Sci. 2024, 49, 12046. [Google Scholar] [CrossRef]
- Park, S.; Kim, J. Landslide Susceptibility Mapping Based on Random Forest and Boosted Regression Tree Models, and a Comparison of Their Performance. Appl. Sci. 2019, 9, 942. [Google Scholar] [CrossRef]
- Gu, T.F.; Duan, P.; Wang, M.G. Effects of non-landslide sampling strategies on machine learning models in landslide susceptibility mapping. Sci. Rep. 2024, 14, 7201. [Google Scholar] [CrossRef]
- Ke, C.; Sun, P.; Zhang, S. Influences of non-landslide sampling strategies on landslide susceptibility mapping: A case of Tianshui city, Northwest of China. Bull. Eng. Geol. Environ. 2025, 84, 123. [Google Scholar] [CrossRef]
- Chang, Z.L.; Huang, J.S.; Huang, F.M.; Bhuyan, K.; Meena, S.R.; Catani, F. Uncertainty analysis of non-landslide sample selection in landslide susceptibility prediction using slope unit-based machine learning models. Gondwana Res. 2023, 117, 307–320. [Google Scholar] [CrossRef]
- Zhai, S.; Sun, Y.; Lei, J. An improved information quantity method for non-landslide selection to enhance landslide susceptibility evaluation: A case study in Yongfeng, South China. Nat. Hazards 2025, 121, 11773–11797. [Google Scholar] [CrossRef]
- Hong, H.Y.; Wang, D.S.; Zhu, A.X. Landslide susceptibility mapping based on the reliability of landslide and non-landslide sample. Expert Syst. Appl. 2024, 243, 122933. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, D.; Wen, H. Considering the effect of non-landslide sample selection on landslide susceptibility assessment. Geomat. Nat. Hazards Risk 2024, 15, 392–409. [Google Scholar] [CrossRef]
- Dou, H.Q.; He, J.B.; Huang, S.Y. Influences of non-landslide sample selection strategies on landslide susceptibility mapping by machine learning. Geomat. Nat. Hazards Risk 2023, 14, 5719. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, A.P.; Huang, D.L. Exploring the uncertainty of landslide susceptibility assessment caused by the number of non–landslides. Catena 2023, 227, 107109. [Google Scholar] [CrossRef]
- Wang, C.; Lin, Q.; Wang, L. The influences of the spatial extent selection for non-landslide samples on statistical-based landslide susceptibility modelling: A case study of Anhui Province in China. Nat. Hazards 2022, 112, 1967–1988. [Google Scholar]
- Zhu, Y.; Liu, S.; Yin, K. Impact of negative sampling strategies on landslide susceptibility assessment. Adv. Space Res. 2025, 76, 592–613. [Google Scholar] [CrossRef]
- Huang, F.; Xiong, H.; Jiang, S. Modelling landslide susceptibility prediction: A review and construction of semi-supervised imbalanced theory. Earth-Sci. Rev. 2024, 250, 104700. [Google Scholar]
- Jiang, W.; Li, L.; Niu, R. Impact of non-landslide sample sampling strategies and model selection on landslide susceptibility map. Appl. Sci. 2025, 15, 2132. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.L.; Huang, F.M.; Huang, L.; Wang, X.M. Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 2023, 123, 198–216. [Google Scholar]
- Yu, X.; Chen, H. Research on the influence of different sampling resolution and spatial resolution in sampling strategy on landslide susceptibility map results. Sci. Rep. 2024, 14, 1549. [Google Scholar] [CrossRef]
- Sun, D.L.; Gu, Q.Y.; Wen, H.J. Assessment of landslide susceptibility along mountain highways based on different machine learning algorithms and mapping units by hybrid factors screening and sample optimization. Gondwana Res. 2023, 123, 89–106. [Google Scholar]
- Wang, Z.; Chen, J.; Lian, Z. Influence of buffer distance on environmental geological hazard susceptibility assessment. Environ. Sci. Pollut. Res. 2024, 31, 9582–9595. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, B.P.; Dhakal, S.; Tsou, C. Assessing the Prediction Accuracy of Frequency Ratio, Weight of Evidence, Shannon Entropy, and Information Value Methods for Landslide Susceptibility in the Siwalik Hills of Nepal. Sustainability 2024, 16, 2092. [Google Scholar] [CrossRef]
- Bharadwaj, D.; Sarkar, R. Landslide Susceptibility Mapping Using Probabilistic Frequency Ratio and Shannon Entropy for Chamoli, Uttarakhand Himalayas. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2024, 48, 377–395. [Google Scholar] [CrossRef]
- Ahmad, M.S.; MonaLisa Khan, S. Comparative analysis of analytical hierarchy process (AHP) and frequency ratio (FR) models for landslide susceptibility mapping in Reshun, NW Pakistan. Kuwait J. Sci. 2023, 50, 387–398. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lin, Q.; Zhang, Z.H.; Yang, Z.H. Co-seismic landslides susceptibility evaluation of Bayesian random forest considering InSAR deformation: A case study of the Luding Ms6.8 earthquake. Geomat. Nat. Hazards Risk 2024, 15, 238–253. [Google Scholar] [CrossRef]
- Wen, H.; Zhao, S.Y.; Liang, Y.H. Landslide development and susceptibility along the Yunling-Yanjing segment of the Lancang River using grid and slope units. Nat. Hazards 2024, 120, 6149–6168. [Google Scholar] [CrossRef]
- Wang, P.; Deng, H.W.; Liu, Y. GIS-based landslide susceptibility zoning using a coupled model: A case study in Badong County, China. Environ. Sci. Pollut. Res. 2024, 31, 6213–6231. [Google Scholar] [CrossRef]
- Nath, N.K.; Gautam, V.K.; Pande, C.B. Development of landslide susceptibility maps of Tripura, India using GIS and analytical hierarchy process (AHP). Environ. Sci. Pollut. Res. 2024, 31, 7481–7497. [Google Scholar] [CrossRef]
- Yang, L.; Cui, Y.; Xu, C. Application of coupling physics–based model TRIGRS with random forest in rainfall-induced landslide-susceptibility assessment. Landslides 2024, 21, 2179–2193. [Google Scholar] [CrossRef]
- Yao, J.M.; Yao, X.; Zhao, Z. Performance comparison of landslide susceptibility mapping under multiple machine-learning based models considering InSAR deformation: A case study of the upper Jinsha River. Geomat. Nat. Hazards Risk 2023, 14, 2212833. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, Z.; Wei, Z.L. Assessment of earthquake-triggered landslide susceptibility considering coseismic ground deformation. Front. Earth Sci. 2023, 10, 3975. [Google Scholar] [CrossRef]
- Martinello, C.; Mercurio, C.; Cappadonia, C. Using Public Landslide Inventories for Landslide Susceptibility Assessment at the Basin Scale: Application to the Torto River Basin (Central-Northern Sicily, Italy). Appl. Sci. 2023, 13, 9449. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Xu, P.Y.; Liu, J. Comparison of LR, 5-CV SVM, GA SVM, and PSO SVM for landslide susceptibility assessment in Tibetan Plateau area, China. J. Mt. Sci. 2023, 20, 979–995. [Google Scholar] [CrossRef]
- Dang, K.B.; Nguyen, C.Q.; Tran, Q.C. Comparison between U-shaped structural deep learning models to detect landslide. Sci. Total Environ. 2024, 912, 169113. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.C.; Zhang, R.; Shama, A. Exploring the spatial patterns of landslide susceptibility assessment using interpretable Shapley method: Mechanisms of landslide formation in the Sichuan-Tibet region. J. Environ. Manag. 2024, 366, 121921. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Pradhan, B.; Beydoun, G. A novel method using explainable artificial intelligence (XAI)-based Shapley Additive Explanations for spatial landslide prediction using Time-Series SAR dataset. Gondwana Res. 2023, 123, 107–124. [Google Scholar] [CrossRef]
- Liu, X.M.; Su, P.C.; Li, Y. Spatial distribution of landslide shape induced by Luding Ms6.8 earthquake, Sichuan, China: Case study of the Moxi Town. Landslides 2023, 20, 1667–1678. [Google Scholar] [CrossRef]
- Sun, D.L.; Ding, Y.K.; Wen, H.J. SHAP-PDP hybrid interpretation of decision-making mechanism of machine learning-based landslide susceptibility mapping: A case study at Wushan District, China. Egypt. J. Remote Sens. Space Sci. 2024, 27, 508–523. [Google Scholar] [CrossRef]
- Rabby, Y.W.; Li, Y.; Hilafu, H. An objective absence data sampling method for landslide susceptibility mapping. Sci. Rep. 2023, 13, 1740. [Google Scholar] [CrossRef]
- Tien, B.D.; Tuan, T.A.; Hoang, N.D.; Thanh, N.Q.; Nguyen, D.B.; Liem, N.V.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2017, 14, 447–458. [Google Scholar] [CrossRef]
- Xu, W.; Cui, Y.L.; Wang, J.Z. Landslide susceptibility zoning with five data models and performance comparison in Liangshan Prefecture, China. Front. Earth Sci. 2024, 12, 1417671. [Google Scholar] [CrossRef]
- Yang, S.; Li, D.; Sun, Y. Effect of landslide spatial representation and raster resolution on the landslide susceptibility assessment. Environ. Earth Sci. 2024, 83, 132. [Google Scholar] [CrossRef]
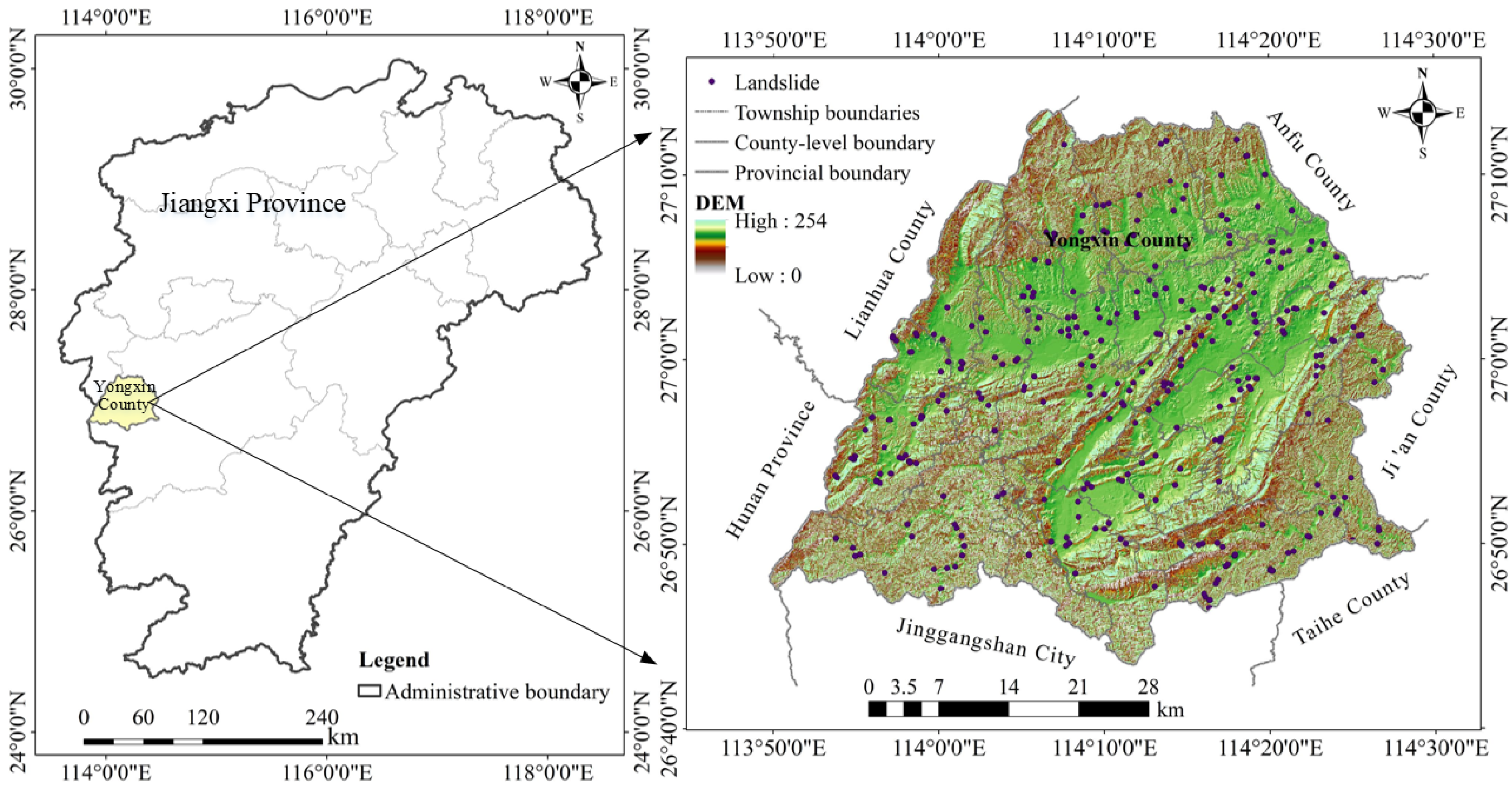




| Number | Data | Introduction | Source | Purpose | Coordinate System |
|---|---|---|---|---|---|
| 1 | Sentinel-2 data | Sentinel-2 Level-2A multispectral imagery (with a 10 m spatial resolution raster) | European Space Agency website (https://earth.esa.int/eogateway/catalog) | used for extracting NDVI data and constructing landslide characteristic factors | World Geodetic System 1984 (WGS84) |
| 2 | Land use data | 10 m spatial resolution raster | Analysis of landslide characteristic factors | ||
| 3 | Meteorological data | 1 km spatial resolution raster | https://gpm.nasa.gov | Used for extracting the characteristic factor of average annual rainfall | |
| 4 | Lithology | Polygonal vector data | Yongxin County Natural Resources Bureau | Landslide characteristic factor | China Geodetic Coordinate System 2000 |
| 5 | 1:50,000 Geological Hazard Risk Survey Results | Text, Vector | Yongxin County Natural Resources Bureau | Analyze the historical landslide characteristics of the study area | |
| 6 | Fault | linear vector data | Yongxin County Natural Resources Bureau | Construct landslide characteristic factors by converting to raster imagery through Euclidean distance calculation. | |
| 7 | River | linear vector data | Yongxin County Natural Resources Bureau | ||
| 8 | Road | linear vector data | Yongxin County Natural Resources Bureau | ||
| 9 | DEM | 5 m spatial resolution raster | Yongxin County Natural Resources Bureau | Extract landslide characteristic factors such as elevation, slope, and aspect. |
| / | / | Prediction Result | |
|---|---|---|---|
| Actual situation | class | Positive | Negative |
| Positive | TP | FN | |
| Negative | FP | TN | |
| Number | Evaluation System | Computing Formula |
|---|---|---|
| 1 | Accuracy | |
| 2 | Precision | |
| 3 | Recall | |
| 4 | F1-score |
| Evaluation Factor | Grading Interval | Number of Landslides | FR | IV | CF |
|---|---|---|---|---|---|
| lithology | metamorphic rock | 77 | 0.6806 | −0.3848 | −0.3186 |
| carbonatite | 54 | 2.6100 | 0.9594 | 2.0793 | |
| clasolite | 174 | 1.2714 | 0.2401 | 0.2560 | |
| magmatite | 28 | 0.4494 | −0.8000 | −0.6741 | |
| Fault distance (m) | (0, 200] | 73 | 1.6140 | 0.4787 | 0.2838 |
| (200, 400] | 43 | 1.0967 | 0.0923 | 0.6513 | |
| (400, 600] | 35 | 1.0281 | 0.0277 | −0.0344 | |
| (600, 800] | 19 | 0.6419 | −0.4434 | −0.6041 | |
| (800, 1000] | 27 | 1.0949 | 0.0907 | 0.0998 | |
| >1000 | 136 | 0.8486 | −0.1641 | −0.1354 | |
| Elevation (m) | (0, 69] | 23 | 0.9598 | −0.0411 | −0.0949 |
| (69, 117] | 39 | 0.9214 | −0.0818 | −0.0019 | |
| (117, 160] | 73 | 1.3954 | 0.3332 | 0.7391 | |
| (160, 204] | 126 | 0.8404 | −0.1739 | −0.2004 | |
| (204, 254] | 72 | 1.1169 | 0.1105 | −0.0972 | |
| Slope (°) | (0, 14] | 13 | 0.1529 | −1.8779 | −0.8865 |
| (14, 33] | 47 | 0.9222 | −0.0810 | −0.2071 | |
| (33, 52] | 116 | 2.0657 | 0.7255 | 0.9495 | |
| (52, 69] | 124 | 1.8448 | 0.6124 | 1.1963 | |
| (69, 88] | 33 | 0.4481 | −0.8027 | −0.6488 | |
| aspect | horizon | 0 | 0.0000 | 0.0000 | −1.0000 |
| north | 0 | 0.0000 | 0.0000 | −1.0000 | |
| northeast | 4 | 0.1457 | −1.9264 | −0.9466 | |
| east | 30 | 0.7571 | −0.2782 | −0.5145 | |
| southeast | 63 | 1.2811 | 0.2477 | 0.2944 | |
| south | 101 | 2.6549 | 0.9764 | 2.0951 | |
| southwest | 78 | 2.8607 | 1.0511 | 2.6100 | |
| west | 42 | 1.0997 | 0.0950 | −0.2732 | |
| northwest | 15 | 0.3284 | −1.1134 | −0.8962 | |
| Annual rainfall (mm) | (1488, 1526] | 237 | 1.4638 | 0.3811 | 0.4430 |
| (1526, 1570] | 64 | 0.7610 | −0.2731 | −0.1876 | |
| (1570, 1628] | 23 | 0.4509 | −0.7965 | −0.4684 | |
| (1628, 1708] | 7 | 0.2822 | −1.2652 | −0.8740 | |
| (1708, 1880] | 2 | 0.1789 | −1.7210 | −0.9157 | |
| River distance (m) | (0, 200] | 42 | 1.9600 | 0.6730 | 1.0349 |
| (200, 400] | 28 | 1.4682 | 0.3840 | 0.5975 | |
| (400, 600] | 28 | 1.3604 | 0.3078 | 1.0491 | |
| (600, 800] | 31 | 1.4584 | 0.3774 | 0.5194 | |
| (800, 1000] | 15 | 0.7119 | −0.3398 | −0.4167 | |
| >1000 | 189 | 0.8232 | −0.1946 | −0.2498 | |
| NDVI | (0, 0.22] | 31 | 2.4309 | 0.8883 | 4.1690 |
| (0.22, 0.37] | 220 | 9.3440 | 2.2347 | 8.3501 | |
| (0.37, 0.48] | 58 | 0.8229 | −0.1949 | −0.5237 | |
| (0.48, 0.57] | 23 | 0.1875 | −1.6739 | −0.8962 | |
| (0.57, 0.78] | 1 | 0.0097 | −4.6402 | −0.9933 | |
| Road distance (m) | (0, 200] | 95 | 3.0577 | 1.1177 | 2.7311 |
| (200, 400] | 34 | 1.2211 | 0.1998 | 0.6002 | |
| (400, 600] | 25 | 0.9852 | −0.0149 | −0.3121 | |
| (600, 800] | 30 | 1.2969 | 0.2600 | 0.2874 | |
| (800, 1000] | 17 | 0.8087 | −0.2123 | −0.1707 | |
| >1000 | 132 | 0.6453 | −0.4381 | −0.4724 | |
| Land cover | woodland | 92 | 0.3918 | −0.9370 | −0.7857 |
| bush | 0 | 0.0000 | 0.0000 | −1.0000 | |
| water | 1 | 0.3625 | −1.0149 | −0.4500 | |
| herbaceous wetland | 0 | 0.0000 | 0.0000 | −1.0000 | |
| grassland | 21 | 1.1928 | 0.1763 | 0.8575 | |
| cultivated land | 14 | 0.2530 | −1.3744 | −0.8391 | |
| built-up area | 15 | 1.4231 | 0.3528 | −0.3006 | |
| bare land or sparse vegetation | 190 | 16.3083 | 2.7917 | 18.9321 |
| Model | max_depth | min_samples_split | n_estimators |
|---|---|---|---|
| RF_SJ | 7 | 8 | 150 |
| RF_HC | 6 | 4 | 200 |
| RF_GZ | 6 | 8 | 150 |
| RF_FR | 8 | 4 | 150 |
| RF_IV | 9 | 8 | 250 |
| RF_CF | 8 | 4 | 200 |
| Non-Landslide Samples | Susceptibility Classification | Index Range | Area/km2 | Area Proportion | Number of Landslides | Landslide Proportion | Frequency Ratio |
|---|---|---|---|---|---|---|---|
| RF_SJ | Very Low | [0, 0.14] | 672.31 | 31.17% | 1 | 0.30% | 0.01 |
| Low | (0.14, 0.24] | 600.86 | 27.86% | 5 | 1.50% | 0.05 | |
| Moderate | (0.24, 0.36] | 514.04 | 23.84% | 25 | 7.51% | 0.31 | |
| High | (0.36, 0.53] | 279.59 | 12.96% | 56 | 16.82% | 1.30 | |
| Very High | (0.53, 0.97] | 89.79 | 4.16% | 246 | 73.87% | 17.74 | |
| RF_HC | Very Low | [0, 0.12] | 701.84 | 32.54% | 2 | 0.60% | 0.02 |
| Low | (0.12, 0.25] | 614.31 | 28.49% | 2 | 0.60% | 0.02 | |
| Moderate | (0.25, 0.40] | 442.18 | 20.50% | 13 | 3.90% | 0.19 | |
| High | (0.40, 0.59] | 265.96 | 12.33% | 33 | 9.91% | 0.80 | |
| Very High | (0.59, 1] | 132.29 | 6.13% | 283 | 84.98% | 13.85 | |
| RF_GZ | Very Low | [0, 0.12] | 691.26 | 32.05% | 2 | 0.60% | 0.02 |
| Low | (0.12, 0.26] | 621.70 | 28.83% | 2 | 0.60% | 0.02 | |
| Moderate | (0.26, 0.4] | 421.46 | 19.54% | 9 | 2.70% | 0.14 | |
| High | (0.4, 0.58] | 287.60 | 13.34% | 75 | 22.52% | 1.69 | |
| Very High | (0.58, 0.99] | 134.57 | 6.24% | 245 | 73.57% | 11.79 | |
| RF_FR | Very Low | [0, 0.13] | 666.36 | 30.90% | 0 | 0.00% | 0.00 |
| Low | (0.13, 0.24] | 741.29 | 34.37% | 3 | 0.90% | 0.03 | |
| Moderate | (0.24, 0.37] | 453.07 | 21.01% | 7 | 2.10% | 0.10 | |
| High | (0.37, 0.58] | 225.07 | 10.44% | 39 | 11.71% | 1.12 | |
| Very High | (0.58, 0.99] | 70.80 | 3.28% | 284 | 85.29% | 25.98 | |
| RF_IV | Very Low | [0, 0.14] | 645.84 | 29.95% | 0 | 0.00% | 0.00 |
| Low | (0.14, 0.27] | 759.45 | 35.22% | 0 | 0.00% | 0.00 | |
| Moderate | (0.27, 0.42] | 471.09 | 21.84% | 8 | 2.40% | 0.11 | |
| High | (0.42, 0.65] | 183.04 | 8.49% | 30 | 9.01% | 1.06 | |
| Very High | (0.65, 0.99] | 97.17 | 4.51% | 295 | 88.59% | 19.66 | |
| RF_CF | Very Low | [0, 0.1] | 968.21 | 44.90% | 0 | 0.00% | 0.00 |
| Low | (0.1, 0.22] | 679.42 | 31.50% | 3 | 0.90% | 0.03 | |
| Moderate | (0.22, 0.39] | 271.64 | 12.60% | 11 | 3.30% | 0.26 | |
| High | (0.39, 0.62] | 132.83 | 6.16% | 32 | 9.61% | 1.56 | |
| Very High | (0.62, 1] | 104.49 | 4.85% | 287 | 86.19% | 17.79 |
| Source | Model | Non-Landslide Sample | AUC |
|---|---|---|---|
| Dou et al. [42] | Logistics regression | Buffer zone method (600 m) | 0.936 |
| Buffer zone method (900 m) | 0.95 | ||
| Buffer zone method (1200 m) | 0.954 | ||
| Buffer zone method (1500 m) | 0.946 | ||
| Condition factor method | 0.991 | ||
| Information value model | 0.997 | ||
| Artificial neural networks | Buffer zone method (600 m) | 0.942 | |
| Buffer zone method (900 m) | 0.952 | ||
| Buffer zone method (1200 m) | 0.956 | ||
| Buffer zone method (1500 m) | 0.946 | ||
| Condition factor method | 0.989 | ||
| Information value model | 0.995 | ||
| Zhu et al. [41] | Random Forest | District-wide random selection method | 0.7483 |
| Buffer method | 0.777 | ||
| Frequency ratio method | 0.857 | ||
| Analytic hierarchy process | 0.9164 | ||
| XGBoost | District-wide random selection method | 0.7553 | |
| Buffer method | 0.7619 | ||
| Frequency ratio method | 0.8668 | ||
| Analytic hierarchy process | 0.9217 | ||
| Trinh et al. [43] | SVM | Frequency ratio method | 0.969 |
| Analytic hierarchy process | 0.963 | ||
| Bayesian | Frequency ratio method | 0.87 | |
| Analytic hierarchy process | 0.817 | ||
| KNN | Frequency ratio method | 0.896 | |
| Analytic hierarchy process | 0.86 | ||
| This study | Random Forest | random selection method | 0.9768 |
| Buffer method | 0.978 | ||
| Regular distribution method | 0.9708 | ||
| Frequency ratio method | 0.9696 | ||
| Information value method | 0.9878 | ||
| Certainty factor method | 0.9857 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, L.; Chen, M.; Leng, P.; Liu, S.; Liu, M.; Luo, W.; Mao, Y. Improving Landslide Susceptibility Assessment Through Non-Landslide Sampling Strategies. Land 2025, 14, 2059. https://doi.org/10.3390/land14102059
Tu L, Chen M, Leng P, Liu S, Liu M, Luo W, Mao Y. Improving Landslide Susceptibility Assessment Through Non-Landslide Sampling Strategies. Land. 2025; 14(10):2059. https://doi.org/10.3390/land14102059
Chicago/Turabian StyleTu, Liping, Meiqiu Chen, Peng Leng, Shengwei Liu, Mei’e Liu, Wang Luo, and Yaqin Mao. 2025. "Improving Landslide Susceptibility Assessment Through Non-Landslide Sampling Strategies" Land 14, no. 10: 2059. https://doi.org/10.3390/land14102059
APA StyleTu, L., Chen, M., Leng, P., Liu, S., Liu, M., Luo, W., & Mao, Y. (2025). Improving Landslide Susceptibility Assessment Through Non-Landslide Sampling Strategies. Land, 14(10), 2059. https://doi.org/10.3390/land14102059





