Objective Parameterization of InVEST Habitat Quality Model Using Integrated PCA-SEM-Spatial Analysis: A Biotope Map-Based Framework
Abstract
1. Introduction
2. Materials and Methods
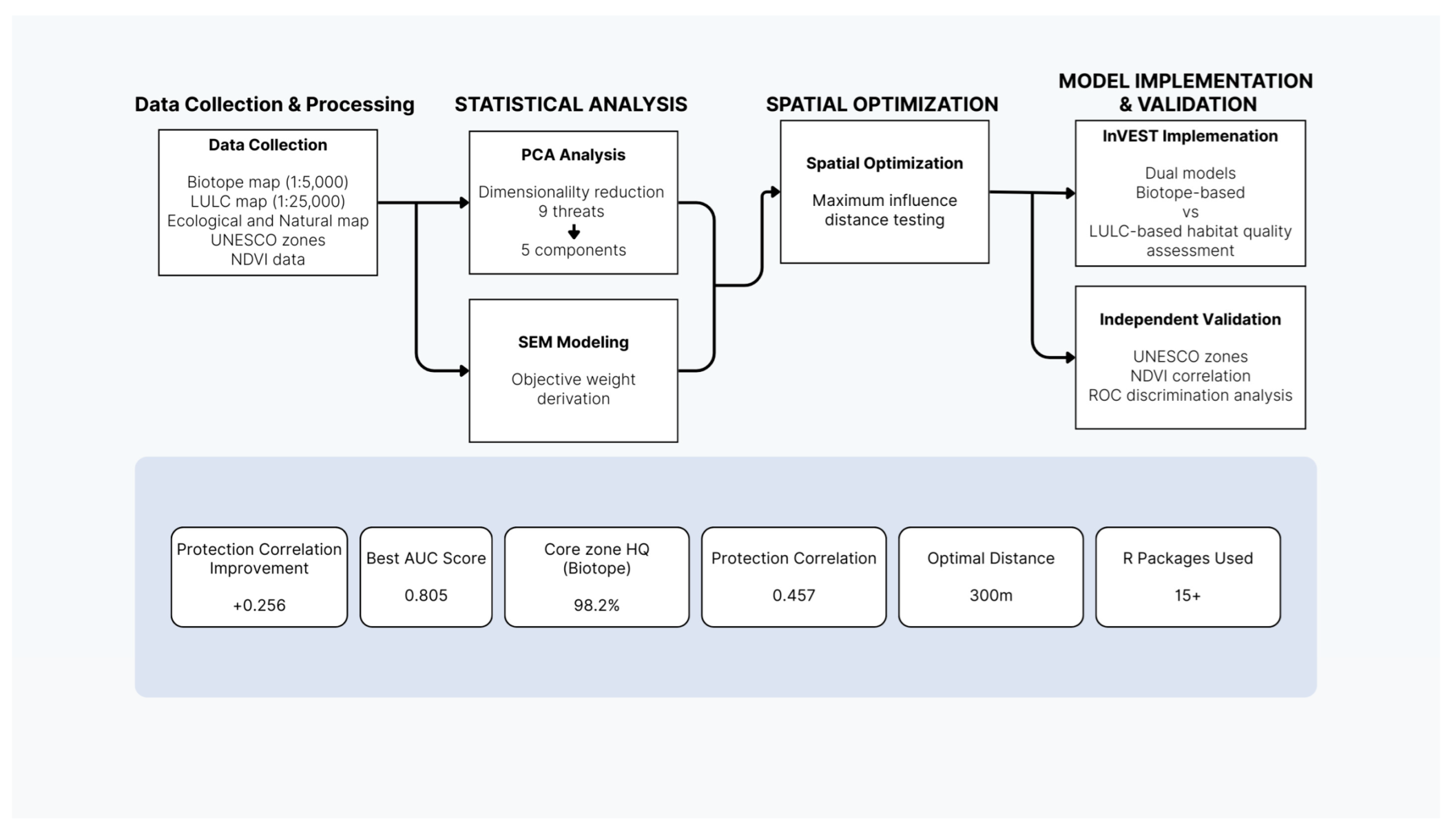
2.1. Analytical Framework Overview
2.2. Study Area
2.3. Data Sources and Biotope-Based Habitat Classification
2.3.1. Spatial Data Sources and Specifications
2.3.2. Data Processing and Integration
2.4. Integrated Threat Analysis Approach
2.4.1. Principal Component Analysis for Threat Dimensionality Reduction
2.4.2. Structural Equation Modeling for Causal Relationships
2.4.3. Spatial Parameter Optimization
2.5. InVEST Habitat Quality Implementation
2.5.1. Model Configuration and Parameter Integration
2.5.2. Model Execution and Quality Control
2.6. Comparative Performance Evaluation Framework
2.6.1. Reference Data Preparation and Sampling Strategy
2.6.2. Multi-Domain Performance Assessment
2.6.3. Ecological Gradient Verification
2.7. Statistical Analysis and Implementation
2.7.1. Comprehensive Software Framework
2.7.2. Analysis Workflow and Quality Control
2.7.3. Reproducibility and Quality Assurance
2.7.4. Statistical Significance and Effect Sizes
2.7.5. Performance Integration Framework
3. Result
3.1. Threat Variable Analysis and Reduction
3.1.1. PCA Results
3.1.2. SEM Results
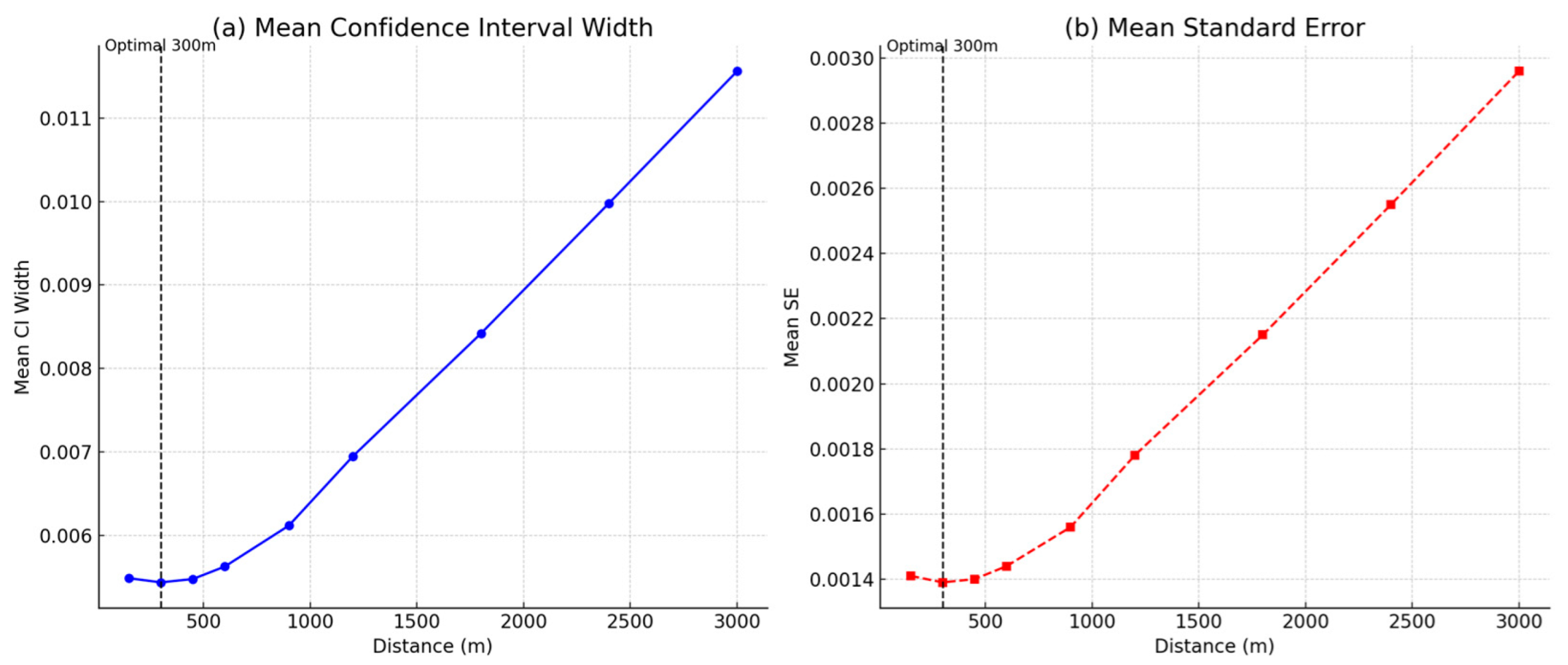
3.2. Spatial Parameter Optimization
3.2.1. Distance Parameter Selection and Performance
3.2.2. Model Stability and Precision
3.3. Biotope vs. LULC Performance Comparison
3.3.1. Correlation Analysis with Validation Indicators
3.3.2. ROC Analysis for Protected Area Prediction
3.3.3. UNESCO Biosphere Reserve Validation
3.3.4. Spatial Overlap Analysis
3.4. Model Performance Summary
3.4.1. Comprehensive Performance Evaluation
3.4.2. Practical Significance Assessment
- NDVI correlation: +0.078 points (0.247 vs. 0.169);
- Biosphere Reserve correlation: +0.232 points (0.390 vs. 0.158);
- Special Management Zone correlation: +0.075 points (0.179 vs. 0.104);
- Any protected area correlation: +0.256 points (0.457 vs. 0.201).
4. Discussion
4.1. Methodological Development and Validation
4.2. Regional Parameterization and Ecological Insights
4.3. Addressing Methodological Limitations
4.4. Policy and Conservation Planning Implications
4.5. Future Research Directions
- (1)
- (2)
- (3)
- Integration with climate change projections will enable scenario-based conservation planning that accounts for both bioclimatic shifts and species responses [52,53]. In particular, linking bioclimate and population models offers improved forecasts for extinction risk, while iterative scenario testing may strengthen adaptive planning [52,53].
- (4)
- Development of automated parameter updating procedures is essential for operational applications. Advances in iterative near-term ecological forecasting [46] and Bayesian updating methods [64,65] provide promising pathways, and recent workflow frameworks demonstrate how automation can enhance reproducibility and transparency [66,67].
5. Conclusions
5.1. Research Accomplishments
5.2. Scientific and Methodological Contributions
- Objective parameter derivation substantially reducing expert judgment bias;
- Enhanced ecological realism through detailed biotope mapping;
- Comprehensive validation across independent ecological indicators;
- Transferable methodology applicable to diverse regional contexts.
5.3. Policy and Conservation Implications
5.4. Future Research and Applications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Liang, X.; Wang, J. Parameter assignment for InVEST habitat quality module based on principal component analysis and grey coefficient analysis. Math. Biosci. Eng. 2022, 19, 13928–13948. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Gou, A. Habitat quality evolution characteristics and multi-scenario prediction in Shenzhen based on PLUS and InVEST models. Front. Environ. Sci. 2023, 11, 146347. [Google Scholar] [CrossRef]
- Wu, J.; Hou, Y.; Cui, Z. Coupled InVEST-MGWR modeling to analyze the impacts of changing landscape patterns on habitat quality in the Fen River basin. Sci. Rep. 2024, 14, 13084. [Google Scholar] [CrossRef]
- Convention on Biological Diversity (CBD). Kunming–Montreal Global Biodiversity Framework; CBD COP15: Montreal, QC, Canada, 2022; Available online: https://www.cbd.int/gbf (accessed on 1 August 2025).
- Convention on Biological Diversity (CBD). Protected Areas and Other Effective Area-Based Conservation Measures; CBD SBSTTA/22/L.2, 2018; Available online: https://www.cbd.int/doc/c/9b1f/759a/dfcee171bd46b06cc91f6a0d/sbstta-22-l-02-en.pdf (accessed on 1 August 2025).
- Taskforce on Nature-Related Financial Disclosures (TNFD). Metrics and Targets Guidance v0.4; TNFD: London, UK, 2023; Available online: https://tnfd.global/metrics (accessed on 1 August 2025).
- IPBES. Global Assessment Report on Biodiversity and Ecosystem Services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services; Brondizio, E.S., Díaz, S., Settele, J., Watson, R.T., Eds.; IPBES Secretariat: Bonn, Germany, 2019; Available online: https://ipbes.net/global-assessment (accessed on 1 August 2025).
- Dasgupta, P. The Economics of Biodiversity: The Dasgupta Review; HM Treasury: London, UK, 2021. Available online: https://www.gov.uk/government/publications/final-report-the-economics-of-biodiversity-the-dasgupta-review (accessed on 1 August 2025).
- Nelson, E.; Mendoza, G.; Regetz, J.; Polasky, S.; Tallis, H.; Cameron, D.R.; Chan, K.M.A.; Daily, G.C.; Goldstein, J.; Kareiva, P.M.; et al. Modeling multiple ecosystem services, biodiversity conservation, commodity production, and tradeoffs at landscape scales. Front. Ecol. Environ. 2009, 7, 4–11. [Google Scholar] [CrossRef]
- Sánchez-Canales, M.; Benito, A.L.; Passuello, A.; Terrado, M.; Ziv, G.; Acuña, V.; Schuhmacher, M.; Elorza, F.J. Sensitivity analysis of ecosystem service valuation in a Mediterranean watershed. Sci. Total Environ. 2012, 440, 140–153. [Google Scholar] [CrossRef] [PubMed]
- Vigerstol, K.L.; Aukema, J.E. A comparison of tools for modeling freshwater ecosystem services. J. Environ. Manage. 2011, 92, 2403–2409. [Google Scholar] [CrossRef] [PubMed]
- Sharp, R.; Douglass, J.; Wolny, S.; Arkema, K.; Bernhardt, J.; Bierbower, W.; Chaumont, N.; Denu, D.; Fisher, D.; Glowinski, K.; et al. InVEST 3.8.0 User Guide; The Natural Capital Project, Stanford University: Stanford, CA, USA, 2020; Available online: https://naturalcapitalproject.stanford.edu/software/invest (accessed on 1 August 2025).
- LI, Y.; Duo, L.; Zhang, M.; Yang, J.; Guo, X. Habitat quality assessment of mining cities based on InVEST model—A case study of Yanshan County, Jiangxi Province. Int. J. Coal Sci. Technol. 2022, 9, 28. [Google Scholar] [CrossRef]
- LI, D.; Sun, W.; Xia, F.; Yang, Y.; Xie, Y. Can habitat quality index measured using the invest model explain variations in bird diversity in an urban area? Sustainability 2021, 13, 5747. [Google Scholar] [CrossRef]
- Berta Aneseyee, A.; Noszczyk, T.; Soromessa, T.; Elias, E. The InVEST Habitat Quality Model Associated with Land Use/Cover Changes: A Qualitative Case Study of the Winike Watershed in the Omo-Gibe Basin, Southwest Ethiopia. Remote Sens. 2020, 12, 1103. [Google Scholar] [CrossRef]
- Ye, H.; Song, Y.; Xue, D. Multi-Scenario Simulation of Land Use and Habitat Quality in the Guanzhong Plain Urban Agglomeration, China. Int. J. Environ. Res. Public Health 2022, 19, 8703. [Google Scholar] [CrossRef]
- Hong, H.-J.; Kim, C.-K.; Lee, H.-W.; Lee, W.-K. Conservation, Restoration, and Sustainable Use of Biodiversity Based on Habitat Quality Monitoring: A Case Study on Jeju Island, South Korea (1989–2019). Land 2021, 10, 774. [Google Scholar] [CrossRef]
- Wang, X.; Liu, B.; Chen, J.; Arash, M.; Zhang, B.; Chang, Q.; Liu, J.; You, W. Assessing the impact of land use change on habitat quality in Zhongwei through multiscenario simulation using the PLUS and InVEST models. Sci. Rep. 2025, 15, 12355. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Liu, S.; Huang, Z.; Yan, W. Parameter optimization, sensitivity, and uncertainty analysis of an ecosystem model at a forest flux tower site in the United States. J. Adv. Model. Earth Syst. 2014, 6, 405–419. [Google Scholar] [CrossRef]
- Wang, R.; Xu, W.; Wang, H.; Li, Y. Sensitivity analysis of activity scheduling parameters with a parameter optimization framework. Environ. Model. Softw. 2020, 127, 104664. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Zhao, W.; Wang, R. Exploring the most important indicators for environmental condition assessment using structural equation modeling and InVEST habitat quality model. Ecol. Indic. 2021, 131, 108186. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, J.; Shirkey, G.; John, R.; Wu, S.R.; Park, H.; Shao, C. Applications of structural equation modeling (SEM) in ecological studies: An updated review. Ecol. Process. 2016, 5, 19. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer, 1st ed.; John Wiley & Sons: Chichester, UK, 2008; pp. 1–292. [Google Scholar]
- Rykiel, E.J. Testing ecological models: The meaning of validation. Ecol. Model. 1996, 90, 229–244. [Google Scholar] [CrossRef]
- Jacobs, S.; Burkhard, B.; Van Daele, T.; Staes, J.; Schneiders, A. ‘The Matrix Reloaded’: A review of expert knowledge use for mapping ecosystem services. Ecol. Model. 2015, 295, 21–30. [Google Scholar] [CrossRef]
- Kim, T.Y.; Song, C.H.; Lee, W.K.; Kim, M.I.; Lim, C.H.; Jeon, S.W.; Kim, J.S. Habitat quality valuation using InVEST model in Jeju Island. J. Korean Env. Res. Tech. 2015, 18, 1–11. [Google Scholar]
- Kim, J.C.; You, C.H.; Kim, D.W.; Oh, W. A Study on the Development of Biotope Type and Evaluation Map of Gochang-gun. GEO DATA 2023, 5, 277–285. [Google Scholar] [CrossRef]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M.; et al. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Olenin, S.; Ducrotoy, J.P. The concept of biotope in marine ecology and coastal management. Mar. Pollut. Bull. 2006, 53, 20–29. [Google Scholar] [CrossRef]
- Jung, H.-J.; Ryu, J.-H. Sustaining a Korean Traditional Rural Landscape in the Context of Cultural Landscape. Sustainability 2015, 7, 11213–11239. [Google Scholar] [CrossRef]
- Kim, E.Y.; Seo, H.Y.; Lee, D.K.; Nam, K.J. Structural implications of traditional agricultural landscapes on the functional diversity of birds near the Korean Demilitarized Zone. PLoS ONE 2020, 15, e0240890. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.; Choi, C.; Park, S. Impacts of changes in climate and land use/land cover under IPCC RCP scenarios on streamflow in the Hoeya River Basin, Korea. Water 2013, 5, 1374–1393. [Google Scholar] [CrossRef]
- Hong, S.; Jang, K.; Choi, S.; Kim, S.W.; Jung, J.; Kim, J.S. An assessment of land cover changes and their impacts on ecosystem services in South Korea from 2000 to 2010. Remote Sens. 2017, 9, 1181. [Google Scholar]
- Grace, J.B. Structural Equation Modeling and Natural Systems; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 4th ed.; Guilford Publications: New York, NY, USA, 2015. [Google Scholar]
- Rosseel, Y. lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–1006. [Google Scholar]
- Kim, D.U.; Kim, J.C.; You, C.H.; Oh, W. Occurrences Status of Biota in Gochang-gun, South Korea. GEO DATA 2024, 6, 123–143. [Google Scholar] [CrossRef]
- Salata, S.; Grillenzoni, C. A spatial evaluation of multifunctional Ecosystem Service networks using Principal Component Analysis: A case of study in Turin, Italy. Ecol. Indic. 2021, 127, 107758. [Google Scholar] [CrossRef]
- Gochang-gun. The First Carbon Neutrality and Green Growth Master Plan (2023–2030); Gochang-gun: Gochang, Republic of Korea, 2025; Available online: https://www.2050cnc.go.kr/storage/board/base/2025/07/02/BOARD_ATTACH_1751432565310.pdf (accessed on 1 August 2025).
- Bentler, P.M. Comparative fit indexes in structural models. Psychol. Bull. 1990, 107, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Hamel, P.; Guswa, A.J. Uncertainty analysis of a spatially explicit annual water-balance model: Case study of the Cape Fear basin, North Carolina. Hydrol. Earth Syst. Sci. 2015, 19, 839–853. [Google Scholar] [CrossRef]
- Scherr, S.J.; McNeely, J.A. Biodiversity conservation and agricultural sustainability: Towards a new paradigm of ‘ecoagriculture’ landscapes. Phil. Trans. R. Soc. B 2008, 363, 477–494. [Google Scholar] [CrossRef]
- Lopes, A.S.; Cavalcanti, I.F.A.; Müller, G.V. Ecosystem Services Modeling as a Tool for Defining Priority Areas for Conservation. PLoS ONE 2016, 11, e0154573. [Google Scholar]
- Dietze, M.C.; Fox, A.; Beck-Johnson, L.M.; Betancourt, J.L.; Hooten, M.B.; Jarnevich, C.S.; Keitt, T.H.; Kenney, M.A.; Laney, C.M.; Larsen, L.G.; et al. Iterative near-term ecological forecasting: Needs, opportunities, and challenges. Proc. Natl. Acad. Sci. USA 2018, 115, 1424–1432. [Google Scholar] [CrossRef]
- Park, S.; Jeon, S.; Kim, S.; Choi, C. Prediction and comparison of urban growth by land suitability index mapping using GIS and RS in South Korea. Landsc. Urban Plan. 2011, 99, 104–114. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Fortin, M.J.; Dale, M.R.T. Spatial Analysis: A Guide for Ecologists; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Dormann, C.F.; McPherson, J.M.; Araújo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Kissling, W.D.; et al. Methods to account for spatial autocorrelation in species distributional data. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Brook, B.W.; Akcakaya, H.R.; Keith, D.A.; Mace, G.M.; Pearson, R.G.; Araujo, M.B. Integrating bioclimate with population models to improve forecasts of species extinctions under climate change. Biol. Lett. 2009, 5, 723–725. [Google Scholar] [CrossRef] [PubMed]
- Urban, M.C.; Bocedi, G.; Hendry, A.P.; Mihoub, J.B.; Pe’er, G.; Singer, A.; Bridle, J.R.; Crozier, L.G.; De Meester, L.; Godsoe, W.; et al. Improving the forecast for biodiversity under climate change. Science 2016, 353, aad8466. [Google Scholar] [CrossRef] [PubMed]
- Morandi, B.; Piquer-Rodríguez, M.; Kuemmerle, T.; Dara, A.; Gavier-Pizarro, G.I.; Ginzburg, R.; Gasparri, N.I. Expert-based and correlative models to map habitat quality: Which gives better support to conservation planning? Glob. Ecol. Conserv. 2018, 16, e00513. [Google Scholar] [CrossRef]
- Cord, A.F.; Bartkowski, B.; Beckmann, M.; Dittrich, A.; Hermans-Neumann, K.; Kaim, A.; Lienhoop, N.; Locher-Krause, K.; Priess, J.; Schröter-Schlaack, C.; et al. Towards systematic analyses of ecosystem service trade-offs and synergies: Main concepts, methods and the road ahead. Ecosyst. Serv. 2017, 28, 264–272. [Google Scholar] [CrossRef]
- White, J.T.; Foster, L.K.; Fienen, M.N.; Knowling, M.J.; Hemmings, B.; Winterle, J.R. Toward reproducible environmental modeling for decision support: A worked example. Front. Earth Sci. 2020, 8, 50. [Google Scholar] [CrossRef]
- Schmolke, A.; Thorbek, P.; DeAngelis, D.L.; Grimm, V. Ecological models supporting environmental decision making: A strategy for the future. Trends Ecol. Evol. 2010, 25, 479–486. [Google Scholar] [CrossRef]
- Republic of Korea. National Biodiversity Strategy and Action Plan (2021–2030); Convention on Biological Diversity Repository: Montreal, QC, Canada, 2021; Available online: https://www.cbd.int/doc/world/kr/kr-nbsap-v5-en.pdf (accessed on 25 September 2025).
- Cook, C. Diverse approaches to protecting biodiversity: OECMs. Conserv. Lett. 2024, 17, e13027. [Google Scholar] [CrossRef]
- Petza, D.; Amorim, E.; Lamine, E.B.; Colloca, F.; Crisóstomo, E.D.; Fabbrizzi, E.; Fraschetti, S.; Galparsoro, I.; Giakoumi, S.; Kruse, M.; et al. Assessing the potential of Other Effective area-based Conservation Measures (OECMs). Conserv. Biol. 2024, 38, e10539721. [Google Scholar] [CrossRef]
- Luo, Y.; Schuur, E.A.G. Model Parameterization to Represent Processes at Unresolved Scale and Changing Properties of Evolving System. Glob. Change Biol. 2020, 26, 1109–1117. [Google Scholar] [CrossRef]
- Giakoumi, S.; Richardson, A.J.; Doxa, A.; Moro, S.; Andrello, M.; Hanson, J.O.; Hermoso, V.; Mazor, T.; McGowan, J.; Kujala, H.; et al. Advances in systematic conservation planning to meet new biodiversity targets. Trends Ecol. Evol. 2025, in press. [Google Scholar] [CrossRef]
- Mclntosh, E.J.; Pressey, R.L.; Lloyd, S.; Smith, R.J.; Grenyer, R. The impact of Systematic Conservation Planning. Annu. Rev. Environ. Resour. 2017, 42, 677–697. [Google Scholar] [CrossRef]
- Klepper, O.; Scholten, H.; van de Kamer, J.P.G. Prediction uncertainty in an ecological model of the Oosterschelde estuary. J. Forecast. 1991, 10, 191–209. [Google Scholar] [CrossRef]
- O’Hagan, A. Bayesian analysis of computer code outputs: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 1290–1300. [Google Scholar] [CrossRef]
- White, E.P.; Yenni, G.M.; Taylor, S.D.; Christensen, E.M.; Bledsoe, E.K.; Simonis, J.L.; Ernest, S.M. Developing an automated iterative near-term forecasting system. Methods Ecol. Evol. 2019, 10, 1645–1658. [Google Scholar] [CrossRef]
- Barros, C.; Luo, Y.; Chubaty, A.M.; Eddy, I.M.S.; Micheletti, T.; Boisvenue, C.; Andison, D.W.; Cumming, S.G.; McIntire, E.J.B. Empowering ecological modelers with a PERFICT workflow. Methods Ecol. Evol. 2023, 14, 1802–1816. [Google Scholar] [CrossRef]
- Botelho, L.L.; Jeynes-Smith, C.; Vollert, S.; Bode, M. Ecosystem models cannot predict the consequences of conservation decisions. arXiv 2024, arXiv:2401.10439. Available online: https://arxiv.org/abs/2401.10439 (accessed on 1 August 2025). [CrossRef]
- Dai, P.; Ye, J.; Liu, J.; Zhou, D.; Cheng, X.; Wang, Y. Evolution of habitat quality and multi-scenario simulation based on the InVEST model. Environ. Chall. 2025, 13, 100975. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Wu, W.; Tang, D. Integrating Multi-Model Coupling to Assess Habitat Quality Dynamics: Spatiotemporal Evolution and Scenario-Based Projections in the Yangtze River Basin, China. Sustainability 2025, 17, 4699. [Google Scholar] [CrossRef]




| Data Type | Description | Resolution | Source | Encoding |
|---|---|---|---|---|
| HQ Outputs | ||||
| Biotope base HQ | biotope-based InVEST | 30 m | This Study | Continuous (0–1) |
| Biotope base DG | ||||
| LULC base HQ | LULC-based InVEST | |||
| LULC base DG | ||||
| Reference Data | ||||
| Biosphere Reserve | UNESCO Biosphere Reserve zones | 30 m | UNESCO MAB | Categorical (0, 1, 2) |
| Management Area | Separately managed conservation area | Min. of Environment | Binary (0, 1) | |
| Ecological Grade | Grade 1 ecological natural map | Binary (0, 1) | ||
| Vegetation Index | Normalized Difference Vegetation Index (NDVI) | This Study | Continuous (−1, 1) |
| Category | Evaluation Indicator | Score | Description |
|---|---|---|---|
| Structure | Area | 3/2/1 | ≥10 ha/1–10 ha/<1 ha |
| Slope | ≥25°/8–25°/<8° | ||
| Elevation | ≥100 m/50–100 m/<50 m | ||
| Shape Index | ≥2.0/1.5–2.0/<1.5 | ||
| Naturalness | Vegetation Layers | Multi/Two/Single layer | |
| Land Use Intensity | Conservation/Mixed/Developed | ||
| Distance from Road | ≥100 m/50–100 m/<50 m | ||
| Green Coverage | ≥60%/40–60%/<40% | ||
| Permeable Surface | ≥60%/40–60%/<40% | ||
| Function | Biodiversity Core | Highest | Priority conservation zones |
| Buffer Zones | High | Secondary conservation areas | |
| Cultural Heritage | High | Designated cultural properties | |
| Species Habitat | High | Endangered species locations | |
| Connectivity | Variable | ≥50% connectivity index |
| Domain | Metric | Method | Interpretation |
|---|---|---|---|
| Ecological Coherence | NDVI correlation | Pearson r | Higher values indicated ecological alignment |
| Policy Alignment | Protection correlations | Pearson r (4 type) | Higher values indicate policy concordance |
| Prediction Accuracy | AUC values | ROC analysis | Values > 0.7 indicate good discrimination |
| Spatial Precision | Overlap Rate, Precision | Spatial overlay | Higher values indicate spatial accuracy |
| Analysis Component | Package | Version | Key Function | Primary Purpose |
|---|---|---|---|---|
| Data Processing | Dply | 1.1.0 | Select (), filter (), mutate () | Data manipulation |
| Readr | 2.1.4 | Read_csv (), read_rds () | Data import/export | |
| tibble | 3.2.1 | Tibble (), as_tibble () | Data structure management | |
| PCA Analysis | FactoMineR | 2.8 | PCA (), get_eigenvalue () | Principal component analysis |
| Facroextra | 1.0.7 | Fviz_pca_var (), fviz_contrib () | PCA visualization | |
| Corrplot | 0.92 | Corrplot (), corrplot.mixed () | Correlation matrix visualization | |
| SEM Modeling | Lavaan | 0.6-15 | Sem (), cfa (), fitMeasures () | Structural equation modeling |
| semPlot | 1.1.6 | semPaths (), semPlotModel () | SEM path diagrams | |
| Spatial analysis | Terra | 1.7-29 | Rast (), extract (), global () | Raster data processing |
| Sf | 1.0-12 | St_read (), st_trensform () | Vector spatial operations | |
| Gstat | 2.1-1 | Variogram (), fit.variogram () | Variogram analysis | |
| Automap | 1.1-9 | autofitVariogram () | Automated variogram fitting | |
| Performance Evaluation | pROC | 1.18.0 | Roc (), auc (), roc.test () | ROC analysis |
| Caret | 6.0-94 | trainControl (), confusionMatrix () | Model validation | |
| MLmetrics | 1.1.1 | RMSE (), MAE (), Accuracy () | Performance metrics |
| Analysis Step | Sample Size | Method | Statistical Test | Quality Control |
|---|---|---|---|---|
| Data Sampling | 6000 pixels | Stratified random (seed = 42) | Distribution normality | Shapiro–Wilk test |
| Missing Data | [Final N] pixel | Listwise deletion | Completeness Assessment | Missing pattern analysis |
| PCA Execution | Full sample | Standardized variables | Kaiser-Maeyer- Olkin test | KMO > 0.8 Threshold |
| SEM Fitting | Full sample | Maximum likelihood | Model fit indices | RMSEA < 0.08 CFI > 0.95 |
| Variogram Analysis | Systematic sample | Exponential/Spherical models | Range parameter estimation | Cross-validation |
| Correlation Analysis | Full sample | Pearson coefficients | Significance testing | Cor.test () |
| ROC Analysis | Full sample | Binary classification | AUC calculation | 95% confidence intervals |
| Spatial Concordance | Top 20% HQ | Quantile threshold | Overlap analysis | Precision/recall metrics |
| Gradient Analysis | 3 protection levels | Group comparison | ANOVA | Descriptive statics |
| Component | Eigenvalue | % of Variance | Cumulative % | Dominant Loading |
|---|---|---|---|---|
| PC1 | 3.82 | 42.47 | 42.47 | Urban (0.89), Industrial (0.84), Road (0.76) |
| PC2 | 1.75 | 19.45 | 61.92 | Crop (0.91), Pasture (0.68) |
| PC3 | 1.19 | 13.26 | 75.18 | Hydropower (0.82), Recreation (0.74) |
| PC4 | 0.946 | 11.42 | 86.60 | Greenspace (0.88) |
| PC5 | 0.67 | 7.42 | 94.02 | Bareground (0.91) |
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | Cluster Value |
|---|---|---|---|---|---|---|
| Urban | 0.89 | 0.12 | −0.08 | 0.15 | 0.09 | 0.89 |
| Industrial | 0.84 | 0.19 | 0.21 | −0.12 | 0.18 | 0.92 |
| Road | 0.76 | 0.34 | 0.28 | 0.19 | −0.08 | 0.91 |
| Crop | 0.23 | 0.91 | −0.15 | 0.12 | 0.08 | 0.94 |
| Pasture | 0.41 | 0.68 | 0.18 | −0.21 | 0.31 | 0.89 |
| Hydropower | 0.19 | −0.12 | 0.82 | 0.08 | 0.15 | 0.96 |
| Recreation | 0.28 | 0.31 | 0.74 | 0.23 | −0.11 | 0.93 |
| Greenspace | 0.15 | −0.19 | 0.23 | 0.88 | 0.12 | 0.94 |
| Bareground | −0.08 | 0.21 | 0.09 | 0.18 | 0.91 | 0.92 |
| Fit Index | Value | 90% CI | Acceptable Threshold |
|---|---|---|---|
| RMSEA | 0.042 | 0.038~0.047 | <0.05 |
| CFI | 0.968 | - | >0.90 |
| TLI | 0.954 | - | >0.90 |
| χ2/df | 1.99 | - | <3.0 |
| Principal Component | β | SE | t-Value | p-Value | InVEST Weight |
|---|---|---|---|---|---|
| PC1 (Development pressure) | −0.47 | 0.018 | −26.11 | <0.001 | 0.47 |
| PC2 (Agricultural Pressure) | −0.31 | 0.021 | −14.76 | <0.001 | 0.31 |
| PC3 (Infrastructure development) | −0.28 | 0.019 | −14.74 | <0.001 | 0.28 |
| PC4 (Greenspace management) | −0.19 | 0.020 | −9.50 | <0.001 | 0.19 |
| PC5 (Bareground disturbance) | −0.15 | 0.022 | −6.82 | <0.001 | 0.15 |
| Distance (m) | R2 | AIC | BIC | Performance Category |
|---|---|---|---|---|
| 150 | 0.610 | −4503.07 | −4475.06 | Good |
| 300 | 0.611 | −4504.67 | −4476.66 | Optimal |
| 450 | 0.610 | −4503.12 | −4475.11 | Good |
| 600 | 0.592 | −4485.23 | −4457.22 | Moderate |
| 900 | 0.523 | −4431.45 | −4403.44 | Poor |
| 1200 | 0.478 | −4389.67 | −4361.66 | Poor |
| 1800 | 0.412 | −4323.89 | −4295.88 | Very Poor |
| 2400 | 0.381 | −4278.12 | −4250.11 | Very Poor |
| 3000 | 0.354 | −4234.56 | −4206.55 | Very Poor |
| Metric | Value | Interpretation |
|---|---|---|
| Average Confidence Interval Width | 0.00544 | Minimal uncertainty |
| Average Standard Error | 0.00139 | Optimal precision |
| Bootstrap CV (n = 1000) | <5% | High stability |
| Total Coefficient Magnitude | 0.0742 | Maximum signal detection |
| Moran’s I (residuals) | 0.031 (p = 0.124) | No spatial autocorrelation |
| Distance Range | CV for Threat Weights | Reliability Assessment |
|---|---|---|
| 150~450 m | <5% | High reliability |
| 450~900 m | 5~8% | Moderate reliability |
| 900~1200 m | 8~12% | Low reliability |
| >1200 m | >12% | Poor reliability |
| Validation Indicator | Biotope Model | LULC Model | Improvement |
|---|---|---|---|
| NDVI | 0.247 | 0.169 | +0.078 |
| Biosphere Reserve Status | 0.390 | 0.158 | +0.232 |
| Special Management Zone | 0.179 | 0.104 | +0.075 |
| Natural Monument | −0.023 | 0.038 | −0.061 |
| Protect Area | 0.457 | 0.201 | +0.256 |
| Protection Type | Biotope AUC | LULC AUC | Improvement | Performance Level |
|---|---|---|---|---|
| Biosphere Reserve | 0.794 | 0.744 | +0.050 | Good -> Excellent |
| Protected Area | 0.805 | 0.755 | +0.050 | Good -> Excellent |
| Zone Type | Sample Size | Biotope HQ Mean | LULC HQ Mean | Biotope DG Mean | LULC DG Mean |
|---|---|---|---|---|---|
| Core | 268 | 0.982 | 0.869 | 0.067 | 0.100 |
| Buffer | 2757 | 0.956 | 0.841 | 0.115 | 0.143 |
| General | 861 | 0.881 | 0.721 | 0.211 | 0.216 |
| Method | High HQ in BR | Total High HQ | Total BR | Overlap Rate | Precision |
|---|---|---|---|---|---|
| Biotope | 761 | 811 | 3025 | 0.938 | 0.252 |
| LULC | 763 | 811 | 3025 | 0.941 | 0.252 |
| Performance Category | Biotope Winner | LULC Winner | No Difference |
|---|---|---|---|
| Correlation Metrics | 4/5 | 1/5 | 0/5 |
| AUC Metrics | 2/2 | 0/2 | 0/2 |
| Spatial Metrics | 0/3 | 2/3 | 1/3 |
| Overall | 6/10 | 3/10 | 1/10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.U.; Yoon, H.Y. Objective Parameterization of InVEST Habitat Quality Model Using Integrated PCA-SEM-Spatial Analysis: A Biotope Map-Based Framework. Land 2025, 14, 2050. https://doi.org/10.3390/land14102050
Kim DU, Yoon HY. Objective Parameterization of InVEST Habitat Quality Model Using Integrated PCA-SEM-Spatial Analysis: A Biotope Map-Based Framework. Land. 2025; 14(10):2050. https://doi.org/10.3390/land14102050
Chicago/Turabian StyleKim, Dong Uk, and Hye Yeon Yoon. 2025. "Objective Parameterization of InVEST Habitat Quality Model Using Integrated PCA-SEM-Spatial Analysis: A Biotope Map-Based Framework" Land 14, no. 10: 2050. https://doi.org/10.3390/land14102050
APA StyleKim, D. U., & Yoon, H. Y. (2025). Objective Parameterization of InVEST Habitat Quality Model Using Integrated PCA-SEM-Spatial Analysis: A Biotope Map-Based Framework. Land, 14(10), 2050. https://doi.org/10.3390/land14102050







